Perceptually relevant parameters for virtual listening simulation of small room acoustics

Abstract

Various physical aspects of room-acoustic simulation techniques have been extensively studied and refined, yet the perceptual attributes of the simulations have received relatively little attention. Here a method of evaluating the perceptual similarity between rooms is described and tested using 15 small-room simulations based on binaural room impulse responses (BRIRs) either measured from a real room or estimated using simple geometrical acoustic modeling techniques. Room size and surface absorption properties were varied, along with aspects of the virtual simulation including the use of individualized head-related transfer function (HRTF) measurements for spatial rendering. Although differences between BRIRs were evident in a variety of physical parameters, a multidimensional scaling analysis revealed that when at-the-ear signal levels were held constant, the rooms differed along just two perceptual dimensions: one related to reverberation time (T₆₀) and one related to interaural coherence (IACC). Modeled rooms were found to differ from measured rooms in this perceptual space, but the differences were relatively small and should be easily correctable through adjustment of T₆₀ and IACC in the model outputs. Results further suggest that spatial rendering using individualized HRTFs offers little benefit over nonindividualized HRTF rendering for room simulation applications where source direction is fixed.

INTRODUCTION

Binaural technology has enabled realistic virtual listening simulation of a variety of room environments from anechoic rooms to concert halls. These “auralization” techniques not only allow users the unique opportunity to listen and evaluate the acoustics of different environments without being physically present in the environments but they also afford architectural acousticians, sound engineers, and scientists (among others) levels of control of the acoustic stimulus reaching the listeners’ ears that would be impractical or perhaps even impossible in real acoustic listening spaces. Although many aspects of the complex methods underlying particularly model-based auralization techniques (Kleiner et al., 1993; Vorländer, 2008) continue to be improved and refined (see Rindel, 2000), perceptual evaluation of the end results has received relatively little attention. Arguably the most severe form of perceptual testing for evaluating auralization methods would be to determine whether listeners could discriminate sound signals in a real room from virtual simulations designed to emulate the same source signal in the same room. For anechoic listening rooms, such tests have been conducted and under the best conditions of the simulation, real and virtual are indistinguishable (Zahorik et al., 1995; Hartmann and Wittenberg, 1996; Kulkarni and Colburn, 1998; Langendijk and Bronkhorst, 2000). Analogous testing in more complicated reverberant room environments has yet to be conducted and for good reason. Best evidence suggests that even the most sophisticated model-based auralization techniques cannot reproduce the acoustic stimulus measured in a real room to less than the just-noticeable limits for human listeners on a host of room-acoustic parameters when estimated in isolation (Vorländer, 1995; Bork, 2000). Although this implies that even the best virtual room simulations would be discriminably different from real-room listening, the simulations are perhaps no less “natural” or “room-like” or different on perceptual properties that might depend on multiple naturally covarying physical parameters. Alternative methods are therefore needed to more fully assess the perceptual similarity of real and virtual room simulations. This article describes and implements one type of alternative method in which similarity ratings between both acoustically measured and modeled rooms are evaluated using multidimensional scaling (MDS) techniques. A principal advantage of this method over simple discrimination testing is that it allows the potentially multiple perceptual aspects or dimensions by which listeners rate the similarities of different measured or modeled room-acoustic simulations to be explicitly determined.

MDS techniques have been applied to a variety of problems in the hearing sciences, including the perception of vowels (Kewley-Port and Atal, 1989), consonant confusions (Bilger and Wang, 1976; Soli and Arabie, 1979), vocal qualities (Kempster et al., 1991), timbre (Grey, 1977), and the perceptual properties of concert hall acoustics (Yamaguchi, 1972). In general, MDS techniques seek to determine a configuration of the experimental stimuli in a hypothetical Euclidean space that optimally describes or represents participants’ judgments of similarity (or disimilarity) between all possible pairs of stimuli in the experiment. Stimulus pairs that are judged to be similar will lie close together in this “perceptual” space, and stimuli that are judged to be very different will lie far apart in the perceptual space. Different (independent) dimensions in the derived perceptual space can then be interpreted as the different perceptual attributes or quantities by which participants base their judgments. Further interpretation of the perceptual space dimensions is often accomplished by noting relationships in these dimensions to physical aspects of the stimuli. For example, work by Yamaguchi (Yamaguchi, 1972) concluded that listeners’ judgments of similarity between various seating positions within two concert halls were based on three perceptual parameters, since the MDS solution for the listeners’ similarity judgments was found to be three-dimensional. The first two dimensions of this solution were highly correlated with the physical parameters of sound pressure level and reverberation time, and therefore likely represent perceptual correlates of these parameters. The third dimension in the scaling solution was not easily interpretable in relation to any physical stimulus quantities. Although the precise relationship between physical aspects of concert hall acoustics and relevant perceptual aspects is an area of active study and debate, the pioneering results of Yamaguchi using MDS procedures are in many ways similar to other results using both related (Schroeder et al., 1974) and relatively unrelated means for assessing perceived similarity or preference (Barron, 1988; Beranek, 2004).

In the work described here, MDS was used to assess the perceptual similarity between auralizations using both measurements from real rooms and simple room-acoustic models. The perceptual accuracy of the models is then reflected in their proximity in the MDS solution to stimuli based on measurements from real rooms. Given the results of past room modeling evaluations (Vorländer, 1995; Bork, 2000), some perceptual differences between measured and modeled stimuli are expected. Interpretation of the perceptual dimensions resulting from the scaling solutions will allow for more detailed assessment of the particular perceptual aspects in which the models depart from real rooms.

One obvious issue related to the MDS methods as described here is that substantial variability in similarity ratings from participant to participant might naturally be expected. Although classical MDS procedures offer no way of accounting for this variability, more recent weighted MDS procedures (e.g. INDSCAL; Carroll and Chang, 1970) allow the extent to which individual participants’ responses are based on a given dimension in the stimulus-space to be determined. Each individual participant can then be characterized by the weight they place on each stimulus dimension. In this way, individual differences can be effectively analyzed. Although previous studies of perceptual similarity in room acoustics have not implemented methods to scale individual differences (Yamaguchi, 1972; Schroeder et al., 1974), it seems clear that the potential for considerable individual differences exists in this application. As such, INDSCAL methods are implemented in the current study.

A variety of techniques for producing auralizations based on acoustic models of a room environment have been proposed (see Kleiner et al., 1993; Rindel, 2000 for review) and implemented in commercially available software (e.g. ODEON and CATT-ACOUSTIC packages). Most techniques rely on assumptions of geometrical acoustics (Kuttruff, 2000), and many use separate methods for simulating early reflections and late reverberation. Because early reflections are typically more distinct both temporally and spatially than the late reverberant energy, which is more diffuse and homogeneous in time, they are modeled with more precise, and therefore more computationally demanding techniques. The modeling techniques implemented here adopt this same strategy, based loosely on methods described by Heinz (1993). An image-model (Allen and Berkley, 1979) is used to model early reflections and a statistical model is used for late reverberant energy modeling. Both individualized and nonindividualized head-related transfer functions (HRTFs) are used for spatially rendering the direct-path and early reflections. The end result of the model is an estimated binaural room impulse response (BRIR). Modeled BRIRs can then be compared to measured BRIRs, which are complete descriptions of the transfer characteristics of the various acoustical components of a given real listening situation including characteristics of the source, the room, and the listener’s head and external ears. Overall, the model implemented here is rudimentary at best, and results in a variety of compromises related to the simulation of the acoustics of analogous real rooms. Areas of known compromise include appropriate simulation of source directionality, appropriate simulation of non-specular aspects of early reflections (i.e. scattering and diffraction), and appropriate simulation of late reverberant energy (correct effect of diffusion, etc.). No claims are therefore made as to the superiority of this modeling technique over other techniques. Nevertheless, the model is believed to maintain many of the essential perceptual aspects of small-room acoustics, while still allowing the experimenter complete control of all modeling methods and procedures—something that is often compromised in commercially available auralization packages.

The primary goal of this study is to evaluate the perceptual similarity of rooms simulated using these highly simplified modeling techniques to simulations based on measurements from a real room. As part of the evaluation, judgments of similarity will also be solicited for other rooms, with differing size, reverberant properties, and simulation fidelity. This will allow for determination of the acoustical factors that are most relevant for judgments of perceptual room similarity in this, and perhaps other similar sets of rooms, while at the same time providing a means for perceptual validation of the proposed room modeling techniques.

A secondary goal of this study is to determine the necessity of individualized HRTFs for realistic spatial rendering in the room simulation, which is one potentially important aspect of room simulation fidelity. Although individualized HRTFs are known to result in superior spatial rendering of sound source direction (Wenzel et al., 1993), the process of measuring HRTFs for each potential user of an auralization system is a significant logistical difficulty. It is therefore important to carefully quantify the potential benefits of individualized HRTFs for room auralization applications.

The majority of past work both related to room modeling techniques and to the perceptual aspects of room acoustics has focused on concert hall environments, many of which have interior volumes of 20 000 m³ or more. The current study, however, is concerned primarily with smaller room listening environments (between approximately 14 and 7800 m³), which are more representative of everyday listening environments in which the vast majority of our auditory functioning takes place. Given that the acoustic contributions of a room are known to affect many critical auditory abilities, such as speech intelligibility (Peutz, 1971; Nabelek and Robinson, 1982) and sound localization in both direction (Hartmann, 1983) and distance (Zahorik, 2002), further understanding of the perceptual attributes of the acoustic properties themselves from everyday room environments is essential. In addition to addressing an important and generally understudied area, focus on small-room acoustics, particularly with simple rectangular shapes, has the methodological benefit of lessening the computational complexity in theory required for effective room modeling. It is important to note that the room modeling techniques implemented here become inappropriate in cases where wave behavior of sound in an enclosed space can no longer be ignored, such as when room dimensions and source∕receiver distances become small relative to sound wavelength (Lam, 2005). Such behavior should be largely irrelevant for the situations examined in this study.

Related work by Berkley and Allen (1993) used classical MDS techniques to determine the perceptual similarity between 5 small rooms (constant interior volume of 75.5 m³ with variable surface absorptions and source distances in each room), all simulated using an image model (Allen and Berkley, 1979) and presented monaurally without HRTF spatial rendering. Results from this important and highly relevant work suggest that listeners base their judgments of room similarity on two perceptual dimensions: one related to reverberation time and one related to variation in the sound spectrum. Although a number of methodological differences exist between Berkley and Allen’s study (1993) and the work described here, their results will nevertheless serve as a basis for comparison of the results reported here in which model-based room simulations are compared both physically and perceptually to simulations based on measurements from a real room.

METHODS

Room-acoustic measurements and modeling

Participants

Nine listeners (6 female) ages 18–31 years participated in the acoustical measurement phase of this study.

BRIR measurements

BRIRs were measured for each participant in a single rectangular room using methods fundamentally identical to those described in Zahorik 2002. The room was large rectangular office room with dimensions of 5.7×4.3×2.6 m³ (L×W×H). Walls were painted drywall material. The floor was carpeted (short, dense weave), and the ceiling was a suspended type, constructed of acoustical tile materials. The participant was seated (1.3 m from floor to ear level) in the approximate center of the room: 3.8 m from the front wall, and 2 m from the left-hand side wall. All measurements were made using binaural microphones (Sennheiser KE4-211-2) placed at the entrance of the acoustically sealed ear canals (i.e. blocked-meatus configuration). Previous research has shown that this measurement configuration when paired with appropriate headphones and compensation will produce results vary similar to those obtained using probe-microphones placed near the tympanic membrane (Hammershøi and Møller, 1996). An additional benefit of this microphone configuration is that is allows larger microphones to be used, with frequency response and noise characteristics that are generally superior to probe-microphones. The sound source was a small full-range loudspeaker (Cambridge SoundWorks Center∕Surround IV) with high-quality amplification (D-75, Crown, Inc.) positioned at ear level directly in front of the participant at a distance of 1.4 m Standard system identification techniques using a maximum-length sequence (MLS) signal (Rife and Vanderkooy, 1989) were used to measure BRIRs for each participant. The responses to a 16th order MLS signal (65535-sample) presented periodically were averaged coherently (ten averages) in order to improve signal-to-noise ratio, which was at least 55 dB (broadband) in all cases after averaging. Impulse responses were derived from the averaged responses via circular cross-correlation (Rife and Vanderkooy, 1989). All signal generation and data acquisition was performed using MATLAB software (Mathworks, Inc.), and high-quality D∕A and A∕D hardware (DD1, Tucker-Davis Technologies, Inc.) using 16-bit quantization and a 48 kHz sampling frequency. No compensation for the response characteristics of the loudspeaker was applied to the measurements. The loudspeaker was relatively omni-direction up to approximately 1 kHz, as is evident in its directional response data (Fig. 1) measured using procedures detailed in ISO-3382 (ISO-3382, 1997). Additional details of the measurement room are shown in Table 1, along with parameters for subsequent physical and psychophysical testing including whether the BRIR measurements originated from the listener’s own ears (ID 1) or from another participant’s ears (IDs 2–3).

Figure 1.

Directional responses of the measurement loudspeaker (Cambridge SoundWorks Center∕Surround IV) in octave bands (125–4000 Hz) expressed in decibels (1 dB∕division) relative to the 360° (energetic) average response (0 dB, white curve). The 0° orientation indicates that the loudspeaker was oriented directly facing the (omni-directional) measurement microphone. Shaded tolerance regions for source omni-directionality from ISO-3382 (1997) are shown for each octave band. Below 2 kHz, the measurement loudspeaker deviates from omni-directional specifications by at most 1.2 dB. Above 2 kHz, the directional characteristic of this loudspeaker becomes more pronounced, but still only deviates from omni-directionality by at most 5.2 dB at 4 kHz.

Table 1.

Description of measured (IDs 1–3) and modeled (IDs 4–15) BRIRs evaluated in this study. For each BRIR, dimensions (length×width×height), volume (V), surface area (SA), and source distance (d) are listed. Individualized and nonindividualized HRTF implementations are also indicated (subject ID code listed for nonindividualized sets), along with the number of HRTF sets (n) used for generating the full stimulus set in each room. For the modeled BRIRs, early and late energy absorption coefficients (α) entered into the model are also indicated.

ID	HRTF set	n	L (m)	W (m)	H (m)	V (m3)	SA (m2)	d (m)	Early α	Te (ms)	Late α
											125	250	500	1000	2000	4000
Meas.
1	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
2	SXB	1	5.7	4.3	2.6	62.4	99.6	1.4	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
3	SZM	1	5.7	4.3	2.6	62.4	99.6	1.4	⋯	⋯	⋯	⋯	⋯	⋯	⋯	⋯
Modeled
4	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	0.29	55	0.40	0.30	0.30	0.30	0.22	0.20
5	SXB	1	5.7	4.3	2.6	62.4	99.6	1.4	0.29	55	0.40	0.30	0.30	0.30	0.22	0.20
6	SZM	1	5.7	4.3	2.6	62.4	99.6	1.4	0.29	55	0.40	0.30	0.30	0.30	0.22	0.20
7	Indiv.	7	3.4	2.6	1.5	13.5	35.9	1.4	0.29	34	0.40	0.30	0.30	0.30	0.22	0.20
8	Indiv.	7	8.5	6.4	3.9	210.5	224.1	1.4	0.29	83	0.40	0.30	0.30	0.30	0.22	0.20
9	Indiv.	7	11.3	8.5	5.2	499.0	398.4	1.4	0.29	112	0.40	0.30	0.30	0.30	0.22	0.20
10	Indiv.	7	28.4	21.3	12.9	7797.4	2490.0	1.4	0.29	283	0.40	0.30	0.30	0.30	0.22	0.20
11	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	0.05	55	0.05	0.05	0.05	0.05	0.05	0.05
12	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	0.10	55	0.10	0.10	0.10	0.10	0.10	0.10
13	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	0.30	55	0.30	0.30	0.30	0.30	0.30	0.30
14	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	0.29	55	1.00	1.00	1.00	1.00	1.00	1.00
15	Indiv.	7	5.7	4.3	2.6	62.4	99.6	1.4	1.00	55	1.00	1.00	1.00	1.00	1.00	1.00

BRIR models

Simple models of BRIRs were constructed using a three-dimensional image-model (Allen and Berkley, 1979) to simulate early specular reflections within a hypothetical rectangular room and a statistical model of the late diffuse reverberant energy. This approach, while relying on a variety of assumptions and simplifications, is fundamentally similar to that described by Heinz (1993), and is shown schematically in Fig. 2. Twelve different listening situations (“rooms”) were modeled, all with an omni-directional sound source directly in front of the listener’s location in the approximate center of each room, at a distance of 1.4 m, and 1.3 m above the floor surface (approximately ear level when seated). The rooms differed in various physical parameters such as size and the amount of surface absorption, as well as other details of the simulation methods, which are described below and in Table 1. Certain room simulations were designed to closely approximate the measurement room environment in which the BRIR measurements described in Sec. 2A2 were conducted (e.g., IDs 4–6). Other room simulations were designed for comparative use in subsequent psychophysical scaling experiments. For example: room 15 was anechoic, and room 14 had only early reflections and no late reverberant energy, rooms 7–10 differed in size, and rooms 11–13 differed in surface absorption.

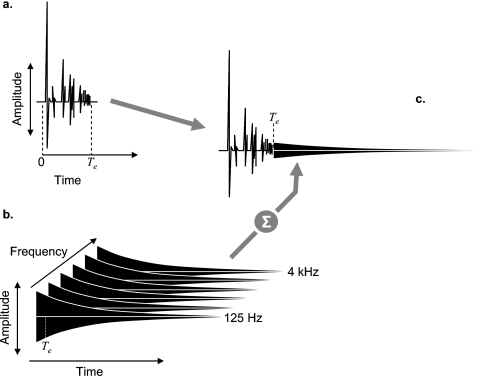
Figure 2.

Schematic representation of the BRIR modeling procedure. (a) Stylized representation of the early portions of the BRIR (one ear only) estimated using an image model (Allen and Berkley, 1979) and then spatially rendered using HRTFs. The time axis represents the duration of the early response, T_e, relative to the start of the direct-path response (0). (b) Stylized representation of the late response modeling procedure in which noise samples shaped by exponentially decaying envelopes are generated in each of six octave bands (125 Hz–4 kHz) and then summed and scaled (see text for details). (c) Representation of the combined early and late responses for one ear. Identical procedures were implemented to estimate the response of the other ear.

a. Early response modeling. The direct-path and 500 early reflections were all spatially rendered with head-related transfer functions (HRTFs) measured using techniques similar to those described by Wightman and Kistler (1989). HRTFs were measured for each participant from a spherical grid of 541 spatial locations surrounding the listener (10° spacing, full 360° in horizontal angle; vertical angles from −60°. below to 90° above ear level) in an anechoic chamber using miniature electret microphones (Sennheiser KE4-211-2) in a blocked-meatus configuration. The spherical grid of measurements was conducted using vertically-oriented semi-circular (1.4 m radius) array of 16 loudspeakers that could be rotated horizontally around the participant’s head location at the center of the grid. A given spatial location in the grid was selected by rotating the arc to the appropriate horizontal (azimuth) angle, and then energizing the loudspeaker on the arc corresponding to the appropriate vertical (elevation) angle. Arc rotation was accomplished using a high-torque computer-controlled motor (model HA5C, Haas, Inc.) with 0.01° rotational precision. Loudspeaker switching was performed prior to audio signal amplification (D-75, Crown, Inc.) using a computer-controlled switching device (AM-16∕B, 360 Systems, Inc.). The measurement signal was a 20.48 ms broad band (0.2–25 kHz) noise constructed with a phase-spectrum that minimized the peak-factor of the signal (Schroeder, 1970). For each measurement location, 100 repetitions of this signal were presented periodically at a level producing 70 dBA at the recording location (center of the participant’s head). The signals were presented and the responses from the binaural microphones were recorded using the same high-quality D∕A-A∕D hardware (DD1, Tucker-Davis Technologies, Inc.) at a sampling frequency of 100 kHz, with 16-bit precision. Responses were averaged coherently (100 averages) in order to improve signal-to-noise ratio. Transfer-functions were derived for each measured response via frequency-domain division by the measurement signal. Results for each measurement location were then down-sampled to 50 kHz and windowed to 1024-points in order to facilitate efficient storage and later convolution operations. Using these techniques, a set of 541 measurements could be completed in approximately 30 min.

These “HRTF” measurements differed from most standard types of HRTF measurements in one important respect: They were not referenced relative to the measured response from a reference microphone in the absence of the head. This was done in order to preserve the response of the measurement loudspeakers in each of the transfer function measurements, for later comparison with the room BRIR measurements which also contained the response of the loudspeaker (same make and model).

Reflection locations determined from the image-model were rendered to the nearest HRTF measurement angle. No interpolation was implemented. Individualized HRTFs were used for spatial rendering in certain simulation conditions (e.g. simulation IDs 4 and 7–15). Nonindividualized HRTFs from different human participants were used in other conditions (e.g., rooms 5 and 6). All reflections were modeled as ideal specular reflections resulting from a point-source (omni-directional), with no frequency-dependent absorption characteristics and no dependencies on angle of incidence. Broadband levels of each reflection were determined based on path-length (r), an average broadband energy absorption coefficient (α) for all surfaces in the room, the reflection order (n), and a constant loss factor (f) designed to help offset level discrepancies due to scattering and∕or other factors. The gain for the jth reflection relative to the direct-path (with pathlength r₀) was

$$20{\log }_{10}\left[\frac{r_0\sqrt{1-f\alpha }}{r_j{n}_j}\right]\mathrm{dB}.$$ (1)

For certain models, average α was estimated based on published α values for common building materials (Moulder, 1991) averaged across frequency octave-band frequencies from 125 to 4000 Hz and weighted by the relative surface area of each material in the modeled room. Other models used experimentally altered values for average α. Table 1 displays the specific choices for HRTF-individualization and (early response) α values for the simulated rooms evaluated in this study. Also displayed in Table 1 is the delay relative to the direct-path of the last image (500th) in the estimates of the early response, T_e. The constant loss factor, f, was determined via pilot testing and set to a value of 3 for all models. A schematic early response is shown in Fig. 2a.

b. Late response modeling. Diffuse late reverberation was simulated using independent Gaussian noise samples for each ear shaped by separate decay functions applied to each of six octave-bands ranging from 125–4000 Hz [see Fig. 2b]. The decay functions were derived from the Sabine equation (Sabine, 1922):

$$T_{60}=0.163\frac{V}{S{\overline{\alpha }}_i},$$ (2)

which estimates the amount of time (s) required for sound level to decay by 60 dB (T₆₀) following the offset of a source signal, from the parameters of room volume (V), total surface area of the reflecting surfaces (S), and the average absorption coefficient for all surfaces within the ith octave band $\left({\overline{\alpha }}_i\right)$. Average absorption coefficients in each band were again based on published α values for common building materials (Moulder, 1991) weighted by the relative surface area of each material. These estimated T₆₀ values were used to define decay functions for each octave band of the following form:

$$d\left(t\right)={10}^{-3t∕T_{60}},$$ (3)

where t is measured in seconds. The parameters used to estimate T₆₀ and compute all decay functions for modeling late reverberant responses are shown in Table 1. Broadband late responses were created by summing the decay-shaped noise samples across octave bands.

c. Combining early and late responses. The levels of early and late responses were first matched by noting the rms level (broadband) in the last 10 ms of the early response (i.e. T_e−10 ms to T_e) and then scaling the late response such that its rms level (broadband) over the same period (T_e−10 ms to T_e) was identical to the early response. All energy in the late responses between 0 and T_e was then removed, and the resulting late response for each ear was summed with the early response for each ear to create an estimated BRIR, as shown schematically in Fig. 2c. The resulting BRIR was then down-sampled to 48 kHz and stored for subsequent analysis and psychophysical testing. All room model and signal processing was implemented using MATLAB® (Mathworks, Inc.) software.

Equalization for headphone presentation

In order to facilitate accurate reproduction of the appropriate pressure waveform at both eardrums using headphone-based virtual auditory space techniques, the transfer characteristics of an acoustically open headphone (Beyerdynamic DT 990 Pro) when coupled to the head were measured for each participant. These measurements were obtained during the same measurement sessions as the BRIR and anechoic HRTF measurements using the same binaural microphones (Sennheiser KE4-211-2) in a blocked-meatus configuration and similar techniques for system identification. Results of these measurements were used to construct headphone equalization filters to correct for the response of the headphone when coupled to the head of each participant, following logic described and evaluated by Møller, Hammershøi, and colleagues (Møller, 1992; Møller et al., 1995). Because the equalization quality can depend on the degree to which the microphone position in the ear canal was similar for both headphone and HRTF or BRIR measurements, two sets of equalization filters were made for each participant: one based on headphone measurements during the BRIR measurement session and the second based on measurements during the HRTF session. The former equalization filters were then used for virtual room simulation using the measured BRIRs, and the later equalization filters were used for model-based room simulation. Methods to construct the equalization filters were similar to those described in previous work (Zahorik, 2002). The magnitude spectrum from each measurement was inverted, smoothed (20% of a critical bandwidth), and low-pass filtered at 20 kHz. The results were then defined to have linear phase, and used to implement a 256-coefficient finite impulse response filter for headphone equalization (48 kHz sampling rate).

Physical testing

Measured and modeled BRIRs were evaluated physically using two general methods: one in which the BRIRs were directly compared between the measured room and the best-case model, and one in which various common room acoustical parameters were computed from the BRIRs for each room. Parameter values were then compared and used to provide a basis for interpretation of subsequent psychophysical testing.

BRIR comparisons

The direct analysis of BRIR similarity compared BRIRs from the measured room (ID 1) to those from the best-case modeled room (ID 4) for each of nine participants. Comparisons were made by first bandpass filtering (third-order Butterworth as specified by ANSI-S1.11, 2004) the BRIRs (left and right ears separately, un-equalized for headphone reproduction) into 1∕3 octave bands, with center frequencies ranging from 125 to 8000 Hz. In each band, the normalized cross-correlation function, CF, was computed between measured and modeled BRIRs:

$${\mathrm{CF}}_{L\text{or}R}\left(\tau \right)=\frac{{\int }_0^{t_{\max }}{p}_1\left(t\right)p_4(t+\tau )dt}{\sqrt{{\int }_0^{t_{\max }}{p}_1^2\left(t\right)dt{\int }_0^{t_{\max }}{p}_4^2\left(t\right)dt}}.$$ (4)

CF was computed for each ear separately, where p₁ and p₄ are the FIRs from rooms 1 and 4, respectively, for a given ear (L or R). A variable maximum integration time, t_max, which represents the maximum integration time applied to the impulse responses was also implemented. Here three different values of t_max were evaluated: 5 ms, 20 ms, and full impulse response, which will be denoted as t_max=∞. These different choices of t_max where chosen to determine how the degree of match may be influenced by the direct-path alone (t_max=5 ms), the inclusion of early reflections (t_max=20 ms), and the inclusion of early reflections as well as late reverberant energy (t_max=∞). Each 1∕3-octave-band CF was then summarized by computing the cross-correlation coefficient, CC, defined as

$$\mathrm{CC}=\max \mid \mathrm{CF}\left(\tau \right)\mid \text{for}-1\mathrm{ms}<\tau <1\mathrm{ms},$$ (5)

which is simply the maximum magnitude of CF CC may be interpreted as the degree of linear association between the two impulse responses that is independent of delay or polarity. High similarity between measured and modeled BRIRs will yield CC values near 1.

Acoustical parameter comparisons

Five different room-acoustic parameters were estimated from the measured and modeled BRIRs in this study. The majority of the estimated parameters were commonly used room-acoustic parameters (ISO-3382, 1997), including reverberation time (T₆₀), clarity index (C₅₀), center time (T_c), and the interaural cross-correlation coefficient (IACC) based on full-duration BRIRs. An additional spectral centroid parameter, f_c, not described in ISO-3382 (1997) was also estimated in an attempt to characterize any potential timbral differences between the BRIRs. All parameters were estimated from the BRIRs for each measured∕modeled room (un-equalized for headphone reproduction) for each participant.

Estimation procedures for T₆₀, C₅₀, T_c, and IACC were based on those described in ISO-3382 (1997) with the following important differences: (1) All BRIRs in this study resulted from measurements made with directional microphones placed in the ears of individual listeners. Although this technique is valid for estimation of IACC, ISO-3382 (1997) recommends that estimates of T₆₀, C₅₀, T_c be made from measurements with an omni-directional microphone in the absence of the head. Here, these parameters were instead estimated from the left ear portion of the BRIRs. (2) ISO-3382 (1997) also requires that an omni-directional source be used for all parameter estimation. The source used for all measured BRIRs in this study had directional response properties that deviated from true omni-directionality. Although both of these departures from ISO-3382 (1997) recommendations may have biased the parameter estimates reported in this study, the bias due to directional microphones used in the measurements should be relatively constant across all measurements, and the bias due to source directionality in the measure BRIRs is believed to be relatively low below 2 kHz (see Fig. 1).

Estimation of the spectral centroid parameter, f_c, for each BRIR was accomplished as follows. Each BRIR was first passed through a bank of 1∕6th-octave rectangular bandpass filters, with center frequencies, cf_i, ranging from 125 to 16 000 Hz. Let E_i be the resulting energy in the ith 1∕6th octave band specified in decibels. The spectral centroid, f_c, in hertz is therefore defined as

$$f_c={10}^{({\sum }_{i=1}^n\left(\log 10\left({\mathrm{cf}}_i\right)E_i\right)∕{\sum }_{i=1}^n\left(E_i\right))},$$ (6)

where n=43 in this case, corresponding to the number of bandpass filters used in the analysis. Conceptually, the spectral centroid is the center of mass of a signal’s magnitude spectrum, and has been shown to be related to the perceptual quality of timbre (Grey and Gordon, 1978). Since previous work has identified the importance of spectral∕timbral aspects in small-room acoustics (Bech, 1995, 1996), and informal observation suggests that mismatches in HRTF processing can cause changes to the timbre of reproduced sound, this spectral centroid parameter may be particularly relevant for the listening situations examined in this study.

Due to specific experimental and measurement procedures of this study, three additional and common room-acoustic parameters (all described in ISO-3382, 1997) were not estimated in this study: sound strength, lateral energy fraction, and early decay time. Sound strength, which is a measure of sound energy in a given room relative to energy at a fixed source-receiver distance (typically 10 m) in the acoustic free-field, was not estimated here because overall sound presentation level was equalized across all sound stimuli in this study. This caused sound strength to be essentially fixed, and therefore not a useful acoustic parameter for describing acoustical differences across the measured and simulated rooms in this setting. Lateral energy fraction, which is the proportion of laterally arriving sound energy relative to omni-directional energy, was also not estimated, since this parameter requires measurements from a figure-eight microphone which was not available for this study. Finally, early decay time was not separately estimated because preliminary testing revealed that it was almost perfectly correlated with measures of T₆₀ for the rooms examined in this study.

Psychophysical testing

Participants

Seven listeners (six female) ages 18–31 years participated in the experiment. All had normal hearing, as verified by standard (ANSI-S3.9, 1989) audiometric screening at 15 dB HL from 125 to 8000 Hz, and were experienced in sound localization tasks. All listeners participated in the previous physical measurement phase of this study. Listeners SXB and SZM (see Table 1) did not participate in this phase of the study.

Stimuli and presentation apparatus

15 different stimuli were constructed based on the 15 different measured or modeled room simulations detailed in Table 1. The source signal for all stimuli was a high-quality speech sample (3.4 s duration) from a male talker recorded in anechoic space. This signal was convolved with BRIRs from each room. Overall level of the convolved stimulus was then equalized across all stimuli by matching the rms amplitudes. This was done in an attempt to remove overall level as a potential means for perceptually classifying the stimuli. Stimuli were presented in a double-walled sound booth over equalized headphones (Beyerdynamic DT-990-Pro) using Tucker-Davis Technologies equipment for D∕A conversion (16-bit, 48 kHz) and headphone amplification (fixed gain). All signal processing was implemented using MATLAB® (Mathworks, Inc.) software.

Design and procedure

Participants listened to all possible pairs of different stimuli (210 total), presented with an inter-stimulus interval of 1 s. Participants were told to rate the perceived disimilarity between each stimulus in the pair using a 100-point rating scale, ranging from 0=“exact same” to 99=“completely different.” Participants were allowed to listen to the stimulus-pair as many times as they wished prior to making their rating response, which the participant entered numerically on a computer keypad. No feedback was given to participants as to the type of trial or the nature of their responses. The experiment was run in blocks of 210 trials consisting of one set of all possible pairs of different stimuli, presented in random order. Participants required approximately 45 min to complete one trial block. Each listener completed nine blocks of trials, resulting in a total of 1890 trials, or nine similarity ratings for each stimulus pair. Listeners were explicitly instructed to note any stimuli in which the sound source location was not perceived external to the head.

RESULTS

Physical testing

Overall, the simple virtual room modeling techniques described in this study produced a reasonably good physical match to the measured room (a large office space). Quantitative assessment of the degree of physical matching was conducted both via direct analysis of BRIR similarity and via an indirect analysis of various room-acoustic parameters derived from the BRIRs. Results from these analyses are reported in Secs. 3A1, 3A2.

BRIR comparisons

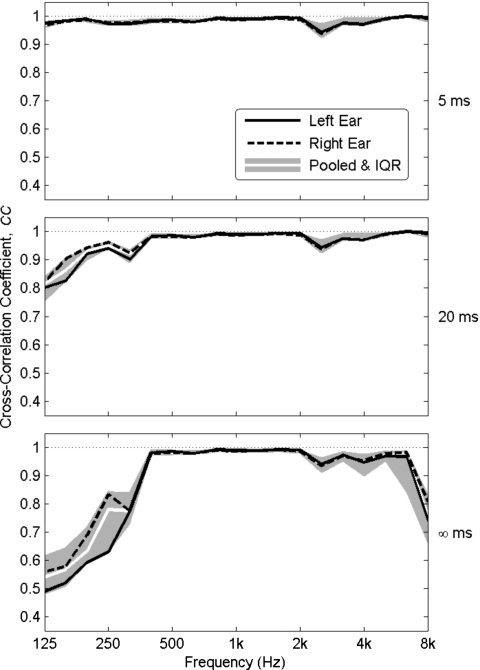
Figure 3 displays results from the BRIR correlation analysis comparing a measured BRIR to the best-case modeled BRIR. When t_max=5 ms, the cross-correlation coefficient was greater than 0.93 at all frequencies. This high degree of association was not particularly surprising, given that this time range was dominated by the direct-path response, which should have been very similar in both cases (e.g. same participant, same source, and direction). When t_max=20 ms, some decrease in correlation (mismatch) may be observed at frequencies below 400 Hz. This effect becomes more pronounced at t_max=∞, and additional decreases in correlation may be observed above 6 kHz. Overall, this analysis suggests that the modeled BRIRs are in good agreement with the measured BRIRs within the 400–6000 Hz bandwidth, but show increasing mismatch above and particularly below this frequency range when the full BRIRs are analyzed (t_max=∞). Increased mismatch is also accompanied by increased variability across participants [i.e., greater interquartile range (IRQ)].

Figure 3.

Results of a correlation analysis between measured (ID 1) and best-case modeled (ID 4) BRIRs for all participants (n=9). The dependent measure is a cross-correlation coefficient, CC, which is the maximum magnitude of the cross-correlation function, CF(τ) between measured and modeled impulse responses computed separately in each 1∕3-octave band ranging from 125 to 8 kHz (see text for details). Three different maximum integration times for the cross-correlation function are shown: 5, 20, ∞ ms. In each plot panel, the median CC across all participants is displayed for left ear responses only (solid curve), right ear responses only (dashed curve), and for responses pooled across both ears (white curve). Shaded regions indicate the IRQ for all CC values.

Acoustical parameter comparisons

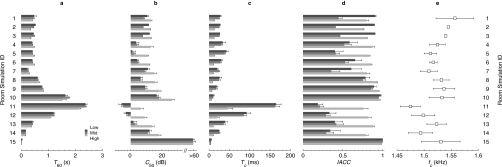
Estimates of five acoustical parameters derived from the BRIRs from each room are displayed in Fig. 4. Results for the T₆₀, C₅₀, T_c, and IACC parameters [Figs. 4a, 4b, 4c, 4d] were condensed into three two-octave frequency ranges: low (125 and 250 Hz bands), medium (500 and 1000 Hz bands), and high (2 and 4 kHz bands), following methods described in ISO-3382 (1997). This process was performed separately for each participant in a given measured or modeled room. Figure 4e displays the spectral centroid parameter for each measure∕modeled room. All values displayed in Fig. 4 represent mean estimates across participants. Standard deviation values across participants are also displayed (error bars).

Figure 4.

Estimated room-acoustic parameters for 15 BRIR types (see Table 1 for ID coding and descriptions): reverberation time T₆₀ (a), clarity index C₅₀ (b), center time T_c (c), interaural cross-correlation IACC (d), and spectral centroid f_c (e). Separate estimates are shown for low (125 and 250 Hz bands), medium (500 and 1000 Hz bands), and high (2 and 4 kHz bands) frequency ranges in (a)–(d). In all cases, the displayed estimates are means across participants. Error bars represent one standard deviation.

Overall, considerable variation in the parameter estimates may be observed across the sample of rooms. This variation across rooms is generally much larger than the between-participant variation, with the exception of the f_c parameter where large individual variability was observed. This individual variability in f_c is likely due to differences in the HRTFs across participants, which is controlled through the use of individualized HRTFs in subsequent psychophysical testing. Two additional points regarding individual variability are noteworthy. First, there was zero individual variability between rooms 2 and 3, since each room was based on measured BRIRs from only a single participant. Second, although rooms 5 and 6 were also based on anechoic HRTF measurements from single participants, these rooms had non-zero parameter standard deviations. This is because the room models, which used independent samples of Gaussian noise for simulating the late reverberant energy, were re-computed for each participant in the study, even though the HRTF set was held constant. Hence the variability in these parameters was due solely to variability in late reverberant energy, not HRTF differences.

To further assess the adequacy of the room modeling procedures, parameter estimates between the measured room (ID 1) and the best-case modeled room (ID 4) were compared. Table 2 displays broadband parameter estimates for each room, and parameter estimate differences between rooms. Estimates of the just-noticeable difference for each parameter in isolation are also displayed based on results from previous studies that most closely approximated the listening conditions present in this study. Only the differences in C₅₀ and IACC were greater than 1 just noticeable difference (JND), suggesting that rooms 1 and 4 would likely be discriminable based differences in either of these parameters alone.

Table 2.

Broadband acoustical parameters estimates (means across all frequency bands) for measured (ID 1) and best-case modeled (ID 4) BRIRs. Differences (and % changes) are also shown, as are estimates of the JND for each acoustical parameter determined from previous studies.

		Measured (ID 1)	Modeled (ID 4)	Difference		JND
Broadband Parameter	T60 (ms)	445.8	432.3	13.5	(3%)	24 ms	(Seraphim, 1958)
	C50 (dB)	10.6	6.8	3.8	(36%)	1.1 dB	(Bradley et al., 1999)
	Tc (ms)	21.8	24.9	−3.1	(−14%)	5.7–11.4 ms	(Cox et al., 1993)
	IACC	0.718	0.659	0.1	(8%)	5%	(Okano, 2002)
	fc (Hz)	1557	1525	32	(2%)	7%	(Emiroglu and Kollmeier, 2008)

An additional and important aspect of the room-acoustic parameter estimates for this set of rooms is that many parameters are highly correlated. These relationships are visible in Table 3, which displays the Pearson correlation matrix between all pairs of parameters. Statistically significant correlation may be observed in many of the cells, particularly between the different frequency ranges for a given parameter. Significant correlations are also observed across parameters, particularly in relationship to the T_c parameter which appears to be highly correlated with many of the other parameters.

Table 3.

Correlation matrix between physical room acoustic parameters for 15 BRIR types (see Table 1 for BRIR descriptions).

		T60			C50			Tc			IACC			fc
		Low	Mid	High	Low	Mid	High	Low	Mid	High	Low	Mid	High
	Low	1.000
T60	Mid	0.998a	1.000
	High	0.990a	0.993a	1.000
	Low	−0.396	−0.392	−0.426	1.000
C50	Mid	−0.331	−0.330	−0.355	0.980a	1.000
	High	−0.296	−0.295	−0.317	0.968a	0.998a	1.000
	Low	0.757a	0.726a	0.738a	−0.498	−0.373	−0.341	1.000
Tc	Mid	0.753a	0.723a	0.735a	−0.493	−0.372	−0.341	0.998a	1.000
	High	0.737a	0.704a	0.707a	−0.456	−0.359	−0.340	0.971a	0.977a	1.000
	Low	−0.287	−0.266	−0.309	0.582b	0.463	0.429	−0.704a	−0.708a	−0.618b	1.000
IACC	Mid	−0.116	−0.083	−0.081	0.644a	0.618b	0.627b	−0.582b	−0.592b	−0.610b	0.749a	1.000
	High	−0.106	−0.071	−0.049	0.509	0.533b	0.562b	−0.483	−0.498	−0.589b	0.495	0.926a	1.000
	fc	−0.419	−0.407	−0.448	0.329	0.215	0.178	−0.703a	−0.722a	−0.647a	0.873a	0.537b	0.352	1.000

^aCorrelation is significant at the 0.01 level (two-tailed).

^bCorrelation is significant at the 0.05 level (two-tailed).

In an attempt to reduce the redundancy and dimensionality of this set of parameters, a principle-components analysis with varimax rotation was performed on the mean parameter estimates shown in Figure 4. From this analysis (implemented using SPSS® software), four principle components were found to account for 97.8% of the variance in the full set of parameter estimates (13 parameters for each of 15 room simulations). This suggests that the original 13-dimensional parameter space with a relatively high degree of redundancy can be effectively represented with only 4 dimensions. Components 1–4 accounted for 35.3%, 24.8%, 19.7%, and 18% of the variance, respectively, suggesting relatively equal contributions of components 1–4. The rotated component loadings resulting from this analysis are shown in Table 4, where each value may be interpreted as the correlation between a given component and room-acoustic parameter. From these results, it appears that component 1 is most strongly associated with T₆₀ (relatively independent of frequency), component 2 is most strongly associated with C₅₀ (also relateively independent of frequency), component 3 is most strongly associated with f_c, and component 4 most strongly associated with high-frequency IACC. This suggests that broadband T₆₀, broadband C₅₀,f_c, and high-frequency IACC make up a set of four independent physical room-acoustic parameters for this set of room simulations.

Table 4.

Rotated principal component matrix for acoustic parameters estimated from 15 measured and modeled room simulations (see Table 1 for room descriptions). The strongest loadings for each component are indicated in bold.

		Component
		1	2	3	4
	Low	0.975	−0.159	−0.101	−0.009
T60	Mid	0.972	−0.169	−0.090	0.037
	High	0.961	−0.198	−0.148	0.078
	Low	−0.243	0.916	0.232	0.185
C50	Mid	−0.173	0.959	0.099	0.198
	High	−0.141	0.959	0.057	0.234
	Low	0.720	−0.118	−0.489	−0.437
Tc	Mid	0.715	−0.113	−0.499	−0.447
	High	0.713	−0.087	−0.376	−0.566
	Low	−0.147	0.312	0.886	0.275
IACC	Mid	0.019	0.448	0.447	0.764
	High	−0.008	0.352	0.165	0.899
	fc	−0.316	0.037	0.901	0.162

Consistent with correlation results shown in Table 3 where T_c is shown to be highly correlated with many other room-acoustic parameters, T_c also does not appear to be strongly related to any principle component in this analysis. Instead, T_c is only moderately related to the principal component 1, which is the same component to which T₆₀ is much more strongly related. This result, in conjunction with the correlation results (Table 3), suggests that T_c is not independent of T₆₀, and that T₆₀ is a better predictor of one source of independent variability in the acoustic parameters for the rooms in this study. For this reason the T_c parameters will be excluded from subsequent analyses.

Psychophysical testing

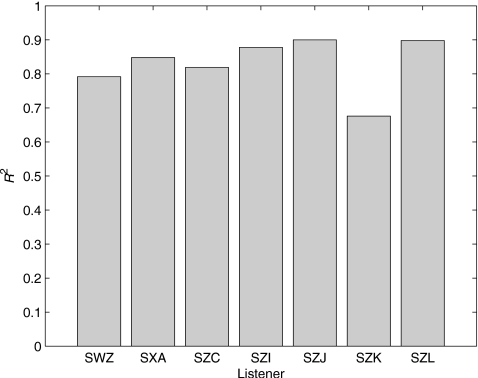
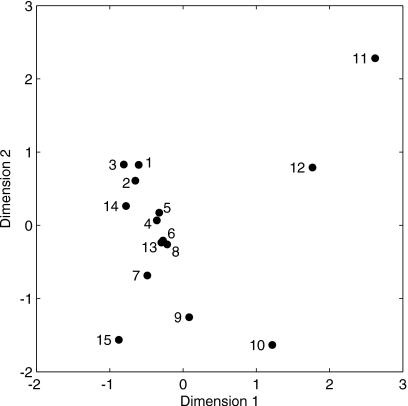
A MDS analysis was performed on the mean perceived similarity ratings (interval measurement scale assumed) from each listener between all possible pairs of measured∕modeled room simulations listed in Table 1. This analysis (INDSCAL, implemented using SPSS® software) allowed for a scale of perceived room similarity to be determined, as well as a characterization of each individual listener’s use of the resulting scale. Here, the scale of perceived similarity in room acoustics was determined to be two-dimensional (R²=0.830), since solutions with higher dimensionality did not account for a substantially greater proportion of the total variance (0.871≤R²≤0.889, for solutions with three to six dimensions). The two-dimensional solution also resulted in high R² values associated with each individual listener’s data, as shown in Fig. 5. There were no reports of non-externalized sound sources from any of the listeners.

Figure 5.

Proportion of variance accounted for (R²) in a two-dimensional scaling solution as a function of individual listener.

Figure 6 displays the resulting two-dimensional scale of perceived room acoustics. To further interpret the scale, each dimension in the scale was correlated with physical room-acoustic parameters that were found to be most representative of the acoustical variability between rooms in this study. Table 5 displays the correlation between each of the two dimensions in the psychophysical scale with four “most representative” physical parameters: those found to produce factor loadings with magnitude ≥0.9 in any of the four dimensions from the principal components analysis described in Sec. 3A (see Table 4). Because Dimension 1 from the scaling solution was highly correlated (r>0.94) with T₆₀, at all frequencies, it likely represents a perceptual quantity related to reverberation time. The relationship is direct: Increases in Dimension 1 scale values correspond to increases in T₆₀ parameter values. Dimension 1 also appears to be more moderately related (inversely) to the f_c parameter (r=−0.58), which may suggest that this perceptual dimension may also depend somewhat on sound timbre. Dimension 2 of the scaling solution appears to be most strongly related to the IACC parameters in the mid- and high frequencies (r<−0.82). As a result, it may represent a spatial aspect of the perceived sound, perhaps related to image size or diffuseness. The relationship is inverse, however: Increases in Dimension 2 scale values generally correspond to decreases in mid- and high-frequency IACC. More moderate (but still statistically significant) negative correlations between Dimension 2 and the C₅₀ parameters as well as low-frequency IACC are present.

Figure 6.

Derived two-dimensional scale (R²=0.830) of perceived room similarity (see Table 1 for room simulation ID coding and descriptions).

Table 5.

Correlation between physical stimulus parameters and values in the two-dimensional perceptual scaling solution. The T_c parameter was excluded from this comparison, because it was found to be highly correlated with T₆₀ (see Table 3).

		Dim. 1	Dim. 2
	Dim. 1	1.000	0.355
	Dim. 2	0.355	1.000
	Low	0.946a	0.383
T60	Mid	0.943a	0.344
	High	0.948a	0.330
	Low	−0.412	−0.571b
C50	Mid	−0.309	−0.530b
	High	−0.264	−0.536b
	Low	−0.452	−0.554b
IACC	Mid	−0.183	−0.822a
	High	−0.086	−0.837a
	fc	−0.575b	−0.389

^aCorrelation is significant at the 0.01 level (two-tailed).

^bCorrelation is significant at the 0.05 level (two-tailed).

Also evident from the scaling solution shown in Fig. 6 is that the modeled BRIRs (IDs 4–6) designed to approximate BRIRs measured from a particular room do not exactly match the percepts elicited by the measured BRIRs (IDs 1–3). In general, the modeled BRIRs lie slightly higher on Dimension 1 and slightly lower on Dimension 2, which based on the proposed interpretation of the two dimensions of the perceptual scale suggests that the modeled BRIRs are perceived as having slightly longer reverberation time and slightly less diffusivity than the measured BRIRs. For Dimension 1, this relationship is consistent with the observed physical values of T₆₀ in the high frequencies, where modeled BRIRs had approximately 23% greater reverberation time than measured BRIRs (see Table 2). For Dimension 2, the relationship is consistent with the observed physical values of IACC in the mid- and high frequencies, where modeled BRIRs had approximately 16% and 9% greater IACC values (see Table 2). Although these perceptual mismatches between measured and modeled rooms do suggest shortcomings of the modeling procedures, it is important to note that the mismatches are limited to two perceptual dimensions with relatively clear physical correlates. As such, methods to improve the perceptual match should be relatively straightforward.

Of further note is the close proximity of modeled BRIRs using individualized HRTFs (IDs 1 and 4) to those using nonindividualized HRTFs (IDs 2, 3, 5, and 6) in Fig. 6. This suggests that the perceptual effects of manipulating properties of the reverberant sound are much larger than the effects due to the potentially degraded spatial rendering of the direct-path and early reflections with nonindividualized HRTFs. This result has important implications for the implementation of virtual room simulations, suggesting that individualized HRTFs may not be required to effectively simulate different room-acoustic environments when the source direction is fixed.

An additional and potentially interesting aspect of the perceptual scale shown in Fig. 6 is the relative location of room 14: a room with no late reverberant energy (see Table 1 for details). This “degraded” room is, in fact, closer to the measured rooms (1–3) than any of the modeled rooms (4–6) expressly designed to emulate the measured rooms. Although the enhanced match on Dimension 1 is perhaps predictable, based on the interpretation that Dimension 1 is a direct perceptual correlate of reverberation time and that room 14’s reverberation time is reduced given the truncation of its late reverberant energy, it also clearly suggests that simulation of late reverberant energy may be relatively unimportant for the overall accurate perceptual recreation of small-room acoustics.

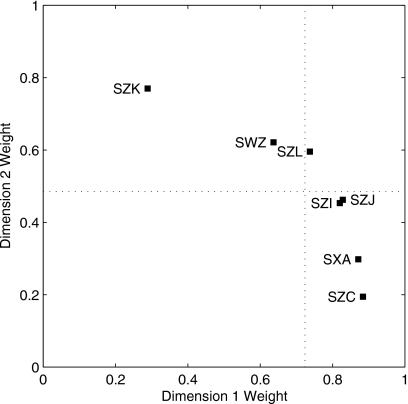
The relative importance of the two dimensions in the scaling solution for each listener are shown in Fig. 7. Substantial differences in the importance, or weight, each listener placed on the dimensions of the scaling solution are evident. The majority of listeners tended to place greater weight on Dimension 1, and relatively less weight on Dimension 2. The mean weight across all listeners for Dimension 1 was 0.72 (SD=0.21). For Dimension 2, the mean weight was 0.49 (SD=0.20). This suggests that for most listeners, aspects of room reverberation time are perhaps the primary bases for judging the similarities between room simulations in this study. Some listeners, however, appear to place approximately equal weight on the two dimensions, and one listener (e.g., SZK) appears to base their judgments of room similarity primarily on the perhaps spatially oriented aspects of Dimension 2.

Figure 7.

Individual listener weights for the two-dimensional scaling solution (R²=0.830). Dotted lines indicated the mean weight for each dimension.

DISCUSSION

Physical testing

BRIR comparisons

Although the simplified room modeling techniques described in this study were capable of producing reasonable approximations to measured BRIRs in a real-room, closer analysis of BRIR similarity revealed that the approximations were least good in the frequency extremes of the late reverberant energy (see Fig. 3). Differences in the high frequencies were most likely due to the method of modeling the late reverberant energy, which was limited to frequencies below 4 kHz. Explanations of the differences at low frequencies are more complicated, however. Some of the differences likely resulted from the mere fact that correlational procedures were used to assess similarity of signals that were designed to have uncorrelated late reverberant energy. Other explanations of the differences include potential errors in the estimation of absorption coefficients used to model the late reverberant energy, as well as the lack of diffraction effects in the model. Previous studies have demonstrated the sensitivity of room modeling techniques to accurate estimates of surface absorption properties as well as low-frequency errors due to the lack of diffraction modeling (Vorländer, 1995; Bork, 2000) Although precise explanations of these differences observed in the BRIRs at the frequency extremes is beyond the scope of this study, it is also important to recognize the generally high degree of similarity observed using the same correlational procedures between measured and modeled BRIRs in the midfrequencies (400–6000 Hz). This result is encouraging, because it suggests that even greatly simplified room modeling techniques can produce reasonable physical matches to measured BRIRs from simple room environments at least over a somewhat restricted mid-frequency region.

Acoustical parameter comparisons

Given that direct comparison of the BRIRs demonstrated differences between measured and modeled results, it is not surprising that room-acoustic parameters derived from the BRIRs also show differences between models and measurements, as displayed in Table 2. To better interpret the magnitude of these differences, they were compared relative to psychophysically determined just-noticeable differences (JNDs) for each parameter in isolation (see Table 3). Two recent evaluative comparisons of commercially available room modeling software have used a similar approach (Vorländer, 1995; Bork, 2000). From the results shown in Table 3, it is apparent that only the differences in C₅₀ and IACC parameters were greater than 1 JND. This suggests that these rooms would likely have been discriminable based on either of these parameters in isolation, and not any of the other parameters (e.g. T₆₀, T_c, and f_c). Of course comparison of particularly the C₅₀, T₆₀, and T_c parameters from this study that were estimated from the response of a directional microphone (i.e., placed in the ear) to JND values from other studies where this was not the case (Seraphim, 1958; Cox et al., 1993; Bradley et al., 1999) must be made with considerable caution. The IACC comparison is perhaps more valid, given that comparable source directionality (at least in the low frequencies) and binaural recording techniques were used both to estimate the parameters in this study and by Okano (2002) to estimate IACC JND. The observed difference in IACC between measured and modeled rooms is most likely related to the directional properties of the measurement sound source at high frequencies (see Fig. 1). Finally, it is important to note that the differences between measured and modeled rooms in this study, expressed in terms of parameter JNDs, are within the range of differences reported in recent evaluative comparisons of various commercially available auralization packages relative to parameters based on measurements from real auditoria (Vorländer, 1995; Bork, 2000).

Independence of acoustical parameters

Although a large number of room-acoustic parameters were estimated from BRIR measurements in this study (see Fig. 4), results from the principal components analysis suggest that there are really only four independent parameters for this set of rooms: broadband T₆₀, broadband C₅₀,f_c, and high-frequency IACC. Given that the sample of rooms in this study was in no way intended to be representative of all moderate-sized rooms, it is premature to extend this result to other sets of listening rooms. Nevertheless, there are potentially important similarities between this set of independent parameters, and results from four other studies based on physical measurements from mostly concert hall listening environments (Schroeder et al., 1974; Ando and Schroeder, 1985; Beranek, 2004; Cerdá et al., 2009): All find a relatively small number of independent parameters (2–6) and all sets of independent parameters include some measure of reverberation time and some measure of interaural coherence. These results are potentially important because they may suggest that a small set of independent physical parameters are invariant across a wide range of listening environments, and thus may be of considerable benefit to understanding general perceptual aspects of room acoustics. Beyond this, it is difficult to find other similarities in the results across studies, although Ando and Schroeder (1985), Beranek (2004), and Cerdá et al. (2009) did all report that strength factor was an additional independent physical parameter. Strength factor was not considered in Schroeder et al., 1974, or in the current study, because in both studies sound level was equalized at the ear across all stimuli during psychophysical testing, thus removing strength factor as a basis for similarity judgments.

Psychophysical testing

Perceptual scale results

Even though the simplified methods used to model room acoustics did not produce exact physical matches to measured BRIRs, the modeling techniques still provide valuable insight into the perceptual differences between rooms—either simulated or real—with different acoustical properties. Based on the results of the MDS analysis of the participants’ disimilarity ratings of all possible pairs of rooms, it is concluded that the scale of perceptual differences between the rooms is two-dimensional. Dimension 1 of this perceptual scale appears to be related to reverberation time and Dimension 2 appears to be related to sound spaciousness within the room. Overall, these results are consistent with several aspects of previous work in which perceptual scales of mostly concert hall listening environments have been estimated. First, the perceptual scales of room acoustics appear to be relatively low-dimensional. That is, a relatively few number of independent perceptual aspects of the room’s acoustical properties comprise the entire room-acoustic percept. In complex listening environments, such as concert halls, there appears to be a greater number of independent perceptual parameters, although the exact number and makeup of the set of parameters has been an active area of study over the past quarter-century or more (Beranek, 1992; Cerdá et al., 2009). In one study that examined perceptual scales of the acoustics of smaller listening rooms, the scale was found to be two-dimensional (Berkley and Allen, 1993). A second area of consensuses across nearly all studies is the primacy of reverberation time in percepts related to room acoustics. In this study, reverberation time appears to account for the majority of variance in most listeners’ judgments of acoustical similarity. Work by Berkley and Allen (1993) also in small rooms demonstrated a similarly strong relationship between reverberation time and perceptual similarity. A number of other studies of concert hall acoustics draw similar conclusions regarding the perceptual importance of reverberation time (see Beranek, 1992 for review), although debate as to the exact perceptual relationship between reverberation time and other room-acoustic parameters continues. In general, this apparent primacy of reverberation time in the perceptual aspects of room acoustics is clear testament to practical importance placed on the physical quantification of reverberation time in a variety of listening environments dating at least to the work of Sabine (Sabine, 1922).

At least two aspects of the derived perceptual scale in this study depart from results of previous studies related to perceived small-room acoustics. First, the interpretation of Dimension 2 as a spatial dimension of perceived room acoustics is inconsistent with the second dimension of the perceptual scale reported by Berkley and Allen (1993). Although both studies conclude that the primary determinant of perceived small-room acoustics is reverberation time, Berkley and Allen (1993) suggested that a secondary determinant is related to a spectral variance parameter, which has been shown by other to relate to the ratio of direct-to-reverberant sound energy (Jetzt, 1979), instead of the spatial aspects of Dimension 2 reported here. One likely explanation for this difference is that the Berkley and Allen (1993) scaling study was conducted under monaural listening conditions, which would have eliminated any binaural information that is critically important for reproduction of the spatial aspects of room acoustics. Had spatial information been eliminated in the current study through monaural sound presentation, closer agreement on Dimension 2 of the scaling solutions in the two studies may have been observed. It is also interesting to note that the measured and modeled BRIRs in this study differed most along Dimension 2, suggesting that these two classes of BRIRs are perhaps most different perceptually in terms of spatial attributes related to IACC. A second departure from the results of past work is the seemingly minimal contribution of spectral∕timbre aspects to perceived small-room acoustics. This result is surprising, given that results of past work suggest that spectral coloration caused by the acoustics of small rooms is an important perceptual aspect of such rooms (Olive and Toole, 1989; Bech, 1995, 1996). Although results from the physical parameter analyses in this study do suggest that timbre (as measured by f_c) is an independent physical parameter in this set of rooms, it does not appear to be an independent perceptual parameter. Instead, f_c is found to be related to Dimension 1 of the scaling solution, but more weakly related than reverberation time. As such, one might conclude that timbre does, in fact, contribute to the perceptual aspects of small-room acoustics in the current study, but it does so much less than reverberation time and is not perceptually independent of reverberation time, at least for this set of room simulations. Recent data from Rumsey et al. (2005) show similar inter-relationships between spatial and timbral aspects of reproduced sound, although these authors find that timbre tended to dominate space under conditions of degraded multi-channel audio reproduction.

An additional important result from the perceptual scaling analysis in this study is that individual listeners differ considerably in the relative importance they place on the two perceptual dimensions related two reverberation time and spaciousness. Although most listeners weight the reverberation time dimension most heavily, clear exceptions to this rule were observed, where some listeners placed increased weight on the spaciousness dimension. Because past studies of preference in room acoustics have not generally used the multidimensional methods to analyze individual differences implemented in this study, results are difficult to compare directly. Reports of large individual differences in concert hall acoustics preference appear to be relatively common (Wilkens, 1977; Barron, 1988; Morimoto et al., 1988), however.

Finally, it is important to note that the perceptual scaling results reported here were determined from a single source∕listener location within each room, using a single set of speech source material. As a result, the sensitivity of these particular scaling results to source location or source material is not currently known, although past studies of concert hall preference have demonstrated effects of both factors (Yamaguchi, 1972). Clearly this is an area in need of study within smaller listening environments.

Practical implications

Results from the psychophysical scaling analysis have a number of practical implications for virtual listening simulation of small rooms. First, the greatly simplified room modeling techniques used here still provided reasonable matches to measured rooms. Physically, the matches in room-acoustic parameters were generally similar to the matches typically seen from other room modeling software packages (Vorländer, 1995; Bork, 2000). Perceptually, the modeled rooms did differ from the measured rooms, but only along the two dimensions of the perceptual similarity space thought to relate to reverberation time and spaciousness. Had very poor perceptual matches between measured and modeled rooms been present, one might have expected that the scaling solution would have included an additional dimension that independently differentiated between measured and modeled rooms: a “realism” dimension. Such a dimension was not observed. This result is encouraging, because it suggests that optimization of the model to perceptually match the measured response characteristics should be easy to accomplish via appropriate adjustments to the physical acoustic parameters of T₆₀ and IACC that closely correspond to the two perceptual dimensions. Evaluation of such perceptual optimization strategies applied to room-acoustic modeling techniques, perhaps in conjunction with comparisons to results from more physically sophisticated models, is an area for additional study.

A second implication from these room scaling results is that individualized HRTFs do not appear to be necessary for realistic room simulation, since both measured and modeled BRIRs with nonindividualized HRTFs fall very near those with individualized HRTFs in the scaling solution (Fig. 6). Given the logistical challenges of obtaining individualized HRTF sets for each potential user in virtual listening simulations, this result is of particular practical importance. It is essential to note, however, that the testing situation in this study involved only a single static source location directly in front of the listener. As such, the relevance of the likely small directional errors in source rendering resulting from the use of nonindividualized HRTF did not play a major role in listeners’ judgments of room similarity. It is also likely that in listening situations such as those reproduced here, the directional information contained in at least some of the early reflections may be suppressed through a process commonly known as the precedence effect (Wallach et al., 1949; Litovsky et al., 1999), thus further minimizing the need for highly accurate simulation of the directional information in the early reflections using individualized HRTFs. Although there can be no doubt that a variety of room simulation applications would be well-served through accurate simulation of a single fixed-direction sound source, other more complicated applications with variable source direction would likely benefit from the increased directional accuracy afforded by individualized HRTFs, as has been demonstrated in previous work within anechoic space (Wenzel et al., 1993).

A final somewhat more tenuous implication relates to the simulation of late reverberant energy. In the physical analyses of the measured and modeled BRIRs, it was noted that one significant source of error appeared to stem from the modeling of the late reverberant energy. Hence, modeling techniques for this portion of the response are an obvious place for improvement. Surprisingly, however, the modeled room stimulus which had its late reverberant energy artificially removed (room 14) was closer on the perceptual scale than other modeled rooms which included simulated late reverberation. Perhaps no reverberation, which is analogous to the simulation situations originally described by Allen and Berkley (1979), is better than poor reverberation. Clearly additional research is required to more fully examine this effect.

CONCLUSIONS

The simple room simulation methods described in this study provide a reasonable physical approximation to BRIRs measured in a real room. Modeling errors generally increased at the frequency extremes. When room-acoustic parameters were estimated from the BRIRs, differences between modeled and measured rooms for most parameters were on the order of those reported for other room modeling algorithms (Bork, 2000). Potential causes for these differences are not fully understood, but likely include model limitations related to directional sound sources, as well as inadequacies in the model’s treatment of late reverberant energy.

Four independent acoustics parameters derived from the measured or modeled BRIRs resulting from the 15 room simulations examined in this study were found. These parameters were broadband T₆₀, broadband C₅₀,f_c, and high-frequency IACC.

MDS results suggest that only two dimensions are perceptually relevant for judging the similarity between the 15 room simulations examined in this study. Dimension 1 of the scaling solutions was highly correlated with T₆₀ (∣r∣>0.94). Dimension 2 was highly correlated with mid- and high-frequency IACC (∣r∣>0.82). Measured and modeled rooms were relatively close together in the scaling solution, suggesting a good degree of perceptual similarity.

Most listeners based their judgments of room similarity primarily on reverberation time (Dimension 1), although relatively large individual differences were observed.

Effects of spatial rendering quality (individualized HRTFs) were small, which has important practical implications for virtual auditory display and room auralization applications.