Blind location and separation of callers in a natural chorus using a microphone array

Abstract

Male frogs and toads call in dense choruses to attract females. Determining the vocal interactions and spatial distribution of the callers is important for understanding acoustic communication in such assemblies. It has so far proved difficult to simultaneously locate and recover the vocalizations of individual callers. Here a microphone-array technique is developed for blindly locating callers using arrival-time delays at the microphones, estimating their steering-vectors, and recovering the calls with a frequency-domain adaptive beamformer. The technique exploits the time-frequency sparseness of the signal space to recover sources even when there are more sources than sensors. The method is tested with data collected from a natural chorus of Gulf Coast toads (Bufo valliceps) and Northern cricket frogs (Acris crepitans). A spatial map of locations accurate to within a few centimeters is constructed, and the individual call waveforms are recovered for nine individual animals within a 9×9 m². These methods work well in low reverberation when there are no reflectors other than the ground. They will require modifications to incorporate multi-path propagation, particularly for the estimation of time-delays.

INTRODUCTION

The determination of individual interactions in animal choruses is of wide interest to behavioral researchers. Participants in a chorus can dynamically adjust spacing and acoustic call timing to influence behaviors such as mate choice, defense of territory and group cohesion (Kroodsma et al., 1983; Sullivan et al., 1995; Gerhardt and Huber, 2002; Simmons et al., 2002). But the number of participants, their spatial distribution, and the overlap between calls makes it difficult to precisely locate the individuals and separate their voices. Consequently, spatial and temporal characteristics of a chorus are typically studied in smaller subsets of the chorus, where it may be easier to visually locate callers and record the sound of one or a few individuals. What would be of benefit to researchers is a technique for mapping a chorus that simultaneously locates callers and separates their voices over a much larger scale. Such a spatio-temporal map would make it possible to address questions on large-scale chorus dynamics. The research reported here is a step in the direction of chorus mapping. Building on past work and new research, it outlines techniques for locating callers and separating their voice using a microphone array. The application discussed here is a frog chorus, but the techniques can be applied to other chorusing species as well.

Anuran choruses

Vocally communicating anurans such as frogs and toads congregate in dense choruses around bodies of water and vocalize to attract females. This is a lek-like breeding system (Bradbury, 1981) where males contribute sperm but do not otherwise control a resource. Females are therefore free to choose mates. Anuran choruses are usually heterospecific and their notable feature is high call density. Numerous individuals from many different species may be calling at the same time with a high degree of temporal and spectral overlap. While species calls are stereotypical and sufficiently distinct in their temporal and spectral features to reproductively isolate the species (Blair, 1958; Bogert, 1960), call overlap and the presence of large numbers of callers in close proximity can give rise to acoustic jamming and masking interference (Ehret and Gerhardt, 1980; Narins, 1982; Gerhardt and Klump, 1988; Schwartz and Wells, 1983a, 1993b; Schwartz and Gerhardt, 1995; Wollerman, 1999).

At the individual level, communication in dense choruses presents several challenges to signalers (males) and receivers (females). Females approaching the chorus must detect, locate, and identify calling conspecific males in the presence of masking interference. Thus, a target call must be sufficiently intense and well-separated from interfering sources. On the other hand, males are confronted with the problem of defending their acoustic space so that they may time their calls to be heard above the background (see Gerhardt and Huber, 2002, for a review). Thus, location and spatial separation, in combination with call intensity, timing, and overlap, are important parameters that may be actively controlled to maximize mate attraction and selection.

Earlier studies have shown that frogs have evolved strategies for utilizing time, frequency, and space in energetically efficient ways to minimize wasteful calling. Most of this evidence comes from small-scale studies involving a few frogs (Zelick and Narins, 1985; Gerhardt et al., 1989; Wilczynski and Brenowitz, 1988; Brush and Narins, 1989; Grafe, 1997; Simmons et al., 2006, 2008; Schwartz, 2001) but there are little data on the spatial and temporal structures of natural choruses involving large numbers of callers. Evidence from these studies point to interactions between local groups of callers with males typically paying greater attention to the calls of nearest neighbors (Brush and Narins, 1989; Schwartz, 2001). Such interactions will ncessarily weaken with increasing inter-male separation because of sound attenuation. Wagner and Sullivan (1992) suggested that males move when the number density of callers increases while preferring to remain stationary when densities are low. But little is known about the adjustment in individual call timing as a function of spacing (see Brush and Narins, 1989, for an exception). Such data are not easy to obtain without physically moving calling individuals and disrupting the natural scene. These concerns demonstrate the need for wider non-invasive spatial sampling in conjunction with call extraction.

At the chorus level a different set of questions arises particularly with regard to sexual selection. Broadly, anurans can be classified as prolonged or explosive breeders (Wells, 1977). Prolonged breeders have a long breeding season and the number density of males is relatively low. Explosive breeders, on the other hand, have a short breeding season and sustain higher densities. Both types of breeders can be sympatric as is the case for the two species considered here. A motivation for measuring chorus density, and to a lesser extent chorus size, has been the determination of operational sex ratios and female behavior, and male mating success. A major theoretical direction has been to determine how these factors influence sexual selection.

The data on chorus density are highly variable, being governed by physical environmental parameters and by species characteristics. Consequently density of callers and chorus size are subject to large variability between days in a given season, between seasons, between locations, and between species (see Wagner and Sullivan, 1992). As stated before, gross chorus parameters have usually been measured from the point of view of studying sexual selection and not with the aim of taking a census (for instance, see Gerhardt, 1994; Friedl and Klump, 2005; Murphy, 1994, 2003; Stewart and Pough, 1983). Most of the available data are restricted to a single species and to breeding sites that can be rapidly covered for censusing, typically in one night. By necessity this restricts the size of the choruses that can be covered. In particular, census data for heterospecific choruses are sparse.

For the two species that are studied here, Blanchard’s cricket frog (Acris crepitans blanchardi, a prolonged breeder) and the Gulf Coast toad (Bufo valliceps, an explosive breeder), some data are available. For cricket frogs, Perrill and Shepherd (1989) reported that 10–30 marked males were observed in small ponds over a 3 year period. Their separation was almost always greater than 50 cm, they called for durations ranging from 3 to 6 h, and they typically remained at the same position, sometimes returning to the same location on different nights. Unfortunately no data on the size of the ponds are available, nor is it known whether all marked individuals called in a chorus bout, or indeed whether unmarked males were present.

Wagner and Sullivan (1992), and Sullivan and Wagner (1988) observed Gulf Coast toads over a period of four seasons in two locations. They reported a mean number of toads ranging from 4 to 25 per nightly chorus, with densities ranging from 0.01 to 0.5 toads∕m of shoreline. Nearest-neighbor distances were about 5.5 m with large variability (standard deviation of 5.1 m). The number of chorus participants ranged from 2 to 65 males∕night and was highly variable between days in a given season, between seasons, and between locations. Males generally remained stationary, moving only when the density increased.

While direct observation and a manual census are often necessary and are unlikely to be replaced, they are arduous and time-consuming, and limited in spatial coverage. Thus, there is a pressing need for locating chorusing frogs if only to assess densities and numbers on a much larger scale, and over multiple species. Likewise, in the temporal domain, it is difficult to manually determine how many individuals are calling at any given time and to determine the call densities (number of callers per unit time). Such data are not readily available and form a major motivation for this work. An automated procedure that does not require direct observation and manual counting would be a valuable adjunct to on-going research. Thus, the case for automatically localizing and separating callers stems from these observations. The major question is: can it be accomplished? The problem is non-trivial especially when the chorus density is high and there are multiple overlapping heterospecific callers. To further understand the issues, we review some of the methods that can be employed.

Microphone-array techniques

A chorus can be mapped acoustically using a spatially dispersed microphone array by following a two-step process. First, the spatial position of each individual caller (source) is determined from the differences in the time of arrival of sounds at the microphones (a procedure akin to triangulation). Second, the known location of each source is used to estimate a steering vector to that source. Then an adaptive spatial filter steers to the selected source and recovers it while suppressing all other sources.

Source localization

Many algorithms have been proposed for source localization using intermicrophone time delays (see Carter, 1981). For airborne signals assuming a constant velocity of sound, the time-of-arrival differences (TOADs) are proportional to the differences in source-to-microphone range (range differences), with the locus of points that satisfy a constant range difference being described by hyperboloids (van Etten, 1970). In this method the sensors form the foci of the hyperboloids and the source lies at their intersection. In general, a minimum of three or four sensors are required for locating a source in two dimensions, and four or five sensors are required for locating in three dimensions with redundant measurements being used to provide improved accuracy when measurements are noisy (Hahn and Tretter, 1973). The method of hyperbolic range-difference location originated in the Loran navigation system and suffers from several drawbacks. It is a two-step process that requires an estimate of the TOADs before solving for the locations. Thus, it is suboptimal. For instance, when multi-path propagation is present, the arrival-time estimates are not accurate (but see Hahn and Tretter, 1973, for a maximum-likelihood etimator). Further, it does not have a closed-form solution, it is computationally expensive, and it is not amenable to statistical analysis when measurement noise is present.

Several variations of the method have been proposed to overcome some of these drawbacks including a simpler localization scheme where the source location forms the focus of a general conic (Schmidt, 1972). To incorporate measurement noise a generalized least-squares location estimator based on the approach of Schmidt (1972) was proposed by Delosme et al. (1980). And to overcome the computational difficulties engendered by manipulating hyperboloids, closed form localization based on spherical methods have been proposed by Schau and Robinson (1987), and Smith and Abel (1987). Additionally, several frequency-domain methods have been proposed. For the general case of multiple sources and sensors, and when the spectral density matrices of the sources and noise are known, Wax and Kailath (1983) extended the single-source results due to Hahn and Tretter (1973) by deriving a maximum-likelihood localizer and the Cramer–Rao lower bound on the error covariance matrix. The method includes the case of multi-path propagation and is a bank of beamformers each directed toward a particular source. More recently Mohan et al. (2008) derived a localizer for multiple sources using small arrays (where the number of sensors may be less than the number of sources). They exploit the sparse time-frequency structure and spatial stationarity of certain sources like speech, by using a coherence test to identify low-rank time-frequency bins. The data can be combined coherently or incoherently to arrive at directional spectra which yield the location estimates.

Biologically inspired source localization

Of particular interest to this work are approaches taken by bioacoustics and auditory researchers. Two lines of research are notable, namely, those with applications to human hearing and those with applications to animal call monitoring and localization. A biologically-inspired model that exploits time differences in the signals arriving at two sensors was originally proposed by Jeffress (1948) to explain how humans localize sounds using two ears. The model uses a coincidence detection mechanism with a dual delay-line to estimate the direction-of-arrival (DOA) of a sound (with two microphones only the direction of a sound can be estimated in a plane, typically the azimuthal plane, but not the source position). Mathematically, these operations are the same as cross-correlating the signals arriving at the two sensors and determining the time instant of the peak. The peak time is an estimate of the delay between the two sensors, and so the method provides a means for calculating the DOA. The Jeffress model has been validated anatomically and physiologically in the brain of the barn owl (Konishi, 1992) and the cat (Yin and Chan, 1990), and has inspired a number of two-sensor models for estimating DOAs. Most of these models have been applied to auditory processing and have used combinations of time-delays or phase differences, and intensity differences at the sensors to estimate DOAs (Blauert, 1983; Lindemann, 1986; Banks, 1993; Bodden, 1993; Gaik, 1993; Liu et al., 2000).

Source localization for bioacoustics monitoring

In field bioacoustics where it is necessary to monitor a population of callers, some of the early multisensor applications were in marine (Watkins and Schevill, 1971; Clark, 1980) and terrestrial (Magyar et al., 1978) domains. However, until recently most applications were confined to localizing and tracking marine mammals (Clark, 1980, 1989; Clark et al., 1986; 1996), and only a few studies have focused on techniques for localization of terrestrial callers2 (Spiesberger and Fristrup, 1990; Grafe, 1997; McGregor et al., 1997; Mennill et al., 2006). The report of McGregor et al. (1997) utilizes the technique due to Clark et al. (1996) for locating songbirds. The accuracy of these terrestrial acoustic localization systems, and several of their variants, have been evaluated under both reverberant (Mennill et al., 2006) and non reverberant or moderately reverberant conditions (McGregor et al., 1997; Bower and Clark, 2005). Spiesberger and Fristrup (1990) rigorously derived localization estimates using broadband cross-correlation and Wiener filtering under a variety of signal and environmental conditions. Subsequently Spiesberger developed a technqiue for estimating arrival-time delays from cross-correlation functions that had multiple peaks due to multipath propagation (Spiesberger, 1998), and used it to locate calling birds (Spiesberger, 1999).

The first known application of array localization to frog choruses is the work by Grafe (1997) who used methods due to Clark (1980), Magyar et al. (1978), and Spiesberger and Fristrup (1990) to localize a small population of African painted reed frogs. More recently, Simmons et al. (2006, 2008) used a small array and a localizer based on a dual-delay line cross-correlator to estimate locations of callers in a bullfrog chorus. To the authors’ knowledge, these are the only published reports on localizing callers in a frog chorus. None of the localization methods reported above attempts source recovery, which would be a crucial and necessary technique for detailed analysis of calling behavior.

Source recovery

To recover a single sound source with fidelity from a mix of sources, a spatial filter must be designed that passes the target source without distortion but cancels all other competing sources perfectly. The filtering (also known as beamforming) is performed with an array of spatially dispersed sensors. Based on the array data, target to sensor impulse responses (steering vectors) are estimated and a set of filter coefficients are computed. The microphone data are then filtered to yield the required target. Many different beamforming techniques have been developed for a range of applications (Brandstein and Ward, 2001; van Veen and Buckley, 1988). Filter coefficients may be fixed or adapted to the signal and noise conditions, implementation may be in the time or frequency domain, or the beamformer may actively cancel interfering sources by steering nulls in their directions. We briefly review some of the developments pertinent to this work.

Time-domain beamforming

The simplest beamformer is the fixed (i.e., nonadaptive) delay-and-sum beamformer, which for two microphones, is the average of the two microphone signals after one of them is shifted in time to compensate for the intermicrophone delay induced by a target source. This produces on average a 3 dB gain for the target source. However, it is often possible to do much better than a fixed beamformer by adapting the beamformer parameters. There are many techniques and real-time algorithms that are available for adaptive beamforming (Brandstein and Ward, 2001; van Veen and Buckley, 1988). Two commonly used iterative time-domain adaptive beamformers were developed by Frost (1972), and Griffiths and Jim (1982). The relative merits of these processors are discussed in Lockwood et al., 2004, where it is noted that they perform well when canceling interference sources that are statistically stationary and uncorrelated with the target source, but their slow adaptation causes poor performance when confronted with more sources than sensors and when the sources are nonstationary. This is of particular interest as bioacoustic sources in a dense chorus are nonstationary and likely to be more numerous than the sensors. An explicit solution of the optimal beamformer proposed by Capon (1969) avoids the convergence problems of iterative algorithms but for broadband sources requires the inversion of large time-domain correlation matrices. This can be computationally difficult.

Frequency-domain beamforming

Implementing a beamformer in the frequency domain eliminates some problems encountered in the time domain. The frequency-domain technique of Liu et al. (2000) first localizes sources (see above) and then cancels interfering sources in each frequency band. It can often cancel more sources than sensors. The LENS algorithm (Deslodge, 1998) uses n sensors to actively steer n−1 spatial nulls for interference cancellation. More efficient than these algorithms are a class of frequency-domain minimum variance distortionless response (MVDR) beamformers that minimize the energy from interfering sources (minimum variance) while allowing the signal to pass through with unity gain in all frequency bins (distortionless response) (Cox et al., 1986, 1987; Lockwood et al., 2004). Briefly, given the impulse response from the target-source to sensors (the steering vector) and the correlation matrix, an optimum weight vector that specifies how the sensor outputs are to be combined is obtained using the method proposed by Capon (1969). This weight vector is obtained for each frequency bin and applied to the sensor outputs. The weights are computed afresh whenever a new block of data is processed (Lockwood et al., 2004). A variant of this beamformer has also been proposed and applied to small-aperture arrays, and the reported target-source gain ranges from 11 to 14 dB (Lockwood and Jones, 2006). Beamformers using two sensors or a combination of sensors incorporated in two separate packages have found extensive application in the development of binaural hearing aids. Interested readers are referred to Lockwood et al. (2004) and Lockwood and Jones (2006) for a review and summary of these algorithms.

On-going challenges in bioacoustical monitoring

While localization of vocalizing frogs has been attempted in a few studies (see above), extraction of sources has hardly received any attention. The only attempts in this direction have been highly specialized and have utilized close-mic recording methods to isolate individual callers. For instance, the voice of individual callers has been recovered in artifical ponds using a microphone placed close to a calling perch (Schwartz, 2001), and another study has tracked the voice onset and offset times of individual callers in a natural chorus of coqui frogs (Brush and Narins, 1989). While these techniques are elegant and have provided valuable data on call interactions, they cannot generally be applied to natural choruses. These studies nevertheless provided a motivation for the current work. To take one example, Brush and Narins (1989) were able to determine that a male coqui frog actively avoided call interference with at most two neighbors by adjusting its call timing. Such detailed timing information on each individual caller would be of great benefit to studies on vocal communication if they could be determined on a larger spatial scale. Hitherto it has been difficult to determine the temporal interactions between callers and the spatial distances over which they persist. Thus, determining the spatio-temporal interactions in a chorus requires both source localization and source recovery. The current work is motivated by a need to develop a systematic and overarching framework for tackling this problem. Its development would assist not just the anuran vocalization community, but it would be of interest to other researchers in vocal communication, ethology, ecology, and environmental monitoring.

Current work

This report takes a step toward unifying source localization and source recovery into one scheme. It details a processor for blind localization and blind recovery of sources using a microphone array. A large-aperture microphone array is deployed around a frog spawning site. Callers are localized using a gradient-descent approach to solve for the intersection of the hyperboloids resulting from the TOADs. For each localized caller, a steering vector is estimated. This is followed by source recovery using a modified version of the MVDR proposed by Lockwood et al. (2004). The result is a spatial and temporal map of the chorus as it evolves in time. Along with theoretical methods, algorithms that detail the link between the various steps are provided. The method is independent of the array size or the number of microphones, and the array can be deployed in any configuration. Tests were carried out using four microphones in a chorus of nine individuals calling in a 9×9 m² area. We show that sources can be localized and recovered under non-reverberant or mildly reverberant conditions. The method has not been tested when there is multi-path propagation. We believe that without improving time-delay estimation, source localization will be difficult under such conditions. This is an important direction for future work.

A NOVEL METHOD FOR UNDERDETERMINED BLIND SOURCE LOCALIZATION AND RECOVERY

Consider a chorus with Q distinct species each with L_k, k=1,…,Q individual callers. Each caller is denoted by $C_i^k$, with k=1,…,Q denoting the species, and i=1,…,L_k denoting the individual within a species. Let $s_i^k\left(t\right)$ be the temporal waveform of the caller $C_i^k$ originating from spatial location ${\mathbf{\zeta }}_i^k∊R^3$. The total number of sources L is the sum over all L_k. The caller waveforms [s(t)], spatial locations (ζ), and number of callers (L) are all unknown, but the number of species (Q) is assumed to be known. The following assumptions apply: (i) The spectrum $S_i^k\left(f\right)$, considered over all individuals i in species k, is bandlimited to $f∊[f_l^k,f_u^k]$. The lower $\left(f_l^k\right)$ and upper $\left(f_u^k\right)$ cut-off frequencies are known. They define the frequency band B_k for the species k. (ii) If $s_i^k\left(n\right)$ are the samples at times t=nT, the data sampling interval is set at a fixed T=1∕f_s so that the sampling rate $f_s\ge 2{\max }_{\mathrm{k}}\left\{f_u^k\right\}$. (iii) The individual source waveforms are independent and block stationary, i.e., over adjacent N-sample intervals, the sources $s_i^k\left(n\right)$ are stationary and $E\left[s_i^k\left(n\right)s_j^m(n-l)\right]=0$, ∀k,m, and ∀i≠j when k=m, ∣l−n∣<N. (iv) The source locations ${\mathbf{\zeta }}_i^k$ are spatially stationary over the same time scale.

Consider a sensor array with M microphones at known locations ξ_j∊R³j=1,…,M. Let z(n)∊R^M be the discrete-time signal at the array output after sampling at the rate f_s. No assumptions are made about the impulse response between source and sensor other than that it incorporates a time delay dependent on the source-sensor distance. For each species k, the signal z(n) is filtered to pass B_k, resulting in a set of species-specific signals y^k(n)∊R^M, k=1,…,Q.

Given the species-specific signals y^k(n) and microphone locations ξ, the goal is to estimate the location ${\mathit{\zeta }}_i^k$ and the call $s_i^k\left(n\right)$ for each individual i belonging to species k.

This section is divided as follows. Theoretical methods for locating a source are presented in Sec. 2A and those for adaptive beamforming are presented in Sec. 2B. The implementation requires sources to be localized first, and then recovered using the beamformer. The algorithms and analysis that integrate localizing and beamforming are detailed in Sec. 2C.

Acoustic source localization

Let vector ξ_j denote the spatial coordinate (x,y,z) of sensor j with reference to an aribitrary origin. Let the source coordinate be denoted by ζ. The source-sensor distance is defined as D_j=‖ξ_j−ζ‖. Only one source is considered because the processing scheme considered below selects only those time-frames where a single source is dominant. The range difference between two sensors i and j will be denoted by

$$d_{ij}=D_i-D_j,i,j=1,\dots ,M.$$ (1)

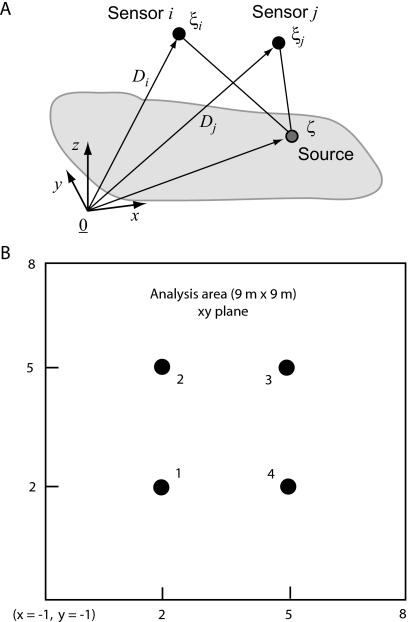
Let the vector of all possible range differences be denoted by d. There will be M(M−1)∕2 distinct range-difference measurements for all microphone pairs. For localizing sources in three dimensions the system is over-determined whenever M≥4 or M≥5 depending on the source sensor geometry (see footnote n1). In this case the redundant measurements can provide improved estimates in noise. The geometrical relationship between the source and sensors are depicted in Fig. 1.

Figure 1.

Source and sensor geometry. (A) Shown is a single source located at ζ and two sensors i and j at locations ξ_i and ξ_j, respectively. Directed arrows represent vectors from an arbitrary origin $\underset{̱}{0}$. Source-to-sensor distances are marked as D_i and D_j. The arrival-time differences are τ_ij=c⁻¹(D_i−D_j), where c is the velocity of sound, or equivalently the range differences d_ij=D_i−D_j. (B) Deployment of sensors in the field test, looking down on to ground (along z-axis). Ground is xy plane with z=0. Omnidirectional microphones numbered 1–4 (filled circles) were placed in a square with the following (x,y,z) coordinates. (1) (2.0, 2.0, 1.69), (2) (2.0, 5.0, 1.74), (3) (5.0, 5.0, 1.76), and (4) (5.0, 2.0, 1.65). The analysis area extended to a square 9 m on either side (solid line, not to scale) with the lower-left corner at x=−1, y=−1.

The source location ζ is to be determined given the vector of range-difference measurements d and the microphone locations ξ. An iterative gradient-descent optimization technique is followed. Given an estimate $\widehat{\mathbf{\zeta }}$ of the unknown source location, the range-difference estimate $\widehat{\mathit{d}}=\Vert \mathbf{\xi }-\widehat{\mathbf{\zeta }}\Vert$ is formed. The error in the delay $\mathbf{ϵ}=\mathbf{d}-\widehat{\mathbf{d}}$ is determined and the goal is to minimize the squared delay error, i.e.,

$$\min \left\{{\mathbf{ϵ}}^T\mathbf{ϵ}\right\}.$$ (2)

For a fixed location step Δζ the gradient of the squared error is calculated, and the new estimate of $\widehat{\mathbf{\zeta }}$ is determined from

$$\widehat{\mathbf{\zeta }}\leftarrow \widehat{\mathbf{\zeta }}-\mu \frac{\Delta \left({\mathbf{ϵ}}^T\mathbf{ϵ}\right)}{\Delta \mathbf{\zeta }}.$$ (3)

The parameter μ is adaptively adjusted so that the squared error ϵ^Tϵ is made smaller. The initial value of $\widehat{\mathbf{\zeta }}$ is taken to be some suitable value, say, the mean value of ξ. An approximate solution to the problem of intersecting hyperboloids based on spherical interpolation has been proposed by Smith and Abel (1987). The authors suggest that their solution could be used as an initial condition in iterative nonlinear minimization methods, such as the gradient-descent method proposed here, so as to improve convergence. But this has not been attempted here.

Acoustic beamforming

Recovery of the individual vocalizations by beamforming requires a steering vector, which at each frequency defines the relative amplitude and phase relationships of a signal from the location of interest for all microphones in an array. A MVDR beamformer preserves any signal exhibiting the exact amplitude and phase relationships defined by the normalized steering vector (distortionless response) while minimizing the interference energy in the output (minimum variance) from sources with any other amplitude and phase relationships between sensors (Capon, 1969). This precision potentially allows the separation of vocalizations of even closely spaced frogs.

Let the microphone signals be denoted by y(n)∊R^M. Data frames of length N_F are windowed and Fourier-transformed via an N-point FFT (Fast Fourier Transform). The frequency-domain signals are denoted by Y(f) where f represents frequency. The cross-correlation matrix R(f) at frequency f (an M×M matrix) is computed from E[YY^H(f)], where Y^H represents the transposed complex conjugate (Hermitian) of Y. For the remainder of the discussion the frequency f will be omitted for notational simplicity and it will be assumed that the quantities are confined to a frequency bin unless otherwise stated. If there is only a single source i that is present in the data frame, then the cross-correlation matrix consists of the outer product of the steering vector e_i times the power of the signal $\left({\sigma }_s^2\right)$,

$$\mathit{R}={\sigma }_s^2{\mathit{e}}_i{\mathit{e}}_i^H.$$ (4)

The cross-correlation matrix R from each data frame is computed. Because only one source dominates the microphone data, R is rank-1 with an eigenvector that is an energy-normalized version of e_i. The eigenvector ${\tilde{\mathit{e}}}_i$ corresponding to the largest eigenvalue of R is an estimate of the steering vector for that source at each frequency. The estimated steering vector is scaled so that the steering-vector element at some selected microphone m is 1, i.e.,

$${\mathit{e}}_i={\overline{\mathit{e}}}_i{e}_{m,i}.$$ (5)

With known steering vectors e_i to source i, the optimal weights $\left({\mathit{w}}_i^{*}\right)$ for combining the different microphone channels are obtained from the solution to a linearly constrained quadratic optimization problem. The MVDR beamformer minimizes the output power subject to the constraint that the gain of the target signal is unity, i.e.,

$$\underset{e_i^H{w}_i=1}{\min }\mathit{E}\left[{\mid {\mathit{w}}_i^H\mathit{Y}\mid }^2\right].$$ (6)

In this case the optimal weights are (Capon, 1969)

$${\mathit{w}}_i^{*}=\frac{{\mathit{R}}^{-1}{\mathit{e}}_i}{{\mathit{e}}_i^H{\mathit{R}}^{-1}{\mathit{e}}_i}.$$ (7)

The optimal frequency weight ${\mathit{w}}_i^{*}$ is applied to each frequency bin (of the Fourier-transformed data) at each time frame over which the correlation matrix R was computed. Then an inverse Fourier transform is performed to recover the source. The time-frames are then pieced back together to recover the entire vocalization from the given source for all times. By determining the steering vector and optimum weights for each source location, all individual callers can be extracted with minimum distortion.

Algorithms and analysis procedure

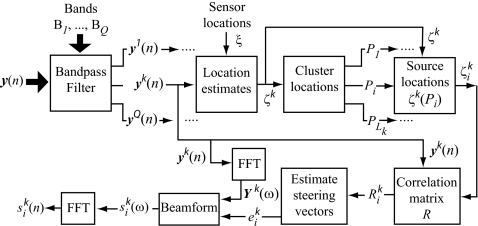
Acoustic data from a chorus are recorded synchronously at multiple microphones positioned around a spawning site. Subsequently, using an offline procedure, the location of each individual caller in the neighborhood of the microphone array is estimated using a source localizer (Sec. 2A), and its call recovered using an acoustic beamformer (Sec. 2B). The localization and beamformer steps are linked in a six-step procedure, and schematically reproduced in Fig. 2.

• (1)Bandpass filter raw microphone data. For each species k, microphone data z(n) are bandpass filtered into bands B_k resulting in microphone data sets y^k(n). Bandpass filtering retains the spectral range of that species (the “focal species”) while minimizing interference from other species. Even if there is some overlap with the frequency band of other species, isolating the bandwidth of the focal species leads to greater localization accuracy, as it reduces interference and improves beamformer performance. Subsequent steps are applied individually to each band B_k; i.e., analysis of a focal species is independent of other species present in the chorus.
• (2)
  Find time intervals with single dominant call. Experimental data indicate that even in a dense chorus, many time intervals contain only a single strong call within the spectral range of a given species from an individual within or near the sensor array. From these times the location of the single caller can be determined by cross-correlating the signals at the various microphone pairs (i,j) and finding the relative time-delay $\left({\tau }_{ij}^{*}\right)$ of maximum correlation between each pair of sensors. Let $y_i^k\left(n\right)$ and $y_j^k\left(n\right)$ be the bandpass-filtered outputs for species k from microphones i and j, respectively. The correlation coefficient of the cross-correlation at the maximizing delay, ${\tau }_{ij}^{*}$, is

  $${\rho }_{ij}=\frac{{\sum }_{r=l}^n{y}_i^k\left(r\right)y_j^k(r+{\tau }_{ij}^{*})}{\sqrt{{\sum }_{r=l}^n{\left(y_i^k\left(r\right)\right)}^2}\sqrt{{\sum }_{r=l}^n{\left(y_j^k(r+{\tau }_{ij}^{*})\right)}^2}},$$ (8)

  where l and n are the start and end times of the interval of analysis, and the correlation frame length is n−l+1. If the waveforms from the different microphones are identical replicas (within a scale factor and a time-delay), then the correlation coefficient ρ_ij at the maximizing delay ${\tau }_{ij}^{*}$ will be 1. If there are multiple sources of similar power originating from different locations, ρ_ij will be considerably smaller. Thus, we apply a threshold γ to all pairwise coefficients so that whenever ρ_ij≥γ the interval is considered to be dominated by a single source. The value of γ is determined experimentally. The set of frames for which ρ_ij≥γ will be denoted by P. For a given frame in P, the maximizing delay ${\tau }_{ij}^{*}$ for every pair of microphones is denoted by the vector τ^*. For all frames in P this step yields a set of τ^* which can be used to estimate the source location. In certain situations it may be advantageous to consider pairwise correlations from subsets of sensors instead of all sensors, for instance, when some sources are close to a subset of sensors but much farther away from the remaining sensors.

• (3)Find location of dominant source intervals by least-squared delay error. For any given τ^* the measured range differences are given by d=cτ^*, where c is the velocity of sound. The location of the source corresponding to the range difference is obtained via the gradient-descent procedure outlined in Sec. 2A. The localization is performed on every frame in P and results in a set of location estimates, each corresponding to a single caller. The identities of the callers $C_i^k$ are, however, still unknown.
• (4)Cluster the location estimates to identify individual frogs. If the data record y^k is sufficiently long, then each caller is likely to dominate one or more frames with indices P_i such that ζ^k(P_i) corresponds to a single caller $C_i^k$. These location estimates will be somewhat variable due to measurement noise even though the individual is stationary. However, it is assumed that the variability in the estimates is smaller than the mean spacing between frogs, thus providing a natural way to cluster the location estimates ζ^k into sets ζ^k(P_i) each corresponding to a caller $C_i^k$. From this cluster, the averaged spatial location ${\mathbf{\zeta }}_i^k$ of each actively calling frog can be determined. Here the clusters are determined visually from localization plots, although automatic clustering procedures can be applied to extract the sets ζ^k(P_i).
• (5)Estimate beamformer steering vectors. Small deviations in the steering vectors can cause the adaptive beamformer to treat the target source as interference and to cancel it as well. In frog choruses variations in the steering vector can result from (1) minor deviations in microphone placement, (2) any reflections or absorption of sound from the ground, (3) presence of other objects such as vegetation in the environment, or (4) direction-dependent acoustic radiation patterns in vocalizations. These can make recovery of calls difficult if not impossible with current methods. The following new procedure has proven effective in blindly estimating the steering vectors from field recordings with high accuracy.

  The cross-correlation matrix R [see Eq. 4] is computed for the frames y^k(P_i) and averaged in each frequency band. Recall that this set of frames corresponds to the cluster of location estimates ζ^k(P_i) for caller $C_i^k$. Because only one caller $C_i^k$ dominates the cluster, the rank of R is essentially 1 and the eigenvector corresponding to the largest eigenvalue of R is an estimate of the steering vector ${\mathit{e}}_i^k$ for the caller. The steering vectors are renormalized across all frequencies according to Eq. 5 to reconstruct the frog vocalization without distortion at the closest microphone. The procedure is repeated to estimate the steering vectors for each individual in the chorus.

• (6)
  Beamform to recover individual acoustic signal at all times. For each caller $C_i^k$ the optimal weights $\left({\mathit{w}}_i^{k*}\right)$ for combining the different microphone channels of the MVDR adaptive beamformer are computed in each frequency bin according to Eq. 7 and the beamformer output is calculated using

  $$S_i^k\left(f\right)={\mathit{w}}_i^{k*}{\left(f\right)}^H{\mathit{Y}}^k\left(f\right).$$ (9)

The vocalization $s_i^k\left(n\right)$ of caller $C_i^k$ is obtained via the inverse Fourier-transform of $S_i^k\left(f\right)$. The procedure is repeatedly applied to recover all sources.

Figure 2.

The source localization and source recovery processor. The procedure is outlined for localization and recovery of a single source i from a single species k. These quantities are ${\mathbf{\zeta }}_i^k$ and $s_i^k\left(n\right)$, respectively. Notation follows text.

FIELD TESTING

Recordings of choruses were carried out at a spring-fed marsh located in the Cibolo Nature Center (Boerne, TX). The site coordinates were 29°47^′7.51^″ N, 98°42^′37.92^″ W at an elevation of 422 m. A 7×7 m² grid (1 m spacing) was marked using short stakes driven into the ground. The grid was used for visually locating calling individuals, but the analysis was carried out over an 81 sq m area (9 m to a side). Four omnidirectional microphones numbered 1–4 (Sennheiser MKE-2, 0.02–20 kHz) were positioned at the vertices of a square 3 m on each side centered in the grid [Fig. 1B]. All microphones were mounted on poles. In this coordinate system ξ represents (x,y,z) with the z axis being normal to the ground (where z=0). Microphone data from the array (number of sensors, M=4) were used for source localization and source separation. Note that the ground was planar (z=0); therefore each source could be located precisely with four microphones (see footnote n1).

The omnidirectional microphone outputs were amplified using battery-powered field amplifiers (Sound Devices MP-1) and the cables from the array were led into a blind that housed the data-acquisition system and other components. Microphone data were acquired synchronously at a sampling rate of 20 kHz (National Instruments PXI 4472, eight-channel, 24 bit) by a data-acquisition computer (National Instruments PXI-8186 controller running Windows XP, mounted in a PXI 1031DC chassis). Data-acquisition programs were developed in the LabVIEW environment (National Instruments Inc.). All equipment were powered using DC (battery) sources. Recorded data were analyzed offline using MATLAB (The MathWorks Inc.)

Once the chorus was in progress the frogs and toads that could be visually located within the grid area were identified, and their x and y locations were marked on a chart (the z coordinate was assumed to be 0, as all the located individuals were calling from the ground). The uncertainty of the visual estimates were estimated to be about 10 cm along x and y directions. The area was then vacated and microphone data were acquired for a period ranging from 5 to 10 min. Then the positions of the previously marked frogs were once again determined, and new entrants if any were noted. This procedure was repeated for the duration of the session. At the end of the session only the microphones were removed, but the grid and microphone stands were left intact at the site. This ensured that microphone locations between sessions were unchanged.

RESULTS

Recordings were carried out in mid-March 2007 between 2100 and 2400 h. Two species were present on all days in this period. They were Bufo valliceps (Gulf Coast toad) and Acris crepitans blanchardi (Blanchard’s cricket frog), abbreviated Bv and Ac, respectively. Cricket frogs outnumbered Gulf Coast toads in the entire site. The Rio Grande leopard frog Rana berlandieri was present from late February to early March. It was identified visually and by voice but was not present during the days the chorus was recorded. Data presented here are for a mixed Bv and Ac chorus, and were collected on March 21, 2007. Average temperature was 21 °C, relative humidity was 78%, and pressure was 1019.5 hPa.

For the duration of the recording, two Bv males were identified visually in the 9×9 m² arena [Bv1: (2.6, 4.5), Bv2: (2.0, 4.5)]. Cricket frogs were harder to identify due to their small size and coloration, and only one was visually located [Ac1: (1.95, 4.6)]. Although not all callers within the arena were visually located, as will be seen in the results below, the known locations of Bv1, Bv2, and Ac1 will be compared to the computed locations so as to verify the accuracy of the localization algorithm.

Call characteristics

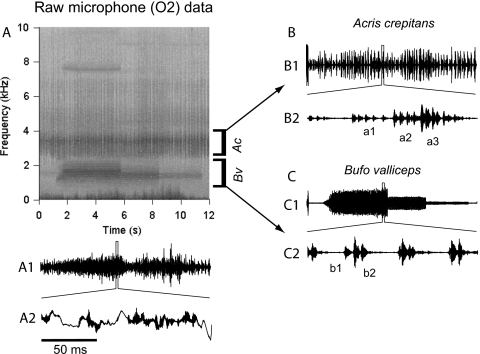
Figure 3A depicts the spectrogram for a 12 s segment of the chorus recorded at microphone 2. The dominant call frequencies of Bv (species 1) and Ac (species 2) were spectrally separated into non-overlapping frequency bands: 680–2300 Hz (spectral band B₁) and 2700–4000 Hz (spectral band B₂), respectively. Several individuals from both species were calling in this segment, and there was extensive temporal overlap within and across species. Calls of one Bv individual contained some harmonic components, most notably the fifth harmonic of the dominant frequency [between 7 and 8 kHz; see call spectrogram Fig. 3A, 1.5–5.5 s]. Power in this band was attenuated by 32 dB with respect to B₁. Calls of Ac also possessed harmonics but because of their pulsatile nature, energy was distributed over a broad range of frequencies (between 4.5 and 7 kHz). Power in this band was attenuated by 20 dB with respect to B₂.

Figure 3.

Bandpass filtering of raw microphone data into species-specific bands. (A) Spectrogram of mic 2 output. Two distinct species-specific bands marked Bv and Ac can be discerned. Panel A1 shows the time waveform of the signal. A 150 ms window from the segment is expanded and shown in detail in panel A2. (B) depicts the bandpass-filtered waveform corresponding to band Ac for the cricket frog (panel B1), with fine temporal details corresponding to the 150 ms window shown in panel B2. Three individuals marked a1, a2, and a3 are calling in this window. (C) depicts similar results for the Gulf Coast toad filtered into band Bv. The window depicts two callers b1 and b2, with b2 being more intense than b1.

In general, harmonic components were greatly attenuated with respect to the bands B_k and so it was assumed that neglecting the higher harmonics would not make a significant difference to either call localization or separation. Further, the harmonics could get washed out in background noise depending on the proximity and orientation of the caller with respect to the microphones. The Bv individual mentioned above was close to mic 2 and positioned so that the fifth harmonic was captured, whereas those of the other toads calling at the same time (see panel C) were not distinguishable from the background. Thus the use of higher harmonics may not provide additional benefit and could, in fact, degrade localization and beamformer performance by reducing signal-to-noise ratio. Small changes in the upper and lower cut-off frequencies of the bands did not significantly affect processing. Energy in the band below 500 Hz was primarily from wind and other abiotic sources. Microphone data corresponding to the spectrogram are shown in Fig. 3(A1). Panel A2 shows waveform details of a 150 ms segment selected from Panel A1 (windowed portion). The high-frequency fluctuations (dark bands) are Bv and Ac callers. The slow fluctuations are due to wind and other low-frequency noise sources.

The spectrogram demonstrates that the two species are reasonably well separated in frequency space and that their calls can be processed independently of one another by bandpass filtering the data into two parallel data streams. Accordingly, data from each microphone were filtered into two streams y¹ (Bv) and y² (Ac) restricted to bands B₁ and B₂, respectively. The filter outputs for the mixed waveforms shown in [Fig. 3(A1)] are depicted in (Figs. 3B, 3C), for the bands B₁ and B₂, respectively. The fine temporal details corresponding to the 150 ms segment (panel A2) are shown in panels B2 and C2. Multiple callers within each species can be discerned. There are three Ac individuals (a1, a2, and a3), and two Bv individuals (b1 and b2) distinguishable by their relative amplitudes. Leakage of calls from one species into the band of the other was insignificant. Broadly, panels B and C demonstrate that calls can be unmixed into species-specific streams. The results shown in Figs. 3B, 3C are analogous to the spectral filtering that takes place in the inner ears of anurans (Capranica, 1965).

Localization of callers

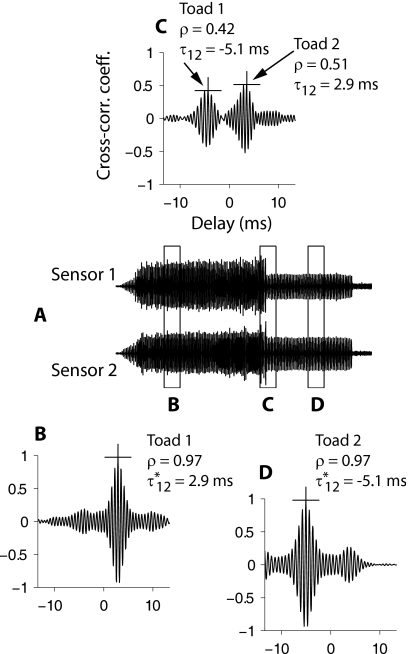
Hereafter the same procedure was applied to data from both species. Location was computed on a frame-by-frame basis using a correlation block size of 500 ms (Bv) and 20 ms (Ac). For each frame the pairwise normalized cross-correlation function was computed and its maximum value ρ was determined. A threshold γ=0.65 was apllied to ρ. When ρ was greater than γ the frame was assumed to contain only a single caller and was retained; otherwise, it was discarded. Figure 4 illustrates the process. To illustrate the procedure, the bandpass-filtered traces from microphones 1 and 2 are shown in Fig. 4A [filterband B₁ corresponding to Bv, identical to the segment shown in Fig. 3(C1)]. Three representative time frames at which the cross-correlation functions were evaluated are shown in panel A as rectangles marked B, C, and D. Cross-correlation functions in each of these frames are shown in the respective panels. The selected frames show two toads 1 and 2. In frame B only toad 1 is present [Fig. 4B: ρ=0.97, ${\tau }_{ij}^{*}=2.8\mathrm{ms}$], in frame D only toad 2 is present [Fig. 4D: ρ=0.97, ${\tau }_{ij}^{*}=-5.1\mathrm{ms}$], whereas in frame C both toads were present [Fig. 4C: ρ=0.42, and ρ=0.51 ms at the maximizing delays shown in Figs. 4B, 4C, respectively]. After applying the threshold only frames B and D were retained for estimating steering vectors because they contained only one dominant caller, whereas frame C was discarded.

Figure 4.

Time-domain cross-correlation to test for the presence of a single caller in a selected frame. (A) shows bandpass (B₁) filtered outputs from two sensors 1 and 2. Three representative time frames B, C, D are shown as rectangular windows. The corresponding cross-correlation functions are shown in panels B, C, and D, respectively. For frames B and D, the maximum in the cross-correlation function is marked (+), and the ρ and maximizing delay ${\tau }_{12}^{*}$ are also shown. These frames have one dominant caller each: toad 1 (frame B) and toad 2 (frame D) and ρ exceeds threshold (γ=0▷65). Frame C has both callers as seen from the two peaks in the cross-correlation function at the delays exhibited by toad 1 (panel B) and toad 2 (panel D). Consequently, the cross-correlation function is broad and neither peak exceeds γ. This frame was discarded. Note that the two callers can be visibly distinguished in the sensor data except in the overlapping region (see also the identical segment shown in Figs. 3(B1) and 3(B2)).

In a 1 min interval approximately 3% of the frames for cricket frogs were identified as having one dominant caller (totaling at least six callers). For Gulf Coast toads the number of frames with a single caller was approximately 34% (totalling four callers). All calling individuals were represented at least once in the selected frames as most of them positioned their calls to avoid overlap. For each frame the maximizing delays τ^* were converted to a range-difference estimate d=cτ^* [see Eq. 1 and Step 3 in Sec. 2C]. This set of frames is denoted by P.

After analyzing all frames and determining the vector d(P), the source-localization procedure outlined in Sec. 2A was applied to each frame in P and a raw position estimate was obtained for that source. Position estimates of single callers ζ^k(P) (k=1: Bv; k=2, Ac) were graphically plotted. The identities of the callers at this point were still unknown because the location estimates differed across individuals (due to spatial separation). However, estimates for a single individual were also subject to variability due to measurement noise. Thus the frames P_i∊P which correspond to individual i had to be determined by a clustering procedure. This visual procedure relied on the small variability in an individual’s location in comparison with the inter-individual spacing.

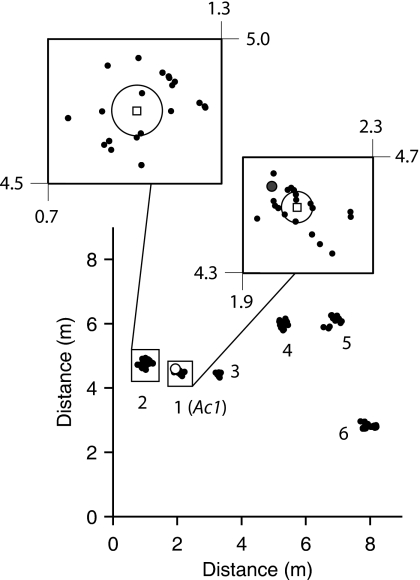
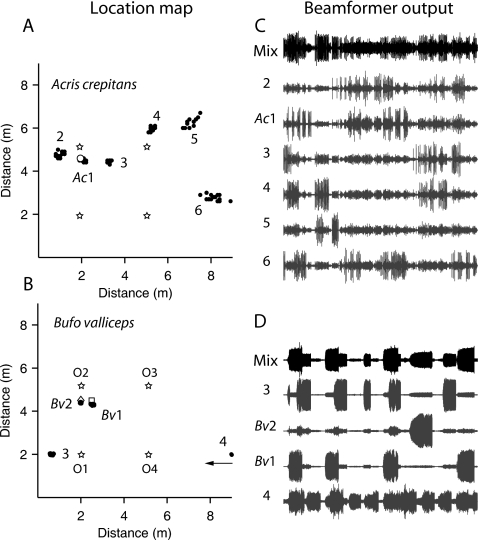
This is illustrated in Fig. 5 for cricket frogs. Based on a visual clustering procedure, six cricket frogs were identified. Their estimated mean positions are listed in Table 1. The individual who had been visually located (frog 1 or Ac1) is listed and his position marked on the graph in Fig. 5 (open circle). An identical procedure was applied to the spectral band B₂ to estimate the locations of Gulf Coast toads. The results are listed in Table 1 along with the locations from visual estimates for Bv1 and Bv2. For both species, the location estimates from the data were in good agreement with the visual estimates where available. Location maps for both species are shown in Figs. 6A, 6B.

Figure 5.

Two-dimensional map of cricket-frog locations. Frames of 20 ms duration containing only one caller were identified by cross-correlation, and the location of the calling individual was determined within the 9 m−9 m area. Point estimates were clustered visually, and six frogs (numbered 1–6) were estimated to be present in the arena. Frog 1 (Ac1) was visually located prior to the recording at the position marked with an open circle. Insets show the clustering procedure for frogs 1 (Ac1) and 2. The point estimates were clustered visually by selecting the bottom-left and top-right corners of a bounding box. Points within the box were assigned to a single caller with mean position indicated by a square. The circle defines the positions within one standard deviation of the mean position.

Table 1.

Coordinates (x,y) of individual callers in meters (z=0 for all individuals). “Algorithm”: locations calculated from microphone data. “Visual”: locations determined visually for some individuals. Standard deviations are indicated below the coordinates. No. 4 under B. valliceps was a cluster of two toads with the x and y positions beyond the range of the algorithm. See also location maps in Figs. 6A, 6B.

No.	B. valliceps (x,y)		A. c. blanchardi (x,y)
	Algorithm	Visual	Algorithm	Visual
(1)	(−0.51,1.17)		(2.03, 4.53)	Ac1: (1.95, 4.6)
	(±0.031,±0.024)		(±0.064,±0.067)
(2)	(2.03, 4.37)	Bv2: (2.0, 4.5)	(1.0, 4.75)
	(±0.003,±0.003)		(±0.145,±0.108)
(3)	(2.55, 4.27)	Bv1: (2.6, 4.5)	(3.28, 4.43)
	(±0.006,±0.004)		(±0.036,±0.04)
(4)	(>9,<2.0)		(5.26, 5.96)
	2 toad cluster		(±0.051,±0.067)
(5)			(6.9, 6.16)
			(±0.217,±0.184)
(6)			(8.01, 2.77)
			(±0.195,±0.076)

Figure 6.

Location maps [(A) and (B)] for cricket frogs and Gulf Coast toads in the xy plane (ground), and their beamformer outputs [(C) and (D)]. Microphone locations are shown as 1–4 [open stars in (A) and (B)]. The location of each individual is a numbered cluster. Visually observed individuals are marked Ac1 (panel A, ○) and Bv1 and Bv2 (panel B, ◇ and ◻, respectively). In panel B cluster 4 represents two toads located outside the analysis arena (x>9 m, y<2 m). See text for further explanation. Beamformer outputs for each individual are shown in gray. The filtered bandpass output from a representative microphone (mic 2) are shown in black (“Mix”).

Beamforming and call separation

The clustering procedure identified the data frames P_i for each individual. From these frames the mean location ${\mathbf{\zeta }}_i^k$ and the mean correlation matrix R_i was computed, and the steering vector was estimated following the proceedure outlined in Step 5 in Secs. 2C, 2B. The minimum-variance beamformer used the estimated steering vector e_i for each individual to recover its calls for all times, while suppressing all other interfering sources. For each recovered source, the beamformer output is a single channel, one per individual, available at the same sampling rate as the raw data (20 kHz). Traces of the recovered sources are shown in Figs. 6C, 6D, and numbered according to the source depicted in Figs. 6A, 6B, respectively. The Bv source marked with an arrow (cluster 4, in panel B) was a cluster of two toads located at x>9 and y<2. This cluster could not be localized due to the large range. That this cluster has more than one individual can be readily seen from the beamformer output in which the call density is higher than the density for toad 3, Bv1, and Bv2. Some degree of cross-talk between channels is visible in some of the recovered source channels. For example, the Bv1 and toad 3 channels crossover to the Bv2 channel.

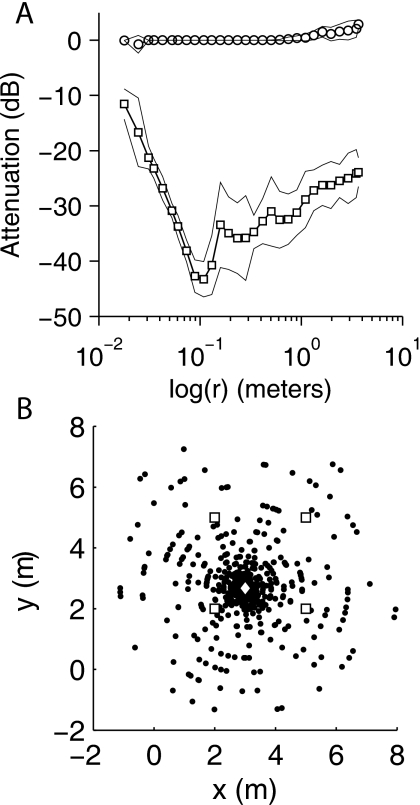
There is no general characterization (such as a beam-pattern) of adaptive beamfomer performance, as it depends on the exact array and source configurations and their individual spectra and calling times. But an empirical estimate of the performance can be arrived at by simulations. Sources corresponding to two of the Gulf Coast toads (Bv1 and Bv2) were synthetically presented to the same array. The toad Bv1 was placed at coordinates (3.0, 2.67, 0), and Bv2 was located at random on a circle around Bv1. Twenty-nine circles with radii spaced logarthmically from 0.02 to 5 m were selected, and around each circle 30 random locations were determined for a total of 870 locations. Figure 7B shows the caller Bv1 (◇) and all the locations of Bv2 tested in the simulations (●). For each pair of Bv1 and Bv2 locations, the procedure used for localizing and extracting the sources as outlined above was followed. Each source was extracted in turn while suppressing the other.

Figure 7.

Beamformer performance as a function of inter-source distance. Calls from two Gulf Coast toads were synthetically combined so that they appeared to originate from distinct locations. Each source was localized and then extracted with the beamformer while the second source was treated as an interference. (A) The average attenuation (dB, ordinate) of the interfering source in the target source (◻) is shown as a function of the logarithm of distance (abcissa). Thin lines represent the standard deviations of the attenuation over repeated trials. Also shown are self-cancellation (○), the degree to which a target is canceled by the beamformer. (B) The results in (A) were obtained by fixing one of the toads (◇) at (3.0, 2.67, 0) while the second toad had a variable location (●). The plot shows all the 870 locations (●) that were used to generate the plots in (A). Microphone locations (◻) as in Fig. 1B. See text for details.

Let E₁ and E₂ be the energies of the Bv1 and Bv2 calls, respectively, that were selected for mixing. Following recovery let ${\widehat{E}}_{ij}$ with i,j=1,2 be the energy of the source j in target channel i. Attenuations were calculated in dB as $a_{ij}=10{\log }_{10}({\widehat{E}}_{ij}∕E_i)$. The term a₁₂ represents the amount of residual energy (cross-talk) from Bv2 in the recovered Bv1 channel. The term a₂₁ represents the cross-talk resulting from Bv1 in the recovered Bv2 channel. These should be large and negative. The terms a₁₁ and a₂₂ represent self-cancellation and should ideally be close to 0 dB. The results are shown in Fig. 7A. The averages of a₁₂ and a₂₁ (over 30 locations at each distance) are shown with standard deviations (thin lines). In general there is a sharp decline in cross-talk as the sources are spatially separated up to a critical distance of about 10 cm. At this separation the attenuation is about 45 dB. For progressively larger separations the attenuation gradually decreases to about 25 dB due to increasing relative time-delay differences between the sources. The average self-cancellation of the target source (○) is almost 0 dB over the range of distances indicating that the recovery does not appreciably subtract the desired target.

DISCUSSION

This report details a passive microphone array technique for locating and recovering the calls of vocalizing frogs in a natural chorus. The technique is blind in that it makes no specific assumptions about the sources (callers). Instead, it utilizes heuristics that stem from biological plausibility, in particular, time-frequency sparseness (Mohan et al., 2008). At the core of the processor are two powerful theoretical methods originating from array signal processing: (1) Localization of a source using the TOADs between pairs of microphones and (2) recovering a source by adaptive beamforming. The two parts (localization and recovery) are linked by a novel, yet simple procedure for estimating steering vectors from the location information and then actively steering the array toward the source for recovery. The procedures are repeatedly applied to every source. The end result is a spatio-temporal map of the chorus. The core methods—localization and source recovery using beamforming—have been widely investigated (see Sec. 1). What is new in this report is the processing system, and, in particular, the steering-vector estimation. They are motivated by biological mechanisms for listening in noise. The method will not work without modifications when there are significant multi-path reflections.

Segregating data into species-specific spectral bands

The first step takes a set of raw sensor data and bandpass filters it into species-specific bands. The segregated streams of data, one for each species, are subsequently processed in parallel as they are independent of one another. There is good reason to follow this strategy although it increases the computational effort. If the assumption is that conspecific callers avoid overlap, as has been suggested by many studies (see Bee and Micheyl, 2008; Feng and Ratnam, 2000; Gerhardt and Huber, 2002, for reviews), then removing potentially overlapping heterospecifics will make it more likely to find temporally segregated callers. Location estimates become more accurate as there is less energy from spatially separated interfering sources. The step is no different from the matched filtering that takes place in the frog ear originally proposed by Capranica (1965). Namely, the inner ear acts a spectral filter matched to the species-specific mating call, thereby selectively enhancing the calls of its own species while suppressing calls from other species. It is possible to bandpass filter the data into a spectral band that exactly matches the data but it has not been attempted here. In the case of partial spectral overlap between species, location and individual calling times can easily be determined by limiting the recovery to only the nonoverlapping portions of the spectral band. One concern about this step is that it requires a priori information on the number of species. For most recordings and locations, this does not present a significant problem as the information is easily obtained by listening to the recorded microphone data.

Source localization

To localize a calling individual and estimate the steering vector to his location, it is necessary to find at least one data frame where the frog is the only individual vocalizing near a group of at least four to five microphones in his spectral band. This is possible when data are collected for long durations, giving each individual the opportunity to find temporal gaps when he can vocalize without interference. For instance, in the case of cricket frogs the percentage of data frames where only one caller was present was about 3%, whereas for Gulf Coast toads it is about 34%. The difference in numbers is a result of the call duration and rate. Cricket frogs produce brief pulsatile call notes of about 30 ms duration with a low duty cycle, whereas Gulf Coast toads have a call duration that is about 5 s. Individuals from both species appear to avoid overlap with conspecific callers. This is a general feature of communication in choruses and highlights a common strategy for hearing in noisy environments (see Feng and Ratnam, 2000; Gerhardt and Huber, 2002; Bee and Micheyl, 2008).

The localizer presented here also exploits the biological strategy of “listening in the gaps” to accurately estimate the location of a single dominant caller. It uses a time-domain cross-correlator that selects only those time frames where a single frog is vocalizing [e.g., Figs. 4B, 4D] while ignoring frames with more than one caller [Fig. 4C]. Stated another way, for single-caller frames the sensor covariance matrix R has unity rank. This strategy can be used in choruses that are more dense than the chorus studied here, as the following argument demonstrates.

Typically callers tend to attend to interfering callers in a local neighborhood while callers further away are ignored or remain unnoticed because they are greatly attenuated. Thus we can increase the likelihood of finding single-caller frames by restricting the analyses to data from subsets of sensors that are close together. Reducing the number of sensors in this way would reduce the spatial extent or coverage of the sensors, and restrict the chorus area to a neighborhood in the vicinity of the selected sensors (casting a “spotlight” on the neighborhood). The total energy from interfering sources that are further away is reduced. In these restricted neighborhoods, there is a greater likelihood of finding time windows where the call from a single individual dominates all other callers, and the covariance matrix from the selected subset of sensors will effectively have unity rank. Thus, dense choruses or arrays of large size can be analyzed by selectively restricting the array geometry during post-processing. For these reasons the array geometry (sensor placement) is not critical provided that the number of sensors in a subset is at least 4 or 5 (for locating in three dimensions) and they are not coplanar (Schmidt, 1972).

The localizer that has been implemented here employs a gradient-descent procedure and solves an unconstrained quadratic minimization problem to determine the intersection point of a locus of hyperboloids satisfying a given range difference. The exact procedure is not important, and any of a number of methods found in the literature can be employed. Nevertheless it should be kept in mind that as the number of sources and sensors becomes large, algorithm efficiency and computational speed become important. It may become necessary to refine the procedure by improving the initial estimate to bring it close to the global minimum (as suggested in Smith and Abel, 1987) or by pre-processing the data to select only those microphones that are closest to the source (i.e., microphones where the signal has the most energy). Further, once the set of single-source data frames have been identified, the localization can be parallelized to simultaneously extract all source locations as these operations are independent of one another. This report has not exmained issues of convergence nor has it tried alternate procedures or computational schemes. These are important problems for future work.

Certain factors constrain localization accuracy and the ability to resolve two sources located close to one another. For a single source, localization accuracy reduces as the source-to-array distance increases. Failure to accurately resolve two sources that are close to one another also occurs when the distance from the sources to the array increases. This is due to a reduction in the angular separation and hence relative time delay between two sources (as viewed from one of the sensors) with increasing distance, leading to misidentifying both callers as belonging to one source. Increasing the array aperture by spreading out the microphones can improve this, but the increased relative delay may reduce the beamformer’s ability to reject other sources during recovery, as is discussed further below. Enlarging the array by adding more sensors over more area can overcome both problems and can be used to cover arbitrarily large choruses. These tests are on-going.

The effect of source-sensor distance and angular separation between sources can be seen in the reported results. In Fig. 6A, cricket frogs 5 and 6 are much further away from the sensors than the remaining frogs. The location estimates for these frogs are more variable than for the remaining clusters (standard deviations are reported in Table 1). Similarly the toad cluster 4 shown in Fig. 6B represents a cluster of two toads. The area of analysis was a square 9 m wide. The cluster is shown at the right boundary (x=9) but this is because the algorithm projects all sources outside the selected area of analysis on to the boundary. In actuality the x-coordinate exceeded 9 m (see Table 1). Increasing the area of analysis beyond the 9 m² did not improve the accuracy nor did it resolve the two toads into their component sources (analysis not shown). In this case the toads could have been resolved by adding more microphones to the right of mics 2 and 3.

These examples illustrate that array geometry is not critical to the analyis, but it is important to provide adequate spatial coverage of the section of the chorus of interest. In this study, four microphones covered about 100 sq m, but this number depends on the elevation of the microphones and required spatial resolution. The preferred array geometry, placement, and trade-offs warrant further investigation, but the proposed methods can be applied to any microphone configuration.

The clustering procedure assigns a set of estimated locations to a given caller (i.e., the data frames P_i∊P to a single source i). The procedure is valid if the variance of source-location estimates are small in comparison with the inter-source spacing, and if the source is spatially stationary on the time-scale over which the cluster is determined. The data on the within-location and across-location variability can be inferred from Table 1. The callers did not exhibit significant movement over a cluster interval of about 1 min, and so this was the interval employed in the study. In other situations or for other species, the clustering interval may need to be established by trial and error before selecting a suitable time-frame for analysis.

Clusters were evaluated visually. This is readily performed even for several hours of data because it involves the selection of a bounding box for each individual, as shown in Fig. 5. However, an automated clustering algorithm can be implemented, for instance, by examining the histogram of locations for peaks, although it has not been tried here. This is an area for future work.

Estimation of steering vectors

To recover the individual vocalizations with little attenuation or distortion, the steering vectors must be estimated accurately. This was accomplished by a novel blind field steering-vector estimation that utilized only those time-frames where a single source was present. These frames were obtained from the localization step. The clustering procedure then assigned a unique source to every cluster. The steering vectors were evaluated from the sensor covariance matrix averaged over the cluster, and then they were normalized with respect to the microphone where the source had greatest power. The method provides a fast and accurate estimate of the steering vector.

Adaptive beamforming and source recovery

With known steering vectors the adaptive beamformer output recovers the individual frog vocalizations with little attenuation or distortion. While steering vectors are estimated only in the selected frames of data, the beamformer filters the entire data set based on the assumption that the steering vector does not change between frames. In other words, it makes the biologically plausible assumption that the source does not move in the intervening time intervals.

For widely separated frogs, there is little energy from the other callers in the beamformer output. However, nearby frogs are often only partially attenuated, resulting in interference (cross-talk) within a recovered channel. While the extent of cross-talk resulting from interfering sources is a measure of the beamformer performance, it is not easily evaluated because of the adaptive nature of the spatal filter (see Haykin, 2002, for a discussion). The performance depends on a number of factors including the steering vector, the temporal and spectral characteristics of the target and interfering sources, and the array geometry. Performance is therefore highly dependent on the context.

To illustrate the beamformer capabilities and some of the factors that can influence its performance, simulations were carried out with two sources located over a range of distances (Fig. 7). The recovery of the target demonstrates little or no self-cancellation [Fig. 7A, ○] and the extent of cross-talk is small (<−20 dB) for source separations larger than about 3–4 cm [Fig. 7A, ◻]. While the beamwidth is sharp, it reaches an apparent minima at about 0.1 m. This minima is due to the tonal nature of the Bv call which has a spectral peak around 1700 Hz corresponding to a half wavelength λ∕2≈0.1 m. At this separation the distinction between the steering vectors of the target and interferer is maximum and results in maximal attenuation or minimal cross-talk. For greater source separation, the attenuation reduces progressively because the increasing relative delays between microphones increase the intrinsic time-domain length of the optimal spatial cancellation filters. For practical reasons, these filters are limited to a (fixed) FFT length, and therefore there is an effective truncation of the filters that limits the beamformer performance.

Research into biologically inspired binaural beamformers for hearing aids has led to new methods that exploit some of the mechanisms found in the auditory system (Liu et al., 2000; Lockwood et al., 2004). These mechanisms enhance the performance of the beamfomer even with two microphones in complex cocktail-party scenes (Cherry, 1953) containing many simultaneous speech sources. This is a situation similar to that of a frog chorus.

A chorus contains a high density of spatially localized nonstationary interfering sources that exhibit time-frequency sparseness. That is, at any given instant energy is present only in a small region of time-frequency space. By exploiting the time-frequency sparseness of the target and interfering sources, the complex scene could be separated into individual time-frequency bins with much less overlap (Mohan et al., 2008). This makes it easier to identify the direction of sources and to beamform independently in these sparse channels to obtain improved cancellation of interference. The most efficient of these beamformers for small arrays, a particular frequency-domain MVDR beamformer implementation, combines very rapid independent adaptation in each time-frequency bin with low computational complexity (Lockwood et al., 2004). This implementation is particularly suited to the complex dynamics of a frog chorus. The rapidly varying nonstationarity and time-frequency sparseness of the frog vocalizations, the presence of many more frogs than microphones, and their small spatial separation combine to make the use of this particular adaptive beamformer very appropriate.

Monitoring choruses and future directions

The procedures outlined in this work can be used to monitor heterospecific choruses where the number of individuals exceeds the number of microphones. A total of 9 individuals from two species were localized. Large natural choruses can involve many more frogs and several species in breeding sites that exceed several thousand sq m. While there is variability in the size of natural choruses reported (see Sec. 1A), there is no doubt that the spatial extent of the chorus and the number of individuals reported here are small compared to many natural choruses. Thus, it is of interest to ask whether the methods can be applied to large choruses, and what are the limits on the chorus sizes that can be analyzed.

There are no clear answers to these questions at this time although they form the focus of on-going work. However, several features of the processing scheme should be noted in this regard.

• (1)The array is scalable. That is, more microphones can be added to increase the spatial extent of the array, and increase coverage of larger choruses. For example, in the scheme presented here, two additional microphones (say, mics 5 and 6) could have been added to the right of mics 3 and 4 to increase the coverage beyond x=9 m. The size of the array is only limited by practical considerations. The methods presented here are independent of the array size or geometry.
• (2)The analysis of a chorus does not require data from all microphones. As discussed earlier, there is much greater advantage in focusing or applying a spotlight to a neighborhood around a set of microphones. At a practical level this would mean ignoring data from microphones that are much further away from the neighborhood. A group of five microphones deployed as one module (in the configuration of an irregular polyhedron) would be adequate to cover a neighborhood around the module and localize in three-dimensions. More modules could be added to increase the array size.
• (3)The number of callers localized and separated 9 exceeded the number of microphones 4. This is a major advance, as blind source separation requires as many sensors as there are sources (Hyvarinen et al., 2001). By exploiting the time-frequency sparseness of the system and applying biologically motivated strategies, the processor is able to separate more sources than sensors. We have no data as yet on the upper limit on the number of sources that can be extracted by a fixed number of microphones. These tests are on-going. If we were to increase the number of microphone modules as suggested above, then in principle the processor could analyze larger choruses. This work is a step in that direction.

A significant drawback of the method is that it does not include multi-path propagation. As a result the cross-correlation function between pairs of sensors will demonstrate multiple peaks, and it may not be possible to determine the correct time delay without errors. We note that only time-delay estimation via cross-correlation is affected; the localizer and the beamformer are unaffected by multi-path propagation. Thus, a major future goal is to estimate the arrival-time differences to the microphones by incorporating multi-path propagation.