Analysis of flow-structure interaction in the larynx during phonation using an immersed-boundary method

Abstract

A recently developed immersed-boundary method is used to model the flow-structure interaction associated with the human phonation. The glottal airflow is modeled as a two-dimensional incompressible flow driven by a constant subglottal pressure, and the vocal folds are modeled as a pair of three-layered, two-dimensional, viscoelastic structures. Both the fluid dynamics and viscoelasticity are solved on fixed Cartesian grids using a sharp-interface immersed boundary method. It is found that the vibration mode and frequency of the vocal fold model are associated with the eigenmodes of the structures, and that the transition of the vibration mode takes place during onset of the sustained vibration. The computed glottal waveforms of the volume flux, velocity, and pressure are reasonably realistic. The glottal flow features an unsteady jet whose direction is deflected by the large-scale vortices in the supraglottal region. A detailed analysis of the flow and vocal fold vibrations is conducted in order to gain insights into the biomechanics of phonation.

INTRODUCTION

Flow-structure interaction (FSI) between the air expelled by the lungs and the vocal fold (VF) tissues is the essential process that generates sound. A high-fidelity model that describes the air∕VF interaction could complement experimental studies, thereby helping us understand the physics of voice production. It may also eventually help assess voice related pathologies.1 A number of mathematical models of different complexity have been developed in the past for describing the FSI during phonation. Among them, the spring-mass-damper models are frequently used to investigate various aspects of phonation, such as the chaotic motion and asymmetry in VF vibrations.2, 3 In addition to the lumped-mass approaches, models based on the continuum mechanics of either airflow or VF tissues, or both, have been developed to simulate the laryngeal dynamics. Using the finite-element method (FEM) for the structural dynamics, Berry and Titze4 studied the free vibration modes of a brick-shaped VF model. Berry et al.5 and Alipour et al.6 developed a two-∕three-dimensional (2D∕3D) hybrid FEM model of the VFs incorporating three tissue layers and the anisotropic material properties. Coupling this model with a 2D flow solver, they qualitatively compared the eigenmodes of the VF model with the vibration modes extracted from the FSI simulations. Recently, Thomson et al.7 used the 2D FEM simulations to study the energy transfer from the airflow to the VF during the FSI, and Tao and Jiang8 combined a 3D VF model and Bernoulli’s law to investigate the anterior-posterior biphonation phenomenon.

Much work has been devoted in studying the flow field close to the VFs, the gross characteristics of the flow, and the aerodynamic forces on the VF surfaces. For example, Alipour et al.6, 9 studied the glottal waveforms and flow separation in the glottis. Scherer et al.10, 11 studied the pressure within the glottis in both stationary and driven mechanical models. Rosa et al.12 presented a fully 3D model in which the dynamics of the three-layer and transversely isotropic VF was coupled with an incompressible flow solver to simulate the FSI. Using the model, the authors studied the phase difference in the VF tissue deformation and the effect of the false vocal folds (FVFs) on the pressure distribution over the laryngeal surfaces. Recently, Duncan et al.13 applied an immersed-boundary (IB) method to model the FSI and examined the vorticity around the glottal exit; Tao et al.3 considered a 2D viscous flow and a two-mass model to study the asymmetric glottal jet and VF vibration.

The unsteady vortex motion and turbulence are essential for the broadband noise in the human voice and thus have an important effect on the voice quality. It has also been argued that the fluctuating force produced by the vortex structures has direct impact on the VF dynamics, which in turn influences the flow and sound generation.14 Rich fluid dynamics has been reported in a few recent experimental studies. From their particle image velocimetry measurements of a pulsatile flow through a stationary VF model, Erath and Plesniak15 observed the cycle-to-cycle flipping of the glottal jet from one side of the VF to the other. Triep et al.16 found that the flow field downstream the VF model is highly three-dimensional, and the vortex structures in the flow have a frequency of five times higher than the fundamental frequency of the VF. In a self-oscillating physical model experiment, Neubauer et al.17 observed that the axis of the jet oscillates and exhibits an interesting wavy form. In addition, they found that the flow is marked by roll-up and convection of the large-scale vortices. Physical understanding of the phenomena reported in these works is still lacking. The asymmetry in the jet is often explained by the so called Coanda effect,3, 10, 15 i.e., the tendency of the jet to attach to one of the VF medial surfaces when the glottis has a divergent shape. However, it has been found that the parallel flow entering a suddenly enlarged channel through a slit without divergence is generally asymmetric at moderate Reynolds numbers due to the downstream recirculating flow.18 Therefore, a divergent shape of the glottis does not seem to be necessary for the flow to become asymmetric. Neubauer et al.17 hypothesized that the asymmetric flow observed in their experiments is induced by the vortices downstream from the VFs. This hypothesis appears to be more plausible considering that the glottal jet indeed experiences a sudden expansion after leaving the glottis and it is likely that the jet would interact with the downstream vortices. To examine the hypothesis and understand more general behavior of the vortex motions in the supraglottal area, a computational fluid dynamics (CFD) simulation that resolves the domain away from the VFs is necessary.

One of main challenges for the CFD study of phonation is that the complex∕moving geometry of the larynx is difficult to address. For this, Luo et al.19 recently developed an IB method to handle the complex boundaries for a class of FSI problems. In this method, both the incompressible Navier–Stokes equation governing the flow and the Navier equation governing the elasticity of the solid are solved on stationary Cartesian grids. Details of this method and its relevance to other variants of the IB methods available in literature are provided by Luo et al.19

The goal of the present paper is to extend the work of Luo et al.19 and to study the mechanism of the sustained vibration and the interaction between the glottal jet and the downstream unsteady vortices. Compared to the previous VF modeling research, the present work advances the continuum-based model using an efficient and accurate IB method and captures features of the VF vibration and glottal flow with a high level of detail. In addition, the authors will focus on the connection between the flow-induced vibration and the eigenmodes of the VFs for both the transient stage and sustained vibration. Although the relationship between the sustained vibration mode and the eigenmodes has been studied before and it was found that a particular eigenmode typically dominates the sustained vibration,5, 8 the issue has not been looked at for the transient vibration. The transient process is important as it may affect the voice onset qualities as perceived by experts.20 Furthermore, the authors will investigate the pressure distribution on the VFs and the role of pressure during the opening and closing phases of VF vibration. Generally speaking, the pressure does positive work on the VF during the opening phase and negative work during the closing phase. However, several factors such as the air∕tissue inertia and viscosity complicate the situation. Previously, linear stability analysis21, 22 has been used to examine the issue of pressure work. In another work by Thomson et al.,7 the authors found that the sign of the pressure work approximately corresponds to the glottal opening∕closing. They also found that the VFs rely on their own elasticity to recover their shape during the closing phase and an auxiliary pressure force does not exist. In the present work the authors will re-examine the role of pressure during both the opening and closure of the VFs.

SIMULATION SET-UP AND MODELING APPROACH

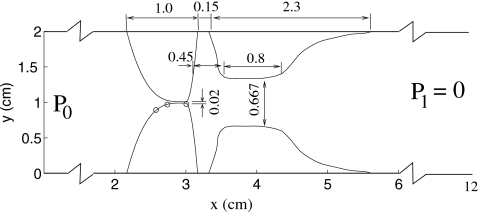
The 2D computational domain representing the coronal section of the larynx located at the VF anterior-posterior midplane is shown in Fig. 1. It consists of a straight channel, a pair of deformable true VFs, and a pair of rigid FVFs downstream the true VFs. The domain is symmetric about the centerline of the channel. The geometries of the true∕false VFs are chosen based nominally on the computed tomography scan data of a live person,19 and the dimensions of the various features are described in Fig. 1. The VFs have a three-layer structure including the cover, ligament, and body,6 as described in detail by Luo et al.19

Figure 1.

The 2D computational domain (to scale) including the true VFs and FVFs where the length unit is cm. The three points marked with circles on the lower VF are chosen for analysis of the VF vibration in Sec. 3.

The shortest distance between the two VFs along the medial surfaces is time-varying during the VF deformation and is defined as the glottal gap, denoted by d. In the simulations, a small threshold, d_min=0.02 cm, is set on the glottal gap between the two VFs to prevent the flow domain from being disconnected during the VF closure. A simple contact model is incorporated to handle the VF collision. Two collision lines are set at ±d_min∕2 off the midplane, which are non-penetrable and non-slippery for the VFs. When a point on the medial surface of one VF reaches the collision line of its side and tends to cross over, the VF is deemed to be in collision at the point. The contact point on the VF is then simply fixed on the collision line. As the VF starts to open, the kinematic constraint on the contact point is released. The VF is considered to be opening at the contact point if (1) the y velocity component at a selected point that is close to the contact point but located inside the VF points into the VF, and (2) the y force component on the VF surface at the contact point points out of the VF, meaning that the VF tends to “pull away” from the contact point while opening. For this contact model to be valid, both the asymmetry in the VF vibration and the VF movement in the inferior-superior direction during closure need to be small. The former condition is confirmed in the simulations presented in Sec. 3. The latter condition is valid as seen from the high-speed imaging of the VF vibration of the excised human larynx.23

The longitudinal stretching and 3D shear in the VFs during deformation due to anterior∕posterior attachment to cartilage cannot be directly incorporated into the current 2D model. The authors therefore choose a set of elastic constants so that the lowest eigenmodes of the VFs resemble the corresponding 3D modes in the midplane presented by Luo et al.19 where the physiological parameter ranges were adopted. In addition, the elastic constants are chosen so that when the subglottal pressure P₀ is in the physiological range, around 1 kPa, the glottal gap width would be in the physiological range too, i.e., on order of 1 mm. The viscoelastic model of the VFs is described by Luo et al.,19 and here the authors only give a summary of the material properties. Each of the three VF layers is isotropic, and the shear modulus is μ=10, 15, 5 kPa for the body, ligament, and cover, respectively. Poisson’s ratio, density, and viscosity for all three layers are ν=0.3, ρ_s=1.0 g∕cm³, and η=10 P. The lowest four eigenmodes for the chosen parameters are identical to those of Luo et al.,19 and the associated eigenfrequencies are 64, 151, 170, and 297 Hz. The eigenmodes have distinct patterns. The first mode corresponds to inclination of the VFs in the streamwise (x) direction, the second mode to stretching∕compression in the transverse (y) direction, and the third and fourth modes represent the higher-order deflection forms.

The viscous incompressible Navier–Stokes equations are discretized using a second-order, centered finite-difference scheme in space and a second-order Crank–Nicolson scheme in time. The boundary conditions for both the flow and linear viscoelasticity of the VFs are treated with an IB method, which is described in detail by Mittal et al.24 and Luo et al.19 A non-uniform grid of 288×256 points is used for domain discretization with the minimum grid intervals Δx=0.0234 cm and Δy=0.0078 cm, and the time step size is Δt=0.005 ms for all simulations. The system is deemed to have reached a stationary state if the variations in the VF vibration amplitude are within 1%. A refined simulation has been performed with the grid points around the VFs doubled and Δt reduced by half. The simulation shows that changes in all the characteristics listed in Table 1 are below 10% and therefore confirms that the results are effectively independent of the grid resolution and time step size.

Table 1.

Characteristics of the volume flux waveform, including the fundamental frequency, f, duration of the open phase T_o, rising and dropping time of Q during the open phase, T_p and T_n, and the ratios τ₀=T_o∕T, τ_s=T_p∕T_n, and q_r=Q_mean∕Q_max. The units are kPa for P₀, Hz for f, ms for T_o, T_p, and T_n, and cm²∕s for Q_max and Q_mean.

P0	f	To	Tp	Tn	Qmax	Qmean	τ0	τs	qr
0.8	162	4.74	2.55	2.19	405	180	0.77	1.16	0.444
1.0	163	4.43	2.40	2.03	545	248	0.72	1.18	0.456
1.2	164	4.43	2.47	1.97	755	314	0.73	1.26	0.416

RESULTS AND DISCUSSIONS

Three simulations were performed with the subglottal pressure at P₀=0.8, 1.0, and 1.2 kPa. These values are above the phonation threshold, which is found to be around 0.5 kPa for the present model,25 and they are within the physiological range.26 Different values are chosen here to ensure that the obtained results can be generalized to a range of subglottal pressures, from somewhat above the onset threshold to 2.4 times as high. The authors present the simulation results for the VF deformation and flow physics separately in Secs. 3A, 3B, 3C, 3D.

VF deformation

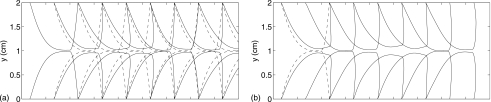
Figure 2a shows a series of snapshots of the VF deformation immediately after the subglottal pressure, P₀=1.2 kPa, is imposed at time t=0. Due to the finite slope of the subglottal surface of the VFs, the suddenly imposed pressure produces not only a pushing force in the streamwise direction on the VFs but also a compressive force in the transverse direction. As a result, the VFs are displaced in both the x and y directions, and the glottis starts to open due to the VF deformation. Meanwhile, the flow is accelerated through the glottis and a jet is formed, the dynamics of which will be discussed in detail later. In the subsequent cycles, the VFs oscillate in both the x and y directions. Close inspection reveals that the streamwise and transverse motions are close to the first and second eigenmodes of the VF model, respectively. In Fig. 2a, the frequency of the transverse deformation mode is approximately twice as high as the frequency of the streamwise deformation mode. This is indicated by the observation that the glottis opens and closes twice in one oscillation cycle. The VF deformation at this stage can be roughly described by the superposition of the two eigenmodes. The glottis formed by the two medial surfaces of the VFs changes shape, switching between convergent, straight, and divergent shapes. The convergent shape occurs when the closed VFs start to open from the subglottal side. From the eigenfunctions of the VFs,19 neither the first nor the second eigenmode of the VFs contains such a deformation pattern. Therefore, the convergent shape in the present case could be caused by excitation of higher eigenmodes such as the third and fourth eigenmodes, which display the convergent shape of the glottis.

Figure 2.

A series of snapshots (shifted in the horizontal direction by 0.5 cm) of the deformed VFs, spaced by 1.5 ms, for P₀=1.2 kPa. (a) Transient vibration starting from t=0 and (b) sustained vibration. The undeformed VFs are shown as dashed lines.

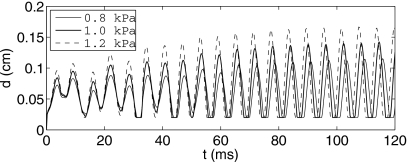
After a few cycles, the streamwise oscillation mode diminishes, and the VFs settle down to a displaced position in the x direction. Meanwhile, the transverse oscillation mode is amplified, and then this vibration mode is saturated and sustained for the cycles thereafter. Similar mode transition before the sustained vibration is also observed for P₀=0.8 and 1.0 kPa. Figure 3 shows the glottal gap width, d, defined as the minimal distance between the two VFs at any given instance, plotted against time for P₀=0.8, 1.0, and 1.2 kPa. In all cases, the glottal gap displays a transient stage that lasts for several cycles. The first few cycles contain double peaks, indicating that there are two oscillation frequencies present, which is consistent with the mode transition observed in Fig. 2a. During the transition, the gap width gradually grows and finally settles down to a nearly periodic motion. Overall, the observed transient behavior can be roughly explained from a point of view of a general dynamical system. If the authors consider the coupled flow∕VF an inhomogeneous system which is forced by the subglottal pressure and has a stable limit cycle, then the transient process can be viewed as a combination of the asymptotic decay of the initial condition and the asymptotic approach to the limit cycle. For the present system, both components of the process feature the eigenmodes of the VF structure. Finally, it should be pointed out that in this work, the authors only consider the situation where the VFs are initially at rest, and a constant subglottal pressure is suddenly imposed at t=0. In reality, the transient vibration can be complicated by the initial posture of the VFs and the pressure ramp in the trachea.

Figure 3.

Gap width between the VFs. d(t).

Figure 2b shows the self-sustained vibration pattern, demonstrated by a series of snapshots of the deformed VFs, for P₀=1.2 kPa. The maximum asymmetry in the deformation of the two VFs throughout the simulation is below 5% of the maximum glottal opening size. Therefore, the VF vibration is nearly symmetric. The glottis starts to open from the subglottal side as expected, and the two medial surfaces form a convergent shape blended in with the subglottal surfaces of the VFs. When the glottis is open, the majority portion of the medial surfaces forms either a straight or a divergent channel. Figure 2b shows that the glottis closes first from the subglottal side during the VF closing phase, which is consistent with the in vivo observation of the VF vibration26 and the simulation of Thomson et al.7 The geometric pattern of the glottis is an important topic in VF modeling, and the authors will discuss this issue in detail in Sec. 3C. As the subglottal pressure is raised, the mean displacement of the VFs in the x direction becomes larger. As a result, the glottal opening size is widened, allowing a higher volume flow rate. In addition, the divergence angle between the two VFs becomes larger during the opening phase due to the increased inclination of the VF body. In the present simulations, the maximum included angles are around 18°, 24°, and 26° for P₀=0.8, 1.0, 1.2 kPa, respectively.

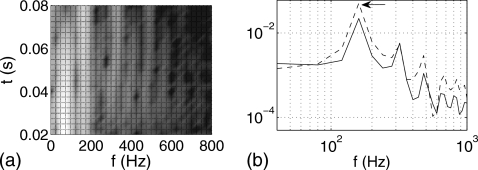
To better show the transient frequency components, the authors compute the time-frequency map of the x-displacement of the superior tip of the VFs using the short-time Fourier transform for the initial stage between t=0 and 100 ms. The map in Fig. 4a, where P₀=1.0 kPa, displays two frequency bands around 70 and 163 Hz, which are close to the first two eigenfrequencies of the VF model. It can be seen that the 70 Hz component decreases in time, while the 163 Hz component increases in time. For sustained vibration at the same P₀, the frequency spectra are shown in Fig. 4(b), where the highest peak in the figure (indicated by an arrow) corresponds to the fundamental frequency at f=163 Hz, and the smaller peaks correspond to the harmonics of the fundamental frequency. The fundamental frequencies at the two other subglottal pressure levels are given in Table 1 and are discussed in Sec. 3B. In all cases, the frequency is around 160 Hz and is slightly higher than the second eigenfrequency. During the stationary state (i.e., state of periodic vibration), the amplitude of the glottal gap width is d=1.17 mm for P₀=0.8 kPa, 1.42 mm for P₀=1.0 kPa, and 1.65 mm for P₀=1.2 kPa. These values are in the physiological range of human phonation where the amplitude is found to be on order of 1 mm.27

Figure 4.

(a) The time-frequency map during the transient stage. (b) The Fourier components of the x- (solid line) and y-coordinates (dashed line) of the VF superior tip during the sustained vibration.

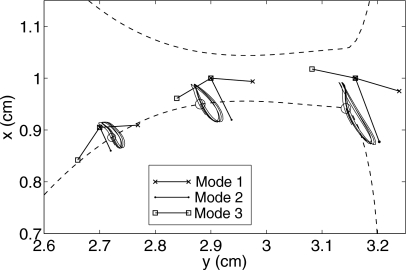
Figure 5 shows the trajectories of the three selected points on the VF surface (as seen in Fig. 1) during the stationary-state vibration for P₀=1.2 kPa. A similar approach of analysis has been adopted previously.28, 29 All three trajectories show a nearly elliptical shape, and the points on the trajectories travel in the counterclockwise direction. These trajectories are in qualitative agreement with the recent observation of the vibration pattern of an excised human larynx.23 Next to the ellipses are plotted the trajectories predicted by the first three eigenmodes of the VF model, which are simply straight lines. Note that the absolute lengths of the straight lines are arbitrary since the amplitude of the eigenmodes is undetermined. It can be seen that the elliptical trajectories are in general oriented along the lines corresponding to the second eigenmode, indicating that the flow-induced VF vibration pattern in the present case closely resembles this particular mode. The elliptical paths indicate that the deviation from the second eigenmode is mainly in the streamwise direction. This is caused by the streamwise oscillating load on the VFs during the VF opening∕closure. Furthermore, the trajectories during the FSI are not strictly periodic. The aperiodic motion is closely related to the unsteady vortex motion in the flow, which will be discussed in Sec. 3B.

Figure 5.

The trajectories of three selected points on the VF during the stationary-state vibration for P₀=1.2 kPa. The start point is marked by a circle. The straight lines indicate the trajectories predicted by the first three eigenmodes (shifted from the VF for clarity).

The typical pressure force on one of the VF surfaces during a stationary-state vibration cycle is shown in Fig. 6a for P₀=1 kPa. The shear stress has been neglected when calculating the aerodynamic load on the VFs. This is because the dimensional analysis indicates that the shear stress is about one to two orders of magnitude lower than the pressure force during the VF vibration. The pressure fluctuation (pressure subtracted by its local temporal mean) is also shown here. The force on the medial surface of the VF is found to vary significantly during the cycle. When the glottis opens [first two frames in Fig. 6a], the pressure within the glottis reduces rapidly to zero (i.e., the atmospheric pressure level) along the streamwise direction. As the glottis opens further, the force on the medial surface diminishes. During this stage, the pressure produces a nominally compressive load on the VFs, forcing the glottis to open. Detailed analysis of the role of pressure will be provided in Sec. 3C. When the glottis closes [right frame in Fig. 6a], the intraglottal pressure becomes negative, causing a local “pulling” force on the VF. On the subglottal surface of the VF, the pressure changes slightly around 1 kPa, while on the supraglottal surface, the temporal variation is notable.

Figure 6.

(a) Velocity of the VF, pressure (thin solid line), and pressure fluctuation (multiplied by 2, dashed line) during a cycle for P₀=1.0 kPa where the three frames are spaced by 1.5 ms. (b) Corresponding energy flow intensity. The pressure indentation into the VF means positive p, while the energy indentation means positive energy flow into the VF.

Glottal jet

Figure 7 shows the volume flux per unit spanwise length, Q=∫v₁dy, streamwise velocity v₁, and pressure p measured at the location x=3 cm on the centerline of the channel during the sustained vibration for the three cases. Note that the point of measurement is located within the glottis, as can be seen in Fig. 5. The volume flux has a pulsatile waveform whose amplitude increases as the subglottal pressure is raised. The statistical quantities of the volume flux are shown in Table 1. These quantities include the maximum and mean volume flow rate, Q_max and Q_mean, fundamental vibration frequency f=1∕T, where T is the period of 1 cycle, duration of the open phase T_o, rising time T_p and dropping time T_n of Q during the open phase, open quotient, τ₀=T_o∕T, skewness quotient, τ_s=T_p∕T_n, and the mean-to-maximum ratio of the volume flux, q_r=Q_mean∕Q_max. These quantities are either within the physiological range established in literature26 or consistent with previous numerical studies of phonation.13

Figure 7.

(a) The volume flow rate Q, (b) streamwise velocity v₁, and (c) pressure p at x=3.0 cm and y=1 cm, and (d) glottal gap width d during sustained vibration for P₀=0.8 (dashed line), 1.0 (solid line), and 1.2 kPa (dashed-dotted line).

As P₀ is raised from 0.8 to 1.2 kPa, the volume flux increases by 74%, from 180 to 314 cm²∕s, and Q_max increases by 86%, from 405 to 755 cm²∕s. However, f changes only slightly from 162 to 164 Hz. Therefore, the subglottal pressure within the range considered here has little effect on the fundamental frequency of the VF vibration, and the fundamental frequency primarily depends on the inherent frequency of the VF structure, in the present case, the second eigenmode. The present relative independence of f on P₀ at the moderate frequency and subglottal pressure is consistent with the observation of Zemlin26 and the simulations of Rosa et al.12 Recent experiments using excised canine larynges suggest that f has a nonlinear dependence on P₀.30 The discrepancy between the simulations here and the experiments is probably caused by the linear VF model assumed in the present work. Due to the nonlinear nature of the dynamics, the fundamental frequency is shifted from the eigenfrequency by 8%. The P₀=0.8 kPa case has the largest open quotient among the three, meaning that the glottis has the longest open time. The P₀=1.2 kPa case has the highest skewness quotient but the lowest mean-to-maximum volume flux ratio.

The fluid velocity at the centerline shown in Fig. 7b has a quick rise as the glottis opens and then increases at a slower rate. It reaches a maximum during the closing phase and then reduces rapidly to a minimum. As P₀ is raised, the fluid velocity during the open phase increases. In addition, P₀ has a significant effect on the waveform of the fluid velocity. For P₀=1.2 kPa, there is a second quick rise in the velocity before the flow is shut off. The intraglottal pressure shown in Fig. 7c drops continuously during most of the open phase, and its minimum is well below zero. As P₀ is raised, the amplitude of the pressure oscillation increases, and the pressure waveform is also somewhat modified. The velocity and pressure waveforms presented here are qualitatively in agreement with the theoretical estimates by Titze.31 In addition, the waveform of the fluid velocity is consistent with the experimental measurements of a mechanically driven model by Krane et al.32 Finally, the general trends of the glottal pressure and velocity agree with the waveforms measured in excised canine larynges [e.g., Figs. 8(b) and 8(c) in Ref. 33]. Quantitative differences, however, do exist and are most likely due to the particular choices of the present VF geometry and material properties.

Throughout the VF vibration, the jet exhibits time-varying asymmetry and may attach itself to either one of the FVFs (Fig. 8). A similar phenomenon was also observed in previous experiments and numerical simulations.3, 10, 15, 19 As noted by Luo et al.,19 the steady channel flow with a sudden expansion is known to bifurcate in its solution at a critical Reynolds number that depends on the expansion ratio.18 Beyond the bifurcation point, the symmetric solution becomes unstable, and the steady flow becomes asymmetric even though the geometry is symmetric. In the present simulations, the peak Reynolds numbers based on the flow rate are Re_Q=(3∕2)Q_max∕ν_a=304, 409, and 566 for P₀=0.8, 1.0, and 1.2 kPa, respectively, and the corresponding Reynolds numbers based on the centerline velocity and channel width are Re_c=4813, 5625, and 6375. These Reynolds numbers are much higher than the critical Reynolds number at the present expansion ratios.18 Therefore, the observed flow asymmetry is a natural effect of the present larynx model. Further discussion on this issue is provided in Sec. 3D.

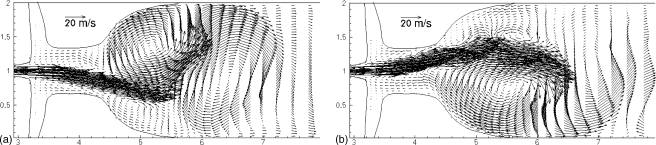
Figure 8.

Two typical instantaneous flow fields for P₀=1.2 kPa.

The downstream flow during the stationary-state vibration is dominated by asymmetric and unsteady vortex motions, as seen in Fig. 8 where two snapshots of typical instantaneous velocity field downstream the FVFs are shown for P₀=1.2 kPa. For clarity, the velocity vectors from every four grid points in the x direction and every five points in the y direction are shown. In Fig. 8a, there are a pair of large counter-rotating vortices downstream the FVFs that are staggered in the channel. The jet downstream the VFs is clearly deflected by the two vortices. Between the FVFs, smaller vortices can be seen, and the jet is directed toward one of the FVFs. The large vortices in the channel evolve in time, changing their size and center locations, and some of them are strengthened by the jet. Consequently, the downstream portion of the jet changes its shape and appears to be flapping. Away from the glottis, the jet core is widened due to the momentum exchange between the jet core and the ambient fluid. As the VFs close, the mean flow diminishes, but the flow in the supraglottal region continues to circulate due to the inertial effect. During this period, the smaller vortices in the flow may disappear due to the viscous dissipation or merge into larger vortices. The surviving vortices will affect the jet behavior in the next cycle. Figure 8b shows the velocity field from another cycle where the jet is diverted toward the other FVF by a clockwise vortex and attaches to that FVF. In all the cycles, the skewness of the jet in the region between the FVFs is relatively persistent for the cycle, while downstream the FVFs, the jet skewness changes rapidly due to the jet-vortex interaction.

Flow separation is of interest during phonation as it significantly affects the pressure distribution on the VF surfaces.3, 34 Since the glottis may form a divergent channel in the open phase, the flow between the two VFs may separate from the medial surfaces. This phenomenon was studied in the numerical simulations of the stationary VF model10 and in the experimental study of the glottal jet.17 In the present simulations, flow separation from the medial surfaces is observed for P₀=1.0 and 1.2 kPa. For P₀=0.8 kPa, recirculation within the glottis is not obvious. The separation zone usually appears between the jet and the medial surface of one VF when the jet is deflected toward the other VF. Throughout the simulation, the location of the separation point and size of the separation zone vary according to the shape of the glottis and deflection of the jet. For example, when the VFs close, the separation point moves from the medial surface to the glottal exit, and in next cycle, it may re-appear on the same side of the glottis or switch to the other side. The similar time-varying separation was also reported in the experimental observation by Neubauer et al.17

Pressure work and energy

Some laryngoscopic studies26 suggest that the glottis may change from a convergent shape during the opening phase to a divergent shape during the closing phase. This vibratory feature has been adopted into many previous VF modeling works, especially those employing two-mass models,3 which necessarily generate a phase difference between the aerodynamically driven mass and the passively following mass. In Ref. 7, the authors argued that a convergent-divergent pattern is necessary for a net amount of energy to be transferred from the fluid to the VFs during a whole vibration cycle and thus for the VFs to maintain the passive vibration. According to their argument, the convergent glottis during the VF opening maintains an intraglottal pressure which is higher than the pressure at the glottal exit and does positive work to the VFs, and the divergent glottis during the VF closing maintains a lower intraglottal pressure which does less amount of work to the VFs than during the opening phase. This temporal asymmetry in the pressure ensures that the net energy flow to the VFs in one full cycle is positive.

In the present simulations, the stationary-state VF vibration pattern also contains a convergent-divergent pattern. Note that, as shown in Fig. 2b, a portion of the glottis forms a convergent shape during the opening phase that is blended in with the subglottal surface. However, as pointed out by Titze,31 the air inertia may be another factor to produce the similar pressure asymmetry to sustain the energy flow. In agreement with his theory, Fig. 7 shows that the fluid velocity in the glottis is not completely in phase with the glottal gap width. When the glottis opens at the beginning of a cycle, the velocity of the subglottal fluid lags behind the glottal gap due to the inertia of the subglottal fluid as well as the resistance from the supraglottal fluid. Similarly, during the closing phase, the fluid velocity does not drop concurrently with the glottal gap since the already-established jet tends to maintain its momentum. In fact, Fig. 7b shows that the intraglottal velocity reaches its maximum when the VFs close. This assertion on the role of the fluid inertia is in line with the argument by Krane et al.32 in explaining their experimental measurement of the glottal velocity at the centerline, which has a similar waveform as shown in Fig. 7b. Corresponding to the velocity waveform, the intraglottal pressure is not in phase with the glottal gap width but is high during the opening phase and low during the closing phase, as suggested in Figs. 6a, 7c. In conclusion, a convergent-divergent vibration mode may not be necessary to maintain the net energy transfer to the VFs or the sustained vibration.

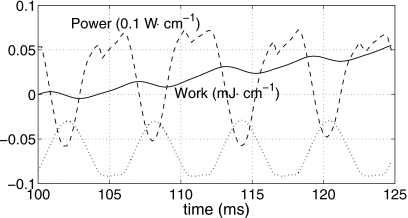
To show the energy transfer between the flow and VFs, the authors compute the total power and work done on one of the VFs by the flow pressure during the sustained vibration. The work done by the shear stress on the VF surface has been neglected since it is very small compared to the work done by the pressure.7 Figure 9 shows that the difference of the work between any two points separated by a full cycle period is always positive, indicating that positive net energy is transferred from the flow to the VF. Note that alternatively one could analyze the work done by the pressure fluctuation [shown in Fig. 6a] only, as the net work done by the temporal mean pressure is zero. The rate of the work varies its sign and is not in phase with the glottal gap width d. During the VF closure and early stage of the following opening phase, the power to the VF is positive, meaning that the VFs are forced to deform. The typical velocity of the VFs and the corresponding pressure distribution at this stage are shown in the left frame of Fig. 6a, and the corresponding energy flow intensity (the dot product of the pressure force and VF velocity) is shown in the left frame of Fig. 6b. The power is computed by integrating the energy flow intensity over the entire VF surface. The power later becomes negative for a time period that involves both the opening phase and closing phase (Fig. 9). During the time period, the pressure force works against the VFs, either preventing them from further deformation or delaying their elastic recoil. It is interesting that the power in Fig. 9 reaches a negative minimum when the glottis has nearly maximum opening. To explain this, the authors plot the velocity of the VF and the pressure load when the glottal gap width reaches its maximum, as shown in the middle frame of Fig. 6a. It can be seen that the VF continues to deform even when d reaches its maximum value, and the subglottal surface of the VF moves against the high pressure, which results in a negative energy flow into the VF [middle frame of Fig. 6b].

Figure 9.

Work (solid line) and the rate of work (dashed line) done to one of the VFs by the flow pressure during the sustained vibration for P₀=1.0 kPa. The glottal gap width d is represented as the thick-dotted line (shifted in ordinate for clarity).

During the late stage of the closing phase, the power to the VF becomes positive again (Fig. 9). This indicates that the pressure force assists the VFs to close. The typical VF velocity, pressure force, and energy flow at this stage are shown in the right frames of Figs. 6a, 6b. Note that beside the medial surface, where the energy flow intensity is positive, there is a significant part of the subglottal surface where the energy flow is positive. That is, the VFs are being pulled at the medial surface while being pushed at the subglottal surface. Therefore, the VFs close not only under the interior elastic recoil but also with the assistance of the pressure. This role of the pressure was not observed by Thomson et al.7 In their simulations, Thomson et al. found that overall, the pressure force never assists the VFs during closure even though there is a negative pressure locally at the medial surface pulling the VFs. To reconcile the difference between the results here and Thomson et al., the present authors point out that the geometric model of the VFs here is significantly different from that of Thomson et al., and as a result, the subglottal surface of their VF model has less movement compared to the present model during the vibration. In conclusion, the exact role of pressure in the VF vibration depends on the chosen model, and it is possible that the pressure force works cooperatively with the elastic force in the VFs to close the glottis.

Mechanism for the flow asymmetry

In the present study, both the geometry of the larynx model and VF material properties are symmetric, but the glottal jet and downstream vortices exhibit highly asymmetric behavior. The attachment of the flow to one of the VF medial surfaces and deflection of the jet core have been observed in both experiments and numerical simulations.3, 10, 15 However, this asymmetry was explained by some of the authors as resulting from the so called Coanda effect.3, 15 According to the argument, when the flow goes through the glottis with a divergent cross section, the fluid trapped between the main stream and one of the VF surfaces is entrained to move, and the evacuating effect combined with the high pressure on the other side of the flow would deflect the flow and attach it to the VF. However, the present simulations show that the jet flow can be severely deflected even when the flow is symmetric within the glottis, as seen in Fig. 8. In addition, the largest curvature of the deflected jet is not in the glottis but somewhere downstream in the supraglottal region. Therefore, the result here is more consistent with the study of the steady symmetric inflow entering a sudden expansion by Drikakis,18 where the flow with the expansion ratio of 10 becomes asymmetric at a very low critical Reynolds number Re_Q=26. According to Drikakis,18 the critical Reynolds number decreases as the expansion ratio is increased. His result suggests that the downstream flow confined by the channel plays a key role in the flow asymmetry. Details of the flow structures presented in the present work reveal that the jet has a strong interaction with the vortices generated due to the confinement of the channel walls. During the interaction, the upstream portion of the jet is deflected by the vortices toward either wall of the FVFs, and the downstream portion displays a wavy form. On the other hand, the jet may strengthen the vortices and cause them to roll up. As a result, the skewness of the jet is time-varying within one vibration cycle, and especially further downstream, the curvature of the jet varies drastically due to the rapid evolution of the unsteady vortices. Note that the similar jet∕vortex interaction is expected to occur in a corresponding 3D flow, even though the details may be different from those presented in Sec. 3B due to the 3D vortex structures. Durst et al.35 showed that a 3D flow over a plane symmetric sudden expansion also becomes asymmetric above a critical Reynolds number. Given that the jet Reynolds number of the glottal flow varies during a vibration cycle, the extent of flow asymmetry should also change, leading the 3D jet to oscillate.

The wavy pattern and flapping motion of the jet have been reported by Neubauer et al.17 in their experimental visualization of the flow downstream a self-oscillating VF model where the Reynolds number and channel expansion ratio are much higher than those in the present work. Therefore, the present findings are consistent to their results. Neubauer et al.17 hypothesized that the jet asymmetry is induced by the flow structures downstream from the VFs. This hypothesis is confirmed by the numerical simulations in this work.

CONCLUSIONS

A recently developed IB method implemented on fixed Cartesian grids is used to solve the governing equations for both the incompressible flow and linear viscoelasticity of the VF model. Compared to the previous research on phonation modeling, the present work advances the use of continuum-based model by using an accurate and efficient method and captures features of the VF vibration and glottal flow with a high level of detail. The transient vibration during onset, the role of pressure in energy transfer, and the oscillatory behavior of the glottal jet have been focused on in this study.

The simulations were performed with three different subglottal pressure levels above the phonation threshold. Self-sustained vibrations of the VFs initially at rest are obtained, and the temporal patterns of the glottal opening and measures of the intraglottal velocity and pressure are reasonably realistic. The results show that the VF vibration undergoes a distinct transition at the start of phonation. The transient stage is dominated by the mode that closely resembles the first mode identified in the eigenmode analysis, whereas the stationary state is identified more closely with the second eigenmode. As expected, the net work done by the flow pressure to the VFs is positive in one vibration cycle. However, the pressure plays distinct roles during different phases of a cycle, and it may promote the VF closure during the closing phase.

The flow structures reveal that in the downstream region away from the VFs, the flow is dominated by unsteady large-scale vortices. The glottal jet interacts with these vortices, and consequently, the direction of the jet is deflected and displays dramatic cycle-to-cycle oscillation. In addition, the downstream part of the jet in the present model appears as a wavy form due to the counter-rotating vortex pairs, and its shape is rapidly altered by the vortices.

Although the present work is limited to a 2D study and the 3D effect is not incorporated, it sheds light on the mechanism of selecting a particular vibration mode from several structural eigenmodes by the nonlinear FSI process and also on the complex flow behavior. Work is currently underway to investigate the corresponding issues in 3D models.