Probabilistic finite element analysis of radiofrequency liver ablation using the unscented transform

Abstract

The main limitation of radiofrequency (RF) ablation numerical simulations reported in the literature is their failure to provide statistical results based on the statistical variability of tissue thermal–electrical parameters. This work developed an efficient probabilistic approach to hepatic RF ablation in order to statistically evaluate the effect of four thermal–electrical properties of liver tissue on the uncertainty of the ablation zone dimensions: thermal conductivity, specific heat, blood perfusion and electrical conductivity. A deterministic thermal–electrical finite element model of a monopolar electrode inserted in the liver was coupled with the unscented transform method in order to obtain coagulation zone confidence intervals, probability and cumulative density functions. The coagulation zone volume, diameter and length were 10.96 cm³, 2.17 cm and 4.08 cm, respectively (P < 0.01). Furthermore, a probabilistic sensitivity analysis showed that perfusion and thermal conductivity account for >95% of the variability in coagulation zone volume, diameter and length.

1. Introduction

Radiofrequency ablation is a commonly used technique for the treatment of localized tumors in liver, with increasing application in other organs such as kidney, bone, lung, adrenal gland and prostate (Gervais et al 2000, Goldberg and Dupuy 2001, McTaggart and Dupuy 2007, Vanderschueren et al 2002).

Deterministic finite element method (FEM) models of RF hepatic ablation have been used extensively to examine the factors that affect ablation zone shape and dimensions, to investigate different algorithms of energy deposition, and to assist in the development of new electrodes (Berjano 2006, Chang and Nguyen 2004, Haemmerich and Wood 2006, Liu et al 2006, 2007, Schutt and Haemmerich 2008). Numerical simulations of RF ablation rely on previously measured thermal–electrical properties of liver tissue, which are inherently variable and uncertain. The measured properties are subject to patient-to-patient variability, site-to-site variability and measurement errors. Consequently, the uncertainties in the measured parameters lead to uncertainties in the simulation results, and reduce the reproducibility of the ablation procedure.

Although the uncertain nature of the thermal–electrical properties of liver tissue is documented (Duck 1990, Gabriel et al 1996, Haemmerich et al 2006, Valvano et al 1985, Van Beers et al 2001), examinations of the influence of these uncertainties in RF ablation are notably absent in the literature. In fact, only in vitro and in vivo experiments provided some statistical parameters regarding ablation zone measurements, e.g., mean and standard deviation. However, previous experimental works did not provide information about the influence of the variability of the thermal–electrical parameters on the variability of the ablation dimensions. In fact, this would be a very difficult task since one would have to measure the thermal–electrical parameters of several tissue samples before using the same samples to perform the ablation experiments. However, this information would be crucial in order to improve current RF ablation techniques and equipment. Conversely, to date, all computer simulations of ablation procedures use one of the two approaches. The first one is a purely deterministic method, in which the thermal and electrical tissue properties are treated as single-value parameters. While this approach is useful to enhance the understanding of the physical process, it has a severe limitation. The underlining assumption for applying this method is that one has to know with absolute accuracy all the thermal and electrical parameters of the simulation domain, which (as mentioned above) cannot be achieved due to both tissue intrinsic tissue variability and measurement errors. Hence, treating each parameter as a single value provides one estimate of tissue temperature and the ablation zone with no data on variance that takes into consideration the known variabilities of tissue properties.

The second approach considers variability of the tissue parameters by varying each parameter by a certain amount (+/−) around the average value (Chang and Nguyen 2004, Liu et al 2006, 2007, Schutt and Haemmerich 2008, Tungjitkusolmun et al 2000). The limitations of this approach are: (1) it does not account for the interaction between the parameters, and (2) it does not give statistical information such as confidence intervals or a probability density function.

In the current study, we used probabilistic tools in order to quantify the variability of the ablation zone dimensions based on the variability of tissue properties. This requires the consideration of uncertainties in the computer simulations; i.e., the parameters are treated as random variables. One way to achieve this is via the Monte Carlo technique (Papoulis 1991), where a large set of random parameter values are used as input parameters to the simulation. This method is not feasible here, as the Monte Carlo approach utilizes several hundred thousand simulations and a single RF ablation simulation typically takes on the order of an hour to complete. Other possible statistical approaches include the first-order-second-moment (FOSM) method with the TLM technique (Ajayi et al 2007), or approaches based on the reduction of the Monte Carlo minimal set (Arulampalam et al 2002). This set is usually constructed from selection of random samples with appropriate characteristics.

In the current study, we used the unscented transform (UT) (Julier and Uhlmann 2004) to approximate a nonlinear mapping by a set of selected points (sigma points), which are deterministically chosen. The expected value and variance of the mapping are available through a weighted average of the deterministically selected points. The UT method was used in combination with FEM computer models in order to investigate the effect of the varying liver tissue properties: specific heat, thermal conductivity, perfusion and electrical conductivity. The goals of this study were:

1. Develop a method based on the UT to determine the extent to which uncertainties in tissue properties affect the coagulation zone during hepatic RF ablation,

2. Determine the probability density function of the coagulation zone dimensions, and

3. Statistically quantify the influence of each tissue property on coagulation zone dimensions and identify the most significant properties.

2. Methods

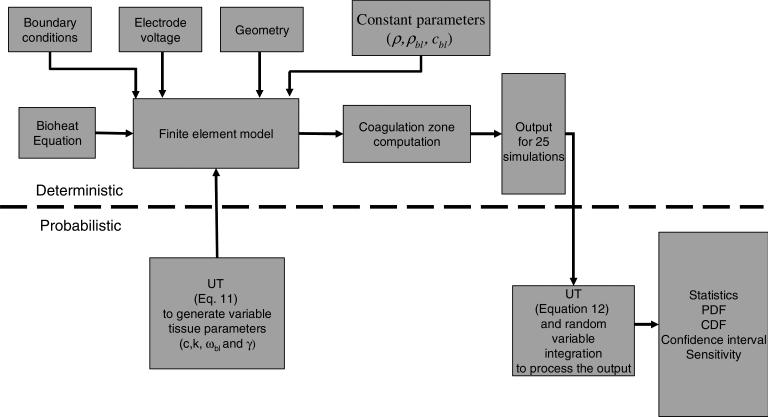
Figure 1 shows an overview of the methods employed in this study and how they are integrated. The top side of the picture shows the deterministic part of the approach, in which the components are the bioheat equation, the FE model and the coagulation zone computation. The bottom side of the picture represents the probabilistic part of the approach, in which the UT is used both to generate the input parameters for the FE model and to obtain the statistical parameters.

Figure 1.

Graphical representation of the probabilistic finite element method based on the unscented transform.

This section is organized as follows. Section 2.1 shows the deterministic model for simulation of RF ablation based on the FEM. In section 2.2, we present the probabilistic method, which includes the UT and the statistics of the tissue parameters.

2.1. Deterministic model

2.1.1. Bioheat equation

We used the Pennes bioheat equation (Pennes 1948) (equation (1)) to model the heating of the tissue during RF ablation:

$$\rho c\frac{\partial T}{\partial t}=\nabla \cdot k\nabla T+\mathbf{J}\cdot \mathbf{E}-{\rho }_{bl}{c}_{bl}{w}_{bl}(T-T_{bl})+Q_m$$ (1)

where ρ is the tissue density (kg m⁻³), c is the specific heat (J kg⁻¹ K⁻¹), k is the thermal conductivity (W K⁻¹ m⁻¹), J is the electric current density (A m⁻²), E is the electric field intensity (V m⁻¹), ρ_bl is the density of blood, c_bl is the heat capacity of blood, ω_bl is the blood perfusion (s⁻¹), T_bl is the basal temperature of blood (K), and Q_m (W m⁻³) is the metabolic heat source, which was neglected since its effect is small when compared to the heat produced by RF energy (Berjano 2006).

2.1.2. Finite element model

We used PATRAN 2005 r2 (The MacNeal-Schwendler Co., Los Angeles, CA) to create the model geometry, mesh and boundary conditions. The software generated data files suitable for use with ABAQUS/STANDARD 6.5 FEM solver software (Hibbitt, Karlsson & Sorensen, Inc., Pawtucket, RI). We used the built-in POST module in ABAQUS for postprocessing to create profiles of the electric potential, temperature and thermal damage integral.

We modeled an internally cooled needle electrode (Cool-tip, Valleylab, Boulder, CO) with an active length of 30 mm. We used a two-dimensional axisymmetric model due to the geometry of this electrode. The electrode was placed at the edge of a block of liver tissue 170 mm high with a radius of 100 mm. The node spacing of the mesh generated by the PATRAN software varied from 0.1 mm (near the electrode) to 4 mm (at the distal edge). The model had 18 000 nodes and 36 000 elements. We verified that no errors were introduced due to the mesh size using convergence tests.

In all simulations, RF power was applied for 12 min. We then simulated a 1 min post-ablation period without internal cooling flow or applied RF power to allow the coagulation zone to form in the region immediately adjacent to the electrode.

During RF ablation, an applied alternating electric field causes tissue heating due to both resistive heating and dielectric losses. At radiofrequencies, however, dielectric losses are negligible (Berjano 2006), and we can determine the resulting electric field in the tissue from Laplace's equation:

$$\nabla \cdot \gamma \nabla V=0,$$ (2)

where γ is the electrical tissue conductivity (S m⁻¹), and V represents the electric potential (V). We assumed the ground potential at the outer model boundary, and applied a varying potential at the electrode; potential was adjusted via a proportional-integral (PI) controller with a target maximum temperature (at the hottest node) of 105 °C.

The initial temperature of all elements and the distal boundary temperatures were set at 37 °C. To simulate the internal cooling of the Cool-tip electrode, a boundary condition of 10 °C (typically seen during clinical procedures with a chilled coolant) was applied to the entire electrode shaft.

2.1.3. Coagulation zone computation

To determine the boundaries of each simulated coagulation zone, we utilized an Arrhenius damage model as shown in (3), where thermal damage Ω(t) is related to the expected cellular survival fraction (4):

$$\Omega \left(t\right)={\int }_0^{t}A{\mathrm{e}}^{-\Delta E∕RT\left(\tau \right)}\mathrm{d}\tau ,$$ (3)

$$\Omega \left(t\right)=-\ln (c\left(t\right)∕c\left(0\right)),$$ (4)

where A is the frequency factor (2.984 × 10⁸⁰ s⁻¹ ΔE is the activation energy (5.064 × 10⁵ J mol⁻¹), T(τ) is the absolute temperature as a function of time, c(t) represents the concentration of living cells as a function of time, and c(0) is the initial concentration of living cells. The values for ΔE and A in equation (3) were previously shown to accurately predict the cell death boundary in an animal model when used with a threshold value of 4.6 for Ω(t) (corresponding to 1.0% cell survival). The volume, short axis (maximum diameter) and long axis (maximal length) of the ablation zone for each simulation were determined from the thermal damage profile using this threshold value.

2.2. Probabilistic model

2.2.1. Theoretical background: unscented transform

This section will give an outline of the UT since it is not generally well known. Any numerical solution procedure involving one or more random variables may be understood as a nonlinear mapping of those variables. Therefore, the statistical characterization of the calculated solution involves the calculation of its statistical moments. This simplifies the problem of quantifying the resulting uncertainty to one of calculating the moments of the solution. In general, the nth order moment of a nonlinear mapped random variable is calculated with (5)

$$E\left\{g{\left(\widehat{x}\right)}^n\right\}=\int g{\left(x\right)}^{n}p\left(x\right)\mathrm{d}x,$$ (5)

where g(x) is the nonlinear mapping function, and p(x) is the probability density function of the random variable $\widehat{x}$.

The UT may also be understood as a discrete approximation of the integral presented in (5). This integral can be calculated in an optimal sense using orthogonal polynomials. The procedure is known as the Gaussian quadrature. Therefore, the integral is approximated by (6)

$$E\left\{g{\left(\widehat{x}\right)}^n\right\}=\int g{\left(x\right)}^{n}p\left(x\right)\mathrm{d}x=\int f\left(x\right)w\left(x\right)\mathrm{d}x\approx \sum _i{w}_{i}f\left(S_i\right),$$ (6)

where f(x) is a nonlinear function (in this case f(x) = g(x)ⁿ), S_i are specially determined points for the integration (sigma points), and w(x) is a weight function (in this case w(x) = p(x)).

The weights and normalized sigma points for the zero-mean Gaussian probability distribution are shown in (7) (de Menezes et al 2008). These parameters were calculated solving (6) up to the forth moment:

$$\begin{array}{cc}\hfill w_0& =\frac{2}{3}{S}_0=0\hfill \\ \hfill w_1& =\frac{1}{6}{S}_1=\sqrt{3}\hfill \\ \hfill w_2& =\frac{1}{6}{S}_2=\sqrt{3}.\hfill \end{array}$$ (7)

Therefore, in the case of a X̄ mean with σ standard deviation Gaussian distribution, the expected value (first moment) and variance (second central moment) of the mapped random variable are shown in (8):

$$\begin{array}{cc}\hfill \stackrel{‒}{G}& =\frac{2}{3}G\left(\stackrel{‒}{X}\right)+\frac{1}{6}G(\stackrel{‒}{X}+\sigma \sqrt{3})+\frac{1}{6}G(\stackrel{‒}{X}-\sigma \sqrt{3})\hfill \\ \hfill {\sigma }_G^2& =\frac{2}{3}{[G\left(\stackrel{‒}{X}\right)-\stackrel{‒}{G}]}^2+\frac{1}{6}{[G(\stackrel{‒}{X}+\sigma \sqrt{3})-\stackrel{‒}{G}]}^2+\frac{1}{6}{[G(\stackrel{‒}{X}-\sigma \sqrt{3})-\stackrel{‒}{G}]}^2.\hfill \end{array}$$ (8)

The multiple random variables case is also modeled by the UT (de Menezes et al 2008). It is possible to include either independent or correlated variables. Although the approach allows modeling correlated variables, it is best to calculate the sigma points for independent random variables. Once these points are known, it is a matter of linear transformation using a covariance matrix.

In such cases, the choice of sigma points and weights is not unique, and it is usually necessary to use additional sigma points. In the case of Gaussian distributions, one set of normalized sigma points is the combination of coordinates of the edges of a four-dimensional cube and its axis (2⁴ + 2 × 4 = 24 combinations). In addition, we have one more sigma point at the center of the cube that represents the parameters average values. One particular set of interest also allows a simple calculation of the statistics of the marginal distributions as shown in (9) and (10):

$$\begin{array}{cc}\hfill & S_{\text{edges}}=(\pm 1,\pm 1,\pm 1,\pm 1)\sqrt{3}\hfill \\ \hfill & S_{\text{axis}}=\{\begin{array}{cc}(\pm 1,0,0,0)\sqrt{3}\hfill & \hfill \\ (0,\pm 1,0,0)\sqrt{3}\hfill & \hfill \\ (0,0,\pm 1,0)\sqrt{3}\hfill & \hfill \\ (0,0,0\pm 1)\sqrt{3}\hfill & \hfill \end{array}\phantom{\}}\hfill \end{array}$$ (9)

$$\begin{array}{cc}\hfill & w_{\text{edges}}=\frac{1}{144}\hfill \\ \hfill & w_{\text{axis}}=\frac{1}{9}.\hfill \end{array}$$ (10)

This set of sigma points has the same normalized value as the one-dimensional case and has different weights that allow the calculation of the full statistical behavior.

2.2.2. Unscented transform in a FEM model for RF ablation

In the case of the FEM modeling of RF ablation, the nonlinear mapping function G is actually the simulation output itself. Specifically, it represents the profile, diameter, length and volume of the coagulation zone. The random variables X₁, X₂, X₃ and X₄ are input variables for the FE model. Since each of the variables will be characterized from a particular known distribution with a known expected value and standard deviation, the process of calculating the mapped sigma points is simply the simulation of the same problem with different input variables (X₁, X₂, X₃ and X₄). In the four-random-variables situation, this results in a set of 25 simulations. The bioheat equation has four dominant random variables, which are equivalent to the tissue properties discussed above: c (X₁: specific heat), k (X₂: thermal conductivity), γ (X₃: electrical conductivity) and w_bl (X₄: perfusion). Each has an average value (${\stackrel{‒}{X}}_1$, ${\stackrel{‒}{X}}_2$, ${\stackrel{‒}{X}}_3$ and ${\stackrel{‒}{X}}_4$) and a standard deviation (σ₁, σ₂, σ₃ and σ₄). Considering the Gaussian distribution for each variable, it is straightforward to calculate the necessary de-normalized sigma points using (11). The values in (11) along with the average values are the input parameters for the FE simulation:

$$\begin{array}{cc}\hfill & S_{\text{edges}}=({\stackrel{‒}{X}}_1\pm {\sigma }_1\sqrt{3},{\stackrel{‒}{X}}_2\pm {\sigma }_2\sqrt{3},{\stackrel{‒}{X}}_3\pm {\sigma }_3\sqrt{3},{\stackrel{‒}{X}}_4\pm {\sigma }_4\sqrt{3})\hfill \\ \hfill & S_{\text{axis}}=\{\begin{array}{cc}({\stackrel{‒}{X}}_1\pm {\sigma }_1\sqrt{3},{\stackrel{‒}{X}}_2,{\stackrel{‒}{X}}_3,{\stackrel{‒}{X}}_4)\hfill & \hfill \\ ({\stackrel{‒}{X}}_1,{\stackrel{‒}{X}}_2\pm {\sigma }_2\sqrt{3},{\stackrel{‒}{X}}_3,{\stackrel{‒}{X}}_4)\hfill & \hfill \\ ({\stackrel{‒}{X}}_1,{\stackrel{‒}{X}}_2,{\stackrel{‒}{X}}_3\pm {\sigma }_3\sqrt{3},{\stackrel{‒}{X}}_4)\hfill & \hfill \\ ({\stackrel{‒}{X}}_1,{\stackrel{‒}{X}}_2,{\stackrel{‒}{X}}_3,{\stackrel{‒}{X}}_4\pm {\sigma }_4\sqrt{3}).\hfill & \hfill \end{array}\phantom{\}}\hfill \end{array}$$ (11)

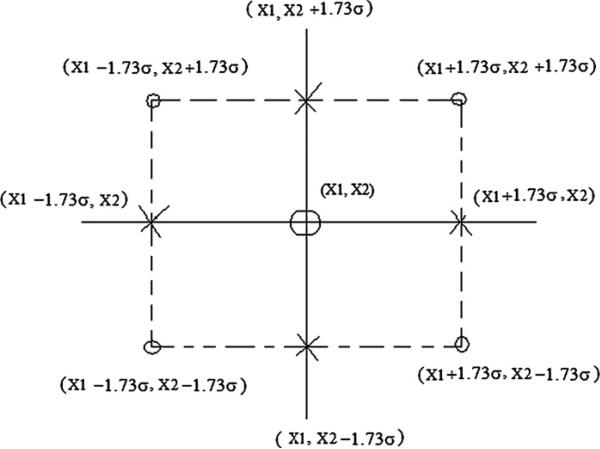
The calculation of the sigma points for the multiple random variable case may be exemplified in a two-random-variables example. The graphical representation is shown in figure 2. In this instance, there are four sigma points for the edges, four sigma points for the axis (and the central sigma point):

$$\begin{array}{cc}\hfill & S_{\text{edges}}=\{\begin{array}{cc}({\stackrel{‒}{X}}_1+\sigma \sqrt{3},{\stackrel{‒}{X}}_2+\sigma \sqrt{3})\hfill & \hfill \\ ({\stackrel{‒}{X}}_1+\sigma \sqrt{3},{\stackrel{‒}{X}}_2-\sigma \sqrt{3})\hfill & \hfill \\ ({\stackrel{‒}{X}}_1-\sigma \sqrt{3},{\stackrel{‒}{X}}_2+\sigma \sqrt{3})\hfill & \hfill \\ ({\stackrel{‒}{X}}_1-\sigma \sqrt{3},{\stackrel{‒}{X}}_2-\sigma \sqrt{3})\hfill & \hfill \end{array}\phantom{\}}\hfill \\ \hfill & S_{\text{axis}}=\{\begin{array}{cc}({\stackrel{‒}{X}}_1+\sigma \sqrt{3},{\stackrel{‒}{X}}_2)\hfill & \hfill \\ ({\stackrel{‒}{X}}_1-\sigma \sqrt{3},{\stackrel{‒}{X}}_2)\hfill & \hfill \\ ({\stackrel{‒}{X}}_1,{\stackrel{‒}{X}}_2+\sigma \sqrt{3})\hfill & \hfill \\ ({\stackrel{‒}{X}}_1,{\stackrel{‒}{X}}_2-\sigma \sqrt{3}).\hfill & \hfill \end{array}\phantom{\}}\hfill \end{array}$$ (12)

Figure 2.

A set of sigma points for the two-random-variables case with means X₁ and X₂ and standard deviation σ . The combination uses four edge sigma points [(X₁ + 1.73σ , X₂ + 1.73σ), (X₁ + 1.73σ, X₂ − 1.73σ), (X₁ − 1.73σ, X₂+1.73σ), (X₁ − 1.73σ, X₂ − 1.73σ)], four axis sigma points [(X₁ + 1.73σ, X₂), (X₁ − 1.73σ, X₂), (X₁, X₂ + 1.73σ), (X₁, X₂ − 1.73σ)] and a central sigma point [(X₁, X₂)].

Once all the de-normalized mapped sigma point values are calculated, the expected value and variance are calculated using (13)

$$\begin{array}{cc}\hfill & \stackrel{‒}{G}=w_{\text{central}}G\left(S_{\text{central}}\right)+\sum _{\text{edges}}{w}_{\text{edges}}G\left(S_{\text{edges}}\right)+\sum _{\text{axis}}{w}_{\text{axis}}G\left(S_{\text{axis}}\right)\hfill \\ \hfill & {\sigma }_G^2=w_{\text{central}}{[G\left(S_{\text{central}}\right)-\stackrel{‒}{G}]}^2+\sum _{\text{edges}}{w}_{\text{edges}}{[G\left(S_{\text{edges}}\right)-\stackrel{‒}{G}]}^2+\sum _{\text{axis}}{w}_{\text{axis}}{[G\left(S_{\text{axis}}\right)-\stackrel{‒}{G}]}^2.\hfill \end{array}$$ (13)

The expected value is the most likely result. If a large number of simulations were performed with varying input parameters, the expected value would be the average result. It divides the output probability distribution into two equal parts.

The UT is based on a polynomial approximation for an arbitrary mapping. This allows a simple form of calculation of the probability density function. The Jacobian approach to calculating a mapped distribution function requires the inverse function of the mapping. Since the UT uses a polynomial to approximate the mapping, the problem is reduced to a root-finding procedure. The case of the second-order approximation has a closed-form representation for the Gaussian probability density function (PDF). The results of the mapping are three points: $G(\stackrel{‒}{X}-\sqrt{3}\sigma )$, $G\left(\stackrel{‒}{X}\right)$ and $G(\stackrel{‒}{X}+\sqrt{3}\sigma )$. The coefficients of the polynomial are shown in (14):

$$\begin{array}{cc}\hfill a_0& =G\left(\stackrel{‒}{X}\right)\hfill \\ \hfill a_1& =\frac{1}{2\sqrt{3}}[G(\stackrel{‒}{X}+\sqrt{3}\sigma )-G(\stackrel{‒}{X}-\sqrt{3}\sigma )]\hfill \\ \hfill a_2& =\frac{1}{6}[G(\stackrel{‒}{X}+\sqrt{3}\sigma )-2G\left(\stackrel{‒}{X}\right)+G(\stackrel{‒}{X}-\sqrt{3}\sigma )].\hfill \end{array}$$ (14)

The resulting probability density distribution is calculated by (15) for the one-parameter case:

$$p\left(G\right)=\frac{1}{\sqrt{2\pi }}\left\{\frac{{\mathrm{e}}^{-\frac{1}{2}{\left[\frac{1}{2}\frac{-a_1+\sqrt{a_1^2-4a_2{a}_0+4a_{2}G}}{a_2}\right]}^2}}{\sqrt{a_1^2-4a_2{a}_0+4a_{2}G}}+\frac{{\mathrm{e}}^{-\frac{1}{2}{\left[\frac{1}{2}\frac{-a_1-\sqrt{a_1^2-4a_2{a}_0+4a_{2}G}}{a_2}\right]}^2}}{\sqrt{a_1^2-4a_2{a}_0+4a_{2}G}}\right\}.$$ (15)

The procedure described in (14) and (15) is well suited for problems with one random variable. However, the thermal ablation problem is a multivariate case. Therefore, the algorithm for the determination of the output PDF is summarized as follows:

1. Calculate mapped de-normalized sigma points (in this problem, there are 25 points).

2. Using the Moore–Penrose pseudoinverse, calculate the coefficients of the second-order polynomial (shown in (18)).

3. Generate the total probability density for all four random variables using the polynomial calculated in (b).

4. Integrate the total probability density with respect to all four variables resulting in a univariate cumulative density function (CDF) of the volume, length, diameter and coagulation zone.

5. Differentiate the CDF to obtain the PDF of the volume, diameter and length.

2.2.3. Sensitivity analysis

A numerical problem with several random variables may be well characterized by a smaller subset of variables. To calculate the effect of each variable, we determined the marginal distributions. These distributions are essentially one-variable distributions, where the calculation is performed for each variable separately using (8). The resulting expected value and variance provide information on the significance of each of the variables.

From the marginal expected value and variance we can estimate the importance of each variable as well as identify any interaction between variables.

We can characterize the influence of each random variable on the variance. Since the UT is based on a Taylor approximation of the nonlinear mapping, the calculation of the marginal statistical moments provides a good estimate of the influence of each parameter in the output result. The second-order approximation of the nonlinear variable is

$$g\left(x\right)=a_0+a_{1}x+a_2{x}^2.$$ (16)

Therefore, in the case of a zero-mean Gaussian distribution, the second central moment (variance) of the mapped function is

$$E\left\{g{\left(x\right)}^2\right\}-E{\left\{g\left(x\right)\right\}}^2=a_1^2{\sigma }_x^4+2a_2^2{\sigma }_x^2.$$ (17)

The second-order approximation of the four-random-variables case is

$$\begin{array}{cc}\hfill & g(X_1,X_2,X_3,X_4)=a_0+a_1{X}_1+b_1{X}_2+c_1{X}_3+d_1{X}_4+c_{x_1{x}_2}{X}_1{X}_2+c_{x_1{x}_3}{X}_1{X}_3+c_{x_1{x}_4}{X}_1{X}_4\hfill \\ \hfill & +c_{x_2{x}_3}{X}_2{X}_3+c_{x_2{x}_4}{X}_2{X}_4+c_{x_3{x}_4}{X}_3{X}_4+a_2{X}_1^2+b_2{X}_2^2+c_2{X}_3^2+d_2{X}_4^2.\hfill \end{array}$$ (18)

The second central moment (variance) of the mapping in the case that all variables are zero-mean random variables is

$$\begin{array}{cc}\hfill & E\left\{g{(X_1,X_2,X_3,X_4)}^2\right\}-E{\left\{g(X_1,X_2,X_3,X_4)\right\}}^2\hfill \\ \hfill & =a_1^2{\sigma }_{x_1}^4+2a_2^2{\sigma }_{x_1}^2+b_1^2{\sigma }_{x_2}^4+2b_2^2{\sigma }_{x_2}^2+c_1^2{\sigma }_{x_3}^4+2c_2^2{\sigma }_{x_3}^2+d_1^2{\sigma }_{x_4}^4+2d_2^2{\sigma }_{x_4}^2+c_{x_1{x}_2}^2{\sigma }_{x_1{x}_2}^2{\sigma }_{x_1}^2{\sigma }_{x_2}^2\hfill \\ \hfill & +c_{x_1{x}_3}^2{\sigma }_{x_1}^2{\sigma }_{x_3}^2+c_{x_1{x}_2}^2{\sigma }_{x_1}^2{\sigma }_{x_4}^2+c_{x_2{x}_3}^2{\sigma }_{x_2}^2{\sigma }_{x_3}^2+c_{x_2{x}_4}^2{\sigma }_{x_2}^2{\sigma }_{x_4}^2+c_{x_3{x}_4}^2{\sigma }_{x_3}^2{\sigma }_{x_4}^2.\hfill \end{array}$$ (19)

Therefore, the influence I of each parameter in the variance is given by (20)

$$I_{x_n}=\frac{E\left\{g{\left(X_n\right)}^2\right\}-E{\left\{g\left(X_n\right)\right\}}^2}{E\left\{g{(X_1,X_2,X_3,X_4)}^2\right\}-E{\left\{g(X_1,X_2,X_3,X_4)\right\}}^2},$$ (20)

where E{g(X_n)²} − E{g(X_n)}² is the variance of the marginal distribution related to the X_n variable, and E{g(X₁, X₂, X₃, X₄)²} − E{g(X₁, X₂, X₃, X₄)}² is the variance of the distribution. Equation (19) provides a second-order estimate of} the effect of each input parameter on the variance of the final result.

The estimation of the effects of each variable in the variance allows minimization of the number of random variables necessary to characterize a particular problem. In fact, the estimate of the influence of each variable shown in (19) is a good indicator of how to reduce the number of input variables. As in the previous case, this approach may be extended to any number of random variables.

The marginal variance was calculated using (13) for each variable. In this calculation, the other variables are considered to be fixed at their average values. It is important to note that this approach models accurately the interaction effects of multiple variables. Such information is difficult to obtain when the individual variations of different variables are performed. In addition to the improved accuracy, the UT provides with useful probability distribution information that allows the determination of the confidence intervals of the solution.

2.2.4. Statistical properties of the thermal and electrical tissue properties used in the FEM

The four random variables examined in this study were liver thermal conductivity, specific heat, electrical conductivity and blood perfusion. A number of studies have measured the thermal and electrical parameters of liver tissue (Duck 1990, Gabriel et al 1996, Haemmerich et al 2006, Valvano et al 1985, Van Beers et al 2001). Those studies reported both the mean and standard deviation of the measurements. We modeled the thermal conductivity and specific heat as temperature-dependent parameters. We used a reported value of blood perfusion in normal human liver tissue (Van Beers et al 2001). Each probabilistic variable was modeled assuming a Gaussian distribution.

Table 1 shows the values of the variable thermal and electrical properties used in our simulations. The constant parameters (see (1) and figure 1) ρ, ρ_bl and c_bl are 1060 kg m⁻³, 1000 kg m⁻³ and 4180 J kg⁻¹ K⁻¹, respectively. The perfusion and electrical conductivity of the liver tissue were modeled as temperature-independent parameters since there are no statistical data of the influence of the temperature on these parameters.

Table 1.

Thermal–electrical properties.

Property	Relationship	Coefficients		References
k (W m−2 K−1)	k = k0 + k1T	k0 (mean = 0.4692, sd = 0.13)	k1 = 0.001 161	(Nahirnyak et al 2006, Valvano et al 1985)
c (J kg−1 K−1)	c = c0, T < 63.5 c = c0 + c1(T - 63.5), T ≥ 63.5	c0 (mean = 3399.9, sd = 522.34)	c1 = 28.9	(Haemmerich et al 2006)
wbl (s−1)	wbl = w0	w0 (mean = 0.018, sd = 0.005)	N/A	(Van Beers et al 2001)
γ (S m−1)	γ = γ0	γ0 (mean = 0.3, sd = 0.075)	N/A	(Gabriel et al 1996)

Based on (11) and the data from table 1, we simulated 25 RF ablations. Table 2 shows the variable parameters used in each simulation.

Table 2.

De-normalized sigma points used in the simulation.

	Sigma points					Sigma points
N°	k0 (W m−2 K−1)	c0 (J kg−1 K−1)	w0(s−1)	γ0 (S m−1)	N°	k0 (W m−2 K−1)	c0 (J kg−1 K−1)	w0(s−1)	γ0 (S m−1)
1	0.4692	3399.9000	0.0180	0.3000	14	0.2440	4304.6194	0.0267	0.4299
2	0.4692	4304.6194	0.0180	0.3000	15	0.2440	4304.6194	0.0093	0.4299
3	0.4692	2495.1806	0.0180	0.3000	16	0.2440	4304.6194	0.0267	0.1701
4	0.6944	3399.9000	0.0180	0.3000	17	0.2440	4304.6194	0.0093	0.1701
5	0.2440	3399.9000	0.0180	0.3000	18	0.6944	2495.1806	0.0267	0.4299
6	0.4692	3399.9000	0.0180	0.4299	19	0.6944	2495.1806	0.0093	0.4299
7	0.4692	3399.9000	0.0180	0.1701	20	0.6944	2495.1806	0.0267	0.1701
8	0.4692	3399.9000	0.0267	0.3000	21	0.6944	2495.1806	0.0093	0.1701
9	0.4692	3399.9000	0.0093	0.3000	22	0.2440	2495.1806	0.0267	0.4299
10	0.6944	4304.6194	0.0267	0.4299	23	0.2440	2495.1806	0.0093	0.4299
11	0.6944	4304.6194	0.0093	0.4299	24	0.2440	2495.1806	0.0267	0.1701
12	0.6944	4304.6194	0.0267	0.1701	25	0.2440	2495.1806	0.0093	0.1701
13	0.6944	4304.6194	0.0093	0.1701

3. Results

3.1. Coagulation zone

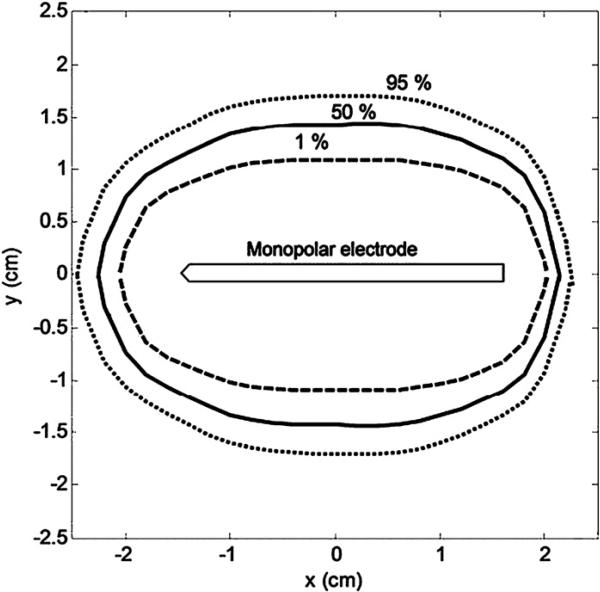
Figure 3 shows the confidence intervals for the coagulation zone dimensions. We plotted the coagulation zone for 1%, 50% and 95% confidence. The average value of the short-axis diameter (maximum measured along the y-axis) was 2.87 cm (range 2.17 (1%) to 3.42 cm (95%)). The average value of the long-axis length (maximum along the x-axis) was 4.40 cm (range 4.08 cm (1%) to 4.71 cm (95%)). These values agree with empirical works reported elsewhere (Mulier et al 2003).

Figure 3.

Coagulation zone dimensions for the 1%, 50% and 95% confidence intervals. For clarification purposes, only the active part of the electrode is shown.

In order to generate the 1%, 50% and 95% curves in figure 3, we segmented the coagulation zone boundaries into 50 points. After that, we obtained the CDF's for each point and calculated the 1%, 50% and 95% confidence coagulation zones.

3.2. Coagulation volume and dimensions

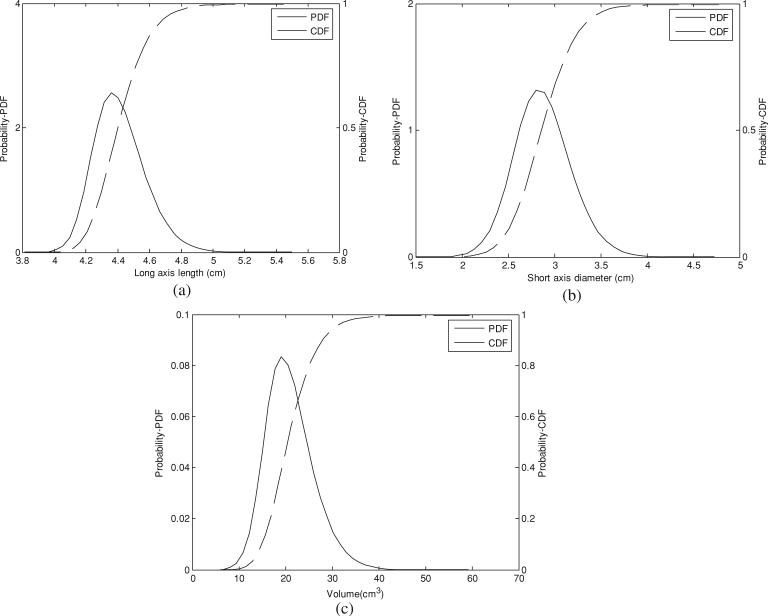
The coagulation zone volume had an approximate mean of 20.52 cm³ and a standard deviation of 5.03 cm³. The probability and cumulative density functions of the coagulation long axis, short axis and volume are shown in figure 4. From the CDFs we determined the confidence interval, which was 10.96 cm³ (P < 0.01).

Figure 4.

Probability density function and corresponding cumulative density function: (a) long-axis length, (b) short-axis diameter and (c) volume.

3.3. Sensitivity

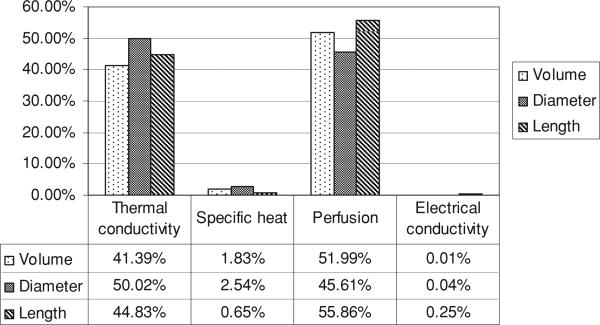
We evaluated the influence of each parameter on the variation of the ablation zone volume, long-axis length and short-axis diameter. Figure 5 shows the influence of each thermal–electrical parameter on the variability of the coagulation zone accordingly (20).

Figure 5.

Influence of each parameter on the variability of the coagulation zone.

4. Discussion

Deterministic FEM models are widely used for predicting coagulation zone dimensions created during RF ablation (Berjano 2006, Chang and Nguyen 2004, Haemmerich and Wood 2006, Liu et al 2006, 2007, Schutt and Haemmerich 2008). However, deterministic simulations provide only a single set of results that do not provide any information on the uncertainty associated with variation of the thermal and electrical tissue parameters. This uncertainty in tissue parameters stems in part from variations between patients and measurement locations, as well as measurement errors.

In this study, we employed a probabilistic approach based on the UT to calculate the expected variation in resulting coagulation zone dimensions due to the uncertainties in tissue parameters. We used the FEM to simulate RF ablations with varied thermal conductivity, specific heat, perfusion and electrical conductivity, with the resulting coagulation zone dimensions providing the input data for the probabilistic model.

Figure 3 shows the confidence interval for the ablation zone. Note that the variation in the short axis is of considerable size, while the long-axis value falls within a very small range; this finding has important implications when planning tumor ablation, in that the uncertainty in the short axis is more likely to result in insufficient coagulation zones.

Figures 4(a)–(c) show the PDF and CDF for the coagulation zone long axis, short axis and volume. From this figure we can obtain several important statistical parameters such as confidence interval, mean and standard deviation. However, it should be noted that we considered variation of tissue properties based on data from normal liver tissue, and results may vary if tumor properties (most of which are currently unavailable in the literature) are considerably different from normal tissue.

Another issue examined in this study was the individual contribution of each tissue parameter to coagulation zone dimensions, quantified in figure 5. It is also important to note that beyond this influence, there is also the cross-effect between the individual variables. The calculation of these effects showed that their influence is of the order of the electrical conductivity. Thus, notably almost all of the variability seen in the coagulation zone can be attributed to variations in tissue perfusion and thermal conductivity. While prior studies have shown the significant effect of tissue perfusion on the size of the coagulation zone (Liu et al 2007, Schutt and Haemmerich 2008), the fact that thermal conductivity variation affects the coagulation zone dimensions to a similar extent is a new finding for hepatic ablation. Moreover, since the variation in electrical conductivity and specific heat has only minor contributions toward ablation zone dimensions, variation of these two properties could be neglected, thereby reducing the number of required computer simulations from 25 to 9 if the UT method is used (figure 2). However, it is worth noting that any parameter might play a bigger role in the variation of the ablation zone if artificially varied, e.g., increasing electrical conductivity (e.g. via saline infusion) or reducing the blood perfusion (e.g. via pharmacologic modulation).

An important application of our findings could be the improved treatment planning of ablation procedures. If tissue perfusion and thermal conductivity at the target ablation site could be measured before the procedure, these data would allow for patient- and location-specific prediction of the resulting coagulation zone dimensions, aiding physicians in guidance of the procedure.

5. Conclusion

Statistical probabilistic models combined with computational simulations allow for estimating the confidence intervals of coagulation zone dimensions based on variability of tissue parameters. This tissue parameter variability has considerable impact on coagulation zone dimensions, but only tissue perfusion and thermal conductivity have major contributions.