Coherent X-ray diffraction from collagenous soft tissues

Abstract

Coherent X-ray diffraction has been applied in the imaging of inorganic materials with great success. However, its application to biological specimens has been limited to some notable exceptions, due to the induced radiation damage and the extended nature of biological samples, the last limiting the application of most part of the phasing algorithms. X-ray ptychography, still under development, is a good candidate to overcome such difficulties and become a powerful imaging method for biology. We describe herein the feasibility of applying ptychography to the imaging of biological specimens, in particular collagen rich samples. We report here speckles in diffraction patterns from soft animal tissue, obtained with an optimized small angle X-ray setup that exploits the natural coherence of the beam. By phasing these patterns, dark field images of collagen within tendon, skin, bone, or cornea will eventually be obtained with a resolution of 60–70 nm. We present simulations of the contrast mechanism in collagen based on atomic force microscope images of the samples. Simulations confirmed the ‘speckled’ nature of the obtained diffraction patterns. Once inverted, the patterns will show the disposition and orientation of the fibers within the tissue, by enhancing the phase contrast between protein and no protein regions of the sample. Our work affords the application of the most innovative coherent X-ray diffraction tools to the study of biological specimens, and this approach will have a significant impact in biology and medicine because it overcomes many of the limits of current microscopy techniques.

Coherent X-ray Diffraction (CXD) imaging is a promising tool for the study of different systems in the nano and micro scales, where speckled diffraction patterns are inverted using an iterative phasing algorithm to obtain an image of the sample. Over recent years, significant advances have been made in the imaging of a large range of objects, including small particles and nanocrystals (1–5). However, most of the studied cases correspond to nonbiological systems, with a few notable exceptions such as Escherichia coli bacteria (6), freeze-dried yeast cell (7), the mineral phase in bone (8), unstained viruses (9), and human chromosome (10). There are severe limitations to the application of CXD to biological samples: one is the evident radiation damage that the samples suffer under the X-ray beam. However, this problem can be overcome by several strategies, depending on the sample characteristics, such as cryo-cooling for unique samples, or by recording a number of patterns from multiple virtually identical samples, the last corresponding to the approach to tackle single molecule imaging in the future free electron lasers. Yet some biological samples can withstand the minimum radiation dose required for their coherent imaging, as we have found it is the case for collagen from rat tail tendon (see Results and Discussion).

A second limitation arises from the fact that in most of the CXD inversion algorithms there is implicit some form of real space constraint, of which the most powerful is probably the “support” constraint, whereby all of the scattering density of the sample is known to be bounded by a finite, well-defined volume of space. The support constraint means that there is a maximum spatial frequency present in the diffraction pattern, so it can be ‘oversampled’ by using fine enough pixels on the X-ray detector (11). There is good experience with successful inversion of such oversampled diffraction patterns for a range of samples, both in forward scattering (1, 2, 5–10) and by Bragg diffraction (3, 4, 12). From the experimental point of view, the support constraint implies the sample being smaller than the illuminating coherent beam. The latest undulator-based sources of synchrotron radiation offer considerable improvements in beam coherence over their predecessors: transverse coherence lengths in the μm range are routinely available with sufficient coherent flux to carry out a variety of diffraction experiments. X-ray optics can allow tradeoffs in the spatial extent of a beam once it has been made coherent by using an aperture. However, the lateral coherence of the X-ray beams is limited to some microns, which limits also the maximum size of the particles/samples that can be imaged by the support constraint-based CXD methods. Images from biological specimens need to extend over a large range of scales, even up to whole organs; therefore the traditional CXD imaging methods are not feasible with these samples.

Several approaches have been developed for the objects that do not comply with a support constraint. Coherent diffraction methods can still be used to image these objects if a piece of the sample can be cut out with some sort of aperture (as performed in Fig. 1). This has been demonstrated for a number of systems, typically looking at domain structures in materials such as magnets, ferroelectric domains, charge density waves, etc. (13, 14). With very few exceptions, these patterns have been found not to be invertible using the algorithms that work for small objects with supports. One exception is the innovation of Eisebitt et al. (15) who included in the sample design a reference pinhole within the coherence length; the resulting interference pattern is then directly invertible as a hologram.

Fig. 1.

Coherent X-ray diffraction pattern obtained from a rat tail tendon sample with an aperture of 10 μm × 10 μm. The bottom image is a zoom over the first meridional reflection, 1/67 nm⁻¹, showing a rich speckled structure.

Ptychography is a recent computational innovation (16) to get around the apparent inability to invert coherent diffraction patterns from continuous objects under finite illumination from an aperture. The method consists of combining diffraction patterns from overlapping regions of a sample, often using a raster scan of the coherent probe beam. Since the diffraction from two overlapping regions partly contains the same information, there is a constraint on the phases of both patterns. A successful algorithm, based on iterative Fourier transforms and a suitable ‘updating’ function, has been proposed by Rodenburg et al. (17) for recovering those phases. The method has the particular advantage of not being limited in spatial extent (field of view) by the inherent beam coherence length, since the raster can be made arbitrarily wide. To date, ptychography has only been successful for complete forward scattering patterns, so a motivation for the study described here is to obtain suitable data by Bragg diffraction and verify the similarity of the diffraction patterns of overlapping probed regions of a sample. Moreover, the fact that ptychography overcomes the support constraint limitation makes this method the ideal candidate for applying CXD to biological samples such as collagen-based or cellulose-based tissues.

Collagen is the most abundant protein in the animal kingdom. It is a highly hierarchical biomaterial: tropocollagen molecules, ca. 300 nm long and 1.5 nm in diameter, self-assemble in staggered arrays, fibrils of ≈100 nm diameter, which subsequently form collagen fibers (1 μm diameter). Collagen materials are very well ordered at the nanoscale as a result of their hierarchical packaging from molecule to fiber, with a paracrystalline supermolecular structure (18–20). The packing gives rise to a periodic axial banding (in the range of 64–69 nm) of the structure known as D-banding (21). Collagen plays an important role in many biological tissues such as bone, tendon, teeth, skin, and cartilage (22–26). The mechanical properties of these tissues are intimately associated with the distribution and structure of the collagen matrix within the tissue. Despite significant research effort over the past years (18–30), many questions about the nanostructure of these tissues remain open. Moreover, defects on the collagen scaffold of these tissues are associated in most cases with diseases (such as bone loss in osteoporosis, skin fibrosis or cornea malfunctions). Therefore, the ability to produce images of the bulk of these tissues with nanometre resolution will offer possibilities for biology and medical sciences; however, currently available imaging methods, such as optical confocal, electron, and atomic force microscopy (AFM) are not, for a number of reasons, ideally suited for this purpose.

X-ray ptychography using synchrotron radiation is a powerful alternative because high resolution images with bulk information can be obtained from samples with little preparation. Furthermore, collagen offers a particular attraction for dark-field imaging. Since the diffraction signal is contained within a relatively confined region of reciprocal space due to the relatively high order in the collagen hierarchical nanostructure (18–20), it can be separated to a great degree from all other contributing matter. Such an imaging method would be specific to just the collagen parts of a complex tissue structure in 3D, with sensitivity to the distribution and orientation of the collagen fibrils. We demonstrate here just the first step of this potential imaging technique: that suitable speckled X-ray diffraction patterns can be obtained from a soft collagen-containing tissue, namely tendon, implying that these innovative coherence-based methods can be used with such samples.

An important issue for biological samples is whether the CXD information can be extracted with sufficient statistics before the onset of radiation damage. Marchesini et al. (31) have discussed the issue extensively and it has also been considered for electron diffraction by Henderson (32). Howells et al. (33) concluded that there is a minimum dose required for a general sample that is needed to achieve an image with a certain resolution. Conflicting with that, there is a second curve documenting the dose accumulated by a sample that will extinguish the diffraction data at each resolution. The two curves are found to cross at about 10 nm feature resolution, implying that individual objects cannot be imaged beyond that resolution. The argument concerning the required dose assumes that the sample is disordered, so exceptions are to be expected for ordered materials. Collagen is particularly favourable in this regard because of its native ordered nanostructure: the regular D-banding confines the diffraction orders into narrow rings at 67 nm spacing (Fig. 1). The collagen samples from rat tail tendon examined here are additionally ordered by alignment with the tendon axis, which further narrows the powder ring into two arcs of a few degrees wide (depending on the sample quality). Our work demonstrates that sufficiently long exposures can be performed before the onset of radiation damage in rat tail tendon to obtain high quality coherent diffraction patterns. The methodology could be adapted and extended to other biological specimens in the near future.

Results and Discussion

Speckle Patterns from Collagen-Rich Soft Tissues.

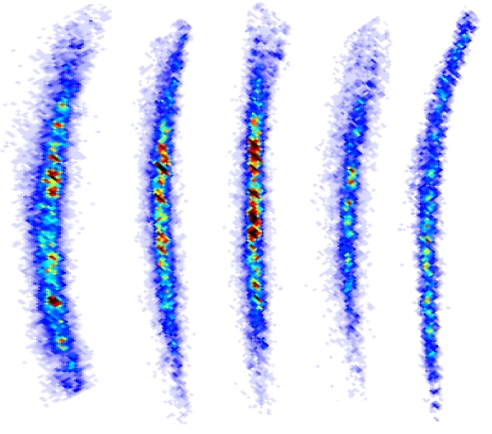
We present Speckle patterns from collagen soft tissue (Figs. 1 and 2 and Movie S1). The obtained diffraction patterns show two arcs along the meridian, the first order reflections, at a spacing equivalent to 1/67 nm⁻¹, subtending ≈40° in the azimuthal direction (Fig. 1), as expected from a relatively ordered collagen sample (28). Due to the substantial spatial coherence of the illuminating beam, the reflections contain high contrast 50-μm speckles, as expected for an aperture d = 10 μm and a detector to aperture distance D = 3.8 m, with λD/d = 53 μm (corresponding to 2.6 CCD pixels). The speckle contrast in the Bragg peak, calculated as the ratio (I_max − I_min)/(I_max + I_min) in the reflection, is around 63%. We observed both an intensity decay of ≈30% and a drop in the spacing (ca. 0.5 nm) of the first meridional reflections due to radiation damage after 5-min exposure time. These values are an average as some variation from sample to sample was observed. To our knowledge, no such speckled data have been reported, and it has been only possible now because of the use of a suitable aperture size and a detector to aperture distance tailored to the beam coherence; hence improving the conventional Small Angle X-ray Scattering (SAXS) setup (see Materials and Methods).

Fig. 2.

First meridional reflection from rat tail tendon obtained by scanning the coherent probe in five positions spaced 60 μm apart. Note the changes in the intensity and position of the speckles.

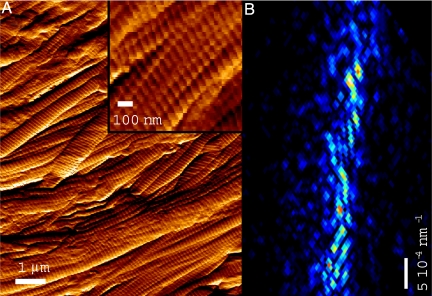
The main features of the diffraction patterns obtained experimentally can be reproduced with a simulation of the collageneous tissue made using AFM images from the same specimen (Fig. 3). We have combined the topological signal (height, H) with the feedback signals (amplitude A and phase P) of the AFM tip oscillation to generate in multiple ways real, pure phase, and complex density objects that simulate our collagen specimens. The diffraction patterns from all of the models show the characteristic collagen meridional arcs at spacings 1/67 nm⁻¹. The parameters of the simulated diffraction patterns (number of pixels, pixel size) have been derived to match the experimental conditions. These two parameters define the size of the Fast Fourier Transform (FFT) used for calculating the simulated diffraction patterns. The FFT size acts as a ‘virtual’ coherence aperture in the simulation. Speckles were only observed in the simulated pattern when the parameters matched the values for the aperture size and the detector to aperture distance used in the X-ray experiment. This fact confirms that the speckled substructure observed in the X-ray reflections is related to the beam coherence properties.

Fig. 3.

Atomic force microscope based simulations. (A) AFM image (tip oscillation amplitude signal) from rat tail tendon samples used to calculate simulated diffraction patterns. Size is 10 μm x 10 μm, which is the same lateral dimension as the X-ray experiment. Inset: The 1-μm diameter collagen fibers show the characteristic D-banding at ca. 67 nm. Note the relative small spread of orientations of about 10° from parallel. (B) Simulated first meridional reflection from complex density collagen model, which should be compared with X-ray diffraction data in Fig. 1.

Contrast Mechanism in the Diffraction Patterns.

We need to know about the contrast mechanisms in the samples under study to interpret the resultant images after reconstruction in terms of the real features present in the samples. We have simulated the effects in the diffraction patterns for absorption, phase, and a mixture of both contrast mechanisms using the AFM data. Fig. 3B shows the best simulation, from a complex density model where the amplitude and the phase have been simulated from the sample H image and the A image respectively. The phases were allowed to vary between 0 and π. The speckle size and shape is reproducible. The arc length is about the same in both the X-ray and the simulated patterns, meaning that the angular distribution of fiber orientation is consistent in the AFM model. The fact that the simulated reflection is wider in the radial direction implies that the fibers are straight over a shorter distance in the AFM experiment compared with the X-ray one. This could be explained assuming that the sample surface suffers damage during preparation and handling (as can be appreciated in some areas in Fig. 3A), whereas in the sample bulk the fibers reflect more their native ordering and orientation. The pure phase object model also worked satisfactorily, although the speckles showed less contrast than in the complex density model (ca. 40% less visibility). Poorer agreement was obtained with the real object model (visibility of 5%), suggesting that the contrast mechanism in collagen is predominantly phase type, as expected for biological specimens. It is noteworthy that even though X-ray diffraction is sensitive to the sample bulk (around 100 fibers) and AFM can only probe the sample surface, the main structural details of our collagen samples agree between both techniques.

Speckle Changes Between Positions in the Ptychography Scan.

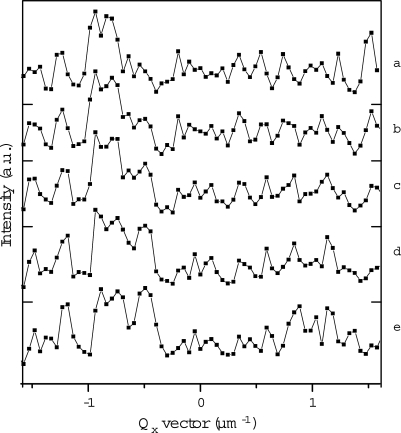
The speckles change in position and intensity when the sample moves between adjacent positions under the illuminating beam (shown in Figs. 2 and 4 and Movie S1). Two kinds of changes are noticeable: first, the arcing of the reflection, total intensity within, and width change. These modifications are related to spreading of the fiber orientations within the illuminated area and changes in their orientation with respect to the longitudinal axis of the tendon. Secondly, and more significant, is the change in position and intensity of the speckles within the arcs. Fig. 4 shows how the speckle pattern is modified when moving the probe with smaller steps. The continuity of the pattern between adjacent positions is noticeable, as needed for ptychography to reconstruct the object image. After moving 30 μm, the speckled pattern changes completely. This implies that the speckles effectively contain the information regarding the local structure of the sample.

Fig. 4.

Intensity profile of the central line of the first meridional reflection between five ptychography positions along a line: a) position 0 μm, b) 2 μm, c) 4 μm, d) 6 μm, e) 8 μm. The intensity has been averaged along three neighboring lines (approximately equivalent to the size of one speckle). Each point corresponds to a CCD pixel. Each speckle can be seen to be about 2–3 pixels wide, sufficiently oversampled for phasing to work. Their gradual intensity changes with the probe position are noticeable. See for instance the Q_x = 0.5 μm⁻¹ region, where the intensity increase of one of the speckles is particularly clear.

Implications for Imaging Biological Tissues.

We have demonstrated that an optimized SAXS setup allows coherent diffraction patterns from biological soft tissues to be obtained. Our work will enable CXD to be used to study collagen-rich biological tissues, such as bone, tendon, cornea, connective tissue, or skin. Exploiting the available coherence properties of the X-ray beam is especially relevant to obtain additional information from the nanostructure that could not be accessed with an incoherent beam. Eventually, the phasing of these speckled patterns will allow us to obtain dark field images of such tissue in the illuminated areas, where the alignment, disposition, and orientation of the collagen fibrils within the tissue extracellular matrix (ECM) will be shown. The patterns obtained so far would allow a 2D reconstruction of the tissue, where the third dimension would be projected onto the 2D plane of the image. However, ptychography could be extended to 3D by recording different data sets for different beam-sample angles, following the so called tilt series method, in a similar way to tomographic reconstruction.

Ptychography can have a clear advantage over other CXD methods for imaging extended objects, larger than the beam used. For these cases, the advantages of conventional, “support”- based CXD methods over other microscopy methods are lost because the sample is larger than the coherence length of the illuminating beam. Yet ptychography overcomes this limitation for biological tissues, simplifying the sample preparation requirements as the sample does not need to be cut to the μm scale. Indeed the method promises excellent results in the imaging of collagenous soft tissues when low dose, moderate resolution, and extended field of view are required, filling the gap between other CXD methods and full field X-ray microscopy, which relies on Fresnel zone plate performance. Furthermore, the dark field property will be powerful for discriminating between different contributions in the structural organic tissues, where the density and phase contrast between protein/nonprotein regions is limited. The position and orientation of the collagen fibers within dense matrices of other proteins will be clearly distinguished by their contribution to the unique D-band spacing of collagen. Dark field X-ray ptychography could be adapted to examine the effect of pathological processes in a variety of target tissues, say, in aging; bone loss in osteoporosis (34); diabetes or skin fibrosis; in the study of biomineralization processes (35); and in the evaluation of collagen-based biomaterials under development for regenerative medicine applications (36, 37). Dark field ptychography using an optimized SAXS setup may be also applied to other biomaterials with a suitably repetitive structural ‘signature’, such as those based on cellulose. Structural knowledge about the nanostructure of these vegetal materials would have a relevant impact in the performance optimization of a generation of biocombustibles and in the energy industry (38, 39).

Materials and Methods

Sample Dissection.

Wet tail tendon sections of ca. 5 × 5 mm and about 0.7 mm thick were dissected into saline from young healthy brown rat. The tail was kept frozen (−15 °C) until dissection. The central part of the tendon, between the two ends of the tail, was used. No chemical treatment was performed. Each section was soaked in phosphate buffer solution and sandwiched between two kapton foils for the X-ray measurements.

X-ray Data Acquisition.

The experiment presented was carried out at beamline 34-ID-C at the Advance Photon Source (APS), Argonne, USA. This beamline is characterized by its high coherent flux, in the range of 10¹⁰ photons/s. The beam wavelength λ was set at 0.14 nm (beam energy: 8.92 keV), using a silicon (111) double crystal monochromator. A pair of roller blade slits located 94 cm in front of the sample were used as secondary source, defining a coherent beam probe of 10 μm × 10 μm². Parasitic scattering from the optical system was removed with guard slits 28 cm in front of the sample. A Roper Scientific direct-detection CCD was mounted 2.9 m behind the sample. The beamstop was attached to the CCD external surface.

Each sample was illuminated in 151 overlapping positions, spaced 2 μm apart. We observed evident radiation damage in the samples (thermal denaturation) after 5-min exposure with a clear decrease of both the intensity and spacing (dropping to ca. 66.5 nm) of the reflections. Therefore, we recorded the ptychography data with 50-s exposures, enough for obtaining diffraction patterns with a good signal to noise ratio and without noticing changes due to radiation damage in the first order meridional reflections.

AFM Image Acquisition.

The images were taken using a commercial atomic force microscope (JPK Nanowizard) in intermitted contact mode (RTESP cantilevers; resonant frequency in air f = 300 kHz, nominal spring constant k = 40 N/m) to record both topographic and feedback signals. The same tendon samples used in the X-ray data acquisition were deposited on plain glass slides and gently dried under a weak flow of dry N₂.