Motion Correction in PROPELLER and Turboprop-MRI

Abstract

PROPELLER and Turboprop-MRI are characterized by greatly reduced sensitivity to motion, compared to their predecessors, fast spin-echo and gradient and spin-echo, respectively. This is due to the inherent self-navigation and motion correction of PROPELLER-based techniques. However, it is unknown how various acquisition parameters that determine k-space sampling affect the accuracy of motion correction in PROPELLER and Turboprop-MRI. The goal of this work was to evaluate the accuracy of motion correction in both techniques, to identify an optimal rotation correction approach, and determine acquisition strategies for optimal motion correction. It was demonstrated that, blades with multiple lines allow more accurate estimation of motion than blades with fewer lines. Also, it was shown that Turboprop-MRI is less sensitive to motion than PROPELLER. Furthermore, it was demonstrated that the number of blades does not significantly affect motion correction. Finally, clinically appropriate acquisition strategies that optimize motion correction were discussed for PROPELLER and Turboprop-MRI.

Introduction

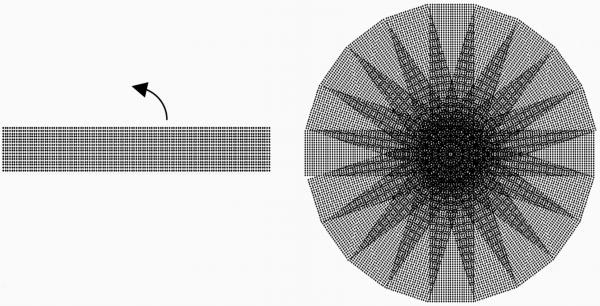
PROPELLER-MRI^1,2 (Periodically Rotated Overlapping Parallel Lines with Enhanced Reconstruction) is characterized by greatly reduced sensitivity to various sources of image artifacts. Data acquisition in PROPELLER is based on multiple-shot fast spin-echo (FSE), in which several k-space lines are acquired in each TR, forming a blade centered at the origin of k-space. The blade is then rotated around its center between shots, resulting in a k-space sampling pattern that resembles a propeller (Fig. 1). The central disc of k-space is sampled by all blades and can be used as a 2D navigator. Comparison of this k-space disc between blades allows correction of the subject's in-plane rotation and translation, as well as identification of blades with corrupted data and exclusion of such blades from the final reconstruction^1,2,3. Furthermore, any residual errors are expressed in a benign fashion due to the radial nature of the acquisition. Therefore, PROPELLER-MRI is less sensitive to bulk motion than conventional FSE.

Figure 1.

A) A single PROPELLER blade with 16 lines, and 128 samples per line. B) A PROPELLER sampling pattern with 12 blades produced by rotation of (A).

However, data acquisition in PROPELLER is at least 50% longer than that of conventional FSE, due to oversampling in the central part of k-space¹. This issue is addressed in Turboprop-MRI⁴, an accelerated version of PROPELLER, in which multiple lines of k-space are acquired around the spin-echo produced after each 180° pulse, similar to the gradient and spin-echo (GRASE) sequence. Hence, Turboprop-MRI allows acquisition of more k-space lines per blade than PROPELLER, in less time, thereby increasing scanning efficiency. Also, Turboprop reduces the number of 180° pulses required in PROPELLER acquisitions with the same k-space sampling pattern, and thus reduces the specific absorption rate (SAR). However, collecting a large number of gradient-echoes per spin-echo in Turboprop-MRI results in images that have similar characteristics to those produced by spin-echo echo-planar imaging (EPI), such as field inhomogeneity-related artifacts etc. For Turboprop acquisitions with a relatively small number of gradient-echoes per spin-echo, the effects of field inhomogeneities are not detectable.

PROPELLER and Turboprop-MRI have been applied in studies of the heart¹, brain^2,5-7, spinal cord^8,9, abdomen¹⁰, cartilage¹¹, and liver¹². In general, it was demonstrated that the two techniques provided superior results in regions with significant field inhomogeneities and in objects undergoing motion, compared to EPI-based and FSE-based methods, respectively. However, compensation for motion in the PROPELLER family of sequences has not been thoroughly investigated. It is unknown how acquisition parameters such as the number of blades, number of lines per blade, number of spin-echoes and gradient-echoes per blade, affect motion correction. Furthermore, since the introduction of PROPELLER and Turboprop, the approach used for motion compensation has not been evaluated and optimized. Thus, the goals of this study were: to investigate the effects of various PROPELLER and Turboprop-MRI acquisition parameters on motion correction, identify an optimal rotation correction approach, and propose clinically appropriate acquisition strategies that minimize motion-related artifacts.

Theory

Motion-correction in PROPELLER and Turboprop-MRI

Since PROPELLER and Turboprop-MRI allow acquisition of images free of distortions, motion correction for objects such as the human head becomes a rigid body registration problem. Any in-plane motion of a rigid body is geometrically equivalent to a rotation about the center of the image and a linear translation. Hence, in-plane rigid body motion correction can be separated into a rotation correction and a translation correction¹³. Out-of-plane motion cannot be corrected in PROPELLER and Turboprop-MRI, but the effects of out-of-plane motion can be minimized during reconstruction, by assigning low quality weights to blades affected by out-of-plane motion². Therefore, in the rest of this work we only discuss methods for correction of in-plane motion.

Rotation of the object around the center of image-space is equivalent to rotation of the k-space representation of the object around the center of k-space, whereas translation of the object in image space is equivalent to a linear phase change in the k-space representation of the object. Therefore, motion in image space can be measured and corrected using k-space data. Since in PROPELLER and Turboprop-MRI all blades share only the central disc of k-space with diameter equal to the width of each blade, rotation and translation between blades can be estimated using only the common data in that disc of k-space.

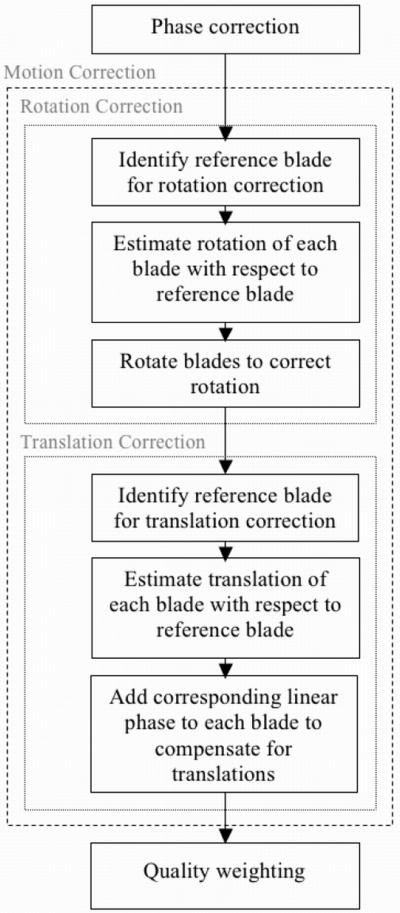
The blade with the highest correlation between its data in the central disc of k-space and the mean of the same data from all blades, is selected to be the reference blade (Fig. 2). In the following discussion we assume that A and B represent the central disc of k-space data from two different blades. We also assume that A corresponds to the reference blade, and B to a blade obtained in a rotated and translated position of the object relative to the position during acquisition of the reference blade. Also, a and b are the low-resolution images reconstructed from the central region of k-space from blades A and B respectively,

Figure 2.

Flow-chart outlining the procedure used for motion correction in PROPELLER and Turboprop-MRI.

$$a(x,y)=F{T}^{-1}(A(K_X,K_Y))=\sum _{K_X=1}^N\sum _{K_Y=1}^{N}A(K_X,K_Y)e^{2\pi i(K_{X}x+K_{Y}y)},$$ (1)

$$b(x,y)=F{T}^{-1}(B(K_X,K_Y))=\sum _{K_X=1}^N\sum _{K_Y=1}^{N}B(K_X,K_Y)e^{2\pi i(K_{X}x+K_{Y}y)},$$ (2)

Rotation Estimation and Correction

Estimation of the rotation of the object between two blades is equivalent to estimating the rotation in the data of the central disc of k-space from the two blades. In the presence of image-space translation adding different phases in the k-space representation of the two blades, estimation of rotation of the object can be achieved by estimating the rotation in the magnitude data of the central disc of k-space from the two blades. Furthermore, in polar co-ordinates (K_r, K_θ), rotation around the center of k-space is equivalent to translation along K_θ. Thus, estimation of the rotation of the object can be achieved by estimating the translation between ‖A(K_r, K_θ)‖ and ‖B(K_r, K_θ)‖ along K_θ, where ‖ ‖ denotes magnitude. If λ_θ is the translation of ‖B(K_r, K_θ)‖ relative to ‖A(K_r, K_θ)‖, then:

$$\Vert B(K_r,K_{\theta })\Vert =\Vert A(K_r,K_{\theta }-{\lambda }_{\theta })\Vert ,$$ (3)

The Δθ for which the cross-correlation between corresponding K_r lines from the two data sets is maximum,

$$cc(K_r,\mathrm{\Delta }\theta )=\int {\Vert A(K_r,K_{\theta })\Vert }^{\ast }\Vert B(K_r,K_{\theta }+\mathrm{\Delta }\theta )\Vert d{K}_{\theta },$$ (4)

represents an estimate of the rotation λ_θ between the two blades, where “*” denotes the complex conjugate (Fig. 2), and based on Parceval's theorem can be estimated rapidly³ by identifying the maximum of:

$$cc(K_r,\mathrm{\Delta }\theta )=F{T}_{K_{\theta }}^{-1}({(F{T}_{K_{\theta }}(\Vert A(K_r,K_{\theta })\Vert ))}^{\ast }(F{T}_{K_{\theta }}(\Vert B(K_r,K_{\theta })\Vert ))),$$ (5)

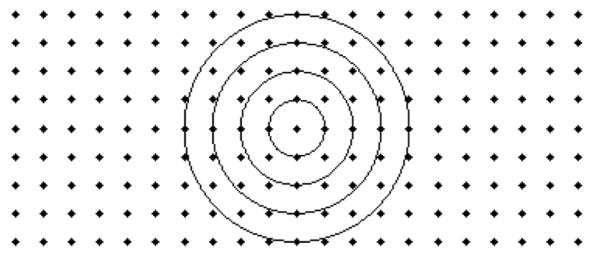
where FT_Kθ is the one-dimensional Fast Fourier Transform (FFT) along K_θ. This cross-correlation can be estimated separately for different K_r, as long as K_r is lower than half of the width of each blade (Fig. 3). However, although there is only one rotation of the object between two blades, the Δθ for which the cross-correlation in Equation 5 is maximum varies for different K_r, due to noise and interpolation errors primarily along K_θ. K_r lines that are near the center of k-space contain information from few k-space samples of each blade, leading to significantly inaccurate estimates of λ_θ (Fig. 3). In contrast, K_r lines that are distant from the center of k-space contain information from multiple k-space samples of each blade, leading to more accurate estimates of λ_θ (Fig. 3). However, K_r lines that are far from the center of k-space contain more noise than information about the object, resulting in less accurate estimates of λ_θ.

Figure 3.

Image of the locations of k-space samples (represented by dots) of a hypothetical blade with 9 lines and 21 samples per line, and an example of the K_r lines that would be used for rotation correction. The outermost K_r line defines the border of the central disc of k-space sampled by all blades.

The estimation of the final λ_θ from the available K_r lines has not been optimized for acquisitions with the PROPELLER family of sequences. Based on the above discussion, one approach would be to first estimate λ_θ,r for each K_r line separately, and then calculate the final λ_θ by either taking a weighted average of all λ_θ,r (using as weights the squared distances of the K_r lines from the center of k-space¹), or by simply averaging λ_θ,r for a few outer K_r lines. In the rest of this work the two methods will be referred to as the AL (all lines) and OL (outer lines) methods. Pipe et al³ followed the Decoupled Automated Rotation and Translation registration (DART) algorithm¹³, which ignores K_r lines nearest to, and most distant from the center of k-space, and estimates λ_θ based on a composite cross-correlation function produced by averaging the cross-correlations between only the middle half range of all K_r lines of a blade and the reference blade (from K_r-MAX/4 to 3*K_r-MAX/4). A method that combines the composite cross-correlation idea of DART and the weighted average of AL will be investigated in this work.

Finally, after estimation of the rotation between A and B, the k-space co-ordinates of blade B are rotated accordingly and the same process is repeated for all remaining blades (Fig. 2).

Translation Estimation and Correction

If image b is translated by λ_x along the x-axis, and λ_y along the y-axis, relative to image a, then:

$$b(x,y)=a(x-{\lambda }_x,y-{\lambda }_y),$$ (6)

The Δx, Δy for which the cross-correlation between a and b is maximum,

$$cc(\mathrm{\Delta }x,\mathrm{\Delta }y)=\iint a^{\ast }(x,y)b(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y)\mathit{\text{dxdy}},$$ (7)

represent estimates of the translation λ_x, λ_y between the two blades. Considering Equations 1, 2, 7, and Parceval's theorem, the estimates of the translation between the two blades can be obtained by identifying the Δx, Δy for which the following expression is maximized^3,13:

$$cc(\mathrm{\Delta }x,\mathrm{\Delta }y)=F{T}^{-1}(A^{\ast }(K_X,K_Y)B(K_X,K_Y)).$$ (8)

After estimation of the translation λ_x, λ_y between the two blades, the complete k-space data of the blade corresponding to image b are corrected by multiplying with the corresponding phase (Fig. 2).

Methods

Simulations

PROPELLER-MRI

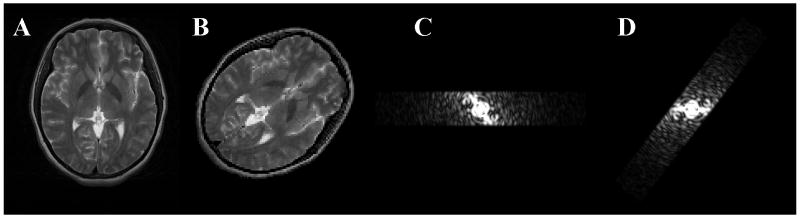
A high-resolution (512×512 image matrix, 24cm × 24cm field of view), axial, T₂-weighted image was first acquired from the brain of a healthy human volunteer, using a 3T GE MRI scanner (Waukesha, WI, USA) and conventional FSE (Fig. 4A). Appropriate consent was obtained. PROPELLER acquisitions were then simulated using the actual data. For this purpose, the acquired image was rotated and re-sampled on 128×128 Cartesian grids (Fig. 4B). Two-dimensional inverse Fourier transform was applied on the rotated images (Fig. 4C) and simulated k-space blades were obtained at angles exactly opposite to those the original image was rotated to (Fig. 4D). The same procedure was repeated for several different angles to simulate PROPELLER sampling patterns with {12, 16, 20, 24, 28, 32} blades, {16-128} lines per blade in increments of 4, and 128 samples per line. T₂ decay was also simulated for each blade. The T₂ value was assumed to be 90ms throughout the brain, and the first echo was acquired at 85ms for all blades.

Figure 4.

A) High-resolution (512×512) T2-weighted axial image from the brain of a healthy human volunteer. B) Image of the same slice obtained by rotating image (A) clockwise by 60° and resampling it on a 128×128 Cartesian grid. C) Truncated magnitude image of the 2-dimensional Fourier transform of (B). D) Simulated k-space blade obtained by rotating (C) counter-clockwise by 60°.

Rotations and translations were simulated in the blades of all sampling patterns by appropriately rotating the k-space co-ordinates and adding linear phases to the k-space data of each blade, respectively. The magnitude and sign of the added rotations and translations was generated randomly by sampling from Gaussian distributions with zero mean and standard deviation of 5° and 5 pixels, respectively. Furthermore, Gaussian noise with zero mean was added in k-space. The variance of the added Gaussian noise was such that the SNR in a frontal lobe white matter region was approximately 20 when images were reconstructed from the sampling pattern with 32-blades and 20 lines per blade. All resulting datasets were motion corrected prior to final image reconstruction.

In the rotation correction step, rotation was estimated using four different approaches. The first three were the AL, OL and DART, described in the theory section, which use all, outer two, and middle half K_r lines, respectively. In the fourth method, which was a variant of DART, each K_r line of a blade and the reference blade was multiplied by the square of its distance from the center of k-space, and a composite cross-correlation function was estimated from the cross-correlations (Equation 5) between all available K_r lines of the two blades. Rotation was then estimated as the angle for which the value of the composite cross-correlation was maximum. In the following discussion this method is referred to as the DART_w approach.

The performance of all motion correction approaches was assessed for all sampling patterns. First, the error in rotation estimation was measured for each blade as the absolute value of the difference between the added and estimated rotations. The mean of the rotation errors over all blades was then used to assess the error in rotation estimation for each sampling pattern. A similar process was used to assess the error in translation estimation along the x and y axes. All simulations (i.e. simulating rotation and translation, adding noise in k-space, motion correction) were repeated 100 times, and the mean rotation and translation errors were computed for every sampling pattern over the 100 repetitions of the simulations. Plots of the mean rotation and translation errors as a function of the number of blades and lines per blade were produced for each motion correction approach.

All the simulations described above were repeated for added rotations and translations generated by sampling from Gaussian distributions with zero mean and standard deviation of 10° and 10 pixels, respectively. The simulations were also repeated with no added motion.

Plots of the mean rotation and translation errors as a function of the number of blades, and number of lines per blade, were generated. The mean rotation and translation errors were compared between sampling schemes and motion correction approaches. The Wilcoxon signed rank test was used to assess the significance of any differences between distributions of rotation or translation errors. Only differences with p<0.05, were considered significant. The mean rotation and translation errors were also compared for different amounts of added motion. In this case, the Mann-Whitney U-test was used to assess the significance of any differences between distributions of rotation or translation errors. Only differences with p<0.05, were considered significant. Finally, all simulations described above were repeated with the first echo of all blades acquired at 58ms for all sampling patterns.

Turboprop-MRI

Turboprop-MRI acquisitions were also simulated from the high-resolution human brain data following a process similar to that for the simulations of PROPELLER acquisitions. In Turboprop-MRI, the number of lines in each blade is equal to the product of the number of spin echoes per excitation (echo train length, ETL) and the turbofactor, which represents the number of lines acquired with each spin echo. Turboprop sampling patterns with {12, 16, 20, 24, 28, 32} blades, ETL of {4, 6, 8, 10, 12, 14, 16}, turbofactor of {1, 3, 5, 7, 9}, and 128 samples per line were simulated. T₂* decay was also simulated for each blade. The T₂* value was assumed to be 50ms throughout the brain, and the first echo was acquired at 85ms for all blades of all sampling patterns. Rotation, translation, and k-space noise were added to all Turboprop data as described above. Motion correction and estimation of the mean rotation and translation error were also performed for each sampling pattern. Rotation estimation was performed using all four methods discussed above. Surface plots of the mean rotation and translation errors as a function of ETL, turbofactor, and number of blades, were produced. All simulations were repeated for different amounts of added motion and a different time for acquisition of the first echo, as described above for PROPELLER-MRI. The distributions of rotation and translation errors were compared between sampling schemes, motion correction approaches, and amounts of added motion, using similar statistical analysis as in PROPELLER-MRI.

Phantom and Human studies

PROPELLER and Turboprop-MRI sequences were implemented on a 3T GE MRI scanner (General Electric, Waukesha, WI). Data were acquired on a phantom and a cooperative human volunteer, after appropriate consent, using the following imaging parameters: 10 blades, 128 samples per line, TR = 5000ms, axial slices with slice thickness of 5mm, and a field of view of 24cm × 24cm. Images of the phantom were obtained for all combinations of ETL = {4, 6, 8, 10, 12, 14, 16} and turbofactor = {3, 5, 7, 9}. The imaging time was the same for all acquisitions, since it is determined by the number of blades. The SNR was measured in a uniform region of interest within the phantom. A table of the SNR as a function of the ETL and turbofactor was produced.

The human volunteer was asked to move his head in the scanner avoiding as much as possible motion through the axial plane. Brain data were acquired with ETL = {4, 6, 8} and turbofactor = 5. Images were reconstructed using all four motion correction approaches, as well as without motion correction.

Results

Simulations

PROPELLER-MRI

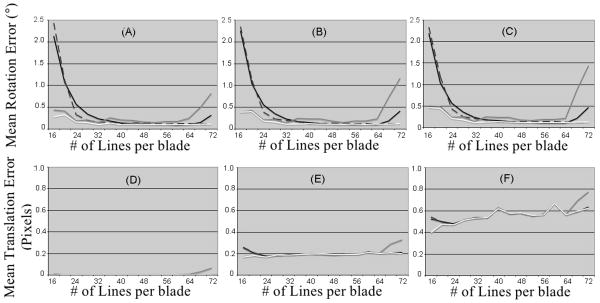
In PROPELLER-MRI, when using the DART and AL approaches to estimate rotation between blades, the mean rotation error was high for sampling patterns with 16 lines per blade and decreased for patterns with increasing number of lines per blade (Fig. 5 A, B, C). When using the DART_W and OL methods, the mean rotation error for sampling patterns with a number of lines per blade between 16-32 was significantly lower than that obtained with DART and AL (for example, for 20 lines per blade p<2.6×10^-11 when comparing DART and AL to DART_W). For blades with 32-56 lines, all rotation estimation approaches produced similar mean rotation errors. However, for blades with more than 60 lines, the mean rotation error was significantly higher when using the OL method compared to all other approaches for rotation estimation (p<2.2×10^-8) (Fig. 5 A, B, C). Also, for blades with more than 64 lines, the mean rotation error was significantly higher when using the AL compared to the DART_W and DART methods (p<3.3×10^-13). Furthermore, DART_W consistently provided the lowest mean rotation error for 16-72 lines per blade. Additionally, for DART and DART_W, the mean rotation error was relatively insensitive to increasing amounts of added motion. For the OL and AL, the mean rotation error increased for increasing amounts of added motion when the number of lines per blade was higher than 64, but the increase was not significant (p>0.057).

Figure 5.

Graphs of the mean rotation error (A, B, C) and mean translation error (D, E, F) in PROPELLER-MRI as a function of the number of lines per blade, when no motion is added (A, D), and when the simulated motion in each blade is sampled from a Gaussian distribution with standard deviation of 5° and 5 pixels (B, E), or 10° and 10 pixels (C, F). Rotations were estimated using AL (solid black curve), DART_w (white curve), DART (dotted curve), and OL (grey curve). 12 blades were used for all sampling patterns in this example.

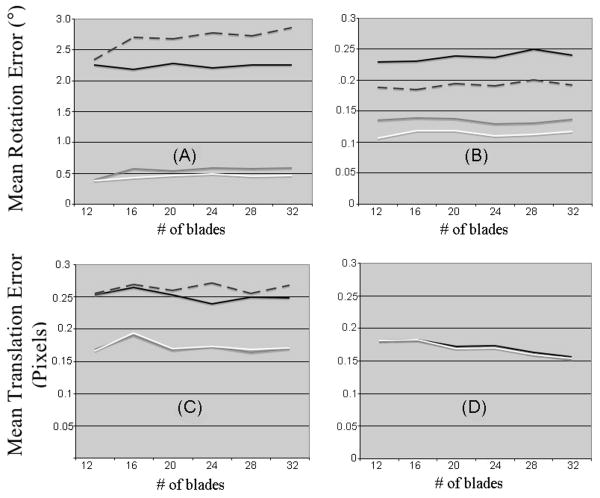
A generally similar behavior was observed for the mean translation error as a function of the number of lines per blade (Fig. 5 D, E, F). When motion was added and the DART_W or OL methods were used, the mean translation error for sampling patterns with a number of lines per blade between 16-24 was significantly lower than that obtained with DART and AL (for example, for 20 lines per blade p<0.003, when comparing DART and AL to DART_W) (Fig. 5E, F). In contrast to the mean rotation error, the mean translation error significantly increased for increasing amounts of added motion, independent of the number of lines per blade, or the method used for the preceding rotation correction (for example, p<10^-40 for DART_W and different amounts of added motion). For several sampling patterns, the mean translation error was approximately equal to zero when no motion was added (Fig. 5D). In addition, the mean rotation and translation errors were relatively independent of the number of blades of the PROPELLER sampling pattern, for all rotation correction approaches (Fig. 6). Finally, similar results were obtained when the first echo of all blades was acquired at 58ms.

Figure 6.

Graphs of the mean rotation error (A, B) and mean translation error (C, D) in PROPELLER-MRI as a function of the number of blades, for blades with 16 lines (A, C) and 32 lines (B, D). The amount of added motion in each blade was simulated by sampling from a Gaussian distribution with standard deviation of 5° and 5 pixels. Rotations were estimated using AL (solid black curve), DART_w (white curve), DART (dotted curve), and OL (grey curve).

Turboprop-MRI

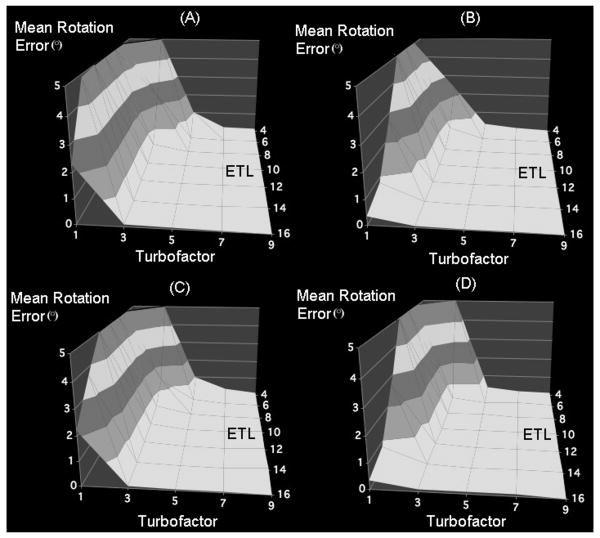
For Turboprop sampling patterns and almost all combinations of ETL and turbofactor investigated, the mean rotation error was minimized when using the DART_W approach for rotation correction (for example, for ETL=8 and turbofactor=3, p<2×10^-22 when comparing DART, AL, OL to DART_W) (Fig. 7). Only for ETL=6 and turbofactor=3 OL provided lower mean rotation error than all other approaches (p<2.3×10^-148) (Fig. 7). In the special case of turbofactor=1, Turboprop-MRI essentially becomes PROPELLER, and the fact that the minimum mean rotation error was obtained with DART_W was in agreement with the PROPELLER results of Figure 5. The mean rotation error in Turboprop-MRI was in general high for sampling patterns with few lines per blade and decreased for patterns with increasing number of lines per blade (Fig.7). Also, for all ETL investigated, the mean rotation error for turbofactor=1 (PROPELLER) was significantly higher than for turbofactor>1 (Turboprop). Finally, the mean rotation error was relatively insensitive to increasing amounts of added motion.

Figure 7.

Surface plots of the mean rotation error in Turboprop-MRI for different combinations of ETL and turbofactor, when using DART (A), DART_w (B), AL (C), OL (D). The amount of added motion was simulated by sampling from a Gaussian distribution with standard deviation of 5° and 5 pixels. 12 blades were used for all sampling patterns in this example. The combinations of ETL=16, turbofactor=9, and ETL=4, turbofactor=1 were not investigated.

A similar behavior was observed for the mean translation error as a function of the number of lines per blade. However, in contrast to the mean rotation error, the mean translation error increased for increasing amounts of added motion, independent of the number of lines per blade, or the method used for rotation correction (for example, p<2.6×10^-3 for DART_W and different amounts of added motion). For several sampling patterns, the mean rotation and translation errors were greater than zero when no motion was added. Furthermore, the mean rotation and translation errors were relatively independent of the number of blades of the Turboprop sampling pattern, for all rotation correction approaches. Finally, similar results were obtained when the first echo of all blades was acquired at 58ms.

Phantom and Human studies

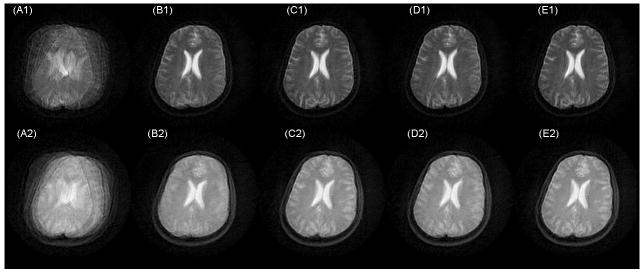
Table 1 contains SNR values from a uniform region of the phantom for different combinations of ETL and turbofactor, expressed as percentages of the maximum SNR measured. For increasing ETL, SNR values initially decreased and then increased, or reached a plateau. Images of the brain of a human volunteer moving his head in the scanner contained significant artifacts when no correction for motion was performed (Fig 8 A1, A2). When using the DART_W or OL methods for rotation correction, images were significantly improved compared to the uncorrected ones, as well as to those produced using DART or AL (Fig.8).

Table 1.

SNR values from a uniform region of the phantom for different combinations of ETL and turbofactor, expressed as a percentage of the maximum SNR value measured.

Turbofactor	3	5	7	9
ETL
16	80.1	72.8
14	69.0	65.7	64.8
12	66.2	70.8	69.2
10	74.2	58.6	70.1	67.0
8	77.6	67.9	71.1	69.7
6	87.7	82.4	84.4	79.2
4		100.0	93.5	93.1

Figure 8.

Axial Turboprop images through the brain of a trained human volunteer moving his head in the scanner during data acquisition. The subject was instructed to refrain from moving through the axial plane as much as possible. Each row corresponds to a different scan session. For images in the first row the first echo was acquired at 85ms, and in the second row at 50ms. Motion correction was not used for images (A1) and (A2). DART motion correction was used for images (B1, B2), DART_w for (C1, C2), AL for (D1, D2), and OL for (E1, E2). Image quality was significantly improved in images (C1, C2) and (E1, E2) compared to (A1, A2, B1, B2, D1, D2). The sampling pattern used for the data acquisitions in this example contained 20 blades, ETL=4, turbofactor =5.

Discussion

Greatly reduced sensitivity to motion is probably the most significant feature of PROPELLER and Turboprop-MRI compared to their predecessors, FSE and GRASE, respectively. However, since the introduction of PROPELLER and Turboprop-MRI, the method used for motion compensation has not been evaluated and optimized. In this work, we studied how acquisition parameters that determine k-space sampling affect motion correction, and we identified an optimum rotation correction approach that also improves translation correction. In the following discussion we analyze our findings and provide insights on clinically appropriate PROPELLER and Turboprop-MRI acquisition strategies that minimize motion-related artifacts.

For sampling schemes with a relatively small number of lines per blade, the outer K_r lines provide significantly more accurate estimates of rotation than those near the center of k-space. Rotation estimation in DART_W is primarily based on the outer K_r lines, due to the strong weighting of cross-correlations from these lines, and in OL, rotation estimation is based exclusively on the outer K_r lines. In contrast, in the DART approach for rotation correction, only the K_r lines from K_r-MAX/4 to 3K_r-MAX/4 are utilized, and in AL, although the estimates of rotation from the outer K_r lines are weighted more than those from lines near the center of k-space, the latter contain large errors that are eventually included in the weighted average. As a result, when blades with a relatively small number of lines were used for PROPELLER-MRI, significantly higher mean rotation errors were measured for DART and AL compared to DART_W and OL. For increasing lines per blade, the range of K_r lines used in DART includes lines that allow more accurate estimation of rotation, in AL and DART_W more lines that provide a better assessment of rotation are used and multiplied with higher weights, and in OL, the rotation estimation is based exclusively on lines that provide more accurate estimates of the rotation. Therefore, the mean rotation error decreased for all methods (but most significantly for DART and AL) until it reached approximately the same plateau. For sampling schemes with large numbers of lines per blade, the outer K_r lines contain mostly noise. Therefore, the mean rotation error in OL and AL increased significantly, since the former is based exclusively on the outer K_r lines, and in the latter, large weights are assigned to estimates of the rotation originating from the outer K_r lines. In contrast, the mean rotation error remained relatively unchanged for DART and DART_W (for the number of lines per blade investigated), since in the former, the problematic outer lines were not used, and in the latter the cross-correlations from the problematic outer K_r lines were averaged with those from K_r lines that provided accurate assessment of the rotation. Overall, DART_W provided the lowest mean rotation error for all PROPELLER sampling patterns and amounts of added motion used here.

It was demonstrated that, the behavior of the mean translation error as a function of the number of lines per blade in PROPELLER-MRI exhibited similarities to that of the mean rotation error. This may be due to the fact that, in the motion correction process, blades are corrected for rotation before translation, and any residual rotations due to inaccurate rotation correction may lead to inaccuracies in translation correction. In addition, the mean translation error increased with increasing amounts of added motion, while the mean rotation error was shown to be relatively insensitive to the amount of motion added. However, the increase in mean translation error was less than half a voxel, which is negligible from a practical point of view.

The performance of motion correction in Turboprop-MRI as a function of the number of lines per blade and amount of motion was generally similar to that in PROPELLER. DART_w was shown to provide the lowest mean rotation and translation errors for Turboprop. In addition, it was demonstrated that the mean rotation and translation errors for Turboprop (turbofactor>1) were lower than those for PROPELLER (turbofactor=1) for all values of ETL investigated (Fig.7). This is due to the fact that, for any ETL, increasing the turbofactor to a value higher than one, significantly increases the number of lines per blade, allowing one to perform: a) rotation correction using K_r lines that are further away from the center of k-space, and b) translation correction with wider blades containing higher spatial frequencies. Thus, Turboprop-MRI is less sensitive to motion than PROPELLER.

For the sampling patterns investigated in this work, the number of blades did not have any effect on the accuracy of motion correction in PROPELLER and Turboprop-MRI. This is relatively intuitive, since after identifying the reference blade, all corrections are performed for each non-reference blade separately. However, in the case of extremely uncooperative subjects, acquisitions with a small number of blades may not contain any blade with high quality data that could be used as a reference blade. That, of course, would lead to unsuccessful motion correction. Furthermore, the number of blades in a sampling pattern is tightly linked to the imaging time and the SNR of the reconstructed images. A small number of blades requires less scan time, but also results in lower SNR.

Based on the discussion above and figures 5 and 7, optimal motion correction in PROPELLER-MRI could be achieved when using blades with at least 16 lines, and the DART_w approach for rotation correction. However, PROPELLER blades with multiple lines require an equal number of 180° RF pulses, thereby depositing significant amounts of energy per unit time (high SAR) in the subject's body. Furthermore, acquisition of multiple lines with an FSE approach increases the effective TE, leading to significant signal decay, and limiting the maximum width of PROPELLER blades. In contrast, blades in Turboprop-MRI can be wider than those in PROPELLER, using fewer 180° RF pulses and producing lower SAR. Furthermore, it was shown that Turboprop is less sensitive to motion than PROPELLER for all values of ETL investigated. Considering the results shown in Table 1 and Figure 7, Turboprop acquisitions with ETL≥8 and turbofactor≥3 lead to low mean rotation and mean translation errors, and produce images with sufficient SNR. Of course increasing the ETL in Turboprop-MRI to values much higher than 8 will lead to similar heating and signal decay as in PROPELLER, and increasing the turbofactor to values much higher than 3 will produce artifacts due to magnetic field inhomogeneities. Considering all of the above, we conclude that, in the presence of motion, Turboprop-MRI with {8 ≤ ETL ≤ 12 and 3 ≤ turbofactor ≤ 7}, or {4 ≤ ETL ≤ 6 and 5 ≤ turbofactor ≤ 7}, and using the DART_w approach for motion correction, is recommended for low mean rotation and translation errors, sufficient SNR, and acceptable SAR.

Finally, in the simulations we assumed only in-plane motion, and that motion does not occur during the acquisition of a blade. Out of plane motion, or motion that takes place during acquisition of a blade, significantly alter the quality of the blade's data. Such blades are typically removed by the quality weighting procedure², which follows motion correction. Therefore, we anticipate that in actual experiments on uncooperative subjects, significantly corrupted blades will be removed by the quality weighting procedure, and motion correction in the remaining blades will be accomplished as described in this work. Our results on the human subject are a good example of that. Although the subject was instructed to avoid through-plane motion, there was nothing restricting the subject from doing so, and thus such motion probably contaminated the data. However, our results from the experiments on the human subject were in agreement with the findings from the simulations.

Conclusion

In this study, we evaluated the accuracy of motion correction in PROPELLER and Turboprop-MRI, and determined acquisition strategies for optimal motion correction. It was demonstrated that, in both techniques, blades with multiple lines allow more accurate estimation and correction of motion than blades with fewer lines. Four rotation correction approaches were evaluated, and the DART_W approach was shown to significantly improve compensation for motion, particularly in blades with few lines. This approach is particularly important for PROPELLER-MRI, where the maximum number of lines per blade is limited. Furthermore, it was shown that for all typical values of ETL, Turboprop-MRI is less sensitive to motion than PROPELLER. Additionally, it was demonstrated that the performance of motion correction is not affected by the number of blades included in PROPELLER or Turboprop sampling patterns. Finally, acquisition strategies that optimize motion correction were identified.