Computation of conformational transitions in proteins by virtual atom molecular mechanics as validated in application to adenylate kinase

Abstract

Many proteins function through conformational transitions between structurally disparate states, and there is a need to explore transition pathways between experimentally accessible states by computation. The sizes of systems of interest and the scale of conformational changes are often beyond the scope of full atomic models, but appropriate coarse-grained approaches can capture significant features. We have designed a comprehensive knowledge-based potential function based on a Cα representation for proteins that we call the virtual atom molecular mechanics (VAMM) force field. Here, we describe an algorithm for using the VAMM potential to describe conformational transitions, and we validate this algorithm in application to a transition between open and closed states of adenylate kinase (ADK). The VAMM algorithm computes normal modes for each state and iteratively moves each structure toward the other through a series of intermediates. The move from each side at each step is taken along that normal mode showing greatest engagement with the other state. The process continues to convergence of terminal intermediates to within a defined limit—here, a root-mean-square deviation of 1 Å. Validations show that the VAMM algorithm is highly effective, and the transition pathways examined for ADK are compatible with other structural and biophysical information. We expect that the VAMM algorithm can address many biological systems.

Large-scale conformational transitions mediate allosteric regulation and play other critical roles in protein function (1, 2). Crystallographic studies have provided various snapshots of some proteins in different conformational states, yet the transition mechanisms and the allosteric couplings of these proteins remain incompletely understood at best. In addition to experimental techniques, the near-native state dynamics of proteins have been studied using various full atomic (3) and coarse-grained computational approaches (4). Conformational changes may span an extensive range of amplitudes and time scales, and relevant systems can be quite large. Such transitions typically entail the crossing of large energetic and entropic barriers and involve the collective motions of very large protein complexes that are not readily accessible to experiments and not easily modeled for computations. Accurate and efficient molecular mechanics approaches are needed to analyze such large-scale motions and relate the complex dynamic behaviors of proteins to their function.

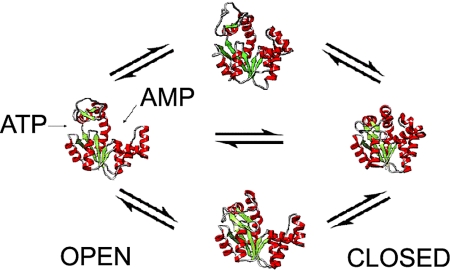
Adenylate kinase (ADK) is prototypic of proteins that undergo large-scale conformational change during functional transitions (5). ADKs regulate energy homeostasis in cells by catalyzing the transfer of a phosphate group from ATP to AMP to yield two ADP molecules. ADK comprises three domains: a core domain, an ATP-binding lid domain, and an AMP-binding lid domain. It has been well characterized by structural (5–9), biophysical (9, 10), and theoretical (11–14) studies that large conformational transitions of ATP lid and AMP lid domains are coupled to ligand binding and catalysis by ADK. Hinge-bending motions allow the ATP- and AMP-binding domains to close onto their ligands and form the catalytic site (closed state) and to open up for product release and substrate rebinding (open state). Crystal structures are known in a comprehensive set of ADK conformational states from multiple orthologs (Fig. 1).

Fig. 1.

A schematic representation of ADK conformational transitions. The open state (Left; PDB ID: 2RH5) is in the apo state. The closed state (Right; PDB ID: 2RGX) is bound to Ap5A nucleotide. The semiopen state (Upper; PDB ID: 2AK3) is in complex with AMP, and its AMP lid is in a closed conformation. The other semiopen state (Lower; PDB ID: 1DVR) is in complex with an ATP analog (phosphodifluoromethylphosphonic acid-adenylate ester), and its ATP lid is in a closed conformation.

Several computational methods have been proposed in recent years to study conformational transitions of macromolecules, notably for ADK. Rigorous atomistic molecular dynamics simulations have proven useful in revealing the trajectory of the ADK transition (11–13); however, such approaches are computationally expensive and still problematic for very large complexes, such as ribosomes and RNA polymerase. Alternatively, coarse-grained normal-mode analyses (15–17) or plastic network model approaches (18) using different forms of simple harmonic potentials have generated transition pathways of the ADK; however, these approaches are questionable because the simple harmonic potential approximation becomes less valid as the intermediate structures lie far away from the native states.

Motivated largely by transition pathway applications, we recently defined a knowledge-based potential function for large systems undergoing large conformational changes (19). We call this coarse-grained approach virtual atom molecular mechanics (VAMM). The VAMM pseudo force field accurately describes the structure and fluctuations of proteins around their native states. Here, we establish an algorithm based on the VAMM force field to compute transition pathways of conformational change in proteins. We applied both the VAMM algorithm and control algorithms to generate transition trajectories for the open/closed transformation of ADK. Our analyses of these trajectories validate the VAMM-based algorithm as being significantly more efficient and accurate than control algorithms based on simple harmonic potential approaches. The transition trajectory generated by the VAMM-based approach is further analyzed to gain insight into the conformational pathway between the open and closed states of ADK.

Algorithm Validation

Transition Pathway Computations for ADK.

We developed an algorithm for using VAMM in transition pathway computations, and we have compared this VAMM algorithm with control algorithms based on simple coarse-grained harmonic potentials. Briefly, at each step we computed the normal modes from each of the starting states, chose the normal mode with greatest involvement as directed toward the alternate state, and made those two structural moves. We then iterated this process to convergence (see Methods for details). The VAMM algorithm was perfected in calculations on conformational transitions in ADK based on crystal structures from the thermophile Aquifex aeolicus in open [Protein Data Bank (PDB) ID: 2RH5 chain A] and closed (PDB ID: 2RGX) conformations (14). Tests with the open and closed structures of Escherichia coli ADK gave similar results.

We first performed transition calculations using a control algorithm with a simple harmonic potential. Then, hoping to reduce geometric distortions, we used that same algorithm with a harmonic potential modified to include restraints on the virtual Cα–Cα bonds. Finally, we devised the VAMM approach, which adds other restraints to give a complete potential function for virtual atoms, improves the algorithm for transition pathway calculations, and also includes periodic energy minimizations and periodic reassessments of secondary structure as needed for the VAMM force field.

Convergence of ADK Transition Pathway Intermediates.

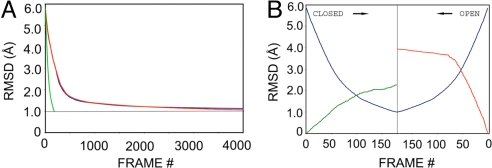
Transition pathway calculations converged slowly for the control algorithm, as seen in the progression of rmsd between the alternative intermediates generated from initial open and closed structures of ADK (Fig. 2 and Fig. S1). These deviations dropped from an rmsd of 5.85 Å initially to 1.5 Å in 637 and 699 iterations for the simple harmonic and bond-restrained potentials, respectively; however, convergence beyond this point was very inefficient. To reach 1 Å rmsd required 7,655 total steps with only bond restraints, and the system stalled at ≈1.1 Å rmsd with the simple harmonic potential and was discontinued after 7,500 iterations. This situation indicates a very ineffective algorithm.

Fig. 2.

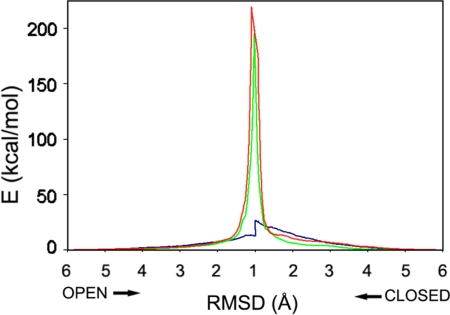
Structural deviations along ADK transition pathways. (A) Deviations (rmsd) between the succession of two intermediate states generated from open and closed ADK, respectively, as analyzed with the simple harmonic potential (blue), with the bond-restrained potential (red), and with the VAMM potential (green). (B) Deviations during the VAMM-based transition calculations. An expanded view is shown for deviations (rmsd) between the succession of VAMM intermediate states as they move, frame by frame, from the respective closed (Left) and open (Right) states toward similar terminal intermediates (blue). Deviations between the closed state and intermediates generated from the closed state (green) and deviations between the open state and intermediates generated from the open state (red) are also shown.

On the other hand, the VAMM algorithm yielded a transition pathway that converged strikingly fast, requiring only 178 steps to reach 1 Å rmsd (Fig. 2B). As moves proceeded toward convergence, the involvement coefficients of engaged normal modes decreased, and the frequencies of these modes tended to increase (Fig. S2). The increased efficiency of the VAMM algorithm, reflecting the more comprehensive energetic restraints, also implies lowered computational strain along the transition pathway and structurally more realistic intermediates. Intermediates generated from the open state deviated from the initial structure more than those generated from the closed state. For VAMM, the rmsd between the open-state crystal structure and its terminal intermediate was 3.94 Å, whereas that between the closed-state crystal structure and its terminal intermediate was only 2.26 Å (Fig. 2B). This result is in accord with FRET experiments (9), which indicate that the unliganded, open state samples a much larger conformational space.

Accuracy of Calculated Cα–Cα Virtual Bond Lengths.

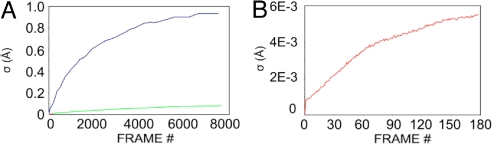
Distances between adjacent Cα atoms are strictly confined to the vicinity of 3.8 Å for trans-peptide bonds of the protein molecules. We find that the distribution of the Cα–Cα bonds in the EVA database (20) has a 3.78-Å mean value and an SD (σ) of 0.0093 Å; Cα–Cα distances below 3.45 Å and above 4.15 Å are almost never observed, and even the next nearest values (in the range of 3.45–3.65 Å and 3.95–4.15 Å) are very rare, with p[3.45,3.65] = 6.3 × 10⁻³ and p[3.95,4.15] = 3.6 × 10⁻⁴. Thus, even minor deviations from the equilibrium values are not usually allowed for Cα–Cα virtual bond distances.

In violation of this reality, the SDs of Cα–Cα distances along transition pathways (Fig. 2A) reveal gross distortions for the simple harmonic potential (terminal σ = 0.93 Å) and even unacceptable departures for the bond-restrained potential (terminal σ = 0.08 Å). Many distances fell into the highly disallowed range for trans-peptides (3.5 Å < d > 4.1 Å), with maximum distances of 7.21 Å and 4.03 Å for simple and bond-restrained potentials, respectively. Iterative fitting of normal modes computed by using simple harmonic potentials clearly generates unrealistic bond distances.

In sharp contrast with the control algorithms, the Cα–Cα distances from the VAMM algorithm conformed to standard values throughout the transition (Fig. 3C). The terminal intermediate state originated from the open ADK had σ = 0.0055 Å, in the same range as that deduced from the entire EVA database. All of the virtual trans-bond distances fell within the range between 3.7 Å and 3.9 Å. Thus, VAMM provides an accurate tool for preserving the integrity of virtual bond distances during a pathway calculation.

Fig. 3.

SDs (σ) of Cα–Cα virtual bonds during trajectories starting from the open state of ADK (rmsd between intermediate- and starting-state distances). (A) Comparison of trajectories based on different potential functions: simple harmonic potential (blue), bond-restrained harmonic potential (green), and VAMM potential (red). (B) VAMM-based trajectory in an expanded view.

Accuracy of Virtual Bond and Dihedral Angles.

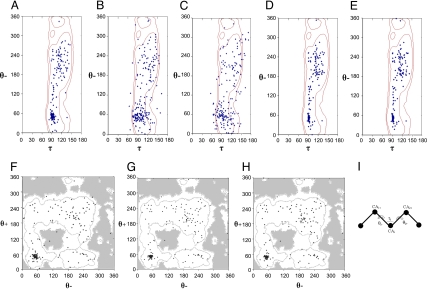
Protein conformations are well defined by their backbone (ϕ,ψ) dihedral angles, and distributions of polypeptide conformations in accurate crystal structures allow for the definition of probability contours in familiar Ramachandran (ϕ,ψ) plots (21). Although (ϕ,ψ) angles are not defined in Cα virtual-atom representations of proteins, a comparable picture of the conformational state is specified by the virtual Cα–Cα–Cα bond angles τ and the virtual Cα–Cα–Cα–Cα dihedral angles θ. Distributions of (τ,θ) pairs are plotted in Fig. 4 A–E for the open-state crystal structure and terminal intermediate states generated from it. Probability contours deduced from the Top500 database (21) are drawn at the MolProbity levels of 95% (favored) and 99% (allowed). Similar distributions of virtual bond and dihedral angles were reported previously (22).

Fig. 4.

Distributions of virtually bonded conformation parameters. Conformational values from defined ADK structures are spotted (blue dots) onto contour plots based on the MolProbity Top500 database (21). (A–E) θ⁻ vs. τ profile. Contour levels are at 95% (favored) and 99% (allowed). (A) Crystal structure of open ADK. (B) The terminal intermediate state generated from open ADK using the simple harmonic control algorithm. (C) The terminal intermediate state generated from open ADK using the bond-restrained control algorithm. (D) The open ADK structure after energy minimization with VAMM. (E) The terminal intermediate state generated from open ADK using the VAMM-potential algorithm. (F–H) The θ⁻ vs. θ⁺ profile. Contour levels are at 95% (favored) and 99% (allowed). (F) Crystal structure of open ADK. (G) The open ADK structure after energy minimization with VAMM. (H) The terminal intermediate state generated from open ADK using the VAMM algorithm. (I) Definition of virtual bond (τ) and virtual dihedral (θ) angles.

For the crystal structure of open ADK, no outlier (>99%) was observed (Fig. 4A), and only two residues were outside the favored (>95%) region (Table S1). The virtual dihedral angle vs. bond angle plots for the VAMM-minimized open ADK structure (Fig. 4D) and for the open-state terminal intermediate state calculated by the VAMM algorithm (Fig. 4E) were both similar to the experimental result, with no outliers for either and only one residue for each outside the favored region.

In contrast to VAMM, intermediate states generated by using the control algorithms contained several outlier residues [nine from the simple harmonic model (Fig. 4B), and 24 from the bond-restrained model (Fig. 4C)]. Interestingly, restraining the virtual bond distances caused more unrealistic curvilinear distortions in ADK as a payoff for the more realistic Cα–Cα distances (Fig. 3A). Pathway calculations based on simple harmonic potentials clearly yield distorted molecules.

The distributions of virtual bond angles in (τ,θ) pairs from VAMM-based structures conform statistically with observations from the PDB (Fig. 4), which further validates VAMM as being sufficient to calculate intermediate states that are in accordance with the physical laws imposed on macromolecules. Moreover, because outliers occur frequently when simple harmonic potentials are used, we conclude that VAMM has a clear superiority in pathway calculations.

Distributions of Neighboring Dihedral Angles.

The analysis of virtual bond and dihedral angle distribution plots reveals that allowed virtual bond angles were confined to the interval 80° to 150°, whereas allowed dihedral angles spanned the entire range, from 0° to 360° (Fig. 4 A–E). Thus, an alternative approach is needed to analyze accuracy of the virtual dihedral angles. Here, we analyze distributions of the consecutive virtual dihedral angles preceding (θ⁻) and following (θ⁺) a given Cα atom, again deriving probability contours from the Top500 database. Values for open ADK were spotted on contoured θ⁻ vs. θ⁺ plots (Fig. 4 F–H).

The θ⁻/ θ⁺ plot from the open-state ADK crystal structure conformed well to the contours of allowance (Fig. 4F), but there were three outlier residues. These outlier dihedrals all joined central glycine residues, however, indicating a greater dihedral liberty at glycine positions, as is also seen in Ramachandran plots. The number of outliers dropped to two in the θ⁻/θ⁺ plot from the minimized open structure (Fig. 4G) and to one in the plot from the terminal intermediate state (Fig. 4H), both of which derived from VAMM. The θ⁻/θ⁺ plots from control-based structures showed 14 outliers (i.e., outside the 99% probability level) from the simple harmonic model, and 15 outliers from the bond-restrained potential (Table S1). Here again, we see that VAMM maintains structural integrity, in keeping with a realistic transition pathway, whereas unrealistic distortions are encountered in calculations from simple potentials.

Strain Energy of ADK Intermediates.

The strain energy of intermediate structures from ADK transitions was calculated with a double-well potential (see Methods). This strain energy is a measure of deviation from native contacts that exist in the initial input structures. Computational strains are shown for transition pathways based on each of the potential function algorithms (Fig. 5).

Fig. 5.

Energetics of ADK transitions. The strain energies stored in intermediate states are shown for trajectories computed with the simple harmonic (red), bond-restrained (green), and VAMM (blue) potentials. In each case, the strain energies in trajectories from both the open and the closed states are plotted against rmsd values between intermediates as they approach one another, ultimately reaching terminal intermediates.

The comparison shows that the VAMM-based conformational transition generated significantly less computational strain (maximal strain energy of 26.6 kcal/mol) than happened with the control algorithms (up to 219.1 kcal/mol and 199.5 kcal/mol from the simple harmonic and bond-restrained approaches, respectively). Values from harmonic potentials were in the same high range as those found with other coarse-grained approaches using similar potentials (17, 18). Thus, the VAMM algorithm significantly decreases the energy barrier for transition pathways, which is in accord with the more realistic geometric features and the greater efficiency of the method.

In summary, all of our tests validate the performance of the VAMM algorithm, and we describe results of our applications to ADK based entirely on VAMM computations.

Application Results

Conformational Transition Pathways in ADK.

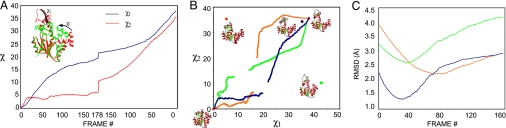
Differences between fully open (no ligand) and closed (Mg²⁺, Ap5A) states of ADK (9) are accounted for almost entirely by rigid hinge-bending rotations of the ATP-lid domain (χ₁) and the AMP-lid domain (χ₂) relative to the core domain, which we measured here relative to their dispositions in the closed state. By using program TOSS (23), we found that rotations of (χ₁ = 38.1°, χ₂ = 35.2°) superimpose the two lid domains from the open-state crystal structure onto those of the closed state, and thereby reduce the rmsd from 5.85 Å to 1.40 Å. The two terminal intermediates from the VAMM algorithm have very similar lid conformations (χ₁ = 21.6°, χ₂ = 10.6°) vs. (χ₁ = 19.4°, χ₂ = 6.1°), as generated from the open and closed states, respectively, and the terminal rmsd (1 Å) is even less than that from direct rigid-body superposition (1.40 Å).

The conformational transition between open and closed states of ADK is constructed as the joining of two trajectory segments, closure computed from a fully open state and opening from a fully closed state. We used the two lid-domain angles (χ₁ and χ₂) to monitor evolution of the trajectory and, because the terminal intermediates meeting from opposite directions are so similar, we invoked reversibility to reconstruct the entire transition from closed to open or vice versa (Fig. 6A). Closure from the open state proceeded quickly to reach (χ_1, χ₂) of (27.4°, 25.3°) after only 60 steps on way to the terminal intermediate (21.6°, 10.6°) at 178 steps. Further closure of the ATP lid (χ₁) proceeded more slowly, but the AMP lid (χ₂) closure continued at the same pace. Opening from the closed state proceeded sharply for the AMP lid (χ₂) for a few steps and then meandered slowly toward the terminal intermediate, whereas the ATP lid (χ₁) opened more smoothly over the course of ≈100 steps to (15.7°, 5.3°) before ultimately reaching the terminal intermediate (19.4°, 6.1°) at 178 steps. The juncture between forward and reverse directions was relatively smooth (Fig. 6 A and B).

Fig. 6.

The conformational transition of ADK. (A) The evolution of χ angles along the progression of ADK trajectories from closed (Left) and open (Right) states toward similar terminal intermediates (Middle). (B) The coupling of χ₁ and χ_2. The conformations of intermediate crystal structures are shown on the χ_1, χ₂ domain angle space alongside dots at respective χ_1, χ₂, color-coded corresponding to C. Trajectories are plotted starting from closed-state ADK (Left) and open-state ADK (Right): entire structure involved in targeting (blue), AMP-lid domain excluded from targeting (red), and ATP-lid domain excluded from targeting (green). (C) Deviations (rmsd) between the trajectory intermediate states and respective intermediate crystal structures: semiclosed apo state (PDB ID: 2RH5) vs. the fully targeted trajectory (blue); complex with ATP analog AMPPCF₂P (PDB ID: 1DVR) vs. the ATP-lid-directed trajectory (orange); and complex with AMP (PDB ID: 2AK3) vs. the AMP-lid-directed trajectory (green).

The computed transition pathway can be visualized in an animation of the course for closing from the open state through the terminal intermediate states to complete closure by reversal of opening from the closed state (Movie S1). This trajectory shows a very large rearrangement of the open state to a semiclosed form during the initial stages. This is consistent with the FRET experiments that showed the rapid partial closure of the open state (9). After the semiclosed state formed, the transition slowed down and did not sample a large space around this semiclosed form. The closed state sampled a narrower portion of the conformational space, with a limited opening of the ATP- and AMP-lid domains.

Comparison with Crystallographic Intermediate States.

We studied trajectories that targeted only one or the other lid domain as well as that for the entire ADK molecule. The couplings of χ₁ and χ₂ angles during these conformational transitions of ADK are shown in Fig. 6B together with the locations of intermediate ADK crystal structures in the (χ_1, χ₂) space. The trajectories, viewed from open (Fig. 6B Upper Right) to closed (Fig. 6B Lower Left) states, can be thought to mimic the binding of Ap5A (Fig. 6B, blue curve) and, in some sense, of ATP (Fig. 6B, red curve) and AMP (Fig. 6B, green curve). The entire structure was included in the transition pathway calculation for the blue curve, but the AMP-lid domain was excluded from calculations of involvement coefficients for the red curve, and the ATP-lid domain was excluded for the green curve. Such domain-selected calculations can be used for dissecting potential allosteric couplings; based on our calculations, the two closures in ADK are relatively uncoupled.

When both lid domains were targeted, ADK followed an initial trajectory roughly diagonal in the (χ_1, χ₂) space. It passed at (χ₁ = 36.1, χ₂ = 33.3°), very close to values (χ₁ = 35.1°, χ₂ = 34.3°) of a semiclosed structure (PDB ID: 2RH5, chain C), which has been shown to lie on the trajectory of ADK closure (9). When only the core and ATP-lid domains were targeted, as in a trajectory that might be induced by binding of an ATP analog (7), intermediate states approached (χ₁ = 18.2°, χ₂ = 30.2°), the conformation (χ₁ = 5.1°, χ₂ = 35.4°) of an ATP-lid closed/AMP-lid open crystal structure (PDB ID: 1DVR). When only the core and AMP-binding domains were targeted, intermediate states approached (χ₁ = 34.1°, χ₂ = 25.0°) the conformation (χ₁ = 42.8°, χ₂ = 10.3°) of the crystal structure (PDB ID: 2AK3) of an AMP complex (24).

Deviations of computed trajectory intermediates from crystal structures of intermediate states are consistent with the preceding (χ_1, χ₂) plot analysis. Minima close to experimental intermediates occurred in each of the respective rmsd plots against intermediate crystal structures (Fig. 6C). The closest approaches of trajectory intermediates to the observed crystal structures were at 1.34 Å rmsd for the semiclosed apo state (Fig. 6C, blue), 2.21 Å rmsd for the ATP analog complex (Fig. 6C, orange), and 2.59 Å for the AMP complex (Fig. 6C, green). The red and green domain-selected trajectories are biased toward the respective ATP and AMP complex structures, but their more distant close approaches may reflect either coupling between the lid domains or calculation defects.

Discussion

In all respects, the VAMM force field with its associated algorithm for iterative fitting of normal modes and energy minimization is superior in conformational transition calculations to algorithms based on simple harmonic potentials. This is not to diminish that elastic network models are highly effective for analyzing motions near the native state. First, transition pathway calculations are significantly more efficient with the VAMM-based algorithm. Second, with simple potentials, the Cα–Cα bond distances show absurd deviations from their equilibrium states, whereas the VAMM preserves the virtual Cα–Cα bond integrity. Third, the VAMM-based algorithm generates accurate virtual bond and dihedral angles compared with the simple network models. Fourth, the VAMM-based algorithm generates a transition trajectory with significantly lower computational strain.

Several computational and experimental studies of protein dynamics show that proteins in an unbound state can fluctuate with varying populations over an ensemble of conformations that sample states adopted in complexes with ligands or binding partners (25–27). The conformational space accessible to an uncomplexed apo state is likely to be greater than that accessible in a state closed down onto a ligand. The transition pathways found here for ADK are consistent with this view. In our calculations, ADK moves quite freely and rapidly away from the open state but more slowly and with greater restriction away from the closed state (Figs. 2B and 6A). Indeed, the most populated subspaces may not necessarily lie on the most likely trajectory. Relaxed states that approach the “closed-state ensemble” defined by the restricted fluctuations about the closed state dictate the most likely conformational trajectory. In our current description of the ADK system, slight openings of the ATP- and AMP-lid domains are followed by further opening of the ATP-lid domain within the narrow conformational space of the closed system. Open states that can adapt to this confine are selected to drive the full conformational transition. A more realistic description of such conformational transitions will require inclusion of stochastic processes in the algorithm to yield an ensemble of transition pathways populated around the most likely pathway.

The VAMM algorithm for conformational transition pathway calculations is very versatile and not restricted by ADK-specific characteristics. Because of its coarse-grained nature, it is not limited by protein size; because it uses iterative normal-mode fittings rather than simulations requiring short integration time intervals, it is not limited by the amplitude or time scale of the conformational change. Moreover, because the VAMM potential is completely general, the algorithm is not limited to hinge-bending motions. It is directly applicable as well to shear motions, as in citrate synthase (28), or more complicated conformational changes such as in HIV envelope glycoprotein gp120. Being coarse-grained, VAMM necessarily has limitations; for example, there is insufficient detail for calculation of energetic barriers. Nevertheless, we expect that the VAMM algorithm for conformational transition calculations will be useful quite generally in describing large conformational transitions in even the largest of protein complexes.

Methods

Potential Functions.

We have performed parallel calculations based on three different coarse-grained potential functions.

A simple harmonic potential function, which models all interactions between residues within a cutoff radius (13 Å) as springs to calculate a subset of the slow normal modes (29), serves as a control. It is given by

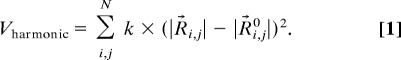A uniform spring constant k of value 1 kcal/molŲ is adopted for all residues that are closer than the cutoff distance. R_ij represents the displacement vector, and R_ij⁰ represents the equilibrium distances between positions of Cα atoms i and j. N is the number of residues.

An alternative approach is taken to introduce additional restraints to the neighboring Cα atoms to model pseudo bonds between each residue. The modified potential becomes

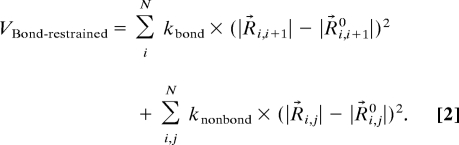In this bond-restrained model, k_bond is the spring constant of the interaction between neighbor Cα atoms, and k_nonbond is the spring constant of the interaction between nonbonded neighbor Cα atoms. A value of 70 kcal/molŲ is adopted for k_bond based on the statistical analysis and Boltzmann inversion of the crystallographic data.

The fully elaborated VAMM force field is

where each of the terms is defined in a companion paper (19). In brief, V_bonded is the same bond-restraint term as for V_{Bond-restrained} in Eq. 2, including separate definitions for trans- and cis-peptide bonds and for disulfide bonds; V_angle is for restraints on virtual bond angles τ, which depend on type of secondary structure; V_dihedral is for restraints on virtual dihedral angles θ, which also depend on secondary structure; V_nonbonded is for restraints on nonbonded interactions between atom pairs more than five residues apart, which are specific to amino acid identities; and V_local is for restraints that maintain local geometries.

Iterative Normal-Mode-Driven Transitions.

We computed the transition pathway between two alternative conformations, A (e.g., open-state ADK) and B (e.g., closed-state ADK), by moving each structure toward the other in iterations of moves directed at each step along the normal mode of greatest engagement with its target structure. Only protein residues are modeled; bound ligands are implicit. For each structure, from the starting points at A₀ and B₀ through intermediates A_i and B_i at each step i, the Hessian matrix is constructed from the particular potential function used in that analysis (Eq. 1, 2, or 3) and diagonalized to compute normal modes (30, 31).

In general, 20 slow modes are considered sufficient to span the slow fluctuations of macromolecules that sample the functional motions (17). Thus, we screened the 20 lowest-frequency normal modes for each of conformations A_i and B_i to find that normal mode from each vibrating state having the greatest Marques–Sanejouand overlap factor (32) with the alternate, target state. This factor, also called the involvement coefficient by Ma and Karplus (33), measures how much a given normal mode contributes to the molecular displacement between two conformers. The involvement coefficient, I_ik, is the projection of the normal-mode vector onto the linear displacement:

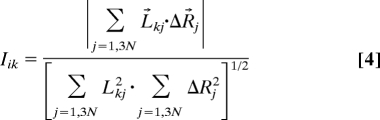where at step i, L_kj is the component from eigenvector k acting on atom j, and ΔR_j is the displacement vector between the intermediate states generated from alternative starting structures. Both for the mode from A_i with highest involvement coefficient into the direction of B_i and for the mode of B_i with highest involvement coefficient into the direction A_i, each direction of the mode must be tested, which we do by calculating the pairwise rmsd values between four possible conformers generated from states A_i and B_i after applying shifts dictated by the respective modes in each of the alternative directions.

The shifts for each move for residue j are found by

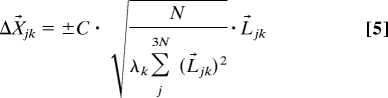where C is a constant chosen as 0.005, λ_k is the eigenvalue of mode k, L_jk is the eigenvector for mode k acting at atom j, and ± refers to the alternative directions for this mode. Tests showed that the nature of conformational transitions is relatively insensitive to the value of C within a certain interval (Table S2), and 0.005 was chosen so that the calculations are performed within a feasible CPU time and without unrealistic distortions due to large step sizes.

The two new conformers from shift sets giving minimal rmsd values then become the input structures for the next iteration step. The process continues until intermediate conformers A_i and B_i converge to within the convergence criteria, which is usually set as an rmsd value of 1 Å. This cutoff value is appropriate because the normal modes calculated from two structures that are closer than 1 Å rmsd are not significantly different (34), and two such structures are generally very similar, except at flexible loops. A more lenient criterion might be set in cases where complicated motions, such as in flexible loops or local folding events, are also involved in contrast to the transition observed in ADK.

Control Algorithm.

Computations of conformational transitions with the simple harmonic potential (Eq. 1) or the bond-restrained harmonic potential (Eq. 2) use the algorithm shown in Fig. S3. Normal modes and iterative moves are made as described above, sampling the 20 lowest-frequency modes and moving in the direction of normal modes having greatest involvement in the directions toward the respective target structures.

VAMM Algorithm.

Computations of conformational transitional pathways with the VAMM potential function (Eq. 3) use the algorithm shown in Fig. S4. The VAMM algorithm is similar to the control algorithm, but additional requirements are imposed. In the initial step, secondary structures needed for VAMM are assigned from the crystal structure coordinates of conformers A₀ and B₀ by using the DSSP algorithm (35). This step is followed by a truncated Newton minimization of the Cα system in the VAMM force field to a gradient of 0.1 kcal/molÅ (36). Hessian matrices are constructed from each of these minimized structures by using VAMM and are then diagonalized for normal-mode evaluations. The procedure is iterated as described above to generate successive intermediates A_i and B_i. As the calculation proceeds, secondary structures of the computed intermediate states are updated at intervals of 0.1 rmsd (rmsd_UPDATE) between the calculated intermediate states. The rmsd_UPDATE values between 0.1 and 0.5 Å generated reliable and consistent results on calculation of the ADK transition. In addition, energy minimizations of the intermediate states are performed whenever the energy gradient rises above 1 kcal/molÅ. This approach keeps the system near-local energy minima and also helps to relax artificially high strains. The convergence criterion is again 1 Å rmsd.

Distributions of Virtually Bonded Conformation Parameters.

Probability contour plots for relevant conformational parameters were evaluated from the same Top500 database (21) as used to produce Ramachandran plots by the MolProbity software (37). Details are in SI Text.

Strain Energy of Intermediate States.

Strains that accumulate during conformational transitions are calculated with a double-well potential similar to that for the plastic network model (18). Details are in SI Text.