Classification and energetics of the base-phosphate interactions in RNA

Craig L Zirbel; Judit E Šponer; Jiri Šponer; Jesse Stombaugh; Neocles B Leontis

doi:10.1093/nar/gkp468

. 2009 Jun 14;37(15):4898–4918. doi: 10.1093/nar/gkp468

Classification and energetics of the base-phosphate interactions in RNA

Craig L Zirbel ^1,2, Judit E Šponer ³, Jiri Šponer ³, Jesse Stombaugh ^2,4, Neocles B Leontis ^2,4,^*

PMCID: PMC2731888 PMID: 19528080

Abstract

Structured RNA molecules form complex 3D architectures stabilized by multiple interactions involving the nucleotide base, sugar and phosphate moieties. A significant percentage of the bases in structured RNA molecules in the Protein Data Bank (PDB) hydrogen-bond with phosphates of other nucleotides. By extracting and superimposing base-phosphate (BPh) interactions from a reduced-redundancy subset of 3D structures from the PDB, we identified recurrent phosphate-binding sites on the RNA bases. Quantum chemical calculations were carried out on model systems representing each BPh interaction. The calculations show that the centers of each cluster obtained from the structure superpositions correspond to energy minima on the potential energy hypersurface. The calculations also show that the most stable phosphate-binding sites occur on the Watson–Crick edge of guanine and the Hoogsteen edge of cytosine. We modified the ‘Find RNA 3D' (FR3D) software suite to automatically find and classify BPh interactions. Comparison of the 3D structures of the 16S and 23S rRNAs of Escherichia coli and Thermus thermophilus revealed that most BPh interactions are phylogenetically conserved and they occur primarily in hairpin, internal or junction loops or as part of tertiary interactions. Bases that form BPh interactions, which are conserved in the rRNA 3D structures are also conserved in homologous rRNA sequence alignments.

INTRODUCTION

Structured RNA molecules form compactly folded architectures, superficially resembling folded proteins. This tight packing is remarkable considering that each RNA nucleotide bears a full negative charge. RNA molecules must therefore overcome significant electrostatic self-repulsion to fold compactly. Part of the repulsion is eliminated by mobile as well as structurally bound monovalent and multivalent cations, especially Mg²⁺ (1). Basic proteins also play important roles in facilitating RNA folding and stabilizing the compact biologically active structures of large RNAs (2). As the negative charge of each nucleotide is concentrated on the anionic oxygen atoms of phosphate groups, they can form very strong hydrogen bonds (H-bonds) with appropriate donors. The RNA bases (A, C, G and U) each present multiple H-bond donors that can interact with phosphate groups and thereby help reduce intra-molecular RNA self-repulsion and stabilize compactly folded, functional structures. In this contribution, we examine the stabilizing interactions between nucleotide bases and the phosphate backbone moieties, which we refer to as ‘base-phosphate’ (‘BPh’) interactions.

RNA 3D motifs, ordered arrays of non-Watson–Crick (non-WC) base pairs formed by the nucleotides of hairpin, internal and junction ‘loops' of the secondary structure, mediate most of the tertiary RNA interactions that lead to compact folding (3). Previous work has shown that many recurrent 3D motifs contain specific BPh interactions, in addition to base pairing (BP) and base stacking (BSt) interactions (3,4). The bases forming BPh interactions cited in the literature tend to be highly conserved. For instance, many hairpin loops, including the anti-codon and T-loops of tRNAs (5), contain the ‘U-turn' submotif, a sharp bend in the backbone stabilized by a H-bond between the U(N3) imino position and the phosphate of the N+3 base of the loop (6,7). GNRA hairpin loops contain similar motifs, with the imino N1 and/or amino N2 positions of the conserved G forming the BPh interaction (8). A conserved BPh interaction also involving G is observed in recurrent sarcin/ricin (S/R) internal loop motifs (9). Conserved GU wobble base pairs were observed to bind anionic oxygen phosphate atoms in the minor groove to facilitate tight packing of helical elements (10). These examples suggest that BPh interactions may be widespread in RNA structures and may play significant roles in RNA folding.In this article, we empirically identify and categorize BPh interactions from 3D structures and propose a unified classification and nomenclature for them. We apply ab initio quantum chemical methods to obtain optimized geometries for each empirically identified interaction and to evaluate their intrinsic stabilities. We then use the optimized geometries to define geometric criteria to identify and classify BPh interactions in 3D structures. The classification criteria were implemented in the ‘Find RNA 3D'—FR3D (11) software suite (http://rna.bgsu.edu/FR3D). We assess the significance of these interactions in stabilizing RNA 3D structures by identifying the contexts, occurrences and base conservation of these interactions, using 3D structural alignments of the 16S and 23S ribosomal RNA (rRNA) structures of Escherichia coli and Thermus thermophilus (12). After comparing the rRNA 3D structures to identify conserved BPh interactions, we examine rRNA sequence alignments to determine the base frequencies and substitution patterns at sites where we observe conserved BPh interactions in the 3D structures. Finally, we compare the contributions of BPh interactions, WC and non-WC base pairs and BSt interactions to nucleotide conservation, using linear regression.

Base-phosphate interactions may also affect the properties of nucleic acids by more subtle effects, such as the polarization of the nucleobase rings. Such effects are more difficult to capture and their consideration remains for future investigations. Transient BPh interactions may play a role in RNA catalysis, e.g. by stabilizing transition states or facilitating protonation of leaving groups (13–15).

MATERIALS AND METHODS

Datasets

RNA-containing atomic-resolution X-ray crystal structures of RNA with resolution better than 4.0 Å were downloaded from the Protein Data Bank (PDB, http://www.rcsb.org/pdb/) (16). FR3D was used to add hydrogen atoms to experimental 3D structures by fitting ab initio calculated base geometries containing hydrogens to experimental base coordinates (11). Sequence alignments for 16S and 23S rRNAs were downloaded from the European Ribosomal RNA Database (17), in January 2007 from http://bioinformatics.psb.ugent.be/webtools/rRNA/.

Software

We used MATLAB version 7.5.0.338 (R2007b) for program development and Microsoft Excel for tables. PDB files were analyzed and classified using the ‘FR3D' program (11) available at http://rna.bgsu.edu/FR3D/. To eliminate redundant sequences from sequence alignments, we used the SeqQR program (18) obtained from http://www.scs.uiuc.edu/∼schulten/software/.

Hardware

Data were analyzed using a MacBook (Mac OS X) with an Intel Core Duo running at 2 GHz and with 2 GB of RAM along with a Dell Optiplex GX280 with two Intel Pentium 4 processors running at 3.4 GHz and with 1 GB of RAM.

Selection of non-redundant sequences for BPh analysis

We identified the most complete 16S or 23S sequences for each species in the rRNA sequence alignments obtained from the European Ribosomal RNA Database as previously described (12) and employed the SeqQR program to filter redundant sequences from the alignments, using the following program parameters: (i) sequence identity cutoff of 95%; (ii) gap scale of 0.5 and (iii) norm value of 2 (18). The final sequence alignments comprise 717 16S sequences and 136 23S sequences (12).

Selecting a reduced-redundancy set of PDB files for analysis

The RNA-containing 3D structures deposited with the PDB contain multiple versions of some RNA structures (e.g. 1ffk, 1jj2 and 1s72 are all 3D structures of the Haloarcula marismortui 23S rRNA). We selected a reduced-redundancy set of PDB files for analysis as previously described (12) and these files are listed in ‘Supplemental Materials S4' of Stombaugh et al. (12). Statistical analyses of this dataset in the current paper were restricted to the 159 files having reported resolution 2.5 Å or better.

Initial geometries used in quantum chemical calculations

Representative interactions from 3D structures were identified through the initial search described in the first section under ‘Results', by calculating the H-bond distance between phosphate oxygens and base H-bond donors. A qualified estimate of the H-bonding distance was obtained from the sum of the van der Waals radii of the H-bond donor group and the acceptor atom (19). This means that the distance of H-bond donor and acceptor atoms was selected to be below 3.2 Å for N-H … O and 3.5 Å for C-H … O H-bonds. After identifying the representative interactions, we constructed model geometries of the representative BPh interactions for quantum mechanical (QM) calculations. Each model consisted of a nucleobase and a phosphate group, with the oxygen atoms representing the O3′ and O5′ atoms of the sugar–phosphate backbone terminated by hydrogen atoms. Thus, the total electrical charge for the studied models was –1. Since the purpose of the QM calculations was to make a general classification of the interaction patterns, we intentionally constructed the simplest possible models. We subsequently performed structural relaxation on these geometries so that the final geometries were not affected by small details of the starting structures.

The QM analysis was performed in two steps. First, we optimized the geometries, and then we used the optimized geometries to derive interaction energies to characterize the strength of each BPh interaction.

Geometry optimizations

Models were optimized using the gradient optimization technique. For each model, we optimized all geometrical parameters (full geometry optimization). The calculations were carried out at the Density Functional Theory (DFT) level of theory using the Gaussian03 program package (20). The density functional was constructed using Becke's three-parameter exchange (21) and Lee-Yang-Parr's (22,23) correlation functional (B3LYP). The 6–31G^** basis set was used for geometry optimizations, augmented by diffuse d-polarization functions on phosphorus (exponent: 0.0348) as well as on the anionic oxygens of the phosphate group (exponent: 0.0845). This is a standard approach used to describe highly polarizable atoms and anions with electron clouds reaching far from the atomic centers (24). Our previous studies have shown that the B3LYP/6–31G^**-optimized structures compare quite well with reference RIMP2/cc-pVTZ data for H-bonded systems and are entirely sufficient for subsequent high-quality interaction energy calculations (25).

Because all systems in the present study have a formal charge equal to –1, all computations were carried out in a dielectric continuum using the COSMO solvation model (26–28), setting the dielectric constant at ϵ = 78.4 (the value for pure water). This method reasonably represents the balance of various stabilizing forces acting in charged intermolecular complexes (29). QM interaction energies are usually calculated in the gas phase (in vacuo). However, for electrically charged systems, the interactions in vacuo are dominated by long-range molecular ion-molecular dipole contributions. For biomolecules in their normal environments, these long-range interactions are compensated by solvation. Therefore, to make the calculations more relevant to RNA molecules in solution, we included solvation effects in the calculations so as to quench the full expression of the anionic electrostatic interactions (30). In addition, use of continuum solvent prevents formation of irrelevant H-bonds in the course of geometry optimization and helps us to determine more reliably the relative stability order of the individual types of BPh interactions.

Interaction energies

Interaction energies were calculated for the optimized geometries. The BPh interaction energy (ΔE^BPh) is used to characterize the strength of the direct intermolecular forces acting between the phosphate and the nucleobase. ΔE^BPh is defined in Equation (1).

Here E^BPh stands for the electronic energy of the whole system, and E^B and E^Ph are the electronic energies of the isolated subsystems, i.e. nucleobase (B) and phosphate (Ph). The interaction energy is usually derived assuming in vacuo environment, and in this case, (Equation 1) corresponds to the change in enthalpy, without the zero point vibrational energy contribution, of a hypothetical in vacuo dimerization process at a temperature of 0 K. This describes the electronic structure part of the interaction energy, which modern QM methods can derive with very high accuracy (31).

In general, the interaction energy (Equation 2) has two components, the Hartree–Fock (HF) term, ΔE^HF, and the electron correlation term, ΔE^corr (32). They are calculated consecutively.

The ΔE^HF term accounts mainly for the electrostatic (Coulombic) effects. This term also includes a large portion of the polarization (induction) and charge-transfer effects. Besides these attractive contributions, the ΔE^HF term also contains the short-range exchange repulsion reflecting the mutual repulsion of the electronic clouds once they start to penetrate each other. The ΔE^corr term includes dispersion attraction and corrections to other terms arising from the correlated motion of the electrons.

In this study, we derived the interaction energies in the frame of the COSMO dielectric continuum approach that adds the mean-field effect of solvent screening of the electrostatic forces (26–28). The calculations were done at the RIMP2 level of theory using the aug-cc-pVDZ basis set of atomic orbitals. The RIMP2/aug-cc-pVDZ method achieves a close to quantitative accuracy for H-bonded and ionic molecular clusters and is entirely sufficient for the purpose of this study. The RIMP2 method for calculating interaction energies has been validated in previous studies (25,33). These calculations were done as follows: first we computed interaction energies in the gas-phase using the optimized geometries obtained with the COSMO solvation model (see above). We carried out these calculations with and without correction for the ‘basis set superposition error'—BSSE (34). BSSE is a mathematical artifact that arises from using a finite basis set of atomic orbitals. All calculations should be corrected for BSSE, as explained in Sponer et al. (35). The difference of the BSSE-corrected and uncorrected interaction energies gives the BSSE correction (δ^BSSE). In the next step we computed the BSSE-uncorrected interaction energy at the RIMP2/aug-cc-pVDZ level using the COSMO dielectric continuum model (ΔE_COSMO). Then, the final BSSE-corrected interaction energy, computed with the COSMO dielectric continuum model (ΔE_COSMO^BSSE), was calculated using Equation (3).

This represents the desired interaction energy, i.e. ΔE^BPh from (1) with the added solvent screening correction. For simplicity, we rename and refer to this quantity as E^INT. Thus,

All RIMP2 calculations were performed with the Turbomole code (36–38). For the sake of completeness, gas-phase interaction energies derived without the solvent screening are given in the supporting information (Supplementary Data S1).

Modifications to the FR3D program suite

New modules were written for FR3D to find and classify BPh interactions in RNA 3D structures. These modules have been incorporated in the new release of FR3D, http://rna.bgsu.edu/FR3D/. With this new release, users can launch searches for RNA motifs using as search criteria BPh or near-BPh (nBPh) interactions as constraints between specified pairs of nucleotides.

Construction of rRNA 3D structural alignments

The FR3D program suite, modified as described above was used to identify and classify BPh interactions from selected 3D files of the 16S and 23S rRNAs of E. coli—PDBs: 2avy and 2aw4 (39)—and T. thermophilus—PDBs: 1j5e (40) and 2j01 (41). The BPh lists generated by FR3D for homologous rRNA structures were imported into Excel and aligned horizontally to identify conserved BPh positions. The complete BPh 3D alignments for 16S and 23S rRNA are provided in Supplementary Data S2 as MS Excel files to allow the reader to access and manipulate the data as desired. BPh interactions are listed in the alignments in the order of the number of the nucleotide that H-bonds using its base. Column A in the Excel file provides a running index to restore the original order of the alignment after manipulation. Column B is used to indicate BPh interactions that are conserved between the E. coli and T. thermophilus structures (an ‘X' indicates conservation). The nucleotide number and base identity for the H-bond donor in each BPh interaction are listed in columns E and F for the E. coli structure and in N and O for the T. thermophilus structure. BPh acceptor nucleotide data are listed in columns G and H (E. coli) and P and Q (T. thermophilus). Occurrence frequencies from homologous rRNA sequence alignments were computed for each H-bond donor base (columns V-AA) and phosphate acceptor (columns AC-AH) in the BPh alignment using the E. coli structure as the reference. Columns AJ and AK provide comments describing those BPh interactions that could not be aligned between the E. coli and T. thermophilus 3D structures.

RESULTS

Identification of BPh interactions in 3D structures

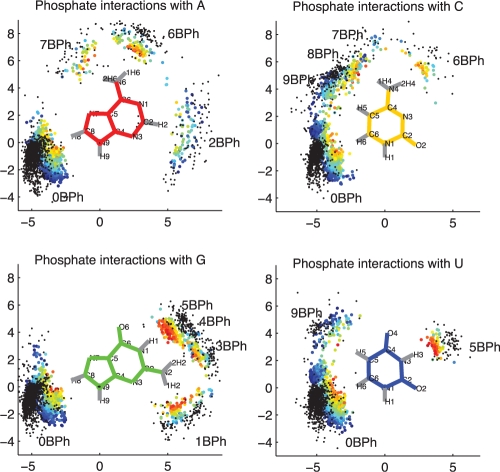
We searched the reduced-redundancy set of RNA 3D structures to locate all phosphate groups within H-bonding distance of some nucleobase (12). To visualize the potential interactions, we superposed the interacting bases for each potential BPh interaction and then plotted the positions of the phosphorous and the phosphate oxygen atoms that are closest to the corresponding H-bond donor atom of the base. Projections of these data onto the plane of the donor base are shown in Figure 1, color-coded according to the distance between the H-bond donor and the nearest phosphate oxygen atom.

The data in Figure 1 show that all four RNA bases can form more than one BPh interaction. Most interactions involve H-bonding to a single phosphate oxygen, but the C and G bases have interactions in which two oxygen atoms of the same phosphate simultaneously H-bond to distinct base H-bond donors. For C, these simultaneous interactions involve N4 and C5 on the Hoogsteen edge, and for G, they involve N1 and N2 on the WC edge. These H-bond donors can also make non-simultaneous interactions, bringing the total number of distinct potential BPh interactions to 17. Rather than simply labeling them 1–17, we categorize the interactions as indicated in Figure 1, using labels 0BPh through 9BPh, so that the label indicates, in a consistent way for all four bases, the location of the base H-bond donor group relative to the glycosidic bond and the base edges. The 4BPh and 8BPh labels are used for the simultaneous interactions made by G and C, respectively. There are a few instances in which a single phosphate oxygen H-bonds simultaneously to G(N1) and G(N2). These instances involving bifurcated H-bonding are also classified as 4BPh.

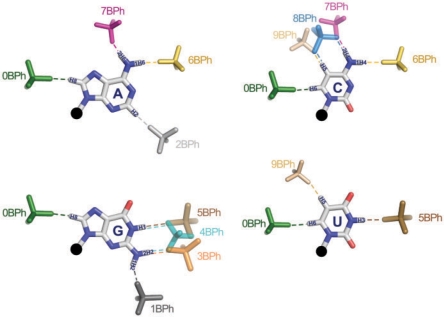
Idealized BPh interactions and the corresponding category labels are shown in Figure 2. While each base presents distinct combinations of H-bond donors and acceptors, certain bases have electropositive functional groups at equivalent positions and therefore can form equivalent BPh interactions, as shown in Figure 2. BPh interactions which are formed by more than one base include 0BPh, 5BPh, 6BPh, 7BPh and 9BPh. All bases can form 0BPh interactions using the purine H8 or pyrimidine H6 proton as H-bond donor. Both A (upper-left panel) and C (upper-right panel) can form 6BPh and 7BPh interactions using equivalent exocyclic amino groups at the A(N6) and C(N4) positions. Similarly, G (lower-left panel) and U (lower-right panel) can form equivalent 5BPh interactions using the G(N1) or U(N3) imino groups on their WC edges. The 3BPh, 4BPh and 5BPh interactions all occur on the WC edge of G and are possibly interchangeable during conformational changes or thermal fluctuations of RNA molecules. Likewise, the 7BPh, 8BPh and 9BPh interactions all occur on the Hoogsteen edge of C and may also be interchangeable. The other interactions are specific to individual bases: 1BPh, 3BPh and 4BPh are specific to G, 2BPh is specific to A and 8BPh is specific to C. We refer to BPh interactions that occur on the same edge of the same base as neighboring interactions. When comparing homologous 3D structures, we expect to observe the same or possibly neighboring BPh interactions at homologous locations where the base forming the BPh interaction is conserved. When a base substitution occurs, we expect that for the BPh interaction to be maintained without a large conformational change or disruption of the structure, an equivalent BPh interaction must form. This suggests BPh interactions that are crucial for RNA folding, stability and function constrain the sequence variation of homologous RNA molecules. This idea will be examined in detail later in the paper.

Quantum chemical calculation of optimized geometries and interaction energies for BPh interactions

Quantum calculations were carried out for each of the 17 distinct potential BPh interactions identified above. As described in the ‘Materials and Methods’ section, model geometries were constructed for each interaction formed by each base using the empirical structures as a guide. The geometries were optimized quantum mechanically and then interaction energies were calculated. PDB files with the optimized geometries can be viewed and downloaded at http://rna.bgsu.edu/FR3D/BasePhosphates. We present the calculated interaction energies and optimal distances in Table 1 and summarize the results base by base in this section.

Table 1.

Energies and H-bond distances for BPh interactions (0BPh-9BPh) by nucleotide (A, C, G, U)

	A		C		G		U
	E^INT (kcal/mol)	H-Bond Distance (Å)	E^INT (kcal/mol)	H-Bond Distance (Å)	E^INT (kcal/mol)	H-Bond Distance (Å)	E^INT (kcal/mol)	H-Bond Distance (Å)
1BPh					−4.3	2.85 (N2)
2BPh	−0.1	3.41 (C2)
3BPh					−5.4	2.80 (N2)
4BPh					−10.1	2.85 (N2)⁽¹⁾
						2.89 (N1)⁽²⁾
5BPh					−4.0	2.92 (N1)	−4.2	2.81 (N3)
6BPh	−3.1	2.90 (N6)	−3.5	2.89 (N4)
7BPh	−2.8	2.77 (N6)	−4.8	2.85 (N4)
8BPh			−5.6	2.86 (N4)⁽¹⁾
				3.53 (C5)⁽²⁾
9BPh			−0.6	3.35 (C5)			−0.6	3.34 (C5)
0BPh	−1.1	3.22 (C8)	−1.0	3.21 (C6)	−1.1	3.25 (C8)	−1.1	3.23 (C6)

Open in a new tab

Each nucleotide is represented by two columns:

⁽¹⁾The calculated interaction energy (kcal/mol);

²Distance (in Å) from H-bond donor to acceptor. The H-bond donor site is given in parentheses.

Adenine

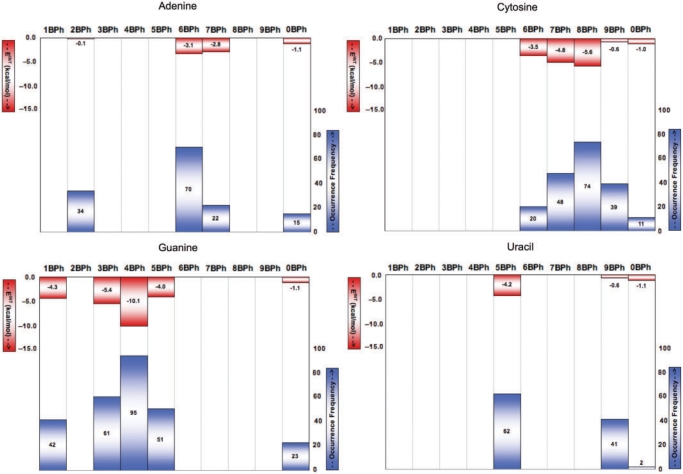
Adenine can H-bond to phosphates with the exocyclic amino group (N6) as well as the polarized C2-H2 and C8-H8 groups (Table 1, columns 1–2, and Supplementary Data S3). H-bonding with the less polarized C-H groups is markedly weaker (interaction energies are –0.1 and –1.1 kcal/mol for C2-H2 and C8-H8, respectively) than with the N6-amino group (computed interaction energies are –3.1 kcal/mol for 1H6 and –2.8 kcal/mol for 2H6).

Cytosine

Cytosine forms five different binding patterns with phosphate, utilizing its N4 exocyclic amino group as well as the C5-H5 and C6-H6 groups (Table 1, columns 3–4, and Supplementary Data S4). The strongest binding mode for cytosine occurs on the Hoogsteen edge when the H-bond from the N4 amino group to the phosphate is supplemented by an H-bond from C5-H5. We have found three different types of stable binding that differ as to which phosphate oxygens are involved: (i) N-H binds to an anionic oxygen, while C-H binds to O3′ or O5′; (ii) N-H and C-H both bind to anionic oxygens and (iii) N-H and C-H both bind to O3′/O5′. While the first two variants possess almost identical stabilities (computed interaction energies are –5.4 and −5.6 kcal/mol, respectively), the Bph contact is noticeably weaker in the third case (interaction energy is −2.5 kcal/mol). We have also attempted to optimize a fourth possible variant, i.e. when C-H binds to an anionic oxygen and N-H to O3′ or O5′. We could not locate the corresponding minimum energy geometry on the potential energy hypersurface, since after a couple of steps the optimization was driven into the first geometry, with the amino group binding to the anionic oxygen. These results indicate that the most stable binding occurs when cytosine N6 H-bonds to an anionic oxygen and C5 H-bonds either to an anionic or ester oxygen.

Each of the other four binding patterns is stabilized by single H-bonds between the nucleobase and one of the anionic oxygens of the phosphate.

Guanine

Guanine establishes H-bonds with the phosphate group in five different ways (Table 1, columns 5–6, and Supplementary Data S5), three of which use the exocyclic N2 amino group. In addition, the endocyclic imino group (N1) and the C8-H8 bond are capable of donating H-bonds to phosphate oxygens.Guanine is unique in forming the 4BPh interaction, which is overall the most stable BPh interaction by far. The 4BPh interaction comprises two strong H-bonds between nitrogen donor groups of the base (N2 and N1) and two distinct oxygen acceptors of the phosphate group. The acceptor groups can be the anionic oxygens of the phosphate group or the O3′ or O5′ atoms of the riboses. Depending on the type of acceptor oxygens, the computed interaction energy pattern ranges from –5.3 to –10.1 kcal/mol. In the weakest form of the 4BPh interaction (with an interaction energy of –5.3 kcal/mol) N2 and N1 of guanine interact with O3′ and O5′ of the same phosphate group. The interaction is noticeable stronger (–7.8 and –8.3 kcal/mol) when N1 and N2 interact with one anionic phosphate oxygen and one O3′ or O5′ atom. Finally, the highest stability is obtained when N1 and N2 both H-bond to anionic oxygens (−10.1 kcal/mol).

In addition, we have found a peculiar alternative for 4BPh, a bifurcated binding mode in which N2 and N1 bind to the same anionic oxygen of the phosphate group (Supplementary Data S5). The computed stability of this binding mode is relatively high (–8.8 kcal/mol). Note that this is the only bifurcated binding pattern found for BPh interactions. For example, we tried to optimize the bifurcated analog of 8BPh for cytosine but this failed since the optimized geometry was identical to 7BPh of cytosine, showing that the bifurcated binding is not stable if the H-bonding ability of the adjacent H-bond donors differ markedly (the 8BPh binding mode of cytosine combines C–H and N–H H-bonds.). This does not rule out the occurrence of such an interaction in RNA molecules, however, the geometry would have to be constrained by some other interactions, in contrast to the BPh interactions that are intrinsically stable.

Due to the significant stability of the 4BPh binding pattern, we could not optimize the geometry of the G 5BPh binding pattern which involves exclusively N1 of guanine. All optimization attempts resulted in the significantly more stable 4BPh combined binding mode. To avoid H-bond formation by the N2 amino group during geometry optimization, we replaced the N2-H2 atom with a methyl group. This electronically neutral substitution blocks H-bond formation by the N2 amino group and allowed for optimizing the geometry and calculating the energy of the 5BPh model representing G(N1)-binding.

Uracil

Uracil may bind to phosphates using its N3 endocyclic H-bond donor group on the WC edge or its C5-H5 and C6-H6 groups on the Hoogsteen edge (Table 1, columns 7–8, and Supplementary Data S6). Of these three phosphate-binding modes, the H-bond formed with the N-donor is markedly stronger (with interaction energy of –4.2 kcal/mol) than those having C-donors (interaction energies are –0.6 kcal/mol and –1.1 kcal/mol for C5 and C6, respectively). Since the N3 position of uracil is on the WC edge, while C5 and C6 are on the Hoogsteen edge, no combined binding modes involving an N-H donor are possible for uracil.

Significance of computed BPh interaction energies

The interaction energies reflect the intrinsic binding energy between the base and phosphate in a given geometry and report the difference in electronic energy between the bound and unbound systems. The relationship between the geometry and the energy complements the purely geometrical information obtained experimentally. The interaction energy describes the most interesting component of the binding that comes from the electronic structure, which tells us how the electronic shells of base and phosphate communicate with and adapt to each other (42). However, these calculations do not include non-electronic contributions to binding and thus cannot be directly compared with the free energies of binding. The non-electronic terms, including entropy terms, are highly variable and depend on the specific contexts of the interactions, while the electronic component reports on the intrinsic strength of the interaction. Since the BPh systems are not electrically neutral, we report the interaction energies derived with continuum solvent screening, to attenuate the long-range ionic electrostatic effects. In summary, the interaction energies provide the basic stability ranking for the individual BPh interaction types reflecting the strength of the bond formed between the H-bond donor and acceptor. The actual contributions to free energy may be further modulated by the specific context of each interaction.

We refer the reader to Supplementary Data S7, where we present the results of calculations mapping the potential energy hypersurface at the optimized minima for the 6BPh interaction of cytosine, to represent nitrogen H-bond donors, and the 2BPh interaction of adenine, to represent carbon H-bond donors.

Relative stabilities of BPh interactions

The QM calculations show that all of the experimentally identified BPh interactions, with the exception of 5BPh, are stable in that they occupy minima in the potential energy hypersurface. Moreover, the calculations show that 5BPh is not separated from the adjacent and more stable 4BPh interaction by a significant energy barrier. One therefore expects that 5BPh will tend to convert to 4BPh unless the overall local arrangement favors the 5BPh. One must bear in mind that the energy difference between the 4BPh and the 5BPh or 3BPh interactions, results from the fact that 4BPh is associated with two direct N-H … O H-bonds between the base and phosphate while 3BPh and 5BPh contain only one. Although the COSMO solvation model includes overall solvent screening effects, this treatment is not equivalent to the explicit consideration of the eventual second direct H-bond to the phosphate group provided by another H-bond donor, possibly water, in the case of the 3BPh or 5BPh interactions. In other words, we have some uncertainty in the quantitative comparison of the strength of 4BPh versus 5BPh interactions. The saturation of the phosphates by direct H-bonds in these computations is unequal and the energy difference between 4BPh and 5BPh probably is somewhat exaggerated. While our stability order, 4BPh>>3BPh>5BPh is correct, the scale of energy differences is likely reduced when all possible interactions, including directly bound water molecules, are considered.

Comparison of BPh to base pair interaction energies

Comparison of the relative strength of the BPh interactions to base pairs is not straightforward, as BPhs are electrically charged systems which respond differently to solvent screening than do base pairs, most of which are electrically neutral. Nevertheless, the interaction energy of the strongest BPh interactions (∼–10 kcal/mol) exceeds in absolute value the interaction energy of the cis WC/WC (cWW) GC base pair calculated with the identical protocol (∼–7 kcal/mol). Therefore, it is reasonable to conclude that the most stable BPh interactions involve very strong H-bonds and provide stabilization fully comparable with strongly H-bonded base pairs. We note that assessment of the overall thermodynamics contribution of a given interaction in a complex nucleo-protein structure such as the ribosome is a more delicate issue than is often assumed, as the reference state may be defined in different ways. The bound state is usually compared to the state with entirely unbound base and phosphate in aqueous solution. However, in the folded ribosome, it may be more relevant to compare the stability of the formed BPh with respect to the alternative substates where the interaction is locally disrupted. The free energy balance will depend not only on the direct strength of a given interaction, but also on the cooperative formation of other interactions in its vicinity. The present calculations obviously ignore differences in solvation and cannot capture ion displacement effects (surely an important issue in BPh interactions) and other context-dependent effects. The stabilizing effect of a given type of BPh interaction in a given specific context will depend on the details of its neighborhood, including, for example, whether direct competitive binding of a positive ion to the phosphate is sterically allowed. Another open issue is competition between direct and water-mediated BPh interactions. Nevertheless, the intrinsic interaction energies, as captured by QM calculations, reflect the direct (electronic structure) communication between the interacting systems, which is the single most important term contributing to the final energy balance. Their knowledge is fundamental for basic understanding of the interactions. Although such knowledge is not sufficient for unambiguous quantitative free energy predictions in individual cases, it can at least prevent misleading interpretations that sometimes do occur in the structural biology literature when judgments are based purely on observed geometries.

Thus, the main purpose of the present QM calculations is to refine and verify the basic classification of the BPh interactions and to qualitatively assess the strengths of distinct BPh interaction patterns relative to each other and to base pair interactions. Further analysis of the stability of such interactions will require in-depth studies specifically dealing with distinct BPh patterns, while considering broader aspect of their structural contexts. The present data nevertheless suggest that BPh interactions have the potential to provide substantial stabilization that is energetically comparable to well-bonded base pairs.

Base-phosphate classification in RNA 3D crystal structures

The quantum calculations indicate the optimal bond lengths for the H-bonds in BPh interactions. In RNA 3D structures, the observed bond lengths and angles of non-covalent interactions are rarely optimal; they vary for a variety of reasons including thermal agitation of interacting partners, limited resolution of the experimental data and model-building errors. Here we discuss the variability in the bond length and angle parameters and how we set classification cutoffs for BPh interactions.

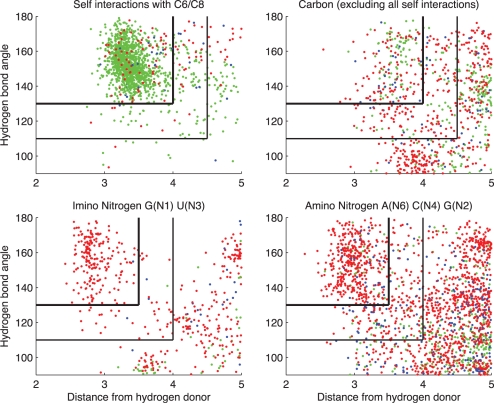
Figure 3 displays the data behind Figure 1 in another way, by showing each BPh interaction as a point on a graph with the horizontal coordinate indicating the distance between the H-bond donor and the nearest phosphate oxygen and the vertical coordinate indicating the H-bond angle, defined as the angle between the donor-H vector and the H-O vector. The data are color-coded to indicate which phosphate oxygen atom is H-bonding. Four disjoint subsets of BPh interactions are plotted: (i) upper-left, only intra-nucleotide (self) 0BPh interactions; (ii) upper-right, all other BPh interactions involving C-donors; (iii) lower-left, imino N-donors and (iv) lower-right, amino N-donors. These data show that the H-bond lengths for BPh interactions involving carbon atoms are longer than for nitrogen atoms, consistent with the QM calculations (Table 1 and Supplementary Data S7). Furthermore, the data show that certain oxygen atoms more often participate in some interactions than others.

Clear clusters for discriminating ‘interacting' from ‘not interacting' instances are only evident in the scatterplot for intra-nucleotide interactions (upper-left panel of Figure 3). These interactions are by far the most numerous BPh interactions in RNA structures and are probably most consistently modeled. We use these data as a guide to set cutoffs for BPh interactions involving carbon H-bond donors. To be classified as a BPh interaction, we require that the distance from a carbon H-bond donor to oxygen acceptor atom be <4 Å and the bond angle >130°. When these conditions are not met, but the H-bond length is <4.5 Å and the bond angle is >110°, the interaction is labeled ‘nBPh'. We use the same cutoffs for non-self interactions with carbon (upper-right panel of Figure 3). For interactions with nitrogen donors, we use the data in the lower-left panel of Figure 3 to set the H-bond length cutoff to 3.5 Å and the bond angle cutoff 130°, and extend this to the case illustrated in the lower-right panel of Figure 3. Cutoffs for nBPh interactions with N-donors were set at 4 Å and 110°, as illustrated. Using ‘near' interaction categories softens the sharp divisions produced by a dichotomous classification scheme and has been found to be useful in classifying BP interactions (11). The data in Figure 3 also show that the phosphate oxygen making each type of BPh interaction is usually the one predicted from the quantum calculations to form the more stable H-bond (see section ‘Quantum chemical calculation of optimized geometries and interaction energies for BPh interactions’). Thus for N-H donors, the acceptor is almost exclusively an anionic oxygen, while for C-H donors a large proportion of O3′ and O5′ acceptors is observed.

Annotation of BPh interactions in secondary structures

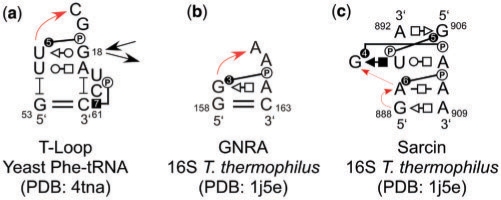
In the previous work (43), we proposed annotating BPh interactions in secondary structures with the letter ‘P' inside a circle, to indicate the phosphate, connected by a line to a circle, square or triangle symbol, to indicate the base edge of the H-bond donor, consistent with the Leontis–Westhof annotations for base pairs (44), where circles represent WC edges, squares Hoogsteen edges and triangles Sugar edges. Now we propose to add a number within the symbol representing the base edge to designate the BPh type (0–9). Figure 4 shows the annotated secondary structures of three RNA 3D motifs that contain BPh interactions (two hairpin loops and one internal loop). Figure 4a shows a T-Loop motif (6,7), where U55 forms a 5BPh with A58 (the circle represents the WC edge of U55) and C61 forms a 7BPh with C60 (the square represents the Hoogsteen edge of C61); panel (b) represents a GNRA motif (8), where G159 forms 3BPh with A162 and panel (c) shows a sarcin motif (45), where A889 forms a 6BPh with A908, G890 forms a 4BPh with A907 and G906 forms a 5BPh with U893.

Figure 4. — 2D annotations for (a) T-Loop from yeast Phe-tRNA (b) GNRA from *T. thermophilus* 16S rRNA and (c) Sarcin/ricin motif from *T. thermophilus* 16S rRNA.

Occurrence of BPh interactions in structured RNA molecules

In this section we report the number of BPh interactions in selected reference structures, the distribution over the different types of interaction, and the locations of BPh interactions in secondary structures.

A large number of intra-nucleotide (self) interactions were identified, almost all of which are 0BPh interactions involving purine (C8) or pyrimidine (C6) positions as H-bond donors. These interactions stabilize the default ‘anti' configuration of nucleotides, but are of little interest for understanding RNA 3D motifs and tertiary interactions and so were excluded from analysis. However, we included the small number of inter-nucleotide 0BPh interactions.

Occurrence of BPh interactions by type and interaction energy

We used FR3D to classify the BPh interactions in the reduced-redundancy subset of the PDB as described in the ‘Materials and Methods’ section. We counted the number of instances of each category of interaction, in structures having resolution 2.5 Å or better and present these data for comparison with the calculated interaction energies, in Figure 5. Generally, the more stable (lower energy) interactions occur more frequently for each base type. In particular, the most frequent interactions by base are the 6BPh of adenine (upper-left panel), the 8BPh of cytosine (upper-right panel), the 4BPh of guanine (lower-left panel) and the 5BPh of uracil (lower-right panel). These are also the lowest energy interactions calculated for each base.

Figure 5. — Comparison of calculated BPh interaction energies (red) and BPh occurrence frequencies (blue) from a reduced-redundancy set of crystal structures with resolution better than 2.5 Å (blue). Each panel represents one of the four nucleotides: Adenine (upper-left), Cytosine (upper-right), Guanine (lower-left) and Uracil (lower-right).

When lower resolution structures are included in this analysis (resolution 4.0 Å or better), we find slightly more 3BPh than 4BPh interactions for G. This suggests that neighboring BPh interactions are less well resolved in lower resolution structures.

Locations of BPh interactions in relation to the secondary structure

We studied the locations of BPh interactions in relation to the secondary structure of E. coli 16S and 23S (PDB files 2avy and 2aw4, respectively). We extracted 504 classified non-self BPh interactions involving 480 distinct bases and the phosphate groups of 473 distinct nucleotides. (Bases and phosphate groups can simultaneously make more than one BPh interaction.) There are a total of 4488 nucleotides in these two structures and they make 1303 canonical or wobble cWW base pairs (AU, UA, CG, GC, GU or UG) and 690 non-WC base pairs. Thus, the number of BPh interactions is on the same order of magnitude as the number of non-WC base pairs.

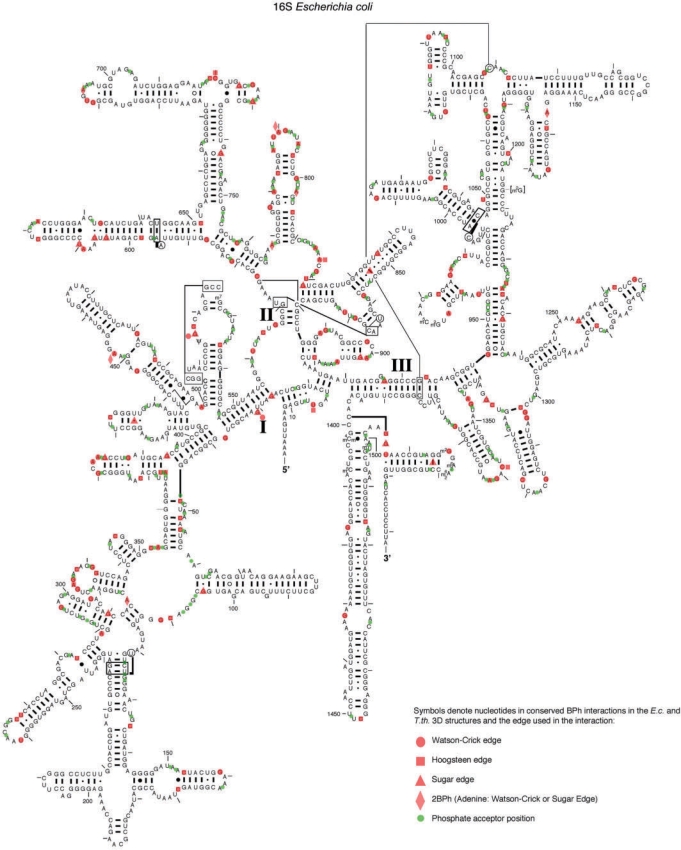
Bases making BPh interactions are fairly evenly distributed along the length of the nucleotide chain, although they tend to occur in small clusters, in which several successive nucleotides form BPh interactions. Such clusters of BPh interactions usually occur in multi-helix junctions, as is apparent for 16S rRNA in Figure 6. Secondary structure diagrams of E. coli 16S and 23S rRNA (46), annotated with the BPh interactions that are conserved between the E. coli and T. thermophilus rRNA structures, are shown are in Figure 6 and Supplementary Data S8–S9, respectively. In these diagrams, each base that acts as an H-bond donor in a conserved BPh interaction is marked by a semi-transparent red symbol, according to the base edge involved in the BPh interaction (circle for WC edge, square for Hoogsteen edge and triangle for Sugar edge). A red diamond is used for the Adenine 2BPh interaction, which straddles the WC and Sugar edges. A green dot placed between consecutive nucleotide letters indicates phosphates that act as BPh acceptors. 1BPh interactions conserved at the base pair level are annotated with red triangles placed between bases forming the WC base pair.

Figure 6. — BPh interactions conserved between *E. coli* and *T. thermophilus* rRNA 3D structures mapped on the 2D structure of *E. coli* 16S rRNA (46). Red symbols were used to denote the edge used by each base donor (circle for Watson–Crick edge, square for Hoogsteen edge, triangle for Sugar edge and diamond for the Adenine 2BPh which straddles the WC and Sugar edges). The 1BPh interactions that are conserved at the base pair level, are marked by red triangles placed between the bases forming the WC base pair. Green circles denote the locations of phosphate acceptors.

To study the contexts in which BPh interactions occur, we annotated each nucleotide in the E. coli 16S and 23S rRNA structures with the kind of secondary structure element to which it belongs (Helix, Hairpin Loop, Internal Loop or Junction Loop). Table 2 shows the number of each such element that contains one or more BPh interactions in which both the base and the phosphate forming the interaction belong to the same element. We find that most hairpin, internal and junction loops in the rRNAs contain at least one BPh interaction, but few helices do so. Indeed, the BPh interaction is quite rare in helices and only occurs between adjacent, stacked WC base pairs at the ends of helices.

Table 2.

Fraction (%) of secondary structure elements in E. coli 16S and 23S rRNA (2avy and 2aw4) that contain one or more BPh interactions internal to that element

Secondary structure element	Number with BPh Total number
Number of secondary structure elements containing at least one internal BPh interaction
Helices
Hairpin loops
Internal loops
Multi-helix junction loops

Open in a new tab

BPh interactions occur between structural elements (helices, hairpin, internal and junction loops) as well as within them. We define as ‘short-range' all BPh interactions that are internal to a single element (Table 2) or involve nucleotides in adjacent elements, such as a hairpin loop and its helical stem. We define as ‘long-range' all BPh interactions between distinct structural elements that are not adjacent in the secondary structure. We present an analysis of short-range and long-range BPh interactions in the E. coli 16S and 23S rRNA structures according to the locations of base H-bond donors and phosphate acceptors in Table 3. The diagonal entries in Table 3 show the numbers of internal BPh interactions according to the type of structural element. These numbers are larger than the corresponding numbers in Table 2 because some elements of each type have more than one internal BPh interaction. This is especially true for multi-helix junctions, where we find that 35 junctions out of total 44 contain 113 BPh interactions or more than an average of 3 BPh per junction.

Table 3.

Number of BPh interactions occurring between secondary structure elements in E. coli 16S and 23 S rRNA (2avy and 2aw4), according to the range of the interaction

	Phosphate location
	Helix	Hairpin	Internal	Junction	Total
Short-range base–phosphate interactions
Helix	8	19	25	14	67
Hairpin	3	83	0	0	86
Internal	3	0	69	0	72
Junction	13	0	1	113	127
Total	27	102	95	127	353
Long-range base–phosphate interactions
Base location
Helix	24	5	5	6	42
Hairpin	10	7	9	11	37
Internal	15	2	5	5	27
Junction	15	4	7	4	31
Total	67	19	27	27	143

Open in a new tab

The data are tabulated according to the location of the base H-bond donor (rows) and phosphate acceptor (columns).

Adjacent short-range BPh interactions occur mostly between bases located at the ends of helices and adjacent phosphates in hairpin, internal or junction loops. Long-range BPh interactions occur in every combination, but in largest numbers between phosphates located in helices and bases located in hairpin, internal or junction loops, or in helices and between bases located in hairpin loops and phosphates in internal loops.

Ribosomal RNAs are rich in BPh interactions, having about one BPh for about every eight nucleotides. The average over the entire reduced-redundancy dataset is only 1BPh for every 24 nucleotides. However, this list contains many small RNAs that consist only of short duplexes or single strands that do not contain any junctions and few if any internal or hairpin loops, which are the primary locations at which BPh interactions are found. Generally speaking, the BPh frequency increases as the number of non-cWW base pairs per nucleotide increases, while the BPh frequency decreases as the number of cWW base pairs per nucleotide increases. Thus 3D structures that consist primarily of helical regions have few BPh; those with many non-cWW base pairs tend to have relatively many BPh interactions.

Sequence conservation of BPh interactions

The significant energies of BPh interactions and their widespread occurrence in hairpin, internal and junction loop motifs and tertiary interactions suggest they play an important role in stabilizing RNA 3D structure. We can therefore expect that the locations of BPh interactions are likely to be conserved in homologous RNA molecules. Furthermore, most BPh interactions are base specific as to the identity of the donor base. Thus, on the one hand, we may also expect that the H-bond donor base for most BPh interactions is likely to be conserved or to be substituted only by bases which can make geometrically and energetically equivalent interactions. On the other hand, we do not expect to observe much effect of BPh interactions on the base identity of phosphate acceptors, since all four nucleotides have the same phosphate group.

In this section, we report four tests of the conservation of BPh interactions in homologous RNA molecules. In ‘Conservation of BPh interactions between homologous RNA 3D structures’ section, we consider the conservation of these interactions between the 3D structures of E. coli and T. thermophilus 16S and 23S rRNA. In ‘Conservation of H-bond donor bases in BPh interactions among homologous rRNA sequences’ section, we examine the conservation of the H-bond donor between the 3D structures and multiple sequence alignments of homologous molecules. In ‘Predicting base conservation in sequences using pairwise interactions in 3D structures’ section we compare the contributions of BPh interactions and other interactions (WC and non-WC base pairs, BSt and protein interactions) to base conservation at homologous sites. Finally, in ‘Conservation of BPh interactions at the base pair level’ section we discuss conservation of certain BPh interactions at the base pair level.

Conservation of BPh interactions between homologous RNA 3D structures

Using FR3D, we extracted, classified and aligned all BPh interactions for the 16S and 23S rRNA structures of E. coli (2avy and 2aw4) and T. thermophilus (1j5e and 2j01), as described in the ‘Materials and Methods’ section. This alignment is provided as an Excel file in the Supplementary Data S2. We found a total of 592 BPh interactions in the E. coli. rRNA structures (195 in E. coli 16S and 397 in 23S rRNA) and 601 total BPh interactions in the T. thermophilus structures (203 in T. thermophilus 16S and 398 in 23S rRNA). Since some bases form more than one BPh interaction, we found a total of 557 distinct bases in the E. coli rRNA and a total of 562 distinct bases in T. thermophilus rRNA acting as H-bond donors in BPh interactions, or about 13% of bases. These data are summarized in Table 4.

Table 4.

Frequencies of non-self BPh interactions in E. coli and T. thermophilus 16S and 23S rRNAs

	16S rRNA 3D structures		23 S rRNA 3D structures
	Escherichia coli (2avy) (1j5e)	Thermus thermophilus (lj5e)	Escherichia coli (2aw4)	Thermus thermophilus (2j01)
Total nucleotides	1530	1513	2841	2772
Number of distinct bases involved in BPh interactions	185 (12.1%)	191 (12.6%)	372 (13.1%)	371 (13.4%)
Total number of BPh interactions	195	203	397	398
Number of BPh interactions at corresponding E. coli and T. thermophilus positions	174		338
Conserved bases at corresponding BPh positions

Open in a new tab

About 13% of all bases in the bacterial rRNA structure from BPh interactions and ∼86% of these interactions are common to the E. coli and T. thermophilus rRNA structures. For the corresponding BPh interactions, the base is ∼95% conserved between E. coli and T. thermophilus.

Comparing the lists of BPh interactions in the E. coli and T. thermophilus rRNA 3D structures, we found 512 ‘corresponding' BPh interactions (174 in 16S rRNA and 338 in 23S rRNA) for which the nucleotide positions of both the base H-bond donor and the phosphate acceptor can be aligned in the structures. BPh interactions were counted as aligned if FR3D detected a BPh interaction in both structures at aligned positions or if FR3D detected a nBPh interaction in one structure at aligned positions annotated with a full BPh interaction in the other structure. Thus, ∼86% ((2 × 512)/1193) of the BPh interactions are common to the E. coli and T. thermophilus rRNA 3D structures. Furthermore, in 484 out of the 512 aligned BPh interactions (∼95%), the H-bond donor base is the same in the E. coli and T. thermophilus structures (164 in 16S and 320 in 23S rRNA, Table 4).

Thus, <15% of the BPh interactions found in the E. coli 16S or 23S rRNA structure are not found at the corresponding position of the homologous T. thermophilus structure and vice versa. We have examined each of these instances manually and find that they belong to one of five categories: (i) In the first category, data are missing in one of the two structures due to crystallographic disorder (∼2%). Thus, for these instances one cannot tell at present whether the interaction is conserved. (ii) In the second category, there is a major structural difference between the E. coli and T. thermophilus molecules at the position in question, such as a motif swap or a difference in length of a peripheral element. For such instances, about 3% of the total, no comparison can be made and these are best excluded from analysis. (iii) The third category consists of instances where the structures are modeled differently at the nucleotide level (∼5%). Most such instances involve a difference in modeling of the glycosidic bond conformations of the corresponding nucleotides acting as H-bond donors. For example, A65 is modeled ‘syn' in E. coli 16S but ‘anti' in T. thermophilus 16S and is only able to form the 2BPh interaction in the E. coli structure. Differences in modeling the glycosidic conformation, which may indicate possible errors in one or both structures, are not infrequent in large RNA structures solved at moderate resolution (12) and can be resolved with better crystal data. Thus, some of these instances may also prove to be conserved BPh interactions. (iv) In the fourth category, the BPh interaction is conserved at the base pair level rather than the nucleotide level (∼1% of instances). This case will be discussed in more detail in ‘Conservation of BPh interactions at the base pair level’ section. (v) The fifth category comprises actual base substitutions that preclude forming equivalent BPh interaction in both structures. These cases (about 3% of instances) are genuine instances where a BPh interaction does not appear to be conserved. Even in these cases, however, a conformational change between the two structures can compensate for the base change. An example is position 121 in 16S which is U in E. coli 16S and C in T. thermophilus 16S. Both bases are bulged and both form a BPh interaction with helix 7. U121 forms a 5BPh with the C234 phosphate and C121 forms a 7BPh with the G236 phosphate.

Focusing on the ∼86% of BPh interactions which can be aligned between the E. coli and T. thermophilus 16S and 23S rRNAs, we estimated the conservation rate of the H-bond donor base between structures. These data are shown in Table 5, which organizes the BPh interactions according to the base edges to which the H-bond donors belong. The cells along the diagonal correspond to BPh interactions which are identical as to interaction type and base identity in the E. coli and T. thermophilus rRNA structures. These constitute ∼75% of the BPh interactions. Examination of the off-diagonal cells shows that those with the highest counts involve neighboring BPh interactions in which the base is the same in the two structures. These cells are indicated by dotted red lines and correspond to guanine 3BPh, 4BPh and 5BPh neighboring interactions (56 instances) or cytosine 7BPh, 8BPh and 9BPh neighboring interactions (27 instances). Combining these instances of neighboring interactions with the instances of identical interactions on the diagonal, we find 92% of BPh instances have the same base in the E. coli and T. thermophilus rRNA structures making the same or neighboring BPh interaction. Of the remaining ∼8% of BPh instances from the rRNA 3D structures, 11 instances (∼2%) are cases of equivalent BPh interactions formed by bases which are different in the E. coli and T. thermophilus structures. These are indicated by solid red outlines in Table 5 and include cases of 0BPh, 5BPh, 6BPh, 7BPh and 9BPh. Another set of instances involves neighboring BPh interactions with base changes, for which there are 16 instances (∼3%). This leaves only 12 instances (∼2%) that involve changes of base edge (pink background). Thus, the data in Table 5 clearly show that when changes occur, the interacting edge of the base is almost always conserved (yellow cells).

Table 5.

Corresponding BPh interactions observed in the 3D structures of E. coli and T. thermophilus 16S and 23S rRNAs

Open in a new tab

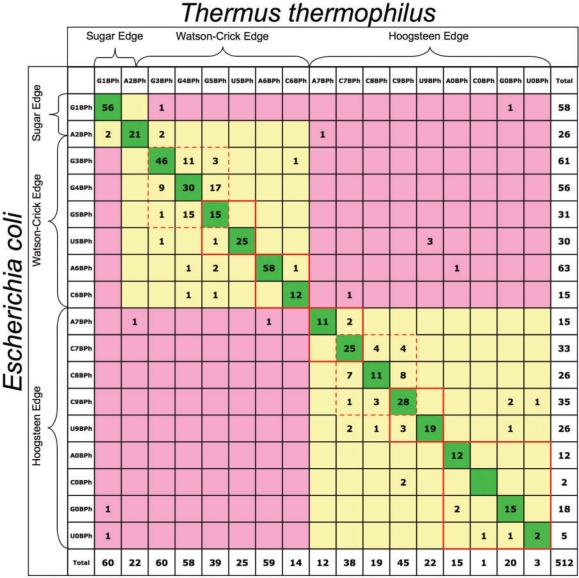Diagonal entries (dark green) correspond to identical BPh interactions (same base donor and BPh category). Yellow shaded cells correspond to differences in base or BPh category that preserve the geometry of the interaction. Pink cells indicate differences that do not preserve the BPh geometry.

Conservation of H-bond donor bases in BPh interactions among homologous rRNA sequences

In the previous section we obtained direct evidence for conservation of BPh interactions by comparing the 3D structures of the homologous but phylogenetically distant E. coli and T. thermophilus rRNA molecules. The BPh interactions common to these structures are likely to be present in other 16S and 23S rRNAs, because they are observed in both structures and are found within the core regions of the rRNA secondary structures (12). In this section, we examine rRNA multiple sequence alignments to obtain larger numbers of instances of BPh interactions for more robust statistical analysis of BPh sequence variations. We use the multiple sequence alignments of 717 16S and 136 23S sequences that we previously reported in a study of base pair substitutions (12). For each aligned BPh interaction identified in the 3D alignment, we examined the column corresponding to the H-bond donor in the multiple sequence alignment and tallied the number of instances of A, C, G and U observed in that column. By restricting our attention to locations of BPh interactions that are conserved between the E. coli and T. thermophilus rRNA 3D structures we gain assurance that the interaction is also found in other homologous rRNA molecules for which we only have sequences.

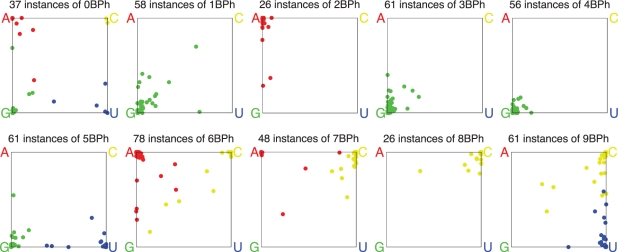
Figure 7 presents on separate plots the data obtained from the alignments, for each BPh type of interaction observed in the E. coli 3D structures. We first consider the 9BPh subplot. This BPh interaction is specific to C and U. The blue dots represent instances in which U is the H-bond donor in a 9BPh interaction in the E. coli 3D structures. Those blue dots clustered near the corner of the graph labeled ‘U' correspond to instances that are also predominantly U in the sequence alignments. Likewise, the yellow dots clustered near the C corner represent instances that are predominantly C in the sequence alignments, while the blue and yellow dots along the edge that connects the U and C corners of the square indicate instances that vary exclusively between U and C in alignments. Together these account for most instances and provide support for the idea that mutations that interchange U and C are structure-neutral as either U or C can support the 9BPh interaction. There is one instance with about 60% U and 40% G (blue dot on bottom edge of the square) and only a handful of yellow dots with significant fractions of A and G as well as C and U. These may represent regions where the alignments are less certain or sites where the 9BPh interaction is not conserved in all structures.

Some BPh interactions are highly conserved in the sequence alignments. For example, the 3BPh and 4BPh interactions, which are specific to G (all green dots), are also largely G in the sequence alignments (all dots map close to the G corner). Likewise, the 8BPh interaction, which is specific to C (all yellow dots) is also largely C in the sequences (all dots close to the C corner), with the exception of one instance that is mainly A. The 1BPh interaction is also specific to G and most instances in sequences are also G, but some sites have significant percentages of C, U or A. This interaction, which occurs on the minor groove, sometimes involves an interesting base pair covariation, which may explain the dots on the diagonal between the G and C corners of the 1BPh subplot and will be discussed in more detail in ‘Conservation of BPh interactions at the base pair level’ section.

The 2BPh interaction is specific to A, but is geometrically similar to the 1BPh or 3BPh formed by G. The 3D structure alignment reported in ‘Conservation of BPh interactions between homologous RNA 3D structures’ section provides examples of A2BPh to G1BPh substitutions, Table 5. This interpretation may explain the red dots along the A–G edge of the 2BPh subplot, which are instances for which we see significant fractions of G in the sequence alignments.Category 5BPh is only made by G or U and we see some G ↔ U variation, as expected.

Category 6BPh is only made by A or C. The 5BPh and 6BPh interactions, which can be made by A, C, G or U, all involve the WC edge of the base, so it is no surprise to see wider sequence variation in these subplots. Table 5 shows that such substitutions are observed in 3D structures. Even so, most locations show near-total conservation; in each subplot, there are only ∼12 instances out of total 139 5BPh or 6BPh interactions that are not close to a corner.

Finally, the 0BPh interaction is not base-specific and shows the greatest sequence variation of all.

Predicting base conservation in sequences using pairwise interactions in 3D structures

The results presented in the previous two sections indicate that when a BPh interaction is observed in one RNA 3D structure, it is very likely to be present at the corresponding location in homologous RNA molecules. Moreover, the bases acting as H-bond donors in BPh interactions tend to be very conserved in homologous molecules. We can ask whether this conservation should be attributed to the BPh interaction itself, or to other interactions that the base makes. In other words, are BPh interactions primarily incidental, or do they have a selective effect on RNA sequence? It is difficult to answer this question conclusively for individual instances of BPh interactions, but we gain some understanding if we examine more globally the degree of base conservation in RNA molecules in relation to other factors that are known to constrain sequence variation.

We mapped the 3D structures of E. coli 16S and 23S rRNA (PDB files: 2avy and 2aw4) to the sequence alignments (described above), to determine for each nucleotide in the 3D structure, which bases appear in the corresponding column of the multiple sequence alignment. We define the conservation of each base in the structure as the percentage of bases (A, C, G or U) in the corresponding column of the alignment that are identical to it. For this calculation, we ignore gaps and symbols indicating incomplete data in the sequence alignment. Thus, if the 3D structure has an A and in the corresponding column there are 200 As, 100 Cs, 50 Gs, 50 Us, 85 gaps and 35 Ns, the conservation percentage is calculated 200/(100 + 200 + 50 + 50) = 50%.

We investigated possible factors that might influence nucleotide conservation as defined in the previous paragraph. Presumably the interactions the nucleotide makes in the folded RNA structure have a major effect. We therefore used FR3D to tabulate all the annotated interactions that each nucleotide in the structure makes, including the number of cWW base pairs in which the nucleotide is involved (either 0 or 1), the number of non-cWW base pairs (0, 1, 2 or 3), the number of distinct BPh interactions in which the base of the nucleotide is the H-bond donor (0, 1 or 2) and the number of interactions in which the phosphate of the nucleotide is the acceptor (0, 1 or 2). We also calculated whether a nucleotide is within 3.7 Å of a protein residue in the 3D structure (1 if so, 0 if not). Protein contacts were found using Swiss PDB Viewer (47), by selecting all nucleotides within a neighboring radius of 3.7 Å of a protein moiety. Finally, to account for the general level of conservation among neighboring nucleotides, for each nucleotide we calculated the average conservation percentage for the nucleotides which base stack on it (‘stacking partners'), or, if there are no stacking partners, the average conservation percentage of the nucleotides immediately before and after it in the chain (‘adjacent nucleotides'). Treating these numbers as the predictors of base conservation, we performed a simple linear regression on these parameters, resulting in the following model:

Conservation percentage of base in sequences
= 26.3 (constant term)
+ 58.1 × conservation percentage of stacking partners or adjacent nucleotides, divided by 100
+ 8.0 × number of non-cWW pairs it forms
+ 7.4 × number of BPh interactions in which it is the H-bond donor
+ 2.7 × near a protein (1) or not (0)
+ 1.8 × number of BPh interactions in which it is the phosphate acceptor
+ 0.3 × number of cWW pairs it forms

All coefficients except the last two are non-zero at the 0.05 significance level. The conservation percentage of stacking partners makes the strongest contribution. It accounts for the general level of conservation of the RNA region in which the nucleotide occurs and for possible base specificity of stacking interactions. With that accounted for, nucleotides which participate in one or more non-cWW base pairs have elevated conservation percentages. Non-cWW base pairs generally exhibit less variation between structures (12). Bases that are H-bond donors in one or more BPh interactions also have elevated conservation percentages, with roughly the same strength of effect as the number of non-cWW base pairs formed. Proximity of the nucleotide to a protein has a moderate effect. The last two factors are the weakest, and may be statistical fluctuations rather than real effects. We do not expect nucleotides which act as phosphate acceptors to be more or less conserved due to this interaction, since it is not base specific. The very small contribution to conservation due to a nucleotide making a cWW pair is consistent with our understanding that the AU, UA, CG, GC cWW pairs are isosteric and can freely substitute for one another, in the absence of further constraints. Any base specificity of stacking for cWW pairs is accounted for by the conservation percentage of stacking partners.

This is a simple but fairly complete model for the dependence of base conservation in homologous RNA sequences on the type and number of pairwise interactions a nucleotide makes. The model indicates that bases that act as H-bond donors in BPh interactions are subject to sequence constraints comparable to those of bases forming non-WC base pairs.

In Supplementary Data S10, we use boxplots to show the statistical distribution of conservation percentages for subsets of nucleotides having all possible combinations of three binary attributes: (i) whether the nucleotide makes a cWW pair, (ii) whether the nucleotide makes at least one non-cWW pair and (iii) whether the nucleotide is the H-bond donor in at least one BPh interaction. The boxplots provide additional evidence that a base, i.e. the H-bond donor, in a BPh interaction is more conserved than one that is not.

Conservation of BPh interactions at the base pair level

In previous sections, we examined the conservation of individual nucleotides making BPh interactions by comparing the corresponding positions in two 3D structures or the 3D structures and homologous sequence alignments. We found some cases where Gs forming 1BPh interactions in one rRNA structure did not appear to be conserved in the other structure. Closer examination revealed that for these cases the 1BPh interaction is in fact conserved on the base pair level rather than the nucleotide level. Figure 8 shows an example: G2692 in E. coli 23S makes a 1BPh with G2848 and a cWW base pair with C2717. The corresponding base pair in T. thermophilus has GC replaced with CG, but the G again makes a 1BPh interaction. This is possible because when superposing a GC cWW base pair on a CG cWW base pair, the G(N2) amino groups of the Gs coincide in space so that the G(N2) group is positioned to participate in an equivalent 1BPh interaction with a phosphate located in the same place in the middle of the minor (shallow) groove.

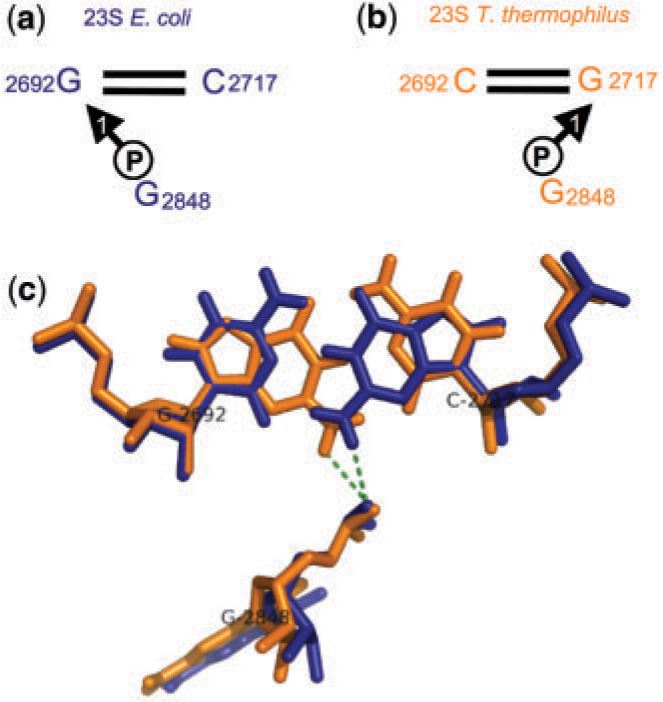
Figure 8. — Conservation of 1BPh interaction at the level of base pairs. The G2692/C2717 cWW base pair of *E. coli* 23S rRNA (a) corresponds to the C2692/G2717 base pair in *T. thermophilus* 23S (b). The G in each structure forms a conserved 1BPh interaction with the phosphate of nucleotide 2848, as shown (c).

We have identified two other instances of GC ↔ CG substitutions in the E. coli and T. thermophilus rRNA 3D structures that preserve 1BPh interactions. In Table 6, we summarize these cases and four others in which a GC cWW base pair in one structure is substituted by a UG or CA cWW base pair in the other structure and the purine in each pair makes a similar BPh interaction (G makes 1BPh, A makes 2BPh).Table 6 also presents base pair substitution data from the rRNA sequence alignments for the seven identified instances of base pair level BPh conservation. In six of the seven cases, the base combinations observed in the 3D structures are the combinations most often seen in the sequence alignments as well. These data offer confirmation that the base pair substitutions observed in the 3D structures occur with some frequency in other homologous molecules. As noted previously (12), base pair substitutions occur most often between base combinations that make isosteric base pairs. Thus, GC base pairs are most often substituted by CG, AU and UA (isosteric, red boxes), but also by GU, UG, AC and CA (near isosteric, yellow boxes). This explains the very low counts in the boxes shaded blue and gray.

Table 6.

Substitution tables for identified cWW base pairs in 16S and 23S bacterial rRNAs involved in 1 BPh conservation at the base pair level

Open in a new tab

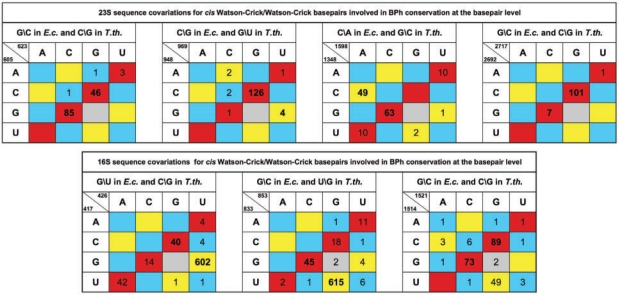For each substitution table the sequence for E. coli and T. thermophilus are given in the header, while the corresponding nucleotide numbers are given in the upper-left corner of each table. The cells are colored according to whether the base pair is isosteric (red), near isosteric (yellow), or non-isosteric to the GC cWW base pair as discussed in (12).

We have identified 20 other aligned positions in the E. coli and T. thermophilus rRNA 3D structures where Gs form 1BPh interactions as well as cWW GC pairs. In these cases both structures have the G in the same position. We compiled base pair substitutions for each of these 20 instances from the sequence alignments and find that thirteen of these show 90% or greater conservation of the GC base pair per se, while the other seven show patterns of variation similar to those shown in Table 6. Including the three cases in Table 6, of which one shows 90% or greater conservation of the GC base pair, there are 23 cases of GC cWW pairs making 1BPh in both structures and nine of them (∼40%) exhibit significant levels of base pair substitutions in the sequence alignment. Moreover, most of the variability involves GC, CG, GU or UG covariations which, as we have seen, preserve the 1BPh interaction in the minor groove. This phenomenon can help to explain some of the variability in the 1BPh subplot of Figure 7. When a GC in the 3D structure in which the G makes a 1BPh is substituted by a CG or UG base pair in the sequence alignment, the 1BPh subplot of Figure 7 will show non-conservation of the G, but this masks the fact that the BPh interaction may still be conserved at the base pair level. Figure 9 shows the data in the 1BPh subplot of Figure 7 separated according to whether the G making the 1BPh interaction also forms a cWW base pair. Those that do make a cWW base pair show higher tendency toward substitution, consistent with the phenomenon described above.

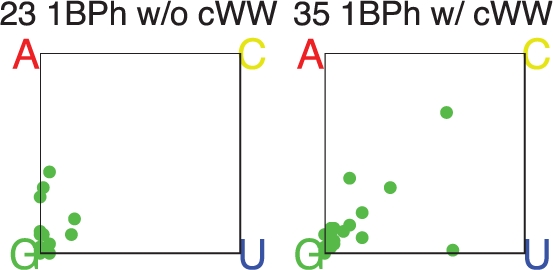
Figure 9. — Base substitution data for G1BPh interactions, as described in the caption for Figure 7. The left subplot shows cases in which the G does not make a cWW base pair, while the right panel shows cases in which the G does make a cWW base pair.

DISCUSSION

The analysis of the 3D structures of E. coli and T. thermophilus 16S and 23S rRNAs indicates that a significant fraction of bases in structured RNA molecules (about 13%) form conserved inter-nucleotide BPh interactions. Moreover, they are widespread in hairpin, internal and multi-helix junction loops. We find that ∼87% of hairpin loops, ∼80% of junction loops and ∼71% of internal loops of E. coli 16S and 23S rRNA contain one or more BPh interactions involving nucleotides of the same loop. As many of these motifs are recurrent, it is likely that BPh interactions are also found widely in other structured RNAs. A significant number of the conserved BPh interactions are long-range (143 out of 496), which suggests that BPh interactions also play significant roles stabilizing the tertiary structures of structured RNA molecules.

Our analysis revealed 17 unique phosphate-binding sites on the standard RNA bases (A, C, G and U). Based on the reported quantum chemical calculations and consideration of the locations of these binding sites along the base perimeters (edges), we decided to classify them in 10 families. This groups together, under the same designation, phosphate-binding sites that occur at equivalent sites on different bases. Thus, 5BPh designates the imino nitrogen H-bond donors on the WC edges of G and U with a phosphate oxygen. Other BPh interactions that are shared by more than one base are 6BPh, on the WC edges of A and C, 7BPh, on the Hoogsteen edges of A and C, 9BPh, on the Hoogsteen edges of U and C and the non-specific 0BPh, also on the Hoogsteen edge. The other BPh interactions are base-specific. BPh interactions that occur on the same base edge, such as the 3BPh, 4BPh and 5BPh interactions of G, are called ‘neighboring interactions' and are very conserved.

We developed the proposed BPh nomenclature to facilitate integration of structural and sequence data. Comparing the 3D structures of E. coli and T. thermophilus 16S and 23S rRNA we found that at least 86% of the BPh interactions detected in the homologous E. coli or T. thermophilus structures are common to both structures. As E. coli and T. thermophilus are distantly related bacteria, it is likely that most of these interactions also occur at corresponding sites in homologous bacterial rRNAs. This degree of conservation over billions of years of evolution provides further evidence that BPh interactions play significant roles in the ribosome. Comparing the annotations of conserved BPh interactions in the E. coli and T. thermophilus structures we find in most cases (about 75%) the base and the class of interaction are the same in the E. coli and T. thermophilus structures. Closer examination showed that most of the differences could be accounted for in two ways: in many cases, the base is conserved, but the BPh annotations of the E. coli or T. thermophilus structures indicated neighboring interactions, that is BPh interactions involving the same edge, such as G 4BPh in one structure and G 5BPh in the other. In other cases, the bases were not the same in the two structures, but the interactions were the same, as in U 9BPh in one structure and a C 9BPh in the other, or the structures had neighboring interactions, e.g. A 6BPh in one structure and G 5BPh in the other. Therefore, we conclude that, taking into account conservative base substitutions and neighboring interactions which allow BPh interactions to form without drastic changes in geometry, close to 98% of BPh interactions that occur at homologous sites are conserved. This number includes 1BPh interactions in the minor groove of RNA helices that are conserved at the level of the base pair, a novel kind of sequence covariation described here for the first time. A linear regression model developed to compare the influences of BPh to other interactions that are known to constrain sequences shows that bases which form BPh interactions are strongly constrained, in a manner comparable to bases forming non-WC base pairs.

Auffinger et al. showed by analyzing X-ray crystal data and MD simulations that mobile anions can intrude into the first hydration shell of nucleic-acid bases (48). They observed a number of anion-binding sites and inferred or proposed several more. They identified about 13 anion-binding sites along the base edges. They designated binding sites according to the H-bond donor base (ADE, CYT, GUA or CYT) and interacting base edge (WC, S, H and CH, for the WC, Sugar and Hoogsteen/CH edges). The following correspondences can be made between the two classifications: Auffinger et al. GUA_S anion-binding site corresponds to our 1BPh class; the inferred GUA_WC_S site corresponds to 3BPh; GUA_WC corresponds to 4BPh or 5BPh; ADE_WC_H and the inferred CYT_WC_CH correspond to 6BPh; CYT_CH corresponds to 7BPh or 8BPh. In addition, Auffinger et al. propose bifurcated (B) anion binding to both amino hydrogen atoms simultaneously (ADE_B, CYT_B, GUA_B) and binding to A or C protonated on the WC edge (ADE+_WC and CYT+_WC).

Role of BPh interactions in stabilizing RNA structures

The quantum computations show that experimentally identified BPh interactions are intrinsically stable. We did not find it necessary to apply constraints to maintain the observed interaction patterns during geometry optimization, except in the case of G5BPh interactions, which minimize to 4BPh when not constrained. The QM studies clearly indicate that the observed geometries are energetically stable per se and do not depend on neighboring stabilizing interactions. By contrast, in related QM studies of certain non-WC base pairs we had to apply constraints to maintain the experimentally observed geometries (49). Moreover, BPh interactions are directional and can stabilize specific RNA geometries. Further, the BPh interaction energies are large enough to play significant roles in RNA folding and stability, corroborating our findings based on comparative structure and sequence analysis that these interactions are very conserved in rRNA evolution. It is likely that this is also the case for other structured RNAs. We found that for each base the relative abundances of the various BPh-binding patterns roughly correlate with the computed interaction strengths, providing further evidence of their relevance and importance in RNA structure. These observations also indicate that the intrinsic energetics of molecular interactions can contribute to modulating or supplementing the primary geometrical (isostericity) signatures of molecular interactions. Thus, relative energies can also affect the evolution of sequences of otherwise isosteric structures (see ‘Comparison of BPh to base pair interaction energies’ section for a discussion of the limitations of the energy analysis). While the classification of molecular interactions in RNAs was until now based solely on structural information, the present study suggests that complementary energy calculations can help to refine and better understand the classification. In fact, the present energy calculations helped to classify the BPh-binding patterns and clarified the nature of several binding modes.

There is evidence from several sources that BPh interactions effectively ‘solvate' the negatively charged phosphate groups of the RNA backbone. The first line of evidence is the size of the interaction energies themselves. Second, the ‘internal' solvation they provide can modulate or limit the formation of deep pockets of negative electrostatic potentials (ESP). For example, the bacterial 5S Loop E motif and the S/R Loop motif (which is also present in Loop E of eukaryal and archaeal 5S rRNAs) comprise some of the same non-WC base pairs (50). However, the S/R loop contains at least three conserved BPh interactions, all in the major groove, that are not observed in the bacterial Loop E motif. Consistent with these observations, only bacterial Loop E exhibits a deep negative ESP pocket in its major groove, which is known, moreover, to be a strong binder of cations (51–54). The conserved BPh interactions in the S/R loop are formed by the conserved purine (usually G) of the AR tHS base pair (R = A or G), the conserved G of the cHS UG base pair and the conserved A of the AM tHH pair (M = A or C). The first two BPh interactions occur on the WC edge of the base and as we have seen, the strongest BPh interactions on the WC edge are formed by Gs. G is observed exclusively as the second base in the cHS base pair and is by far most frequent as the second base in the tHS pair. Substitution of A for G in the tHS can be accommodated by a slight adjustment in the backbone to form an A 6BPh, but substitution of U or C does not allow a BPh interaction to form in this context. In other motifs, such as T-loops, substitution of U for a G, to form a 5BPh interaction is possible, but requires a small adjustment in the backbone, as shown by superposition of T-loops containing U or G at the site forming this conserved BPh interaction.

In a recent survey of base pair frequencies by geometric base pair family (12), we found that 69% of tHS base pairs are AG, 71% of tHH base pairs are AA and 47% of cHS base pairs are UG. Searching the non-redundant 3D database using FR3D, we find that the nucleotides in these non-WC base pairs also frequently have a BPh interaction between them (45). The fact that these base combinations can simultaneously form strong BPh interactions may in part account for their high frequencies.

How these data can be used

This work shows that the presence of BPh interactions in RNA 3D structures strongly constrains the sequences of homologous RNA molecules. The base acting as H-bond donor in conserved BPh interactions is very likely to be identical at corresponding positions in homologous sequences, when the sequences are properly aligned. We now provide annotations of BPh interactions for all RNA-containing PDB/NDB structures, in addition to BP and BSt interactions. Annotations can be accessed on the FR3D website (http://rna.bgsu.edu/FR3D/AnalyzedStructures/) annotations index page, by clicking on the link labeled ‘FR3D' in the second column of the record corresponding to each PDB entry.

Knowledge that a particular BPh interaction occurs at a particular position in a 3D structure also indicates possible base substitutions that may occur in homologous sequences, although with generally small probabilities. If a 1BPh interaction is observed in the 3D structure and the G H-bond donor also forms a GC or GU WC base pair, the interaction is likely to be conserved at the base pair level, as described in ‘Conservation of BPh interactions at the base pair level’ section. In homologous sequences, the base pair is most likely to be conserved as GC or GU or to be substituted by CG or UG. If the G forming the 1BPh is not forming a WC base pair, the G is most likely to be conserved as G in homologous sequences, or, with much lower probability, to be substituted by A, forming a neighboring 2BPh interaction. Likewise the presence of a 2BPh interaction in a 3D structure indicates the A acting as H-bond donor is most likely to be conserved as A in homologous sequences, or with lower probability, to be substituted by G to form either a neighboring 1BPh or 3BPh interaction, as the 2BPh straddles the Sugar and WC edges.

Gs forming BPh interactions on their WC edges can, with small probabilities, be substituted by As or Us, depending on the context. As and Cs forming 6BPh on the WC edge show more variability and can be substituted by each other or by G. Cs forming 7BPh or 8BPh are quite conserved but can be substituted by A with small probabilities. Of all BPh interactions the pyrimidine 9BPh interaction showed the most regular variations in sequences, almost exclusively between C and U. The inter-nucleotide 0BPh interaction is dominated by purines, which show some tendency to substitute.

Comparison of the E. coli and T. thermophilus 3D structures, which at best are based on moderate-resolution data, shows that the corresponding BPh interactions on the WC edges of Gs or the Hoogsteen edges of Cs are modeled differently in a number of cases (e.g. G4BPh in one structure and G 3BPh or 5BPh in the other). In higher resolution structures, we find higher fractions of interactions modeled as the more stable G4BPh or C8BPh interactions. Thus, limited resolution is probably one factor contributing to differences between the structures. Another factor may be the inherent dynamics of BPh interactions. Base pairs are known to open and close on the milli-second time-scale (55,56). As BPh interactions have intrinsic stabilities comparable to base pairs, it is possible that they fluctuate between neighboring interactions (e.g. C 7BPh or 9BPh and 8BPh, or G 3BPh or 5BPh and 4BPh) in response to structural dynamics of the RNA. Thus, the uncertainty in the X-ray structures may in part reflect intrinsic dynamics of the structures themselves at some sites.

Given the intrinsic stabilities of BPh interactions, comparable to base pairs, it is not surprising that the presence of BPh interactions protects the base from reactive chemical probes. In a landmark study, published long before the 3D structures were known, Noller and coworkers (57) probed E. coli 16S rRNA with chemical probes that react with the WC edges of RNA bases. They detected reactive sites by primer extension assays. Their data, in combination with the FR3D annotations of the 3D structures, show clearly that WC edges of the bases acting as H-bond donor are protected when forming 3BPh, 4BPh, 5BPh or 6BPh interactions, once the 16S achieves its native fold. The reported protection is complete for most bases annotated with these BPh interactions in the 3D structures and at least partial for the rest. For Gs, bases annotated as making G 3BPh or 5 BPh interactions were more likely than G 4BPh to be partly accessible to probes, consistent with the partial exposure of the WC edge in these cases.

CONCLUSIONS

By combining empirical and quantum chemical methods, we have identified optimal phosphate-binding geometries for each RNA base and implemented software in FR3D to find and classify these interactions in 3D structures (http://rna.bgsu.edu/FR3D/BasePhosphates). We have shown that BPh interactions are highly conserved in homologous rRNA molecules. We have shown that BPh interactions strongly constrain the sequences of homologous structured RNAs. We suggest that conclusions we have drawn based on studies of rRNA may also apply to other homologous structured RNAs. These data should be useful in the interpretation of chemical probing experiments and should provide better understand of RNA sequence variability, to improve algorithms for aligning homologous sequences and predicting RNA 3D structure and motifs.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Grants to NBL from the National Institutes of Health (2 R15GM055898-04), from the National Science Foundation (Research Coordination Network Grant No. 0443508), and from Bowling Green State University (Research Capacity Expansion Program, funded by the Ohio Board of Regents Research Incentive Fund); Academy of Sciences of the Czech Republic (grants no. AV0Z50040507 and AV0Z50040702); the Grant Agency of the Academy of Sciences of the Czech Republic (grants No. IAA400550701, IAA400040802 and 1QS500040581); Grant Agency of the Czech Republic (grant GA 203/09/1476) and Ministry of Education of the Czech Republic (grant LC06030). Funding for open access charge: National Science Foundation (Research Coordination Network Grant No. 0443508).

Conflict of interest statement. None declared.

Supplementary Material

[Supplementary Data]

gkp468_index.html^{(762B, html)}

ACKNOWLEDGEMENTS

We would like to thank Zdeněk Salvet for the maintenance of our computing facilities.

REFERENCES

1.Draper DE. A guide to ions and RNA structure. RNA. 2004;10:335–343. doi: 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Klein DJ, Moore PB, Steitz TA. The roles of ribosomal proteins in the structure assembly, and evolution of the large ribosomal subunit. J. Mol. Biol. 2004;340:141–177. doi: 10.1016/j.jmb.2004.03.076. [DOI] [PubMed] [Google Scholar]
3.Leontis N, Westhof E. Analysis of RNA motifs. Curr. Opin. Struct. Biol. 2003;13:300–308. doi: 10.1016/s0959-440x(03)00076-9. [DOI] [PubMed] [Google Scholar]
4.Leontis NB, Lescoute A, Westhof E. The building blocks and motifs of RNA architecture. Curr. Opin. Struct. Biol. 2006;16:279–287. doi: 10.1016/j.sbi.2006.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Auffinger P, Westhof E. An extended structural signature for the tRNA anticodon loop. RNA. 2001;7:334–341. doi: 10.1017/s1355838201002382. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Quigley GJ, Rich A. Structural domains of transfer RNA molecules. Science. 1976;194:796–806. doi: 10.1126/science.790568. [DOI] [PubMed] [Google Scholar]
7.Jaeger L, Verzemnieks EJ, Geary C. The UA_handle: a versatile submotif in stable RNA architectures. Nucleic Acids Res. 2009;37:215–230. doi: 10.1093/nar/gkn911. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Jucker FM, Pardi A. GNRA tetraloops make a U-turn. RNA. 1995;1:219–222. [PMC free article] [PubMed] [Google Scholar]
9.Correll CC, Munishkin A, Chan YL, Ren Z, Wool IG, Steitz TA. Crystal structure of the ribosomal RNA domain essential for binding elongation factors. Proc. Natl Acad. Sci. USA. 1998;95:13436–13441. doi: 10.1073/pnas.95.23.13436. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Mokdad A, Krasovska MV, Sponer J, Leontis NB. Structural and evolutionary classification of G/U wobble basepairs in the ribosome. Nucleic Acids Res. 2006;34:1326–1341. doi: 10.1093/nar/gkl025. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Sarver M, Zirbel CL, Stombaugh J, Mokdad A, Leontis NB. FR3D: finding local and composite recurrent structural motifs in RNA 3D structures. J. Math. Biol. 2008;56:215–252. doi: 10.1007/s00285-007-0110-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Stombaugh J, Zirbel CL, Westhof E, Leontis NB. Frequency and isostericity of RNA basepairs. Nucleic Acids Res. 2009;37:2294–2312. doi: 10.1093/nar/gkp011. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Rupert PB, Massey AP, Sigurdsson ST, Ferre-D'Amare AR. Transition state stabilization by a catalytic RNA. Science. 2002;298:1421–1424. doi: 10.1126/science.1076093. [DOI] [PubMed] [Google Scholar]
14.Torelli AT, Krucinska J, Wedekind JE. A comparison of vanadate to a 2′-5′ linkage at the active site of a small ribozyme suggests a role for water in transition-state stabilization. RNA. 2007;13:1052–1070. doi: 10.1261/rna.510807. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Ditzler MA, Sponer J, Walter NG. Molecular dynamics suggest multifunctionality of an adenine imino group in acid-base catalysis of the hairpin ribozyme. RNA. 2009;15:560–575. doi: 10.1261/rna.1416709. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Deshpande N, Addess KJ, Bluhm WF, Merino-Ott JC, Townsend-Merino W, Zhang Q, Knezevich C, Xie L, Chen L, Feng Z, et al. The RCSB Protein Data Bank: a redesigned query system and relational database based on the mmCIF schema. Nucleic Acids Res. 2005;33:D233–237. doi: 10.1093/nar/gki057. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Wuyts J, Perriere G, Van De Peer Y. The European ribosomal RNA database. Nucleic Acids Res. 2004;32:D101–103. doi: 10.1093/nar/gkh065. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Sethi A, O'Donoghue P, Luthey-Schulten Z. Evolutionary profiles from the QR factorization of multiple sequence alignments. Proc. Natl Acad. Sci. USA. 2005;102:4045–4050. doi: 10.1073/pnas.0409715102. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Atkins P, de Paula J. Physical Chemistry. 7th. Oxford: Oxford University Press; 2002. [Google Scholar]
20.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery J, JA, Vreven T, Kudin KN, et al. 2004. Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford, CT. [Google Scholar]
21.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
22.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Physical Rev. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
23.Miehlich B, Savin A, Stoll H, Preuss H. Results obtained with the correlation energy density functionals of becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989;157:200–206. [Google Scholar]
24.Gresh N, Sponer JE, Spackova N, Leszczynski J, Sponer J. Theoretical study of binding of hydrated Zn(II) and Mg(II) cations to 5′-guanosine monophosphate. Toward polarizable molecular mechanics for DNA and RNA. J. Phys. Chem. 2003;107:8669–8681. [Google Scholar]
25.Sponer J, Jurecka P, Hobza P. Accurate interaction energies of hydrogen-bonded nucleic acid base pairs. J. Am. Chem. Soc. 2004;126:10142–10151. doi: 10.1021/ja048436s. [DOI] [PubMed] [Google Scholar]
26.Barone V, Cossi M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. 1998;102:1995–2001. [Google Scholar]
27.Cossi M, Rega N, Scalmani G, Barone V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comp. Chem. 2003;24:669–681. doi: 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
28.Klamt A, Schuurmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993;2:799–805. [Google Scholar]
29.Sponer JE, Reblova K, Mokdad A, Sychrovsky V, Leszczynski J, Sponer J. Leading RNA tertiary interactions: structures, energies, and water insertion of A-minor and P-interactions. A quantum chemical view. J. Phys. Chem. 2007;111:9153–9164. doi: 10.1021/jp0704261. [DOI] [PubMed] [Google Scholar]
30.Orozco M, Luque FJ. Theoretical methods for the description of the solvent effect in biomolecular systems. Chem. Rev. 2000;100:4187–4226. doi: 10.1021/cr990052a. [DOI] [PubMed] [Google Scholar]
31.Sponer J, Riley KE, Hobza P. Nature and magnitude of aromatic stacking of nucleic acid bases. Phys. Chem. Chem. Phys. 2008;10:2595–2610. doi: 10.1039/b719370j. [DOI] [PubMed] [Google Scholar]
32.Hobza P, Sponer J. Structure, energetics, and dynamics of the nucleic acid base pairs: nonempirical ab initio calculations. Chem. Rev. 1999;99:3247–3276. doi: 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]
33.Jurecka P, Nachtigall P, Hobza P. RI-MP2 calculations with extended basis sets – a promising tool for study of H-bonded and stacked DNA base pairs. Phys. Chem. Chem. Phys. 2001;20:4578–4582. [Google Scholar]
34.Boys SF, Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970;19:553–566. [Google Scholar]
35.Šponer J, Jurečka P, Hobza P. In: Computational Studies of RNA and DNA. Sponer J, Lankas F, editors. Vol. 2. Berlin Heidelberg: Springer; 2006. pp. 343–388. [Google Scholar]
36.Eichkorn K, Treutler O, Ohm H, Haser M, Ahlrichs R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995;242:652–660. [Google Scholar]
37.Weigend F, Haser M. RI-MP2: first derivatives and global consistency. Theoret. Chem. Accounts: Theory Comput. Model. 1997;97:331–340. [Google Scholar]
38.Weigend F, Haser M, Patzelt H, Ahlrichs R. RI-MP2: optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998;294:143–152. [Google Scholar]
39.Schuwirth BS, Borovinskaya MA, Hau CW, Zhang W, Vila-Sanjurjo A, Holton JM, Cate JH. Structures of the bacterial ribosome at 3.5 A resolution. Science. 2005;310:827–834. doi: 10.1126/science.1117230. [DOI] [PubMed] [Google Scholar]
40.Wimberly BT, Brodersen DE, Clemons W.M., Jr, Morgan-Warren RJ, Carter AP, Vonrhein C, Hartsch T, Ramakrishnan V. Structure of the 30S ribosomal subunit. Nature. 2000;407:327–339. doi: 10.1038/35030006. [DOI] [PubMed] [Google Scholar]
41.Selmer M, Dunham CM, Murphy F.Vt, Weixlbaumer A, Petry S, Kelley AC, Weir JR, Ramakrishnan V. Structure of the 70S ribosome complexed with mRNA and tRNA. Science. 2006;313:1935–1942. doi: 10.1126/science.1131127. [DOI] [PubMed] [Google Scholar]
42.Sponer J, Leszczynski J, Hobza P. Electronic properties, hydrogen bonding, stacking, and cation binding of DNA and RNA bases. Biopolymers. 2001;61:3–31. doi: 10.1002/1097-0282(2001)61:1<3::AID-BIP10048>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
43.Nasalean L, Stombaugh J, Zirbel CL, Leontis NB. In: Non-Protein Coding RNAs. Walter NG, Woodson SA, Batey RT, editors. Vol. 13. Berlin Heidelberg: Springer; 2009. pp. 1–26. [Google Scholar]
44.Leontis NB, Westhof E. Geometric nomenclature and classification of RNA base pairs. RNA. 2001;7:499–512. doi: 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Leontis NB, Westhof E. A common motif organizes the structure of multi-helix loops in 16 S and 23 S ribosomal RNAs. J. Mol. Biol. 1998;283:571–583. doi: 10.1006/jmbi.1998.2106. [DOI] [PubMed] [Google Scholar]
46.Cannone JJ, Subramanian S, Schnare MN, Collett JR, D'Souza LM, Du Y, Feng B, Lin N, Madabusi LV, Muller KM, et al. The comparative RNA web (CRW) site: an online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinfo. 2002;3:2. doi: 10.1186/1471-2105-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Guex N, Peitsch MC. SWISS-MODEL and the Swiss-PdbViewer: an environment for comparative protein modeling. Electrophoresis. 1997;18:2714–2723. doi: 10.1002/elps.1150181505. [DOI] [PubMed] [Google Scholar]
48.Auffinger P, Bielecki L, Westhof E. Anion binding to nucleic acids. Structure. 2004;12:379–388. doi: 10.1016/j.str.2004.02.015. [DOI] [PubMed] [Google Scholar]
49.Sponer JE, Leszczynski J, Sychrovsky V, Sponer J. Sugar edge/sugar edge base pairs in RNA: stabilities and structures from quantum chemical calculations. J. Phys. Chem. 2005;109:18680–18689. doi: 10.1021/jp053379q. [DOI] [PubMed] [Google Scholar]
50.Leontis NB, Stombaugh J, Westhof E. Motif prediction in ribosomal RNAs lessons and prospects for automated motif prediction in homologous RNA molecules. Biochimie. 2002;84:961–973. doi: 10.1016/s0300-9084(02)01463-3. [DOI] [PubMed] [Google Scholar]
51.Spackova N, Sponer J. Molecular dynamics simulations of sarcin-ricin rRNA motif. Nucleic Acids Res. 2006;34:697–708. doi: 10.1093/nar/gkj470. [DOI] [PMC free article] [PubMed] [Google Scholar]
52.Reblova K, Spackova N, Stefl R, Csaszar K, Koca J, Leontis NB, Sponer J. Non-Watson–Crick basepairing and hydration in RNA motifs: molecular dynamics of 5S rRNA loop E. Biophy. J. 2003;84:3564–3582. doi: 10.1016/S0006-3495(03)75089-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Correll CC, Freeborn B, Moore PB, Steitz TA. Metals, motifs, and recognition in the crystal structure of a 5S rRNA domain. Cell. 1997;91:705–712. doi: 10.1016/s0092-8674(00)80457-2. [DOI] [PubMed] [Google Scholar]
54.Auffinger P, Bielecki L, Westhof E. The Mg2+ binding sites of the 5S rRNA loop E motif as investigated by molecular dynamics simulations. Chem. Biol. 2003;10:551–561. doi: 10.1016/s1074-5521(03)00121-2. [DOI] [PubMed] [Google Scholar]
55.Leroy JL, Broseta D, Gueron M. Proton exchange and base-pair kinetics of poly(rA).poly(rU) and poly(rI).poly(rC) J. Mol. Biol. 1985;184:165–178. doi: 10.1016/0022-2836(85)90050-6. [DOI] [PubMed] [Google Scholar]
56.Gueron M, Leroy JL. Studies of base pair kinetics by NMR measurement of proton exchange. Meth. Enz. 1995;261:383–413. doi: 10.1016/s0076-6879(95)61018-9. [DOI] [PubMed] [Google Scholar]
57.Moazed D, Stern S, Noller HF. Rapid chemical probing of conformation in 16 S ribosomal RNA and 30 S ribosomal subunits using primer extension. J. Mol. Biol. 1986;187:399–416. doi: 10.1016/0022-2836(86)90441-9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]

gkp468_index.html^{(762B, html)}

gkp468_1.pdf^{(5.7MB, pdf)}

gkp468_nar-00671-m-2009-File012.xls^{(328.5KB, xls)}

[B1] 1.Draper DE. A guide to ions and RNA structure. RNA. 2004;10:335–343. doi: 10.1261/rna.5205404. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] 2.Klein DJ, Moore PB, Steitz TA. The roles of ribosomal proteins in the structure assembly, and evolution of the large ribosomal subunit. J. Mol. Biol. 2004;340:141–177. doi: 10.1016/j.jmb.2004.03.076. [DOI] [PubMed] [Google Scholar]

[B3] 3.Leontis N, Westhof E. Analysis of RNA motifs. Curr. Opin. Struct. Biol. 2003;13:300–308. doi: 10.1016/s0959-440x(03)00076-9. [DOI] [PubMed] [Google Scholar]

[B4] 4.Leontis NB, Lescoute A, Westhof E. The building blocks and motifs of RNA architecture. Curr. Opin. Struct. Biol. 2006;16:279–287. doi: 10.1016/j.sbi.2006.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] 5.Auffinger P, Westhof E. An extended structural signature for the tRNA anticodon loop. RNA. 2001;7:334–341. doi: 10.1017/s1355838201002382. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] 6.Quigley GJ, Rich A. Structural domains of transfer RNA molecules. Science. 1976;194:796–806. doi: 10.1126/science.790568. [DOI] [PubMed] [Google Scholar]

[B7] 7.Jaeger L, Verzemnieks EJ, Geary C. The UA_handle: a versatile submotif in stable RNA architectures. Nucleic Acids Res. 2009;37:215–230. doi: 10.1093/nar/gkn911. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B8] 8.Jucker FM, Pardi A. GNRA tetraloops make a U-turn. RNA. 1995;1:219–222. [PMC free article] [PubMed] [Google Scholar]

[B9] 9.Correll CC, Munishkin A, Chan YL, Ren Z, Wool IG, Steitz TA. Crystal structure of the ribosomal RNA domain essential for binding elongation factors. Proc. Natl Acad. Sci. USA. 1998;95:13436–13441. doi: 10.1073/pnas.95.23.13436. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B10] 10.Mokdad A, Krasovska MV, Sponer J, Leontis NB. Structural and evolutionary classification of G/U wobble basepairs in the ribosome. Nucleic Acids Res. 2006;34:1326–1341. doi: 10.1093/nar/gkl025. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B11] 11.Sarver M, Zirbel CL, Stombaugh J, Mokdad A, Leontis NB. FR3D: finding local and composite recurrent structural motifs in RNA 3D structures. J. Math. Biol. 2008;56:215–252. doi: 10.1007/s00285-007-0110-x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B12] 12.Stombaugh J, Zirbel CL, Westhof E, Leontis NB. Frequency and isostericity of RNA basepairs. Nucleic Acids Res. 2009;37:2294–2312. doi: 10.1093/nar/gkp011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] 13.Rupert PB, Massey AP, Sigurdsson ST, Ferre-D'Amare AR. Transition state stabilization by a catalytic RNA. Science. 2002;298:1421–1424. doi: 10.1126/science.1076093. [DOI] [PubMed] [Google Scholar]

[B14] 14.Torelli AT, Krucinska J, Wedekind JE. A comparison of vanadate to a 2′-5′ linkage at the active site of a small ribozyme suggests a role for water in transition-state stabilization. RNA. 2007;13:1052–1070. doi: 10.1261/rna.510807. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B15] 15.Ditzler MA, Sponer J, Walter NG. Molecular dynamics suggest multifunctionality of an adenine imino group in acid-base catalysis of the hairpin ribozyme. RNA. 2009;15:560–575. doi: 10.1261/rna.1416709. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B16] 16.Deshpande N, Addess KJ, Bluhm WF, Merino-Ott JC, Townsend-Merino W, Zhang Q, Knezevich C, Xie L, Chen L, Feng Z, et al. The RCSB Protein Data Bank: a redesigned query system and relational database based on the mmCIF schema. Nucleic Acids Res. 2005;33:D233–237. doi: 10.1093/nar/gki057. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] 17.Wuyts J, Perriere G, Van De Peer Y. The European ribosomal RNA database. Nucleic Acids Res. 2004;32:D101–103. doi: 10.1093/nar/gkh065. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B18] 18.Sethi A, O'Donoghue P, Luthey-Schulten Z. Evolutionary profiles from the QR factorization of multiple sequence alignments. Proc. Natl Acad. Sci. USA. 2005;102:4045–4050. doi: 10.1073/pnas.0409715102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B19] 19.Atkins P, de Paula J. Physical Chemistry. 7th. Oxford: Oxford University Press; 2002. [Google Scholar]

[B20] 20.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery J, JA, Vreven T, Kudin KN, et al. 2004. Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford, CT. [Google Scholar]

[B21] 21.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]

[B22] 22.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Physical Rev. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]

[B23] 23.Miehlich B, Savin A, Stoll H, Preuss H. Results obtained with the correlation energy density functionals of becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989;157:200–206. [Google Scholar]

[B24] 24.Gresh N, Sponer JE, Spackova N, Leszczynski J, Sponer J. Theoretical study of binding of hydrated Zn(II) and Mg(II) cations to 5′-guanosine monophosphate. Toward polarizable molecular mechanics for DNA and RNA. J. Phys. Chem. 2003;107:8669–8681. [Google Scholar]

[B25] 25.Sponer J, Jurecka P, Hobza P. Accurate interaction energies of hydrogen-bonded nucleic acid base pairs. J. Am. Chem. Soc. 2004;126:10142–10151. doi: 10.1021/ja048436s. [DOI] [PubMed] [Google Scholar]

[B26] 26.Barone V, Cossi M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. 1998;102:1995–2001. [Google Scholar]

[B27] 27.Cossi M, Rega N, Scalmani G, Barone V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comp. Chem. 2003;24:669–681. doi: 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]

[B28] 28.Klamt A, Schuurmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 1993;2:799–805. [Google Scholar]

[B29] 29.Sponer JE, Reblova K, Mokdad A, Sychrovsky V, Leszczynski J, Sponer J. Leading RNA tertiary interactions: structures, energies, and water insertion of A-minor and P-interactions. A quantum chemical view. J. Phys. Chem. 2007;111:9153–9164. doi: 10.1021/jp0704261. [DOI] [PubMed] [Google Scholar]

[B30] 30.Orozco M, Luque FJ. Theoretical methods for the description of the solvent effect in biomolecular systems. Chem. Rev. 2000;100:4187–4226. doi: 10.1021/cr990052a. [DOI] [PubMed] [Google Scholar]

[B31] 31.Sponer J, Riley KE, Hobza P. Nature and magnitude of aromatic stacking of nucleic acid bases. Phys. Chem. Chem. Phys. 2008;10:2595–2610. doi: 10.1039/b719370j. [DOI] [PubMed] [Google Scholar]

[B32] 32.Hobza P, Sponer J. Structure, energetics, and dynamics of the nucleic acid base pairs: nonempirical ab initio calculations. Chem. Rev. 1999;99:3247–3276. doi: 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]

[B33] 33.Jurecka P, Nachtigall P, Hobza P. RI-MP2 calculations with extended basis sets – a promising tool for study of H-bonded and stacked DNA base pairs. Phys. Chem. Chem. Phys. 2001;20:4578–4582. [Google Scholar]

[B34] 34.Boys SF, Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970;19:553–566. [Google Scholar]

[B35] 35.Šponer J, Jurečka P, Hobza P. In: Computational Studies of RNA and DNA. Sponer J, Lankas F, editors. Vol. 2. Berlin Heidelberg: Springer; 2006. pp. 343–388. [Google Scholar]

[B36] 36.Eichkorn K, Treutler O, Ohm H, Haser M, Ahlrichs R. Auxiliary basis sets to approximate Coulomb potentials. Chem. Phys. Lett. 1995;242:652–660. [Google Scholar]

[B37] 37.Weigend F, Haser M. RI-MP2: first derivatives and global consistency. Theoret. Chem. Accounts: Theory Comput. Model. 1997;97:331–340. [Google Scholar]

[B38] 38.Weigend F, Haser M, Patzelt H, Ahlrichs R. RI-MP2: optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998;294:143–152. [Google Scholar]

[B39] 39.Schuwirth BS, Borovinskaya MA, Hau CW, Zhang W, Vila-Sanjurjo A, Holton JM, Cate JH. Structures of the bacterial ribosome at 3.5 A resolution. Science. 2005;310:827–834. doi: 10.1126/science.1117230. [DOI] [PubMed] [Google Scholar]

[B40] 40.Wimberly BT, Brodersen DE, Clemons W.M., Jr, Morgan-Warren RJ, Carter AP, Vonrhein C, Hartsch T, Ramakrishnan V. Structure of the 30S ribosomal subunit. Nature. 2000;407:327–339. doi: 10.1038/35030006. [DOI] [PubMed] [Google Scholar]

[B41] 41.Selmer M, Dunham CM, Murphy F.Vt, Weixlbaumer A, Petry S, Kelley AC, Weir JR, Ramakrishnan V. Structure of the 70S ribosome complexed with mRNA and tRNA. Science. 2006;313:1935–1942. doi: 10.1126/science.1131127. [DOI] [PubMed] [Google Scholar]

[B42] 42.Sponer J, Leszczynski J, Hobza P. Electronic properties, hydrogen bonding, stacking, and cation binding of DNA and RNA bases. Biopolymers. 2001;61:3–31. doi: 10.1002/1097-0282(2001)61:1<3::AID-BIP10048>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]

[B43] 43.Nasalean L, Stombaugh J, Zirbel CL, Leontis NB. In: Non-Protein Coding RNAs. Walter NG, Woodson SA, Batey RT, editors. Vol. 13. Berlin Heidelberg: Springer; 2009. pp. 1–26. [Google Scholar]

[B44] 44.Leontis NB, Westhof E. Geometric nomenclature and classification of RNA base pairs. RNA. 2001;7:499–512. doi: 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B45] 45.Leontis NB, Westhof E. A common motif organizes the structure of multi-helix loops in 16 S and 23 S ribosomal RNAs. J. Mol. Biol. 1998;283:571–583. doi: 10.1006/jmbi.1998.2106. [DOI] [PubMed] [Google Scholar]

[B46] 46.Cannone JJ, Subramanian S, Schnare MN, Collett JR, D'Souza LM, Du Y, Feng B, Lin N, Madabusi LV, Muller KM, et al. The comparative RNA web (CRW) site: an online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinfo. 2002;3:2. doi: 10.1186/1471-2105-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B47] 47.Guex N, Peitsch MC. SWISS-MODEL and the Swiss-PdbViewer: an environment for comparative protein modeling. Electrophoresis. 1997;18:2714–2723. doi: 10.1002/elps.1150181505. [DOI] [PubMed] [Google Scholar]

[B48] 48.Auffinger P, Bielecki L, Westhof E. Anion binding to nucleic acids. Structure. 2004;12:379–388. doi: 10.1016/j.str.2004.02.015. [DOI] [PubMed] [Google Scholar]

[B49] 49.Sponer JE, Leszczynski J, Sychrovsky V, Sponer J. Sugar edge/sugar edge base pairs in RNA: stabilities and structures from quantum chemical calculations. J. Phys. Chem. 2005;109:18680–18689. doi: 10.1021/jp053379q. [DOI] [PubMed] [Google Scholar]

[B50] 50.Leontis NB, Stombaugh J, Westhof E. Motif prediction in ribosomal RNAs lessons and prospects for automated motif prediction in homologous RNA molecules. Biochimie. 2002;84:961–973. doi: 10.1016/s0300-9084(02)01463-3. [DOI] [PubMed] [Google Scholar]

[B51] 51.Spackova N, Sponer J. Molecular dynamics simulations of sarcin-ricin rRNA motif. Nucleic Acids Res. 2006;34:697–708. doi: 10.1093/nar/gkj470. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B52] 52.Reblova K, Spackova N, Stefl R, Csaszar K, Koca J, Leontis NB, Sponer J. Non-Watson–Crick basepairing and hydration in RNA motifs: molecular dynamics of 5S rRNA loop E. Biophy. J. 2003;84:3564–3582. doi: 10.1016/S0006-3495(03)75089-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[B53] 53.Correll CC, Freeborn B, Moore PB, Steitz TA. Metals, motifs, and recognition in the crystal structure of a 5S rRNA domain. Cell. 1997;91:705–712. doi: 10.1016/s0092-8674(00)80457-2. [DOI] [PubMed] [Google Scholar]

[B54] 54.Auffinger P, Bielecki L, Westhof E. The Mg2+ binding sites of the 5S rRNA loop E motif as investigated by molecular dynamics simulations. Chem. Biol. 2003;10:551–561. doi: 10.1016/s1074-5521(03)00121-2. [DOI] [PubMed] [Google Scholar]

[B55] 55.Leroy JL, Broseta D, Gueron M. Proton exchange and base-pair kinetics of poly(rA).poly(rU) and poly(rI).poly(rC) J. Mol. Biol. 1985;184:165–178. doi: 10.1016/0022-2836(85)90050-6. [DOI] [PubMed] [Google Scholar]

[B56] 56.Gueron M, Leroy JL. Studies of base pair kinetics by NMR measurement of proton exchange. Meth. Enz. 1995;261:383–413. doi: 10.1016/s0076-6879(95)61018-9. [DOI] [PubMed] [Google Scholar]

[B57] 57.Moazed D, Stern S, Noller HF. Rapid chemical probing of conformation in 16 S ribosomal RNA and 30 S ribosomal subunits using primer extension. J. Mol. Biol. 1986;187:399–416. doi: 10.1016/0022-2836(86)90441-9. [DOI] [PubMed] [Google Scholar]

PERMALINK

Classification and energetics of the base-phosphate interactions in RNA

Craig L Zirbel

Judit E Šponer

Jiri Šponer

Jesse Stombaugh

Neocles B Leontis

Abstract

INTRODUCTION

MATERIALS AND METHODS

Datasets

Software

Hardware

Selection of non-redundant sequences for BPh analysis

Selecting a reduced-redundancy set of PDB files for analysis

Initial geometries used in quantum chemical calculations

Geometry optimizations

Interaction energies

Modifications to the FR3D program suite

Construction of rRNA 3D structural alignments

RESULTS

Identification of BPh interactions in 3D structures

Figure 1.

Figure 2.

Quantum chemical calculation of optimized geometries and interaction energies for BPh interactions

Table 1.

Adenine

Cytosine

Guanine

Uracil

Significance of computed BPh interaction energies

Relative stabilities of BPh interactions

Comparison of BPh to base pair interaction energies

Base-phosphate classification in RNA 3D crystal structures

Figure 3.

Annotation of BPh interactions in secondary structures

Figure 4.

Occurrence of BPh interactions in structured RNA molecules

Occurrence of BPh interactions by type and interaction energy

Figure 5.

Locations of BPh interactions in relation to the secondary structure

Figure 6.

Table 2.

Table 3.

Sequence conservation of BPh interactions

Conservation of BPh interactions between homologous RNA 3D structures

Table 4.

Table 5.

Conservation of H-bond donor bases in BPh interactions among homologous rRNA sequences

Figure 7.

Predicting base conservation in sequences using pairwise interactions in 3D structures

Conservation of BPh interactions at the base pair level

Figure 8.

Table 6.

Figure 9.

DISCUSSION

Role of BPh interactions in stabilizing RNA structures

How these data can be used

CONCLUSIONS

SUPPLEMENTARY DATA

FUNDING

Supplementary Material

ACKNOWLEDGEMENTS

REFERENCES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases