Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Aug 26.
Published in final edited form as: Psychon Bull Rev. 2008 Feb;15(1):64–69. doi: 10.3758/PBR.15.1.64

Temporal associative processes revealed by intrusions in paired-associate recall

Orin C Davis 1, Aaron S Geller 2, Daniel S Rizzuto 3, Michael J Kahana 4
PMCID: PMC2731933  NIHMSID: NIHMS129246  PMID: 18605481

Abstract

Although much is known about the factors that influence the acquisition and retention of individual paired associates, the existence of temporally defined associations spanning multiple pairs has not been demonstrated. We report two experiments in which subjects studied randomly paired nouns for a subsequent cued recall test. When subjects recalled nontarget items, their intrusions tended to come from nearby pairs. This across-pair contiguity effect was graded, spanning noncontiguously studied word pairs. The existence of such long-range temporally defined associations lends further support to contextual-retrieval models of episodic association.

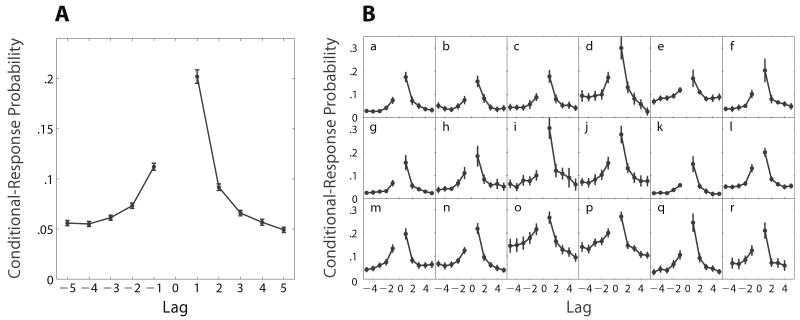
The law of contiguity states that experiences occurring in close temporal proximity become associated. This oldest and perhaps most venerable of the laws of association implies that items studied in neighboring list positions serve as more effective retrieval cues for one another than do items studied in remote list positions. Consider the contiguity effect in free recall. When recalling the words on a previously studied list in any order, subjects tend to recall words from neighboring list positions in succession. As shown in Figure 1, the probability of recalling a word from serial position i + lag immediately following a word from serial position i is a decreasing function of | lag |. This contiguity effect exhibits a forward bias, with associations being stronger in the forward direction than in the backward direction (Kahana, 1996).

Figure 1.

Figure 1

Open in a new tab

The contiguity effect in free recall. (a) The conditional-response probability as a function of lag (or lag-CRP) shows the probability of recalling an item from serial position i + lag immediately following an item from serial position i. This curve depicts data averaged across 18 different studies shown separately in panel B. (B) Lag-CRP curves from each of the following studies: (a) Murdock (1962) (list length 20, 2 sec/item). (b) Murdock (1962) (list length 30, 1 sec/item). (c) Murdock and Okada (1970). (d) Kahana, Howard, Zaromb, and Wingfield (2002) (Experiment 1). (e) Howard and Kahana (1999) (Experiment 2). (f) Murdock (1962) (list length 20, 1 sec/item). (g) Murdock (1962) (list length 40, 1 sec/item). (h) Murdock and Metcalfe (1978). (i) Howard and Kahana (1999) (Experiment 1). (j) Kahana et al. (2002) (Experiment 2). (k) Roberts (1972). (l–m) Zaromb et al. (2006) (Experiments 1 & 2). (n) Thapar et al. (unpublished). (o) Kimball and Bjork (2002). (p) Kimball, Bjork, and Bjork (unpublished). (q) Kahana and Howard (2005). (r) Kahana, Dolan, Sauder, and Wingfield (2005). From Handbook of Latent Semantic Analysis (p. 123), by T. K. Landauer, D. S. McNamara, S. Dennis, and W. Kintsch (Eds.), 2007, Mahwah, NJ: Erlbaum.

One observes similar evidence for temporally or positionally defined associations in the serial recall task. When subjects recall the words on a previously studied list in the order in which they were presented, incorrect recalls tend to be words that were studied in positions near that of the correct response (Lee & Estes, 1977; Nairne, 1990). The temporal gradient of errors in serial recall is strikingly similar to the temporal gradient of correct responses in free recall (Klein, Addis, & Kahana, 2005).

The contiguity effects observed in free and serial recall could reflect one of a number of underlying processes. One could envision direct item-to-item associations among neighboring items, as predicted by classic associative chaining theories (Ebbinghaus, 1885/1913; Lewandowsky & Murdock, 1989; Metcalfe & Murdock, 1981). An alternative is Raaijmakers and Shiffrin's (1980) dual-store model of recall, in which items from contiguous positions tend to share time in a short-term store, or rehearsal buffer. This shared time, in turn, strengthens their interitem associations in long-term memory (Sirotin, Kimball, & Kahana, 2005). Finally, according to contextual coding models (see, e.g., Brown, Preece, & Hulme, 2000; Burgess & Hitch, 1999; Howard & Kahana, 2002), associations between contiguous items could result from those items having been stored with similar contextual or positional representations. Retrieving the temporal or positional context of a given item will serve as a cue for items studied in nearby list positions (Howard & Kahana, 2002).

Paired-associate memory provides an interesting contrast to both free and serial recall. In the standard paired-associate procedure, subjects are asked to learn a list of word pairs. Following this study phase, subjects are cued for recall of specific pairs (either in the forward or the backward order). Unlike free and serial recall—in which subjects must learn an entire list—subjects in the paired-associate task have no reason to learn associations other than those binding the items within each studied pair. Recall is strictly cued by the experimenter, so there is no benefit to recalling any item other than the one being probed. Although associations in both free and serial recall have a strong forward bias, associations in paired-associate tasks are generally symmetric, with nearly identical recall rates for forward and backward probes (see, for reviews, Ekstrand, 1966; Kahana, 2002). This surprising result led Gestalt psychologists to propose an associative symmetry hypothesis (Asch & Ebenholtz, 1962; Köhler, 1947). According to this view, associations are learned by incorporating the representations of the constituent items into a new holistic representation. Formalized in computational models, this view predicts that the strengths of forward and backward associations are approximately equal and highly correlated (Caplan, Glaholt, & McIntosh, 2006; Kahana, 2002; Rizzuto & Kahana, 2001; Sommer, Rose, & Büchel, 2007).

The present article seeks to answer a straightforward empirical question: When learning a list of paired associates, do subjects form temporal associations beyond those required to learn the pairings set forth in the experiment? Despite more than 100 years of research on paired-associate memory, one can find no definitive answer to this question in the archival literature (for reviews, see Brown & McCormack, 2006; Underwood, 1983).

We approach the question of long-range associations in paired-associate memory by analyzing subjects' intrusion errors. If a common associative process underlies all recall tasks, then we might expect to find that intralist intrusions (ILIs) are more likely to come from neighboring list pairs. We can further ask whether intrusions to nearby pairs are biased toward the position of the correct target item. That is, after subjects study the list [A1−B1, A2−B2, …, An−Bn], will an intrusion made to the cue “Ai−?” more likely be Bj than Aj, with j≠i? Alternatively, we may ask whether intrusions are biased toward the member of a pair that is more temporally proximate to the target pair, so that “Ai−?” is more likely to evoke Ai+1 than Bi+1. As in free recall, we expected prior-list intrusions (PLIs) in paired-associate tasks to exhibit a temporal gradient, with most PLIs coming from recent lists (Zaromb et al., 2006). We also examined whether PLIs tend to come from the same serial position as the target item (cf. Henson, 1999).

Experiments 1 and 2

Method

Subjects

Seventy-five undergraduate students participated in Experiment 1; 14 undergraduate students participated in Experiment 2.

Procedure

In Experiment 1, each list comprised 12 word pairs that were randomly sampled without replacement from the noun subset of the Toronto Word Pool (Friendly, Franklin, Hoffman, & Rubin, 1982). During the study phase, pairs were presented auditorily through a computer speaker. The second word in each pair was presented 2 sec following the onset of the first word in that pair. The first word in the subsequent pair was presented 3 sec following the onset of the second word in the preceding pair. Immediately following the last pair, subjects were given a 15-sec arithmetic distractor task: Problems of the form A + B + C = ? (for A, B, and C integers from 1 to 9) appeared, and subjects were asked to type the correct answer for each problem. A high-pitch tone was given following correct responses; a low-pitch tone followed incorrect responses. This distractor task served to attenuate the end-of-list recency effect (see, e.g., Murdock, 1967).

During the recall phase, subjects were tested on 8 randomly chosen pairs from the 12 that were studied. The order of presentation at test was random with respect to the order at study. For each test probe, a cue word was presented auditorily, and the subject attempted to recall its pair vocally. Half of the tested pairs—chosen at random—were probed in the forward direction; the other half were probed in the backward direction. If unsure of the correct answer, subjects were instructed to say “pass.” Responses were digitally recorded for scoring at a later time. After each study–test trial, subjects were allowed to take a short break.

Each subject studied and attempted to recall 16 unique lists according to the procedures described above. The first of these 16 lists was considered practice, and data from that list were not included in the following analyses. A single experimental session lasted 1–1.5 h. The entire word pool was randomized separately for each subject.

The procedure in Experiment 2 followed that of Experiment 1, except that subjects in Experiment 2 were instructed to give a response to every test cue—even if they were unsure of the correct answer— and studied lists of 18 pairs over 11 trials.

Results

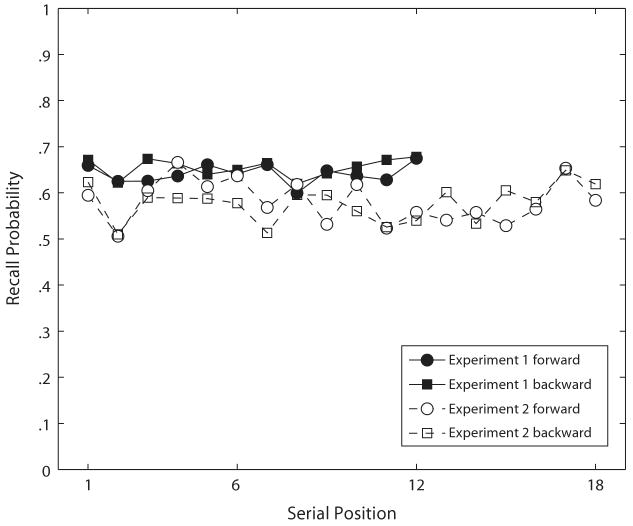
We first compared forward and backward recall probability as a function of serial position (see Figure 2). On the basis of previous work, we did not expect recall probability to vary with either serial position or recall direction. Primacy effects are not usually observed in paired-associate tasks, and recency effects are attenuated or eliminated by an end-of-list distractor, such as the one given in our experiments (Murdock, 1967). As was reviewed in the introduction, the recall of paired associates is usually symmetric with respect to order of study.

Figure 2.

Figure 2

Open in a new tab

Serial position curves for correct recall: Recall probability for forward and backward cues as a function of serial position. Data are shown for the 12 serial positions of Experiment 1 and the 18 serial positions of Experiment 2 and reflect the absence of any serial position effect on recall.

Consistent with these expectations, a repeated measures ANOVA failed to detect any significant serial position effects [F(11,1551) = 1.03, p > .4 for Experiment 1; F(17,442) = 1.12, p > .3 for Experiment 2] or any reliable effects of recall direction [F(1,141) < 1, n.s., for Experiment 1; F(1,26) < 1, n.s., for Experiment 2]. Furthermore, recall direction and serial position did not exhibit a significant interaction in either experiment [F(11,1551) < 1, n.s., for Experiment 1; F(17,442) < 1, n.s., for Experiment 2]. As further evidence for the principle of associative-symmetry hypothesis (Asch & Ebenholtz, 1962), overall recall probabilities in the forward and backward directions were nearly identical (Experiment 1, forward recall = .647 ± .026, and backward recall = .657 ± .024; Experiment 2, forward recall = .536 ± .170, and backward recall = .547 ± .166).

Intrusions constituted approximately 10% of subjects' responses in Experiment 1. In Experiment 2, our use of a forced-recall procedure led subjects to commit many more intrusions. Nearly half of these intrusions were items not presented in the course of the experiment (extralist intrusions; XLIs). Table 1 reports the fraction of subjects' responses that were PLIs, ILIs, and XLIs for Experiments 1 and 2.

Table 1. Probability of Prior List (PLI), Intralist (ILI), and Extralist (XLI) intrusions, and Standard Errors of the Means.

Experiment PLI ILI XLI
p SE p SE p SE
1 .02 .02 .05 .04 .03 .03
2 .09 .10 .13 .08 .19 .16
Open in a new tab

Consistent with studies of intrusions in free recall (Murdock, 1974; Zaromb et al., 2006), we found that PLIs in paired-associate recall tend to come from recent lists. Regressing the probability of a PLI on list lags of 1 through 5 for each subject who met our inclusion criterion,1 we obtained a mean regression coefficient of −0.237 in Experiment 1 [t(38) = −3.079, p < .01] and −.275 in Experiment 2 [t(13) = −1.885, p = .08]. Combining data across both experiments yielded a regression coefficient of −0.245 [t(52) = −3.64, p < .001]. We also examined whether PLIs tend to be items that were studied in the same serial position as that of the target item in the current list. These so-called “protrusion” errors have been taken as strong evidence for positional-coding processes in serial recall (Henson, 1999). We therefore asked whether subjects in our paired-associate task exhibited a similar tendency to commit protrusion errors. A comparison of protrusion errors with PLIs from the three prior and three subsequent list positions for subjects who committed at least three PLIs did not reveal any significant tendency to commit protrusions (mean protrusion rate = 8.34%; mean PLI rate for adjacent lags = 7.52%) [t(34) = .37, p > .7].

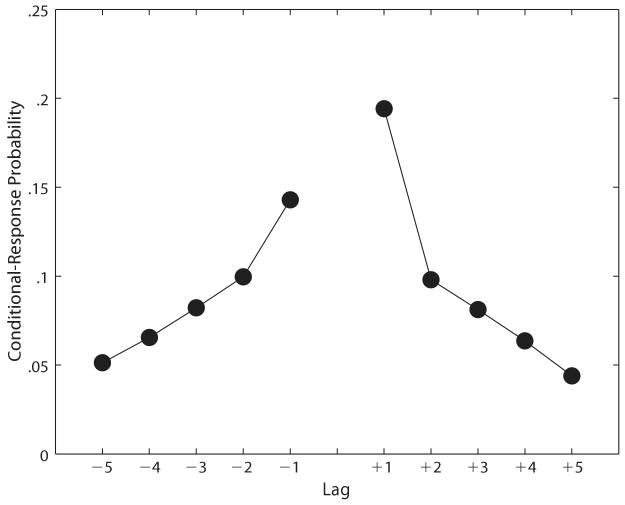
Our primary question of theoretical interest was whether ILIs came from pairs studied in temporal proximity to the target pair. Since we did not find any systematic differences between the two experiments, we report our results based on the combined data. As can be seen in Figure 3, the conditional probability of an ILI decreased monotonically with the number of pairs (lag), separating the ILI from the probed item. (We conditionalized the probability of committing an ILI from a given lag on the availability of pairs at that lag.) A repeated measures ANOVA found a significant effect of lag on the conditional response probability [F(56,504) = 7.71, p < .001].

Figure 3.

Figure 3

Open in a new tab

Effects of across-pair contiguity on paired-associate recall. The probability of an intrusion from pair i + | lag | when the correct response is from pair i decreases monotonically with absolute lag.

To assess the reliability of this across-pair contiguity effect, we conducted two separate analyses. First, we conducted a series of paired-sample t tests in order to compare the conditional probability of ILIs from adjacent and remote lags. These tests revealed significant differences between lags of +1 and +2, +1 and +3, −1 and −2, and −1 and −3 (p < .05 for all comparisons). In addition to conducting these planned comparisons between select adjacent and remote lags, we carried out a second analysis in which we regressed the probability of an ILI on absolute values of lags 1–5 separately for each subject who committed at least four total ILIs across all lists. We obtained an average regression coefficient of −.38 (SE = .06) across all of the 57 subjects who met our inclusion criterion. A t test confirmed that this effect was reliable [t(56) = −6.429, p < .001]. In order to determine whether this across-pair contiguity effect was carried entirely by adjacent pairs—as might be expected if subjects had rehearsed the second member of a given pair with the first member of the subsequent pair—we repeated this analysis using only lags of 2–5. In this analysis, we obtained an average regression coefficient of −.23 [t(56) = −3.23, p < .005]. Thus, the across-pair contiguity effect is not limited to an increased tendency to commit intrusions from adjacent pairs.2

We next examined whether subjects' ILIs were more likely to come from pairs that preceded the target pair or from pairs that followed it. To test for asymmetry in the across-pair contiguity effect, we compared the conditional probability of an ILI to (forward) lags of +1 with the conditional probability of an ILI to (backward) lags of −1. The asymmetry effect seen in Figure 3 was statistically reliable [t(56) = 2.06, p < .05].

Although the preceding analyses focused on the number of pairs separating an ILI from the target item, one can also ask which of the two items in a pair is more likely to be recalled as an ILI. For example, if subjects are probed for recall of the second item in a target pair, one may ask whether their ILIs tend to come from the second item in a nontarget pair, thus preserving the item's within-pair position. Similarly, if subjects are probed for recall of the first item in a target pair, one can ask whether their ILIs will tend to come from the first item in a nontarget pair. We did not find any significant difference between congruent-position ILIs (proportion of all responses = 4.5%, SE = .37%) and incongruent-position ILIs (proportion of all responses = 4.0%, SE = .45%) [t(56) = 1.53, p > .1, n.s.]. Alternatively, one may ask whether subjects' ILIs tend to be the within-pair item that is temporally closest to the target pair. That is, in the case of an ILI that comes from the pair immediately following the target (i.e., lag = +1), one may ask whether it is more likely to have been the first rather than the second item. We did not find any significant difference between the more proximal (proportion of lag−1 ILIs = 53%, SE = 5.7%) and the more distal within-pair positions (proportion of lag−1 ILIs = 47%, SE = 5.7%) [t(56) < 1, n.s.]. These null findings are consistent with Caplan's (2005) hypothesis that the members of a given pair are associated with a single, shared, temporal (or positional) context, but that neighboring pairs are associated with different temporal contexts. According to this hypothesis, once the wrong context (or position) is retrieved, it is just as likely to cue either member of the nontarget pair.

Discussion and Conclusions

The reported experiments provide a clear-cut answer to the question set forth at the beginning of this article (see also Brown & McCormack, 2006). Our analysis of subjects' intralist intrusions revealed strong evidence for the existence of temporal associative processes operating beyond the level of individual studied pairs. This contiguity effect was not limited to adjacently studied pairs, but persisted out to lags of at least four intervening pairs (see Figure 3).

Because the order of test was randomized with respect to the order of study in both experiments, there was no reason for subjects to adopt a strategy of learning inter-pair associations. Indeed, such a strategy would have been counterproductive insofar as it would have induced high levels of associative interference between pairs (Primoff, 1938). Our findings of associative tendencies in subjects' intralist intrusions suggest that these associations arise from a basic and, most likely, obligatory memory process that causes items studied in nearby list positions to become associatively connected (Howard & Kahana, 2002). These results thus argue against previous claims that intentionality is required for learning contiguity-based associations (see Underwood, 1983, for a review).

The present results add critical new evidence to an emerging body of work on temporal associative processes in episodic memory tasks (Brown & McCormack, 2006). The ubiquity of contiguity-based associations and the similarity of their functional form across varied episodic tasks argues for a basic mechanism underlying temporal associations (Buzsáki, 2005). One candidate mechanism is NMDA-dependent synaptic plasticity, which occurs when distinct neural patterns (memories) are activated within a 100- to 250-msec time window (Lisman, Jensen, & Kahana, 2001). But such a mechanism—although appealing on neural grounds—would appear to have a difficult time accommodating our finding of associations spanning multiple pairs, or related findings in free recall, in which associations are preserved across demanding periods of distractor activity (Howard, 2004; Howard & Kahana, 1999). Accounts of associations arising from co-occupancy in a limited-capacity, short-term rehearsal buffer (see, e.g., Kahana, 1996; Sirotin et al., 2005) would also have difficulty explaining the present results. This is because, in dual-store models, associations in long-term store are formed among items that spend time together in the short-term buffer. Our finding of associations spanning multiple pairs of words would thus require dual-store models to allow multiple pairs to be present in the short-term store at the same time. Such an assumption would represent a marked departure from previous implementations of these models in which the capacity of the short-term store is limited to a single pair. In order to prevent the associations across pair boundaries from being as strong as the associations within pairs, the models would need to incorporate a new mechanism for associating pairs of items together. It may be that more sophisticated implementations of the interacting roles of short-term and long-term memory (e.g., Davelaar, Goshen-Gottstein, Ashkenazi, Haarmann, & Usher, 2005) could be more easily extended to explain our findings.

The finding of long-range contiguity effects in the behavioral analysis of associative memory is more consistent with accounts that attribute associative processes—at least in part—to contextual overlap between items studied in nearby list positions. In Howard and Kahana's (2002) temporal context model (TCM), context is a leaky integrator of vector states representing items experienced at each point in time. The contiguity effect is thus a consequence of neighboring items' having been associated with similar contextual states. When an item retrieves its stored contextual associations, those will serve as cues for items studied in similar contexts. In TCM, this retrieved temporal context representation will serve as an asymmetric cue for items studied in neighboring list positions, especially those following the cue item. This result is consistent with our finding that subjects in our task were more likely to commit ILIs from pairs that followed the target than from pairs that preceded the target pair. This forward asymmetry in temporal associative processes mirrors the forward asymmetry observed in recall transitions in both free and serial recall (Kahana, Howard, & Polyn, in press). Although subjects were more likely to commit ILIs from pairs adjacent to the target pair, they were equally likely to commit an ILI with the first member of the pair as with the second. These findings lead us to argue that associations are holistic in nature (Kahana, 2002), but that they include information concerning the temporal context of an item's occurrence.

Acknowledgments

This research was funded by National Institutes of Health Grants MH55687 and MH61975. We thank Gordon Brown for suggesting the analysis of intrusions as a function of temporal separation at study. We thank Marc Howard and Jeremy Caplan for their comments on an earlier version of this article, and we thank Michele Tully, Ben Wellington, and Dan Shiber for their assistance.

Footnotes

1

In order to ensure that PLIs from list lags of 1 through 5 were possible, we restricted our analysis to lists 6 through 16. Only subjects who committed at least one PLI across those 10 recalled lists were included in our analysis.

2

In our experiment, we presented the first and second members of each studied pair successively, rather than simultaneously. We did this in order to permit a direct test of the associative-symmetry hypothesis (see Figure 2 and Kahana, 2002, for a detailed discussion). Because of the successive presentation of the studied items, it is especially important to rule out an encoding or rehearsal-based account of the across-pair contiguity effect.

Contributor Information

Orin C. Davis, Brandeis University, Waltham, Massachusetts

Aaron S. Geller, University of Pennsylvania, Philadelphia, Pennsylvania

Daniel S. Rizzuto, California Institute of Technology, Pasadena, California

Michael J. Kahana, University of Pennsylvania, Philadelphia, Pennsylvania

References

  1. Asch SE, Ebenholtz SM. The principle of associative symmetry. Proceedings of the American Philosophical Society. 1962;106:135–163. [Google Scholar]
  2. Brown GDA, McCormack T. The role of time in human memory and binding: A review of the evidence. In: Zimmer HD, Mecklinger A, Lindenberger U, editors. Binding in human memory: A neurocognitive approach. Oxford: Oxford University Press; 2006. pp. 251–290. [Google Scholar]
  3. Brown GDA, Preece T, Hulme C. Oscillator-based memory for serial order. Psychological Review. 2000;107:127–181. doi: 10.1037/0033-295x.107.1.127. [DOI] [PubMed] [Google Scholar]
  4. Burgess N, Hitch GJ. Memory for serial order: A network model of the phonological loop and its timing. Psychological Review. 1999;106:551–581. [Google Scholar]
  5. Buzsáki G. Theta rhythm of navigation: Link between path integration and landmark navigation, episodic and semantic memory. Hippocampus. 2005;15:827–840. doi: 10.1002/hipo.20113. [DOI] [PubMed] [Google Scholar]
  6. Caplan JB. Associative isolation: Unifying associative and list memory. Journal of Mathematical Psychology. 2005;49:383–402. [Google Scholar]
  7. Caplan JB, Glaholt MG, McIntosh AR. Linking associative and serial list memory: Pairs versus triples. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2006;32:1244–1265. doi: 10.1037/0278-7393.32.6.1244. [DOI] [PubMed] [Google Scholar]
  8. Davelaar EJ, Goshen-Gottstein Y, Ashkenazi A, Haarmann HJ, Usher M. The demise of short-term memory revisited: Empirical and computational investigations of recency effects. Psychological Review. 2005;112:3–42. doi: 10.1037/0033-295X.112.1.3. [DOI] [PubMed] [Google Scholar]
  9. Ebbinghaus H. On memory: A contribution to experimental psychology. New York: Teachers College, Columbia University; 1913. Original work published 1885. [Google Scholar]
  10. Ekstrand BR. Backward associations. Psychological Bulletin. 1966;65:50–64. doi: 10.1037/h0022645. [DOI] [PubMed] [Google Scholar]
  11. Friendly M, Franklin PE, Hoffman D, Rubin DC. The Toronto Word Pool: Norms for imagery, concreteness, orthographic variables, and grammatical usage for 1,080 words. Behavior Research Methods & Instrumentation. 1982;14:375–399. [Google Scholar]
  12. Henson RNA. Positional information in short-term memory: Relative or absolute? Memory & Cognition. 1999;27:915–927. doi: 10.3758/bf03198544. [DOI] [PubMed] [Google Scholar]
  13. Howard MW. Scaling behavior in the temporal context model. Journal of Mathematical Psychology. 2004;48:230–238. [Google Scholar]
  14. Howard MW, Kahana MJ. Contextual variability and serial position effects in free recall. Journal of Experimental Psychology: Learning, Memory, & Cognition. 1999;25:923–941. doi: 10.1037//0278-7393.25.4.923. [DOI] [PubMed] [Google Scholar]
  15. Howard MW, Kahana MJ. A distributed representation of temporal context. Journal of Mathematical Psychology. 2002;46:269–299. [Google Scholar]
  16. Kahana MJ. Associative retrieval processes in free recall. Memory & Cognition. 1996;24:103–109. doi: 10.3758/bf03197276. [DOI] [PubMed] [Google Scholar]
  17. Kahana MJ. Associative symmetry and memory theory. Memory & Cognition. 2002;30:823–840. doi: 10.3758/bf03195769. [DOI] [PubMed] [Google Scholar]
  18. Kahana MJ, Dolan ED, Sauder CL, Wingfield A. Intrusions in episodic recall: Age differences in editing of overt responses. Journals of Gerontology. 2005;60B:P92–P97. doi: 10.1093/geronb/60.2.p92. [DOI] [PubMed] [Google Scholar]
  19. Kahana MJ, Howard MW. Spacing and lag effects in free recall of pure lists. Psychonomic Bulletin & Review. 2005;12:159–164. doi: 10.3758/bf03196362. [DOI] [PubMed] [Google Scholar]
  20. Kahana MJ, Howard MW, Polyn SM. Associative processes in episodic memory. In: Byrne J, Roediger HL III, editors. Learning and memory—A comprehensive reference: Vol. 2. Cognitive psychology of learning. San Diego: Elsevier, Academic Press; in press. [Google Scholar]
  21. Kahana MJ, Howard MW, Zaromb F, Wingfield A. Age dissociates recency and lag recency effects in free recall. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2002;28:530–540. doi: 10.1037//0278-7393.28.3.530. [DOI] [PubMed] [Google Scholar]
  22. Kimball DR, Bjork RA. Influences of intentional and unintentional forgetting on false memories. Journal of Experimental Psychology: General. 2002;131:116–130. doi: 10.1037//0096-3445.131.1.116. [DOI] [PubMed] [Google Scholar]
  23. Kimball DR, Bjork RA, Bjork EL. Retrieval inhibition can increase or decrease false memories. Paper presented at the Third International Conference on Memory; Valencia, Spain. 2001. Jul, [Google Scholar]
  24. Klein KA, Addis KM, Kahana MJ. A comparative analysis of serial and free recall. Memory & Cognition. 2005;33:833–839. doi: 10.3758/bf03193078. [DOI] [PubMed] [Google Scholar]
  25. Köhler W. Gestalt psychology. New York: Liveright; 1947. [Google Scholar]
  26. Lee CL, Estes WK. Order and position in primary memory for letter strings. Journal of Verbal Learning & Verbal Behavior. 1977;16:395–418. [Google Scholar]
  27. Lewandowsky S, Murdock BB., Jr Memory for serial order. Psychological Review. 1989;96:25–57. [Google Scholar]
  28. Lisman J, Jensen O, Kahana MJ. Toward a physiologic explanation of behavioral data on human memory: The role of theta-gamma oscillations and NMDAR-dependent LTP. In: Hölscher C, editor. Neuronal mechanisms of memory formation: Concepts of long-term potentiation and beyond. Cambridge: Cambridge University Press; 2001. pp. 195–223. [Google Scholar]
  29. Metcalfe J, Murdock BB. An encoding and retrieval model of single-trial free recall. Journal of Verbal Learning & Verbal Behavior. 1981;20:161–189. [Google Scholar]
  30. Murdock BB., Jr The serial position effect of free recall. Journal of Experimental Psychology. 1962;64:482–488. [Google Scholar]
  31. Murdock BB., Jr Recent developments in short-term memory. British Journal of Psychology. 1967;58:421–433. doi: 10.1111/j.2044-8295.1967.tb01099.x. [DOI] [PubMed] [Google Scholar]
  32. Murdock BB., Jr . Human memory: Theory and data. Potomac, MD: Erlbaum; 1974. [Google Scholar]
  33. Murdock BB, Metcalfe J. Controlled rehearsal in single-trial free recall. Journal of Verbal Learning & Verbal Behavior. 1978;17:309–324. [Google Scholar]
  34. Murdock BB, Jr, Okada R. Interresponse times in single-trial free recall. Journal of Experimental Psychology. 1970;86:263–267. [Google Scholar]
  35. Nairne JS. Similarity and long-term memory for order. Journal of Memory & Language. 1990;29:733–746. [Google Scholar]
  36. Primoff E. Backward and forward association as an organizing act in serial and in paired-associate learning. Journal of Psychology. 1938;5:375–395. [Google Scholar]
  37. Raaijmakers JGW, Shiffrin RM. SAM: A theory of probabilistic search of associative memory. In: Bower GH, editor. The psychology of learning and motivation: Advances in research and theory. Vol. 14. New York: Academic Press; 1980. pp. 207–262. [Google Scholar]
  38. Rizzuto DS, Kahana MJ. An autoassociative neural network model of paired-associate learning. Neural Computation. 2001;13:2075–2092. doi: 10.1162/089976601750399317. [DOI] [PubMed] [Google Scholar]
  39. Roberts WA. Free recall of word lists varying in length and rate of presentation: A test of total-time hypotheses. Journal of Experimental Psychology. 1972;92:365–372. [Google Scholar]
  40. Sirotin YB, Kimball DR, Kahana MJ. Going beyond a single list: Modeling the effects of prior experience on episodic free recall. Psychonomic Bulletin & Review. 2005;12:787–805. doi: 10.3758/bf03196773. [DOI] [PubMed] [Google Scholar]
  41. Sommer T, Rose M, Büchel C. Associative symmetry versus independent associations in the memory for object-location associations. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2007;33:90–106. doi: 10.1037/0278-7393.33.1.90. [DOI] [PubMed] [Google Scholar]
  42. Underwood BJ. Attributes of memory. Glenview, IL: Scott Foresman; 1983. [Google Scholar]
  43. Zaromb FM, Howard MW, Dolan ED, Sirotin YB, Tully M, Wingfield A, Kahana MJ. Temporal associations and prior-list intrusions in free recall. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2006;32:792–804. doi: 10.1037/0278-7393.32.4.792. [DOI] [PubMed] [Google Scholar]

RESOURCES