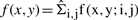Skip to main content
NCBI home page
Bioinformatics logoLink to Bioinformatics
. 2008 Jul 4;24(16):1749–1756. doi: 10.1093/bioinformatics/btn321

A probe-density-based analysis method for array CGH data: simulation, normalization and centralization

Hung-I Harry Chen 1,2, Fang-Han Hsu 1,2, Yuan Jiang 3, Mong-Hsun Tsai 2,4, Pan-Chyr Yang 5, Paul S Meltzer 3, Eric Y Chuang 1,2,4,6,7,8,*, Yidong Chen 3
PMCID: PMC2732214  PMID: 18603568

Abstract

Motivation: Genomic instability is one of the fundamental factors in tumorigenesis and tumor progression. Many studies have shown that copy-number abnormalities at the DNA level are important in the pathogenesis of cancer. Array comparative genomic hybridization (aCGH), developed based on expression microarray technology, can reveal the chromosomal aberrations in segmental copies at a high resolution. However, due to the nature of aCGH, many standard expression data processing tools, such as data normalization, often fail to yield satisfactory results.

Results: We demonstrated a novel aCGH normalization algorithm, which provides an accurate aCGH data normalization by utilizing the dependency of neighboring probe measurements in aCGH experiments. To facilitate the study, we have developed a hidden Markov model (HMM) to simulate a series of aCGH experiments with random DNA copy number alterations that are used to validate the performance of our normalization. In addition, we applied the proposed normalization algorithm to an aCGH study of lung cancer cell lines. By using the proposed algorithm, data quality and the reliability of experimental results are significantly improved, and the distinct patterns of DNA copy number alternations are observed among those lung cancer cell lines.

Contact: chuangey@ntu.edu.tw

Supplementary information: Source codes and.gures may be found at http://ntumaps.cgm.ntu.edu.tw/aCGH_supplementary

1 INTRODUCTION

Genomic alterations that exhibit DNA copy number changes are indicative of numerous diseases including cancer (Lengauer et al., 1998; Schröck et al., 1996). Many studies have demonstrated that locating chromosomal aberrations in genomic DNA samples is an important step in understanding the pathogenesis of many diseases, especially in cancer. Array comparative genomic hybridization (aCGH), developed based on microarray technology (Pinkel et al., 1998; Pollack et al., 1999, is a technique for measuring copy number changes at high-resolution (Bartos et al., 2007; Carrasco et al., 2006; Chin et al., 2006; Katoh et al., 2006; Lai et al., 2005; Neve et al., 2006).

Similar to gene expression profiling, DNA copy number profiling experiment requires a normalization step. With the maturity of microarray technology, various normalization methods that were designed for single or two-dye microarray protocols, such as linear offset, non-linear Lowess/Loess and quantile normalization, have been proposed for analyzing expression-profiling experiments (Quackenbush et al., 2002). Many aCGH experiments conveniently applied these gene expression normalization algorithms for data analysis without careful considerations. It is important to note that the fundamental difference of data characteristics between gene expression profiling and DNA copy number profiling is the dependency of aCGH probes according to their genomic position.

In other words, probes in expression arrays measure are most likely independent activities of target transcripts, whether or not they represent genes that have approximate genomic positions. However, probes in aCGH arrays measure segmental DNA copy number status, which indicates that the measurements of neighboring probes should reflect the same DNA copy number state.

Other problems, such as low intensities at loss regions and the asymmetric nature of copy number alteration (DNA gain states occur with higher frequency than loss states), also cause expression normalization methods to fail when applied to aCGH data. Clearly, the currently available normalization methods for gene expression analysis do not meet these unique characteristics of aCGH.

While most of state-of-the-art aCGH analysis methods concentrated in segmentation algorithms (Marioni et al., 2006; Picard et al., 2007; van de Wiel et al., 2007; Venkatraman and Olshen, 2007; Willenbrock and Fridlyand, 2005), very little attention has been paid to the problem of aCGH data normalization (Khojasteh et al., 2005; Neuvial et al., 2006), where normalization of aCGH data were merely aimed at correcting spatial non-uniformity of the arrays, rather than the intensity-related non-linearity. Recently, Staaf et al. (2007) proposed an aCGH normalization method in which Loess algorithm was applied to probes from normal regions extracted from simple segmentation and k-means clustering. However, the problem of extrapolating smaller dynamic range of normal probes to entire probe intensity range, and impreciseness of k-means algorithm for probe separation may still persist for certain arrays with large number of gain/loss states. Notice that if we generate 2D probe density (see Fig. 3), and then simply follow the highest ridgeline, we avoid the requirement of symmetrical distribution for Loess normalization and avoid data partition algorithm due to possible gain/loss imbalance. This is the motivation of the proposed normalization algorithm. To demonstrate the algorithm, we adopt a two-dye aCGH protocol, where a normal genomic DNA sample (male or female) is used as the common reference sample (reference channel), while the other is used for the test sample (sample channel). To normalize aCGH data, we first perform quantile normalization (Bolstad et al., 2003) to all reference channels from all arrays; then, we generate probe density based on their calibrated intensities from two channels (maintaining same ratio quantity); and regress the highest ridgeline to provide rough normalization. After the rough normalization that corrects dye bias defects, we apply the expectation maximization (EM) algorithm (Dempster et al., 1977) to centralize the copy number ratio. The key points of the proposed normalization method are the regression method for ridgeline regression from 2D probe intensity distribution, and the copy number centralization.

Fig. 3.

Fig. 3.

Open in a new tab

(a) 2D density plot with ridgeline in black ‘+’, and, (b) Regression results. Note that expected normalization reference line (in red) from simulation coincide with ridge-tracing (green line), logistic regression (black line) and cubic-spline fit (light blue line).

To facilitate the study, we have modified the microarray simulation algorithm originally proposed in Balagurunathan et al. (2002) and (Attoor et al., 2004). To apply the algorithm for aCGH arrays, we introduced the hidden Markov model (HMM) to simulate a series of aCGH experiment with random DNA copy number alterations. By using the simulated data, we selected the best normalization algorithm and optimal parameters for different types of biological problems. To demonstrate the algorithm with real aCGH data, we have generated a set of aCGH data from three lung cancer cell lines using two different types of array platforms: the home-made oligonucleotide array designed for expression study and the commercially available Agilent human whole-genome array. The normalization results were reported in the Sections 4 and 5, as well as on the Supplementary Material website. Normalization results obtained from some public datasets from GEO were also reported on the Supplementary material web site.

2 METHODS

A section of aCGH data is illustrated in Figure 1 where the raw probe ratios (log2-transformed) along with their genomic positions on the chromosome are plotted with dots, and their moving-averaged log2-ratios are plotted with gray-bar, positive ratio upward and negative ratio downward. Data were further segmented (black-lines) to reflect their segmental gain, loss or no-change status. As stated before, we adopt the two-dye aCGH protocol in Figure 1. In aCGH analysis, normalization process is commonly referred as the correction method of data non-linearity or other array hybridization artifacts; where a separate step, centralization, is designed specifically for base-line determination due to the imbalance of gain/loss region (Bilke et al., 2005; Lipson et al., 2007).

Fig. 1.

Fig. 1.

Open in a new tab

aCGH data and visualization, where the dots are raw ratios, and the black bars are moving-average ratios (log2 transformed).

The main objective of the article is to study the normalization methods specifically for aCGH, considering its nature of highly correlated adjacent data points and much higher probe-density than expression arrays. The proposed normalization algorithm is divided into two parts: 2D intensity distribution profile and ridge-tracing normalization, which provides a rough normalization over the whole array (normalization step); and the peak detection algorithm to locate the highest peak from intensity density, which provides the refined estimation of chromosome baseline relative to its normal reference sample (centralization step). To facilitate the algorithm development and to illustrate the utilities of the algorithm, we also introduced a simulation procedure based on a HMM combined with the array simulation method proposed in Attoor et al. (2004). By using the simulated data, we compared the proposed normalization method to other commonly used normalization algorithms for expression profiling studies, such as linear regression and Lowess non-linear normalization method (Quackenbush, 2002).

3 ALGORITHM

Figure 2 provides a concise view of the proposed normalization algorithm and aCGH simulation that was used in this study for evaluation of the normalization algorithm. The normalization algorithm is built on a 2D intensity distribution, and the regression is performed along its highest ridgeline, which we assumed to be the concentration of probes with no DNA alteration. Data centralization is achieved via smoothing and then mixture-model estimation in order to precisely locate the peak (or peaks when no dominant peak can be determined) where the data will be shifted to set the highest peak to zero. Sections 3.1 and 3.2 will discuss the normalization and centralization steps in depth.

Fig. 2.

Fig. 2.

Open in a new tab

Block diagram of the normalization algorithm.

The simulation algorithm is adapted from Attoor et al. (2004) with HMM for aCGH segmental data simulation (instead of the exponential distribution for gene expression). Datasets containing 100 × replications under various conditions were simulated, and then applied with the proposed normalization methods with different regression algorithms. Detailed descriptions were provided in Sections 3.3 and 3.4.

3.1 Ridge-tracing normalization algorithm

Many factors unique to aCGH data exist which cause the failure of applying the typical normalization algorithms for gene expression data to aCGH: (1) relatively low intensities and smaller dynamic range in normal state; (2) typically more amplification regions than deletion regions (mean/median shift may not work); (3) multiple gain/loss states causing the Lowess non-linear normalization to yield incorrect regression at lower or higher intensity ends; and last but not least, (4) the dependency of adjacent probes reflecting the segmental states, as illustrated in Figure S7. We proposed a novel normalization method by regressing the highest ridgeline of the 2D probe intensity distribution, rather than performing regression based on the whole dataset. By tracing the ridgeline, we took the full advantage probe dependency on it segmental state (each ridge-line represents a segmental state), while avoiding directly separating probe via clustering algorithm as suggested by Staaf (2007). Key points of the proposed normalization method are the construction of 2D density with kernel smoothing and the regression methods for ridgeline from the 2D probe density. The ridge-tracing normalization algorithm is as follows,

Algorithem 3.1.

Ridge-tracing Normalization.

  1. Perform quantile normalization to all reference channels of all arrays (Bolstad et al., 2003), if multiple arrays are presented,

  2. Generate 2D probe density via 2D kernel smoothing with normalized reference intensity and transformed sample intensity by maintaining the same log-ratio for each probe,

  3. Trace the ridgeline from 2D density by first determining the highest peak and then walking along the ridgeline, and

  4. Regress the ridgeline to provide normalization standard.

Open in a new tab

The construction of a 2D probe density is the key to the preciseness of ridge-line determination. In some situations, due to insufficient probe numbers, the density will be too coarse to be useful. To avoid this potential problem, we extended the 1D kernel smoothing technique (Hastie and Tibshirani, 1990; Wand and Jones, 1995) to construct a smooth 2D distribution, utilizing equality under the condition of independence, or Φ(x, y)=Φ(x)Φ(y) where Φ(·) is the smoothing kernel. Assuming there are n probes in an array, with red and green channel intensities to be R=(r1, …, rn) and G=(g1, …, gn), and the support of the 2D density to be rGrid and gGrid with each contains m intensity bins, a probe-binning-based implementation of kernel smoothing algorithm is described as follows:

Algorithm 3.2.

2D Kernel smoothing (R, G, rGrid, gGrid).

  1. Binning intensity rk (k=1, …, n) into mr bins specified by rGrid.

  2. For each bin rGrid(i), i=1, …, mr
    • 2.1. If there exists sufficient probes, find all probes with rk∈ rGrid(i), and then bin these probes' green channel intensities, gk, into mg bins specified by gGrid.
    • 2.2. Compute kernel density f(x,y; i, j)=ni,jΦ(x, σ r)Φ(y, σ g), where x and y are red and green channel intensity values, σr and σg are Gaussian kernel bandwidth for red- and green-channel, respectively, and ni,j is the number of probes in jth bin of gGrid,

  3. 2D probe distribution is Inline graphic

Open in a new tab

Upon obtaining the 2D intensity density, ridgeline is traced from the peak and then the algorithm ‘walk’ along the ridge toward the lower intensity or higher intensity direction, utilizing the fact that the ridgeline is generally diagonal, since most of the probes in aCGH data maintain in normal state and in good agreement with the reference sample. The 3D ridgeline is then mapped back to 2D and a regression method is selected and performed to extract the normalization reference line. In this study, we implemented four regression methods: linear regression (as an example of traditional normalization method), quadratic regression, logistic regression and cubic spline curve. Linear normalization is the simplest form of normalization while cubic-spline fitting that provides most flexibility in non-linear form. We briefly discussed these normalization methods in the following.

3.1.1 Linear and quadratic regression

For a given set of data points that demarcate the ridgelines, as shown in Figure 3a (black+), we used a polynomial curve fitting method to perform both linear (first-order) and quadratic (second-order) regression. With regressed polynomial parameters, the normalization was then applied to entire dataset. The algorithm was implemented with MATLAB (Natik, MA, USA) built-in function polyfit().

3.1.2 Logistic regression

The logistic function models the S-curve transition, which is commonly observed in M-A plot of microarray data prior to any normalization (Bolstad et al., 2003). The implementation utilized MATLAB built-in function, nlinfit(), to perform a non-linear curve fitting in the least-square sense. See Supplementary website for detailed implementations.

3.1.3 Spline curve fitting

The spline fit is based on the least-squares method with the cubic spline function, constructed of piecewise third-order polynomials which pass through a set of control points. The cubic spline curve fitting was implemented using MATLAB's internal function spline(), and data points along ridgeline were used as control points. The advantages of cubic spline function were obvious: piecewise continuous up to second derivative to avoid the distortion, particular at the beginning and the end of the ridgeline.

3.2 Mode detection and centralization

Differing from the normalization procedure, which aimed at correcting the linear and/or non-linear characteristics because of the two-dye labeling protocol, the objective of aCGH data centralization is to calibrate ‘normal DNA copy number’ to a standard value (0 as the most common choice for log-ratio), assuming the reference channel is a normal DNA sample. As we indicated before, different from expression data (Zien et al., 2001), aCGH data commonly are not symmetrically distributed due to the gain/loss imbalance. Furthermore, many cancer samples contain frequent DNA breakages and aberrations. Thus, the centralization procedure is not a trivial task. There are many different aCGH data centralization methods proposed in Lipson et al. (2007). Many of them are derived from different hypotheses: the minimal aberration location, the longest run-length or the highest mode of probe intensity distribution. The first two methods require segmentation algorithms to be performed before centralization, while the last criterion does not require segmentation. The highest probe intensity mode indicates the majority state in the tissue, which we assumed to be normal, or if f(x) is the probe density with respect to the intensity measurement from probes, the centralization procedure is to find, xmax, such that, xmax=argmaxx(f(x)). To utilize the property of neighboring probe dependency, we applied moving-median filter to the aCGH data (in genomic order) to suppress impulse noises while preserving segmental break-points before applying centralization. We then used yet again the kernel smoothing technique to approximate the probe log-ratio distribution, and then employed the EM algorithm to determine the best mixture Gaussian model (up to 6 components) of ratio distribution. The centralization factor was determined either at the dominant peak, or at the left-most peak that is not smaller than M% (90% in this study) of the highest peak, based on the assumption that copy number loss is less common than copy number gain. The centralization factor was then applied to the normalized aCGH data with a simple linear shift by the amount of xmax. The EM algorithm is supported by the MATLAB Statistical Pattern Recognition toolbox (Franc and Hlavac, 2004).

3.3 Microarray data simulation

Many microarray simulation methods were developed in order to study the process of microarray fabrication and data processing. The purpose of estimating parameters from real aCGH data for microarray simulation, rather than the random number generation as proposed in many studies, is to incorporate common noise models and systematic biases (dye bias, etc.) for evaluation of the proposed normalization algorithm. We adopted a microarray model proposed by Balagurunathan et al. (2002) and Attoor et al. (2004) as follows,

graphic file with name btn321m1.jpg (1)

where tij is the ratio of each probe (for sample i, and probe j), dj the DNA/oligo deposition variation, li the labeling variation, nij the additive measurement noise, bij the background noise and uij is the actual amount of DNA/RNA to be measured. rij is the actual copy number at probe j of i-th sample, which will be simulated by HMM (see next section). The superscripts sam and ref indicate that variables must be drawn independently for the sample and reference channels, respectively. All these random variables take on different distributions (see Attoor et al., 2004 for details).

3.4 HMM of aCGH simulation

Different from the expression profile, in which the gene expression ratio, uij in Equation (1), of a tissue is commonly assumed to possess an independent exponential distribution, genomic DNA data are measurements of segmental copy numbers, and thus, neighboring probes are highly correlated. HMM, widely used in speech recognition (Rabiner et al., 1989) and genomic sequence analysis (Durbin et al., 1999), was employed to simulate segmental changes along the genomic position, where states −1, 1 and 0 represent DNA loss, gain and no-change state, respectively, with the transition probability matrix as T={pij}, as illustrated in Figure S2. A set of parameters for discrete copy number changes along with a known variance were chosen to represent the actual copy number according to the HMM state {0, 1, −1} (Shah et al., 2006). Implementation of HMM is in MATLAB Bioinformatics toolbox.

To illustrate the model parameter estimation from microarray data, we chose a set of publicly available aCGH data (GSE 3264, GEO, NCBI/NIH) derived from a breast cancer study to estimate HMM parameters. As an example, we chose GSM 75166 (a DNA profile of breast cancer cell-line BT474) that has many previously known gain or loss regions (e.g. chromosomes 8, 17 and 20). The transition matrix for each chromosome, trained by HMM, reflected the nature of the DNA copy number gain and loss status. Table 1 provided the transition matrix for chromosome 20, where high probabilities at gain and loss states, rather than at normal state were observed, just as we expected.

Table 1.

Transition matrix trained from GSM 75166, chr20

Current state
Normal Gain Loss
Next state Normal 0.7143 0.1429 0.1429
Gain 0.0071 0.9929 0
Loss 0.0204 0.0102 0.9694
Open in a new tab

For each trained HMM parameter set, we chose three different conditions of noise and/or linearity: (1) normal: least noise and linear bias, (2) noisy: higher level of noise; and (3) Non-linear: non-linear dye-bias presented in lower intensity level and with normal noise level. In order to study the algorithm applicability, we also generated simulated aCGH microarray data with two printing densities: 40 000 probes and 300 000 probes to represent homemade arrays and state-of-the-art high-density commercial arrays. One hundred replicates were generated for each simulation condition and printing density. An example of an array with 300 000 probes in normal condition with HMM parameters derived from GSM 75166 is shown in Figure 4.

Fig. 4.

Fig. 4.

Open in a new tab

aCGH simulation result under normal noise condition, where red and green color indicates copy number gain and loss, respectively. X-axis is the probe index in their genomic order. Other noise conditions were given in supplementary Fig. S3.

4 RESULTS

To demonstrate the capability of the proposed normalization algorithm, we employed the simulation algorithm with HMM for aCGH data, trained with GSM75166 data (in fact, the training can be done with any microarray data), and then performed the normalization algorithm on these simulated data. We used all three simulated noise conditions to evaluate our normalization methods. Sections 4.1 and 4.2 presented the strength and weakness of the proposed normalization under various simulated noisy and dye-bias conditions.

Applications to aCGH data derived from a set of lung cancer cell-lines were presented in Section 4.3. The lung cancer cell line, CL1-0, was created with a poorly differentiated pulmonary adenocarcinoma. CL1-1, CL1-2, CL1-3 CL1-4, and CL1-5 cells, five sublines with progressive invasiveness (Ho et al., 2002), were selected with 4- to 6-fold increased invasive potential as compared with the parental cells, CL1-0, by in vitro measurement with the membrane invasion culture system (Chu et al., 1997). We conducted microarray analysis on CL1-0, CL1-1 and CL1-5 cells using two versions of microarrays: 45K HEEBO oligo (Invitrogen Corp, Carlsbad, CA, USA) arrays fabricated at NHGRI microarry core facility (National Human Genome Research Institute, Bethesda, MD, USA) and Agilent Human Genome CGH 105K oligo array (Agilent Technologies, Santa Clara, CA, USA). Results of the normalizations from both array formats were reported in Section 4.3.

4.1 Performance of ridge-tracing algorithm

Figure 3a showed one of the 2D density plot derived from simulated data, with 300 000 data points and intensity dependent dye-bias. The ridgeline, obtained by Algorithm 3.1, was marked by the black ‘+’ in the figure, which clearly showed a non-linear portion at the low-intensity range (also shown in Fig. 3b). As illustrated in Figure 3b, the normalization curve regression was performed against the ridgeline (or data points marked as ‘+’), rather than being performed against the entire dataset. Finding the center is a difficult task in aCGH data since secondary peaks are often not apparent (e.g. Fig. 3a), nor symmetric. Figure 3b demonstrated all of the four curve-fitting results, along with the actual non-linear dye-bias effect (the expected curve in red color).

4.2 Comparison of four regression methods

To determine which regression methods is the best, we used the rooted mean squared error (RMSE) to quantify the deviation from the expected curve, y=gk(x) where k is the index to regression methods. For any point from the ridge-tracing algorithm, (xi, yi), its nearest point on the expected curve to be {ai, bi∣ bi=gk(ai), and ai=argminz(distance((xi, yi), (z, gk(z)))}, the RMSE is defined as,

graphic file with name btn321m2.jpg (2)

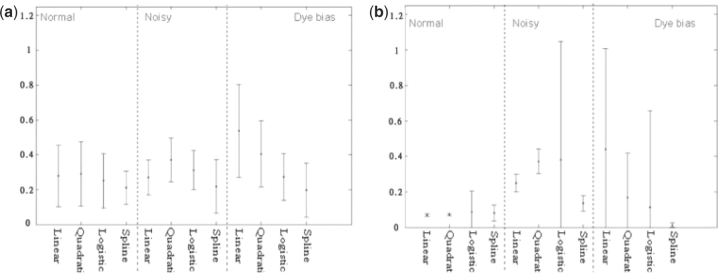
where ɛk is the measurement of fitting error for k-th curve fitting method, obtained from 100 simulated arrays of the same noise condition. Figure 5 depicted the results of four regression methods along with three simulated noise conditions, with 40 000 and 300 000 probes, respectively. We observed that when the noise was low, all these methods generated relatively equivalent performance. With 40 000 data points (Fig. 5a left-hand side), the cubic-spline method performed marginally better, with smaller mean and SD (about 50% reduction of SD) of RMSE. On the contrary, with 300 000 data points (Fig. 5b left-hand side), due to a better 2D density reconstruction and consequently the accurate ridge tracing, the average RMSE for all four methods were strikingly low, with linear regression method to be the best. This result was expected since the low-noise condition was designed to be linear, and thus the linear method provided the most robust result (smallest variation). This result also suggested that when a careful hybridization protocol was carried out, the simplest normalization should be used.

Fig. 5.

Fig. 5.

Open in a new tab

The error bar of rooted mean square error of the simulated data. Tabulated result is also provided in Supplementary Table 1. (a) 40k datasets. (b) 300k datasets.

Under other simulated conditions, noisy and dye-bias, the cubic-spline curve fitting method out-performed regression methods, with a lower average RMSE and a smaller SD, as shown in Figure 5. The logistic method, though expected to perform well, suffered from the well-known least-square convergence problems under some extreme conditions, thus resulted in a large variation. We also noted that normalization results from 300K arrays showed larger variation in dye-bias case under linear and quadratic regressions, because of the larger range covered by ridgeline from the better construction of 2D probe density. Based on these results, we chose the spline curve fitting as our final regression method for the real aCGH data normalization.

4.3 The aCGH data centralization

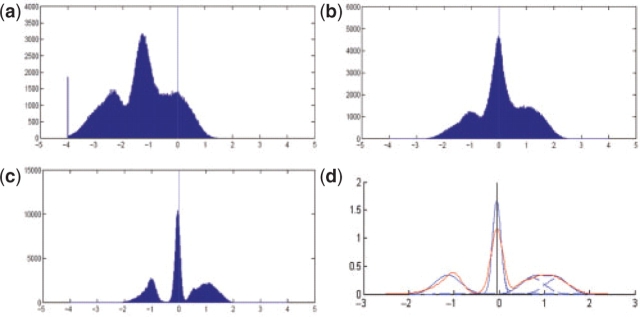
Figure 6 is the illustration of the probe ratio densities at each processing stage. In this illustration, the moving-median window size is fixed to 10 probes. Figure 6a is the histogram of the input raw ratio from one simulated array. Figure 6b to d showed the normalized ratio histogram after cubic spline, after moving-average, and the density plot after EM algorithm, respectively. Similar results for linear, quadratic and logistic regression normalization were provided in Supplementary Figure S4. In Figure 6d, the red line is the actual distribution of the median smoothed ratio; the solid blue line is the mixture model distribution; and dashed-blue lines are Gaussian model components. As we discussed in Section 4.2, the cubic-spline method provided the most distinct peaks (copy number gain or loss states), indicating better normalization results. As expected, the cubic-spline method provided the most distinct peaks, indicating better normalization results. The illustration of data in their genomic positions through various states of processing was provided in supplementary Figure S5.

Fig. 6.

Fig. 6.

Open in a new tab

The illustration of the simulated data. (Centralization factor=−0.0521 in (d).

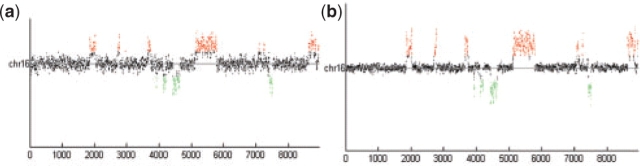
Observed from Figure S4, linear and quadratic regressions failed to correct the non-linear distortion, producing inaccurate results that needed further compensation by centralization with large shift. Contrary to linear and quadratic regression, logistic regression and spline curve fitting accurately matched the highest ridgeline; the moving median method yielded distinct peaks; and the EM algorithm resulted in minor centralization offset. This observation was further strengthened by Figure 7, in which a segment (from chromosome 16) of simulated data was shown and noted in the deletion region (in green color), Figure 7b showed the clearest deletion states after normalization and centralization.

Fig. 7.

Fig. 7.

Open in a new tab

The results of chromosome 16 after implementing aCGH normalization. X-axis is the probe's index on this chromosome. Y-axis is the signal ratio of the probe, exactly the same unit in both axes. (a) Result of linear regression. (b) Result of spline curve fitting.

4.4 Applications of normalization algorithm

We conducted microarray analysis in CL1-0, CL1-1 and CL1-5 cells using two types of microarrays: home-made HEEBO oligo microarray and Agilent human whole-genome 105K microarray. Figure S6, which contained the 2D probe density plots and regression results, showed that data derived from the home-made spotted microarray only had moderate quality, whereas the result of the Agilent array had a consistent high quality. We used an additional median filtering before the 2D density construction for better ridgeline tracing for Agilent array because its careful selection of the oligo probes resulted in a relatively small intensity dynamic range. The cubic-spline method was chosen for the reason aforementioned, and the EM algorithm was performed for centralization.

Normalized results were shown in Supplementary Figures. S7 and S8 for HEEBO microarray and Agilent aCGH arrays, respectively. Apparently, the Agilent aCGH data, due to its high resolution and better oligo design, provided a superior copy number data in terms of the preciseness of gain/loss status and the consistency over entire genome. On the contrary, the home-made array, based on its gene-centric HEEBO oligo design, produced comparable result, but it obviously lacked the dynamic range and consistency. Other supplementary Figures S9 and S10 provided detailed views of those normalized data in genomic position from both platforms, further enhancing our conclusion.

We have also downloaded more than 30 arrays with 244k spots (Agilent Human Genome CGH Microarray 244A) from GEO database to test the performance of our normalization algorithm. The results of these published data can be found on our Supplementary webpage.

5 DISCUSSION

Unlike the algorithms for gene expression that only have the normalization step; our proposed normalization algorithm combined two steps for aCGH data analysis: a ridge-tracing normalization and an EM algorithm based centralization. The ridge-tracing normalization corrects data non-linearity and other array hybridization artifacts. The EM algorithm detects the dominant mode, as well as secondary modes, for data centralization. The centralization step is unique to aCGH data normalization due to the imbalance of gain/loss regions, whereas most of the gene expression data is assumed symmetrical because of the independence of each gene's expression level.

While the linear regression normalization fails to normalize aCGH data in non-linear conditions, can we, as the typical situation in gene expression data analysis, apply Lowess method directly to correct aCGH data? The answer is NO in most situations. This can be further illustrated by Figure S11, where Lowess may regress incorrectly at lower intensity (circled by green line) and/or at higher intensity (circled by red line). To confirm this statement, we took the simulated data under dye-bias condition, and directly applied Lowess normalization to 100 replicates. The RMSE is 0.325 (σ=0.066), much worse than one might achieve with ridge-tracing/cubic-spline curve fitting (Table S1). Therefore, without careful removal of gain and loss regions, Lowess algorithm will regress to the wrong center at lower/high-intensity ends.

Tracing the highest ridgeline avoided the aforementioned weaknesses of direct applying of Lowess and of separating population. However, the Lowess method does not work with data points only from the highest ridgeline (around 300 points for 105K Agilent data), which is the reason that we chose a set of different regression methods to fit the highest ridgeline. In the ridge-tracing normalization, we have presented four regression methods for fitting the highest ridgeline and compared these methods to the simulated data in different conditions. According to the RMSE results, we concluded that cubic-spline curve fitting performed consistently and accurately for all simulated data. However, it is worth noting that when array hybridization/scanning environment and protocols are well designed, one shall choose the linear regression method since it provides the least model constraint with better normalization result (Fig. 5b). Although the logistic regression method was expected to perform well, it was a torment to estimate the parameters via the least-square method, particularly when data are quite linear, or non-linear at both intensity ends.

Whether to apply the moving-median filtering before ridge-tracing normalization or not depends on the data quality. For microarrays with good quality such as Agilent aCGH arrays, signal intensities aggregate together and cause the highest ridgeline difficult to be traced, we chose to apply the moving-median method in order to generate better ridgeline estimation. For microarrays with wider intensity ranges such as home-made microarrays, the highest ridgeline is much easier to be traced. While the moving-median suppresses noise, it would further distort the signal when the intensity-dependent dye-bias condition was presented.

Compared to the raw data of the home-made and the Agilent aCGH microarrays, the normalized data clearly showed that removal of noises achieved more accurate results. The results of the home-made oligo array and the Agilent aCGH array for CL1-0, CL1-1 and CL1-5 were quite similar, as shown in Figures S6 and S7. The results from each chromosome demonstrate similar genetic profiles between different platforms. This newly developed normalization method enables us to remove experimental biases between aCGH microarrays so that other aCGH analysis algorithms, such as segmentation algorithms and aberration region determination algorithms, can achieve much accurate results.

6 CONCLUSION

In this study, we demonstrated a novel method for analyzing aCGH data and for profiling abrupt changes in the relative copy number ratios between test and reference DNA samples. The ridge-tracing normalization algorithm can accurately fit the highest ridgeline in various noisy and non-linear conditions. Data centralization employed the EM algorithm for accurately locating the dominant mode and secondary modes. EM algorithm was performed against the copy number ratio distribution derived from the moving-median filtering by utilizing the dependency of neighboring probes.

By estimating the HMM parameters from published aCGH data, we can simulate aCGH data in different conditions. Furthermore, by using various simulated conditions, our results indicated that cubic-spline curve fit provided the best normalization result. The application of the proposed normalization algorithm to a set of cancer cell line aCGH profiling provided excellent results for the genome-wide copy number change visualization, and enabled accurate segmentation and other downstream analysis.

Supplementary Material

[Supplementary Data]
btn321_index.html (701B, html)

ACKNOWLEDGEMENTS

Funding: This research was supported in part by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research, 95HM0032 (E.Y.C.) and 95HM0033195R0066-BM01-01 (E.Y.C.) from National Taiwan University, and DOH96-TD-G-111-014 (E.Y.C.) from Department of Health, Executive Yuan, ROC (Taiwan).

Conflict of Interest: none declared.

REFERENCES

  1. Attoor S, et al. Which is better for cDNA-microarray-based classification: ratios or direct intensities. Bioinformatics. 2004;20:2513–2520. doi: 10.1093/bioinformatics/bth272. [DOI] [PubMed] [Google Scholar]
  2. Balagurunathan Y, et al. Simulation of cDNA microarrays via a parameterized random signal model. J. Biomed. Opt. 2002;7:507–523. doi: 10.1117/1.1486246. [DOI] [PubMed] [Google Scholar]
  3. Bartos JD, et al. aCGH local copy number aberrations associated with overall copy number genomic instability in colorectal cancer: coordinate involvement of the regions including BCR and ABL. Mutat. Res. 2007;615:1–11. doi: 10.1016/j.mrfmmm.2006.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bilke S, et al. Detection of low level genomic alterations by comparative genomic hybridization based on cDNA micro-arrays. Bioinformatics. 2005;21:1138–1145. doi: 10.1093/bioinformatics/bti133. [DOI] [PubMed] [Google Scholar]
  5. Bolstad B, et al. A comparison of normalization methods for high density oligonucleotide array data based on bias and variance. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
  6. Carrasco DR, et al. High-resolution genomic profiles define distinct clinico-pathogenetic subgroups of multiple myeloma patients. Cancer Cell. 2006;9:313–325. doi: 10.1016/j.ccr.2006.03.019. [DOI] [PubMed] [Google Scholar]
  7. Chin K, et al. Genomic and transcriptional aberrations linked to breast cancer pathophysiologies. Cancer Cell. 2006;10:529–541. doi: 10.1016/j.ccr.2006.10.009. [DOI] [PubMed] [Google Scholar]
  8. Chu YW, et al. Selection of invasive and metastatic subpopulations from a human lung adenocarcinoma cell line. Am. J. Respir. Cell Mol. Biol. 1997;17:353–360. doi: 10.1165/ajrcmb.17.3.2837. [DOI] [PubMed] [Google Scholar]
  9. Dempster AP, et al. Maximum likelihood from incomplete data via the EM algorithm, J. R. Stat. Soc. B. 1977;39:1–38. [Google Scholar]
  10. Durbin R, et al. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge, UK: Cambridge University Press; 1999. [Google Scholar]
  11. Franc V, Hlavac V. Statistical Pattern Recognition Toolbox for Matlab User's guide. Czech Technical University; 2004. [Google Scholar]
  12. Hastie TJ, Tibshirani RJ. Generalized Additive Models. New York: Chapman and Hall; 1990. [Google Scholar]
  13. Ho C-C, et al. Up-regulated caveolin-1 accentuates the metastasis capability of lung adenocarcinoma by inducing filopodia formation. Am. J. Pathol. 2002;161:1647–1656. doi: 10.1016/S0002-9440(10)64442-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Katoh H, et al. Genetic inactivation of the APC gene contributes to the malignant progression of sporadic hepatocellular carcinoma: a case report. Genes Chromosomes Cancer. 2006;45:1050–1057. doi: 10.1002/gcc.20362. [DOI] [PubMed] [Google Scholar]
  15. Khojasteh M, et al. A stepwise framework for the normalization of array CGH data. BMC Bioinformatics. 2005;6:274. doi: 10.1186/1471-2105-6-274. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lai WR, et al. Comparative analysis of algorithms for identifying amplifications and deletions in array CGH data. Bioinformatics. 2005;21:3763–3770. doi: 10.1093/bioinformatics/bti611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lengauer C, et al. Genetic instabilities in human cancers. Nature. 1998;396:643–649. doi: 10.1038/25292. [DOI] [PubMed] [Google Scholar]
  18. Lipson D. Computational Aspects of DNA Copy Number Measurement. Israel Institute of Technology: Computer Science Department; 2007. PhD Dissertation. [Google Scholar]
  19. Marioni JC, et al. BioHMM: a heterogeneous hidden Markov model for segmenting array CGH data. Bioinformatics. 2006;22:1144–1146. doi: 10.1093/bioinformatics/btl089. [DOI] [PubMed] [Google Scholar]
  20. Neuvial P, et al. Spatial normalization of array-CGH data. BMC Bioinformatics. 2006;7:264. doi: 10.1186/1471-2105-7-264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Neve RM, et al. A collection of breast cancer cell lines for the study of functionally distinct cancer subtypes. Cancer Cell. 2006;10:515–527. doi: 10.1016/j.ccr.2006.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Picard F, et al. A segmentation/clustering model for the analysis of array CGH data. Biometrics. 2007;63:758–766. doi: 10.1111/j.1541-0420.2006.00729.x. [DOI] [PubMed] [Google Scholar]
  23. Pinkel D, et al. High resolution analysis of DNA copy number variation using comparative genomic hybridization to microarrays. Nat. Genet. 1998;20:207–211. doi: 10.1038/2524. [DOI] [PubMed] [Google Scholar]
  24. Pollack JR, et al. Genome-wide analysis of DNA copy-number changes using cDNA microarrays. Nat. Genet. 1999;23:41–46. doi: 10.1038/12640. [DOI] [PubMed] [Google Scholar]
  25. Quackenbush J. Microarray data normalization and transformation. Nature Genetics. 2002;32:496–501. doi: 10.1038/ng1032. [DOI] [PubMed] [Google Scholar]
  26. Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE. 1989;77:257–286. [Google Scholar]
  27. Schröck E, et al. Multicolor spectral karyotyping of human chromosomes. Science. 1996;273:494–497. doi: 10.1126/science.273.5274.494. [DOI] [PubMed] [Google Scholar]
  28. Shah SP, et al. Integrating copy number polymorphisms into array CGH analysis using a robust HMM. Bioinformatics. 2006;22:e431–e439. doi: 10.1093/bioinformatics/btl238. [DOI] [PubMed] [Google Scholar]
  29. Staaf J, et al. Normalization of array-CGH data: influence of copy number imbalances. BMC Genomics. 2007;8:382. doi: 10.1186/1471-2164-8-382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. van de Wiel MA, et al. CGHcall: calling aberrations for array CGH tumor profiles. Bioinformatics. 2007;23:892–894. doi: 10.1093/bioinformatics/btm030. [DOI] [PubMed] [Google Scholar]
  31. Venkatraman ES, Olshen AB. A faster circular binary segmentation algorithm for the analysis of array CGH data. Bioinformatics. 2007;23:657–663. doi: 10.1093/bioinformatics/btl646. [DOI] [PubMed] [Google Scholar]
  32. Wand MP, Jones MC. Kernel Smoothing, Monographs on Statistics and Applied Probability. London, UK: Chapman & Hall; 1995. [Google Scholar]
  33. Willenbrock H, Fridlyand J. A comparison study: applying segmentation to array CGH data for downstream analyses. Bioinformatics. 2005;21:4084–4091. doi: 10.1093/bioinformatics/bti677. [DOI] [PubMed] [Google Scholar]
  34. Zien A, et al. Centralization: a new method for the normalization of gene expression data. Bioinformatics. 2001;17:323–331. doi: 10.1093/bioinformatics/17.suppl_1.s323. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btn321_index.html (701B, html)
btn321_1.pdf (1.1MB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES