mlegp: statistical analysis for computer models of biological systems using R

Abstract

Summary: Gaussian processes (GPs) are flexible statistical models commonly used for predicting output from complex computer codes. As such, GPs are well suited for the analysis of computer models of biological systems, which have been traditionally difficult to analyze due to their high-dimensional, non-linear and resource-intensive nature. We describe an R package, mlegp, that fits GPs to computer model outputs and performs sensitivity analysis to identify and characterize the effects of important model inputs.

Availability: http://www.biomath.org/mlegp

Contact: kdorman@iastate.edu

Supplementary information: See http://www.biomath.org/mlegp for a user manual and examples.

1 INTRODUCTION

Gaussian processes (GPs) commonly facilitate analysis of computer models that are high-dimensional, non-linear and resource-intensive (Santner et al., 2003) by serving as fast and accurate emulators of these models. GPs play a prominent role in computer model calibration and validation (Bayarri et al., 2007; Kennedy and O'Hagan, 2001)), as well as sensitivity analysis (SA) to rank inputs in order of importance [based on functional analysis of variance (FANOVA) decomposition] and to characterize their effects (through visual plots of main and two-way factor interactions) (Schonlau and Welch, 2006).

We describe an R package, mlegp, that implements GP modeling with power exponential correlation structure (Santner et al., 2003), the SA methods described in Schonlau and Welch (2006) and the modeling of functional computer model output described in Heitmann et al. (2006). In addition, mlegp extends previous GP models to handle stochastic computer output with non-constant (heteroscedastic) variance by no longer requiring a constant nugget term across observations.

The package is appropriate for what Kitano (2002) describes as simulation-based research in systems biology. In this context, computer models have been used to simulate gene expression and signal transduction pathways, e.g. in Escherichia coli (Dobrzyński et al., 2007); and infectious disease at the cellular level, e.g. Mycobacterium tuberculosis infection (Segovia-Juarez et al., 2004). We demonstrate the capabilities of mlegp by analyzing a computer model of parasitic infection.

2 STATISTICAL METHODS

2.1 The Gaussian process

Let z_obs=[z(x⁽¹⁾), …, z(x^(m))] be a vector of observed computer model outputs for m choices of the input vector x⁽ⁱ⁾=[x⁽ⁱ⁾₁, …, x⁽ⁱ⁾_p]. We are interested in predicting output z(t) at untried input t. The correlation between any two computer model outputs is assumed to have the form

(1)

Let μ(x) be the unconditional mean E[z(x)]. Define the mean matrix

Under the GP model, computer output follows a multivariate normal distribution

(2)

where I is the m×m identity matrix, C≡{C_ij} from Equation (1), σ²_GP is the unconditional variance of mean computer model output and the nugget σ²_e accounts for computer model stochasticity. For convenience, denote the variance–covariance matrix as V. Then, the GP predictive distribution of z(t) is normal with mean and variance

where r=[r₁,…,r_m]′, with r_i=cor(z(t), z(x⁽ⁱ⁾)) following Equation (1). For more details, see Santner et al. (2003).

2.2 Sensitivity analysis

Schonlau and Welch (2006) describe SA of computer models using GPs. For independent marginal priors on the components of x, the total variance of the GP predictor can be decomposed into contributions from single and interacting inputs, a technique called FANOVA decomposition. The percent-age of total functional variance attributed to the main effect of an input or the interaction effect among inputs provides a measure of the importance of that effect. The main effect E[z(x)∣z_obs, x_k] of the k-th input variable predicts output, given x_k and known results z_obs, by integrating against a prior π(x_−k) on all remaining variables in x. The two-way interaction effect E[z(x)∣z_obs, x_k, x_l] is similarly defined. Main effects plots and contour plots conveniently illustrate main effects and two-factor interactions as functions of the model inputs x_k and (x_k,x_l).

3 SOFTWARE

The package mlegp, available in R (R Development Core Team, 2007)), finds maximum likelihood estimates of Gaussian process parameters using the likelihood that follows from Equation (2). The package extends previous GP models by allowing the user to replace the identity matrix I in (2) with a user-defined diagonal matrix N. This extension leads to more accurate GP emulators of heteroscedastic computer models when the variance is known or well estimated. Another approach to this problem is implemented in the R package tgp, which fits separate GPs to a partitioned input space using a fully Bayesian approach (Gramacy, 2007). Not all non-constant variance can be partitioned in this way. On the other hand, our model requires knowledge of the nugget matrix up to a multiplicative constant.

GPs with constant mean functions (i.e. μ(x)≡μ₀) or linear functions in x are supported. For high-dimensional or functional output such as time-series data, the user can opt to fit independent GPs to individual outputs or, instead, to the most important principle component weights following singular value decomposition of the output (Heitmann et al., 2006). For each GP, the R package provides cross-validated diagnostics, performs FANOVA decomposition, and produces plots for all main and two-way factor interaction effects. Main effects for functional output can also be produced.

4 EXAMPLE APPLICATION: ANALYSIS OF A COMPUTER MODEL OF DISEASE

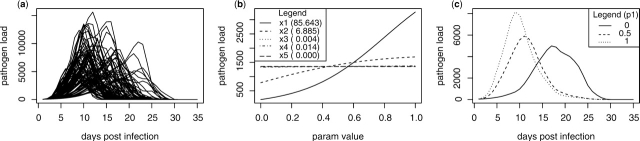
The SA methods we describe have been used to analyze computer models with up to 40 input variables (Schonlau and Welch, 2006). For demonstration purposes, we use mlegp to analyze the effects of five input variables (x=[x₁,…,x₅]) in a computer model of Leishmania major infection (Dancik et al., 2006). Inputs are scaled between 0 and 1 and are described in Supplementary Material. Computer model output consists of pathogen load over time (Fig. 1a). Using mlegp, we fit a GP to 100 observations of pathogen load at 5 days post infection (dpi). Main effects for all inputs and their FANOVA contributions are provided in Figure 1b. Lastly, we use mlegp to calculate the main effect of x₁ (pathogen growth rate) on the temporal evolution of pathogen load by fitting independent GPs to the six most important principle component weights (Fig. 1c). The SA shows that the input variable x₁ is the most important input for determining pathogen load at 5 dpi and has a positive relationship with this response (Fig. 1b). Low values of x₁ result in a gradual increase in pathogen load and a relatively longer infection, whereas high values of x₁ result in a sharp increase in pathogen load and a higher peak, but a fast resolution of the infection (Fig. 1c).

Fig. 1.

Sensitivity analysis of a computer model of parasitic infection using the R package mlegp. (a) Computer model output, consisting of pathogen load over time, for 100 simulations obtained by varying inputs x₁ through x₅, (b) main effects for all inputs on pathogen load at 5 dpi, along with the percentage contribution of each effect to the total functional variance of the GP predictor and (c) main effect of x₁ on pathogen load over time.

In Supplementary Material, we report additional output from mlegp, including GP diagnostic plots, the FANOVA decomposition, and two-way interaction contour plots, for pathogen load at both 5 and 18 dpi. We also illustrate the advantage of using a non-constant nugget term for heteroscedastic computer model output.