Accelerating and focusing protein–protein docking correlations using multi-dimensional rotational FFT generating functions

Abstract

Motivation: Predicting how proteins interact at the molecular level is a computationally intensive task. Many protein docking algorithms begin by using fast Fourier transform (FFT) correlation techniques to find putative rigid body docking orientations. Most such approaches use 3D Cartesian grids and are therefore limited to computing three dimensional (3D) translational correlations. However, translational FFTs can speed up the calculation in only three of the six rigid body degrees of freedom, and they cannot easily incorporate prior knowledge about a complex to focus and hence further accelerate the calculation. Furthemore, several groups have developed multi-term interaction potentials and others use multi-copy approaches to simulate protein flexibility, which both add to the computational cost of FFT-based docking algorithms. Hence there is a need to develop more powerful and more versatile FFT docking techniques.

Results: This article presents a closed-form 6D spherical polar Fourier correlation expression from which arbitrary multi-dimensional multi-property multi-resolution FFT correlations may be generated. The approach is demonstrated by calculating 1D, 3D and 5D rotational correlations of 3D shape and electrostatic expansions up to polynomial order L=30 on a 2 GB personal computer. As expected, 3D correlations are found to be considerably faster than 1D correlations but, surprisingly, 5D correlations are often slower than 3D correlations. Nonetheless, we show that 5D correlations will be advantageous when calculating multi-term knowledge-based interaction potentials. When docking the 84 complexes of the Protein Docking Benchmark, blind 3D shape plus electrostatic correlations take around 30 minutes on a contemporary personal computer and find acceptable solutions within the top 20 in 16 cases. Applying a simple angular constraint to focus the calculation around the receptor binding site produces acceptable solutions within the top 20 in 28 cases. Further constraining the search to the ligand binding site gives up to 48 solutions within the top 20, with calculation times of just a few minutes per complex. Hence the approach described provides a practical and fast tool for rigid body protein-protein docking, especially when prior knowledge about one or both binding sites is available.

Availability: http://www.csd.abdn.ac.uk/hex/

Contact: d.w.ritchie@abdn.ac.uk

1 INTRODUCTION

Genome-wide proteomics studies (Gavin et al., 2002; Ho et al., 2002; Ito et al., 2001; Uetz et al., 2000) provide a growing list of putative protein–protein interactions, but understanding the function of these predicted interactions requires further biochemical and structural analysis. However, protein–protein hetero-complexes currently constitute <2% of the known protein structures in the Protein Data Bank (PDB; Berman et al., 2002). Protein docking algorithms aim to bridge this gap by using computational techniques to predict the three dimensional (3D) structures of protein–protein complexes starting from the unbound or model-built monomers. For recent reviews, see Ritchie, (2008) and references therein.

Proteins have intrinsically dynamical molecular structures which can often change conformation to some extent on complexation. However, in order to make the calculation tractable, most protein docking algorithms begin by assuming that the structures to be docked are rigid. This essentially reduces the problem to a 6D rotational–translational search space. The fast Fourier transform (FFT) correlation approach, introduced by Katchalski-Katzir et al. (1992), revolutionized this part of the docking calculation by making it computationally feasible to systematically explore and evaluate in the order of billions (O(10⁹)) of trial orientations without using any a priori information on the expected structure. The first FFT scoring function of Katchalski-Katzir et al., (1992) was based only on shape complementarity within a Cartesian grid, but was later extended to include additional terms representing electrostatic interactions (Gabb et al., 1997; Mandell et al., 2001), or both electrostatic and desolvation contributions (Chen et al., 2003). Each of these terms adds a new correlation function to the potential. More recently, we have shown that the use of pairwise structure-based potentials can improve the generation of near-native docking predictions by up to 50% (Kozakov et al., 2006). Other investigators have also reported considerable success with knowledge-based docking potentials (Ritchie, 2008). To be used with FFT-based docking, all such potentials need to be expressed as sums of correlation functions. Furthermore, in order to simulate protein flexibility during docking calculations, several groups use FFT techniques to dock ensembles of rigid body structures (Grünberg et al., 2004; Mustard and Ritchie, 2005; Smith et al., 2005), which further increases the computational cost of FFT-based approaches. Hence there is a need to develop more powerful and more versatile FFT docking techniques.

Several groups have demonstrated considerable success with ‘data-driven’ docking techniques, perhaps best exemplified by the HADDOCK program (Dominguez et al., 2003), which use external biochemical or biophysical knowledge about binding sites or interaction residues to filter rigid body docking predictions. However, due to the translational nature of the Cartesian FFT, which cannot be easily constrained to search around a putative binding site, data-driven filters generally cannot be used to focus and accelerate conventional Cartesian FFT-based approaches.

The other disadvantage of Cartesian FFT-based approaches is that new FFT grids must be computed for each rotational increment of the rotating molecule. Because fully covering the search space requires many thousands of rotational samples, Cartesian docking algorithms commonly take several hours to complete, and the efficiency of the approach decreases with increasing complexity of the potential. On the other hand, the Hex spherical polar Fourier (SPF) representation (Ritchie and Kemp, 2000) avoids the grid sampling overhead of the Cartesian-based methods and naturally allows up to two angular constraints to be used to constrain the search space. Hence Hex docking runs typically take from a few minutes to around 1 h, even though the original algorithm uses only a 1D FFT to accelerate the calculation. However, the efficiency of the Hex algorithm also decreases with the increasing complexity of the potential.

Because the FFT allows a problem that formally requires O(N²) operations to be computed in O(N log N) steps, greater computational speed-ups should be expected when the FFT is applied to as many degrees of freedom as possible. A 5D FFT rotational correlation technique was described by Kovacs et al., (2003) to superpose 3D electron microscopy (EM) density maps. However, conventional FFT-based techniques require that each FFT grid dimension be a power of two. Hence the approach described was limited to relatively crude low order correlations for the 5D FFT grid to fit into computer memory. Recently, multi-dimensional mixed radix FFT implementations have become available (e.g. MKL: http://www.intel.com/, FFTW: http://www.fftw.org/ and Kiss FFT: http://sourceforge.net/projects/kissfft/), thereby eliminating the radix constraint on the FFT grid dimensions. Nonetheless, no 5D FFT protein–protein docking algorithm has been described to date, and it would appear that implementing a practical 5D EM density correlation also remains a challenge. For example, Garzón et al., (2007) found it necessary to remove two FFT dimensions from the 5D rotational space in order to implement a practical 3D EM density fitting algorithm.

This article shows that by representing the properties to be correlated as expansions of SPF basis functions, it is relatively straight-forward to develop an analytic 6D correlation master equation in which each pairwise interaction is concisely represented as a fully factorized sum over a product of complex exponentials and SPF translation matrix elements. This master equation may then be used to derive generating functions (GFs) for 5D, 3D and 1D FFT rotational correlations. Surprisingly, 5D shape-only and low order shape plus electrostatic correlations are found to be slower than 3D correlations. However, due to the fully factorized form of the GF, 5D FFTs are expected to be advantageous when correlating more complex multi-term potentials. Nonetheless, regardless of the dimension of the FFT correlation, the SPF approach provides a natural way to define one or two simple angular constraints with which to focus docking searches around known or hypothesized binding sites. This accelerates the calculation and can significantly reduce the number of false-positive predictions.

Here, the approach is applied to the 84 complexes of the Protein docking benchmark (Mintseris et al., 2005) using shape-only and shape plus electrostatic correlations. Blind 3D shape-only docking correlations find acceptable solutions within the top 20 in 6 cases, whereas including electrostatics in the calculation gives 16 solutions within the top 20. Applying a single loose angular constraint to focus the calculation around the receptor binding site is sufficient to produce acceptable solutions within the top 20 in 28 cases. Further constraining the search to the ligand binding site in a similar manner gives up to 48 solutions within the top 20.

2 METHODS

2.1 SPF correlations

The main goal of Fourier-based docking algorithms is to calculate rapidly and accurately multiple overlap integrals of the form

(1)

where dr=r² dr sinθdθdφ is the 3D volume element in polar coordinates, φ(r) and ρ(r) represent 3D scalar functions such as the electrostatic potential and charge density, and E represents the classical electrostatic energy of the system, for example. Protein shape complementarity may also be expressed as sums of overlap integrals Ritchie and Kemp, (2000). In the SPF approach, each real scalar property of interest, A(r), is represented as a polynomial expansion to order N as

(2)

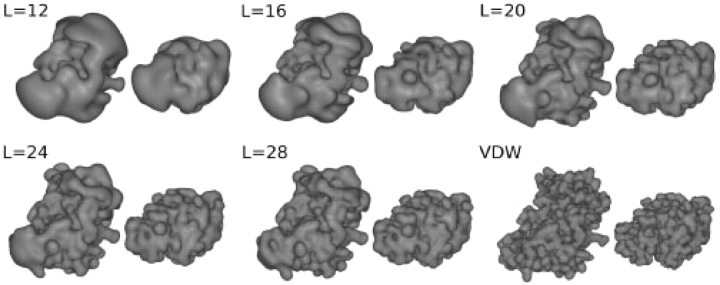
where a_nlm are real expansion coefficients, calculated just once for each property by numerical integration, y_lm(θ,φ) are normalized real spherical harmonics (SHs) and R_nl(r) are orthonormal Gaussian-type orbital (GTO) or exponential-type orbital (ETO) radial basis functions (Ritchie and Kemp, 2000). Calculating the expansion coefficients corresponds to performing a forward Fourier transform in conventional FFT-based approaches. The cost of this step scales linearly with the number of atoms or the volume of the protein. All subsequent calculations depend only on the expansion order. For consistency with previous work (Ritchie, 2005, Ritchie and Kemp, 2000), the radial index, n, counts from unity. Hence the highest harmonic order and highest polynomial power in any individual coordinate is L=N−1. Until now, Hex docking runs typically used 1D real correlations of a two-term (van der Waals plus surface skin) shape density representation of each protein using L=24 (N=25) GTO expansions. Electrostatic interactions may be calculated similarly using the ETO basis functions. Figure 1 shows some example SPF representations of the complex between the HyHel-5 antibody and hen egg lysozyme (PDB code 3HFL), calculated from the GTO expansion coefficients at various orders.

Fig. 1.

SPF steric density isosurfaces of various 3D GTO expansions for the complex between the HyHel-5 antibody Fv domain (left) and hen egg lysozyme (right). The subunits are separated by 15 Â for clarity. The bottom right pair shows atomic Gaussian representations of the van der Waals surfaces from which the SPF expansions are derived.

Here, it is convenient to use both real and complex SHs, with the complex functions denoted as Y_lm(θ,φ). The two types of function are related by a unitary transformation matrix, U^(l), which mixes pairs of functions with the same absolute value of the circular frequency, m, Biedenharn and Louck, (1981):

(3)

Hence, Equation 2 may be written in complex form as

(4)

where the complex coefficients, A_nlm, are related to the real expansion coefficients by

(5)

SH expansions are useful in rotational problems because each group of SHs with the same order l transform amongst themselves under rotation according to the Wigner D^(l) matrices (Biedenharn and Louck, 1981):

(6)

where 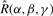represents a rotation operator expressed in terms of the Euler rotation angles α, β and γ about the z, y and z axes, respectively, with the γ rotation being applied first. Equation (6) essentially says that a rotated SH function can always be expressed as a linear combination of unrotated SH functions. Consequently, once the SPF expansion coefficients have been calculated, the effect of rotating a protein may be simulated by transforming only the original coefficients. Because the SPF basis functions are orthonormal, the overlap between a pair of SPF expansions may be calculatedas the scalar product of the expansion coefficients using, for example,

(7)

In a rigid body docking search, the overall aim is to compute the overlap between such representations over a given range of coordinate transformations. In the SPF representation, it is natural to partition the search space into one translational and five rotational degrees of freedom and to make the translational direction coincide with the intermolecular axis located on the z-axis. Figure 2 illustrates this arrangement. Letting A(r) and B(r) represent 3D scalar properties of the receptor and ligand, respectively, and assuming both molecules are initially co-located at the origin, then the overlap between these functions in a general orientation may be expressed as:

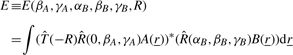(8)

where the asterisk denotes complex conjugation, and where the operators 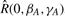, 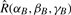and 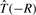represent the actions of rotating the receptor and ligand about the origin, and translating the receptor along the negative z-axis, respectively. A positive translation of the rotated ligand could equally be used. Figure 3 illustrates the main processing steps in this approach.

Fig. 2.

Left: the relationship between the spherical polar (r,θ,φ) and Cartesian (x,y,z) coordinate systems; right: schematic illustration of the 6D rigid body search space in terms of one translational coordinate, R, and five Euler rotational coordinates, (β_A,γ_A) and (α_B,β_B,γ_B), assigned to the receptor and ligand, respectively. Following the usual Euler angle convention, β rotations refer to the y−axis, and α and γ rotations refer the z-axis.

Fig. 3.

Conceptual flowcharts showing the main processing steps in the SPF approach to protein–protein docking. In practice, the rotations for the ligand or for both the ligand and receptor are computed en masse in 3D or 5D FFT rotational grids, respectively.

Now it can be shown (Ritchie, 2005) that a positive translation of the SPF basis functions by an amount R along the positive z-axis may be expressed as:

(9)

where T^(|m|)_kj,nl(R) represents a matrix element of the translation operator. These real quantities are independent of the sign of m, but they vanish if |m|>l or |m|>j, and also if j≥k or l≥n. From the orthogonality of the basis functions, it follows that translated expansion coefficients may be calculated as:

(10)

Similarly, it can be shown that rotated expansion coefficients may be calculated using the Wigner D^(l) matrices:

(11)

Hence the overlap expression becomes

(12)

Summing over the k and n radial subscripts then gives

(13)

where S(R) is a reduced translation/overlap matrix given by

(14)

The Wigner rotation matrix elements are defined as

(15)

where the real d^l_mm′(β) are often expressed in terms of Jacobi polynomials (Biedenharn and Louck, 1981). Here, it is convenient to expand d^l_mm′(β) as a product of complex exponentials (Edmonds, 1957):

(16)

Then, writing

(17)

and collecting constants

(18)

gives

(19)

Substituting Equation (19) twice into Equation (20) gives the fully factorized result

(20)

where the summation ranges over all subscript values that satisfy |r|≤j, |s|≤j, |t|≤l, |v|≤l and |m|≤min(l, j)≤L. In this equation, r and t enumerate azimuthal frequency components, and s, v and m enumerate circular frequencies. We call Equation (20) the docking correlation master equation.

2.2 An analytic 5D FFT generating function

Equation (20) gives a compact analytic recipe for calculating the overlap function for an arbitrary point in the 6D docking space from the initial SPF expansion coefficients. However, considering the number of subscripts in Equation (20), performing point-wise summations at a given set of coordinates would clearly cost O(N⁷) arithmetic operations per point. Hence it is essential to use FFT techniques to accelerate the calculation. However, because Euler rotation angles have the ranges 0≤α,γ<360° and 0≤β<180°, it is useful to change the sign of the γ_A rotation and to scale the β rotation angles so that all rotational coordinates map to the natural phase and period of the FFT. If this is not done, the FFT calculation will over sample the β coordinates to give duplicate solutions, each at half the desired resolution. Scaling the β coordinates eliminates this effect and allows a smaller FFT grid to be used, thus halving the amount of computer memory required for each β dimension and speeding up the FFT calculation.

Dealing with the sign of γ_A is straightforward. For example, putting γ_A^′=−γ_A, and writing

(21)

and using the orthogonality of the exponentials to solve for the coefficients, η_sq, gives

(22)

where δ is the Kronecker delta, and q≡−q. Similarly, the β rotations may be scaled by putting β′=2β and writing

(23)

and again using the orthogonality of the exponentials to solve for the coefficients λ_tu. In this case, it can be shown using basic trigonometric relations that the coefficients are given by

(24)

In other words, there exist exact solutions when t is even, and convergent power series solutions when t is odd. However, for current purposes, the coefficients λ_tu may be determined to reproduce exactly a finite set of M_β rotational samples by treating Equation (23) as a discrete Fourier transform analysis equation:

(25)

Other angular ranges may be scaled onto the natural FFT period in a similar manner. Substituting the above changes of variable into Equation (20) and applying an inverse Fourier transform to the result gives

(26)

Collecting coefficients as

(27)

gives the final recipe for calculating the FFT grid:

(28)

Applying a forward Fourier transform to this expression will produce a 5D array of E(β_A,γ_A,α_B,β_B,γ_B, R) function values for unique combinations of Euler rotation angles. Hence Equation (28) may be interpreted as an analytic GF for 5D FFT docking correlations. This is the main theoretical contribution of this article.

2.3 Multi-dimensional FFTs

In Equation (28) it can be seen that the double sum over the jl subscripts means that the cost of initializing each 5D FFT grid cell scales as O(N²) and therefore the overall cost of setting up a 5D FFT scales as O(N⁷). Hence it is expedient to calculate Equation (28) as

(29)

and

(30)

Thus, by using a temporary array, W, the O(N⁷) ‘set-up’ cost of a 5D FFT can be computed practically using two O(N⁶) steps. The double sum in the expression for the reduced overlap matrix, Equation (14), may be calculated efficiently in a similar way. However, using a large intermediate array makes significant additional demands on the available computer memory. One way to reduce the memory requirement is to set γ_A=0 in the correlation expression and to explicitly rotate the receptor expansion coefficients before applying the FFT to obtain the 4D GF:

(31)

where

(32)

and A_kjq(γ_A) represents a rotated expansion coefficient. In principle, a 6D docking search could be performed by iterating over pairs of (R,γ_A) samples and by calculating 4D FFTs of the remaining rotation angles. However, this approach can immediately be seen to be impractical because the triple sum in Equation (31) indicates that the set-up cost of initializing a 4D FFT grid is still O(N⁷). On the other hand, the GF complexity falls significantly if the β_A rotation angle is dropped from the FFT. For example, by explicitly transforming the receptor expansion coefficients using Equations (10) and (11):

(33)

the 3D GF is found to be:

(34)

where

(35)

Hence, it can be seen that the set-up cost for a 3D rotational FFT essentially scales as O(N⁴) per receptor orientation. For the sake of completeness, the 2D GF has the same structure and set-up complexity as above, and may be stated as

(36)

Therefore, like the 4D case, 2D correlations may be dismissed as being computationally impractical. The 1D GF [FFT set-up complexity O(N³) per α_B twist angle search] was implemented previously in real form (Ritchie and Kemp, 2000) and is given by

(37)

2.4 Multi-property FFTs

It is well known that the correlation between two pairs of real properties may be calculated simultaneously using one complex FFT. For example, if the in vacuo electrostatic potential and charge density of a system of two proteins, A and B, are written as

(38)

and if linear combinations of the SPF expansions are formed as

(39)

where U^T is the transpose of the complex-to-real unitary transformation matrix U [c.f. Equations (1), (3), and (5)], then the electrostatic interaction energy for a pairwise orientation may be calculated as:

(40)

Similarly, dropping summation subscripts and using matrix notation for the 6D electrostatic interaction energy GF [Equation (28)] gives:

(41)

However, it follows from the linearity of this expression that multiple interaction energy correlations e=0,1,2, … may be computed simultaneously by first summing the distance-dependent part of each potential/density interaction:

(42)

to give

(43)

Thus, arbitrary combinations of correlations may be evaluated together in a single 5D FFT with very little additional cost.

2.5 Multi-resolution FFTs

It is worth noting that there is no requirement for the FFT grid dimensions to correspond exactly to the polynomial order of the SPF basis functions. For example, a low order GF may be evaluated on a high order FFT grid and vice versa. This corresponds to padding the FFT grid with zeros or excluding components that exceed the grid boundaries, respectively. Therefore, it is important to consider carefully both the polynomial expansion order and the FFT grid dimensions, as each can significantly influence overall performance. It was shown previously (Ritchie, 2003; Ritchie and Kemp, 2000) that the use of polynomial expansion orders in the range L=24 to 30 is often sufficient to give satisfactory resolution when docking globular protein domains. According to Shannon sampling theory, this implies an angular FFT grid dimension of at least M=2L=48 should be used for thorough rotational sampling. This corresponds to using an angular search increment of 360°/48=7.5°, which is somewhat finer than the rotational step sizes conventionally used in Cartesian FFT algorithms. Nonetheless, because two of the five rotational degrees of freedom can be described using Euler angles which range from 0° to 180°, it is evident that a 5D FFT grid of, e.g.48³ × 24² cells can be accommodated in<1GB of computer memory if grid values are stored as single precision complex numbers (8 bytes per grid cell). Because 1 GB of memory is normally available on contemporary 32-bit computers, this level of angular resolution will be used in the following calculations.

3 RESULTS AND DISCUSSION

3.1 FFT performance comparison

As a first test of the utility of the multi-dimensional FFT approach, the HyHel-5/lysozyme complex (Fig. 1) was docked at a range of expansion orders, L, using the conformation of the bound antibody Fv fragment and unbound lysozyme. Table 1 presents a comparison of the accuracy and execution times of shape-only and shape plus electrostatic correlations for this example. All calculations sampled 53 translational steps of ±0.75Â from the initial orientation of the complex. To facilitate comparison of the 3D and 5D correlations with the existing 1D radix-2 FFT implemented in Hex, M_α=64 was used for the twist angle dimension. The 3D and 5D grids each used M_γ=48 and M_β=24 to give (β,γ) increments of 7.5°. The remaining rotational degrees of freedom in the 3D and 1D cases, respectively, used one and two icosahedral tesselations of the sphere, each of 812 vertices, to generate rotational samples with an average angular separation of around 7.7°. Considering that the Euler grids tend to oversample near the poles, this scheme gives broadly equivalent sampling densities with around 1.7, 2.5 and 3.5 billion docking orientations for the 1D, 3D and 5D cases, respectively.

Table 1.

Comparison of shape-only and shape plus electrostatic docking correlations for the HyHel-5/lysozyme complex

L	1D shape-only		1D shape+electro		3D shape-only		3D shape+electro		5D shape-only		5D shape+electro
	Rank (RMS)	Time/m	Rank (RMS)	Time/m	Rank (RMS)	Time/m	Rank (RMS)	Time/m	Rank (RMS)	Time/m	Rank (RMS)	Time/m
16	646 (6.8)	28.7	428 (8.0)	52.0	864 (7.1)	15.1	254 (8.2)	18.1	–	37.5	669 (6.0)	40.3
20	336 (1.2)	52.7	20 (1.3)	102.7	410 (1.2)	23.5	17 (1.3)	29.2	336 (7.9)	39.3	29 (1.3)	46.5
24	417 (1.2)	92.4	52 (1.2)	184.2	501 (1.2)	33.2	53 (1.2)	51.2	833 (1.2)	53.0	82 (1.2)	56.2
26	49 (1.2)	123.3	15 (1.2)	243.1	48 (1.2)	43.5	15 (1.6)	69.0	45 (1.2)	58.7	13 (1.6)	63.1
28	54 (1.5)	158.1	8 (1.2)	315.6	22 (5.2)	54.2	11 (1.3)	92.2	19 (5.5)	64.5	13 (1.2)	71.7
30	113 (2.2)	203.5	43 (1.3)	403.0	47 (1.6)	69.8	20 (1.6)	122.5	61 (1.6)	74.3	19 (1.6)	108.0

In the table L is the polynomial order of the expansion, Rank is the rank of the first orientation found in which the ligand is within 10 Å RMS (shown in parentheses) of the crystal structure after clustering with the default Hex clustering threshold. A hyphen indicates no near-native orientation found within the top 2000 solutions. Time is the total computation time in minutes on a single processor 1.8 GHz Pentium Xeon PC. The 3D and 5D FFT calculations used Kiss FFT. For those calculations, the time spent within the FFT library is essentially constant at 13.1 and 34.3 min, respectively. All timings exclude the calculation of the translation matrix elements.

As expected, Table 1 shows that high order expansions generally assign a better rank to near-native orientations than low order expansions, but this trend is not necessarily monotonic. The best combination of a good rank and low ligand root mean squared (RMS) deviation from the complex is typically obtained with L=28 or L =30. This table also shows that shape-only 3D FFTs are around three times faster than the 1D calculation and, surprisingly, are also generally faster than 5D FFTs. However, due to the linearity of the GF, the cost of including electrostatics in 3D and 5D correlations is low compared to the cost of computing 1D shape plus electrostatic FFTs. Indeed, 5D FFTs of shape plus electrostatics are faster than 3D FFTs when L≥26. These differences would become more pronounced if more potentials were included in the calculation.

Nonetheless, considering the enormous size of the search space, the vast majority of the orientations computed in the FFT are vacuous. As it is reasonable to expect that good docking orientations should score well at all expansion orders, one way to reduce the amount of computation is to perform an initial scan of the search space using low order expansions and to rescore only the best orientations at high order. Table 2 shows the results obtained using this approach in which the best 30 000 partial (β_A,γ_A,β_B,γ_B, R) orientations are each resampled using up to four translational steps of ± 0.2 Â and rescored using 1D correlations in α_B using L=30. To avoid oversampling rotations near the (β,γ) poles in the 3D and 5D scans, all orientations from the FFT grids were mapped to icosahedral tesselation samples using a look-up table, and only distinct pairs of tesselation orientations were retained for rescoring. Table 2 shows that this two-stage scoring approach finds comparable orientations to high order searches in considerably less time, with only a small drop in the quality of the solutions. Because higher order scans tend to give better RMS deviations, we use L=20 as a good compromise between speed and accuracy.

Table 2.

Two-stage shape plus electrostatic docking results for HyHel-5/lysozyme

L	1D		3D		5D
	Rank (RMS)	Time/m	Rank (RMS)	Time/m	Rank (RMS)	Time/m
16	23 (1.5)	27.7	19 (1.5)	21.3	26 (1.6)	30.3
18	27 (1.3)	37.2	22 (1.3)	27.5	27 (1.3)	29.7
20	32 (1.3)	45.2	29 (1.3)	29.5	17 (1.3)	37.5

The table shows the results obtained by performing blind low order shape-only scans of the search space at the given order, followed by 1D L=30 shape plus electrostatic refinement of the top 30 000 orientations.

3.2 Protein docking benchmark performance

In order to evaluate the approach more exhaustively, the above correlation protocol was applied to the 84 complexes of version 2 of the Protein Docking Benchmark (Mintseris et al., 2005). To provide a consistent pseudo-random starting orientation, all proteins were initially oriented by least-squares fitting to the complex, and a small off-grid rotation, 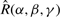=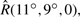, was then applied to the ligand. The orientations calculated in each docking run were clustered using a greedy algorithm with a 9 Â clustering threshold (Kozakov et al., 2005), and the lowest energy member of each cluster was selected as the ‘solution’ for that cluster. All other members of each cluster were discarded.

Seven different docking runs were performed for each complex to assess the shape-based and electrostatic components of the scoring function, and to investigate the difference between blind docking and the use of prior knowledge of one or both protein's binding sites. The results are shown in Table 3. The first set of figures in this table give the results for blind shape-only docking of bound subunits, presented as the rank and deviations of the first solution found within 10 Â RMS deviation of the complex (here called a ‘hit’) along with the total number of such hits found within the top 2000 solutions. This threshold broadly corresponds to the definition of an ‘acceptable’ prediction under the CAPRI assessment criteria (Méndez et al., 2003). Although the final goal is to dock unbound subunits, consideration of bound docking results provides a practical way to identify complexes which will a priori be expected to be difficult to dock acceptably in the unbound case. Encouragingly, acceptable solutions are found within the top 10 in 33 cases, and within the top 20 in 37 cases. This shows that the Hex shape-based scoring function can often identify near-native crystallographic orientations.

Table 3.

Hex results for the Docking Benchmark (version 2)

Code	B–B shape-only		U–U shape-only		U–U shape+elec		U–U shape-only		U–U shape+elec		U–U shape-only		U–U shape+elec
	Blind search		Blind search		Blind search		One Constraint		One Constraint		Two Constraints		Two Constraints
	Rank (RMS)	Hits	Rank (RMS)	Hits	Rank (RMS)	Hits	Rank (RMS)	Hits	Rank (RMS)	Hits	Rank (RMS)	Hits	Rank (RMS)	Hits
Rigid-Body (63)
1AVX	46 (4.8)	20	108 (8.9)	7	111 (8.9)	4	40 (8.9)	12	75 (9.0)	14	18 (9.0)	43	12 (9.0)	45
1AY7	40 (8.9)	16	645 (9.9)	4	–	–	99 (3.5)	20	234 (9.8)	1	17 (6.7)	39	17 (9.7)	18
1BVN	1 (1.1)	29	63 (9.1)	20	389 (9.6)	7	29 (9.6)	35	3 (6.6)	36	4 (5.1)	49	2 (9.6)	39
1CGI	1 (0.7)	24	42 (9.4)	17	47 (4.6)	9	20 (9.4)	14	42 (9.8)	11	4 (9.4)	31	4 (4.6)	24
1D6R	273 (1.3)	24	447 (7.7)	1	119 (7.6)	4	49 (7.7)	8	31 (7.7)	8	8 (7.7)	37	5 (7.7)	31
1DFJ	167 (4.2)	14	17 (9.5)	14	1 (4.2)	30	3 (9.5)	24	1 (4.2)	30	2 (9.5)	32	1 (4.2)	35
1E6E	1 (2.1)	14	109 (5.6)	10	5 (2.2)	24	24 (5.6)	19	3 (1.5)	29	5 (5.6)	38	1 (7.7)	49
1EAW	1 (1.0)	17	9 (5.0)	20	1 (4.0)	37	7 (5.0)	25	1 (4.0)	35	1 (5.0)	42	1 (4.0)	42
1EWY	19 (7.7)	16	76 (9.1)	12	24 (9.7)	14	114 (8.1)	12	103 (6.8)	7	9 (8.1)	37	9 (7.6)	23
1EZU	2 (0.9)	13	–	–	–	–	–	–	–	–	86 (6.7)	10	287 (6.2)	4
1F34	1 (1.4)	25	124 (6.7)	11	–	–	48 (7.1)	15	–	–	11 (5.4)	22	26 (6.5)	11
1HIA	3 (1.2)	30	51 (8.7)	6	8 (8.9)	15	72 (8.7)	21	15 (9.9)	22	15 (6.7)	33	6 (8.3)	32
1MAH	1 (0.9)	16	2 (1.2)	20	1 (1.1)	28	1 (1.2)	27	1 (1.2)	30	1 (1.2)	33	1 (1.2)	30
1PPE	1 (1.0)	42	2 (9.7)	47	4 (3.0)	31	1 (9.7)	49	1 (3.0)	46	1 (3.0)	43	1 (3.0)	45
1TMQ	1 (2.1)	19	356 (5.9)	9	427 (6.0)	6	45 (5.9)	21	264 (2.3)	7	7 (5.9)	39	10 (6.6)	38
1UDI	1 (1.6)	17	8 (6.2)	9	20 (6.2)	10	4 (6.2)	22	7 (6.2)	25	1 (6.2)	32	5 (6.2)	37
2MTA	11 (1.4)	18	136 (9.0)	4	79 (9.8)	20	38 (9.0)	17	12 (8.4)	24	15 (7.7)	33	15 (8.7)	31
2PCC	1007 (9.1)	1	–	–	18 (6.9)	33	14 (9.3)	20	12 (5.1)	31	5 (9.3)	37	14 (6.3)	44
2SIC	3 (0.7)	10	57 (8.8)	8	–	–	21 (8.9)	10	44 (1.0)	9	4 (8.9)	31	4 (1.0)	35
2SNI	1 (1.5)	18	256 (9.6)	7	101 (9.6)	6	39 (7.1)	15	40 (4.4)	11	5 (7.1)	31	5 (4.4)	25
7CEI	5 (1.3)	17	61 (8.7)	5	4 (8.4)	19	11 (8.7)	17	3 (8.4)	22	2 (8.7)	29	1 (8.4)	35
1AHW1	6 (1.9)	10	234 (8.0)	3	7 (8.0)	12	31 (8.0)	12	5 (8.0)	40	3 (8.0)	42	5 (8.0)	38
1BVK1	44 (1.5)	6	–	–	508 (6.7)	7	134 (9.4)	7	184 (6.8)	10	71 (9.9)	23	22 (6.8)	24
1DQJ1	–	–	–	–	–	–	216 (8.6)	6	440 (9.9)	2	22 (8.6)	24	73 (8.1)	11
1E6J1	–	–	–	–	–	–	26 (8.9)	12	16 (8.4)	22	2 (8.9)	37	4 (8.4)	41
1JPS1	24 (1.3)	5	–	–	36 (8.8)	11	170 (6.6)	9	14 (6.6)	27	15 (6.6)	29	1 (8.8)	30
1MLC1	62 (1.2)	5	408 (3.6)	2	–	–	25 (3.6)	13	22 (3.7)	28	3 (3.6)	29	2 (3.7)	23
1VFB1	23 (1.1)	3	–	–	–	–	97 (9.1)	14	51 (7.1)	10	14 (9.1)	36	12 (7.1)	35
1WEJ1	–	–	–	–	–	–	26 (1.7)	13	2 (1.7)	20	8 (1.7)	29	1 (1.7)	37
2VIS1	–	–	–	–	–	–	–	–	–	–	–	–	–	–
1A2K	29 (5.4)	12	–	–	–	–	–	–	–	–	186 (9.3)	5	274 (9.1)	4
1AK4	–	–	–	–	–	–	–	–	–	–	–	–	–	–
1AKJ	30 (8.4)	25	209 (9.6)	10	17 (9.4)	27	110 (6.3)	15	23 (2.7)	35	23 (9.6)	36	5 (9.6)	48
1B6C	3 (1.8)	19	593 (9.0)	2	755 (8.9)	2	88 (9.0)	5	133 (8.5)	5	19 (9.0)	27	7 (9.7)	36
1BUH	28 (1.0)	9	743 (7.7)	2	289 (7.8)	4	52 (7.7)	14	19 (7.7)	13	28 (7.7)	19	8 (7.7)	18
1E96	133 (1.1)	5	–	–	302 (8.6)	2	246 (9.4)	6	119 (8.6)	8	37 (9.7)	13	43 (8.5)	20
1F51	3 (1.4)	21	371 (9.6)	5	–	–	149 (9.6)	12	58 (9.3)	3	9 (7.6)	19	8 (7.5)	27
1FC2	605 (6.5)	2	–	–	–	–	–	–	–	–	–	–	297 (7.7)	10
1FQJ	7 (1.0)	14	41 (8.0)	12	7 (7.9)	14	14 (8.0)	21	7 (7.7)	28	5 (7.8)	31	4 (7.7)	41
1GCQ	1 (1.0)	16	–	–	–	–	–	–	–	–	92 (6.2)	6	–	–
1GHQ	–	–	–	–	–	–	828 (8.9)	2	–	–	30 (8.9)	13	175 (6.7)	6
1HE1	1 (1.5)	24	37 (6.4)	18	88 (6.3)	15	10 (6.4)	26	28 (7.2)	25	2 (7.6)	39	9 (7.2)	39
1I4D	31 (1.5)	19	–	–	–	–	–	–	–	–	505 (8.1)	1	481 (9.4)	1
1KAC	36 (1.2)	7	687 (8.7)	1	271 (8.9)	5	7 (4.4)	19	4 (4.4)	26	4 (4.4)	33	2 (4.4)	32
1KLU	–	–	–	–	–	–	–	–	–	–	591 (9.7)	2	–	–
1KTZ	–	–	–	–	–	–	–	–	–	–	238 (9.4)	4	25 (6.0)	10
1KXP	1 (1.1)	22	36 (9.4)	13	1 (7.5)	13	15 (9.4)	19	1 (6.9)	30	7 (9.4)	24	1 (6.9)	29
1ML0	–	–	–	–	–	–	7 (9.1)	8	33 (7.0)	11	1 (9.1)	22	3 (5.6)	27
1QA9	86 (5.9)	7	–	–	161 (9.9)	3	587 (7.5)	8	481 (6.8)	4	25 (5.3)	28	23 (4.5)	28
1RLB	409 (8.8)	2	–	–	–	–	–	–	–	–	305 (6.3)	7	384 (6.3)	6
1SBB	–	–	–	–	–	–	–	–	–	–	–	–	–	–
2BTF	5 (0.8)	8	–	–	–	–	133 (8.6)	13	16 (6.7)	22	32 (8.6)	19	4 (6.7)	34
1BJ11	–	–	–	–	–	–	–	–	–	–	7 (6.7)	13	10 (6.9)	10
1FSK1	10 (1.3)	16	5 (1.8)	16	6 (1.4)	10	1 (1.8)	31	1 (1.8)	31	1 (1.8)	43	1 (1.8)	46
1I9R1	5 (5.7)	14	82 (2.1)	8	4 (2.1)	15	23 (2.1)	19	13 (2.1)	26	7 (2.1)	29	5 (2.1)	26
1IQD1	42 (0.7)	8	–	–	760 (1.4)	3	276 (6.1)	7	5 (6.1)	16	5 (9.4)	27	3 (6.1)	29
1K4C1	24 (0.7)	4	21 (9.6)	1	–	–	4 (9.6)	3	311 (9.6)	2	2 (9.6)	17	46 (9.6)	19
1KXQ1	6 (5.5)	10	488 (7.1)	5	35 (6.3)	12	48 (7.1)	16	27 (7.1)	15	27 (7.1)	18	24 (7.1)	16
1NCA1	1 (1.1)	11	116 (1.2)	5	139 (1.9)	3	20 (1.2)	13	8 (0.9)	16	2 (9.9)	22	3 (0.9)	30
1NSN1	11 (1.7)	8	142 (1.5)	6	–	–	18 (1.5)	19	14 (1.5)	12	6 (1.5)	22	3 (1.5)	23
1QFW1	–	–	–	–	–	–	–	–	–	–	333 (6.3)	3	37 (6.3)	6
2QFW1	–	–	–	–	–	–	–	–	–	–	522 (9.7)	1	–	–
2JEL1	10 (1.1)	10	164 (6.0)	3	–	–	7 (6.0)	27	4 (5.6)	29	6 (6.0)	39	2 (6.0)	38
Mean	25 (4.1)	11	242 (8.4)	5	156 (8.1)	7	66 (7.6)	13	46 (7.0)	14	15 (7.3)	25	13 (6.7)	25
Medium Difficulty (13)
1ACB	36 (0.9)	8	694 (8.3)	3	674 (8.5)	2	156 (8.3)	7	163 (8.3)	1	10 (8.3)	33	88 (8.4)	14
1KKL	–	–	–	–	–	–	48 (8.6)	18	94 (8.4)	10	8 (8.7)	40	14 (8.0)	31
1BGX1	1 (3.0)	3	–	–	–	–	–	–	–	–	–	–	–	–
1GP2	–	–	–	–	419 (6.9)	5	–	–	137 (7.1)	8	113 (5.6)	12	68 (7.1)	17
1GRN	1 (1.3)	13	914 (9.1)	2	586 (2.5)	5	661 (7.1)	4	27 (6.3)	23	14 (7.4)	31	20 (6.3)	29
1HE8	–	–	–	–	–	–	–	–	–	–	–	–	–	–
1I2M	1 (1.8)	17	–	–	29 (5.4)	24	754 (8.5)	3	15 (8.5)	24	107 (6.7)	14	21 (8.5)	24
1IB1	10 (5.0)	13	–	–	–	–	–	–	–	–	14 (9.8)	13	22 (9.9)	7
1IJK	189 (3.0)	10	1012 (8.7)	3	–	–	145 (8.7)	5	383 (8.7)	1	14 (8.7)	18	70 (8.7)	5
1K5D	406 (5.9)	4	–	–	146 (7.6)	3	–	–	128 (9.1)	5	377 (7.6)	4	21 (9.7)	17
1M10	429 (9.1)	4	514 (9.5)	2	48 (9.2)	4	130 (9.5)	4	46 (9.3)	6	13 (9.5)	8	124 (8.4)	12
1N2C	–	–	–	–	–	–	–	–	–	–	–	–	–	–
1WQ1	1 (1.5)	26	125 (7.1)	10	16 (7.2)	17	34 (7.1)	14	13 (7.1)	20	6 (7.1)	27	3 (7.1)	33
Mean	50 (5.5)	8	782 (9.5)	1	329 (8.2)	5	306 (8.8)	5	153 (8.7)	8	58 (8.4)	15	66 (8.6)	15
Difficult (8)
1ATN	–	–	–	–	–	–	–	–	–	–	–	–	–	–
1DE4	–	–	946 (8.6)	1	15 (8.4)	3	164 (8.6)	3	–	–	184 (8.5)	8	35 (9.9)	8
1EER	1 (4.0)	25	609 (9.2)	8	43 (9.2)	16	106 (7.6)	18	30 (7.7)	18	34 (7.6)	23	39 (7.7)	13
1FAK	–	–	–	–	–	–	–	–	–	–	768 (7.0)	2	221 (7.0)	8
1FQ1	162 (5.6)	5	–	–	–	–	469 (8.4)	2	–	–	82 (8.4)	5	508 (8.4)	3
1H1V	–	–	–	–	–	–	–	–	–	–	–	–	–	–
1IBR	4 (3.0)	27	–	–	–	–	–	–	–	–	314 (8.8)	4	68 (8.4)	6
2HMI1	–	–	–	–	–	–	–	–	–	–	–	–	–	–
Mean	168 (7.8)	7	933 (9.7)	1	399(9.7)	2	549 (9.3)	3	359 (9.3)	3	325 (8.8)	5	238 (8.9)	5

In the table, B–B and U–U denote bound–bound and unbound–unbound docking, respectively. A hyphen denotes no acceptable solution within the top 2000, in which case a value of 10Å is used when calculating the mean RMS deviation. Means of ranks were calculated using the MLR formula, Equation (44). for antibody/antigen complexes (1AHW, 1BVK, 1DQJ, 1E6J, 1DQJ, 1JPS, 1MLC, 1VFB, 1WEJ, 2VIS, 1BJ1, 1FSK, 1I9R, 1IQD, 1K4C, 1KXQ, 1NCA, 1NSN, 1QFW, 2QFW, 2JEL, 1BGX, 2HMI), the Cα coordinates of heavy chain residue 37 were used as the antibody coordinate origin. For all other structures, the centre of mass was used as the coordinate origin. It should be noted that the Docking Benchmark includes several antibody complexes (1BJ1, 1FSK, 1I9R, 1IQD, 1K4C, 1KXQ, 1NCA, 1NSN, 1QFW, 2QFW, 2JEL, 2HMI) for which only the bound antibody Fab coordinates are available.

However, these results also show that Hex fails to find an acceptable bound–bound solution for 22 of the Benchmark complexes. Visual inspection of these complexes shows that several (1AK4, 1GHQ, 1KTZ, 1BJ1, 1QFW, 2QFW and 1ATN) have particularly small interface areas, which would therefore be expected to be difficult for any shape-based docking algorithm to identify. Furthermore, several of the other failing complexes include at least one large protein domain (e.g. 1KLU, 1ML0, 1KKL, 1HE8, 1N2C, 1DE4, 1H1V and 2HMI) which cannot accurately be encoded in the standard Hex radial function. Hence, these cases will also be difficult for the Hex scoring function. Of the remaining failing complexes, several are antibody/antigen complexes (e.g. 1DQJ, 1E6J, 1WEJ, 2VIS), and it is generally not necessary to perform completely blind docking calculations on such well understood systems.

The rest of Table 3 presents results for docking unbound structures. As expected, the rank of the best shape-only blind docking solution is often considerably poorer compared to docking bound components, with only 6 complexes being ranked within the top 20. On the other hand, including the ETO electrostatic interaction term in the correlation often improves the rank of the best solution, giving 16 complexes within the top 20. However, using electrostatic correlations can worsen the prediction in some cases, but it is not clear how to predict ab initio as to which those cases might be.

Nonetheless, in practice, it is becoming increasingly rare that completely blind docking is necessary because, like the antibody families, biochemical or biophysical knowledge is often available to indicate the identities of key interaction residues. Hence, four further constrained docking runs were performed for each complex to simulate such data-driven docking scenarios. Here, the range of the FFT searches were constrained by applying the restriction β_A≤45° to simulate using knowledge of the receptor binding site (tabulated as ‘One Constraint’), and additionally β_B≤45° corresponding to using knowledge of both the receptor and ligand binding sites (‘Two Constraints’). These constraints each reduce the size of the search space and corresponding FFT grid dimensions by a factor of about four, and speed up the FFT scan correspondingly. Thus, for constrained docking runs, overall calculation times of just a few minutes arise largely from the L=30 rescoring stage. Specifying a receptor constraint of β_A=45° would physically correspond to spinning an antigen over the antibody hypervariable loop region in an antibody/antigen complex, as illustrated in Figure 2, for example. In general, Hex allows a given receptor and ligand residue to be rotated onto the z-axis before each docking run. Hence, for example, by setting small values for the β_A and β_B angular ranges, it is straightforward to focus a docking calculation around a given pair of residues in a known or hypothesized protein–protein interface.

As can be seen from Table 3, the above rather loose constraints are often sufficient to improve considerably the rank of near-native solutions. For example, using only the receptor constraint is sufficient to increase the rate of acceptable solutions from 6 to 17 within the top 20. Adding the Hex electrostatic correlation term boosts this improvement to 28 within the top 20. Applying a similar ligand constraint further improves the success rate to 48 in the top 20 and 35 in the top 10 for shape only correlations, or 45 in the top 20 and 37 in the top 10 for shape plus electrostatics. It is worth noting that constrained docking also improves the results for several complexes that the rigid body docking runs indicated would be intrinsically difficult to dock predictively (specifically 1GHQ, 1KTZ, 1ML0, 1BJ1, 1QFW, 1KKL and 1DE4).

In order to compare such trends more objectively, Table 3 presents overall average results for each set of calculations. Here, we calculate the mean rank using the mean of the logarithm of the rank (MLR) of each first acceptable hit according to:

(44)

where N_C is the number of complexes in each Benchmark category. Limiting poor results to a value of 1000 in this formula helps to prevent outliers from adversely biasing the overall score. Hence the MLR score ranges from 1 (rank 1 hits for all complexes) to 1000 (no hits for any complex). The MLR figures in Table 3 readily show the benefit of using just one, or preferably two, loose constraints to enrich the number of high ranking predictions in each Benchmark category. This benefit is most dramatic in the Rigid-Body category, although using two constraints also significantly enhances the results for both the Medium Difficulty and Difficult categories.

4 CONCLUSION

Analytic GF expressions have been presented for calculating multi-dimensional multi-property rotational FFT docking correlations. Scaling Euler angle ranges onto the natural period of the FFT provides a straightforward way to accelerate the calculation and to focus the correlation around the region(s) of interest. This also reduces overall memory requirements and, for the first time, allows 5D FFT docking to be performed on an ordinary PC. Here, 3D shape-only and shape plus electrostatic FFTs are found to be around three times faster than the 1D FFT previously implemented in Hex but, surprisingly, 3D FFTs are also often faster than 5D FFTs. On the other hand, multiple properties may be correlated simultaneously in the 5D FFT, and this is expected to be particularly advantageous when calculating high order correlations of multi-term knowledge-based protein–protein interaction potentials.

Currently, a two-stage search protocol using 3D shape-only rotational FFT scans with L=20 followed by 1D shape plus electrostatic rescoring with L=30 gives a good trade-off between speed and accuracy. When biochemical or biophysical knowledge about a complex is available, this information may easily be exploited to constrain the angular search to the interface region(s), and docking times are reduced to just a few minutes. For a clear majority of the Docking Benchmark examples, constraining the docking search in this way dramatically improves the quality of the predictions, producing acceptable predictions in the top 20 in 28 cases using one constraint, and giving up to 45 in the top 20 and 37 in the top 10 using two constraints. Hence the approach provides a practical and fast tool for rigid body protein–protein docking, especially when some prior knowledge about one or both binding sites is available.