Specific alignment of structured RNA: stochastic grammars and sequence annealing

Abstract

Motivation: Whole-genome screens suggest that eukaryotic genomes are dense with non-coding RNAs (ncRNAs). We introduce a novel approach to RNA multiple alignment which couples a generative probabilistic model of sequence and structure with an efficient sequence annealing approach for exploring the space of multiple alignments. This leads to a new software program, Stemloc-AMA, that is both accurate and specific in the alignment of multiple related RNA sequences.

Results: When tested on the benchmark datasets BRalibase II and BRalibase 2.1, Stemloc-AMA has comparable sensitivity to and better specificity than the best competing methods. We use a large-scale random sequence experiment to show that while most alignment programs maximize sensitivity at the expense of specificity, even to the point of giving complete alignments of non-homologous sequences, Stemloc-AMA aligns only sequences with detectable homology and leaves unrelated sequences largely unaligned. Such accurate and specific alignments are crucial for comparative-genomics analysis, from inferring phylogeny to estimating substitution rates across different lineages.

Availability: Stemloc-AMA is available from http://biowiki.org/StemLocAMA as part of the dart software package for sequence analysis.

Contact: lpachter@math.berkeley.edu; ihh@berkeley.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Computational and experimental whole-genome screens suggest that there are thousands of undiscovered non-coding RNAs (ncRNAs) in eukaryotic genomes, and there has been much recent progress in cataloging these functional elements (Rose et al., 2007; Ruby et al., 2007; Torarinsson et al., 2008). In order to group these elements into families and understand their evolutionary relationships at the single-nucleotide level, we need sensitive, specific and efficient methods for accurately aligning structured RNA, even in the presence of highly diverged sequence or structure.

Accurate alignment of homologous ncRNAs is notoriously difficult. Because functional constraint largely acts at the level of structure, rather than sequence, alignment programs which fail to take structure into account cannot effectively align ncRNAs with low sequence identity (Gardner et al., 2005). The Sankoff algorithms (Sankoff, 1985) for structural alignment offer a solution; structural alignment methods attempt to simultaneously infer both the consensus secondary structure and sequence alignment.

While in principle structural alignment allows for accurate, structurally aware inference of ncRNA multiple alignments, in practice the RNA alignment problem is still unsolved. The full Sankoff algorithms, O(L^3N) in time for N sequences of length L, are prohibitively expensive. Structural alignment programs use heuristics such as restricting the sets of possible alignments and folds considered by the algorithm in order to reduce time and memory usage of the algorithm, but even so practical programs can make only pairwise comparisons when building multiple alignments. We therefore need robust methods for building a multiple alignment from many pairwise structural alignments.

Most existing RNA multiple alignment programs suffer from one or both of the following problems: like most alignment methods, they maximize sensitivity, even at the expense of specificity, and furthermore, they build multiple alignments with variations on progressive alignment, despite its well-known shortcomings.

A good alignment algorithm must be both sensitive and specific. High sensitivity is meaningless unless we can be reasonably confident that aligned characters are truly homologous. Because increased sensitivity generally means decreased specificity, and vice versa, we want to be able to dynamically adjust the sensitivity/specificity tradeoff of our alignment method depending on the target application. For example, phylogeny reconstruction and tree building require very precise alignments, and it is better to have a reduced number of correctly aligned characters than many imperfectly aligned characters (so we want to maximize specificity, even at expense of sensitivity).

Furthermore, a good multiple alignment algorithm must have a good technique for searching the space of multiple alignments. Although popular, progressive alignment (Feng and Doolittle, 1987) suffers from serious flaws. In particular, homology relations are fixed at each step, so mistakes made early in the alignment construction are uncorrected. Progressive structural alignment, which commonly corresponds to choosing a consensus structure at the very first step of the algorithm, is particularly problematic. While improvements on basic progressive alignment, such as iterative refinement (Gotoh, 1996), can partially ameliorate these problems, the fundamental limitations of the approach remain (and furthermore, iterative refinement is undesirable for computationally costly structural alignment).

We present a novel method for RNA multiple alignment which successfully addresses both of these problems. The sensitivity/specificity tradeoff of our method is controlled by a single adjustable parameter, allowing users to choose a setting appropriate to their intended application. Furthermore, we search the RNA multiple alignment space with the sequence annealing technique introduced for protein multiple alignment (Schwartz and Pachter, 2007), thereby sidestepping the inherent limitations of progressive alignment.

In contrast with progressive alignment methods, which take large steps through alignment space, sequence annealing takes the smallest steps possible. We begin with the null alignment, where all sequences are unaligned, and merge single columns (align characters) according to the corresponding expected increase in an objective function, the alignment metric accuracy (AMA), which takes both the expected sensitivity and specificity into account. Put plainly, sequence annealing constructs a multiple alignment by iteratively aligning characters which have a high posterior probability of being aligned.

The posterior probabilities which inform the annealing algorithm are calculated by summing over all possible structural alignments of sequences X and Y with a pairwise Sankoff algorithm. Sequence annealing of RNA is therefore informed by structural considerations, but outputs only a multiple sequence alignment, not a structure. We treat structure as an unobserved random variable to be marginalized over in order to calculate the alignment probabilities used by sequence annealing; many competing structures are allowed to contribute to these probabilities. After sequence annealing has produced a multiple sequence alignment, if desired a corresponding consensus structure can be predicted with a phylo-grammar-based method such as PFOLD (Knudsen and Hein, 2003) or xrate (Klosterman et al., 2006).

We have implemented our methodology in Stemloc-AMA, a probabilistic structural alignment program which builds upon Stemloc (Holmes, 2005), a progressive RNA structural aligner, and AMAP (Schwartz and Pachter, 2007), an implementation of sequence annealing for protein alignment. Benchmarking against the BRalibase II (Gardner et al., 2005) and BRalibase 2.1 (Wilm et al., 2006) databases of RNA multiple alignments, we find that our approach has sensitivity comparable to that of the best competing methods and superior specificity. The comparative gain in specificity increases in the presence of low sequence identity or structurally diverged sequence. We use a random-sequence experiment to demonstrate that this increase in per-column specificity makes our approach far more robust than any other tested method when presented with non-homologous sequence.

2 RESULTS

Structural alignment methods can be divided into two categories, thermodynamic or energy-attributed models and probabilistic models, where by ‘probabilistic model’ we mean a generative model which assigns a joint likelihood to both alignment and structure. We hypothesize that this natural modeling of both alignment and structure, combined with their robustness under uncertainty, allows probabilistic models to outperform thermodynamic methods.

Originally developed for single-sequence structure prediction, thermodynamic models associate a free energy term to each possible RNA structure, corresponding to the estimated change in free energy from a random coil to a folded state, and (generally) attempt to find the minimum free energy structure. This single-sequence structure model is then extended to multiple structural alignment by adding ‘cost’ terms for the sequence alignment, predicted structures and/or observed covariation (Hofacker et al., 2004; Mathews and Turner, 2002). The parameters of thermodynamic models often have clear biophysical interpretations and are frequently experimentally determined (Mathews et al., 1999; Turner et al., 1987). Thermodynamic models are probabilistic insofar as they implicitly assign a probability to each possible structure via the partition function (McCaskill, 1990), but they generally lack a principled way to incorporate alignment information into this probability distribution.

Probabilistic models, in contrast, simultaneously model both alignment and structure and associate a probability to each possible structural alignment. There is no explicit biophysical model and the parameters rarely have obvious interpretations; rather, they reflect the prevalence of particular features of the structural alignments in the training data.

Despite the intuitive appeal of thermodynamic approaches, we believe that probabilistic models offer significant advantages. There is no clearly correct way to weight the different contributions from cost terms for sequence alignment, predicted structures and covariation when building a thermodynamic model; each worker does this differently. In contrast, probabilistic models naturally account for all of these terms, and there exist robust methods for automatically learning the corresponding parameters from the data (Durbin et al., 1998). Most importantly, as discussed below, probabilistic models offer a principled way to cope with alignment uncertainty.

Stemloc-AMA relies on the probabilistic version of the Sankoff algorithms (Sankoff, 1985) for pairwise structural alignment implemented in the Stemloc program.

2.1 Probabilistic models and the multiple alignment problem

Probabilistic models are robust under uncertainty. This is crucial for accurate multiple alignment; our models are, at best, approximations to biological reality, and so appropriate homology assignments will rarely be obvious. When creating a multiple alignment, we must avoid being wrong (introducing false homology) as much as possible.

Sequence annealing, introduced for protein multiple alignment and implemented in the AMAP program (Schwartz and Pachter, 2007), attempts to achieve exactly that. There are two crucial insights of the sequence annealing technique: first, that a measure of alignment quality should assess both sensitivity and specificity, and second, that when constructing a multiple alignment, we should first align characters whose homology we are certain of and only later align characters of unclear homology. It thereby addresses both of the problems laid out in Section 1.

Described more fully in Section 4, sequence annealing greedily maximizes a scoring function which depends on both the sensitivity and specificity of the alignment. The tradeoff is specified by the user-controlled ‘gap factor’. Multiple alignments are constructed one match at a time by iteratively aligning pairs of characters with high posterior probabilities of being aligned. These posterior probabilities, P(x_i∼y_j∣X,Y), are calculated by summing over all possible structural alignments of X and Y.

The comparative advantage of using a probabilistic approach for multiple alignment increases with growing uncertainty. Stemloc-AMA does comparatively better as the alignment problem grows more difficult, whether because of low sequence identity, structural divergence or many sequences.

2.2 Comparison with thermodynamic algorithms

We benchmarked our RNA alignment algorithm against BRalibase II (Gardner et al., 2005) and BRalibase 2.1 (Wilm et al., 2006), both databases of RNA multiple alignments. BRalibase II contains multiple alignments from four ncRNA families, 5S ribosomal RNA (rRNA), transfer RNA (tRNA), U5 spliceosomal RNA and Group II introns. Each family contains approximately 100 multiple alignments of five sequences. We benchmarked against all families for BRalibase II. For experiments on BRalibase 2.1, which contains over 18 000 multiple alignments, we benchmarked against alignments with 15 sequences (the hardest alignment problems in the database) and restricted our analysis to families of length <150 nt. We also excluded rRNA and tRNA sequences because they are already represented in BRalibase II. Section 4.1 lists the families analyzed.

We compared our method against four thermodynamically informed multiple alignment programs, FoldalignM (Torarinsson et al., 2007), LocARNA (Will et al., 2007), RNASampler (Xu et al., 2007) and MASTR (Lindgreen et al., 2007), as well as MXSCARNA (Tabei et al., 2008) and Murlet (Kiryu et al., 2007), thermodynamic/probabilistic hybrid models. FoldalignM (Torarinsson et al., 2007) is an extension of Foldalign (Gorodkin et al., 1997; Havgaard et al., 2005, 2007), the first lightweight implementation of the Sankoff algorithms, and builds multiple alignments progressively. LocARNA (Will et al., 2007) uses aggressive heuristics to reduce the cost of the Sankoff algorithms and builds multiple alignments progressively. RNASampler (Xu et al., 2007) and MASTR (Lindgreen et al., 2007) use sampling techniques to explore the space of multiple alignments. MXSCARNA (Tabei et al., 2008) progressively aligns candidate stem sequences along a guide tree. Murlet (Kiryu et al., 2007) uses the thermodynamic RNAAlifold program in the ViennaRNA package (Hofacker et al., 2002, 2004) to calculate base-pairing probabilities, scores pairwise alignments heuristically according to a probabilistic measure related to the one which we propose here and builds multiple alignments progressively. We also included the popular program ClustalW (Larkin et al., 2007) as a control.

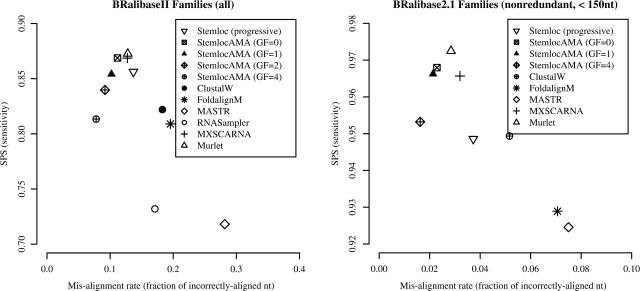
Table 1 and Figure 1 compare Stemloc-AMA's performance against that of other RNA structural alignment methods. Stemloc-AMA has comparable sensitivity to Murlet, the best competing method, and better specificity than all other programs. The advantage of our method is most apparent on the more-challenging datasets, U5 and Group II intron, which exhibit significant structural divergence. Surprisingly, we found that the aging algorithm ClustalW outperformed several of the thermodynamic methods on these datasets (Table 1).

Table 1.

Sensitivity and positive predictive value (SPS/PPV) for the BRalibase II alignments (calculated by averaging over all alignments)

Program	rRNA	tRNA	U5	g2intron
	(SPS/PPV)	(SPS/PPV)	(SPS/PPV)	(SPS/PPV)
Stemloc-AMA	94.1 / 94.3	93.4 / 94.7	83.2 / 86.7	77.4 / 79.8
ClustalW	92.8 / 92.4	87.2 / 87.2	78.4 / 78.1	71.0 / 69.9
FoldalignM	91.2 / 90.8	94.2 / 93.9	71.2 / 70.9	68.2 / 67.3
LocARNA	94.6 / 94.1	95.6 / 95.3	81.3 / 80.8	73.8 / 72.4
MASTR	75.9 / 75.8	80.8 / 81.2	65.7 / 65.8	65.4 / 65.2
RNASampler	81.8 / 90.7	80.2 / 91.0	67.1 / 78.7	64.6 / 71.7
Murlet	94.4 / 94.0	93.4 / 93.3	83.6 / 83.8	78.2 / 78.1
MXSCARNA	94.3 / 94.3	93.3 / 93.6	82.8 / 83.9	77.6 / 77.8

Stemloc-AMA, run with a gap factor of 0 for more sensitive alignments, has high sensitivity and specificity for all families. See Figure 1 for an illustration of how a higher gap factor yields more specific alignments. ‘g2intron’ is the Group II intron dataset. Bold values indicate the best-performing method on each dataset.

Fig. 1.

Receiver operator characteristic (ROC) curves comparing the performance of our method against other programs on the BRalibase II and BRalibase 2.1 (k=15 sequences) datasets. Stemloc-AMA has better specificity than all competing algorithms, and only Murlet has better sensitivity. Note that the text for Stemloc-AMA (GF=0) and MXSCARNA overlaps on the BRalibase II plot. The BRalibase 2.1 dataset consisted of all alignments of length <150 nt with 15 sequences (the largest alignments), excepting rRNAs and tRNAs, which are already represented in BRalibase II. Our method's computational complexity (see Section 2.5) prevented us from running on sequences longer than 150 nt. The ROC curve for our method was created by varying the gap factor (GF), which controls the sensitivity/specificity tradeoff. We were unable to run RNASampler on the BRalibase 2.1 dataset.

Our Stemloc-AMA program outperforms energy-attributed methods despite the experimentally measured thermodynamic information encoded in their rich models of RNA structure. We hypothesize that this is due to (1) Stemloc's integrated probabilistic modeling of sequence and structure evolution, and (2) Stemloc-AMA's robustness under uncertainty. It is not because Stemloc-AMA does a better job of solving the RNA structure problem.

In contrast, this is the weakest point of our approach: Stemloc-AMA constrains its search of structural-alignment space by individually folding each sequence (‘pre-folding’) with a single-sequence SCFG prior to structural alignment and only iterates over the N best folds during the pairwise structural alignment phase. Single-sequence SCFGs are known to perform relatively poorly at structure prediction; the best grammars have sensitivities and positive predictive values of ∼45% (Dowell and Eddy, 2004). Our structural model incorporates base-stacking effects, but ignores many of the other complex features modeled by thermodynamic approaches. The current best-performing approach, CONTRAFOLD, achieves sensitivity gains of ∼50% over single-sequence grammars like the one which we use. It explicitly models additional features, such as closing base pairs of stems, length distributions over hairpins, stems, bulges and internal loops, internal loop asymmetries, dangling base-stacking and distributions over multi-branch loops. None of these features, which are important in the thermodynamics of RNA structure, are modeled by our approach. Stemloc-AMA's prediction speed and accuracy could be improved by using an approach like CONTRAFOLD to inform the pre-folding stage.

2.3 Alignment in the twilight zone

The twilight zone of RNA alignment begins at ∼60% pairwise sequence identity (Gardner et al., 2005), in contrast to ∼20% for proteins, due to the lower per-site information content of nucleotide sequence. Effective sequence alignment in the twilight zone requires structural information.

Figures in the Supplementary Material show sensitivity and positive predictive value (PPV) for the four families in BRalibase II as functions of average pairwise sequence identity and fraction of gaps in the reference alignments. Stemloc-AMA's improved handling of uncertain homology is most evident on difficult alignments with low sequence identity or significant structural divergence (high fraction of gaps), where it produces alignments with much higher PPV than do the other methods. High PPV is essential for biological inferences ranging from phylogeny, where an incorrect alignment can yield a distorted tree topology, to measurement of substitution rates, where an incorrect alignment can yield poor rate estimates.

The effectiveness of the sequence annealing approach to moving through multiple alignment space becomes clearly visible as the alignment problem becomes more difficult (Supplementary Material). On the three datasets with many alignments in the twilight zone, tRNA, U5 and Group II intron, Stemloc-AMA produces much more specific alignments than the original Stemloc, which uses progressive alignment to build a multiple alignment. The PPV of Stemloc-AMA is ∼10% higher than the PPV of Stemloc below ∼50% pairwise sequence identity, a significant gain on a hard alignment problem.

2.4 Beyond curated alignment benchmarks

The alignment benchmarks such as BralibaseII typically used to compare the performance of alignment algorithms are not representative of the everyday problems faced by biologists. As such, they can subtly bias algorithm developers to create methods which seem robust when tested on these ‘gold-standard’ databases but falter when given real-world problems.

The principal problem with testing on alignment databases is that developers know from the beginning that there is homology present, probably covering almost all of the input sequence. This is not a realistic problem setup for biologists, who generally have sequence of interest embedded in longer sequence of uncertain homology, and furthermore frequently may not know whether there is detectable homology at all in their target sequences. An alignment program should therefore not assume a priori that there is homology present. It should be robust to the situations faced by biologists, where homology is frequently unclear, and not over-align input sequences in order to maximize sensitivity.

Because our method is the most specific of the tested programs at a per-column level, where we measure the accuracy of aligned characters, we hypothesized that it was also the most specific at the ‘sequence homology’ level, where we seek to determine whether two sequences are related. We conducted two experiments to verify this hypothesis: (1) we aligned true ncRNAs of mixed homology and (2) we aligned random sequences of no homology.

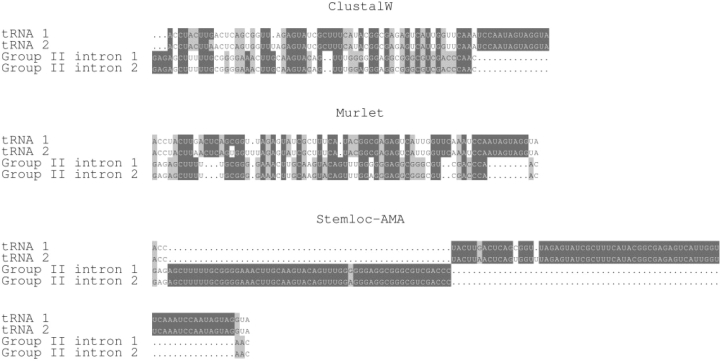
For our first experiment, we randomly picked two tRNA and two Group II intron sequences from BRalibase II and aligned them with ClustalW, Murlet and Stemloc-AMA. Figure 2 shows the resulting alignments. ClustalW and Murlet, assuming homology and attempting to maximize sensitivity, returned near-complete alignments of all four sequences. Stemloc-AMA, in contrast, separately aligned the two tRNAs and two Group II introns and then left the two alignments almost completely disjoint.

Fig. 2.

Standard alignment methods are designed to maximize sensitivity, even to the point of aligning unrelated sequences. We used ClustalW (top), Murlet (middle) and Stemloc-AMA (bottom) to align four randomly chosen sequences from BralibaseII, two of which were tRNAs and two of which were Group II introns. All programs correctly aligned the two tRNAs and two Group II introns, but both ClustalW and Murlet also aligned the tRNAs to the Group II introns. In contrast, Stemloc-AMA correctly detected the lack of homology and did not align the two unrelated families. The two tRNA sequences are Y08502.1-137669_137741 and M20960.1-1_74; the two Group II intron sequences are AP000397.1-37693_37753 and X63625.1-1815_1875.

Our second experiment tested our conjecture that other programs will align non-homologous sequence. We generated 25 datasets, each consisting of five random sequences of 80 nt in length, and used all tested programs to attempt to align the sequences. The results are shown in Table 2 and clearly demonstrate that all tested programs other than Stemloc-AMA give near-complete alignments of even random sequence in an attempt to maximize sensitivity, thereby indicating to biologists that random sequences are evolutionarily related.

Table 2.

Aligning random sequences shows that all tested alignment programs other than Stemloc-AMA dramatically over-align sequence

Program	% of random sequence aligned
Stemloc-AMA (GF=0)	19
Stemloc-AMA (GF=1)	10
Stemloc-AMA (GF=4)	8
ClustalW	93
FoldalignM	99
LocARNA	98
MASTR	91
Murlet	89
MXSCARNA	81

We used each program to align 25 datasets, each consisting of five random sequences of 80 nt in length, and calculated the fraction of possible nucleotide pairs which were aligned. Bold values indicate the best-performing method on each dataset.

2.5 Computational complexity

Stemloc-AMA's computational complexity makes it significantly slower than competing methods. Approximate time complexities for the tested programs on the random sequence dataset are shown in Table 3. Stemloc-AMA's speed can be improved with (1) more aggressive heuristics and (2) a better structural model. Recent advances in heuristics for simultaneous aligning and folding could be incorporated in Stemloc-AMA. For example, FoldalignM prunes low-scoring entries from the dynamic programming matrix in order to reduce memory requirements and computation time. LocARNA uses a cutoff for the minimum-probability base pairs considered by the algorithm, resulting in O(L⁴) complexity in time. Murlet uses a ‘skip’ approximation to limit the number of bifurcations considered by the algorithm. All of these heuristics described are modified versions of the Sankoff algorithm, and as such could readily be implemented in Stemloc-AMA.

Table 3.

Time complexity of tested programs on the Group II intron alignments in BRalibase II

Program	Average time (minutes:seconds) per alignment
Stemloc-AMA	8:53
ClustalW	0:02
FoldalignM	1:09
LocARNA	0:11
MASTR	0:26
RNASampler	0:21
Murlet	0:13
MXSCARNA	0:02

Times reported were calculated on a 1.0 GHz AMD Opteron Processor 248. If there are no clearly best folds or alignments, then Stemloc-AMA imposes few constraints on the search space for the Sankoff algorithms, thereby increasing execution time. Bold values indicate the best-performing method on each dataset.

As discussed earlier, Stemloc-AMA's model of RNA structure is relatively simple, and so in order to get a good alignment Stemloc-AMA must frequently explore a large fraction of the fold space. By using more accurate base-pairing probabilities to calculate appropriate fold envelopes, such as those reported by CONTRAFOLD, Stemloc-AMA could both increase alignment accuracy and decrease execution time (since we could constrain the Sankoff algorithms to a smaller part of the search space).

3 DISCUSSION

Although there are currently only two probabilistic RNA structural alignment tools, Stemloc-AMA and CONSAN (Dowell and Eddy, 2006),¹ the method which we have described is applicable beyond its implementation in Stemloc-AMA. We describe a modular approach to solving the RNA multiple alignment problem, wherein we first build a probabilistic model to compute the pairwise posterior probabilities that two characters are aligned and then use the sequence annealing technique to efficiently explore the space of multiple alignments. We could instead use a different probabilistic model to get posterior alignment probabilities (instead of Stemloc's structural alignment) or an alternate technique for building a multiple alignment from these pairwise probabilities (instead of AMAP's sequence annealing).

The strengths of probabilistic inference for RNA are becoming increasingly clear. The probabilistic CONTRAFOLD program (Do et al., 2006) for single-sequence structure prediction outperforms competing thermodynamic approaches. Similarly, our benchmark against BRalibase II and BRalibase 2.1 (see Section 2.2) indicates that our probabilistic approach to RNA multiple alignment out-performs purely thermodynamic algorithms despite its relatively simple model of RNA structure. We hypothesize that its robustness under uncertainty, as exemplified by the results of the random sequence tests, is due to its probabilistic nature and explicit modeling of the sensitivity/specificity tradeoff.

4 METHODS

4.1 Data

The BRalibase II database (Gardner et al., 2005) was downloaded from http://people.binf.ku.dk/pgardner/bralibase. We used the 5S rRNA, tRNA, U5 and Group II intron datasets used in Gardner et al. (2005) for this study. The BRalibase 2.1 database (Wilm et al., 2006) was downloaded from http://www.biophys.uni-duesseldorf.de/bralibase. We used alignments with 15 sequences, but restricted our analysis to families of length <150 nt and excluded rRNAs and tRNAs, which are already represented in BRalibase II. This left the families HCV_SLIV, Hammerhead_3, S_box, HCV_SLVII, HepC_CRE, HIV_FE, Histone3, Retroviral_psi, TAR, Entero_5_CRE, HIV_GSL3, SECIS, THI, Entero_CRE, HIV_PBS and SRP_bact.

The percent ID of a column was calculated by summing over all pairs of aligned nucleotides and counting the fraction of identical pairs. The gap fraction was calculated as the number of gaps in the alignment divided by the total number of characters, including gaps, in the alignment. Sequences shown in Figure 2 were taken from tRNA/aln75 and g2intron/aln90. RFAM identifiers are given in the figure caption.

4.2 Pairwise structural alignment

The core of Stemloc-AMA is a pairwise implementation of the probabilistic Sankoff algorithm which is constrained by two heuristics, alignment and fold envelopes (Holmes, 1998, 2005), for tractability. An alignment envelope constrains the set of possible pairwise alignments considered by the Sankoff algorithms. Alignment envelopes are computed for each pair of sequences by taking the union of the N-best alignments as calculated by a Pair Hidden Markov Model. A fold envelope constrains the set of possible structures of a sequence considered by the Sankoff algorithm. Fold envelopes are computed for each sequence by taking the union of the N-best structures as calculated by a single-sequence SCFG. The single-sequence SCFG models base stacking, but includes none of the rich features typical of thermodynamic models such as explicit distributions over loop lengths.

The alignment and fold envelope constraints are described more fully in Holmes (2005). They offer a principled way for users to incorporate additional information, such as the known fold of a single sequence, into the structural alignment algorithm.

After calculating the alignment and fold envelopes, Stemloc-AMA's Sankoff algorithm then performs pairwise structural alignments, considering only those alignments and structures contained in the computed alignment and fold envelopes. The Inside and Outside algorithms are used to sum over all possible structural alignments of pairs of sequences to obtain the pairwise posterior probabilities P(x_i∼y_j∣X,Y) that two characters are aligned.

4.3 Searching the space of multiple alignments

The sequence annealing technique implemented in AMAP (Schwartz and Pachter, 2007) is then used to construct a multiple alignment from these posterior probabilities. Sequence annealing uses the pairwise posterior probabilities P(x_i∼y_j∣X,Y) estimated with structural alignment to greedily maximize the expected AMA. AMA, an assessment of alignment fidelity which measures both sensitivity and specificity, is defined for two sequences as the total number of characters which are correctly aligned to either another character or a gap (Schwartz et al., 2006). The definition is extended to multiple sequences simply by taking sum-of-pairs.

We can use the pairwise posterior probabilities P(x_i∼y_j∣X,Y) to calculate the expected AMA as

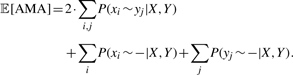More generally, we may want to explicitly control the sensitivity/specificity tradeoff of our alignment algorithm. We introduce a gap factor GF into our definition of the expected AMA,

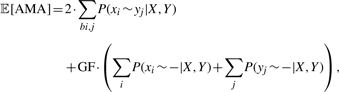such that a lower GF emphasizes sensitivity and a higher GF specificity. Using the expected AMA as an objective function for a greedy maximization, sequence annealing begins with the null alignment (all sequences unaligned) and merges single columns (aligns characters) according to the expected increase in 𝔼[AMA]. A gap factor GF= 1 corresponds to the original AMA, in which case we stop aligning characters when the probability that a character is aligned is equal to the probability that it is unaligned (aligned to a gap).

Sequence annealing greedily maximizes 𝔼[AMA] by annealing single columns of the alignment. The sequence annealing process begins with the null alignment, where all sequences are unaligned, and iteratively aligns single columns according to the posterior probabilities that they are aligned, P(x_i∼y_j∣X,Y), or gapped, P(x_i ∼−∣X,Y) and P(y_j∼−∣X,Y). The consistency of the corresponding multiple alignment is quickly checked with an online topological ordering algorithm (Pearce and Kelly, 2006). A complete description of sequence annealing is given in Schwartz and Pachter (2007), which introduced the sequence annealing approach and applied it to protein multiple alignment with the program AMAP.

4.4 Comparison with other alignment methods

With the exception of Stemloc and Stemloc-AMA, all programs were run with default parameters. Stemloc and Stemloc-AMA were constrained to consider only the 100-best pairwise alignments (-na 100) and 1000-best folds (-nf 1000); the default settings are 100-best alignments and all folds.

Funding

NIH/NHGRI (grant 1R01GM076705); NSF CAREER award (CCF 03-47992 to L.P.); NSF Graduate Research Fellowship (to R.K.B.).

Conflict of Interest: none declared.