ZOOM! Zillions of oligos mapped

Abstract

Motivation: The next generation sequencing technologies are generating billions of short reads daily. Resequencing and personalized medicine need much faster software to map these deep sequencing reads to a reference genome, to identify SNPs or rare transcripts.

Results: We present a framework for how full sensitivity mapping can be done in the most efficient way, via spaced seeds. Using the framework, we have developed software called ZOOM, which is able to map the Illumina/Solexa reads of 15× coverage of a human genome to the reference human genome in one CPU-day, allowing two mismatches, at full sensitivity.

Availability: ZOOM is freely available to non-commercial users at http://www.bioinfor.com/zoom

Contact: bma@csd.uwo.ca, mli@uwaterloo.ca

1 INTRODUCTION

The next generation sequencing technologies provide researchers with the opportunity to sequence a mammalian genome in a matter of weeks at very low cost. These technologies are promoting many exciting biological applications, such as genome resequencing (Bentley, 2006) for SNP detection, histone methylation status (Barski et al., 2007), whole-genome expression profiling (Robertson et al., 2007), small RNA discovery and analysis (Markus et al., 2008), and eventually, personalized medicine.

Inevitable to all these exciting applications is the ‘reads mapping’ process—mapping all reads produced to a reference genome. Mismatches and indel errors are present because of sequencing errors, as well as variations between the sampled genome and the reference genome. This approximate string matching problem can be formulized as: given a query string P of length m, a text string T, and a distance k, find all substrings t of T that are within the distance k from P. The distance measurement could be edit distance or Hamming distance. Many research works have been conducted on this problem, and some earlier ones are reviewed in (Navarro, 2001). In particular, in the context of large-scale DNA sequence search, researchers have exploited the seed method (Altschul et al., 1990; Kent, 2002) and spaced seed method (Ma et al., 2002) to trade search sensitivity for search speed.

Today, the next generation sequencing technologies are producing unprecedented huge amounts of short reads data for the mapping task. For example, the Illumina/Solexa 1G sequencing system can generate one billion bases in a single run, and each read has as small as 25–50 base pairs. While the large data size requires much faster searching speed, the short reads length requires much greater searching sensitivity. The previously mentioned methods are facing difficulties in handling the new situation.

To identify the correct positions for such high throughput reads, filtering strategies are often used. A popular lossless filtering criteria catches the fact that, if two strings of length m are at most k edit distances away, then they share at least one consecutive subsequence of length 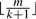, called an l-mer. If either the genome or the reads are indexed, the other can be scanned to filter out the candidates with shared segment of length 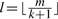, followed by a verification stage for these candidates only. Some mapping software recently developed utilize this filtering criteria. RMAP (Smith et al., 2008) partitions the read into k+1 segments and indexes the l-mers at the start positions of each segment. SXOligoSearch (SynaMatix Co., 2007) indexes the genome and stores exhaustive overlapping l-mers covering whole genome sequences, requiring a 64 GB internal memory machine. Mosaik (Marth Lab, 2007) indexes the reference genome too, adopting a heuristic way to keep only the unique genome l-mers and ignoring those occur more than once.

The filtering criterion using consecutive segments of length 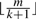has a disadvantage that, with short read length and reasonable number of mismatches, the length of the segment becomes so small that too many false positive hits are produced, resulting in low specificity and efficiency. For example, for read length of 25 bp and two mismatches, the segment length of 8 bp is too small for genome-wide mapping. It can be proved that continuous seeds with length larger than 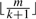can never achieve 100% sensitivity, even when every read position is indexed. Thus, if longer segment length is adopted, the sensitivity will definitely be compromised.

Using certain desiganted positions as filter was shown to provide a better trade-off between searching speed and sensitivity (Burkhardt and Kärkkäinen, 2003; Ma et.al., 2002; Pevzner and Waterman, 1995). The PatternHunter paper (Ma et al., 2002) for the first time used the optimized spaced seed to speed up the homology search while maintaining high sensitivity. To further increase the sensitivity, PatternHunter II (Li et al., 2004) proposed the multiple spaced seeds idea, to use several optimally designed spaced seeds to detect the similarities.

The spaced seed and multiple spaced seeds have also been used to achieve 100% sensitivity for similarity detection. In this direction, Kucherov et al., (2005) tried to minimize the number of multiple spaced seed patterns used. Burkhardt and Kärkkäinen (2003) used a single spaced seed with fixed number of occurrences between the pattern and the text string.

In all of the previously mentioned spaced seed applications, the same seed is used to index each position of the subject sequence or the query sequence. This is largely due to the fact that we do not know the boundaries of the similar regions between the two sequences before conducting the search, and therefore have to treat all the positions equally. However, in the read mapping application, all the reads are short sequences with known boundaries. This allows us to extend the multiple spaced seeds idea, and use different seeds to index different positions of a read. This provides more flexibility to the design of seeds that ‘collaborate’ with each other from different positions, resulting greater hit probability with fewer indexes (and therefore smaller memory consumption).

In this paper, we study the theoretical lower bound of the number of indexes required for each read to gain 100% sensitivity in the mapping process; and design seeds to achieve the theoretical lower bound, for all practical cases.

Based on this framework, we present ZOOM, fast reads mapping software for next generation sequencing, unparalleled in speed, at full sensitivity. We also extend it to allow insertion and deletion type errors, and utilize confidence score information and pair-end sequencing data to enhance mapping accuracy.

2 METHODS

2.1 Theory: designing spaced seeds

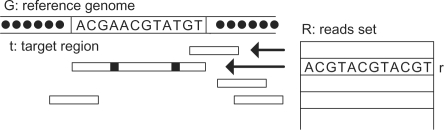
In the simplest case, the reads mapping problem can be stated as: given a set of reads R, for each read r∈R, find its target regions on the reference genome G, such that for each target region t there are at most k mismatches between r and t, Figure 1.

Fig. 1.

The goal is to map each short read to the reference genome, allowing a few mismatches between the read and the target region.

For a read r of length m, the matching status between r and the target region t can be represented by a 0–1 string of length m, where ‘1’ denotes a match and ‘0’ denotes a mismatch. Let (m,k) denote all such regions of length m with k mismatches.

Following Ma et al., (2002), a spaced seed can be denoted by a binary string such as 111010010100110111. A ‘1’ in the spaced seed means it requires a match at that position, and a ‘0’ means ‘don't care’ position. The length of the seed is the string length, and the weight of the seed is the number of 1s in the string.

We extend the idea of spaced seed to use different spaced seeds at several designated positions of the read. Thus, a spaced seed becomes the combination of its pattern and the read position where it is applied. For example, a seed 0001110100000000 is the seed ‘11101’ applied at the fourth position of the read with length 16. In what follows, without specification, a spaced seed has the same length as the read. Therefore, it is only used once to index a read.

Given m and k, we try to design a minimum set of spaced seeds of weight w to achieve full sensitivity for (m,k) regions. We have two competing design goals:

• The seed weight w should not be too small to avoid too many false positives that slow down the mapping process;

• The higher the seed weight, the more seeds would be needed to achieve full sensitivity. This requires more memory, and eventually also slows down the mapping process.

To maximize the performance, for the fixed seed weight, we wish to design as few spaced seeds as possible under the full sensitivity constraint. In another word, we are expecting a tight lower bound on the number of spaced seeds used.

Let LIN(m,k,w) denote the minimum number of weight-w seeds needed to detect all (m,k) regions. We have extensively proved the existence of such tight lower bounds for a wide spectrum of problem settings (the combination of read length m, allowed mismatches k and seed weight w), and constructed corresponding spaced seed sets. The proof and seeds construction procedure is related to problem parameters, and is done case by case. Due to space limitation, we only present the case of LIN(33, 2, 15) and list other results in Table 1, where each single entry involves a proof similar to that of Theorem 1.

Table 1.

The exact number of spaced seeds required and sufficient to detect up to two mismatches for each read length, at full sensitivity

Weight	Read Length
	25	26	27	28	29	30	31	32	33	34	35	36
9	4	4	3	3	3	3	3	3	3	3	3	3
10	4	4	4	4	4	3	3	3	3	3	3	3
11	5	5	5	4	4	4	4	4	3	3	3	3
12	6	6	5	5	5	4	4	4	4	4	4	3
13	7	6	6	6	6	5	5	5	4	4	4	4
14			7	6	6	6	6	5	5	5	4	4
15					7	6	6	6	6	5	5	5
16							7	6	6	6	6	5

Empty entries are considered as impractical cases and we didn't give their exact values.

Theorem 1 —

LIN(33, 2, 15)≥6

Proof —

Let binary string m be the matching status of the read and its target region and S be a set of spaced seeds. Consider s∈S, if for some position p, s[p]=1∧m[p]=0, then m escapes the detection of s, or m[p] rejects s. Denote the set of spaced seeds rejected by m[p]=0 as F(p), so m is detected by S, if and only if there exists at least one seed not rejected by all the mismatch positions of m. That is, ∪_p=1,…,|m|F(p)⊂S.

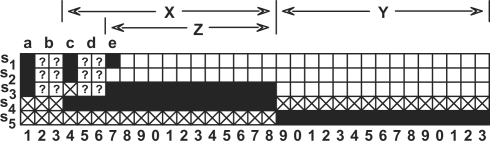
We will use Figure 2 to show that, if only five spaced seeds of weigth 15 are used, then there exists a string with two zeroes out of length 33 that escapes the detection of any combination of these five spaced seeds, formulized as:

By simple observation, we know that the above formula holds in either of the following two cases:

(1)

(2)

Define N_s(p)=|{k∣s_k[p]=1}| as the number of seeds having ‘1’ at position p, and N_p(s,P)=|{p∣s[p]=1, p∈P}| as the number of ‘1’s s having inside position set P. Because , so ∃a, N_s(a)≥3. W.l.o.g, let s₁[a]=s₂[a]=s₃[a]=1, as Figure 2 indicates. Also we know that, s₄[a]=s₅[a]=0, otherwise resorting to case (1).

Due to the failure of case (2), it holds that ∀p,s₄[p]=0∨s₅[p]=0. W.l.o.g, let s₄[X]=1,s₅[Y]=1,|X|=|Y|=15,X∩Y=∅, shown in Figure 2. So, considering two extra positions b and c, we know that,

Because , so ∃d∈X∪Y, N_s(d)≥2+1=3, w.l.o.g, let s₁[d]=s₂[d]=1. We know that s₃[d]=0, otherwise resorting to case (1).

Now let's consider the pattern combination of s₃. It has at least 12 ‘1’s inside X∪Y. But none of they can resident inside Y, otherwise resorting to case (2). So, w.l.o.g, let s₃[Z]=1,Z⊂X,|Z|=12.

Let's divide the pattern combination of s₁ and s₂ into two types:

• type I: if N_p(s₁,Z)=0∧N_p(s₂,Z)=0, then N_p(s₁,Y)+N_p(s₂,Y)≥9+9=18. But |Y|=15, so ∃p∈Y,s₁[p]=1∧s₂[p]=1, resorting to case (2);

• type II: otherwise, w.l.o.g, let s₁[e]=1, and we get that N_p(s₂,Y)=0, otherwise resorting to case (2). So N_p(s₂,Z)≥1. Again we get that N_p(s₁,Y)=0. Now inside position set X, it holds simultaneously that N_p(s₁,X)≥12, N_p(s₂,X)≥12 and N_p(s₃,X)≥12. Because , so ∃p∈X,s₁[p]=s₂[p]=s₃[p]=1, and that finally resorts to case (1);

So, under any possible pattern combination of these five spaced seeds of weight 15, there always exists a string with two zeros that can not be detected by them. This completes the proof. ▪

By manually constructing the spaced seeds, we have obtained the tight lower bounds of the number of spaced seeds required to achieve 100% sensitivity for reads of length ranging from 15 to 64, allowing two mismatches. Table 1 lists part of the results. For example, the following four weight-13 seeds can detect up to two mismatches for read length 33:

As read length increases, so should the number of errors allowed, such as four mismatches for reads of 50 bp. Similar strategies also apply to design spaced seed patterns of 100% sensitivity for wider range of read lengths and error bounds (for example, nine spaced seeds of weight 14 are sufficient to detect four mismatches out of 50 bp). A set of spaced seeds designed for k mismatches with 100% sensitivity can also be used in the case of more than k mismatches, with slightly lower sensitivity.

Fig. 2.

The graph is used to aid the proof of Theorem 1. A solid cell means that a ‘1’ is placed at that seed position, and a crossed cell means that the seed must have a ‘0’ at that position.

2.2 The ZOOM system design

We have implemented ZOOM which maps reads of the Illumina/Solexa 1G sequencing platform to the reference genome. ZOOM utilizes the extended spaced seeds technology which is the key to its mapping efficiency and accuracy.

We will describe the basic model of ZOOM first considering only mismatches between reads and the reference genome. In Sections 2.2.1, 2.2.2 and 2.2.3, we will extend the basic model to allow insertions and deletions, and utilize the sequencing quality scores and pair-end information to enhance mapping accuracy.

To consider the input reads set as a whole, instead of mapping them one by one, ZOOM builds hash tables for the reads set using the spaced seeds designed. For a given seed, the reads sharing the same letters at the 1-positions of the seed are grouped into the same entry of the hash table. Then ZOOM scans the reference genome, and for each genome position finds read candidates from the hash table that have hits with current genome position. These candidates are then further verified. Using appropriate spaced seeds we designed, this filtering strategy of finding read candidates will not miss any true mappings within the mismatch threshold.

For the clarity of presentation, assume that the input reads all have the same length m and we ignore the confidence scores. In general, reads of similar lengths can be grouped or trimmed to a uniform length. ZOOM starts by hashing the reads set using the spaced seeds set, one hash table for a seed. Each read is indexed and stored according to the hash keys generated by these seeds. A hash key is translated from the nucleotide letters picked at positions that correspond to 1-positions in a spaced seed. For example, a read ACGTACGTAC indexed by the weight-3 seed 0001101000 will generate hash key TAG, according to which the read is stored in the read list entry of the hash table for seed 0001101000.

After hashing the input reads set, the reference genome is scanned through, using a sliding window of size m. The same set of spaced seeds are applied to the current window. For each hash key generated, the corresponding hash table entry is fetched and each read inside is checked against the genome segment. In our implementation, each read or genome segment is encoded as two machine words, and bitwise operations are used to calculate the mismatches between them. Finally the number of mismatches can be calculated by counting the number of one bits similar as in (Warren, 2002).

Let N be the size of the reads set, n be total number of spaced seeds used, and w be the maximum weight of the seeds. The space complexity is bounded by O(n*(4^w+N)). The hash tables can be merged to reduce the space complexity to O(4^w+n*N).

2.2.1 ZOOM-C: Mapping with sequencing confidence scores

The Illumina/Solexa 1G sequencing system produces tens of millions of reads of the sampled genome per run, and supplies a confidence score on each read position, based on its base-calling value for four different types of nucleotides. The confidence score shows the sequencing quality of the associated base of an Illumina/Solexa read. Low confidence score hints low sequencing quality at that position. Thus mismatches occurring at high quality positions are less acceptable than those at low quality positions. We extend the ZOOM model to ZOOM-C which allows k mismatches on positions with high quality score. Following the idea in RMAP, with provided confidence threshold, ZOOM-C will ignore mismatches at low quality bases on the basis of ZOOM, without sacrificing much program efficiency.

2.2.2 ZOOM-I: Mapping allowing insertion and deletion

Besides the mismatches, indels (insertion and deletion errors) are another important type of mutation. Although Illumina/Solexa platform is less affected by homopolymers than the 454 sequencing platform, the SNPs can cause indels too. We extend the ZOOM basic model to ZOOM-I allowing insertion and deletion at the verification stage. To detect indels between a genome segment and a read, straightforward but costly dynamic programming can be employed. ZOOM-I chooses a simpler way by enumerating possible indels on the genome segment and compares the mutated segments with each read candidate. Because our encoding of reads enables the use of bit-parallelism in read comparison, this approach is faster than the dynamic programming when the number of indels is limited.

2.2.3 ZOOM-P: Mapping with pair-end information

Several next generation sequencing technologies can also produce paired end reads output to enhance mapping accuracy and help to find genome rearrangement and structure variation (Ng et al., 2005; Shendure et al., 2005; Wei et al., 2006). By sequencing both ends of a sample sequence segment, the reads produced are paired together. Paired reads should be located on the same direction of the reference genome and within a distance range which is related to the sequencing technology. The pairing restriction greatly reduces the possibility of a read mapping to random positions, thus helps to identify their correct positions on the reference genome. ZOOM is extended to ZOOM-P, supporting the mapping of paired end reads by checking the mapping information of each read's counterpart, when this read is mapped to current reference genome position. Only when the mapping distance between two paired reads is within the range limit, their mapping information is reported and collected. Indels are also allowed on both reads, adopting similar strategy as in ZOOM.

3 RESULTS

The efficiency and accuracy of ZOOM are assessed on real experimental data first, then on three larger sets of simulated data to show its speed advantage. The following experiments are all carried out on one core of a AMD Opteron 275 processor, with 8G memory.

3.1 Experiments on real data

Two real data sets were used in our experiments: the BAC data set and the ChIP-Seq transcription factor data set from (Robertson et al., 2007).

The BAC experimental data set was generated using an Illumina/Solexa 1G sequencer at the CSHL genome center. The samples used are two BACs covering a 162 kb sequence segment inside the MHC region, which is an A1-B8-DR3 alternate haplotype assembly of the human chromosome 6 based on the sequence data from the COX library (Stewart et al., 2004). Totally there are 3 415 291 reads of length 36 each, forming an approximately 700× coverage of this 162 kb region. Three target regions are used as the reference genomes:

• MHC-162k: the 162 kb sequence segment with offset from 1878000 to 2040753 inside the MHC region, where the BAC data was sampled;

• chr6: the human chromosome 6 (version hg18), total size 170 Mb, not repeat-masked;

• all: all human chromosomes (version hg18), total size 2.86 Gb, not repeat-masked;

The ChIP-Seq transcription factor data set (Robertson et al., 2007) was generated with STAT1 ChIPs using Hela S3 cells that were stimulated/unstimulated with IFN gama (denoted as STAT1-stimulated and STAT1-unstimulated respectively). The method used was ChIP-sequencing combining chromatin immunoprecipitation and massively parallel sequencing. STAT1-stimulated has 23 980 365 reads of length 27 each and STAT1-unstimulated has 22 175 585 reads of the same length. We used all hg18 human chromosomes as their reference genomes.

Unless stated otherwise, the spaced seeds we used are four weight-13 spaced seeds described in the Section 2.1, and we let the program report all the reads that are uniquely mapped to the reference genome with at most two mismatches.

3.1.1 Efficiency

For the comparison in this section, ELAND, RMAP and ZOOM guarantee 100% sensitivity when there are at most two mismatches, while BLAST, BLAT and Mosaik do not.

• Efficiency compared to BLAST, BLAT, RMAP and Mosaik: On the BAC data set, we compare the speed of our program with BLAST (Altschul et al., 1990) (version 2.2.9), BLAT (Kent, 2002) (version 31x1) which is capable of aligning high similar sequence segments quickly, RMAP (Smith et al., 2008) which has been developed recently, and Mosaik (beta version). Table 2 lists the time used to map the BAC data set onto the reference genomes, allowing two mismatches, together with the memory usage. The table shows the speed advantage of ZOOM. For Mosaik, since it failed to index all chromosomes, we let it map to each chromosome separately. On the two reference genomes MHC-162k and chr6, Mosaik mapped 54.6% and 45.3% of reads, respectively. This is noticeably lower than the full-sensitive RMAP and ZOOM. They both mapped 56.68% and 57.77% of the reads onto the two reference genomes. The remaining unmapped reads are due to various reasons, including more than two mismatches and/or the existence of indels.

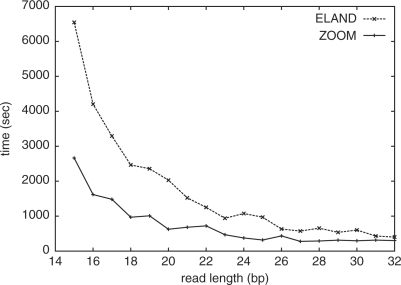
• Efficiency compared to ELAND: ELAND (version 0.2.2.5), which is shipped with Illumina/Solexa platform, is only capable of mapping reads of 15–32 bp, with at most two mismatches. When reads of length 15–25 bp are concerned, ELAND is the most efficient software as we know. To compare the performance of ELAND with ZOOM, we cut each read in the BAC data set to fixed length and map them to chr6. Figure 3 displays the time usage of both programs for various reads length. Clearly, ZOOM is more efficient than ELAND.

Table 2.

Mapping efficiency compared to BLAST, BLAT, RMAP and Mosaik on BAC data

Program	BAC on MHC-162k	BAC on chr6	BAC on all
BLAST	06:56:11 (51M)	>5 days	>8 days
BLAT	00:04:06 (32M)	06:33:03 (32M)	7 days+22:47:16(32M)
RMAP	00:00:51 (1.9G)	00:27:54 (1.9G)	10:09:03 (1.9G)
Mosaik	00:05:33 (214M)	00:07:41 (3.4G)	02:11:15 (3.5G)
ZOOM	00:00:37 (1.1G)	00:06:09 (1.1G)	01:33:03 (1.1G)

Time is represented as hh:mm:ss.

Fig. 3.

Speed comparison of ELAND and ZOOM mapping the BAC data set to chr6, allowing two mismatches on reads length from 15 bp to 32 bp.

ChIP-Seq data is another important output stream of next generation sequencing technology, and we also compared two programs using two ChIP-Seq data sets of length 17 bp from (Robertson et al., 2007). Both ChIP-Seq data sets are too large for ELAND, so we split the data set into two parts and use ELAND to map them separately. ZOOM can handle both complete ChIP-Seq data sets, so we also include the time and memory usage for ZOOM on the unsplit data sets, listed in Table 3. The results show that mapping reads together can save a lot of time.

• SXOligoSearch: We do not have access to the SXOligoSearch software. In addition, the software requires a special hardware of 64G memory. For these reasons, we did not compare it with ZOOM.

Table 3.

Mapping efficiency on ChIP-Seq data. Six spaced seeds with weight 13 were used in ZOOM

Data set	Reads cnt	ZOOM	ELAND
STAT1-stimulated on hg18
Part1	12 471 522	03:24:13 (2.9G)	04:29:57
Part2	11 508 843	03:19:59 (2.9G)	03:41:53
All	23 980 365	04:49:29 (5.1G)	–
STAT1-unstimulated on hg18
Part1	7 667 108	02:48:03 (1.9G)	03:21:10
Part2	14 508 477	03:29:27 (3.4G)	04:28:34
All	22 175 585	04:21:01 (4.8G)	–

3.1.2 Accuracy

• Seed sensitivity: We have proved that ZOOM's approach has 100% sensitivity for up to two mismatches. To examine the sensitivity of ZOOM on reads with more than two mismatches and containing indels, we use the SSearch program (Smith-Waterman algorithm implementation)(Lipman and Pearson, 1985) to align each read in the real BAC experimental data set to the MHC-162k reference region, and use the best alignment result with the highest score for each read as the control sets, grouped by edit distances. The sensitivity using different sets of spaced seeds is evaluated as the percentage of alignment results inside the control set successfully found by ZOOM.

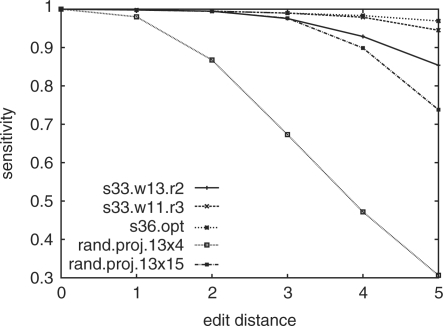
Figure 4 shows the sensitivity under different edit distances ranging from one to five. Three sets of spaced seeds were tested: s33.w13.r2 is our default seed choice, the set of four seeds designed for read length 33 with two mismatches; s33.w11.r3 is the set of 13 seeds designed for read length 33 with three mismatches; and s36.opt, the optimized spaced seed 1101111011111 slided to hash each position of a read. Both s33.w11.r3 and s36.opt have 100% sensitivity for three mismatches.

Fig. 4.

The sensitivity of different spaced seed strategies and random projection. The benchmark is built using SSearch to align the BAC reads onto the MHC-162k region. For each edit distance, the sensitivity reflects its true positive ratio inside the corresponding control set.

It can be seen that our default seed choice, s33.w13.r2, achieves satisfactory sensitivity even if there are indels and the edit distance is greater than 2. If higher sensitivity level is desired, then s33.w11.r3 or even s36.opt is preferred. The latter achieves more than 97% sensitivity even when the edit distance is 5. The speeds of using s33.w11.r3 and s36.opt are approximately six times slower than the default seed. The ability to maintain high sensitivity on reads with indels and more than two mismatches is a big advantage of ZOOM over other software.

On another aspect, spaced seed can be viewed as projection with fixed pattern, such as s33.w13.r2 is four projections on different read positions. An interesting question is whether the same performance of s33.w13.r2 can be achieved by four random projections as done in (Buhler J, Tompa M). To answer this question, the sensitivity (averaged over 10 000 repeats) of four weight-13 random projections is plotted in Figure 4 as rand.proj.13 × 4. Clearly the sensitivity is much worse than s33.w13.r2. To achieve similar sensitivity, the random projection strategy needs to use 15 projections (rand.proj.13 × 15), almost quadrupling the number of seeds needed. This clearly demonstrates the power of seed optimization.

• Coverage: To evaluate the program coverage ratio, we mapped the BAC data set onto human chromosome 6 (chr6), and picked out only the reads that unambiguously mapped into the 162 kb MHC reference region of chr6 (MHC-162k, where the BAC data set was sampled). That is, a mapping into MHC-162k is counted only if the map has fewer mismatches than all the other mappings of the same read on chr6. The coverage of each position on MHC-162k is defined as the number of unambiguously mapped reads that cover this position. The accumulated coverage is defined as the number of positions with coverage no less than a certain coverage threshold.

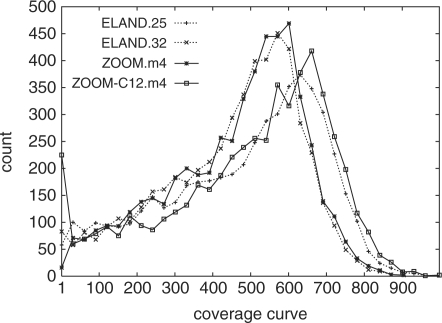
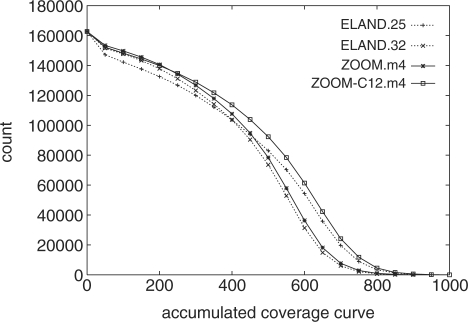
We compared the coverage ratio of four models: ELAND.25 and ELAND.32 are mapping results of ELAND by considering first 25–32 bp of each read during the mapping step (but the full length of 36 bp are used in counting the coverage for fair comparison); ZOOM.m4 is ZOOM's result using s33.w13.r2 seed set, and allowing four mismatches; and ZOOM-C12.m4 is ZOOM-C's result using s33.w13.r2 seed set, and allowing four mismatches on positions with sequencing quality no less than 12.

Figures 5 and 6 show the coverage curve and accumulated coverage curve for four models. Clearly, ZOOM-C12.m4 has the highest average coverage (Fig. 5) and the highest accumulated coverage curve (Fig. 6). This suggests that allowing more mismatches with longer read length (ZOOM) and incorporating sequencing quality scores (ZOOM-C) indeed help to increase the quality of the reads mapping.

Fig. 5.

The 162 kb MHC reference region coverage curve of four models. ELAND.25 and ELAND.32 considers different read lengths, and ZOOM-C incorporating sequencing qualities. For each coverage value, the number of positions having that coverage ratio is counted.

Fig. 6.

The accumulated coverage curve of four models on the 162 kb MHC reference region. For each coverage threshold, the number of positions having coverage ratio no less than that threshold is counted.

3.1.3 Seed weight versus efficiency

For same mismatch threshold on fixed read length, to achieve 100% sensitivity higher weight requires more spaced seeds in the set, hence longer time to construct the hash tables and scan the genome. However, higher weighted seeds will produce much fewer false positive candidates. We compared the performance of three sets of spaced seeds of 100% sensitivity on model of two mismatches out of 36 bp: four weight-14 seeds, four weight-13 seeds and three weight-11 seeds. The experimental results are listed in Table 4. Although consumed more memory, higher weighted seeds contributed a lot to efficiency.

Table 4.

time and memory usage to map BAC data set to three reference genomes, for different seed weights

Run	Weight-14 × 4	Weight−13 × 4	Weight−11 × 3
BAC on MHC-162k	00:00:40 (3.0G)	00:00:37 (1.1G)	00:00:38 (796M)
BAC on chr6	00:04:06 (3.0G)	00:06:09 (1.1G)	00:06:14 (796M)
BAC on all	01:11:55 (3.0G)	01:33:03 (1.1G)	01:45:04 (796M)

Higher weighted spaced seeds used more time to construct the hash tables, but consumed less total time on larger reference genome.

3.2 Experiments on large-scale simulated data

To demonstrate that ZOOM can handle large scale data, we have generated three simulated data sets and mapped them to large reference genomes. Table 5 summarizes the performance.

• chr6.2X.e2: Human genome chromosome 6 (version hg18) was randomly sampled with length of 36 bp. In each read, two random bases were chosen, and mutated to one of the 4 bases with equal probability. Totally 9 494 444 reads were generated, forming 2X coverage of chr6.

• chr6.5X.e2: Similar to the chr6.2X.e2 data set, 23 736 110 reads were generated to simulate 5X coverage of chr6.

• all.0.2X.e2: Similar to above, 15 931 849 reads with two mismatches were randomly sampled on human chromosome 1–22, forming 0.2X coverage of the human genome.

Table 5.

Mapping efficiency evaluation on simulated data sets

Experiment run	ZOOM
Chr6.2X.e2 on chr6	00:09:48 (2.9G)
Chr6.2X.e2 on the human genome	02:37:04 (2.9G)
Chr6.5X.e2 on chr6	00:17:17 (6.5G)
Chr6.5X.e2 on the human genome	04:48:05 (6.5G)
All.0.2X.e2 on the human genome	04:25:40 (4.5G)

Higher weighted spaced seeds used more time to construct the hash tables, but consumed less total time on larger reference genome.

Table 5 demonstrated that ZOOM scales well. The time complexity increases approximately linearly with respect to the genome size and the number of reads, respectively. Note that the 5X coverage reads of chromosome 6 can be mapped back to chromosome 6 in<18 min. Considering the fact that chromosome 6 is above the average chromosome size, if all human chromosomes are sequenced separately with 15X coverage, ZOOM will map all reads to the 23 human chromosomes separately in no more than one day on a single CPU, allowing two mismatches, and with only moderate memory requirement.

With the typical high coverage (100X) of Solexa sequencing applications, ZOOM may also be used as a sequence assembler when a close reference sequence is available (e.g. primate BAC sequencing or population sampling).

4 CONCLUSION AND DISCUSSION

The analysis of next generation sequencing data requires the mapping of short reads back to a reference genome, allowing a few mismatches and indels. We extended the multiple spaced seeds method to design different seeds on different positions of a read. This significantly reduced the number of indexes per read required to achieve 100% sensitivity, resulting less memory consumption and fewer hits. Consequently, the mapping speed is greatly improved. The seeds designed for only mismatches were demonstrated to also have very high sensitivity when indels are present.

We studied the lower-bound for the number of indexes needed to achieve 100% sensitivity, and designed optimal seeds that achieve the lower-bound for all practical cases. In this paper, we deduce such lower-bounds case by case, and to seek for a generalized way to compute the tight lower-bound remains an open problem.

Based on our theoretical studies, we have implemented ZOOM, a short reads mapping program with high efficiency and accuracy. With the extended spaced seed technology, our program can achieve guaranteed sensitivity with low false positive rate. Both real and large simulated data sets are used to benchmark ZOOM. Compared to BLAST, BLAT, RMAP, Mosaik and ELAND, ZOOM is unparalleled in its speed, at full sensitivity.

The ultimate goal of ZOOM is to help personalized medicine, zooming through genome scale of reads to produce SNPs (Hodges et al., 2007), while the patients await. The bottleneck should not be, and will not be, on the computational side.