Biomolecular pleiomorphism probed by spatial interpolation of coarse models

Abstract

In low resolution structures of biological assemblies one can often observe conformational deviations that require a flexible rearrangement of structural domains fitted at the atomic level. We are evaluating interpolation methods for the flexible alignment of atomic models based on coarse models. Spatial interpolation is well established in image-processing and visualization to describe the overall deformation or warping of an object or an image. Combined with a coarse representation of the biological system by feature vectors, such methods can provide a flexible approximation of the molecular structure. We have compared three well-known interpolation techniques and evaluated the results by comparing them with constrained molecular dynamics. One method, inverse distance weighting interpolation, consistently produced models that were nearly indistinguishable on the alpha carbon level from the molecular dynamics results. The method is simple to apply and enables flexing of structures by non-expert modelers. This is useful for the basic interpretation of volumetric data in biological applications such as electron microscopy. The method can be used as a general interpretation tool for sparsely sampled motions derived from coarse models.

Contact: wriggers@biomachina.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Biomolecular assemblies undergo conformational rearrangements as they carry out their biological functions (Alberts, 1998; Gerstein et al., 1994). We are modeling large-scale conformational changes of subcellular systems active in transcription, assisted folding and motility. Ideally, an atomic level of detail of functionally relevant movements is available from X-ray crystallography or NMR spectroscopy. However, the conformational space covered by atomic structures is often limited or isolated from the biological context.

Three-dimensional (3D) imaging techniques enable the visualization of biomolecular assemblies at low and intermediate levels of resolution in their native environment. During the past two decades, cryo-electron microscopy (cryo-EM) has emerged as a powerful approach for the structural investigation of macromolecules. Cryo-EM depicts biomolecular assemblies trapped in vitreous ice during different stages of relevant biological processes (Frank, 2002) without requiring the sample to fit into a crystal lattice. Alternative biophysical techniques such as hydrodynamics (Rai et al., 2005), neutron and X-ray scattering (Niemann et al., 2008), have also been improved in recent years to yield reasonable low-resolution models of solvated biomolecules.

The typical resolution of 3D maps is too low to permit a direct atomic interpretation of the biophysical data. However, it is often possible to build a ‘pseudo-atomic’ model using computational techniques (Baumeister and Steven, 2000). Low-resolution data and atomic subunits are combined by a registration procedure that optimizes a scoring function (Wriggers and Chacón, 2001). The most common scores measure the shape similarity, either by the cross-correlation coefficient (Volkmann and Hanein, 1999) or by quantifying the deviation of coarse models (Birmanns and Wriggers, 2007).

Coarse models in our work are created by a clustering technique known as vector quantization (VQ; Wriggers et al., 1998). VQ brings the modeled data sets to a comparable level of detail. Robust under experimental noise, VQ reliably identifies the gross features of objects and represents them by a small number of points called feature vectors (also known as fiducial or codebook vectors). By closely following the shape and density distribution of the data, the feature vectors reduce the docking to a point cloud matching problem. A rigid body fit of corresponding features may be achieved either in an exhaustive search or more efficiently by anchor-point registration (Birmanns and Wriggers, 2007). The feature vectors enable also a flexible registration when the shapes of the atomic structure and low resolution maps differ. Constrained molecular dynamics (MD) brings deviating features into registration while optimizing the local stereochemistry of the model (Wriggers et al., 2004).

Alternative flexing techniques were recently introduced by a large number of groups both from the cryo-EM and modeling fields. Most flexing methods proposed in the community use some form of dimensionality reduction or coarse-graining for the matching. The reason lies in the mismatch of resolution between atomic and EM data. One can count the number of independent pieces of information available for the fitting of a model in direct space by dividing the volume of the structure by the volume of a resolution element, i.e. a cube whose length corresponds to the spatial resolution. For medium-resolution (∼10–30 Å) EM maps of single molecules, this number is surprisingly small, ranging from the lower single digits to a few dozen (Wriggers and Chacón, 2001). However, the number of degrees of freedom (DOF) of an all atom model is much larger (three times the number of atoms). Therefore, to avoid over-fitting, EM matching methods should use only a small number of parameters. For example, normal mode analysis refinement uses a low-dimensional subspace of orthonormal deformations (Tama et al., 2004), rigid body fitting of fragments uses six rigid body DOF per subunit (Chapman, 1995; Gao and Frank, 2005; Volkmann et al., 2000) and our feature vector based flexing uses three DOF per codebook vector (Wriggers et al., 2004). Constraints on the fitting can also be formulated with the help of rigidity analysis (Jolley et al., 2008) or homology modeling (Topf and Šali, 2005; Velazquez-Muriel et al., 2006). Forcefield guided MD (Chen et al., 2003; Orzechowski et al., 2008; Trabuco et al., 2008) is seemingly less restrictive on the atomic degrees of freedom, but in practical applications to real data such methods are often augmented by additional constraints based on expert knowledge (Chen et al., 2003), to reduce the risk of over-fitting.

While most of the discussed flexing methods use some form of dimensionality reduction, there are notable differences and limitations of the methods: the amplitudes of normal mode sensitively depend on the initial rigid body alignment. The rigid body fragment-based approach requires an (unrealistic) breaking of the polypeptide chain at domain interfaces (also, no intra-domain movements are sampled). Our flexing, while more realistic, requires an expert preparation and parameterization of the system for a MD simulation, which involves significant human effort.

As described below, we believe that our modeling approach holds promise to overcome all of these limitations, but we have been inspired in particular by the competing normal modes approach. Although, the modes do not provide for a ‘chemically correct’ forming and breaking of contacts as the molecule is ‘warped’ between conformations, the technique is particularly easy to use because no physical parametrization of chemical interactions is required (Tama et al., 2004). Our goal was to simplify the original MD based fitting in a similar fashion, such that non-expert users could perform a straightforward exploration of our coarse models and resulting flexible fits. We propose in the following an efficient flexible registration by interpolation methods. This idea has been suggested before (Wriggers, 2004), but in this work we have for the first time tested the performance of three well established interpolation techniques. In the following, we evaluate interpolation for three experimental benchmark systems by comparison with constrained MD results and the corresponding EM maps. Finally, we discuss the practical implications and describe a roadmap for the use of the winning method in the overall modeling workflow.

2 METHODS

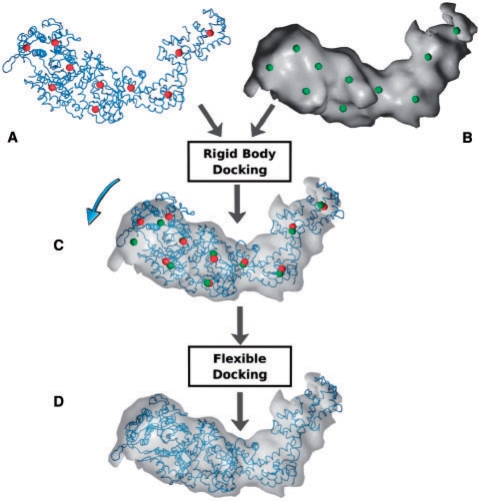
To bring the atomic structure into registration with the volumetric map, we follow a three-step procedure (Fig. 1). First, the data undergoes a well-established coarse-graining in which the feature-vectors of both atomic structure and volumetric map are identified (Fig. 1A and B). These reduced representations are then employed for rigid body registration (Fig. 1C). The third step, the flexible fitting, is the main topic of the present report. We propose to utilize interpolation methods for the flexing of atomic structures in cryo-EM volumetric maps.

Fig. 1.

Flexible registration flowchart. (A) Atomic structure (tube representation) and corresponding feature vectors (red spheres). (B) Cryo-EM volumetric map (isosurface) and corresponding reduced representation (green spheres). (C) Rigid body registration of the multi-resolution datasets is achieved through the alignment of the feature vectors; arrow indicates divergent conformational states in the data sets. (D) Flexible fitting of the atomic structure into the cryo-EM map.

2.1 Coarse-graining and rigid body registration

Clustering techniques are a common approach for reducing the complexity of experimental data sets. We have developed VQ techniques since the 1990s (Wriggers et al., 1998) to identify the major structural features of the atomic structure and of the volumetric map (Fig. 1A and B). The feature vectors correspond to the cluster centers which are identified by minimizing an encoding distortion error (here, the mean-square deviation of the cluster centers from the data points). We denote the feature vectors of the atomic detail subunit by w_i^calc, i=1,…,N, and those corresponding to the cryo-EM map of an assembly by w_j^em, j=1,…,M. Usually, the pairings i,j of corresponding features are readily apparent from visual inspection, or they may be established algorithmically (Birmanns and Wriggers, 2007), even for cases where M>N. In the following we therefore assume i=j for matching features in the two representations, which implies N=M without any loss in generality. Such a mapping of features readily enables the rigid body alignment of the atomic structure with the cryo-EM map by least-squares fitting of the feature vectors (Fig. 1C).

2.2 Flexible registration

The fitting accuracy of atomic models against EM data may reach one order of magnitude above the nominal resolution of the map (Baker and Johnson, 1996; Stowell et al., 1998; Wriggers and Chacón, 2001). For distinctive shapes, features can be accurately tracked to the level of single amino acids (Wriggers et al., 2004). This precision motivated our work of the past 8 years (Wriggers et al., 2000) to allow conformational flexibility for a more precise alignment with low-resolution features that deviate from the atomic model. The flexible docking we developed (Darst et al., 2002; Opalka et al., 2003) is based upon the assumption that local contacts among side chains remain largely intact during the global conformational change.

The flexible docking procedure is based on a connected ‘motion capture’ network of identified features within the atomic model (Wriggers et al., 2004). The atomic model is allowed to move according to displacements tracked by the feature points defined above. The longitudinal distance constraints in the motion capture network reduce the effect of outliers and noise and are typically assigned manually by following the connectivity of the polypeptide chain. Details will be given for each system in section Results below.

The flexing of the structures is then achieved in an additional refinement step (Fig. 1D). The sparsely sampled deformations are extended to the full atomic structure by molecular simulation (Wriggers et al., 2000, 2004). In the past we performed the flexing solely by adding a constraint energy function to the Hamiltonian of a MD simulation that penalizes global shape differences between the data sets (Wriggers and Chacón, 2001). This approach required an expert modeler proficient in MD force field parametrization, system building, and software. Here, we propose a much simpler alternative. Interpolation methods do not require any expert knowledge about the system, but they come initially at the price of missing stereochemical optimization. Therefore, we focus predominantly on the accuracy of alpha carbon (C_α) models derived from interpolation, which we consider a reasonable compromise between robustness of the model under deformation and level of detail for visualization or subsequent modeling.

2.3 Interpolation methods

The following interpolation techniques are based on the assumption that conformational changes of the system may be represented by a continuous function f:ℜ³↦ℜ³ that smoothly warps the embedding space. The smoothness of the warping will depend on the functional form of f and on the level of detail in the coarse feature vector model. To have predictive power at smaller scales, the function f should be sufficiently detailed to allow independent variations at least at the scales of C_α atoms. The functional form of the warping function f depends on the particular interpolation method. Given a particular functional form, the (unknown) parameters are determined from the known displacements at the feature vector locations. Once f has been determined, the full embedding space is warped and the atomic positions of the fitted structure are mapped accordingly. In the following, we introduce and evaluate three well known and widely used interpolation methods: two elastic spline-based methods along with inverse distance weighting (IDW) interpolation.

2.3.1 Spline interpolation

Inspired by physical models, spline interpolation methods are used in a wide range of applications, spanning aircraft design, medical imaging (Bookstein, 1989) and breast cancer diagnosis and evaluation (Davis et al., 1997). The spline techniques considered here are non-linear but can be parameterized with standard linear algebra techniques. We assume in general the following functional form:

(1)

where 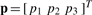is the probe position anywhere in the Cartesian space of the atomic structure, and |p−w_i^calc| is the Euclidean distance between p and a feature w_i^calc in the atomic structure. The 3×3 interpolation kernel U is derived from physical models, originally intended for the modeling of the bending of elastic bodies. In particular, for thin-plate splines (TPS), the kernel U is the solution of the biharmonic equation and minimizes the bending energy of the embedding space (Bookstein, 1989; Harder and Desmarais, 1972), while for elastic body splines (EBS; Davis et al., 1997), U satisfies Navier's equation (Chou and Pagano, 1967). The unknown parameters 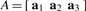(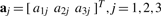), 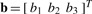and 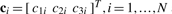are identified from the known feature vector displacements, i.e.

(2)

To set up a linear system of equations, the unknown variables, a_j, j=1,2,3, b and c_i, i=1,…,N, are concatenated into the unknown 3N+12×1 column vector 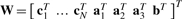. It is straightforward to show that the solution of this system is given by

(3)

where

O₁ is a 12×12 matrix of zeros,

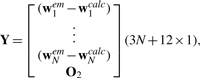O₂ is a column vector of 12 zeros,

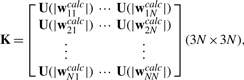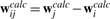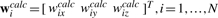, and I is the 3×3 identity matrix.

The first 3N rows in (3) are obtained from the requirement that the spline displacements equal the feature vector displacements in (2). The last 12 rows ensure that the nonlinear displacements relax to an affine (linear) transformation governed only by a_j, j=1,2,3 and b in the asymptotic limit far from the interpolation region (Bookstein, 1989; Davis et al., 1997). Solving the system of equations by matrix inversion of L yields the unknown coefficients W that define the warping function f. The flexed atomic model is then generated with the new atomic coordinates derived from f.

Table 1 presents the interpolation kernels U used in the present study. In the case of TPS, U is the principal solution of the 3D biharmonic equation (Bookstein, 1989; Harder and Desmarais, 1972). The EBS kernels are derived from Navier's equation for a homogeneous, isotropic, elastic body subjected to forces (Chou and Pagano, 1967; Davis et al., 1997). The two kernels in Table 1 are solutions of Navier's equation for two variations of the body forces, and both depend on the elastic properties of the material under constraints. The EBS coefficient ν characterizes the behavior of a material when stretched in one direction, by quantifying the amount of contraction observed in the perpendicular directions. This elasticity coefficient, also known as Poisson ratio, variates between 0 and 0.5 for most common materials and covers soft rubber for ν close to zero and incompressible materials for values up to 0.5. For the evaluation of the interpolation methods, we considered biomolecular systems to be perfectly incompressible when stretched, and thereby we set ν=0.5.

Table 1.

The interpolation kernels U used in the present study, as derived from continuum elastic theory (see text)

Spline type	Deformation term
TPS	U(|p|)=|p|I
EBS Kernel 1	U(|p|)=[(11−12ν)|p|2I−3ppT]|p|
EBS Kernel 2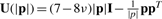

I − the 3 × 3 identity matrix, ν - EBS elasticity coefficient

2.3.2 IDW interpolation

Shepard's IDW method (Gordon and Wixom, 1978) estimates the coordinates of displaced atoms based on their spatial proximity to the feature vectors. IDW assumes that feature vectors in the close neighborhood of an atom have a higher weight in the estimated displacement compared to distant vectors. (Shepard, 1968) formulated the smooth (continuous and once differentiable) function

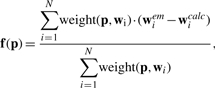(4)

where weight(p,w_i^calc) is the weight of the i-th feature vector. Similar to spline interpolation, IDW ensures the exact fit of the feature vectors (see Equation 2). Usually the weighting function weight(p,w_i^calc) is a monotonously decreasing function of the distance |p − w_i^calc|. (Shepard, 1968) proposed a global weighting scheme based on a negative power function:

(5)

while (Franke and Nielson, 1980) introduced a local IDW interpolation defined as

(6)

where c and R are constant parameters. The weighting exponent c influences the smoothness of the interpolator, and is required to exceed the value of 1 to ensure the differentiability of the function f. Large exponents c>8 render the closest feature vector dominant, thereby decreasing the importance of the others. The influence radius, R, is determined as the distance accommodating a constant number of feature points defined by the user.

2.3.3 Stereochemical idealization

One of the concerns in any refinement method is the stereochemical quality of resulting models. The original constrained MD approach automatically optimized and relaxed bonded and non-bonded interactions during the flexing based on a physical force field. The much simpler interpolation is of course lacking such stereochemical optimization. One could apply MD to such a model in a post-processing step but this would defeat the purpose of the intended simplification. As a compromise between usability by non-experts and the stereochemical quality we tested an optional idealization with the crystallographic refinement tool RefMac (Murshudov et al., 1997) that regularizes abnormal bonds and angles. RefMac has the advantage that it is robust in the case of missing atoms and unknown substrates, whereas MD is very sensitive to such modeling inaccuracies. The tool is freely available to academic users but requires some extra work to be set up, therefore we have evaluated the performance of interpolation both in the presence and absence of the RefMac idealization, to test whether the improvements in stereochemistry justify the added effort.

3 RESULTS

We have tested the interpolation methods on three displacement data sets generated in our recent work: the bacterial RNA polymerase (RNAP), the chaperonin GroEL and the motor domain S1 of myosin. These systems exhibit large conformational changes during their functional cycles. In each case, the experimental cryo-EM map deviates significantly from the atomic structures (Fig. 2), requiring a flexible fit to account for the conformational change. The fitting was validated in discussion with our collaborators to ensure a sound interpretation.

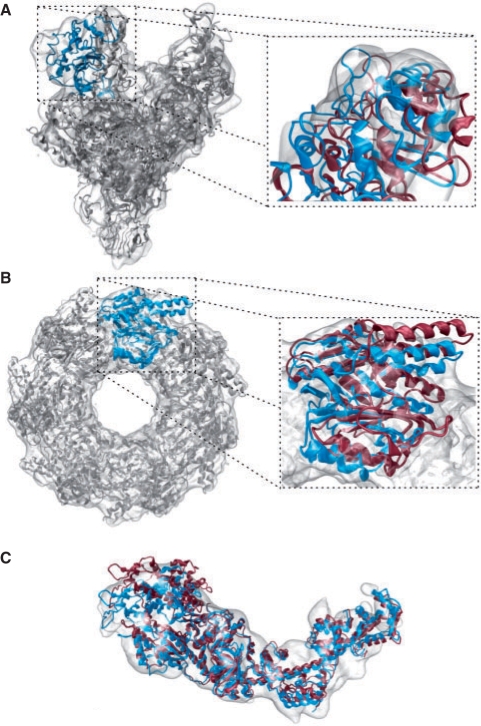
Fig. 2.

Comparison of the interpolation based flexible fitting relative to the rigid body docking. Atomic models of volumetric map are built by rigid body registration (red ribbons), and refined by spatial IDW interpolation (blue, gray ribbons). (A) RNAP; left: side view; right: clamp domain. (B) GroEL; left: top view; right: one monomer. (C) Myosin.

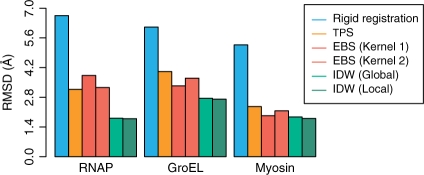
In the following tests, we assess the quality of interpolation methods by comparing the resulting fitted structures with those derived by the well established constrained MD approach (Wriggers et al., 2004) using identical input data (atomic structures and feature-vectors). The docking accuracy is assessed by the root mean square deviation (RMSD) of the C_α as shown in Figure 3. Detailed numerical values and timings of all results are given in Supplementary Table 1.

Fig. 3.

RMSD from models generated with constrained MD.

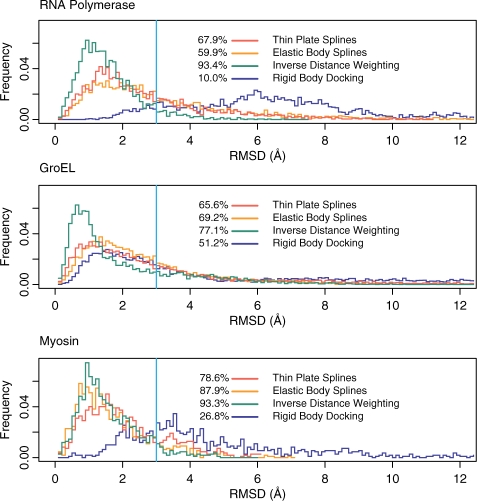
In addition, one can study the structural differences in more detail through the native overlap (NO) well known in the homology modeling field (Fig. 4). The NO quantifies the percentage of atoms with spatial shift below a threshold value. For instance, NO3 represents the percentage of atoms deviating less that 3 Å between the model generated by interpolation and the one obtained by constrained MD.

Fig. 4.

Histogram of observed C_α RMSDs. Shown are observed frequencies as a function of the deviation between the models and constrained MD. The percentage of atoms with deviations below 3Å (NO3) is shown at the left hand side of the legend. Due to similarity with kernel 2, only kernel 1 of the EBS is shown. For the IDW the local weighting scheme with c=4 and R holding nine feature vectors was used. Also shown for comparison are the deviations for the rigid body fit.

An even more detailed view is provided by the histogram of root mean square (RMS) positional deviations. The similarity can be qualitatively assessed by the width of the histogram around small values, i.e. a narrow histogram implies that a large number of atoms have small shifts between the two models while only few atoms have significantly larger ones. For all interpolation methods, the histograms of the RMS positional deviations are compared to those of the rigid body model in Figure 4.

For the cases we studied here there are no known atomic conformations of the target. However, we offer the cross-correlation with the EM map as an ‘absolute’ criterion of accuracy.

3.1 Opening of RNAP

We originally developed our flexible fitting techniques in collaboration with Seth Darst, whose laboratory determined the structure of Escherichia coli core RNAP by cryo-EM and image processing of helical crystals to a resolution of 15 Å. The high sequence conservation between the core RNAP subunits enabled us to interpret the E. coli structure in relation to the high-resolution X-ray structure of Thermus aquaticus core RNAP. A very large conformational change of the T. aquaticus RNAP X-ray structure, corresponding to opening of the main DNA/RNA channel by nearly 25 Å, was required to fit the E. coli map (Fig. 2A). This finding reveals, at least partially, the range of conformational flexibility of the RNAP, which is likely to have functional implications for the initiation of transcription, where the DNA template must be loaded into the channel (Borukhov and Lee, 2005). Darst et al. (2002) flexed the crystal structure of T. aquaticus RNAP into the E. coli 15 Å-resolution cryo-EM map by constrained MD on 15 feature vectors. This simulation induced a 6.65 Å RMSD in the atomic structure. In a later study, the MD flexing technology enabled the location of the transcription elongation factor GreB bound to bacterial RNAP (Opalka et al., 2003).

Based on the displacements measured at 15 feature vector positions (Darst et al., 2002) we have reproduced the earlier MD flexing with the new interpolation methods. With respect to the MD structure, the models flexed by spline interpolations deviate by 3.17 Å for TPS and 3.26-−3.83 Å for EBS (Fig. 3). In contrast, the IDW-refined model deviates by only 1.79 Å using the local scheme with c=4 and cut-off distance R set to include the nine closest feature vectors (Equation 6). A similar deviation was also observed for the model generated by global IDW interpolation for c=8 (Fig. 3). Relative to the initial rigid body docked conformation, the interpolation methods considerably increase the NO3 with the MD structure, from the initial value of 10.0% to at least 59.9%. Moreover, the IDW averaging exhibited the highest NO3 among the interpolation methods (93.4% versus 67.9% for TPS, 59.9% for EBS), and the sharpest histogram of RMS positional deviations (Fig. 4).

3.2 Flexibility of GroEL apical domains

Another system in the benchmark, the bacterial chaperonin GroEL, plays an important role in the native folding of proteins (Fenton and Horwich, 2003). The binding of ATP and of the co-chaperonin GroES initiate a series of allosteric rearrangements in GroEL's structure that allow non-native proteins to interact with the chaperonin's central channel, facilitating their refolding into the native state (Ranson et al., 2001). Despite the large number of solved structures showing GroEL alone or in complex, the mechanism of protein folding by the chaperonin remains unclear.

To shed light on the structure–function relationship, one can investigate functionally relevant conformations. In one such experiment, the mutant Asp155→Ala was imaged by cryo-EM at 14 Å resolution (S.G. Wolf, D. Rivenzon-Segal, W. Wriggers and A. Horovitz, submitted for publication). The significant conformational changes observed in the apical domains of the mutant GroEL motivated us to consider this system in the benchmarking of the interpolation methods. The rigid body docking of the complex identified the locations of the 14 monomers (PDB entry 1xck; Berman et al., 2000) in the 3D map, and emphasized the conformational differences in the datasets (Fig. 2B). The docked crystal structure was refined against the cryo-EM map by MD simulations constrained to 112 feature vectors, or eight vectors per monomer. This refinement procedure induced a large (6.11 Å RMSD) conformational change in the GroEL structure, mainly in the apical domains that exhibit considerable variability. Here, we used the 112 displacements from the MD study for a performance test of the interpolation methods.

Considering the large size of this system, the interpolated models agree reasonably well with the MD result. We achieved RMS deviations of 4.01 Å for TPS and 3.34–3.70 Å for EBS (Fig. 3). However, the IDW-based model deviates only 2.75 Å, in the case of global IDW (c=8), and 2.71 Å in the case of local IDW (c=4, R set to include the nine closest feature vectors). Furthermore, similar to the RNAP case, the NO3 value of the IDW interpolation is superior to that of the splines (77.1% versus 65.6% and 69.2%), while the histogram of RMS positional deviations is also the sharpest (Fig. 4).

3.3 The actin-binding cleft closure of myosin S1

Myosin, the third system in the benchmark, is a molecular motor involved in both intra-cellular motility and muscle contraction (Geeves and Holmes, 1999; Rayment et al., 1993). Here, we focus on the conformational differences induced by binding of S1 to the actin filament. A cryo-EM reconstruction of the actomyosin complex at 14 Å resolution was recently determined by our collaborator Rasmus Schröder (Holmes et al., 2003). A fitted F-actin model (Holmes et al., 2003) allowed us to create a mask for segmenting out a single myosin S1 unit (W. Wriggers and R.R. Schröder, unpublished data). This single myosin S1 map can then be compared to the atomic structure. We first attempted rigid body fitting of the atomic model, taken from the supplementary structure ‘motor_domain.pdb’ published by Holmes et al. (2003). Rigid body docking was not satisfactory with respect to the position of the upper 50 K domain and the lever arm (Rayment et al., 1993) even when performed independently for each structural subunit. Therefore we subjected the predicted atomic model to flexible docking (Fig. 2C) to characterize the observed changes.

The atomic model is allowed to move according to displacements tracked by 10 feature vectors. Our conservative choice of 10 feature vectors (corresponding to a spatial resolution of 26 Å in our coarse model) was sufficient to track shape changes while avoiding an over-fitting of the cryo-EM data. The MD refinement generated an overall 5.27 Å RMSD conformational change. The RMSD of the interpolated models relative to MD ranges from 2.36 Å for TPS, 1.93–2.16 Å for EBS, to 1.80-−1.87 Å for the IDW interpolation (Fig. 3). The NO3 increased significantly from 26.8% for the initial structure to values ranging between 78.6–93.3% for the interpolation-based models, with the highest values achieved again by IDW (Fig. 4).

4 DISCUSSION

In this study, we evaluated three well-known interpolation methods for the flexible fitting of atomic structures into low-resolution data. We introduced interpolation as an efficient and easy-to-use alternative to constrained MD, with the goal of making the flexible fitting techniques available to non-expert users. Sampling the conformational variability by feature vectors limits the effect of experimental noise while avoiding over-fitting of low-resolution data. We expect our work to be generally useful for all applications where sparsely sampled displacements from coarse models are extended to a higher level of detail.

Visual inspection of the fit (Fig. 2) demonstrates a significant improvement of the best performing IDW fitting relative to rigid body docking. The two IDW methods described here rely at most on two parameters for which we provide empirical values based on exhaustive exploration of the parameter space. Our tests showed that the local IDW with a weighting exponent c set from 3–4 and a radius of influence R holding 50–90% of the feature vectors gives optimal results, similar to the global scheme with c set from 7–9. The type of IDW scheme and the exact values within the given ranges of c (or R) are not critical (Supplementary Table 2), and in all cases the results were better or comparable to those of the other interpolation methods. If the number of parameters is a concern, global IDW has only one parameter which can remain fixed at c=8 for all practical purposes.

Our validation strategy was motivated by our goal to emulate the expensive MD results as well as possible with user friendly interpolation. We focused on measurable deviations between MD and interpolation at the carbon alpha level, excluding all possible sources of error except those due to interpolation. There are additional system dependent uncertainties in flexible fitting, for example due to experimental noise in the cryo-EM maps, or as mentioned above, due to the inherent ambiguity of placing many thousands of atoms into a low-resolution dataset (Wriggers, 2004). These sources of error are outside the scope of the current article and discussed in more detail elsewhere (Baker and Johnson, 1996; Stowell et al., 1998; Wriggers and Chacón, 2001). However, we acknowledge that any flexible refinement will be judged by the accuracy of the fit to the experimental data. Therefore, we computed also the overlap between the experimental cryo-EM map and the flexed atomic models (low-pass filtered to experimental resolution) by the standard cross-correlation coefficient (Wriggers and Chacón, 2001). As expected, the flexed correlation values are all higher (Supplementary Table 1) than those of the initial structure. We also confirmed that the interpolated models exhibit very similar cross-correlations compared to the MD fit (Supplementary Table 1). The cross-correlation coefficients are nearly identical for interpolation methods and constrained MD because correlation (at low resolution) is not sufficient to differentiate between alternative models (Wriggers, 2004). However, we found that the IDW interpolation deviates least from constrained MD, showing minimal RMSD, narrowest histogram and maximal NO3 (Figs. 3 and 4) among the tested methods.

To regularize the bonds and angles disturbed by interpolation we carried out an additional idealization with the crystallization refinement tool RefMac (Murshudov et al., 1997). Our tests found very minor improvements in RMSD values that are negligible at the C_α level (Supplementary Table 2). This is to be expected as RefMac mainly regularizes the bonded interactions and the C_α representation is itself a coarse model. Any post-processing of the warped structures with tools like RefMac will be beneficial, especially if all atoms of the system are considered. But our results suggest that for carbon alpha level accuracy it is not necessary to carry out an additional stereochemical refinement step.

In summary, the IDW interpolation methods described in this article are efficient alternatives to the constrained MD, enabling non-expert users to perform multiscale modeling tasks within seconds of compute time (Supplementary Table 1). These methods will be made available both as a command line tool ‘qplasty’ in the Situs package (http://situs.biomachina.org) and as part of the molecular visualization and modeling application Sculptor (http://sculptor.biomachina.org).