MotifMap: a human genome-wide map of candidate regulatory motif sites

Abstract

Motivation: Achieving a comprehensive map of all the regulatory elements encoded in the human genome is a fundamental challenge of biomedical research. So far, only a small fraction of the regulatory elements have been characterized, and there is great interest in applying computational techniques to systematically discover these elements. Such efforts, however, have been significantly hindered by the overwhelming size of non-coding DNA regions and the statistical variability and complex spatial organizations of mammalian regulatory elements.

Results: Here we combine information from multiple mammalian genomes to derive the first fairly comprehensive map of regulatory elements in the human genome. We develop a procedure for identifying regulatory sites, with high levels of conservation across different species, using a new scoring scheme, the Bayesian branch length score (BBLS). Using BBLS, we predict 1.5 million regulatory sites, corresponding to 380 known regulatory motifs, with an estimated false discovery rate (FDR) of <50%. We demonstrate that the method is particularly effective for 155 motifs, for which 121 056 sites can be mapped with an estimated FDR of <10%. Over 28K SNPs are located in regions overlapping the 1.5 million predicted motif sites, suggesting potential functional implications for these SNPs. We have deposited these elements in a database and created a user-friendly web server for the retrieval, analysis and visualization of these elements. The initial map provides a systematic view of gene regulation in the genome, which will be refined as additional motifs become available.

Availability: http://motifmap.ics.uci.edu

Contact: xhx@ics.uci.edu; pfbaldi@ics.uci.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Among the 3 billion bases of the haploid human genome, only a small portion (<2%) corresponds to protein-coding regions. A central challenge of biology is to map and understand the role of the remaining 98% non-coding regions of the human genome. It is commonly believed that many of these non-coding regions are involved in gene regulation, but their specific roles and organization, including which regulatory motifs are contained in which regions, are still poorly known.

Mapping the locations of regulatory motifs across the human genome is challenging because these motifs are typically short, contain fuzzy sequence patterns, and are hidden in the vast background of non-coding sequences. Hence, the key computational challenge is to detect the locations of the motifs without introducing too many false positives.

Comparative genomics provides a powerful tool for detecting regulatory elements in the genome. This is because functional elements often evolve at a much slower rate than neutral sequences, and therefore they often stand out from the surrounding sequences by virtue of their greater levels of conservation. Previous work has demonstrated the power of comparative genomics for discovering novel regulatory motifs in human (Elemento and Tavazoie, 2005; Ettwiller et al., 2005; Xie et al., 2005). However, whether comparative genomics can provide sufficient power for detecting individual motif sites (not just overall motif patterns) in the human genome has not been fully addressed. In particular, a global map of motif sites for all known regulatory motifs in the human genome has not been attempted.

Recent availability of a dozen placental mammalian genomes significantly boosts our power for detecting motif sites in the human genome (Miller et al., 2007). These genomes are closely related to each other, and thus likely share a basic cassette of regulatory motifs. On the other hand, these genomes have been carefully chosen to represent distinct branches of the mammalian evolutionary tree. As such, they are ideal for separating regulatory sequences from neutral ones (Margulies et al., 2005).

When using multiple species for motif site discovery, one must take into consideration the phylogenetic relationship between the species. This is important for distinguishing truly conserved sites from spurious ones due to species proximity. A number of computational algorithms have been proposed (Li andWong, 2005; Moses et al., 2004; Siddharthan and van Nimwegen, 2007). Most of these methods use a probabilistic framework by modeling the evolutionary process of a motif site explicitly and performing statistical inference over the phylogenetic tree. Although these methods have had some success, mostly in yeast, several factors limit their applicability and effectiveness. First, it is not completely clear how to model the evolution of regulatory motif sites. All the previous methods assume that the nucleotides at different positions of a motif site evolve independently. This is clearly an over-simplification. For instance, an insertion or deletion event at a single position can completely abolish a motif site, and consequently relax evolutionary constrains at all other positions. Recent work has demonstrated the importance of considering such inter-position dependencies in modeling motif site evolution (Lusk and Eisen, 2008). Second, most of the previous methods assume that motif sites are conserved throughout the evolution of all the species being compared. In reality, it is often the case that a motif site is conserved and shared in only a subset of the species or lineages. Third, these methods are highly sensitive to the quality of the multiple sequence alignments and to missing sequences. This could be problematic for the mammalian genomes used here, which are repeat-rich and littered with sequencing gaps.

Recently, an alternative method has been proposed for motif site discovery using multiple genomes (Stark et al., 2007). The method works by first identifying the set of species in which the motif occurs, calculating the total branch length score (BLS) of the subtree covering these species and then using BLS to quantify the conservation level of a motif site. The scoring scheme has been successfully applied for motif site discovery in both flies (Stark et al., 2007) and mammals (Xie et al., 2007). This method does not rely on sequence alignments to fit an evolutionary model and, by construction, automatically focuses only on the relevant subset of species that may share a given element. As such, it is not sensitive to the limitations outlined above.

Although useful in practice, the method based on BLS leaves a lot of room for improvement. First, unlike some of the other methods, BLS lacks a solid theoretical foundation. Thus, it is unclear under which circumstances the method will be more effective or more prone to errors. Second, it is often difficult to strictly classify whether a sequence corresponds to motif site or not. It is more desirable to take the uncertainty of motif site matching into consideration. Third, a more principled approach is needed for determining which set of ancestral sequences contains a given motif.

Here we propose a new scoring scheme, the Bayesian branch length score (BBLS), to address these issues. Using BBLS and the genomes of 18 mammals, we are able to derive a genome-wide map of over 380 known regulatory motifs and assess its accuracy. Browsing and visualization of these elements and the corresponding map is achieved through the MotifMap web server.

2 METHODS

2.1 Known motifs and motif-matching z-score

Motifs were extracted from two major transcription factor binding sites databases: Transfac (Wingender et al., 1996) and JASPAR (Sandelin et al., 2004). We used only motifs associated with mammalian cells. In total, we curated 560 motifs, represented in the form of position-specific frequency matrices. We used a log-odds score y to quantify how well a sequence element x matches a motif, defined by y(x|θ) =,log[P(x|θ)/P(x|θ₀)], where θ is the frequency matrix of the motif and θ₀ is the background frequency of the four nucleotides across the entire genome. We further normalized the score to be between 0 and 1, S(x,θ) = (y(x|θ)−y_min)/(y_max−y_min), where y_min and y_max are the minimum and maximum log-odds scores the motif can possibly achieve. Thus S(x,θ) denotes the motif-matching score for sequence x and motif θ.

To determine the threshold score for calling a match, we randomly sampled 10 million locations in nonrepeat regions of the human genome and calculated motif matching scores at these random locations. For each motif, we calculated the mean (μ) and variance (σ²) of the motif-matching scores at these locations. Based on μ and σ, we converted each motif-matching score into a z-score, z(x,θ)=(S(x,θ)−μ)/σ. We used a z-score threshold of 4.27 (corresponding to a threshold S_th(θ)=,μ + 4.27σ on S) for calling a site a match, corresponding to a nominal P-value of 1e−6 for finding a motif purely by chance under a normal distribution model.

2.2 Phylogenetic tree and sequence alignments

Genomes and sequence alignments of 18 mammals used in this study were downloaded from the USCS genome browser (http://genome.ucsc.edu/) (Miller et al., 2007). The phylogenetic tree connecting the species (Supplementary Material) was constructed using the 4-fold degeneracy of the third codon position of coding DNAs (Miller et al., 2007). The tree has a total branch length of 3 mutations per site. We extracted orthologous sequences from the whole genome alignment. When searching for motif sites in other species, we extended the alignment at both ends by 15 bp to account for potential misalignments.

2.3 Bayesian branch length score

Denote the phylogenetic tree of the n species being compared by T and the nodes in the tree by i=,1, … N, where N=,2n−1. Without any loss of generality, we assume that the first n nodes are leaf nodes and the N-th node is the root of the tree. Suppose we are provided with the orthologous sequences of a putative motif site in the genomes of the n species. Denote the set of orthologous sequences by V (visible), and the set of corresponding ancestral sequences associated with the nonleaf nodes of the tree by H (hidden).

We assume that evolution along each edge of the tree is either neutral or constrained (i.e. under selective pressure to preserve a motif site). We use a binary variable σ_i to denote whether the edge leading to node i is evolutionary constrained (σ_i = 1) or not, when traversing the tree from the root to the leaves. For a given assignment vector σ with some nonzero entries, the log-odds score of observing the set V under σ against the neutral model (σ=,0) can be computed as

where the summation is over all ancestral nodes, the sequences of which are not directly observable. It is difficult to know a priori which edges are evolutionarily constrained. One strategy to deal with this uncertainty is to take a Bayesian approach and integrate over both alternatives

where P(σ) is a prior distribution over σ.

To calculate L(V) one must explicitly model the evolution of the motif sequences over all the branches of the tree. Most previous attempts have taken a simplified approach to this problem by assuming independent evolution at different positions of the motif sequence. This is clearly an oversimplification. Here we use a different method to derive an approximation to L(V) that avoids direct modeling of motif site evolution.

Using Jensen's inequality, we note that the L(V) is lower-bounded by

where Q(H|V) =,P(H|Vσ =0) is the posterior distribution of H under the neutral model. Because of the tree structure, the joint distribution P(V,H) can be factorized as a product and the log-odds score becomes

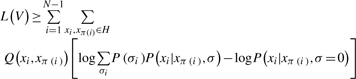where x_i denotes the sequence at node i, and π(i) represents the parent of node i. Q(x_i,x_π(i)) is the posterior distribution of the sequences at two neighboring nodes of the tree, conditioned on the set V under the neutral model. Assuming a non-informative prior on P(σ_ι) applying Jensen's inequality again, we have

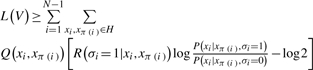where R(σ_i = 1) is the posterior probability for edge i to be constrained.

If the evolution of a motif site at a given edge is truly constrained, we expect the corresponding log likelihood ratio term in L(V), log(P(x_i|x_π(i),σ_ι= 1)/P(x_i|x_π(_i),σ_ι = 0)), to be proportional to the length of the edge (Supplementary Material). Under this assumption, the lower bound on L(V) can be approximated by the sum of the length of all the edges, with edge i weighted by the probability R(σ_i = 1):

and l_i is the length of the edge leading to node i. k and C are a constants.

The BLS can be viewed as a special case of the above approximation, in which R(σ_i =1)=1 for all leaf nodes whose sequences contain a motif site and for the ancestors contained in the subtree connecting these leaf nodes. In other words, the state variables σ_V = (σ₁, σ₂,…, σ_n) of the leaf nodes are now deterministic (σ_i = 1 if leaf node i contains a motif site), and the BLS(σ_V) is calculated by

Here σ_i(σ_V)= 1 if the subtree T_i of node i contains a leaf node with the state variable being 1, and in addition the complement T_i^c of the subtree also contains a leaf node with the state variable being 1. Note that T_i consists of node i and all of its descendents, whereas T_i^c is comprised of all other nodes not included in T_i.

2.4 A specific BBLS proposal

We consider a direct extension of the BLS mentioned above. Suppose there is uncertainty in determining whether a leaf node contains a motif or not, and the uncertainty is described by the probabilities p_i = P(σ_i = 1) for all i = 1,…,n. Given the probabilities for all the leaf nodes p_v = (p₁,p₂,…,p_n), a straightforward extension of the standard BLS is to sum over the uncertainties

where P(σ_V) =P(σ₁) P(σ₂)···P(σ_n) and the sum is over all combinations of possible states for the n leaf nodes. In the context of the general BBLS framework discussed above, this specific proposal corresponds to taking R(σ_i) = Σ_σVP(σ_V)σ_i(σ_V).

BBLS(p_V) involves the summation of 2ⁿ terms. Therefore, in general, it is infeasible to calculate BBLS directly using the above equation when n is large. However, in the Supplementary Methods, we prove that BBLS(p_V) can be calculated in time that scales linearly with n. Specifically, it can be calculated efficiently using the following formula

where c¹(i) and c²(i) denote the two child nodes of node i. P(σ_ι = 1) is the probability that T_i contains at least one leaf node with the state variable being 1, and P(σ_Ti^c = 0) is the probability that T_i^c contains no leaf nodes with the state variable being 1. Both P(σ_ι = 1) and P(σ_Ti^c = 0) can be calculated recursively, bottom-up from the leaf nodes to the root for P(σ_ι = 1), and top-down from the root to the leaf nodes for P(σ_Ti^c = 0)

where s(i) denotes the sister node of node i. The variable l_i* is the effective branch length associated with node i It too can be calculated recursively bottom-up from the leaf nodes to the root according to

with the initialization l_i* = l_i for leaf node i.

The above method does not depend on how P(σ_i = 1) is assigned. For motifs modeled by a positional weight matrix, P(σ_i = 1) is assigned for each leaf node i according to the motif-matching score of the sequence at the corresponding node

That is we assign a nonzero probability only to the nodes with motif-matching score above the threshold S_th. The probability itself is chosen to be linearly proportional to the motif-matching score.

2.5 Estimating the false discovery rate

For each known motif, we generated 10 control motifs by randomly shuffling the columns of the position-specific frequency matrix associated with the known motif, while keeping the frequency of the four nucleotides in each column unchanged. Because the mutation rate of the CG-dinucleotide is typically much higher than the rate of the other 15 dinucleotides, the CG-content of the motif was kept unchanged (i.e. by tying together neighboring columns with a high CG-dinucleotide frequency) during the shuffling. We then applied the same motif-site discovery algorithm to these control motifs. The false discovery rate (FDR) is estimated to be the median number of sites discovered for the control motifs divided by the number of sites discovered for the known motif.

3 RESULTS

We have developed a computational pipeline to search for the sites of 560 known motifs in the non-coding and non-repeat regions of the human genome. Once a putative site is detected in homo, we then determine whether the site also occurs in the orthologous regions of other mammalian genomes (Supplementary Fig. 1). The pipeline returns the species within which the motif occurs and corresponding motif-matching log-odd scores, determined by the position-specific frequency matrix of the motif. We initially retained those sites with motif-matching z-score >4.27 and with matching sites in at least four nonprimate species. For each of these identified sites, we then summarize its conservation level in other species using both the total BLS and the BBLS.

The initial list of candidate motif sites includes 3.9 million sites (corresponding to 1.9 non-overlapping unique sites) throughout the human genome. Because these sites are identified purely by computational methods, it is essential to find ways to rank these sites and estimate the accuracy of these predictions. Next we seek to address these questions.

3.1 Ranking motifs according to their BBLS

Each of the identified motif sites is associated with two conservation scores: BLS and BBLS. We tested which of the two scores can better distinguish bona fide sites from spurious ones. For this purpose, we used the CTCF motif as a benchmark. The CTCF motif is a good testing benchmark because so far it is the only motif whose locations have been experimentally mapped in multiple tissues (T cells and fibroblasts) and with multiple methods, including both ChIP-on-chip (Kim et al., 2007) and ChIP-seq methods (Barski et al., 2007). Altogether, the previous experimental efforts have identified a total number of 26 114 CTCF sites in the human genome.

Our initial list of candidate motif sites includes 25 098 CTCF sites, among which 9761 (39%) overlapped with experimentally identified sites. Using these 9761 sites as our positives, we examined how true positive and false positive rates for CTCF site prediction change when different threshold scores are chosen for BLS or BBLS. The ROC curves for these two different scoring schemes are shown in Figure 1A. Although both of the scoring methods clearly have predictive power at separating true CTCF sites from spurious ones, there are considerable differences in predictive accuracy among them. In particular, the method based on BBLS significantly outperforms BLS. The area under the curve (AUC) of the ROC curve for the BBLS method is 0.81, considerably better than the AUC for BLS (0.75).

Fig. 1.

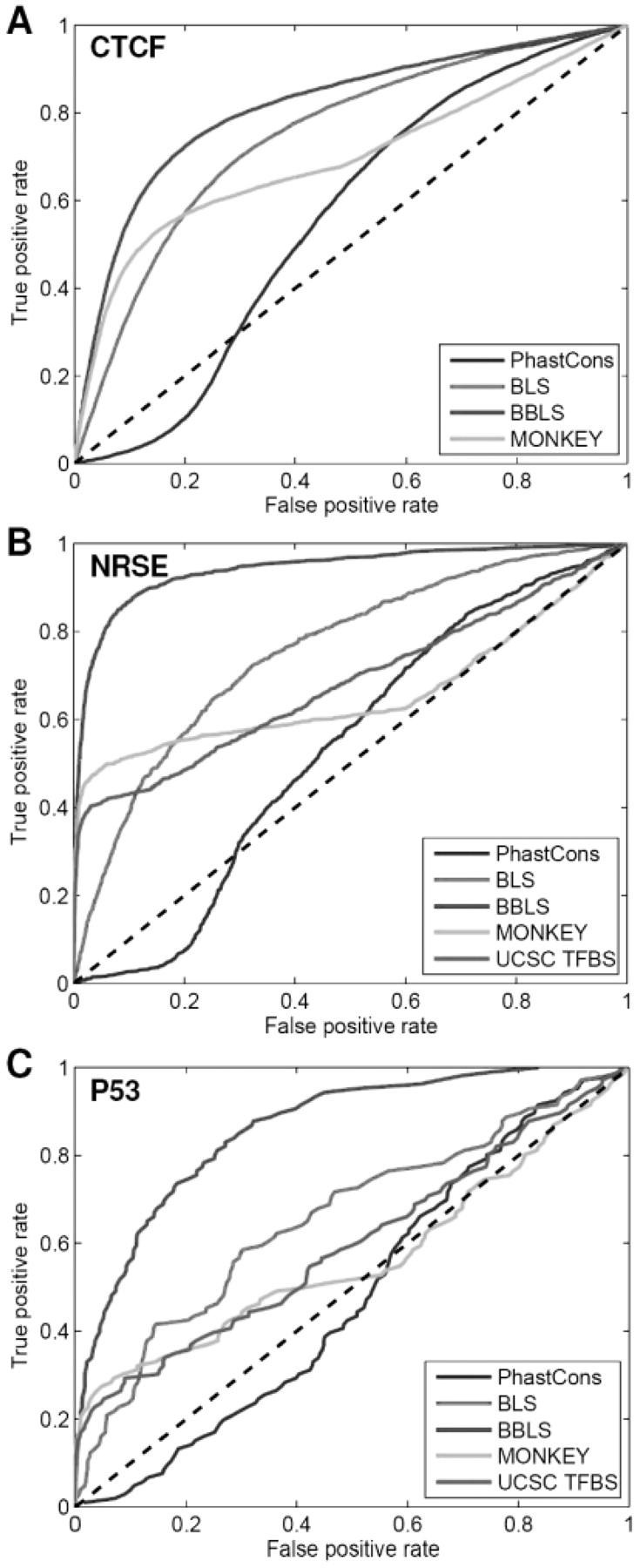
ROC curves for different methods for predicting the sites of CTCF (A), NRSE (B) and P53 (C). PhastCons: PhastCons conservation score; BLS: branch length score; BBLS: Bayesian branch length score; MONKEY: conservation P-value calculated by MONKEY (Moses et al., 2004); and UCSC TFBS: predicted sites from the UCSC genome browser.

As a comparison, we also tested the performance of BBLS against two other commonly used methods for ranking candidate motif sites: PhastCons conservation score (Siepel et al., 2005) and MONKEY (Moses et al., 2004). The PhastCons score is calculated using a phylogenetic hidden Markov model (HMM). It provides a measure of how an individual nucleotide is conserved without referencing the underlying motif model. In contrast to PhastCons, MONKEY specifically models the evolution of a motif site by taking into account the weight matrix model associated with the motif although, similarly to PhastCons, it also assumes that each individual position of the motif evolves independently. We calculated true positive and false positive rates for the CTCF site prediction by choosing different PhastCons and MONKEY conservation score thresholds, and plotted their ROC curves (Fig. 1A). The AUC of the ROC curves for PhastCons and MONKEY is 0.56 and 0.69, respectively, both of which are considerably <0.81 for BBLS (Table 1).

Table 1.

Comparison of the area under the ROC curve (AUC) for five different methods for predicting motif sites of six transcription factors

Factor	CTCF	NRSE	P53	MYC	STAT1	NFkappaB
BLS	0.747	0.756	0.659	0.634	0.554	0.708
BBLS	0.814	0.941	0.861	0.683	0.606	0.722
MONKEY	0.693	0.658	0.566	0.540	0.545	0.558
UCSC TFBS	–	0.681	0.596	0.587	0.529	0.712
PhastCons	0.557	0.533	0.481	0.548	0.494	0.651

Best results are in bold.

In addition to CTCF, we also compared the performance of the different methods for predicting the sites of five other motifs—NRSE (neuron-restrictive silencer element, Johnson et al., 2006), P53 (Wei et al., 2006), STAT1 (Robertson et al., 2007), MYC (Zeller et al., 2006) and NFkappaB (Lim et al., 2005). The binding sites of these five motifs have recently been mapped in human cells using the high-throughput techniques ChIP-seq or ChIP-pet (chromatin immunopreciptation coupled with paired end ditag sequencing). Overall, the experiment work has identified 2274 NRSE sites, 542 P53 sites, 41 515 STAT1 sites, 4296 MYC sites and 488 NFkappaB sites in human cells. We tested the performance of the four methods discussed above for predicting these experimentally identified sites and plotted their ROC curves in Figure 1B and C and Supplementary Figs S3–S8. In addition to the four methods mentioned above, we also tested how the predicted TFBS sites available from the UCSC genome browser (Karolchik et al., 2003) overlap with the experimentally identified sites for the five additional motifs (CTCF predictions are not available from the UCSC TFBS). TFBS uses the sum of the motif-matching scores in different species to score a motif site, without taking into account the phylogenetic relationship between the species. Note that in evaluating the performance of these different methods, we have defined true positive sites as those that are supported by the chip data and that match to a given positional weight matrix. They represent 37% of the 26 114 CTCF sites, 45% of the 2274 NRSE sites, 21% of the 542 P53 sites, 24% of the 4296 MYC sites, 3% of the 41 515 STAT1 sites and 12% of the 488 NFkappaB sites that are identified by the chip experiments. If all experimentally identified sites are used as true positives, the false negative rates corresponding to each method will need to be uniformly scaled down by these factors.

BBLS consistently outperforms all other four approaches mentioned above for predicting the sites of the five motifs (Table 1). The AUC of the ROC curves for BBLS is 0.94, 0.86, 0.68, 0.61 and 0.72 for NRSE, P53, MYC, STAT1 and NFkappaB, respectively, all of which are considerably better than the second best method (BLS for NRSE, P53 and STAT1 and TFBS for NFkappaB). The PhastCons conservation score consistently ranks lower than the four other methods (except for NFkappaB), reinforcing the importance of considering the motif model in measuring cross-species conservation.

Because of the BBLS's better performance, we retained it for further analyses in the following.

3.2 Properties of identified sites

As the motif sites are predicted purely by computational methods, we have followed additional lines of evidence to support the functionality of these sites.

First, we examined how many of the sites are expected to occur purely by chance. For this purpose, for each motif, we generated a set of 10 corresponding control motifs (see Methods section), and identified their sites using the same computational pipeline described above. In total, we obtained 2.6 million sites for these control motifs, based on which we estimate that about one-third of the 3.9 million predicted sites likely correspond to true functional elements. This is encouraging given the high chance of random matches for short motifs in the human genome, and the heterogeneity of the quality of the curated motifs.

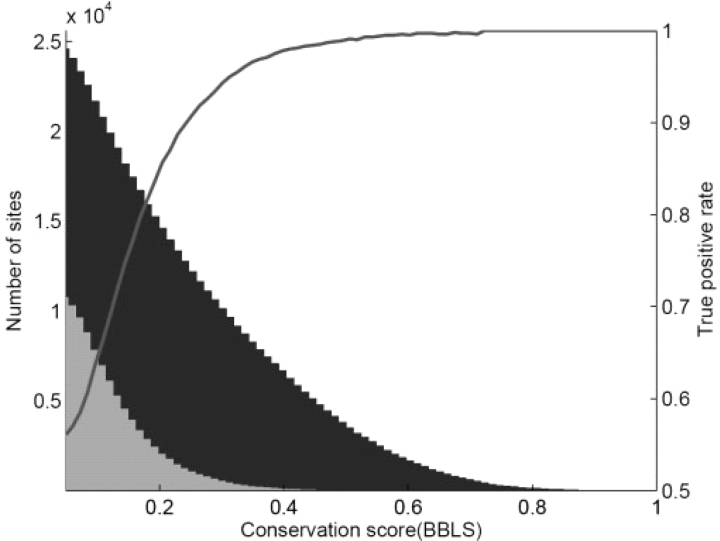
By increasing the threshold cutoffs of the BBLS and motif matching z-score, we can further improve the accuracy of our predictions. Consider, for example, the CTCF motif. The method identified a total number of 25 098 sites, 45% of which were estimated to be false positives (based on control motifs). However, by increasing the BBLS threshold, the prediction accuracy can be improved significantly (Fig. 3). In fact, using a combination of stringent BBLS and motif z-scores, we were able to accurately predict the sites for 155 motifs with FDRs <10%, leading to a total number of 204 421 (corresponding to 122 277 non-overlapping) highly accurate predictions (Table 2, Supplementary Table S1). By relaxing the FDR criterion to 0.5, the sites for an additional 225 motifs can be reliably predicted, corresponding to a total number of 1.5 million (787 517 non-overlapping) sites (Supplementary Table S2). For the remaining 180 motifs, it seems that we still lack the power to pinpoint their locations with high precision. This could result from several causes, including their small size, the incorrect characterization of their position weight matrices or simply because they are lineage-specific and not shared by most of the mammals.

Fig. 3.

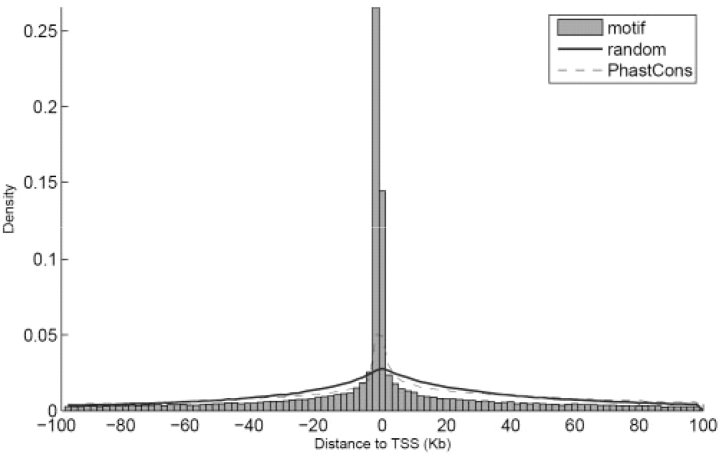
Distribution of the motif sites relative to the TSSs of genes. Also shown are the distributions of random loci (Blue) and the conserved PhastCons elements (excluding coding exons) (Red) relative to TSS.

Table 2.

Top 50 motifs with FDR ⩽0.1 ranked by the number of sites

Name	Number of sites	FDR	Motif score	BBLS	ID
SF-1	15 861	0.10	0.982	0.933	M00727
RFX1	15 319	0.10	0.767	0.500	LM1b
CTCF	12 195	0.09	0.741	0.667	LM2b
Sp1	10 507	0.09	0.912	0.500	M00931
Arnt	7434	0.10	0.874	1.433	MA0004a
AP-1	6513	0.10	0.906	1.167	M00925
Lhx3	5438	0.10	0.894	0.933	M00510
USF1	5081	0.10	0.950	1.133	MA0093a
Oct1	4769	0.10	0.943	1.500	M00342
Nrf-1	4035	0.10	0.900	0.600	M00652
Myf	3808	0.10	0.858	0.967	MA0055a
Elk-1	3130	0.10	0.811	0.667	M00025
ATF3	3106	0.08	0.806	0.500	M00513
ELK4	2777	0.10	0.903	0.867	MA0076a
RP58	2773	0.10	0.907	1.267	M00532
HSF1	2684	0.10	0.892	0.500	M01023
MAX	2623	0.10	0.924	1.033	MA0058a
CREB	2482	0.10	0.825	0.833	M00917
CRE-BP1	2396	0.10	0.939	0.667	M00041
LM4_M2	2176	0.09	0.790	0.500	LM4b
c-Myc	2082	0.10	0.838	0.833	M00615
CREBATF	1931	0.10	0.959	0.933	M00981
NF-Y	1913	0.09	0.804	1.167	M00287
Stra13	1773	0.10	0.868	0.767	M00985
UF1H3B	1750	0.10	0.894	0.567	M01068
ATF	1610	0.10	0.900	0.800	M00338
POU6F1	1547	0.10	0.870	1.000	M00465
AP-4	1537	0.10	0.968	1.800	M00176
GABPA	1426	0.10	0.936	0.933	MA0062a
NRSE	1360	0.09	0.797	0.500	LM9b
ERR	1276	0.08	0.976	0.500	M00511
Tal-1beta	1215	0.10	0.890	1.133	M00070
TGIF	1160	0.10	0.956	1.700	M00418
Staf	1146	0.10	0.893	0.533	MA0088a
USF	1034	0.10	0.912	0.933	M00121
c-Ets-1	941	0.09	0.970	1.467	M00032
MIF-1	880	0.10	0.850	1.000	M00279
YY1	859	0.10	0.950	1.133	M01035
MEF-2	744	0.10	0.767	1.067	M00231
NF-E2	700	0.10	0.988	0.833	M00037
TAL1	651	0.10	0.944	1.567	MA0091a
GFI1B	622	0.10	0.945	0.933	M01058
HNF-6	535	0.10	0.992	0.867	M00639
PPARG	523	0.10	0.830	0.933	MA0065a
MEIS1A	505	0.10	0.895	1.133	M00420
Nrf2	457	0.10	0.934	1.367	M00821
HNF4	446	0.09	0.827	1.500	M01031
HSF	399	0.10	0.978	0.500	M00641
NR2F1	387	0.10	0.914	1.333	MA0017a
GCNF	371	0.10	0.891	0.500	M00526

Most of the motifs are from the Transfac database.

^aFrom JARPAR database.

^bFrom Xie et al. (2007).

The number of sites identified for each motif is highly uneven (Table 2, Supplementary Fig. S1). A few motifs have an especially high number of instances in the genome. For instance, the top four most highly frequent motifs (SF-1, RFX1, CTCF and SP1) each occurred over 10 000 times in the genome, while by contrast the median number of sites among the motifs is only 384. The SF-1 motif contains an 8-mer sequence pattern (TRACCTTG) recognized by many nuclear hormone receptors. Its large number of occurrences (15 492) in the genome may suggest the widespread role of nuclear receptors in gene regulation. The RFX1 motif is similar to the X-box motif that has been extensively studied in nonvertebrates, such as yeast and nematode. In Caenorhabditis elegans, several hundreds X-box sites appear upstream of genes involved in the development of sensory cilia (Efimenko et al., 2005), and play an important role in cilia genesis. In mammals, the RFX1 elements are less well studied. Their high level of occurrence in the mammalian genomes is not expected, and suggests that RFX1 might be involved in roles other than cilia genesis in the mammalian gene regulatory system. The third most frequent motif is recognized by the CTCF protein, which is involved in insulator activity, and plays an important role in demarcating distinct regions of the genome into functionally distinct domains (Kim et al., 2007; Xie et al., 2007).

Second, we examined the distribution of the predicted motif sites in the genome relative to the location of the genes. For this analysis, we focused on the 122 277 sites corresponding to the 155 highly specific motifs discovered above. For each of these sites, we identified its nearest gene and the distance between the motif site and the transcriptional start site (TSS) of the gene. We found a significant enrichment of motif sites in the regions around the TSS (Fig. 2). In fact, as much as 32% of the sites are located within 2 Kb of a TSS. This number corresponds to a 10-fold enrichment over what is expected by chance (for random sites, only 3% are expected). The enrichment near the TSS is of course concordant with a possible involvement in the regulation of the corresponding genes.

Fig. 2.

Estimated false positive rate as a function of BBLS. Blue represents the number of predicted sites for the CTCF motif. Gray represents the number of predicted sites for the CTCF control motif. Red curve plots the rate of true positives as a function of BBLS.

Third, we examined the overlap between the predicted motif sites and the experimentally identified ones. Again we used the CTCF motif as a test case. Altogether, the previous experimental efforts identified a total number of 26 114 CTCF sites in the human genome. In our computational predictions, we identified 12 295 conserved sites with FDR <0.1. Of these sites, 7321 (60%) are also identified by the experimental methods. In contrast, the control motif of CTCF only discovered 1130 sites, out of which only 42 overlapped the experimental identified sites. This demonstrates the high specificity of the computational predictions.

Taken together, these analyses provide strong evidence supporting the functionality of the predicted sites. The predictions have relatively low false positive rates, and as such provide a reliable set of sites for future experimental validations.

3.3 Comparison with PhastCons elements

Previous comparative studies have discovered that a significant portion of the human genome evolves at a much slower rate than that of neutral sequences. For instance, the PhastCons program has identified over 2 million conserved sequence elements in the genome, with average size of about 150 bp (Miller et al., 2007; Siepel and Haussler, 2004). The PhastCons elements also show enrichment in regions near gene TSSs, although less significantly than the enrichment shown by the predicted motif sites (Fig. 3). We checked the overlap between the predicted motif sites and the PhastCons elements, and found that most of the predicted sites (72%) are located inside these PhastCons elements. However, a significant portion (28%) of the motif sites is not detected by the previous method. Most likely, this is because these sites work mostly alone and as such are located in regions without other functional elements. The PhastCons program lacks sufficient power for detecting such short sequence elements. It is worth noting that the FDRs for the predicted sites located outside the PhastCons elements are typically comparable to those located inside the PhastCons elements (Supplementary Fig. S10). Thus our method based on matching conserved motif sites provides a complementary approach to the commonly used PhastCons program for detecting functional elements in the genome.

3.4 Motif sites overlapping SNPs

Recent progress in genome-wide association studies have identified many genetic variations (mostly SNPs) associated with complex phenotypes. One interesting observation emerging from these studies is that most of the discovered SNPs occur outside of protein-coding regions and, in most case, are not associated with any known functions. There is a great deal of interest in figuring out the potential functions of these SNPs.

We checked the overlap between known SNPs and the predicted motif sites. Of the 12 million SNPs deposited in the dbSNP database (version 126), 89 032 SNPs overlap with at least one of the 1.9 million non-overlapping initial candidate motif sites, corresponding to a density of 2.99 SNPs/Kbp. Of the 4 million SNPs (release 22) genotyped in three human populations by the HAPMAP consortium (Frazer et al., 2007), 42 548 overlap with the initial candidate motif sites. If we focus on the high-confidence list of 787 517 million motif sites discovered with FDR <50%, we find 28 294 dbSNPs (density: 2.65 SNPs/Kbp) and 13 535 HAPMAP SNPs overlapping these sites. If we focus on the high-confidence list of 122 277 motif sites discovered with FDR <10%, we find 4293 dbSNPs (density: 2.59 SNPs/Kbp) and 1864 HAPMAP SNPs overlapping these sites. The decrease in SNP density for the three sets of predicted sites likely reflects the stronger purifying selection acting on sites associated with higher prediction confidence. The list of these SNPs and their corresponding motifs (see Supplementary Website) provide a concrete and testable hypothesis regarding the potential functional role of these SNPs. An interesting follow-up study would be to investigate the correlation between the genotype of these SNPs and the variation on the gene expression of their corresponding target genes. The list of the SNPs may also be useful when selecting SNPs for genotyping in disease gene mapping studies or for testing SNPs involved in recent positive selection (Sabeti et al., 2007; Wang et al., 2006).

4 WEB SERVER AND INTERFACE

We have constructed a database and web server for the predicted motif sites, and created a user-friendly web interface for retrieving, analyzing and visualizing these data (Supplementary Fig. S9).

The web interface allows users to filter motif sites using different threshold scores and conservation criteria, including BLS and BBLS, as well as FDR. For a given motif, users can retrieve the genome-wide locations of the motif, and load them into the USCS genome browser for visualization.

5 DISCUSSION

We have created an initial map of candidate regulatory motif sites across the human genome. The map currently contains 3.9 million sites, corresponding to 560 motifs. We have demonstrated that the method is especially effective for 155 motifs, for which the predicted sites have an estimated FDR <0.1.

While here we have focused on the human map, it is clear that the same methods give immediately similar maps for all 17 species. In particular, the mouse and rat maps may also be of general interest and will be made available in the near future through the same web interface.

Because the transcription factors binding to the motifs used in this study are known, it is possible to construct a regulatory network for each genome by connecting these transcription factors and their target genes (estimated from the presence of motif sequences near the corresponding TSS). This could provide an alternative strategy for regulatory network construction and, in future work, it would be interesting to see how the network structures compare with those derived from other methods.

Our prediction methods depend heavily on comparative genomics to boost the signal-to-noise ratio of the motif signals. It has been noticed that many regulatory sites in human are lineage-specific and do not appear to be conserved in other species (King, 2007). For these motif sites, methods other than sequence comparison are required. One potential direction could be to search for a local clustering of motif sites rather than an individual site, and to develop methods for detecting regulatory modules.

The computational analysis of the motif sites presented here is, of course, only a first step towards building a comprehensive map of regulatory elements contained in the human genome. With the identification of additional motifs and better methods for mapping motif sites, the regulatory motif map will be further refined. We intend to provide an active and regularly updated central sever, and make it useful for biologists interested in gene regulation in humans, as well other mammals.