A novel signaling pathway impact analysis

Abstract

Motivation: Gene expression class comparison studies may identify hundreds or thousands of genes as differentially expressed (DE) between sample groups. Gaining biological insight from the result of such experiments can be approached, for instance, by identifying the signaling pathways impacted by the observed changes. Most of the existing pathway analysis methods focus on either the number of DE genes observed in a given pathway (enrichment analysis methods), or on the correlation between the pathway genes and the class of the samples (functional class scoring methods). Both approaches treat the pathways as simple sets of genes, disregarding the complex gene interactions that these pathways are built to describe.

Results: We describe a novel signaling pathway impact analysis (SPIA) that combines the evidence obtained from the classical enrichment analysis with a novel type of evidence, which measures the actual perturbation on a given pathway under a given condition. A bootstrap procedure is used to assess the significance of the observed total pathway perturbation. Using simulations we show that the evidence derived from perturbations is independent of the pathway enrichment evidence. This allows us to calculate a global pathway significance P-value, which combines the enrichment and perturbation P-values. We illustrate the capabilities of the novel method on four real datasets. The results obtained on these data show that SPIA has better specificity and more sensitivity than several widely used pathway analysis methods.

Availability: SPIA was implemented as an R package available at http://vortex.cs.wayne.edu/ontoexpress/

Contact: sorin@wayne.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The typical result of a microarray experiment comparing two groups of samples (e.g. normal and diseased) is a list of differentially expressed (DE) genes together with their estimated expression changes between the groups. Translating such results into a better understanding of the underlying biological phenomenon is key to translating the now abundant high-throughput expression data into biological knowledge. An automated approach to map the list of DE genes onto Gene Ontology (GO) terms is the most widely used attempt at this (Drăghici et al., 2003; Khatri and Draghici, 2005; Khatri et al., 2002). More recently, biological annotations have started to include descriptions of gene interactions in the form of gene signaling networks, such as KEGG (Ogata et al., 1999), BioCarta (www.biocarta.com) and Reactome (Joshi-Tope et al., 2005). This richer type of annotations have opened the possibility of an automatic analysis aimed to identify the gene signaling networks that are relevant in a given condition, and perhaps even the specific signals or signal perturbations involved. This analysis is usually referred to as a pathway analysis. A PubMed search for ‘microarrays and pathway analysis’ returned more than 1800 results, illustrating the numerous attempts to use and develop such techniques. Currently, the pathway analysis with microarray data is primarily performed using the classical approaches inherited from the ontological profiling: over-representation analysis (ORA) (Drăghici et al., 2003; Khatri et al., 2002) and functional class scoring (FCS) (Goeman et al., 2004; Mootha et al., 2003; Pavlidis et al., 2004; Subramanian et al., 2005; Tian et al., 2005). However, both ORA and FCS techniques are limited by the fact that each functional category is analyzed independently without a unifying analysis at a pathway or system level (Tian et al., 2005). This approach is not well suited for a systems biology approach that aims to account for system-level dependencies and interactions, as well as identify perturbations and modifications at the pathway or organism level (Stelling, 2004).

Most of the approaches currently available for the analysis of gene signaling networks share a number of important limitations. First, these approaches consider only the set of genes on any given pathway and ignore their position in those pathways. This may be unsatisfactory from a biological point of view. If a pathway is triggered by a single gene product or activated through a single receptor and if that particular protein is not produced, the pathway will be greatly impacted, probably completely shut off. A good example is the insulin pathway (www.genome.ac.jp/KEGG/pathway/hsa/hsa04910.html). If the insulin receptor (INSR) is not present, the entire pathway is shut off. Conversely, if several genes are involved in a pathway but they only appear somewhere downstream, changes in their expression levels may not affect the given pathway as much. Second, some genes have multiple functions and are involved in several pathways but with different roles. For instance, the above INSR is also involved in the adherens junction pathway as one of the many receptor protein tyrosine kinases. However, if the expression of INSR changes, this pathway is not likely to be heavily perturbed because INSR is just one of many receptors on this pathway. All these aspects are not considered by any of the existing approaches aiming at assessing the impact of a condition on a given signaling pathway. There is a very recent technique (Efroni et al., 2007), however, which takes into account some topological information but this technique aims at phenotype prediction rather than the assessment of given condition which is our primary goal here. Third, and probably the most important current limitation is that the knowledge embedded in these pathways about how various genes interact with each other is largely unexploited. The very purpose of these pathway diagrams is to capture our current knowledge of how genes interact and regulate each other on various pathways. However, the existing analysis approaches consider only the sets of genes involved on these pathways, without taking into consideration their topology. Our understanding of various pathways is expected to improve as more data are gathered. Pathways will be modified by adding, removing or redirecting links on the pathway diagrams. Most existing techniques are completely unable to even sense such changes. Thus, these techniques will provide identical results as long as the pathway diagram involves the same genes, even if the interactions between them are completely redefined over time. Finally, until now, the expression changes measured in these high-throughput experiments have been used only to identify pathways with unexpectedly high number of DE genes (ORA approaches) or pathways whose genes are clustered in the ranked list of DE genes (FCS methods), but not to directly estimate the impact of such changes on specific pathways. This is also an important limitation. For instance, ORA techniques will see no difference between a situation in which a subset of genes is DE just above the detection threshold (e.g. 2-fold) and the situation in which the same genes are changing by many orders of magnitude (e.g. 100-fold). Similarly, FCS techniques can provide the same rankings for entire ranges of expression values, if the correlations between the genes and the phenotypes remain similar. Even though analyzing this type of information in a pathway and system context would be extremely meaningful from a biological perspective, currently there is no technique or tool able to do this.

This article describes a radically different approach that attempts to capture all aspects above. A global probability value, P_G, is calculated for each pathway, incorporating parameters, such as the log fold-change of the DE genes, the statistical significance of the set of pathway genes and the topology of the signaling pathway. We recently proposed a technique that combines the pathway topology with the over-representation evidence with very good results (Draghici et al., 2007). However, in this analysis, the evidence measure captured from the pathway topology was not completely independent from the over-representation evidence. In turn, this made the statistic used to rank the pathways more sensitive to noise in the expression data putting too much emphasis on the magnitude of changes. Also, the false positive rates of this method was higher than expected by chance for short lists of DE genes. The approach described here remedies these weaknesses, while retaining the very novel capability of incorporating the pathway topology. The capabilities of the proposed impact analysis are illustrated on a number of real datasets and simulations. We also show that in this technique, the two types of evidence considered are indeed completely independent.

2 SYSTEM AND METHODS

The impact analysis combines two types of evidence: (i) the over-representation of DE genes in a given pathway and (ii) the abnormal perturbation of that pathway, as measured by propagating measured expression changes across the pathway topology. These two aspects are captured by two independent probability values, P_NDE and P_PERT.

The first probability, P_NDE=P(X≥N_de ∣H₀), captures the significance of the given pathway P_i as provided by an over-representation analysis of the number of DE genes (N_DE) observed on the pathway. In the equation above, H₀ stands for the null hypothesis, that the genes that appear as DE on a given pathway are completely random. From a biological perspective this would mean that the pathway is not relevant to the condition under study. The P_NDE value represents the probability of obtaining a number of DE genes on the given pathway at least as large as the observed one, NDE. These P_NDE values were obtained assuming that N_DE (the number of DE genes on the pathway analyzed) follows a hypergeometric distribution with three parameters: m—the number of all pathway genes present on the array, n—the number of genes on the array not belonging to the pathway, k—total number of DE genes. Any of the existing ORA or FCS approaches can be used to calculate P_NDE, as long as this probability remains independent of the magnitudes of the fold-changes.

The second probability, P_PERT, is calculated based on the amount of perturbation measured in each pathway. We define a gene perturbation factor as:

(1)

In Equation (1), the term ΔE(g_i) represents the signed normalized measured expression change of the gene g_i (log fold-change if two conditions are compared). The second term in Equation (1) is the sum of perturbation factors of the genes g_j directly upstream of the target gene g_i, normalized by the number of downstream genes of each such gene N_ds(g_j). The absolute value of β_ij quantifies the strength of the interaction between genes g_j and g_i. These weights have been introduced in order to allow the model to capture the properties of various types of relationships. The results presented in this article are obtained using all |β|=1 in order to minimize the number of model parameters. The sign of β reflects the type of interaction: +1 for induction (activation), −1 for repression and inhibition, as described by each pathway. Note that β will have non-zero value only for the genes that directly interact with the gene g_i according to the pathway description. The work described here used human signaling pathways from KEGG (Ogata et al., 1999). These pathways contain nodes, representing genes/proteins, and directed edges, representing gene signals or interactions such as activation or repression. Given an edge directed from gene/protein A to gene/protein B, we say A is upstream of B, or B is downstream of A.

Equation (1) essentially describes the perturbation factor PF for a gene g_i as a linear function of the perturbation factors of all genes in a given pathway. In the stable state of the system, all relationships must hold, so the set of all equations defining the impact factors for all genes form a system of simultaneous equations whose solution will provide the values for the gene perturbation factors PF_gi (details are provided in the Supplementary Material). Subsequently, we calculate the net perturbation accumulation at the level of each gene, Acc_g, as the difference between the perturbation factor PF of a gene and its observed log fold-change:

(2)

This subtraction is needed to ensure that DE genes not connected with any other genes will not contribute to the second type of evidence since such genes are already taken into consideration in the ORA and captured by P_NDE. In can be shown (see Supplementary Material) that the vector of perturbation accumulations Acc can be obtained using the matrix equation:

(3)

where B represents the normalized weighted directed adjacency matrix of the graph describing the gene signaling network:

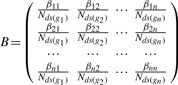(4)

I is the identity matrix, and

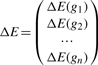(5)

Only the pathways with non-null determinant of I−B matrix were considered for analysis, even though simple, yet reasonable, transformations of B can be performed to avoid such singularities. Out of the 64 human gene signaling pathways available in KEGG, the majority (52 pathways) satisfy this requirement without any other transformations. The situations in which pathways yield a singular matrix and how these situations can be addressed will be described elsewhere. The total net accumulated perturbation in the pathway is computed as t_A=∑_iAcc(g_i). The second probability, P_PERT, will be the probability to observe a total accumulated perturbation of the pathway, T_A, more extreme than t_A just by chance:

(6)

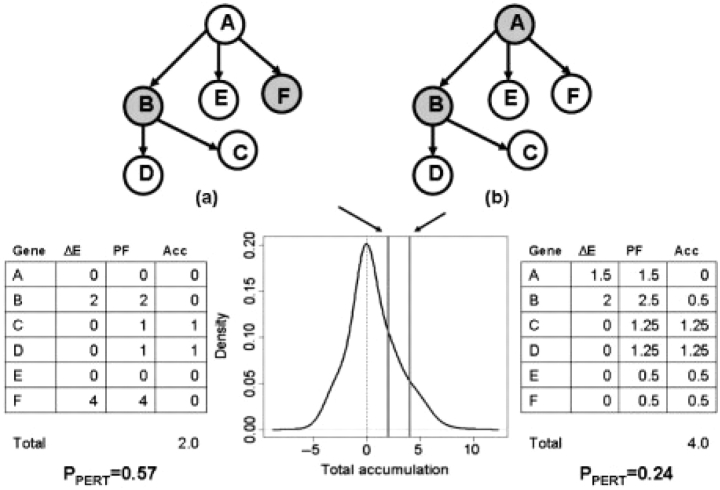
This probability can be calculated using a bootstrap approach. In this procedure, the same number of DE genes as the one observed on the pathway are allowed to occupy any position in the pathway (random gene IDs) and have any possible log fold-change in the range of those considered by the experimenter to be DE. This allows empirical determination of the null distribution of T_A values (details of the bootstrap procedure are given in the Supplementary Materials). Figure 1 illustrates the computation of P_PERT for a simple 6 gene pathway containing two DE genes. Unlike the classical over-representation approach, the perturbation evidence is shown to be able to capture the importance of the position of the DE genes in the pathway as well as their fold-changes.

Fig. 1.

Capturing the topology of the pathways and the position of the gene through the perturbation analysis. The figure shows a six-gene pathway with two DE genes (shown in gray) in two different situations. One of the two DE genes is in common (gene B) while the second gene is either a leaf node (a), or the entry point in the pathway (b). In (a), gene (F) cannot perturb the activity of other genes; in (b) gene (A) has the ability to influence the activity of all the remaining genes in the pathway, as the topology of the pathway indicates. An ORA would find the two situations equally (in)significant (P_NDE=0.48 for a set of 20 monitored genes, out of which five are found to be DE). The perturbation evidence extracted by SPIA will give more significance to the situation in (b) (P_PERT=0.24), even though fold-changes in (b) are almost twice as small as those in (a) (P_PERT=0.57).

The two types of evidence, P_NDE and P_PERT, are finally combined into one global probability value, P_G, that is used to rank the pathways and test the research hypothesis that the pathway is significantly perturbed in the condition under the study. When the null hypothesis is true, the probability of observing a pair of P-values whose product is at least as extreme (low) as the one observed for a given pathway i, c_i=P_NDE(i)·P_PERT(i), can be shown to be (see Supplementary Materials):

(7)

Both components combined within P_G, P_NDE and P_PERT, are independent of the size of the pathways. P_NDE is the probability of observing the given number of DE genes or higher, just by chance. The number of genes expected by chance will increase with the size of the pathway, much like the number of black balls extracted from an urn containing black and white balls will increase with the number of balls extracted in a given trial. Hence, P_NDE will be independent of the size of the pathway, much like the hypergeometric probability of extracting a given number of black balls from the urn will automatically take into consideration the number of balls extracted in that particular trial. The second component, P_PERT is calculated in a bootstrapping process in which both the pathway and the number of DE genes per pathway are fixed. P_PERT will become significant only if the observed fold-changes in the observed pathway nodes yield a significantly different impact compared with what is observed on the same pathway when the same number of fake DE genes are thrown in random locations throughout the same pathway. Again, this bootstrap is calculated for each pathway and hence will be independent of the pathway size.

Since P_G is a combined probability value, it can be used not only to rank the pathways, but also to choose a desired level of type I error. When several tens of pathways are tested simultaneously, as is the case throughout this study, small P_G values can occur also by chance. Therefore, we suggest controlling the false discovery rate (FDR) of the pathway analysis at 5% by applying the popular FDR algorithm (Benjamini and Yekutieli, 2001).

3 RESULTS AND DISCUSSION

3.1 Absence of false positives under the null hypothesis

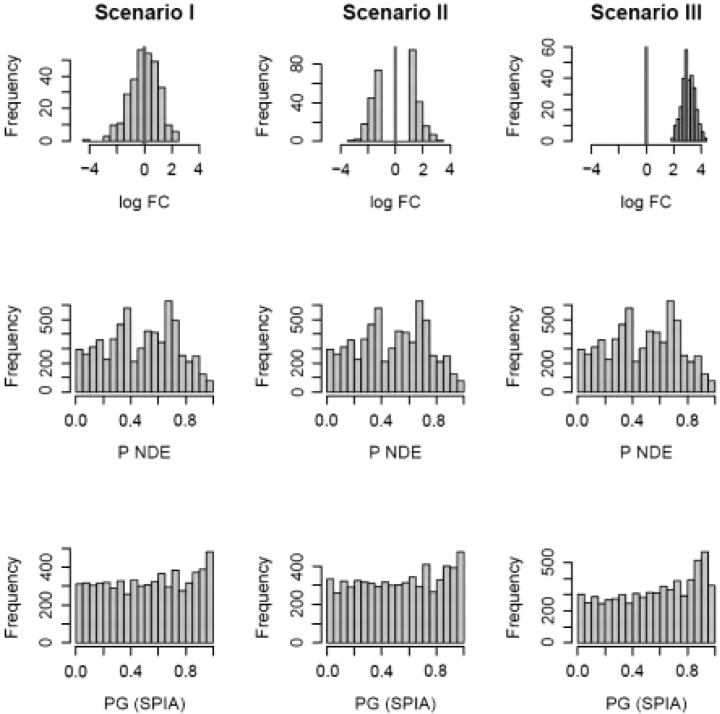
From the specificity perspective, an ideal pathway analysis method should not find any significant pathway when a set of randomly selected genes from the reference array are assigned random log fold-changes, regardless of what type of distribution they are drawn from. However, even if the data are completely random (i.e. the null hypothesis is true), any statistical test will reject the null hypothesis for a number of cases directly controlled by the significance threshold, α. It is important, however, to verify that a proposed test does not provide any false positives beyond this expected proportion. In order to verify that signaling pathway impact analysis (SPIA) does not provide a number of false positives above the significance threshold, we performed a number of simulations of the null hypothesis that can be divided into three scenarios. A reasonable scenario in which one should not find significant pathways is when the DE genes have random normal log fold-changes, and the genes are selected at random. In this setup (further referred to as scenario I), we select N_de random genes as DE from a reference array of size 20 000. The reference array includes all genes from all 52 pathways analyzed. The genes were assigned log fold-changes from a random normal distribution, N(0, 1). This is illustrated in top left panel of Figure 2. An alternative model for the null hypothesis is an experiment in which one compares two groups of samples among which there are no real biological differences. However, due to various reasons, such as improper normalization or array batch effects problems, the values measured for various genes will be different. Thus, one can always falsely identify some genes as DE [using for instance a fold-change selection method (Drăghici, 2002)]. In this case, the distribution of the log fold-changes will be bimodal (scenario II). This is illustrated in the top center panel of Figure 2. In this second scenario, log fold-changes are still drawn from a random normal distribution, N(0, 1) but they are restricted to be at least one SD away from the mean. Another particularly interesting situation is when all DE genes log fold-changes are either positive or negative (all genes are up-regulated or down-regulated). This situation is illustrated in the top right panel of Figure 2. In this case the log fold-changes of the so called DE genes may have a unimodal distribution but they will be all far from 0 and share the same sign, e.g. a random normal distribution with mean 3 and SD of 0.5 (scenario III). It should be noted that, from this perspective, the main limitation of the classical hypergeometric analysis turns into an advantage: since the hypergeometric enrichment analysis does not take into consideration either the specific fold-changes, nor the pathway topology, it will not be susceptible to false positives due to such causes as described above. Indeed, this is illustrated in the middle panel of Figure 2 which shows that the distribution of the hypergeometric P-value is essentially uniform in all three scenarios considered. The results presented in Figure 2 show that SPIA also yields a uniform distribution of P-values under the null hypothesis and therefore will provide no false positives beyond the unavoidable level equal to the chosen significance threshold, α. This is true regardless of the number of DE genes analyzed (Table 1).

Fig. 2.

Distribution of P-values under three null distribution scenarios for the hypergeometric and SPIA models. N_de=300 gene IDs were selected at random out of 20 000 possible IDs containing all genes on all 52 pathways analyzed. The randomly selected gene IDs were assigned log fold-changes from (i) a random normal distribution N(0,1); (ii) a bimodal distribution obtained by sampling from the tails of a N(0,1) distribution; and (iii) random normal N(3,0.5). For each scenario, the experiment was repeated 200 times and P_NDE, P_PERT and P_G were computed for all pathways receiving at least one DE gene. The resulting P-values for all pathways and all iterations were pooled together and shown as histograms for ORA (P_NDE) and SPIA (P_G) on rows 2 and 3, respectively. The false positives rates for SPIA at α = 5% were 4.7%, 5.0% and 4.6%, in scenarios I, II and III, respectively. For ORA, the same positive rates were 4.5% in all three scenarios. False positive rates as an average over these three scenarios are provided in Table 1 for several values of N_de.

Table 1.

The false positive rates and the correlation coefficients between P_PERT and P_NDE, as a function of the number of DE genes analyzed averaged over the three scenarios depicted in Figure 2

Nde	FP(ORA)	FP(SPIA)	R2
100	0.072	0.068	0.0022
300	0.045	0.048	0.0028
500	0.038	0.044	0.0032
1000	0.036	0.045	0.0041
2000	0.038	0.045	0.0041
5000	0.036	0.046	0.0002

The false positive rates and the correlation coefficients between P_PERT and P_NDE, as well as an average false positive rate at the expected 5% level.

3.2 The independence of the perturbation and enrichment statistics

The fact that P_PERT and P_NDE are two independent variables under the null hypothesis, is theoretically justified by the design of the bootstrap procedure used to compute P_PERT. This independence has also been verified using a simulation, as follows. A set of N_de=300 gene IDs was selected at random out of 20 000 possible IDs containing all genes on all 52 pathways analyzed. The randomly selected gene IDs were assigned log fold-changes from (i) a random normal distribution N(0, 1); (ii) a bimodal distribution obtained by sampling from the tails of a N(0, 1) distribution; and (iii) random normal N(3, 0.5). For each scenario, the experiment was repeated 200 times and P_NDE, P_PERT were computed for all pathways receiving at least one DE gene. The resulting pairs of P_NDE and P_PERT are shown as a scatter plot in Figure 3. The squared correlation coefficient was R²=0.0028, indicating essentially no correlation between the two P-values. This remains true regardless of the number of DE genes analyzed (Table 1). These simulations prove that the evidence from perturbations as computed by SPIA is linearly independent from the over-representation evidence under the null hypothesis.

Fig. 3.

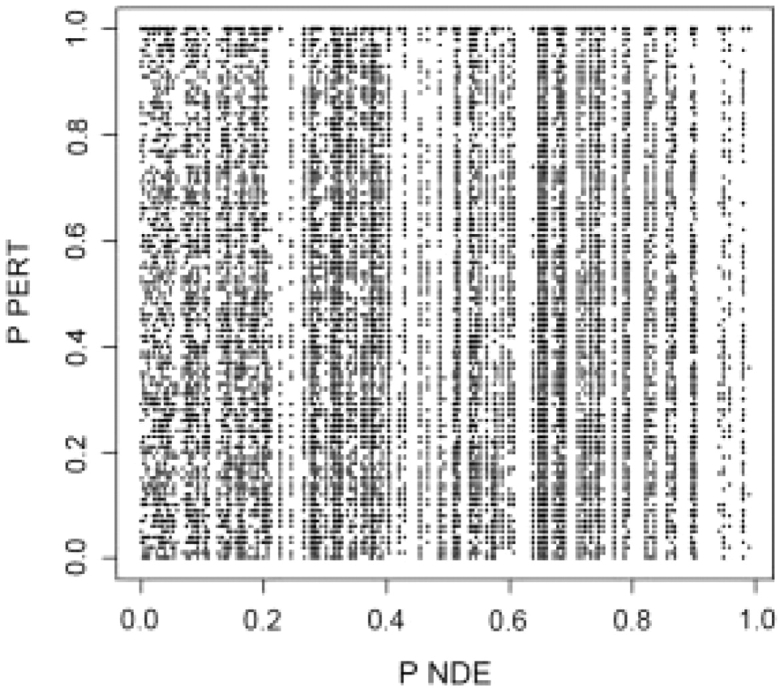
Correlation analysis between P_NDE and P_PERT under the null hypothesis. This scatter-plot shows all pairs of P-values for 52 pathways, 200 random trials and the three fold-change distribution scenarios considered. As shown in Table 1, the squared correlation coefficient, R², was less than 0.005, regardless of the number of genes analyzed, N_de. The current plot was obtained with N_de=300.

3.3 Sensitivity and pathways ranking on real datasets

Assessing the capabilities of any pathway analysis method in real experiments is a challenge in itself because the ground truth is never known. In the absence of a gold standard, the best alternatives are to: (i) analyze the results of the pathway analysis method in the light of the existing biological knowledge regarding the condition studied, and (ii) compare it with the existing methods in the context of the same existing biological knowledge. The absence of a definitive answer regarding the involvement of a given pathway in a given condition makes it impossible to calculate exact values for sensitivity, specificity, ROCs, etc. However, the methods can be compared in terms of the number of pathways that are found to be significant in a given condition and how well the significant pathways fit with the existing biological knowledge. This type of assessment is the current best practice in this area (Subramanian et al., 2005).

We used four datasets in order to illustrate the capabilities of the newly proposed pathway analysis method, SPIA. The first such dataset compares 12 colorectal cancer samples with 10 normal samples (Hong et al., 2007) using Affymetrix HG-U133 Plus 2.0. microarray platform. This dataset is available via the Gene Expression Omnibus (ID=GSE4107) and it will be referred to as the Colorectal cancer dataset. Several pathways are known to be relevant to the colorectal cancer, including the colorectal pathway itself, the PPAR signaling pathway (Shureiqi et al., 2003) and MAPK signaling pathway (Fang and Richardson, 2005).

The second dataset is the result of comparing gene expression levels in cervix tissue samples from women at term with spontaneous labor (TL group) (n=9) and those at term without labor (TNL group) (n=7). The microarray platform used was Affymetrix HG-U133 Plus 2.0. The details of this study and its biological significance are described elsewhere (Hassan et al., 2006, 2007). This dataset will be referred to as LaborC.

The third dataset is the result of comparing gene expression levels between umbilical veins (UV)(n=6) and umbilical arteries (UA) tissues (n=6) using Illumina BeadChips Human-6 V2 arrays. This dataset will be referred to as Vessels dataset. The details of this study and its biological significance are presented elsewhere (Kim et al., 2008). This dataset is available in the Arrays Express repository (ID: E-TABM-368).

The fourth dataset used in this study was produced by comparing gene expression levels in myometrium tissue samples from women at term with spontaneous labor (n=27) and those at term without labor (n=30) using Affymetrix HG-U133 Plus 2.0 platform. In essence, this experiment studies the same medical condition as the second dataset (spontaneous labor at term) except that the investigated tissue is different (myometrium rather than cervix) and the numbers of samples are much larger for each class (27/30 rather than 9/7). The details of this study and its biological significance are not published yet. This dataset will be referred to as LaborM.

After proper preprocessing, including log₂ transformation and quantile normalization (Irizarry et al., 2003), microarray expression data from all three experiments were analyzed in the same way. Differential expression was inferred using a moderated t-test (Smyth, 2005) and aFDR adjustment of the resulting P-values. For the Colorectal cancer and Vessels datasets, genes were considered as DE provided they had a FDR corrected P<0.05. For the LaborC and LaborM datasets, genes were considered as DE provided they had a FDR corrected P-value less than 0.05 and 0.01, respectively, and their fold-change was greater than 2 and 1.5, respectively. The additional stringency used on the gene selection for these later two datasets was implemented in order to be consistent with the original analyzes of the authors.

The richness and suitability of this ensemble of four datasets can be discussed from three different perspectives. First, they were obtained using two different microarray platforms (Affymetrix and Illumina). Second, the distribution of log fold-changes for the DE genes has different properties among the datasets, since for the Colorectal cancer and Vessels data no threshold on fold-changes was used, as opposed to the other two datasets. Finally, for all datasets there are several biological clues about what pathways are expected to be involved. Also, since both LaborC and LaborM datasets studied the impact of spontaneous labor in two closely related uterine regions, a number of similarities can be expected between the pathways impacted in these two experiments.

The SPIA algorithm was compared with several existing pathway analysis methods including the classical over-representation analysis (ORA) using a hypergeometric model, and the gene set enrichment analysis (GSEA) (Subramanian et al., 2005). The comparison was based on statistical power (the ability to find significant pathways), specificity (the ability to limit the number of false positive pathways), as well as the ability to provide a meaningful ranking of the pathways analyzed.

A significance threshold of 5% was used on the FDR corrected P-values in order to infer pathway significance. For both SPIA and ORA the FDR adjusted P-values were computed from the nominal P-values using the R function ‘p.adjust’, while for GSEA, the FDR values (also called Q-values) are reported as provided by the R GSEA V 1.0. Only the top 15 pathways are given in tables for each analysis method, with pathway names being truncated to save space. The correspondence between the pathway IDs shown in these tables and the full KEGG pathway names can be found at ftp://ftp.genome.jp/pub/kegg/xml/organisms/hsa/index.html.

On the colorectal cancer dataset, the three pathway analysis methods were compared in terms of their ability to identify the colorectal cancer pathway, the PPAR signaling pathway (Shureiqi et al., 2003) and MAPK signaling pathway (Fang and Richardson, 2005) as relevant to colorectal cancer disease. Using a 5% cut-off of the FDR adjusted P-values, both ORA and SPIA identified the PPAR signaling pathway and MAPK signaling pathway as significant to the condition under the study (Tables 2 and 3). However, only SPIA identified the colorectal cancer pathway itself as significant (Table 2). This was possible due to additional evidence from perturbations (P_PERT=0.04 in Table 2). In addition, SPIA downgraded the Alzheimers disease pathway from second position in the top with ORA to the fourth position. This pathway is most likely not relevant to colorectal cancer, and it appears among the significant pathways for both ORA and SPIA because 14 genes of this pathway are DE, out of all 22 genes of this pathway that are represented on the reference array. On the other hand GSEA identified no significant pathway on this dataset (Tables 1 and 2 in Supplementary Material). Also, according to GSEA, the top ranked pathways for this dataset are the Huntington's disease and Parkinson's disease pathways, which are not likely to be relevant to colorectal cancer.

Table 2.

SPIA results on colorectal cancer dataset

KEGG pathway	PNDE	PPERT	PG	PFDRa	PFWERb	Status
Focal adhe..4510	0.0001	0.0000	0.0000	0.00000	0.00000	Act.
ECM-recept..4512	0.0001	0.0004	0.0000	0.00001	0.00002	Act.
PPAR signa..3320	0.0000	0.1240	0.0000	0.00011	0.00034	Inh.
Alzheimers..5010	0.0000	0.7260	0.0001	0.00059	0.00235	Act.
Adherens j..4520	0.0001	0.0852	0.0001	0.00090	0.00452	Act.
Axon guida..4360	0.0002	0.2324	0.0006	0.00487	0.02922	Act.
MAPK signa..4010	0.0001	0.7112	0.0007	0.00504	0.03527	Inh.
Tight junc..4530	0.0007	0.5156	0.0032	0.02073	0.16585	Act.
Colorectal..5210	0.0098	0.0432	0.0037	0.02151	0.19359	Act.
Wnt signal..4310	0.0187	0.0704	0.0101	0.05227	0.52268	Inh.
Renal cell..5211	0.0259	0.1048	0.0188	0.08869	0.97561	Inh.
Regulation..4810	0.0046	0.7328	0.0226	0.09797	1.00000	Act.
Thyroid ca..5216	0.0516	0.1032	0.0332	0.13284	1.00000	Inh.
Cytokine-c..4060	0.5049	0.0132	0.0401	0.14880	1.00000	Act.
Antigen pr..4612	0.9948	0.0080	0.0464	0.16094	1.00000	Act.

^abCalculated for P_G; Act., activated, Inh., inhibited. The last pathway considered significant is underlined (FDR<0.05).

Table 3.

ORA results on colorectal cancer dataset

KEGG pathway	PNDE	PFDRa	PFWERb
PPAR signa..3320	0.00000	0.00012	0.00017
Alzheimers..5010	0.00000	0.00012	0.00024
ECM-recept..4512	0.00006	0.00078	0.00308
Focal adhe..4510	0.00007	0.00078	0.00360
Adherens j..4520	0.00008	0.00078	0.00411
MAPK signa..4010	0.00009	0.00078	0.00465
Axon guida..4360	0.00022	0.00165	0.01156
Tight junc..4530	0.00069	0.00450	0.03599
Regulation..4810	0.00461	0.02665	0.23982
Colorectal..5210	0.00983	0.05113	0.51134
Wnt signal..4310	0.01871	0.08843	0.97275
Renal cell..5211	0.02591	0.10365	1.00000
Complement..4610	0.02591	0.10365	1.00000
Insulin si..4910	0.03546	0.13172	1.00000
Gap juncti..4540	0.04630	0.14911	1.00000

^abCalculated for P_NDE. The last pathway considered significant is underlined (FDR<0.05).

For the LaborC dataset, SPIA identified cytokine–cytokine receptor interaction, complement and coagulation cascades, focal adhesion and ECM-receptor interaction pathways as being the most significantly impacted pathways in this condition (Table 4). These pathways are also the top four found by ORA. SPIA clearly indicates that there are no other significant pathways beyond these top four (the next most significant P-value is 0.46 for the FWER correction). This difference of over two orders of magnitude is independent of the type of correction (no correction, FDR or FWER) and represents a clear demarcation, also independent of the choice of any of the usual significance threshold: 1% and 5%. In contrast, the classical ORA results place the pathways in a continuum of P-values in which the choice of the multiple correction method and that of the significance threshold can significantly change the results (Table 5). For instance, two additional pathway are reported as significant at the usual 5% significance on the FDR corrected values, while at the 10%, there are three such additional pathway. Unfortunately, the most ‘significant’ of these additional pathways is the Renal cell carcinoma pathway, which in fact is very unlikely to be truly relevant to pregnancy and labor.

Table 4.

SPIA results on the LaborC dataset

KEGG Pathway	PNDE	PPERT	PG	PFDRa	PFWERb	Status
Cytokine-c..4060	0.0000	0.0000	0.0000	0.0000	0.0000	Act.
ECM-recept..4512	0.0002	0.0008	0.0000	0.0001	0.0002	Act.
Complement..4610	0.0000	0.0652	0.0000	0.0003	0.0008	Inh.
Focal adhe..4510	0.0001	0.0384	0.0000	0.0004	0.0016	Act.
Renal cell..5211	0.0016	0.8032	0.0097	0.0804	0.4652	Act.
Jak-STAT s..4630	0.0028	0.4764	0.0100	0.0804	0.4823	Act.
Phosphatid..4070	0.0111	0.1968	0.0156	0.1067	0.7467	Act.
mTOR signa..4150	0.0238	0.2760	0.0396	0.2378	1.0000	Inh.
Regulation..4810	0.0198	0.5080	0.0563	0.2804	1.0000	Inh.
Type II di..4930	0.0533	0.2568	0.0724	0.2804	1.0000	Inh.
MAPK signa..4010	0.0211	0.6532	0.0729	0.2804	1.0000	Act.
Toll-like..4620	0.0282	0.5104	0.0754	0.2804	1.0000	Act.
Circadian..4710	0.1100	0.1320	0.0759	0.2804	1.0000	Inh.
Huntington..5040	0.1716	0.0996	0.0867	0.2971	1.0000	Inh.
Epithelial..5120	0.6281	0.0308	0.0957	0.3061	1.0000	Act.

^abCalculated for P_G; Act., activated, Inh., inhibited. The last pathway considered significant is underlined (FDR<0.05).

Table 5.

ORA results on the LaborC dataset

KEGG pathway	PNDE	PFDRa	PFWERb
Cytokine-c..4060	0.0000	0.0000	0.0000
Complement..4610	0.0000	0.0004	0.0008
Focal adhe..4510	0.0001	0.0010	0.0030
ECM-recept..4512	0.0002	0.0029	0.0117
Renal cell..5211	0.0016	0.0151	0.0755
Jak-STAT s..4630	0.0028	0.0221	0.1326
Phosphatid..4070	0.0111	0.0760	0.5323
Regulation..4810	0.0198	0.1127	0.9497
MAPK signa..4010	0.0211	0.1127	1.0000
mTOR signa..4150	0.0238	0.1144	1.0000
Toll-like..4620	0.0282	0.1230	1.0000
Type II di..4930	0.0533	0.2100	1.0000
Insulin si..4910	0.0569	0.2100	1.0000
Cell cycle..4110	0.0923	0.3117	1.0000
TGF-beta s..4350	0.0974	0.3117	1.0000

^abCalculated for P_NDE. The last pathway considered significant is underlined (FDR<0.05).

On the other hand, GSEA was unable to find any significant pathways in this condition (after either FDR or FWER) suggesting a more limited power (Tables 6 and 7). Furthermore, GSEA produces two tables, one for the term labor (TL), which is the normal condition in this case, and one for the non-labor at term (TNL). In general, it is unclear what the biological interpretation would be for something which is found to be significantly perturbed in the normal condition (this is not the case here because GSEA does not find any pathway to be significant in this condition).

Table 6.

GSEA results on the LaborC dataset, enrichement in TL group

KEGG pathway	NOM	FDR	FWER	FDR	Global
	P-value	Q-value	P-value	(median)	P-value
Cytokine-c..4060	0.0142	0.58128	0.341	0	0.263
Toll-like..4620	0.0513	0.51643	0.6175	0.38462	0.179
Jak-STAT s..4630	0.0515	0.60647	0.541	0.45455	0.2435
Complement..4610	0.0665	0.41882	0.646	0.3125	0.106
Adipocytok..4920	0.0858	0.33712	0.709	0.26316	0.0525
Type II di..4930	0.0926	0.32744	0.8105	0.25641	0.0425
ECM-recept..4512	0.1102	0.38869	0.6945	0.3	0.0775
Maturity o..4950	0.1407	0.38816	0.786	0.30612	0.063
Focal adhe..4510	0.1421	0.34761	0.7925	0.27778	0.05
Epithelial..5120	0.1626	0.32478	0.8405	0.26471	0.037
MAPK signa..4010	0.1814	0.43041	0.931	0.375	0.0615
Regulation..4810	0.1818	0.44217	0.96	0.38961	0.0515
Renal cell..5211	0.1998	0.41124	0.9385	0.35503	0.046
Type I dia..4940	0.2083	0.40331	0.912	0.34091	0.056
Colorectal..5210	0.3005	0.57367	0.9925	0.55556	0.082

Output from R GSEA V 1.0.

Table 7.

GSEA results on the LaborC dataset, enrichement in TNL group

KEGG pathway	NOM	FDR	FWER	FDR	Global
	P-value	Q-value	P-value	(median)	P-value
Notch sign..4330	0.0468	0.9707	0.5935	0.75	0.382
Tight junc..4530	0.1083	0.5329	0.8295	0.42568	0.1325
Ubiquitin..4120	0.1104	0.7213	0.707	0.55263	0.2715
Dentatorub..5050	0.1554	0.6512	0.805	0.51852	0.2185
Endometria..5213	0.1845	0.7443	0.9475	0.64615	0.26
Phosphatid..4070	0.1934	0.6644	0.971	0.6	0.195
GnRH signa..4912	0.1946	0.6939	0.9625	0.6087	0.221
Olfactory..4740	0.3213	0.5848	0.9725	0.525	0.1295
Hedgehog s..4340	0.3350	0.6803	0.9935	0.64412	0.164
Cell cycle..4110	0.3377	0.5825	0.9805	0.52859	0.1205
Amyotrophi..5030	0.3672	0.7403	0.993	0.7	0.223
Basal cell..5217	0.3685	0.6308	0.9935	0.60577	0.117
Thyroid ca..5216	0.4229	0.6429	0.9955	0.62821	0.1085
Gap juncti..4540	0.4621	0.6696	0.9985	0.66422	0.126
Melanogene..4916	0.5304	0.7081	1	0.7	0.132

Output from R GSEA V 1.0.

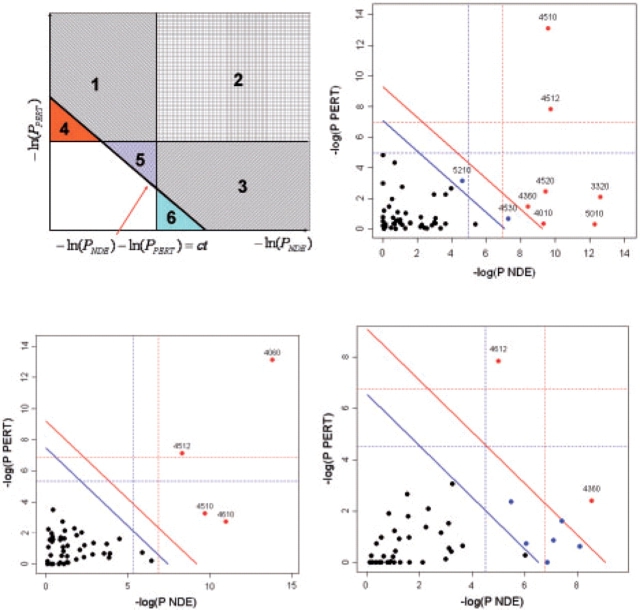
For the Vessels dataset, it can be argued (Kim et al., 2008) that the main difference between the umbilical veins and arteries is their pro-inflammatory behavior, therefore one of the most biologically meaningful pathways is the Antigen processing and presentation (pathway 4612 in Fig. 4, bottom right panel). Indeed, this pathway was identified by SPIA as the most significant (raw P<0.00005, P=0.0016 after either FWER or FDR, see Table 3 in Supplementary Materials). In contrast, the classical ORA ranks this pathway only on the 9th place, with a P-value that may or may not be significant depending on the type of correction and significance threshold (P=0.288 after FWER, P=0.0321 after FDR). With the most stringent correction (FWER) and significance threshold(0.01), SPIA identifies one additional pathway in this condition: Axon guidance. This is in agreement with the ORA which reports this pathway as the most significant in this condition. Both methods report this because 12 out of the 127 genes on this pathway are DE in this condition, which is about four times more than expected by chance. On this data, ORA identified nine significant pathways, SPIA identified eight, while GSEA none (Tables 3–6) in the Supplementary Material).

Fig. 4.

Two-dimensional plots illustrating the relationship between the two types of evidence considered by SPIA. The X-axis shows the over-representation evidence, while the Y-axis shows the perturbation evidence. In the top-left plot, areas 2, 3 and 6 together will include pathways that meet the over-representation criterion (P_NDE<α). Areas 1, 2 and 4 together will include pathways that meet the perturbation criterion (P_PERT<α). Areas 1, 2, 3 and 5 will include the pathways that meet the combined SPIA criteria (P_G<α). Note how SPIA results are different from a mere logical operation between the two criteria (OR would be areas 1, 2, 3, 4 and 6; AND would be area 2). Interestingly, SPIA removes those pathways that are supported by evidence of any one single type that is just above their corresponding thresholds but not supported by the other type of evidence (areas 4 and 6), but adds pathways that are just under the individual significance thresholds but supported by both types of evidence (area 5). The other plots show the pathway analysis results on the Colorectal cancer (top right), LaborC (bottom left) and Vessels (bottom right) datasets. Each pathway is represented by a point. Pathways above the oblique red line are significant at 5% after Bonferroni correction, while those above the oblique blue line are significant at 5% after FDR correction. The vertical and horizontal thresholds represent the same corrections for the two types of evidence considered individually. Note that for the Colorectal cancer dataset (top right), the colorectal cancer pathway (ID=5210) is only significant according to the combined evidence but not so according to any individual evidence P_NDE or P_PERT.

The LaborM dataset studied the same medical condition as the LaborC, except that the samples were collected from the myometrium, rather than cervix, both parts of the (same) uterus. It is therefore reasonable to expect that some of the pathways involved in LaborC and LaborM would be common. Both ORA and SPIA ranked the cytokine–cytokine receptor interaction as the most relevant pathway. The roles of cytokines in the human myometrium in labor have been previously assessed in several investigations, indicating their biological significance in human parturition (Breuiller-Fouche and Germain, 2006). Studies on uterine macrophages in the myometrium showed that the inflammatory cytokines, IL1β and TNFα, are important regulators of PGHS2 and IL8 (Tattersall et al., 2008). An increase in IL1, IL6, IL8 and TNFα within tissues of the laboring uterus and cervix is well known (Osman et al., 2003). Increased mRNA expression of CCL13, CCL19, CCL21, CXCR4 and CXCR5 in the myometrium has also been shown (Bethin et al., 2003; Breuiller-Fouche and Germain, 2006). The cytokine–cytokine receptor interaction pathway was also the most relevant in the LaborC dataset according with these two methods. In contrast, GSEA failed to identify this pathway as significant in either LaborM or LaborC sets (Tables 6 and 7; Supplementary Tables 9 and 10). This is disappointing in the light of the fact that each group had approximately 30 samples, therefore justifying the expectation of a reasonable statistical power. Furthermore, GSEA's rankings of this pathway were not consistent between these two related datasets. Combined with the low false positive rate verified on various null hypothesis simulations, the results on all three datasets suggest a higher statistical power for SPIA when compared with GSEA.

4 CONCLUSIONS

This study introduced the SPIA, which provides increased sensitivity when compared with GSEA, as well as improved specificity and better pathway ranking when compared with ORA. The SPIA algorithm was implemented as a standard R library available at http://vortex.cs.wayne.edu/ontoexpress/.

Funding

The Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH/DHHS (in part); NSF DBI 0234806, CCF 0438970, 1R01HG003491, 1U01CA117478, 1R21CA100740, 1R01 NS045207, 5R21EB000990, 2P30 CA022453 (to S.D.).

Conflict of Interest: none declared.