The PickPocket method for predicting binding specificities for receptors based on receptor pocket similarities: application to MHC-peptide binding

Abstract

Motivation: Receptor–ligand interactions play an important role in controlling many biological systems. One prominent example is the binding of peptides to the major histocompatibility complex (MHC) molecules controlling the onset of cellular immune responses. Thousands of MHC allelic versions exist, making determination of the binding specificity for each variant experimentally infeasible. Here, we present a method that can extrapolate from variants with known binding specificity to those where no experimental data are available.

Results: For each position in the peptide ligand, we extracted the polymorphic pocket residues in MHC molecules that are in close proximity to the peptide residue. For MHC molecules with known specificities, we established a library of pocket-residues and corresponding binding specificities. The binding specificity for a novel MHC molecule is calculated as the average of the specificities of MHC molecules in this library weighted by the similarity of their pocket-residues to the query. This PickPocket method is demonstrated to accurately predict MHC-peptide binding for a broad range of MHC alleles, including human and non-human species. In contrast to neural network-based pan-specific methods, PickPocket was shown to be robust both when data is scarce and when the similarity to MHC molecules with characterized binding specificity is low. A consensus method combining the PickPocket and NetMHCpan methods was shown to achieve superior predictive performance. This study demonstrates how integration of diverse algorithmic approaches can lead to improved prediction. The method may also be used for making ligand-binding predictions for other types of receptors where many variants exist.

Contact: mniel@cbs.dtu.dk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Binding of peptides to receptors plays an important role in many biological interactions. Examples include phosphorylation, recognition of phosphorylated sites by SH2 domains, immune recognition and peptide cleavage. A number of machine learning methods such as artificial neural networks and hidden Markov models have been proposed to predict the specificity of a receptor based on examples of peptide ligands (for review see, Lundegaard et al., 2007). These methods have the ability to interpolate between the training examples so that they can predict if a peptide is likely to be a ligand even if it does not have any obvious similarity to any peptide in the training set.

Some receptor families such as kinases and major histocompatibility complex (MHC) molecules are very large [more than 3000 different MHC molecules have for instance been identified (Robinson and Marsh, 2007)]. It is hence with current technology not feasible to generate enough experimental data for each of the family members and thereby obtain a description of the specificities for all of them. Recently a number of so-called pan-specific MHC binding prediction methods have been proposed that allow not only for interpolation between ligands but also between receptors (Jacob and Vert, 2008; Jojic et al., 2006; Nielsen et al., 2007; Zhang et al., 2005). These methods allow for prediction of the specificities for MHC molecules where no ligands are known. The NetMHCpan method by Nielsen et al. (2007) uses the sequence of the ligand as well as the sequence of the MHC binding cleft as input data to train a neural network ensemble, and this allows for predictions to be made for other MHC molecules than those the method was trained on. It has been experimentally validated that such methods allow for accurate prediction even for MHC molecules where no ligands have previously been described (Nielsen et al., 2007).

Similar approaches have earlier been used to develop the Tepitope method for prediction of binding of peptides to human class II (HLA) molecules (Sturniolo et al., 1999). Phage display techniques were used to elucidate the peptide binding specificity of different MHC class II molecules. The peptide binding groove of MHC molecules has a number of pockets. The amino acids lining each of the pockets mainly interact with one part of the peptide ligand. They therefore generalized their results to make binding predictions for MHC molecules for which they had no experimental knowledge by combining the specificities of other MHC molecules with identical pocket residues.

Generating accurate prediction methods for receptor–ligand interaction using higher order regression methods like artificial neural networks and hidden Markov models require large amount of data being available characterizing the specificity of each receptor (Yu et al., 2002). Likewise, pan-specific prediction approaches rely on sufficient data being available characterizing the close specificity neighborhood of a given receptor (Nielsen et al., 2007). These requirements for large amounts of data pose significant limits to the applicability of the pan-specific algorithms to a broad range of biological problems.

We have earlier shown that it is possible to derive position-specific scoring matrices (PSSMs) from very limited datasets, which accurately describe the MHC binding specificity (Lundegaard et al., 2004). Here, we propose a likewise simple method PickPocket, inspired by this work, Tepitope, and the pan-specific neural network methods. For each residue in a peptide ligand, we use information derived from similar protein structures to infer which residues in the MHC molecule it may interact with. These residues we denote as pocket residues. From a set of MHC molecules with known ligands, we derive a library of the specificity matrices (PSSMs). Each matrix in the library specifies the likelihood for that MHC molecule to bind the different amino acids on each peptide position in the ligand.

In order to construct a specificity scoring matrix for a given query MHC molecule (potentially with no known ligand data), we compare each pocket to the library of pockets from MHC molecules with known specificities. The simplest implementation assumes that the query molecule for each residue in the ligand will have the same specificity as that of the most similar pocket and we therefore pick the specificity of the closest pocket to represent the query. In more advanced implementations, we calculate the specificity as a weighted average based on pocket similarities of all specificities in the database. In both cases, the predicted specificities for each pocket are then combined to a specificity matrix for the query molecule. This matrix can then in turn be used to predict new ligands for the query MHC molecule.

We performed leave-one-out (LOO) experiments to assess the generalization ability of the PickPocket algorithm and investigated to what extent the PickPocket approach for small datasets, where the pan-specific neural network approach fails, could provide an accurate description of the binding specificity of uncharacterized MHC molecules. The PickPocket approach was compared with the performance of the NetMHCpan (Nielsen et al., 2007) method on an extended dataset covering binding data for both human and non-human MHC alleles. We analyzed how the predictive performance of the two methods depended on the similarity to and the number of ligand data available for MHC molecules with characterized binding specificity. Further, the method was compared with two other publicly available pan-specific MHC class I predictor; adaptive double threading (ADT) (Jojic et al., 2006) and Kernel-based Inter-allele peptide binding prediction SyStem (KISS) (Jacob and Vert, 2008).

2 METHODS

2.1 Datasets

Nonamer peptides associated with quantitative binding measurement were retrieved from the IEDB (Sette et al., 2005). Peptide binding was measured as IC50 values. We created three non-overlapping datasets.

EvaluationSet-1 contains a total of 29 336 peptide:HLA binding measurements, covering 35 alleles. The dataset was taken from Peters et al. (2006). EvaluationSet-2 contains 6553 data points covering 33 alleles and was used for evaluation. This dataset was taken from Zhang et al. (2008). EvaluationSet-3 contains data for 19 non-human MHC class I alleles covering primates (Mamu and Patr) as well as mouse and was downloaded from the IEDB (Sette et al., 2005). There is no overlap between the three datasets. Supplementary Table 1 gives a summary of the three datasets. All peptide IC50 values were log-transformed using the relation 1-log(IC50 nM)/log(50 000) to fall in the range between 0 and 1 as described by Nielsen et al. (2003).

2.2 Performance measures

All predictive performance values in the article were measured in terms of the Pearson correlation coefficient (PCC) unless otherwise stated.

2.3 Position-specific scoring matrices

We used the stabilized matrix method (SMM) algorithm to construct PSSM for each MHC molecule. The SMM method (Peters and Sette, 2005) is a matrix solution of a linear equation system that is solved by minimization of the sum of squared errors with a positive penalty to insignificant parameters. The penalty term balances accuracy and stability of parameters against perturbation. In this work, a local implementation of this method was used with a stabilizing penalty value of 0.01 and a combination of sparse and Blosum sequence encoding of the peptides (Nielsen et al., 2003).

2.4 Pseudo-sequences for MHC:peptide binding pockets

Many definitions of which residues in the MHC molecule makes contact to which residues in the peptide ligand exist, and the contact patterns may vary for different MHC molecules and different ligands. For simplicity, we assumed that the contact pattern is conserved for all MHC:peptide pairs and use the contact definition by Nielsen et al. (2007). This approach might not be optimal for each group of MHC specificities (Brusic et al., 2002), but will allow us to make predictions also for MHC molecules that are specificity-wise uncharacterized to us. This contact definition includes MHC residues that are polymorphic in one or more class I alleles and residing within 4.0 Å of the peptide in any of a representative set of HLA-A and -B structures with nonamer peptides. We define nine pockets each consisting of the MHC residues that are in proximity with one of the nine residues in a nonamer ligand, respectively. Note that this is not the standard definition of pockets in MHC molecules and that a residue in the MHC molecule in this definition can be part of more than one pocket. We refer to the MHC residues in contact with a given peptide position as the MHC pocket pseudo-sequence. The MHC pseudo-sequence is thus a sequentially ordered list of polymorphic MHC residues in contact with one or more peptide residues. A table showing the MHC pocket pseudo-sequence is given in Supplementary Table 2.

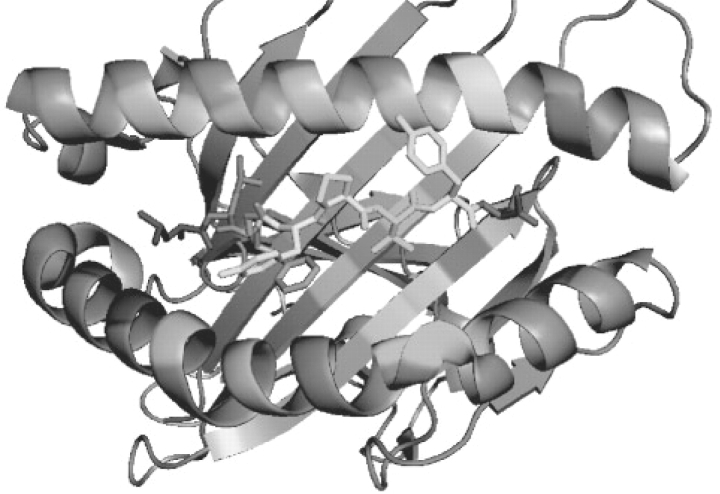
Figure 1 visualizes the pseudo-sequence on the MHC molecule. The residues on the MHC in contact with the peptide are highlighted. It is noted that not all MHC residues in proximity to the peptide are taken into the pocket pseudo-sequence. Those residues conserved across the HLA-A/B alleles are left out. Non-interacting or non-polymorphic residue are displayed in gray. MHC residues that interact with multiple peptide positions are colored in purple. Other contacting residues on the MHC are shown with a different color for each pocket, and the peptide is shown in the same color as the pocket it interacts with.

Fig. 1.

HLA molecule with bound peptide. HLA-A*0201 complexed with a nonameric peptide (LLFGYPVYV) (Khan et al., 2000). The peptide is shown with side-chains in colored sticks, the contacting residues on the MHC are displayed as colored regions, the pockets are distinguished by colors (purple for residues interacting with multiple peptide positions), the rest non-interacting or non-polymorphism residues are displayed in gray.

To formulate a binding specificity vector (i.e. a row in the PSSM scoring matrix) for a pocket in the query MHC molecule, we derived the pocket pseudo-sequence and then used a combination of the vectors representing the same peptide position in the pocket library to construct a virtual vector for the query pocket.

For a given query MHC molecule q, a binding specificity vector 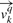can be defined for each of the k positions in a ligand. The 20 elements of 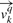corresponds to the binding propensity scores for each of the amino acids. 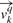is calculated as the weighted sum of the specificities in the pocket library

(1)

The weight w_i is related to the normalized similarity between the pseudo-sequences of the query s_q and target s_i pockets. This similarity is calculated as

(2)

where S(s_q,s_i) is the Blosum62 (Henikoff and Henikoff, 1992) similarity score between the two sequences s_q and s_i. The sequence similarity score is 1 for identical sequences, and can be negative for highly dissimilar sequences. If the similarity score is negative its value is set to zero.

The weight between query pocket with pseudo-sequence s_q, and a pocket in the library, with pseudo-sequence s_i is calculated as

(3)

where l denotes a sum over the entire pocket library. α is a positive parameter that determines the range of similarity scores that give high weights.

3 RESULTS

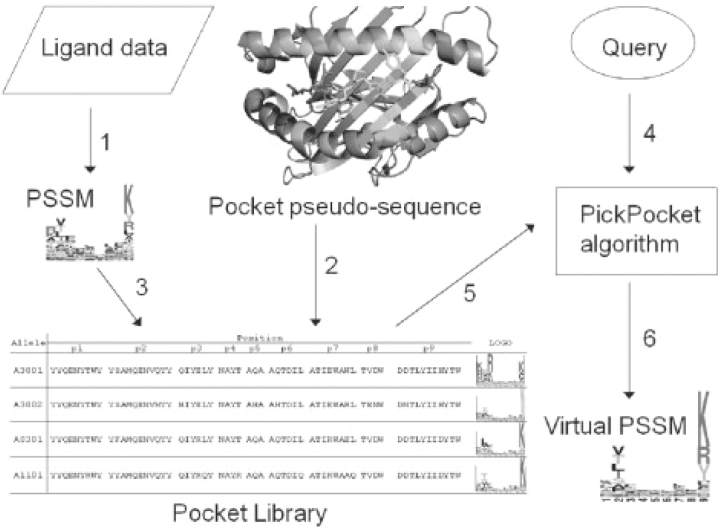
A schematic overview of the PickPocket strategy is shown in Figure 2. Basically the processes of the approach are organized into two parts: construction of a pocket specificity library and construction of the PSSM for the query allele. For each MHC molecule, which is characterized with peptide binding data, a PSSM is derived, and a pocket library is constructed linking these PSSMs to the pocket pseudo-sequences. Next, the ‘virtual’ PSSM for a query MHC is constructed as the average of all library pocket PSSMs weighted by the sequence similarity to the query.

Fig. 2.

Flowchart of PickPocket algorithm. (1) Construct PSSMs from ligands data. (2) Extract pseudo-sequences for the pockets based on the crystal structure of the MHC molecules. (3) Extract the position-specific vectors from the PSSMs in association with pseudo-sequence to construct a pocket library. Each pocket library entry is characterized by nine pairs, where each pair consists of a list of pocket amino acids and a specificity vector. (4 and 5) Input a query MHC, the algorithm retrieves the position-specific vectors and calculates mean vectors weighted by pseudo-sequence similarity. (6) The algorithm constructs a virtual PSSM for the allele in query. A full size version of this figure is available in Supplementary Material Figure S1.

3.1 Optimal weight function

We performed a LOO experiment to simulate the performance of the PickPocket method with uncharacterized MHC receptors. In the LOO experiment, all but one target alleles were included in the PSSM pocket library, which was then used to test against the excluded allele. By rotating the target across the 35 alleles in the EvaluationSet-1, we calculated the mean LOO performance. Two functions determining the virtual PSSM for the query allele were attempted. In the simplest implementation, the query receptor for each residue in the ligand was assumed to have the specificity of the most similar library pocket and we therefore picked the top one highest scoring library pocket according to Equation (2) to represent the query receptor. This approach had an averaged LOO performance value for the 35 alleles of 0.50. In the more advanced implementation, the specificity for the query was calculated as the weighted sum based on pocket similarities of all specificities in the database [see Equation (3)]. We performed a study on an independent dataset to determine the optimal value for the exponential damping factor α in Equation (3). This dataset consists of more than 8000 peptide:MHC pairs with IC50 binding values covering 28 HLA-A and -B alleles with no overlap to any other dataset included in the article. The LOO performance for this dataset reached at a peak when α was close to 10. This advanced weighting function increased the performance to 0.60. This difference between the two pocket assembly methods is statistically significant (P < 0.01, binomial test).

3.2 Construction of virtual vectors for a query allele

The top one approach did perform much poorer than the weighted sum approach for some particular alleles such as HLA-A*3001. Here, the top one approach achieved a performance of 0.25, whereas the weighted sum approach achieved a performance of 0.51. In the top one approach, the query specificity at the two primary anchor positions P2 and P9 is defined by the HLA-A*3002 allele. In spite of the large similarity in the pocket residues of these two HLA molecules [they share all but one amino acid in their P9 pseudo-sequences (Nielsen et al., 2007)], these two alleles have highly different C terminal binding specificities. The HLA-A*3001 has a preference for the basic amino acid K, and HLA-A*3002 has a preference for Y. This difference is not captured by the top one approach.

An example to illustrate the reconstruction procedure adopted in the PickPocket algorithm is shown in Figure 3, where a pocket library was constructed including all alleles in the EvaluationSet-1 except HLA-A*3001. The PickPocket procedure was next applied to construct the binding specificity of the HLA-A*3001 query allele based on similarity between the query and library pocket sequences using Equation (3).

Fig. 3.

PickPocket PSSM assembly for HLA-A*3001. Shown here are P9 pocket pseudo-sequences of HLA-A*3001, HLA-A*3002, HLA-A*0301 and HLA-A*1101, respectively. HLA-A*3002, HLA-A*0301 and HLA-A*1101 are the top ranking library alleles with similarity to HLA-A*3001 at the pocket. The variation of amino acids at the pocket is highlighted with underline. The binding specificity is represented with sequence logos (Schneider and Stephens, 1990) with vertical scale in 2 bits. The Sim score gives the amino acid similarity score as defined by Equation (3), and Weight gives the relative weight of library PSSM.

At position 9 the query pocket sequence is DDTLYIIHYTW for HLA-A*3001, and this sequence is compared with all library entries of position 9 pocket sequences. It is noted that although the pocket pseudo-sequence for HLA-A*3002 is ranking top most against HLA-A*3001 at position 9, and weights 23% of the synthesized vector, the next two pockets from HLA-A*0301 and HLA-A*1101, respectively, accounts for 15% each. After averaging by weight of similarity, the preferential list of amino acids is altered, and Lys (K) shows up as the most preferred amino acid in the constructed specificity vector in accordance with the known P9 binding preference of HLA-A*3001 (Lamberth et al., 2008; Sidney et al., 2008). By adapting the ensemble of multiple pockets, the PickPocket algorithm reduces the bias towards one specific neighborhood pocket and is thus capable of capturing subtle difference in binding specificity between neighboring alleles.

3.3 PickPocket is more robust when data are scarce

To investigate the robustness of the PickPocket method compared with that of the artificial neural network-based methods such as the NetMHCpan method, we constructed two sets of pocket libraries, using a reduced number of only 5 or 10 ligands, respectively, for each of the 35 alleles in the EvaluationSet-1. Likewise, we trained LOO versions of the NetMHCpan method using 5, or 10 ligands for each of the 35 alleles in the EvaluationSet-1. Since the performance of neural networks depends crucially on the presence of negative data, we added 100 randomly chosen natural peptides as negatives for each of the 35 alleles.

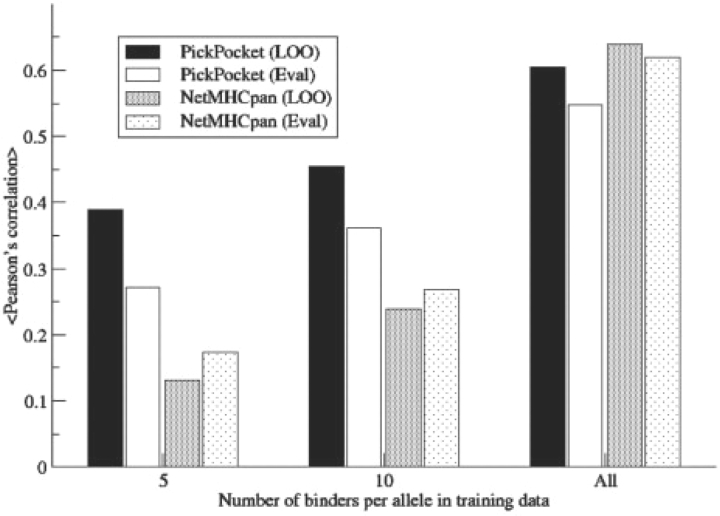
The reduced datasets were also used to construct virtual PSSMs for the alleles in the EvaluationSet-2. Here, a virtual PSSM was constructed for the target allele as weighted sum of all members (including the allele in question if present) in the library according to Equation (3). The NetMHCpan method was likewise trained on the reduced set of ligands including all allelic data. Figure 4 (LOO bars) shows that the PickPocket method significantly outperformed the neural network-based NetMHCpan when the methods were trained on small datasets (P < 0.01, binomial test). NetMHCpan only outperformed PickPocket if the methods were trained on the complete set of data in EvaluationSet-1. A similar pattern was seen when the methods were evaluated on the data in EvaluationSet-2 (Eval).

Fig. 4.

Comparison of the NetMHCpan and PickPocket performances as a function of the number of ligand training data. Prediction methods were trained with 5 ligands, 10 ligands and complete datasets for each allele, respectively. The LOO performance values are average values over the 35 alleles in the EvaluationSet-1, and the Eval performance values are average values over the 33 alleles from the EvaluationSet-2.

3.4 Comparison of performances of PickPocket, ADT, KISS and NetMHCpan methods

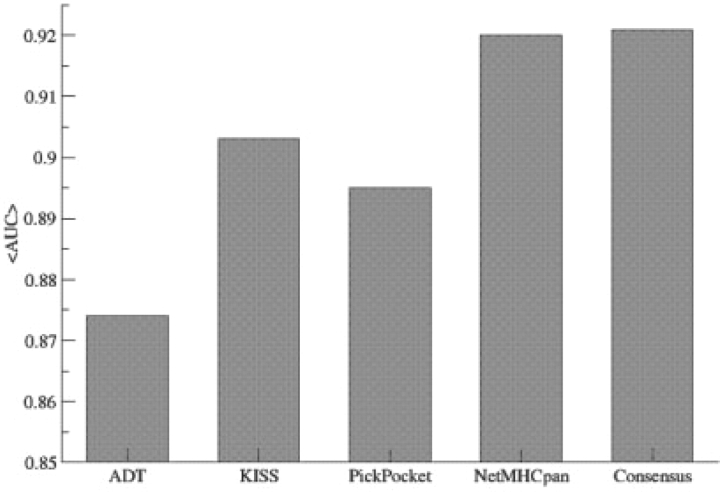
A 5-fold cross-validated training on the EvaluationSet-1 was conducted using the data partitioning of Peters et al. (2006), for the PickPocket, ADT (Jojic et al., 2006), KISS (Jacob and Vert, 2008) and NetMHCpan (Nielsen et al., 2007). The performance values for the ADT and KISS methods are taken from the paper by Jacob and Vert (2008) and are given in terms of the average area under the receiver operating characteristic (ROC) curve (AUC) using a classification threshold of 500 nM. Likewise we here give the performance of the PickPocket and NetMHCpan methods in terms of the average AUC values over the 35 alleles in the benchmark. We further include a Consensus method defined as the average of the output values from the PickPocket and NetMHCpan methods, respectively. The result of the 5-fold cross-validation benchmark is shown in Figure 5. The figure shows that the PickPocket method performs comparably with the other pan-specific prediction methods. It significantly outperforms the ADT method (P < 0.005, binomial test), and performs comparably with KISS (P=0.5, binomial test). NetMHCpan significantly outperforms the three other methods.

Fig. 5.

Average predictive performance values in terms of the AUC for the 35 alleles in the Peters et al. benchmark. ADT and KISS performances were taken from (Jacob and Vert, 2008).

Next, a LOO experiment was performed for the 35 alleles in the EvaluationSet-1 comparing the predictive performance of the PickPocket method to that of the NetMHCpan (Nielsen et al., 2007) method. In this comparison, both methods were trained and evaluated on identical datasets. The predictive performance for the PickPocket method on the data in the EvaluationSet-2 and EvaluationSet-3 was estimated using the complete library of the 35 alleles from EvaluationSet-1. For the EvaluationSet-2 a comparison to the pan-specific MHC class I binding prediction methods ADT (Jojic et al., 2006) and KISS (Jacob and Vert, 2008) is included. The ADT method was also trained on the EvaluationSet1 data, so the predictive performance should be directly comparable. The predictive performance values for the two latter methods were taken from (Zhang et al., 2008). Note, that all prediction methods were trained on human MHC binding data only.

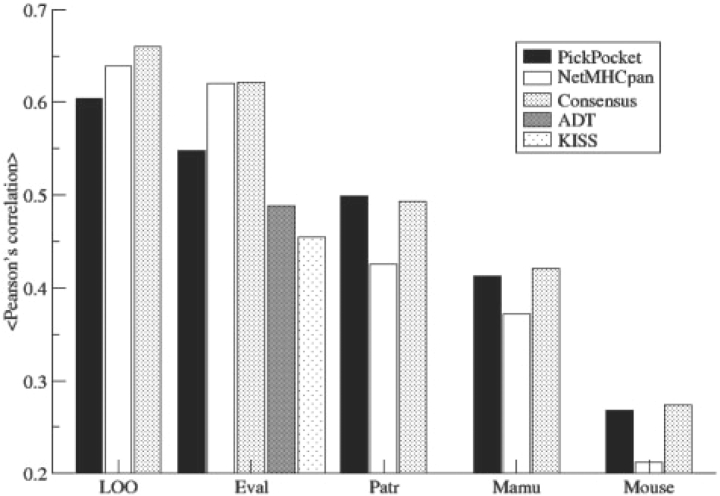
Figure 6 shows that the PickPocket and NetMHCpan methods perform better than the ADT and KISS methods when evaluated on the 33 alleles in the EvaluationSet-2. The NetMHCpan method outperforms the PickPocket method on human MHC data (LOO and Eval). The Consensus method achieved superior or comparable predictive performance to either of the two methods in all five experiments. Both the PickPocket and NetMHCpan methods show a significant though decreased predictive performance for non-human data. This decrease is most likely due to the weaker similarities between these MHC molecules represented by the pseudo-sequences and the MHC molecules forming the pocket library. However, it is striking to observe that the PickPocket method outperforms NetMHCpan on all three non-human datasets. The pan-specific method depends on learning the binding specificity by leveraging information from neighboring MHC molecules. In the PickPocket method, this leveraging is determined from amino acid similarities between the binding pocket amino acids as defined by the Blosum substitution scoring matrix. For the NetMHCpan method, this similarity measure between MHC molecules is inherent to the method, and is learned from the training data implicitly by the neural network. A very large fraction of the alleles in the training set has close distances to their nearest neighbors (Fig. 7). It is hence likely that the NetMHCpan similarity measure is biased towards learning these short distance similarities, and hence performs poorly for weaker similarities that are unknown to the methods. Details of the performance values for the non-human alleles are given in Supplementary Table 3.

Fig. 6.

Performance of PickPocket, NetMHCpan, Consensus, ADT and KISS methods on a large-scale benchmark experiment covering 35 human and 19 non-human primate and mice HLA class I alleles. LOO refers to the LOO experiment for the 35 alleles in the EvaluationSet-1. Eval refers to the 33 alleles in the EvalationSet-2. Patr, Mamu and mouse refer to the eight Chimpanzee (Patr), five Macaque (Manu) and six mouse alleles in the EvaluationSet-3. ADT and KISS performances were taken from (Zhang et al., 2008).

Fig. 7.

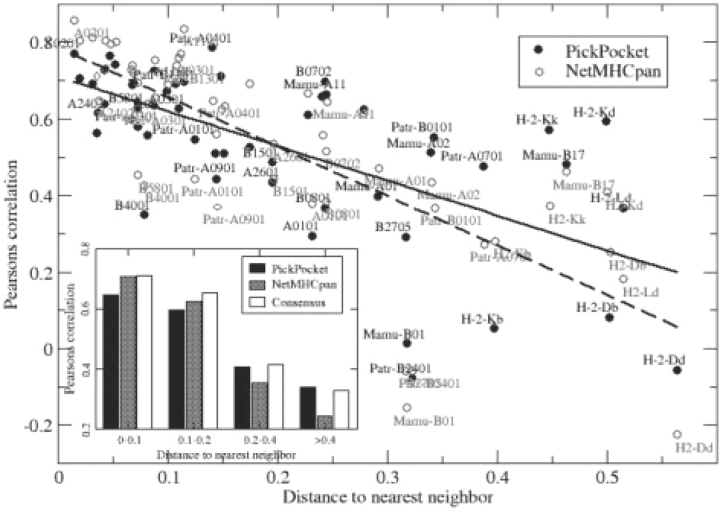
Performance versus the distance to the nearest neighbor of PickPocket and NetMHCpan methods, respectively. The distance to nearest neighbor is estimated from the MHC pseudo-sequence as described in Nielsen et al. (2007). For each HLA-A and HLA-B the predictive performance was calculated using the LOO setup, and for the non-human alleles the performance was estimated using method trained on HLA receptor data only. The solid line gives the least square fit for the PickPocket data, and the dotted line the least square fit for the NetMHCpan data. The insert to figure displays a binned histogram of the performance versus the distance to the nearest neighbor of PickPocket, NetMHCpan and Consensus methods. A full size version of this figure is available in Supplementary Material Figure S2.

The difference in predictive performance between the different methods can further be quantified by investigating how the predictive performance depends on the coverage of the neighborhood surrounding each MHC molecule. It is apparent that both the NetMHCpan and PickPocket methods depend crucially on the ability to leverage from specificities of neighboring MHC molecules. We have earlier demonstrated how the distance (as measured in terms of amino acid similarity between pseudo-sequences) to the nearest specificity-wise characterized MHC molecule relates directly to the predictive performance of the NetMHCpan method for uncharacterized MHC molecules (Nielsen et al., 2007). Figure 7 gives the results of a similar analysis carried out for the PickPocket and NetMHCpan methods, respectively, for the 54 alleles included in the benchmark. From the figure, the strong correlation between the distance to the nearest neighbor and the predictive performance of both the PickPocket and NetMHCpan method is apparent. For both methods, the figure confirms a decreased predictive performance as a function of the distance to the nearest neighbor. However, the decrease appears to be stronger for the NetMHCpan method. Comparing the average predictive performance for the two methods for the set of alleles with a nearest neighbor allele distance >0.2, we find that the PickPocket significantly outperforms the NetMHCpan method (P < 0.01, binomial test). In the insert to Figure 7 is shown the binned histogram of the performance of PickPocket, NetMHCpan and Consensus methods, respectively, versus the distance to the nearest neighbor. This figure demonstrates that the Consensus method achieves superior or comparable predictive performance to either of the two methods in all distance intervals.

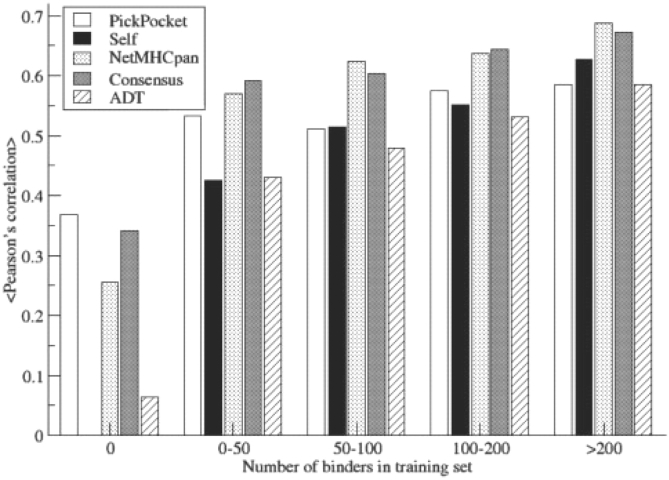
In general, the performance of MHC peptide binding prediction methods depend on sufficient numbers of binders being available characterizing the MHC molecule in question (Yu et al., 2002). In the extreme case where no binding data are available, conventional allele-specific prediction methods will fail to provide meaningful predictions. Pan-specific methods on the other hand can to a high degree also in such cases make accurate predictions (Hoof et al., 2008; Nielsen et al., 2007). Figure 8 illustrates how the performance of the allele-specific and pan-specific methods depends on the number of binding data being available for a given allele. Here, the predictive performance of an allele-specific method is compared with a series of pan-specific predictors as a function of the number of binding data for the particular allele. In this analysis, the Self-method was defined as the corresponding PSSM matrix from the pocket library. The figure shows that for alleles characterized with a large number of binding data (> 200), the allele-specific Self-method performs better than PickPocket. The Self-method on the other hand fails to make any meaningful predictions for the HLA-B*3901 allele, since the allele was not included in the training dataset. For this allele, the PickPocket method maintains a high performance of 0.37. The figure demonstrates that the PickPocket method for allele characterized with less than 50 binders outperforms the allele-specific Self-method. Moreover, the NetMHCpan method is shown to outperform both the PickPocket method for alleles characterized with 50 or more binders, thus confirming earlier finding that artificial neural networks are superior to matrix-based methods in characterizing MHC binding specificities where data are abundant (Peters et al., 2006; Yu et al., 2002).

Fig. 8.

Histogram of the average predictive performance as a function of the number of binding peptides in the training data for the same allele. Each method was trained on the dataset defined in Peters et al. (2006) and evaluated on the EvaluationSet-2 covering 33 human HLA class I alleles. Self: Self–SMM matrix from pocket library. ADT performance values were taken from Zhang et al. (2008). One allele HLA-B*3901 is characterized with zero binding data in the training dataset.

4 DISCUSSION

We have here presented a simple yet powerful method that is capable of generalizing from MHC molecules of known specificity to MHC molecules with unknown specificity. Recently, a number of pan-specific MHC:peptide binding predictive methods have been proposed (Jacob and Vert, 2008; Jojic et al., 2006; Nielsen et al., 2007; Zhang et al., 2005). These methods are all quite complex, making it hard to understand the mechanism behind their generalization abilities. Here, we demonstrate, through a powerful though simple and intuitive algorithm, how pan-specific prediction methods could work. This may help us interpreting the results and make it possible for us to fine-tune and improve the more advanced algorithms. In the context of MHC:peptide binding, we demonstrate that, similar binding pockets share similar binding specificities. From this observation, we are able to construct a library of pockets. In the application of the library, one first formulates the representative sequence of the pockets for the query allele, then searches the library for sequence-similar pockets, and finally reassembles the PSSM by merging the specificity vectors associated with the pockets.

It has earlier been demonstrated that PSSMs in contrast to artificial neural networks, can be constructed with high predictive performance even if they were trained on very limited data examples (Lundegaard et al., 2004; Yu et al., 2002). Here, this result is generalized to pan-specific receptor binding methods. Characterizing each receptor variant using PSSMs constructed from limited amount of ligand data allows for generalization to other receptor variants on which the method is not trained. The performance is demonstrated high in contrast to artificial neural network-based approaches trained on limited datasets. When the number of peptide binders per allele in the training set is 10 or less the accuracy of the neural network-based method NetMHCpan decreased markedly, whereas PickPocket still maintained considerable accuracy. This shows that the PickPocket algorithm, together with PSSM construction algorithms dealing with limited data amounts is especially useful in often encountered situations where there is not enough data available for conventional data-driven approaches to succeed. This is for instance the situation for most non-human species (chicken, cattle, pig, etc.) where very limited amount of peptide binding data exists to characterize the polymorphism of the MHC binding specificities.

To investigate the generalization ability of the PickPocket method, we further used the algorithm to infer the binding specificity for a large set of human and non-human alleles. In the benchmark, we compared the performance of the PickPocket method with that of NetMHCpan, and a consensus method defined in terms of a simple average of the log-transformed binding affinity output values from the PickPocket and NetMHCpan-1.0 methods, respectively. This benchmark demonstrated that the PickPocket method achieved significantly higher predictive performance values than NetMHCpan for alleles that were distant to any MHC molecule with characterized binding specificity. In particular, the benchmark with non-human alleles, demonstrated that the PickPocket method achieved a higher performance than a neural network-based method trained on the same data. Further, the Consensus method was shown to achieve superior or comparable predictive performance to either of the two methods for all datasets, independently on the distance to the nearest MHC molecule with characterized binding specificity. This places great promises to future applications integrating the two approaches to achieve higher predictive performance.

Even though we in this article have only used MHC receptors as examples, the method is general in its nature and may be used in many other contexts where large receptor families are found.

Funding: National Institutes of Health contracts (HHSN26620 0400025C, HHSN266200400083C and HHSN26620040006C).

Conflict of Interest: none declared.