Stimulus ensemble and cortical layer determine V1 spatial receptive fields

Abstract

The concept of receptive field is a linear, feed-forward view of visual signal processing. Frequently used models of V1 neurons, like the dynamic linear filter static nonlinearity Poisson spike encoder model, predict that receptive fields measured with different stimulus ensembles should be similar. Here, we tested this concept by comparing spatiotemporal maps of V1 neurons derived from two very different, but commonly used, stimulus ensembles: sparse noise and Hartley subspace stimuli. We found maps from the two methods agreed for neurons in input layer 4C but were very different for neurons in superficial layers of V1. Many layer 2/3 cells have receptive fields with multiple elongated subregions when mapped with Hartley stimuli, but their spatial maps collapse to only a single, less-elongated subregion when mapped with sparse noise. Moreover, for upper layer V1 neurons, the preferred orientation for Hartley maps is much closer to the preferred orientation measured with drifting gratings than is the orientation preference of sparse-noise maps. These results challenge the concept of a stimulus-invariant receptive field and imply that intracortical interactions shape fundamental properties of layer 2/3 neurons.

The primary visual cortex (V1) has been studied as a way of comprehending cortical function. One of the basic concepts in studying V1 has been the receptive field, the region of visual space from which a neuron's response can be modulated (1). There have been two opposing schools of thought about receptive fields: (i) they can be explained in terms of a model of visual cortical cells as a linear spatiotemporal filter, followed by a spike encoding mechanism, a so-called dynamic linear filter static nonlinearity Poisson spike encoder (LNP) model (reviewed in ref. 2); or (ii) the visual cortex is so nonlinear that one obtains different estimates when attempting to measure receptive fields with different stimuli (3, 4). Our results imply that both schools of thought may be correct in macaque primary visual cortex V1; view i applies to cells in layer 4C, the V1 layer that receives most thalamic input, whereas view ii applies to cells in V1's output layers (layers 2/3 and 5/6) that are heavily interconnected with other cortical neurons.

There is a large diversity of visual properties across cell layers in V1 (4–6), probably because of the variability of excitatory and inhibitory inputs to different V1 neurons (revealed by intracellular recordings; ref. 7) caused by specialized functional circuitry in different macaque V1 layers (8–11). Previously, we reported functional differences between V1 layers in temporal signal processing (12). Here, we present results about profound differences in the spatial processing of different stimulus ensembles across V1 layers.

Spatiotemporal maps have been used to compare visual neurons at different levels of the visual system (13) or V1 cells in different cell layers (12, 14) or to study cortical development (15) or V1 neurons in different species (16). One mapping approach was initiated by Jones and Palmer (17) (cf. refs. 14, 15, and 18), who used randomly positioned bright and dark spots and cross-correlation (reverse correlation; refs. 19 and 20) to map out the visual field regions that caused a cell to fire nerve impulses. The spatial maps that they obtained were consistent with the more qualitative maps obtained by Hubel and Wiesel (1). Other techniques have been developed for mapping, such as reverse correlation with spatiotemporal m-sequences (13, 21) and subspace reverse correlation with a particular set of sinusoidal grating patches termed “Hartley stimuli” (16, 22, 23). The Jones–Palmer method uses “sparse noise” that stimulates only a small fraction of the visual field at any moment in time, whereas the m-sequence and Hartley-subspace methods use “dense noise” that activates signals from many parts of the visual field simultaneously (21).

Frequently used models of V1 neurons, like the LNP model discussed by Carandini et al. (2), predict that spatial maps measured with sparse and dense noise should be the same. Our main experimental result is that spatiotemporal maps obtained from dense and sparse noise are similar for many layer 4C cells but differ qualitatively for layer 2/3 (and layer 5/6) cells. Therefore, the LNP model (2) cannot explain visual responses of neurons in layer 2/3 (and even some layer 4C neurons; see ref. 24). A more elaborate model, LNP with a contrast gain control (25, 26), also is not adequate. One must consider richer models for V1, for instance recurrent, dynamical, nonlinear neuronal networks. Some of these results were previously presented in abstract form (42).

Results

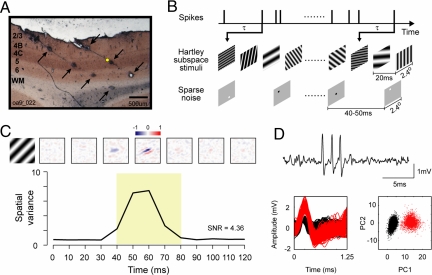
We used a matrix of multiple independently moveable electrodes to record simultaneously from several neurons in the primary visual cortex of adult macaque monkeys. Near the end of each experiment, electrodes were retracted along the electrode track, and 3–4 electrolytic lesions (600–900 μm apart) were made (Fig. 1A). Laminar information for each recording site was assigned through track reconstructions (5, 27, 28). At each recording site, receptive fields were mapped first with Hartley stimuli (22) and then with sparse noise (17). Spatiotemporal maps were estimated by reverse correlation (Fig. 1B; refs. 17, 19, 20, and 22) as R(x, y, τ) = 〈r(t) S(x, y, t − τ)〉, where x and y represent the spatial positions of pixels in the image, S(x, y, t) was the spatiotemporal stimulus, and r(t) was the neuron's spike train. A total of 205 well-isolated single units recorded from four macaque monkeys were included in this study. For each cell, we calculated the spatial map for a series of time delays (in 10-ms steps) between stimulus and response. The spatiotemporal map R(x, y, τ) for a layer 4C cell is shown in Fig. 1C. Typically, for 0 < τ < 30 ms the spatiotemporal map is noise, then the spatial map emerges at some time τ where 40 < τ < 100 ms. Fig. 1D Upper shows a short segment of raw data from the layer 4C example cell recorded from a single quartz platinum/tungsten microelectrode (Thomas Recording). The spike waveforms and principal components analysis (Fig. 1D Lower) indicate that the layer 4C example neuron was well isolated (see refs. 29–31).

Fig. 1.

Mapping with Hartley stimuli and sparse noise and histological labeling of cell layers in V1. (A) A 50-μm cytochrome oxidase-stained brain section with multiple lesions (indicated by arrows) made along 2 recording tracks with quartz platinum/tungsten microelectrodes. (B) The spatiotemporal receptive fields were mapped with Hartley subspace stimuli and sparse noise and calculated by reverse correlation at different time delays (τ). (C) The spatial maps (Upper) and spatial variances (Lower) as a function of time for an example layer 4C simple cell (the yellow dot in A represents the place where the cell was recorded). The spatial maps were normalized by the response at the time when the spatial variance reached the peak. On subregions are shown in red (positive values), and off subregions are in blue (negative values). (D) A short segment of raw data (Upper) for the example layer 4C cell. For spike sorting, we first included waveforms with peaks >0.5 mV and then aligned them at their peaks at 0.25 ms to perform a principal components analysis. (Lower Left) Subsamples of waveforms from a 360-s segment (red: sorted spikes; black: noise). (Lower Right) A scatter plot of the dot product of each waveform with the first and second principal components (PC1 and PC2) of an average waveform from the 360-s segment.

We quantified the time course of the response by estimating the map's spatial variance, σ_xy²(τ) = 〈[R(x, y, τ) − 〈R(x, y, τ)〉]²〉_x,y as a function of time offset τ (Fig. 1C and ref. 32). The time offset at which the spatial variance reached its peak was called the peak time, τ_peak, and used in subsequent data analysis. The signal/noise ratio (SNR) was defined as the ratio 〈σ_xy²(τ_peak)〉/σ_xy²(0) between the map's spatial variance averaged around the peak time, 〈σ_xy²(τ_peak)〉 (defined as the mean variance between τ_peak − 20 ms and τ_peak + 20 ms), and the spatial variance at time offset τ = 0, σ_xy²(0). 〈σ_xy²(τ_peak)〉 is the maximal spatial variance evoked by the stimulus, whereas σ_xy²(0) is response variance caused by noise in the neuron's activity. The criterion for a cell having a “mappable” Hartley receptive field was SNR ≥ 1.8 (n = 81/205).

The Hartley subspace map and the sparse-noise map were fitted with 2D Gabor functions (refs. 33 and 34; see SI Text) to extract neural response properties including the preferred-orientation axis and the number of subregions. We also measured for each cell the orientation tuning curve and the modulation ratio (the ratio between the first harmonic amplitude and the mean firing rate, f1/f0) with drifting sinusoidal grating stimuli, and sorted cells into simple (f1/f0 ≥ 1) and complex (f1/f0 < 1) groups (see Fig. S1) for comparison with previous work.

Laminar Differences in Spatiotemporal Maps: Examples.

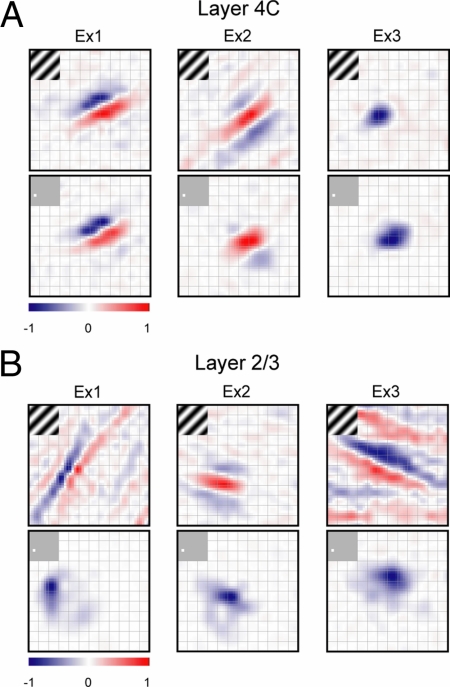
Receptive fields measured with different mapping techniques were highly similar for layer 4C cells but not for cells in other V1 layers (Fig. 2). Maps at the time of peak response (τ_peak) were chosen to compare results obtained with the two techniques. Fig. 2 shows typical examples of the receptive fields of three layer 4C and three layer 2/3 cells (Ex1 and Ex 2: simple; Ex3: complex, based on f1/f0 ratio). Spatial maps are represented as color maps in Fig. 2: on subregions are represented in red and off subregions are in blue.

Fig. 2.

Example spatial maps of V1 cells in layer 4C and layer 2/3. (A) Two simple cells and one complex cell in layer 4C. (B) Two simple cells and one complex cell in layer 2/3. For each example, the Hartley subspace maps are drawn at the top and the sparse-noise maps at the bottom. Spatial maps are shown as color maps (grid size: 0.2°) in which on subregions are represented in red and off subregions are in blue. The SNRs for these six cells from different layers are as follows. For layer 4C: Ex1, Hartley 11.65, sparse 11.34; Ex2, Hartley 4.43, sparse 7.16; Ex3, Hartley 2.14, sparse 2.15. For layer 2/3: Ex1, Hartley 3.47, sparse 10.61; Ex2, Hartley 5.40, sparse 5.81; Ex3, Hartley 2.53, sparse 5.83.

Similarity of Spatiotemporal Maps: Receptive-Field Similarity Index (RFS).

To analyze the entire population of V1 cells we calculated a RFS by computing the spatial correlation between the Hartley subspace map and the sparse-noise map (3, 4):

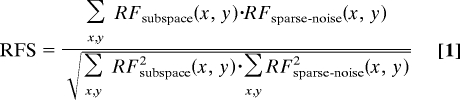RFS = 1 if the two maps are exactly identical, RFS = 0 if the two maps are orthogonal to each other, and RFS = −1 if one map is spatially the same shape but opposite polarity from the other. Note that we calculated the “maximum” spatial correlation between two maps over all x,y displacements to overcome the possible effect on the correlation coefficient of small displacements of the maps (possibly caused by eye movements; see SI Text and Fig. S2 for details; also see ref. 35).

To get an intuition for the RFS index, consider the examples in Fig. 2. The subspace and sparse-noise maps of the first layer 4C example (Fig. 2A Left) have the same number of segregated on and off subregions. In this case RFS = 0.91. The two maps for the second and third layer 4C examples (Fig. 2A Center and Right) are also very similar with RFS = 0.74 and 0.90, respectively. RFS is generally lower for upper layer cells. For the three layer 2/3 examples in Fig. 2B, the subspace maps resemble those of layer 4C in having multiple segregated and elongated on and off subregions, but the sparse-noise maps reveal only a single subregion. The mismatches of the two maps result in lower RFS values: 0.27, 0.34, and 0.38 for the three examples from layer 2/3 given in Fig. 2B.

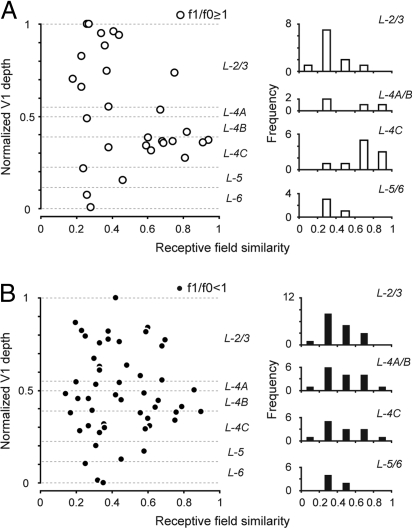
Studying the RFS indices for a population of 81 cells with significant subspace maps (SNR ≥1.8) reveals important functional differences between V1 layers (Fig. 3). Cells were classified as simple (n = 29) or complex (n = 52) based on their responses to drifting gratings (f1/f0 ratio). When only simple cells were considered (Fig. 3A), the average RFS, 〈RFS〉, of layer 4C simple cells (〈RFS〉 = 0.70 ± 0.17, n = 10) was approximately twice as big as the 〈RFS〉 of layer 2/3 simple cells (〈RFS〉 = 0.35 ± 0.16, n = 11, P = 0.0014, Wilcoxon rank sum test) and layer 5/6 simple cells (〈RFS〉 = 0.31 ± 0.10, n = 4, P = 0.007, Wilcoxon rank sum test). The frequency distributions of RFS also reveal interlaminar differences (Fig. 3A Right). Low RFS cells are uncommon in layer 4C, whereas a large fraction of such “mismatched” cells are found in layers 2/3 and 5/6. Note that the subspace maps of many simple cells in layers 2/3 and 5/6 also have multiple elongated and segregated on/off subregions (see Fig. S1).

Fig. 3.

RFSs between subspace and sparse-noise maps across V1. (A) RFS of 29 simple cells (f1/f0 ≥ 1) with significant subspace maps (n = 11 in layer 2/3, 4 in layer 4A/B, 10 in layer 4C, 4 in layer 5/6), plotted verses relative cortical depth. The similarity index is equal to 1 if the two receptive fields are identical (see Eq. 1). (Left) Similarity indices of cells in different layers of V1. (Right) Histograms of the similarity indices for simple cells assigned to different layers of V1. (B) RFSs for complex cells (f1/f0 < 1): individual data points (Left) and histograms (Right) versus depth in V1.

There is little interlaminar difference in 〈RFS〉 for mappable complex cells (Fig. 3B). In all layers the subspace and sparse-noise maps of mappable complex cells were different in shape; therefore, most complex cells had low RFS values. The 〈RFS〉 of layer 4C complex cells (〈RFS〉 = 0.50 ± 0.23, n = 13) was not significantly different from those of layer 2/3 cells (〈RFS〉 = 0.42 ± 0.16, n = 17, P = 0.44, Wilcoxon rank sum test) and from those of layer 5/6 cells (〈RFS〉 = 0.38 ± 0.10, n = 6, P = 0.25, Wilcoxon rank sum test). Also note that layer 4C simple cells had significantly higher 〈RFS〉 than layer 4C complex cells (P = 0.03, Wilcoxon rank sum test).

Laminar Differences in Spatiotemporal Maps: Preferred Orientations.

We also compared the axes of preferred orientations predicted from the best-fitting 2D Gabor functions for the two spatial maps. There were significant laminar differences in the agreement of predicted preferred orientations. For example, for the three 4C cell examples in Fig. 2A the differences in preferred orientation (Δθ) were 2.43°, 1.88°, and 4.48°. However, the three layer 2/3 cells used as examples in Fig. 2B had relatively large differences in preferred-orientation axis (Δθ = 47.44°, 20.15°, and 11.60°).

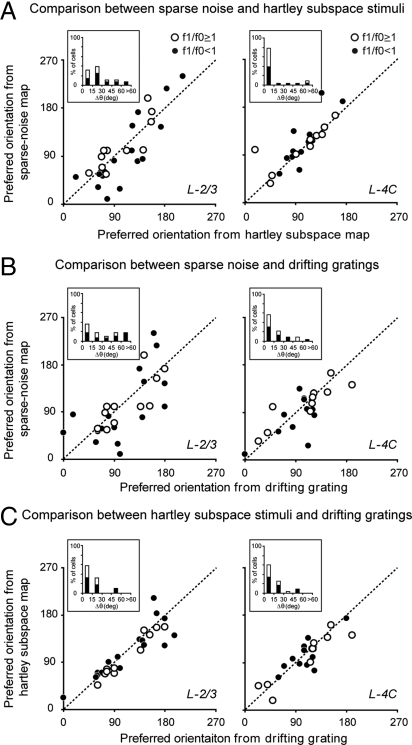
The population analysis of predicted preferred orientations bears out the results shown in the examples (Fig. 4). There was much less agreement in preferred-orientation axes predicted from the subspace and sparse-noise maps for cells in layer 2/3 (Fig. 4A Left) than for cells in layer 4C (Fig. 4A Right). The population-average difference between the two predicted axes was significantly larger for layer 2/3 cells than for layer 4C cells (layer 2/3: 〈Δθ〉 = 27.19° ± 18.50°; layer 4C: 〈Δθ〉 = 15.08° ± 22.26°, P = 0.0016, Wilcoxon rank sum test).

Fig. 4.

Comparisons of preferred-orientation axes predicted from two different maps and measured with drifting gratings. (A) Scatter plots of preferred-orientation axes predicted from the subspace map and the sparse-noise map for neurons in layer 2/3 (Left) and layer 4C (Right) of V1. (B) Scatter plots of preferred-orientation axes measured with drifting gratings and predicted from the sparse-noise map for layer 2/3 cells (Left) and layer 4C cells (Right). (C) Scatter plots of preferred-orientation axes measured with drifting gratings and predicted from the subspace map for layer 2/3 cells (Left) and layer 4C cells (Right). The unity line represents where the values from the two parameters are equal. (Insets) Shown are histograms of Δθ, the difference in preferred-orientation axis between the two parameters.

Which map's predicted orientation preference agrees better with the orientation preference measured directly with drifting gratings? Fig. 4 B and C answers this question. Fig. 4 B and C shows scatter plots of preferred-orientation axis measured with drifting gratings versus that predicted from the sparse-noise map (Fig. 4B) and the subspace map (Fig. 4C) for both layer 2/3 (Left) and layer 4C cells (Right). In layer 2/3, the orientation-preference mismatches from the sparse-noise map were significantly larger than those from the subspace map (sparse noise: 〈Δθ〉 = 34.20° ± 26.86°; subspace: 〈Δθ〉 = 16.03° ± 15.63°, P < 0.0001, Wilcoxon signed rank test). The mismatches were smaller and not significantly different in layer 4C (sparse noise: 〈Δθ〉 = 20.81° ± 19.84°; subspace: 〈Δθ〉 = 15.51° ± 13.20°, P = 0.10, Wilcoxon signed rank test).

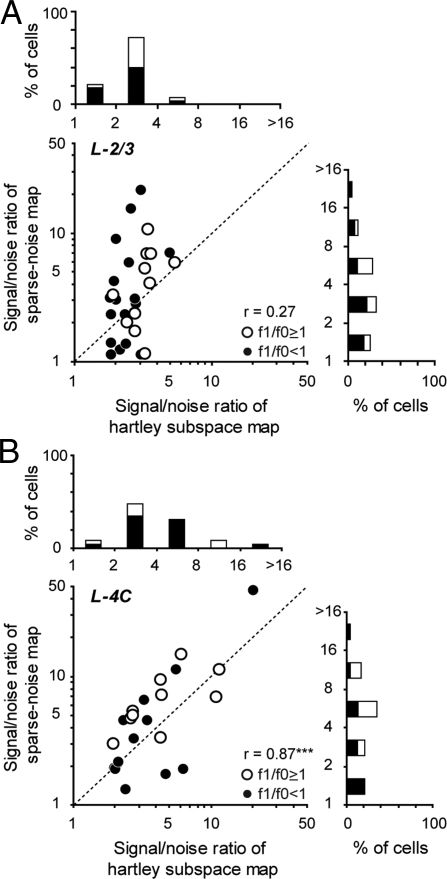
SNRs for Subspace vs. Sparse-Noise Maps: Correlations.

Further evidence for the mismatch of the subspace and the sparse-noise maps in layer 2/3 cells, and the similarity of the spatial maps in layer 4C cells, comes from the comparison of SNR: 〈σ_xy²(τ_peak)〉 /σ_xy²(0). Both kinds of mapping stimuli drove cortical cells very well. On average across the population of mappable cells, for sparse noise SNR = 4.49 ± 6.03, whereas for Hartley stimuli SNR = 3.66 ± 2.80. The SNRs for the two different mapping stimuli were highly correlated for layer 4C cells (Fig. 5B; r = 0.87, P < 0.0001) but not for layer 2/3 cells (Fig. 5A; r = 0.27, P = 0.16). Furthermore, the SNRs of individual neurons from the two stimuli are comparable in layer 4C (Hartley: 4.85 ± 4.29; sparse noise: 6.97 ± 9.29. P = 0.10, Wilcoxon signed rank test), but the sparse-noise SNR is slightly larger than the Hartley stimuli SNR in layer 2/3 (Hartley: 2.79 ± 0.90; sparse noise: 4.85 ± 4.29, P = 0.02, Wilcoxon signed rank test). Therefore, sparse noise can drive both layer 4C and layer 2/3 cells equally well (P = 0.26, Wilcoxon rank sum test).

Fig. 5.

SNRs for subspace maps and sparse-noise maps for layer 4C and layer 2/3 cells. SNR is a measurement of how strongly the mapping stimulus drives the neural response compared with the same neurons' intrinsic noise [defined as 〈σ_xy²(τ_peak)〉/σ_xy²(0)]. The SNRs of subspace and sparse-noise maps for layer 4C cells are highly correlated. However, there is no correlation for layer 2/3 cells. (A) A scatter plot of SNRs from subspace maps and sparse-noise maps for layer 2/3 cells. (B) A scatter plot for layer 4C cells reveals a much higher correlation between the SNRs.

Discussion

Subspace Stimuli and Sparse Noise Generate Different Maps in V1.

The RFS between the subspace maps and the sparse-noise maps was significantly lower for layer 2/3 simple cells than for layer 4C simple cells (Fig. 3A). Many layer 2/3 simple cells had maps consisting of multiple segregated and elongated on and off subregions when mapped with Hartley subspace stimuli, but only a single subregion when mapped with sparse noise (Fig. 2). Furthermore, for layer 2/3 neurons the Hartley subspace maps predict more accurately than the sparse-noise maps the preferred orientation measured with drifting gratings (Fig. 4 B and C; cf. ref. 36).

The mismatch in the spatial maps for neurons in the layer 2/3 of V1 might be because the two stimulus ensembles activate the cortical network differently. Sparse noise (17) consisted of randomly positioned dark and bright spots that appeared one at a time briefly in the visual field, and for most of the time the modulation of each pixel around the mean level was zero (meaning the pixel's luminance was equal to the background luminance). However, Hartley subspace stimuli (22) consisted of a series of sinusoidal gratings that covered a relatively larger region of visual space, and for most of the time the modulation of each pixel of the Hartley stimuli was nonzero (the pixel's luminance was either higher or lower than the background luminance). Therefore, it is possible that Hartley stimuli may activate more cortical neurons (both excitatory and inhibitory) at a given moment and may be more useful for characterizing the first-order spatiotemporal map in a network that has nonlinear spatial interactions (21) than sparse noise. However, the mismatch in layer 2/3 neurons is unlikely to be caused by a simple threshold nonlinearity because we found that sparse noise could drive both layer 4C and layer 2/3 neurons equally well. The SNRs of layer 4C and layer 2/3 neurons under sparse-noise mapping were not significantly different (Fig. 5), indicating that sparse noise could evoke strong suprathreshold responses and provide clear spatial maps for layer 2/3 neurons.

Our results support the idea that V1 cells, even simple cells (f1/f0 ≥ 1), can be highly nonlinear and therefore, as suggested previously, estimates of a neuron's spatial sensitivity may depend strongly on the visual stimuli used (3, 4). Victor et al. (4) used 2D Hermite functions to map V1 neurons and found 73% of them (n = 37/51) had RFS significantly deviated from 1 for visual responses maps from different Hermite basis functions. However, the RFS values we obtained in layer 2/3 neurons (mean = 0.39) were much lower than reported by Victor et al. (ref. 4; mean RFS = 0.76), indicating that the spatial maps obtained with dense and sparse noises were much more different in shape. Moreover, our results provide evidence that the percentage of neurons with unmatched spatial maps (RFS <0.5) depends on which V1 layer the cells are in; the fraction of neurons with unmatched maps was 30% for layer 4C cells (n = 7/23) but 79% for layer 2/3 (n = 22/28) and 90% for layer 5/6 cells (n = 9/10).

A previous study reported that 59% of V1 neurons (n = 26/44) in awake monkeys had different spatial response functions (RFS < 0.5) when mapped with subspace stimuli and natural scenes (3). David et al.'s proposal (3) was that natural scene statistics are so different from those of white-noise-like patterns, and the cortex is so nonlinear, that spatial maps measured with one stimulus set cannot predict what one will measure with the other. However, their results did not take into account the possibility that eye movements could have degraded their estimated RFS. As we show in Fig. S2, translations of spatial maps caused by eye movements can lower RFS significantly even in the anesthetized animal where we minimized eye movements with eye rings (see SI Text), and the effect of eye movements could be even bigger in awake animals (35). Published examples of maps measured with natural images appear similar to white-noise maps (figure 7 of ref. 3, figure 4 of ref. 37, and figure 1 of ref. 38). The very large dissimilarity in spatial maps measured with sparse and dense noise, in output layer neurons, appears to be larger than what one sees in the natural scene examples. It is worth reinvestigating what the actual differences are between spatial maps measured with natural scenes versus white noise and how they depend on laminar location.

Simple Receptive Fields Found Outside of Layer 4C.

One outstanding question regarding V1 organization is whether simple cells are found only in the geniculo-recipient layers of V1. The classic feed-forward model proposes that the receptive field of a simple cell consists of multiple segregated and elongated on and off subregions (1, 39). Studies that used either hand-mapping or reverse correlation with sparse noise reported that simple cells were found mostly or exclusively in the input layers of cat V1 (14, 40).

In this study, using drifting gratings and Hartley subspace mapping, we found a significant number of cells with a high modulation ratio (f1/f0 ≥ 1) for drifting gratings, with multiple segregated and parallel on/off subregions (Fig. 2 and Fig. S1) under Hartley mapping, outside of the input layer 4C (12). The apparent disagreement with earlier findings (14, 40) is likely caused by the discrepancies, in layer 2/3 and layer 5/6 neurons, between the responses to different stimulus ensembles (also see ref. 43). When only sparse noise is used, our results in monkey V1 agree with previous results in cat V1 (14, 40) that cells with multiple on/off subregions are predominantly found in the input layers. Simple cells in layer 4C and layer 2/3 are similar in being sensitive to the spatial phase of flashed stimuli (12), whereas complex cells in both input and output layers are insensitive to phase (but see ref. 41).

Implications for V1 Models.

Models of V1 neurons that are quasi-linear, like the LNP model (reviewed in ref. 2) predict that similar spatial maps should be measured by cross-correlation with sparse and dense noise (21, 22). Our present results indicate that such a model could approximate the responses of some V1 cells in layer 4C with high RFS values. However, for other 4C cells, and most cells outside of layer 4C, the spatiotemporal maps were very dissimilar depending on the visual stimulus ensemble used for mapping. Therefore, the neuronal network that drives most neurons in layer 2/3 and even some layer 4C cells is qualitatively different from the LNP model (2). A more elaborate model of V1 neuronal networks as LNP devices with contrast gain controls (25, 26) will not account for our results either, because in present-generation contrast gain control models the nonlinear feedback scales the contrast gain but has no effect on the spatial map. One must consider richer models for V1, for instance recurrent, dynamical, nonlinear neuronal networks in which excitatory and inhibitory feedback has a spatial structure that can modify the shape of a neuron's spatiotemporal map (3, 4).

Our results suggest that the classical concept of a receptive field (1) is of limited utility for most neurons in V1 especially the cells in the output layers that send signals to other areas of the brain, because the spatial map changes radically when different mapping stimuli are used (Figs. 2 and 3). The maps obtained with sparse noise stimuli are automated versions of the classical receptive field maps obtained with flashing spots, but these sparse-noise maps do not predict orientation preference accurately for most output layer neurons (Fig. 4). Therefore, V1 cortex can teach an important lesson about cortical function in general; intracortical interaction plays an important role in shaping response properties of neurons.

Materials and Methods

Methods are described briefly here and shown in detail in SI Text.

Surgery and Preparation.

Acute experiments were performed on four adult Old World monkeys (Macaca fascicularis). A small craniotomy was made in one hemisphere posterior to the lunate sulcus to provide access for the multielectrode matrix. The animal was maintained on opioid anesthetic (sufentanil citrate, 6–12 μg per kg·h⁻¹, i.v.) and paralyzed with pancuronium bromide (0.1 mg per kg·h⁻¹, i.v.). All vital signs were closely monitored and maintained throughout the experiment.

Receptive Field Mapping.

We used a matrix of seven independently moveable electrodes (Thomas Recording) to simultaneously record from multiple V1 neurons. Both Hartley subspace stimuli and sparse noise were used to map spatiotemporal receptive fields by reverse correlation (17, 22). The subspace stimuli were derived from a low-pass subset of the 2D Hartley functions that consisted of an orthogonal set of stationary sinusoidal gratings (2.4° × 2.4°) with evenly spaced orientations, spatial phases (n = 4) and spatial frequencies (0.6–8.0 cycles/° in visual angle). Each subspace image appeared for 20 ms, and the entire sequence lasted ≈15 min (a total of 1,052 images, each image presented ≈42 times). The sparse noise consisted of a sequence of randomly positioned (on a 12 × 12 sample grid) dark and bright squares (0.2° × 0.2°) against a gray background (luminance: 59 cd/m²). The luminances of bright and dark squares were adjusted so that contrasts from the light increment (luminance: 107 cd/m²) and light decrement (luminance: 11 cd/m²) were equal. Each sparse-noise image (a single dark or bright square) appeared for 40 or 50 ms, and the entire sequence lasted ≈14 or 18 min (a total of 288 images, each image presented 72 times).

Histology.

Cells were assigned to different layers of V1 based on the results of track reconstruction (27). Along each track, we recorded the depths of every recording site during the experiment, and then made 3–4 electrolytic lesions at 600- to 900-μm intervals at the end of the experiment. A lesion was made by passing a 3-μA direct current for 2 s through the quartz platinum/tungsten microelectrodes (Thomas Recording) with a stimulus generator (ALA Scientific Instruments; model number STG-1001).