Estimating the Single Nucleotide Polymorphism Genotype Misclassification From Routine Double Measurements in a Large Epidemiologic Sample

Abstract

Previously, estimation of genotype misclassification of single nucleotide polymorphisms (SNPs) as encountered in epidemiologic practice and involving thousands of subjects was lacking. The authors collected representative data on approximately 14,000 subjects from 8 studies and 646,558 genotypes assessed in 2005 by means of matrix-assisted laser desorption ionization time-of-flight mass spectrometry. Overall discordance among 57,805 double genotypes from routine quality control was 0.36%. Fitting different misclassification models by maximum likelihood assuming identical misclassification for all SNPs, the estimated misclassification probabilities ranged from 0.0000 to 0.0035. When applying the misclassification simulation and extrapolation (MC-SIMEX) method for the first time to genetic data to account for the misclassification in a reanalysis of adiponectin-encoding (APM1) gene SNP associations with plasma adiponectin in 1,770 subjects, the authors found no impact of this small error on association estimates but increased estimates for a more substantial error. This study is the first to provide large-scale epidemiologic data on SNP genotype misclassification. The estimated misclassification in this example was small and negligible for association estimates, which is reassuring and essential for detecting SNP associations. In situations with more substantial error, the presented approach using duplicate genotyping and the MC-SIMEX method is practical and helpful for quantifying the genotyping error and its impact.

Because high-throughput single nucleotide polymorphism (SNP) genotyping is technically feasible today and is readily applied in large epidemiologic studies with thousands of subjects, there is currently a focus in genetic epidemiology on the analysis of SNPs and their associations with diseases or disease markers. However, consistent replication of SNP association signals is a concern. One possible source of bias is error in the genotype (see the Appendix for a short introduction to genetic terminology).

The general effect of errors in predictor variables of regression models is to bias estimates and decrease power (1–4). While nondifferential misclassification in a dichotomous covariate usually induces a bias towards the null (5), the trichotomous covariate case is usually not as predictable (6). There have been numerous studies of the effect of genotyping error on linkage (7, 8), linkage disequilibrium (9), tagging SNPs (10), multiple dimension reduction methods (11), genotype and haplotype distribution (12–15), haplotype assignment (16), and family-based association (17–20). The investigations on how genotyping error affects population-based association have pertained mostly to case-control studies and have applied restricted association models like the chi-squared test or the Armitage trend test that do not allow for covariate adjustment (21–27). There have been few studies for logistic (28) or linear (29) regression models, which apply restricted error models.

The sources of genotyping error are manifold and have already received a great deal of attention (30). When the error cannot be estimated from pedigrees but needs to be derived for unrelated subjects, assumptions or validation/replication data are needed. The use of Hardy-Weinberg equilibrium (HWE) is much debated (31, 32). Validation data implying the availability of a gold standard would be ideal (33), and this approach has already been proposed (25), but it may not be advisable because of the lack of a perfect gold standard genotype and the potential for overcorrecting when a nonperfect standard is used (34). Use of replication from multiple genotype assessments (>2) has been illustrated with small-scale experimental (30) or simulation (28) data, but in practice duplicate genotyping is usually only available for 5–10% of the subjects from routine quality control. Previous attempts to estimate the error from duplicate genotypes involved a limited number of discordant genotype pairs such as 2 (27) or 30 (29) and a restricted error model. To our knowledge, estimation of genotyping error has never been based on routine data from a set of representative epidemiologic studies.

One reason for the lack of previous studies might be that the genotyping error was expected to be small. A situation that is the pride of the laboratory and the joy of the epidemiologist is a problem for the statistician, for a number of reasons: 1) a likelihood with the maximum close to 0 and steep in the vicinity of the maximum is a challenge for robust estimation; 2) huge genotype data sets are required in order to obtain sufficient numbers of discordant repetitions; and 3) the impact of such a small error on association estimates is expected to be negligible. So why bother? Well, the error cannot be deemed to be small in routine genetic epidemiologic association studies before the error has been estimated in such studies. It could well be that rather small experiments in which investigators know the purpose of error assessment contain completely different errors than large studies in which thousands of subjects are routinely genotyped. Methodological investigations of the impact of genotyping error have often assumed large error sizes of 1%–10%—an error size possibly stemming from former times, when sophisticated standard operating procedures or robotics were not available.

We aimed to gather a representative set of large epidemiologic studies with double SNP genotypes to provide an approach to estimation of genotype misclassification in these routine data, and to characterize the model and the size of the error as it can be expected in practice. It was a further objective to elucidate the impact of such misclassification on genetic association estimates in a real example by applying a practical method: the recently developed misclassification simulation and extrapolation (MC-SIMEX) approach (35), which has not yet been used for genetic data.

MATERIALS AND METHODS

Collecting double genotypes

We collected genotype information on all studies with at least 1,000 subjects and 5% double genotypes that had been assessed by laboratory personnel of the Genome Analysis Center of the Helmholtz Zentrum München by matrix-assisted laser desorption ionization time-of-flight mass spectrometry (MALDI-TOF MS) during 2004–2005. There were 2 possible sources of double genotypes: either the DNA of 1 subject was put on 2 positions of the same microtiter plate for routine quality control (routine doubles) or a microtiter plate was processed a second time because of an insufficient call rate in the first run (trouble-shooting doubles). The SNPs in our analysis had met laboratory quality-control requirements (sufficient call rate, polymorphic, and clear spectrometer signals), as they do to be cleared for association analysis. The final data set comprised 8 studies, including 5 distinct samples from the KORA (Kooperative Gesundheitsforschung in der Region Augsburg) studies (36), a Utah study (37), the SAPHIR Study (Salzburg Atherosclerosis Study to Identify Persons with High Individual Risk) (38), and the German part of the AIRGENE (Air Pollution and Inflammatory Response in Myocardial Infarction Survivors) Study (39). All of the studies included had been conducted according to the principles expressed in the Declaration of Helsinki. The investigators in these individual studies had either the written informed consent of all participants for genetic analyses or approval from their institutional review boards for genetic analyses.

Genotypes

For the kth SNP, k = 1, …, K, $X^{\left(k\right)}$ is a subject's true genotype, and $Z_1^{\left(k\right)}$ is the firstly and $Z_2^{\left(k\right)}$ the secondly (if available) observed genotype (omitting indices for the subjects). We denote true and error-prone genotype probabilities by ${\text{π}}^{\left(k\right)}=({\text{π}}_0^{\left(k\right)},{\text{π}}_1^{\left(k\right)},{\text{π}}_2^{\left(k\right)})$ with ${\text{π}}_i^{\left(k\right)}=\mathrm{Pr}ob(X^{\left(k\right)}=i)$ and $\text{π}{*}^{\left(k\right)}=(\text{π}{*}_0^{\left(k\right)},\text{π}{*}_1^{\left(k\right)},\text{π}{*}_2^{\left(k\right)})$ with ${\text{π}}_i^{*\left(k\right)}=\mathrm{Pr}ob(Z_1^{\left(k\right)}=i)$, respectively. For the latter, the observed genotype frequencies, $p{*}^{\left(k\right)}=(p{*}_0^{\left(k\right)},p{*}_1^{\left(k\right)},p{*}_2^{\left(k\right)})$, are a consistent maximum likelihood estimate based on the likelihood

Discordance matrix

For each SNP k, k = 1, …, K, we derived the number of concordant or discordant observed genotype pairs $R^{\left(k\right)}={\left(r_{ij}^{\left(k\right)}\right)}_{i,j=0,1,2}$ (discordance matrix) with $r_{ij}^{\left(k\right)}$ being the number of subjects with $Z_1^{\left(k\right)}=i$ and $Z_2^{\left(k\right)}=j$. Summing the $r_{ij}^{\left(k\right)}$ over i and j yields the total number of observed genotype pairs, for each k = 1, …, K, giving rise to the restriction ${\displaystyle {\sum }_{i,j}{r}_{ij}^{\left(k\right)}=N}$. Without ordering of measurements, the matrix is triangular (Table 1). The overall discordance was computed as the number of discordant pairs across all SNPs relative to the total number of genotype pairs. The SNP-wise discordance was computed accordingly per SNP.

Table 1.

Notation^a for a Triangular Discordance Matrix for the kth Single Nucleotide Polymorphism, k = 1, …, K

Z1(k)	Z2(k)
	0	1	2
0	r00(k)
1	r01(k)	r11(k)
2	r02(k)	r12(k)	r22(k)

^aGenotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

Misclassification matrix and the problem of identifiability

The misclassification problem can be represented by a 3 × 3 matrix for each SNP containing the misclassification probabilities, ${\text{π}}_{ij}\left(k\right)$, which are the probabilities of misclassifying a true genotype $X=j$ as $Z=i$, $i,j=0,1,2$, for SNP k, k = 1, …, K. Solving this problem in general requires more than 2 measurements, but repeated genotyping for routine quality control is not usually performed more than twice. Thus, statistical procedures requiring more than 2 measurements cannot be applied (28, 30). This leaves us with the problem of making this 3 × 3 misclassification problem identifiable with double measurements. “Not identifiable” means there are more parameters to estimate than information available: In the case of K SNPs, the presence of 9 parameters per SNP in the matrix minus 3 due to each column summing up to unity leaves 6K parameters to estimate. The observed number of subjects with genotype pairs i and j (i, j = 0, 1, 2, i < j), $r_{ij}^{\left(k\right)}$, and the restriction ${\displaystyle {\sum }_{i,j}{r}_{ij}^{\left(k\right)}=N}$ for each SNP k leave 5K independent observations.

We achieved identifiability by assuming the misclassification probabilities to be the same for all SNPs and thus to be independent of k. The general misclassification matrix

on the 3-level genotype (i.e., SNPs with nonmissing minor allele homozygote category) with the 3 constraints $1={\displaystyle {\sum }_{j=0,1,2}{\text{π}}_{ij}}$, $i=0,1,2$, thus involved 6 unknown parameters $({\text{π}}_{01},{\text{π}}_{02},{\text{π}}_{10},{\text{π}}_{12},{\text{π}}_{20},{\text{π}}_{21})$ (Table 2).

Table 2.

Notation^a for the General Misclassification Matrix (Unrestricted Model)^b

Observed Genotype Z	True Genotype X
	0	1	2
0	π00	π01	π02
1	π10	π11	π12
2	π20	π21	π22

^aGenotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

^bWith ${\text{π}}_{00}=1-{\text{π}}_{10}-{\text{π}}_{20}$, ${\text{π}}_{01}=1-{\text{π}}_{11}-{\text{π}}_{21}$, and ${\text{π}}_{02}=1-{\text{π}}_{12}-{\text{π}}_{22}$.

Error models

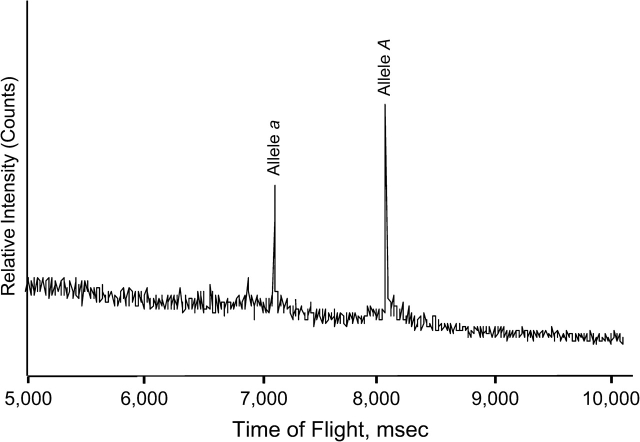
The automated high-throughput MALDI-TOF MS platform (Sequenom, San Diego, California) was used with an example genotyping signal (shown in Figure 1). One or 2 signals are detected when the amplitude exceeds a prespecified detection level for 2 equal (homozygous) alleles or 2 different (heterozygous) alleles. The unavoidable white noise gives rise to specific genotyping error models:

Model A: A true signal falls short of the detection level resulting in allelic dropout, which implies that 1) a heterozygous subject is more likely to be misclassified as homozygous (1 of the 2 signals vanished) than the other way around, 2) a subject homozygous for 1 allele is unlikely to be misclassified as homozygous for the other, and 3) a homozygous subject is more likely to be coded as missing than a heterozygous subject (18).

Model B: The “zero-corner model” (19) assumes 0 probability for a homozygous genotype's being misclassified as the other homozygous genotype (an extreme case of model A2 above).

Model C: The “symmetrical model” assumes no systematic ordering of the major and minor alleles in the assay. It implies that the probability of misclassifying a true homozygous genotype as heterozygous or of falsely classifying a heterozygous genotype as homozygous does not depend upon whether an allele is the minor or major allele of the homozygous genotype.

Model D: The “allele-independent model” assumes that the probability of misclassifying 1 allele for the other is the same as the other way around (9).

Figure 1.

Genotyping signal from the matrix-assisted laser desorption ionization time-of-flight mass spectrometry (MALDI-TOF MS) genotyping platform for 1 single nucleotide polymorphism (SNP) of 1 person. The x-axis displays the mass of the extension primer product and the y-axis the relative intensity of the product. Each of the 2 alleles refers to a product with a specific mass. Therefore, a signal is detected at either of these 2 positions on the x-axis (homozygous genotype of either of the alleles) or at both (heterozygous as shown in the figure). The other signals are white noise.

The other genotyping error models described in the literature are closely related to these 4, except for the “uniform error model” (8), which assumes equal misclassification probabilities and is mathematically appealing but rather unrealistic for this genotyping setting.

The 4 error models correspond to restrictions in the misclassification matrix:

1. The allelic dropout model: ${\text{π}}_{01}>{\text{π}}_{10}$ and ${\text{π}}_{21}>{\text{π}}_{12}$, still involving 6 parameters.

2. The zero-corner model: ${\text{π}}_{20}=0$ and ${\text{π}}_{02}=0$, reducing to 4 parameters.

3. The symmetrical model: ${\text{π}}_{10}={\text{π}}_{12}$, ${\text{π}}_{01}={\text{π}}_{21}$, and ${\text{π}}_{20}={\text{π}}_{02}$, reducing to 3 parameters.

4. The allele-independent model: Prob(allele A is misclassified into allele a) = Prob(allele a is misclassified into allele A) = :ε, reducing to 1 parameter (Table 3).

Table 3.

Misclassification Matrix for the Allele-Independent Model^ab

Observed Genotype Z	True Genotype X
	0	1	2
0	$1-2\text{ϵ}(1-\text{ϵ})-{\text{ϵ}}^2$	$\text{ϵ}(1-\text{ϵ})$	${\text{ϵ}}^2$
1	$2\text{ϵ}(1-\text{ϵ})$	$1-2\text{ϵ}(1-\text{ϵ})$	$2\text{ϵ}(1-\text{ϵ})$
2	${\text{ϵ}}^2$	$\text{ϵ}(1-\text{ϵ})$	$1-2\text{ϵ}(1-\text{ϵ})-{\text{ϵ}}^2$

^aGenotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

^bϵ = Prob(allele A is misclassified into allele a) = Prob(allele a is misclassified into allele A).

Estimating the misclassification matrix via maximum likelihood

The discordance probabilities, ${\text{δ}}_{ij}^{\left(k\right)}=\mathrm{Pr}ob(Z_1=i\wedge Z_2=j)$, $i,j=0,1,2$, $i<j$—that is, the probabilities of observing genotypes i and j for the 2 measurements for SNP k—relate to the misclassification probabilities ${\text{π}}_{ij}$ and the true genotype probabilities ${\text{π}}_i^{\left(k\right)}$ via

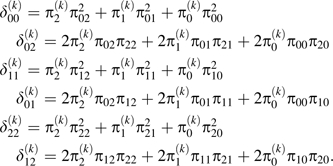(1)

When the true genotype frequencies ${\text{π}}^{\left(k\right)}$ are known, the likelihood for $R^{\left(k\right)}$ given ∏, $L_R\left(\text{∏}\right):=L\left(\text{∏}\right|{\left(R^{\left(k\right)}\right)}_{k=1,\mathrm{\dots },K})$, is

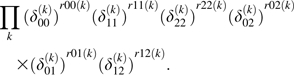(2)

The misclassification probabilities were estimated by maximizing this likelihood.

When the true genotype probabilities ${\text{π}}^{\left(k\right)}$ are unknown, either they can be estimated together with the misclassification probabilities (“extended likelihood”) or assumptions need to be made. Applying the latter approach, we assumed that 1) the observed genotype probabilities $\text{π}{*}^{\left(k\right)}$ reasonably approximated the truth (${\text{π}}^{\left(k\right)}\approx \text{π}{*}^{\left(k\right)}$) and 2) $\text{π}{*}^{\left(k\right)}$ was estimated by $p{*}^{\left(k\right)}$ with negligible sampling error. Therefore, we estimated the misclassification probabilities by maximizing $L_R\left(\text{Π}\right)$ with ${\text{π}}^{\left(k\right)}\approx p{*}^{\left(k\right)}$ (“small misclassification assumption”). Again based on this assumption, exact P values for HWE (see Appendix) were computed using $\text{π}{*}^{\left(k\right)}$.

Maximum likelihood estimates were computed by applying the Nelder-Mead simplex algorithm (Mathematica, version 5.0; Wolfram Research, Champaign, Illinois), and their variances were derived by means of the Fisher matrix. Genotype misclassification was estimated on the basis of error models A–D. Likelihood ratio tests were conducted to compare model fits.

In sensitivity analyses, we evaluated the robustness of error estimation upon violation of the assumption ${\text{π}}^{\left(k\right)}\approx p{*}^{\left(k\right)}$, upon exclusion of SNPs with HWE violation, or upon exclusion of SNPs with sparse data in 1 genotype category. Furthermore, we explored what our results would have looked like had we not opted for the small misclassification assumption but rather estimated the true genotype probabilities simultaneously with the misclassification probabilities (2K + 6 parameters to estimate) via the “extended likelihood” given by the product of equation 2 and

utilizing the relations $\text{π}{*}_0^{\left(k\right)}=1-\text{π}{*}_1^{\left(k\right)}-\text{π}{*}_2^{\left(k\right)}$, $\text{π}{*}_1^{\left(k\right)}={\text{π}}_2^{\left(k\right)}\times {\text{π}}_{12}+{\text{π}}_1^{\left(k\right)}\times {\text{π}}_{11}+{\text{π}}_0^{\left(k\right)}\times {\text{π}}_{10}$, and $\text{π}{*}_2^{\left(k\right)}={\text{π}}_2^{\left(k\right)}\times {\text{π}}_{22}+{\text{π}}_1^{\left(k\right)}\times {\text{π}}_{21}+{\text{π}}_0^{\left(k\right)}{\text{π}}_{20}$.

Method of correcting association analysis for genotype misclassification and real data example

To elucidate the impact of the SNP genotype misclassification on association analysis, we applied the MC-SIMEX method (see brief description in Appendix) in a real data example: We reanalyzed the association of 13 adiponectin-encoding (APM1) gene SNPs with adiponectin plasma levels in the SAPHIR Study (38), including 1,770 unrelated healthy subjects. For each SNP, we computed linear regression association estimates based on log(adiponectin + 1), adjusted for body mass index (weight (kg)/height (m)²), sex, and age, without and with application of the MC-SIMEX method (using the log-linear extrapolation function). We assumed a realistic scenario based on the general misclassification matrix as estimated and an extreme scenario created by multiplying the nondiagonal elements of this matrix by 10.

RESULTS

The analyzed sample

The data set contained 646,558 genotypes with 160,454 doubles involving 283 SNPs from over 10,000 subjects in 8 projects. Among these were 70,539 routine doubles. For 62,318 routine doubles, both genotype measurements were nonmissing; 57,805 of these corresponded to 225 “3-level” SNPs. Table 4 summarizes data on these samples.

Table 4.

Summary of Collected Data from 8 Projects and 646,558 Genotypes Assessed in 2005

	Project Identification No.								Total
	1	2	3	4	5	6	7	8
No. of subjects	1,080	930	1,830	2,489	1,628	1,776	2,907	1,400	14,040
No. of SNPs per subject	98–115	37–46	15–19	13–17	15	9–18	34–44	1–9	283
No. of genotypes	258,517	79,646	36,480	41,999	36,483	41,216	130,383	21,834	646,558
No. of measured person-SNPsa	114,464	37,695	33,590	40,085	24,426	25,794	112,003	10,917	398,974
No. of all doubles (% of person-SNPs)	90,162 (78.77)	17,732 (47.04)	2,787 (8.30)	1,914 (4.77)	5,696 (23.32)	14,260 (55.28)	16,986 (15.17)	10,917 (100)	160,454 (40.22)
No. of SNPs with routine doublesb	111	37	19	17	14	18	37	9	262
No. of routine doubles (% of person-SNPs)	33,262 (29.06)	4,347 (11.53)	2,787 (8.30)	1,914 (4.77)	2,960 (12.12)	590 (2.29)	13,762 (12.29)	10,917 (100)	70,539 (17.68)
No. of routine doubles (% of person-SNPs) without missing genotypes and with 3 genotype values present	26,832 (23.44)	3,199 (8.49)	2,664 (7.93)	1,188 (2.96)	1,980 (8.11)	241 (0.93)	11,957 (10.68)	9,744 (89.26)	57,805 (14.49)

Abbreviation: SNP, single nucleotide polymorphism.

^a“Person-SNPs” = product of the number of persons and the number of SNPs.

^b“Doubles” = double genotypes (i.e., pairs of 2 genotype measurements on the same subject and the same SNP).

Discordance

Table 5 shows the discordance matrix, including routine as well as trouble-shooting doubles, summarizing over all 283 SNPs. This matrix also highlights that the proportion of missing genotypes among the first measurements is 15.65% as opposed to 8.15% among the second, indicating an undesirable informative ordering of the measurements. Restricting the data set to the routine doubles, now including 262 SNPs, yielded symmetry (7.56% vs. 7.60%, respectively; Table 5), indicating that missingness was now independent of the measurement order.

Table 5.

Observed Genotype Doubles Including Missing Genotypes as a Separate Category^a

Z1(k)	Z2(k)				Total
	0	1	2	Missing Genotypes
Routine and Trouble-Shooting Genotype Doubles
0
No.	76,181	156	18	3,934	80,289
%	47.48	0.10	0.01	2.45	50.04
Row, %	94.88	0.19	0.02	4.90
Column, %	87.12	0.32	0.15	30.06
1
No.	80	41,774	43	1,989	43,886
%	0.05	26.03	0.03	1.24	27.35
Row, %	0.18	95.19	0.10	4.53
Column, %	0.09	86.63	0.37	15.20
2
No.	19	160	10,421	564	11,164
%	0.01	0.10	6.49	0.35	6.96
Row, %	0.17	1.43	93.34	5.05
Column, %	0.02	0.33	89.03	4.31
Missing genotypes
No.	11,162	6,132	1,223	6,598	25,115
%	6.96	3.82	0.76	4.11	15.65
Row, %	44.44	24.42	4.87	26.27
Column, %	12.77	12.72	10.45	50.42
Total
No.	87,442	48,222	11,705	13,085	160,454
%	54.50	30.05	7.29	8.15	100.00
Routine Genotype Doubles Only
0
No.	36,202	70	10	1,613	37,895
%	51.32	0.10	0.01	2.29	53.72
Row, %	95.53	0.18	0.03	4.26
Column, %	95.53	0.32	0.18	30.09
1
No.	55	20,746	30	952	21,783
%	0.08	29.41	0.04	1.35	30.88
Row, %	0.25	95.24	0.14	4.37
Column, %	0.15	95.19	0.55	17.76
2
No.	10	37	5,158	320	5,525
%	0.01	0.05	7.31	0.45	7.83
Row, %	0.18	0.67	93.36	5.79
Column, %	0.03	0.17	93.97	5.97
Missing genotypes
No.	1,628	941	291	2,476	5,336
%	2.31	1.33	0.41	3.51	7.56
Row, %	30.51	17.63	5.45	46.40
Column, %	4.30	4.32	5.30	46.19
Total
No.	37,895	21,794	5,489	5,361	70,539
%	53.72	30.90	7.78	7.60	100.00

^aGenotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

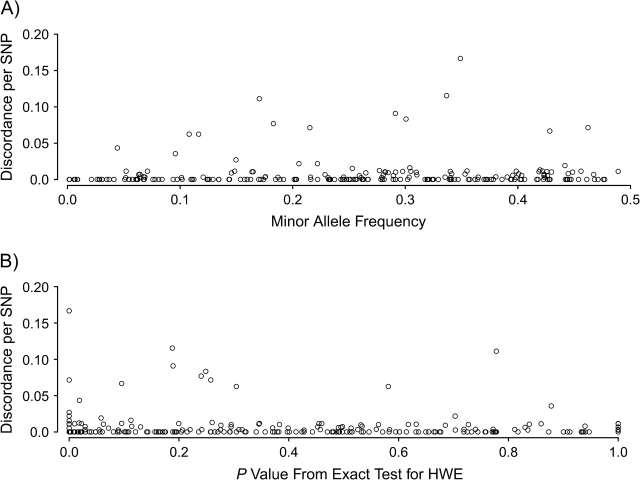
Our main analysis was based on the 225 3-level SNPs with 57,805 routine double genotypes, both nonmissing, which yielded 210 discordant pairs and thus an overall discordance of 0.36%. Table 6 depicts the discordance across all SNPs. The scatterplots of the SNP-wise discordance versus P values from testing for HWE violation (Figure 2, part A) or versus the minor allele frequency (Figure 2, part B) show that some of the larger discordances occurred together with smaller HWE P values, but not all HWE violations implicated large discordance (Spearman correlation coefficient (r) = −0.1362, P = 0.0313). There was no dependency of the discordance on the minor allele frequency (r = 0.0826, P = 0.1927).

Table 6.

Observed Triangular Discordance Matrix^ab

Z1(k)	Z2(k)
	0	1	2
0
No.	32,498
%	56.2201
1
No.	123	19,944
%	0.2128	34.5022
2
No.	20	67	5,153
%	0.0346	0.1159	8.9145

^aGenotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

^bRestricted to routine double genotypes with both measurements nonmissing and 3-level single nucleotide polymorphisms (225 single nucleotide polymorphisms, 57,805 double genotypes).

Figure 2.

Dependency of single nucleotide polymorphism (SNP)-wise observed discordance (proportion) of the 57,805 routine double genotypes with both measurements nonmissing in 225 3-level SNPs versus A) the minor allele frequency of each SNP and B) the P value from testing for violation of Hardy-Weinberg equilibrium (HWE) for each SNP.

Estimation of misclassification probabilities

Table 7 summarizes the misclassification matrices from maximizing the likelihood $L_{R,p*}\left(\text{∏}\right)$ (equation 2) for the various misclassification models. For the general model, the estimated misclassification probabilities ranged between 0.0001 and 0.0024, and for the allele-independent model, they ranged between 0.0000 and 0.0020; the other models yielded a similarly small dimension of the error.

Table 7.

Estimated Misclassification Matrix Under Various Misclassification Models^a

Observed Genotype Z	True Genotype X
	0		1		2
	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI
General misclassification model (6 parameters, unrestricted)
0	0.999505		0.002428	0.001690, 0.003165	0.001380	0.000431, 0.002330b
1	0.000391	0.000014, 0.0007678	0.996023		0.000229	−0.000450, 0.000907
2	0.000104	−0.000050, 0.000258	0.001549	0.001034, 0.002065	0.9983911
Assuming zero-corner model (4 parameters)
0	0.999880		0.003465	0.002720, 0.004210	0c
1	0.000120	−0.000179, 0.000419	0.995136		0.002979	0.001207, 0.004751c
2	0		0.001399	0.000880, 0.001917	0.997021
Assuming symmetric model (3 parameters)
0	0.998740		0.001436	0.000911, 0.001961	0.000264	0.000148, 0.000380c
1	0.000997	0.000257, 0.001736	0.997127		0.000996	0.000257, 0.001736
2	0.000264	0.000147, 0.000380	0.001436	0.000912, 0.001961	0.998740
Assuming allele-independent model (1 parameter); ϵ = 0.000997
0	0.998008		0.000996	0.000867, 0.001124c	0.0000009	0.0000007, 0.0000013c
1	0.001991	0.001734, 0.002249c	0.998009		0.001991	0.001734, 0.002249c
2	0.0000009	0.0000007, 0.0000013c	0.000996	0.000867, 0.001124c	0.998008

Abbreviation: CI, confidence interval.

^aGenotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

^bDoes not include 0; thus, the zero-corner model is not supported.

^cNo overlap with 95% CI of general model.

The estimated parameters and 95% confidence intervals indicated that the allelic dropout characteristics held (${\text{π}}_{10}^{}<{\text{π}}_{01}^{}$ and ${\text{π}}_{12}^{}<{\text{π}}_{21}^{}$); the symmetric model deviated the least from the general model, as the 95% confidence interval from only 1 misclassification probability was disjoint with the corresponding confidence intervals of the general model. This was supported not only by a comparison of the number of discordant genotype pairs observed with the number expected under the various models but also by the likelihood ratio test of model fit (Table 8), which yielded no formal rejection of the symmetrical model (though a “borderline” P value of 0.07), but for the “zero-corner” and “allele-independent” models (P < 10⁻³).

Table 8.

Results From Likelihood Ratio Testing for Goodness of Model Fit in a Comparison of the Restricted Models A–D (See Text) With the General Error Model, Showing the Number of Observed Genotype Pairs and the Number of Discordant Genotype Pairs As Expected Under the Various Error Models

Model	No. of Discordant Genotype Pairs (r02, r01, r12)a	No. of Parameters	Log-Likelihood	λ for Comparison with General Modelb	Degrees of Freedom	P Value
Observed	20, 123, 67
General model (model A)	21.5, 122.5, 64.4	6	−46,768.5
Zero-corner model (model B)	0.2, 146.3, 87.4	4	−46,834.1	131.2	2	<10−3
Symmetrical model (model C)	19.9, 122.1, 68.1	3	−46,772.1	7.2	3	0.07
Allele-independent model (model D)	0.1, 168.7, 61.0	1	−46,861	185	5	<10−3

^aNo. of parameters in restricted model; r₀₂, r₀₁, and r₁₂ refer to the notation in Table 1.

^bWith λ = −2 × (ln L_restricted − ln L_general) ∼ χ_df² (6 df).

Robustness of estimation

Firstly, we explored the impact of violation of the small misclassification assumption (i.e., deviation of ${\text{π}}^{\left(k\right)}$ from $p{*}^{\left(k\right)}$) on the misclassification probability estimates. We chose the deviation such that ${\left(p{*}^{\left(k\right)}\right)}_{1,\mathrm{\dots },225}$ would have been observed, given an allele-independent error with $\text{ε}=0.001$, to be in the ballpark of a realistic error. The new ${\text{π}}^{\left(k\right)}$ were derived from $\text{π}{*}_1^{\left(k\right)}=(1-4\text{ε}+4{\text{ε}}^2){\text{π}}_1^{\left(k\right)}+2\text{ε}-2{\text{ε}}^2$, $\text{π}{*}_2^{\left(k\right)}=(1-2\text{ε}){\text{π}}_2^{\left(k\right)}+(\text{ε}-2{\text{ε}}^2){\text{π}}_1^{\left(k\right)}+{\text{ε}}^2$, and $\text{π}{*}_0\left(k\right)=1-\text{π}{*}_1^{\left(k\right)}-\text{π}{*}_2^{\left(k\right)}$. The misclassification probabilities were again estimated, maximizing $L_R\left(\text{∏}\right)$ given the new ${\text{π}}^{\left(k\right)}$. For the general model, the estimated parameters $({\text{π}}_{01},{\text{π}}_{02},{\text{π}}_{10},{\text{π}}_{12},{\text{π}}_{20},{\text{π}}_{21})$ were similar ((0.0024, 0.0016, 0.0004, 0.0002, 0.0000, 0.0016) instead of (0.0024, 0.0014, 0.0004, 0.0002, 0.0001, 0.0015)); the ε parameter for the allele-independent model remained basically unchanged at 0.0010. Secondly, when we excluded the 29 SNPs with HWE violation (P’s < 0.05), the results did not change markedly. Neither did they change when we excluded SNPs for which fewer than 30 subjects were minor-allele homozygous (leaving 152 SNPs), with the general model parameters being estimated as (0.0018, 0.0013, 0.0009, 0.0002, 0.0002, 0.0018) and the ε estimate being 0.0012. Finally, when estimating true genotype probabilities together with the misclassification probabilities, we had to restrict the data to the 152 SNPs with enough observations in the third genotype category; this yielded (0.0020, 0.0011, 0.0008, 0.0061, 0.0002, 0.0000) and an ε estimate of 0.0012.

Impact of genotyping error in a real data example using the MC-SIMEX method

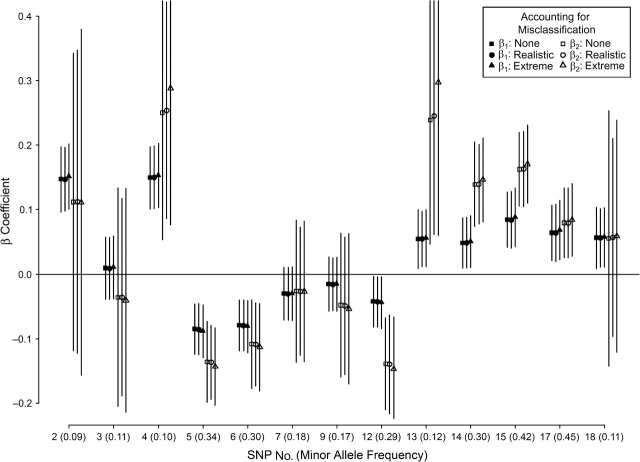
Figure 3 summarizes the uncorrected and MC-SIMEX-corrected β estimates in the example of the 13 3-level APM1 SNPs and their association with plasma adiponectin concentrations. A clear change of the β estimates of up to 15% when correcting for the misclassification was seen only under the extreme scenario for the 2 SNPs with already-high uncorrected estimates (SNP4 and SNP13).

Figure 3.

Impact of genotyping error on the association of 13 single nucleotide polymorphisms (SNPs) of the adiponectin-encoding (APM1) gene with plasma adiponectin in 1,770 subjects from the SAPHIR Study (Salzburg Atherosclerosis Study to Identify Persons with High Individual Risk). The figure shows β estimates computed by linear regression and adjusted for age, sex, and body mass index, 1) without accounting for misclassification (squares), 2) with correction for realistic misclassification (circles; general error model as shown in Table 7), and 3) with correction for extreme misclassification (triangles; using misclassification probabilities for the nondiagonal elements 10-fold as large as those for the realistic scenario). The β coefficients describe the unit increase in log(adiponectin + 1) comparing the heterozygous carriers (β₁) or the homozygous carriers of the minor allele (β₂) with the homozygous carriers of the major allele. The SNP numbering refers to the original publication (38). A clear increase in β coefficients is seen only for the extreme scenario and in cases where the uncorrected estimate was already high (SNP4 and SNP13). Vertical lines, 95% confidence interval.

DISCUSSION

In this study, we collected 646,558 SNP genotypes derived by MALDI-TOF MS from large epidemiologic studies including approximately 14,000 subjects altogether. On the basis of 57,805 double genotypes from routine quality control, estimated genotype misclassification probabilities were 0.001 and below. These data thus underscore the validity of SNP genotypes in situations comparable to that of our study. Note, however, that such a small genotyping error cannot be expected when quality control is relaxed, when the DNA quality is inferior, or when more error-prone genotyping technologies are applied. Furthermore, double genotyping by the same genotyping platform, using the same primer, DNA, and aliquot, does not enable one to grasp all possible sources of genotyping error or the potential mismatch of subject identifiers. Additionally, the error here does not reflect all of the genotypes produced in the laboratory, but rather reflects only the quality-controlled SNPs presented to the data analyst in routine practice. Thus, we can only make conclusions about some aspects of the genotyping error.

While our example of 13 APM1 gene SNPs (38), applying the MC-SIMEX correction method (35), pinpointed only marginal bias in association estimates induced by an error as estimated by our repeated genotype data, it was also illustrated that increased genotyping error would decrease association estimates and that the MC-SIMEX approach can effectively remove this bias. Because the MC-SIMEX method can handle a wide range of error and association models for this trichotomous variable situation also and because it allows adjustment for other covariates, it can be recommended for utilization in future genetic association studies, particularly for conditions that are problematic and when the error is nonnegligible. If it is not possible to conduct repeated genotyping which provides independent replications, re-genotyping by employing a “gold standard” method or formulating a mechanistically motivated error model are further options for obtaining error estimates. If none of these 3 options are possible, the sensitivity of association results to different error sizes can be explored (e.g., using the MC-SIMEX method). Note, however, that when replicate genotypes indicate an extremely low error, as observed in our data, methods such as MC-SIMEX are probably not needed.

It was a great challenge to us to collect a sufficiently large data set with routinely performed repeated genotyping to estimate the genotyping error in epidemiologic practice. The second challenge was to achieve identifiability of the 3 × 3 genotype misclassification problem with double observed genotypes. We did not want a method requiring more than 2 genotype repetitions, nor did we want to restrict the genotyping error model. The first type of method would have prevented our approach from being applicable to routine double genotype data; the second would have omitted the possibility of exploring the misclassification model fit. We thus assumed the same misclassification for all SNPs. Our data supported this assumption, since the discordance did not depend upon the minor allele frequency (see Figure 2, part B). This assumption is also practical when one is interested in the overall error across a full set of SNPs rather than the error of a specific SNP.

We were able to estimate the genotyping error under the most general error model, while the literature covers rather restricted models (Table 9). Note that estimation of all 6 parameters was not as robust as desirable, most likely because of the small error giving rise to only 210 discordant genotype pairs despite the large sample size. Nevertheless, the misclassification probability estimates remained very small throughout, and the fact that we observed discordant genotype pairs with both opposite homozygous genotypes argues against the “zero-corner model.” Our data suggested the allelic dropout model to be appropriate and the symmetrical model to fit reasonably well while being at the same time more parsimonious (involving 3 instead of 6 parameters), and provided evidence against further restrictions.

Table 9.

Overview of Genotype Misclassification Models and Estimated Single Nucleotide Polymorphism Genotyping Error Size in the Literature

Error Model	Description	Parameterization	Reference No(s).	Estimated Error Size
“General” (model A)	No restrictions	${\text{π}}_{ij}$ = Prob(observed genotype = i|true genotype = j), i, j = 0, 1, 2	12, 22, 41
“Allelic dropout”	1 allele signal vanishes beneath white noise, and thus Prob(hom→het)a < Prob(het→hom)	${\text{π}}_{01}>{\text{π}}_{10}$ and ${\text{π}}_{21}>{\text{π}}_{12}$	18, 19
“Zero-corner” (model B)	Hom majorb never misclassified as hom minor and vice versa	${\text{π}}_{20}=0$, ${\text{π}}_{02}=0$	19
“Symmetrical” (model C)	Misclassification does not differ for hom major or hom minor	${\text{π}}_{10}={\text{π}}_{12}$, ${\text{π}}_{01}={\text{π}}_{21}$, and ${\text{π}}_{20}={\text{π}}_{02}$
“Hom-het”	Zero-corner and symmetry as described above	Prob(hom→het) = :ν, Prob(het→hom) = :μ	20, 24, 31
“Directed error”	Error described per allele	Prob(A→a) = :μ, Prob(a→A) = :νc	9, 11, 12, 23, 24, 31, 42
“Allele-independent” (also “stochastic error”) (model D)	Error described per allele, assumed independent from allele	Prob(A→a) = Prob(a→A): = ϵ (see also Table 3)	9, 12, 13, 29, 41, 43, 44	ϵ = 0.0074 (29); 1 study with 1,027 persons genotyped twice (30 discordances)
	Special case of symmetrical model; related to zero-corner model; if e is small, then e2 is close to 0
“Uniform error”	Uniform misclassification probabilities	${\text{π}}_{ij}$ = ϵ for i ≠ j, i, j = 0, 1, 2	7, 8, 10, 18, 21, 22, 32	ϵ = 0.015 (27); 1 study with 1,473 persons genotyped twice (2 discordances)

^aProb(hom→het): transition probability for the true homozygous genotype (either minor or major allele) being misclassified as heterozygous; Prob(het→hom), vice versa.

^bHom minor or hom major: homozygous for the minor or major allele, respectively.

^cProb(A→a): transition probability for the true major allele A being misclassified as the minor allele a; Prob(a→A), vice versa.

It was a strength of our work that we were able to collect a large representative set of epidemiologic studies with double genotypes as would be encountered in practice. Our sample was not an experimental data set, and laboratory personnel were unaware of this project at the time of genotyping. We present an approach as it could be applied in practice: estimating genotyping error from routine double genotypes and a correction method applicable for linear and logistic regression, allowing for covariate adjustment, all genetic effects, and most misclassification models.

It must be considered a limitation that we used categorized genotypes instead of genotype probability scores, which are more sophisticated from a methodological perspective; however, routine association analyses currently use categories, and the epidemiologic practice was our focus here. Our conclusions cannot be transferred to differential error in case-control studies (40) or to more complex genetic variants such as microsatellite markers implying a higher-dimensional misclassification problem.

To our knowledge, this study is the first to provide epidemiologic data with which to estimate and characterize SNP genotype misclassification as it can be expected in practice. For the first time in the genetic context, we have applied the MC-SIMEX method and elucidated it as a method well-suited to account for misclassification in genetic association analysis.

We conclude that SNP genotyping error as presented in our example data—derived from a high-quality laboratory, with experienced personnel, using an established genotyping method, and with quality control before association analysis—is small and possibly negligible for many association studies. This is reassuring and is essential for detecting SNP associations in genetic epidemiology. In cases of very small genotyping error, as in our data, the particular choice of error model is not a concern, and a correction of association estimates applying methods like MC-SIMEX would not be needed. Situations may arise in which more substantial error is encountered. Then the implementation of an allele-independent error model might be appropriate for a first simplified approach, but extension to more complex models might be desirable. In addition, our approach to estimating genotype misclassification from double genotyping and accounting for this misclassification in the association analysis is useful and practical for quantifying the genotyping error and its impact.

Glossary

Abbreviations

HWE

Hardy-Weinberg equilibrium

MALDI-TOF MS

matrix-assisted laser desorption ionization time-of-flight mass spectrometry

MC-SIMEX

misclassification simulation and extrapolation

SNP

single nucleotide polymorphism

APPENDIX

A. Genetic terminology

A (human) single nucleotide polymorphism (SNP) is a position in the DNA where human beings exhibit variation in just 1 nucleotide as opposed to other polymorphisms involving a series of nucleotides. Usually, this SNP variation across subjects involves 2 different nucleotides out of the 4 possible (cytosine, thymine, adenine, guanine) for the 2 alleles that each subject possesses (1 inherited from the mother and 1 from the father). For example, 1 subject could have a cytosine (C) and a thymine (T) at 1 SNP position (subject with a heterozygous genotype); another subject could exhibit 2 C's and again another 2 T's (homozygous genotypes). If T is the nucleotide that is less often found in a population sample, T is considered the minor allele. Thus, a subject's SNP genotype can be coded as 0 (major-allele homozygous), 1 (heterozygous), or 2 (minor-allele homozygous).

Genotype frequencies are typically assumed to be in Hardy-Weinberg equilibrium based on the hypothesis that humans mate randomly and the genotype of the father does not depend upon the genotype of the mother. Hardy-Weinberg equilibrium is thus given when the probability of the heterozygous genotype equals the product of the probability of the 2 involved nucleotides. Violation of Hardy-Weinberg equilibrium is therefore considered a possible indication of genotyping error with allelic dropout.

B. Misclassification simulation and extrapolation approach

Use of the misclassification simulation and extrapolation (MC-SIMEX) approach to account for misclassification in association analysis involves a simulation and an extrapolation step: Starting from the naïve estimate _naive (i.e., the estimate that does not account for the misclassification) and assuming that this was derived with underlying misclassification ∏, data with higher levels of misclassification are simulated. From the estimates resulting from these simulated data, a function (linear, quadratic, or log-linear) is extrapolated back to the case of no misclassification, yielding the corrected estimator 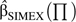_SIMEX(∏). This estimate has already been shown to be consistent, and variance estimates have been developed (35).