Life Course Path Analysis of Birth Weight, Childhood Growth, and Adult Systolic Blood Pressure

Abstract

The inverse associations between birth weight and later adverse health outcomes and the positive associations between adult body size and poor health imply that increases in relative body size between birth and adulthood may be undesirable. In this paper, the authors describe life course path analysis, a method that can be used to jointly estimate associations between body sizes at different time points and associations of body sizes throughout life with health outcomes. Additionally, this method makes it possible to assess both the direct effect and the indirect effect mediated through later body size, and thereby the total effect, of size and changes in size on later outcomes. Using data on childhood body size and adult systolic blood pressure from a sample of 1,284 Danish men born between 1936 and 1970, the authors compared results from path analysis with results from 3 standard regression methods. Path analysis produced easily interpretable results, and compared with standard regression methods it produced a noteworthy gain in statistical power. The effect of change in relative body size on adult blood pressure was more pronounced after age 11 years than in earlier childhood. These results suggest that increases in body size prior to age 11 years are less harmful to adult blood pressure than increases occurring after this age.

Ever since Barker (1) introduced his theory on fetal origins of adult disease, there has been a great amount of interest and controversy about early life factors and later health. Birth weight is associated with later conditions such as heart disease and stroke (2–7), but the magnitude and public health relevance of these associations are debatable. Recent meta-analyses (3, 8), however, have suggested that birth weight is relevant for later adverse outcomes such as higher systolic blood pressure (SBP) and heart disease.

It has been argued that associations between birth weight and later health outcomes are statistical artifacts caused by improper adjustment for adult body mass index (BMI; weight (kg)/height (m)²) (9, 10). Interpretations of results from these analyses are also controversial, as these models can be reparameterized in numerous ways (11–14). Interpretation of the birth weight parameter in a model also including adult BMI relates to the effect of birth weight given adult BMI—for example, comparing a small infant and a large infant who both have the same adult BMI. However, interpretation of the birth weight parameter in a model also including the change in relative size from birth to adulthood relates to the effect of birth weight for given growth—for example, comparing a small infant who has a low BMI in adulthood with a large infant who has a high BMI in adulthood.

If childhood body size is added to the analysis of birth weight and later outcomes, the difficulties in modeling and interpreting results increase. Analyses of childhood body size and adult SBP primarily have been conducted as multiple regression analyses with a number of measurements of size, relative size, or the change in relative size between 2 time points as independent variables (15–25). It is clear that childhood body size is associated with later disease (26), but does change in childhood body size matter, and if so, at what ages does the change matter the most?

Our aim in the present paper is to present a new statistical framework for analyzing and visualizing the impact of body size and change in size in early life on later outcomes based on path analysis techniques, and to compare the results from this framework with results obtained using 3 standard regression methods. We illustrate this by examining the association between childhood body size and adult SBP in a sample of Danish men.

MATERIALS AND METHODS

Sample and study design

Childhood data were obtained from the Copenhagen School Health Records Register (27), which contains data on birth weight and annual height and weight measurements for children who were born between 1930 and 1983 and attended school in Copenhagen, Denmark. These analyses included children aged 7–13 years who were born between 1936 and 1970. BMI was calculated from height and weight. We transformed birth weight and BMI data into age-specific z scores by subtracting age-specific means and dividing by age-specific standard deviations using reference values derived from the cohort (26).

Adult information was obtained via linkage with research data from the Copenhagen Centre for Prospective Population Studies (28–31) (Table 1). The included studies consisted of randomly selected age-stratified samples of subjects who lived in well-defined areas of Copenhagen and its suburbs. Phase 5 SBP was measured on the left upper arm with the subject in the sitting position after at least 5 minutes’ rest. BMI was calculated from measured height without shoes and weight in light clothes. To account for age and study effects on BMI and SBP, we transformed these values into age- and study-specific z scores. Repeated measurements of BMI and SBP were available for a subset of subjects who participated in 5- or 10-year follow-up examinations (Table 1).

Table 1.

Characteristics of Males in a Data Set Created by Linkage Between the Copenhagen School Health Records Register and the Copenhagen Centre for Prospective Population Studies, Denmark

Study (Ref. No.)	Years of First Investigation	No. of Subjects	Mean Age, years	Mean Birth Weight, kg	Mean 7-Year BMIa	Mean 13-Year BMI	Mean Adult BMI	Mean Systolic Blood Pressure, mm Hg
Copenhagen City Heart Study, examination 1 (28)b	1976–1978	376	33.6 (5.9)c	3.42 (0.58)	15.4 (1.3)	18.7 (2.4)	24.5 (3.8)	129.3 (13.0)
Copenhagen City Heart Study, examination 2 (28)d	1981–1983	103	33.5 (8.6)	3.42 (0.55)	15.5 (1.3)	19.0 (2.9)	25.1 (4.3)	135.7 (15.6)
Copenhagen City Heart Study, examination 3 (29)	1991–1994	238	40.2 (8.5)	3.45 (0.58)	15.3 (1.4)	18.6 (2.4)	25.3 (3.7)	132.4 (16.5)
Research Centre for Prevention and Health, 1936 birth cohort (30)b	1976–1977	92	40.4 (0.4)	3.52 (0.61)	15.3 (1.2)	18.9 (2.0)	25.1 (3.4)	131.2 (15.8)
Danish MONICA Study, phase I (31)b	1982–1984	237	36.8 (4.9)	3.42 (0.51)	15.6 (1.3)	19.0 (2.3)	24.5 (3.0)	121.4 (12.7)
Danish MONICA Study, phase II (31)	1986–1987	120	41.8 (7.3)	3.46 (0.58)	15.3 (1.2)	18.3 (2.1)	25.5 (3.4)	122.5 (14.7)
Danish MONICA Study, phase III (31)	1991–1992	118	43.2 (7.4)	3.50 (0.58)	15.5 (1.3)	19.1 (2.7)	26.1 (3.5)	122.2 (15.0)
Total		1,284	37.5 (7.5)	3.45 (0.57)	15.4 (1.3)	18.8 (2.4)	25.0 (3.6)	127.8 (15.2)

Abbreviations: BMI, body mass index; MONICA, Monitoring of Trends and Determinants in Cardiovascular Disease.

^aWeight (kg)/height (m)².

^bA subset of participants had height, weight, and blood pressure measured at a 5-year follow-up examination.

^cNumbers in parentheses, standard deviation.

^dA subset of participants had height, weight, and blood pressure measured at a 10-year follow-up examination.

Because birth weight has different associations with adult SBP in boys and girls (8, 32) and because growth trajectories also differ between the sexes, we chose to focus on boys in the present analyses. Data linkage revealed that information on birth weight, childhood and adult body size, and SBP was available for 1,284 males; they were included in this study.

Statistical analysis

Four different statistical approaches were used to analyze the childhood body size–SBP association: 1) simple linear regressions of SBP on body size, 2) multiple linear regressions of SBP on all or some of the body size measurements, 3) conditional multiple linear regression analyses regressing SBP on a body size measurement with adjustment for all past measurements of body size, and 4) path analysis.

Simple linear regression.

To assess the crude associations between body size and adult SBP, we performed simple linear regressions of SBP from the first investigation on birth weight, BMI at ages 7–13 years, and concurrent BMI, respectively.

Multiple linear regression.

SBP from the first investigation was regressed on birth weight, childhood body size at all ages, and adult BMI simultaneously. The estimates were graphed in a life course plot as suggested by Cole (18).

Conditional linear regression.

We performed a series of conditional regression analyses to obtain estimates conditioned only on past body size. SBP from the first investigation was regressed on body size at a given age, with adjustment for all previous measures of body size.

Path analysis.

The path analysis technique is an extension of regression analysis. It is a joint analysis of 1) the associations between body sizes at different time points and 2) the associations between all body sizes and adult SBP. In this analysis, there was simultaneous estimation of 9 regression equations (33, 34): 1 for each of the 7 measurements of childhood BMI, 1 for adult BMI, and 1 for SBP. In the a priori path analysis model based on a biologic conceptual framework, each measurement of body size depends on all previous measurements of body size, and SBP depends on all measurements of body size. A reduced model was specified by removing all nonsignificant associations from the a priori model. Following this, each association was individually returned to the model, and significance was assessed. The fit of the reduced model was assessed using a χ² test against the a priori model. The robustness of the model was tested by comparing the results with results from alternative models, and Akaike's Information Criterion (35) (see Appendix) was used to compare the fit of nonnested models.

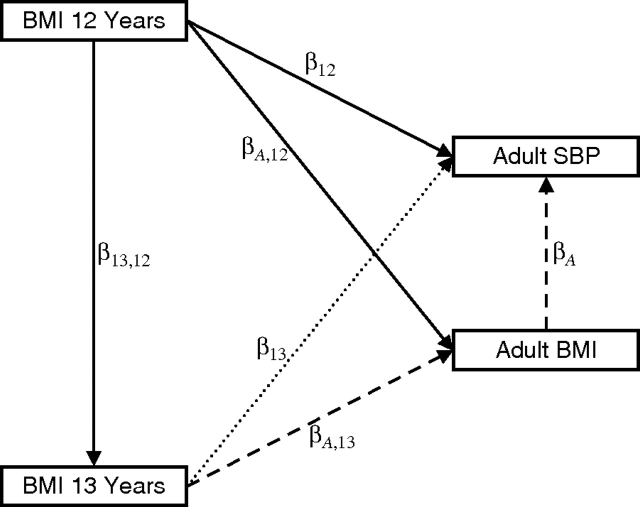
Unlike the situation in the first 3 regression models, with path analysis it is possible to assess direct and indirect effects of, and thus the total effect of, size and change in size in childhood on adult SBP. This is illustrated in Figure 1. The direct effect ${\text{β}}_{12}$ of BMI at age 12 years on adult SBP is the part of the effect that is not mediated through measurements of later BMI. The indirect effect of BMI at age 12 years on adult SBP can be calculated by adding the products of coefficients along all paths from BMI at age 12 years to adult SBP: ${\text{β}}_{A,12}{\text{β}}_A$ + ${\text{β}}_{13,12}{\text{β}}_{13}$ + ${\text{β}}_{13,12}{\text{β}}_{A,13}{\text{β}}_A$; this indirect effect is the part of the effect that is mediated through later measurements of BMI. The total effect is the sum of the direct and indirect effects.

Figure 1.

An example of a path diagram. The arrows represent regression coefficients; thus, adult systolic blood pressure (SBP) is regressed on body mass index (BMI) at ages 12 and 13 years and in adulthood (${\text{β}}_{12},{\text{β}}_{13}$, and ${\text{β}}_A$ being the regression coefficients). The direct effect of BMI at age 13 years on adult SBP ${\text{β}}_{13}$ (dotted line) is the part of the effect that is not mediated by adult BMI. The indirect effect of BMI at age 13 years on adult SBP (dashed line) is ${\text{β}}_{A,13}{\text{β}}_A$, and this indirect effect is the part of the effect that is mediated through adult BMI. (See text for an explanation of direct and indirect effects of BMI at age 12 years.)

To optimize the use of all available data, we expanded the path analysis model to incorporate 2 measurements of adult SBP and concurrent BMI, if available. The multiple measurements were modeled using latent variables (Appendix).

To illustrate the importance of movement in the BMI distribution at different ages, we plotted the total effects of change in body size on adult SBP, given past body size, in a graph that we term a path analysis life course plot.

Missing data is a common problem in data sets with longitudinal information on childhood body size. Data missing at random can easily be handled using path analysis (36), and this contrasts with the complete case analysis requiring missingness completely at random (37). Therefore, including the noncomplete cases is more powerful and less likely to produce biased results. To assess the impact of incorporation of noncomplete data and repeated SBP measurements on the estimates, we performed a path analysis modeling only SBP measured at the first investigation and using complete cases only.

Sensitivity analysis

To avoid the possibility that the timing of puberty influenced the analyses, we performed a path analysis excluding the measurements of BMI at ages 11–13 years, the ages at which the onset of the puberty growth spurt occurs (38). To investigate potential study heterogeneity, we performed path analyses on each individual study.

RESULTS

Simple linear regression

The estimated decrease in adult SBP for an increase in birth weight of 1 standard deviation was 0.066 standard deviations (Table 2), which corresponds to a decrease of approximately 1.8 mm Hg in a 50-year-old man per kilogram of birth weight. Unadjusted regressions of SBP on BMI at school age showed positive though nonsignificant associations (Table 2).

Table 2.

Estimates From Regression of Adult Systolic Blood Pressure z Score on Body Size^a z Score Among Males in a Data Set Created by Linkage Between the Copenhagen School Health Records Register and the Copenhagen Centre for Prospective Population Studies, Denmark

Age at Body Size Measurement, years	Univariate Regressionb		Multiple Regression
			Full Modelc		Reduced Modeld
		95% CI		95% CI		95% CI
0 (birth)	−0.066	−0.126, −0.005	−0.084	−0.177, 0.010	−0.068	−0.137, 0.001
7	0.026	−0.041, 0.093	0.012	−0.171, 0.195	−0.057	−0.154, 0.040
8	0.023	−0.042, 0.088	−0.014	−0.258, 0.229
9	0.022	−0.046, 0.089	0.043	−0.246, 0.331
10	0.021	−0.043, 0.085	−0.126	−0.409, 0.156
11	0.027	−0.039, 0.092	−0.046	−0.338, 0.247
12	0.033	−0.030, 0.096	0.123	−0.171, 0.416
13	0.049	−0.016, 0.113	−0.161	−0.422, 0.099	−0.113	−0.216, −0.009
≥20 (adulthood)	0.259	0.206, 0.312	0.316	0.221, 0.410	0.329	0.255, 0.403

Abbreviation: CI, confidence interval.

^a Birth weight z score or body mass index z score.

^b Estimates from unadjusted regression of adult systolic blood pressure z score on each of the measurements of body size z score.

^c Estimates from a multiple regression of adult systolic blood pressure z score on all measurements of body size z score.

^d Estimates from a multiple regression of adult systolic blood pressure z score on a priori chosen measurements of body size z score.

Multiple linear regression

In the multiple regression of SBP on all body size measurements, all body size measurements except adult BMI were nonsignificant (Table 2). These estimates were graphed in a life course plot (Figure 2). A clear picture of the association between childhood body size and SBP did not emerge because of the inconsistent estimates and the width of the confidence intervals. The inconsistencies suggested that there was a collinearity problem in which high correlation among the body size measurements, because of their close spacing, made the model unable to reliably estimate their individual effects. To reduce the collinearity problem, we performed an alternative multiple regression analysis by regressing SBP on birth weight, BMI at ages 7 and 13 years, and concurrent BMI. The modified life course plot showed a positive association between BMI z score change from age 13 years to adulthood and adult SBP (Figure 2). Parameter estimates from this model are interpreted as the effect of body size at a particular age given past and future size. For example, these estimates compare 2 children, 1 of whom has a 1-standard-deviation higher body size at a given age but the same size at all other measurements. In other words, we are comparing a child who increased in BMI before a measurement at a given age and then decreased before the next measurement with a child who remained BMI-stable.

Figure 2.

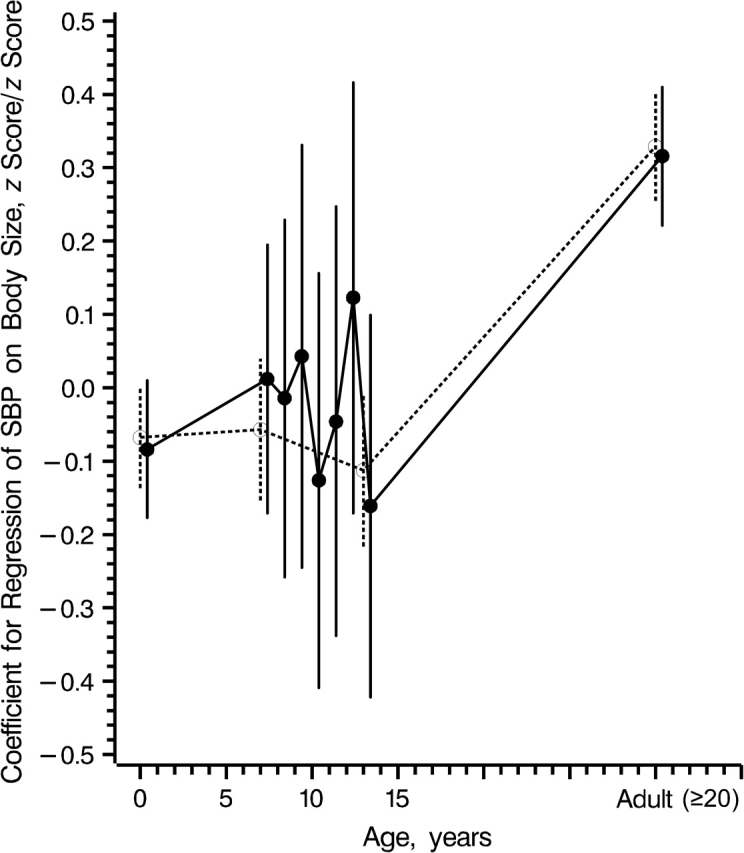
Life course plot (solid line), as suggested by Cole (18). The plot shows multiple regression coefficients (circular points) from the regression of systolic blood pressure (SBP) z scores on birth weight and body mass index z scores, by age at body size measurement. The dashed line represents a modified version of the life course plot using a reduced multiple regression of SBP on body size. Vertical lines, 95% confidence interval.

Conditional linear regression

The effect of birth weight on adult SBP was significantly negative, and the effect of adult BMI adjusted for past body size was significantly positive. The confidence intervals around the estimated effect of the change in body size on SBP from the series of conditional regressions increased from age 7 years to age 13 years (Figure 3, part A). Collinearity and lower numbers of persons with complete data caused these increases. To disentangle these effects, we performed the conditional regressions on the complete cases only (Appendix). A comparison of the results shows that the lower number of persons with complete data has a limited effect on the size of the confidence interval; thus, collinearity is the main reason for the intervals’ increasing size. Parameter estimates from these regressions are interpreted as the effect of body size given past body size, or the effect of change in body size between the measurement in focus and the previous measurement, given body size history. For example, these estimates compare a child who has moved up 1 standard deviation in the size distribution between measurements to a child with an identical body size history who did not move. In contrast to interpretation of the multiple regression model, interpretation of the conditional regression model does not include any assumptions about future body size.

Figure 3.

Regression coefficients (circular points) from the regression of systolic blood pressure (SBP) z score on birth weight and body mass index (BMI) z scores, by age at body size measurement. A) Conditional regression coefficients from the regression of SBP on body size given past body size. For example, the 9-year estimate is the coefficient for regression of SBP on BMI at age 9 years, adjusted for birth weight and BMI at ages 7 and 8 years. B) Path analysis life course plot showing the estimated total effects of body size on adult SBP given body size history. These total effects include the potential indirect effect mediated through future body size. For example, the 9-year estimate is the total effect of BMI at age 9 years on adult SBP given birth weight and BMI at ages 7 and 8 years, including the effect mediated through BMI measured at ages 10 years to adulthood. Interpretation of the estimates shown in both parts of the figure (A and B) is similar. Vertical lines, 95% confidence interval.

Path analysis

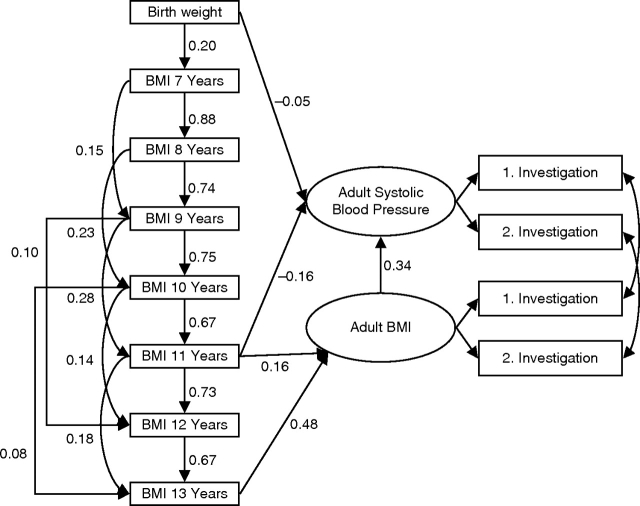
The path diagram illustrates the path analysis model after model reduction (Figure 4). Path analysis showed that SBP was directly and positively associated with concurrent BMI and directly and negatively associated with BMI at age 11 years. A similar direct and negative effect was observed for birth weight, although it was nonsignificant (Table 3). Overall the model had a good fit, and birth weight was retained in the model because it was a priori considered important.

Figure 4.

Path diagram illustrating the final model for the regression of adult systolic blood pressure z score on body size z score. The numbers in the diagram are regression coefficients. For example, the coefficient for the regression of body mass index (BMI) z score at age 7 years on birth weight z score is 0.20. (See Figure 1 for interpretation of a path diagram.)

Table 3.

Estimates^a From Path Analyses of the Effect of Body Size z Score on Adult Systolic Blood Pressure z Score on Body Size^b z Score Among Males in a Data Set Created by Linkage Between the Copenhagen School Health Records Register and the Copenhagen Centre for Prospective Population Studies, Denmark

Age at Body Size Measurement, years	All Measurements of Body Size Included				Body Size Measurements at Ages 11–13 Years Excludedc
	Direct Effectd		Total Effecte		Direct Effect		Total Effect
		95% CI		95% CI		95% CI		95% CI
0 (birth)	−0.046	−0.106, 0.013	−0.039	−0.099, 0.019	−0.051	−0.110, 0.009	−0.043	−0.103, 0.016
7			0.037	−0.009, 0.083			0.038	−0.011, 0.087
8			0.036	−0.008, 0.080			0.035	−0.013, 0.082
9			0.038	−0.009, 0.085			0.049	0.000, 0.097
10			0.034	−0.007, 0.075	−0.148	−0.226, −0.070	−0.005	−0.082, 0.073
11	−0.156	−0.234, −0.077	0.007	−0.056, 0.070
12			0.110	0.071, 0.149
13			0.165	0.108, 0.222
≥20 (adulthood)	0.340	0.255, 0.426	0.340	0.255, 0.426	0.341	0.257, 0.425	0.341	0.257, 0.425

Abbreviation: CI, confidence interval.

^aEstimates from the path analysis model described in Figure 4.

^bBirth weight z score or body mass index z score.

^cSensitivity analysis conducted to investigate whether the timing of puberty affected the results.

^dThe direct effect is the effect on adult systolic blood pressure of the body size measurement given the past body size measurements and not mediated through the future body size measurements or the effect of the body size measurement given the other body size measurements included in the systolic blood pressure regression (i.e., both past and future measurements).

^eThe total effect is the effect on adult systolic blood pressure of a body size measurement given body size history. It is the sum of the direct and indirect effects. The indirect effect is the effect mediated through later body size. The estimate should be interpreted as the total effect of change in body mass index z score at the specified age, given body size history.

The path analysis life course plot illustrates the estimated total effect of body size or change in body size in childhood on adult SBP given body size history (Figure 3, part B). The total effect of body size given body size history was negative at birth (−0.040 standard deviations/standard deviation or approximately 1.1 mm Hg in a 50-year-old male per kilogram of birth weight) and positive at school age. The total effect was small at ages 7–11 years and larger and significant at ages 12 and 13 years (Table 3 and Figure 3, part B). The estimated total effect has the same interpretation as the estimates from the conditional regression analysis, and it accounts for potential indirect effects through later body size.

To investigate the robustness of the estimated total effects, we fitted alternative path analysis models with changes in the associations between body size measurements. These models consistently showed the same general pattern in the estimated total effects, although the direct effect estimates differed (data not shown).

From age 7 years to age 11 years, the total effect of BMI on SBP is small but positive. These small effects result from adding the negative pathways through BMI at age 11 years to SBP with the positive pathways that go through adult BMI. The total effects of BMI at ages 12 and 13 years on SBP are positive and larger, as all pathways from these ages to SBP are positive (Figure 4). Overall, the negative pathway from BMI at age 11 years to SBP causes the size of the total effects to change from being small at ages 7–11 years to large at ages 12 and 13 years. To investigate the specificity of this inflection point, we fitted 6 alternative path analysis models. We defined them by substituting the arrow from BMI at age 11 years to adult SBP in Figure 4 with an arrow from one of the other childhood BMI measurements to adult SBP. Although these alternative models all showed acceptable tests for goodness of fit, none fitted as well as the model in Figure 4 (Appendix).

The negative direct effect of BMI at age 11 years on adult SBP is eliminated by an opposite indirect effect that goes through adult BMI. The estimated total effect of BMI measured at age 11 years on adult SBP is calculated by adding the products of coefficients along all paths from BMI at age 11 years to adult SBP in Figure 4. The estimated effect is −0.16 + (0.16 × 0.34) + (0.73 × 0.67 × 0.48 × 0.34) + (0.18 × 0.48 × 0.34) = 0.01. Thus, children who were larger than average at age 11 years were also larger than average as adults. In turn, this led to higher SBP.

The effect of change in BMI at ages 12 and 13 years is completely indirect and is mediated through adult body size, since the only path from BMI at ages 12 and 13 years to adult SBP goes through adult BMI (Figure 4). At early school age, however, the total effect of change in BMI is smaller than the indirect effect going through adult BMI. The total effect of BMI at these ages is the sum of the negative indirect effect going through BMI at age 11 years and the indirect positive effect going through adult BMI.

We assessed the impact of incorporation of noncomplete data and repeated SBP measurements by performing a path analysis modeling SBP only from the first investigation and using complete data only (Appendix). The impact on the estimates was limited, but the restriction of the data led to some loss of precision, hence wider confidence intervals.

Sensitivity analysis

We performed the path analysis after excluding BMI from age 11 years to age 13 years in order to assess whether the timing of puberty influenced the results (Table 3). Even though the estimated direct effects changed, the general pattern of the total effects remained unchanged, suggesting that puberty timing did not influence the analysis of the early childhood body size–SBP association. The study-specific analyses revealed no signs of heterogeneity (data not shown).

DISCUSSION

In this study, we compared 3 types of standard regression analysis with path analysis in an investigation of the association between childhood body size and adult SBP. In this context, path analysis produced easily interpretable estimates with greater precision than those from the standard regression analyses. Path analysis showed that birth weight is negatively associated with adult SBP; that change in BMI z score at early school age is weakly and positively associated with adult SBP; that the association between change in BMI z score at late school age and SBP is positive and stronger; and that the association between adult BMI and SBP is positively and strongly associated with adult SBP.

Standard regression techniques have largely been inadequate in addressing questions about how body size early in life affects later health. One reason is that reparameterization of a multiple regression analysis can change the interpretation of the model's results (11–14). Another is that multiple regressions using all available measurements of body size, such as those used to produce a life course plot (18), are hindered by collinearity problems—at least in data sets with closely spaced measurement points. Since the use of closely spaced data is essential when the research question is about the timing of change in childhood body size and its association with later SBP, collinearity is problematic. Additionally, the question of whether or not to adjust for a concurrent measurement of body size, because of the so-called reversal paradox, has been debated (9, 10). Path analysis, however, produces an easily interpretable estimate of the total effect of the change in the independent variable. It also efficiently deals with collinearity with only minimal loss of power.

Each analytic method used in this study had a different degree of applicability to the investigation of the childhood body size–SBP association. Simple linear regression had utility in showing the crude associations of the variables, but it could not address the complex associations. The multiple linear regressions suffered from collinearity problems. To avoid this, we performed a reduced multiple linear regression analysis. It showed that change in BMI z score from age 13 years to adulthood is positively associated with SBP in adulthood. The negative estimate at age 13 years should be interpreted cautiously, however, since it is comparing a person who has a relatively large body size at age 13 years and an average body size at birth, at age 7 years, and in adulthood with a person who has an average body size at all times.

Conditional regression analyses are often used in this area of research, since they overcome these interpretation problems. By specifying that the regressions are only conditioned on the past and not the future, we render the results relevant and easily interpretable. The estimate corresponding to the last measurement of body size in such a model is relevant, because it mimics the clinical setting in which the history of body size is known but future body size and health are unknown. In this model, a smaller child and a larger child who have identical body size histories are being compared; that is, we are assessing movement in body size between 2 time points. Just like the standard multiple regression analysis, the conditional regression analyses also have collinearity problems; this implies imprecise estimation of the effects and wide confidence intervals.

Of all the methods, path analysis had the most advantages; it produced easily interpretable results in a model which best reflected the biology of the association between childhood body size and adult SBP. Total effects derived from this model have the same relevant public health interpretation as the estimates obtained from the conditional regression mentioned above. Comparing results from these 2 methods shows no disagreement, but there is a noteworthy gain in statistical power through the use of path analysis, which was illustrated by the smaller confidence intervals. The gain in power can partly be explained by the better utilization of data by the path analysis model, as it can incorporate repeated measures of SBP and incomplete data. The comparison between path analysis and conditional regression on complete data with only 1 measurement of SBP showed that in path analysis there was a noteworthy decrease in the size of the confidence intervals. In the path analysis model, it is also possible to disentangle direct and indirect effects, which makes it possible to distinguish the part of the effect of z score change that operates through later BMI from the part that does not.

Estimates illustrated in the path analysis life course plot are generally positive (Figure 3, part B), and these contrast with the more mixed pattern shown in the life course plot (Figure 2). The 2 plots are based on different models; thus, they have different interpretations. Estimates in the path analysis life course plot come from a path analysis model in which the association between current and future body size is modeled, and therefore they can be interpreted as the effect of a 1-standard-deviation change in body size on SBP, accounting for past body size. Estimates in the life course plot come from a multiple regression model in which the estimates are conditional on both past and future body size. Therefore, interpretation of an estimate from this model involves comparing 2 children with different body sizes at a given age but identical body sizes both before and after that age. In other words, an estimate in the life course plot at a given age can be interpreted as the effect of a 1-standard-deviation gain in body size under the assumption that the gained body size will be lost again before the next measurement. There is a general pattern of differences in the estimates between the plots, and this occurs because the path analysis model does not include any assumptions about future body size, whereas the multiple regression model does.

The path analysis life course plot provides a new way of visualizing the effect of change in body size distribution given past body size on later outcome. This method moves beyond the life course plot (18), where estimates are conditioned on both the future and the past. Integral to path analysis is the path diagram, which illustrates the conceptual framework used to guide the analysis. The combination of the path analysis life course plot with the path diagram eases the interpretation of analyses of the association between childhood body size and later outcome.

Similarly to all other techniques, path analysis also has a set of assumptions and challenges. The first assumption is that there is linearity among all included variables, as opposed to the conditional regression approach, which only assumes linearity between the body size measures and the outcome. The second assumption is that there are no interactions among the variables. The third is that all intermediate or outcome variables have a normal distribution. A challenge in path analysis is the lack of efficient ways to compare different models that are not nested, which can lead to a potentially subjective choice of the final model. It can be overcome by performing an extensive sensitivity analysis assessing all models with an acceptable fit to the data and the impact of these models on the shape of the path analysis life course plot.

This study showed that the effect of a BMI z score change on adult SBP is more pronounced at ages 12 and 13 years than it is in earlier childhood, and that the effect of BMI z score change at ages 12 and 13 years is completely mediated through later body size. However, the total effect of BMI z score change at early school age is smaller than the indirect effect going through adult BMI. This result implies that an early-onset large body size has a smaller impact on adult SBP than a later-onset large body size. Therefore, the body size trajectory matters, since SBP depends on current body size, as well as how the body size was achieved.

Finnish (39), Filipino (15), and British (20) studies have found that a large weight gain at school ages has an adverse effect on adult SBP. Partly, these observed associations probably reflect the beginning of an upward turn in the body size trajectory, which leads to greater body size in later life. In these studies, however, the effect of change in childhood BMI on later SBP was not partitioned into direct and indirect effects operating through later BMI. In the Finnish study (39), the investigators were unable to account for adult BMI; in the Filipino study (15), they used simple regression of changes in weight in childhood on later SBP; and in the British study (20), they used conditional regression.

Our results suggest that a change in the association between BMI z score change and adult SBP occurs around the age of 11 years, but the sensitivity analyses show that the precise timing of this change is uncertain. This uncertainty is probably due to limitations in the statistical power of the study. Because the timing of this change could be affected by puberty, if we had been able to adjust for this the estimate may have become more stable. The timing of puberty onset among Danish boys is close to 11 years (38), thus making this a plausible explanation and suggesting that development of a higher-than-average BMI during or after puberty has a greater impact on adult SBP than development of a higher-than-average BMI before puberty. In these analyses, adjustment for potential childhood confounders such as socioeconomic status was not possible, since this information was not available. We cannot exclude the possibility that unmeasured factors may attenuate the associations we observed. However, in previous studies of the association between birth weight and SBP, a confounding effect of socioeconomic status was not identified (8, 23). It is also possible that genetic factors can account for the larger body size that emerges in earlier life (40), and this type of weight might not lead to a higher adult SBP, or at least might do so to a lesser extent. The data set did not include measurements of body size between birth and school age; hence, we could not investigate the effect of change in body size in early childhood.

From the series of analyses performed, path analysis emerges as a superior method for analyzing the long-term effects of body size early in life on later health outcomes. It has the advantage of producing readily interpretable estimates of public health relevance, and when illustrated using a path analysis life course plot, the estimates are easily visualized. An important step forward will be application of the path analysis method to investigations of time-to-event endpoints so that the effects of body size on these outcomes can be better understood.

Glossary

Abbreviations

BMI

body mass index

SBP

systolic blood pressure

APPENDIX

Collinearity in the conditional regression

The confidence intervals around the estimated effect of the change in body size on systolic blood pressure (SBP) from the series of conditional regressions increase from age 7 years to age 13 years (see Figure 3, part A, in text). This increase is caused by a combination of increasing collinearity and a decreasing number of persons with complete body size measurements as more independent variables are added to the model. To disentangle the effect of collinearity and the effect of a lower number of persons with complete data, we performed the conditional regression analyses on the complete cases only and on the entire sample (Appendix Table 1). A comparison of the results shows that the lower number of persons with complete data has a limited effect on the size of the confidence intervals; thus, collinearity is the main reason for their increasing size.

Appendix Table 1.

Estimates From Conditional Regression and Path Analyses of the Regression of Adult Systolic Blood Pressure z Score on Body Size^a z Score Among Males in a Data Set Created by Linkage Between the Copenhagen School Health Records Register and the Copenhagen Centre for Prospective Population Studies, Denmark

Age at Body Size Measurement, years	Conditional Regression				Path Analysis
	Entire Sample		Complete Case Sampleb		Entire Samplec		Complete Case Sampled
		SE		SE		SE		SE
0 (birth)	−0.066	0.031	−0.085	0.048	−0.039	0.030	−0.082	0.046
7	0.040	0.035	0.026	0.046	0.037	0.023	0.030	0.035
8	0.045	0.074	−0.018	0.092	0.036	0.022	0.029	0.033
9	0.027	0.092	0.068	0.111	0.038	0.024	0.027	0.035
10	0.021	0.105	−0.076	0.123	0.034	0.021	0.037	0.029
11	0.098	0.116	0.152	0.125	0.007	0.032	−0.005	0.044
12	0.143	0.119	0.173	0.122	0.110	0.020	0.168	0.029
13	−0.029	0.136	−0.029	0.136	0.165	0.029	0.132	0.040
≥20 (adulthood)	0.316	0.048	0.316	0.048	0.340	0.044	0.311	0.046

Abbreviation: SE, standard error.

^aBirth weight z score or body mass index z score.

^bExcluding men with incomplete childhood body size measurements.

^cUsing the entire sample and repeated measurement of adult body mass index and systolic blood pressure.

^dExcluding men with incomplete childhood body size measurements and using only adult systolic blood pressure and body mass index from the first investigation.

Path analysis

To take into account the fact that body size at a given time in life affects not only later SBP but also later body size, we performed path analysis (33, 34). It implies the simultaneous estimation of as many regressions as there are intermediate and outcome variables. Model 1 below is an example of such a path analysis model, where each measurement of body size depends on all previous measurements of body size and SBP depends on all measurements of body size. This model is termed the a priori model in the text.

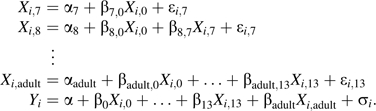(A1)

$X_{i,0},\dots ,X_{i,\text{adult}}$ are the measurements of body size z score, $Y_i$ is the adult SBP z score, and ${\text{ε}}_{i,7},\dots ,{\text{ε}}_{i,13}$ and ${\text{σ}}_i$ are independent normally distributed error terms.

Path analysis with latent variables

To optimize the use of data, we expanded path analysis model 1 to incorporate 2 measurements of SBP and concurrent body mass index (BMI) (if available). To incorporate these multiple measurements into the path analyses, we modeled both SBP and adult BMI using latent variables. The measurements of SBP were assumed to be realizations of a latent SBP variable, and the measurements of adult BMI were assumed to be realizations of a latent BMI variable:

(A2)

where $Y_{i,1},Y_{i,2}$ are the 2 measurements of SBP and $X_{i,\text{adult},1},X_{i,\text{adult},2}$ are the 2 adult measurements of BMI. This type of model is called a structural equation model (33). To allow for the expected greater correlation between BMI and concurrent SBP than between BMI and SBP measured at different time points, the error terms ${\text{ε}}_{i,\text{adult},1}$ and ${\text{σ}}_{i,1}$ and the error terms ${\text{ε}}_{i,\text{adult},2}$ and ${\text{σ}}_{i,2}$ are allowed to be correlated, and all other pairs of error terms are assumed to be independent.

The structural part of path analysis model 2 was reduced to obtain a model with a good fit to the data. Two approaches were used. Firstly, we used an approach that initially focused on all but the last equation, removing all nonsignificant associations in order of significance and, after this reduction, checking to see whether any of the removed associations was significant when added to the reduced model. After this selection procedure in the childhood body size model, the SBP equation was added, and an analogous reduction was made in this model. Secondly, the reduction was made on the entire model. Both approaches gave the same final model:

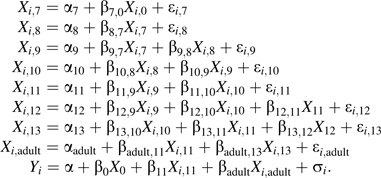(A3)

A path diagram (see Figure 4 in text) was used to illustrate the final model. This model has a very good overall fit; the fit is assessed using a χ² test against model 2 (χ² = 38.43 (41 df); P = 0.59).

We assessed the impact of the incorporation of noncomplete data and repeated SBP measurements, performing a path analysis modeling only SBP from the first investigation and using complete data only (Appendix Table 1). The impact on the estimates was limited, but the restriction of the data led to some loss of precision and hence larger standard errors.

Sensitivity analyses in the path analysis

We performed sensitivity analyses by adding nonsignificant effects to the model and assessing the impact on the path analysis life course plot. The shape of the plot was only minimally influenced by the changes in the model.

From age 7 years to age 11 years, the total effect of BMI on SBP is small but positive (see Table 3 in text). These small effects result from adding the negative pathways through BMI at age 11 years to SBP with the positive pathways that go through adult BMI. The total effects of BMI at ages 12 and 13 years on SBP are positive and larger (see Table 3 in text), since all pathways from these ages to SBP are positive. Overall, the negative pathway from BMI at age 11 years to SBP (₁₁ < 0 in model 3) causes the size of the total effects to change from small at ages 7–11 years to large at ages 12 and 13 years.

To investigate the specificity of this inflection point, we fitted 6 alternative path analysis models. They were defined by substituting ${\text{β}}_{11}{X}_{11}$ in the last equation in model 3 with ${\text{β}}_7{X}_7$, ${\text{β}}_8{X}_8$, …, or ${\text{β}}_{13}{X}_{13}$. All alternative models showed acceptable tests for goodness of fit (Appendix Table 2). Akaike's Information Criterion (35) was used to compare these nonnested models. The criterion is $2k-2\log \left(L\right),$ where k is the number of parameters in the model and L is the likelihood function. None of the alternative models had as good a fit as model 3 (Appendix Table 2). In an additional sensitivity analysis, all models with 2 effects from childhood BMI to adult SBP were fitted. This increased Akaike's Information Criterion by a minimum of 1.93, and there were no changes in the shape of the path analysis life course plot.

Appendix Table 2.

Comparison of the Fit of Alternative Path Analysis Models of the Regression of Adult Systolic Blood Pressure z Score on Body Size^a z Score Among Males in a Data Set Created by Linkage Between the Copenhagen School Health Records Register and the Copenhagen Centre for Prospective Population Studies, Denmark

Model	χ2 Test for Goodness of Fit (41 df)	P Value	AICb	Difference in AIC Between Alternative Model and Final Model
Final modelc	38.43	0.59	21,546.16	0
${\text{β}}_{11}{X}_{11}$ replaced by ${\text{β}}_{\text{7}}{X}_7$d	46.90	0.24	21,554.62	8.46
${\text{β}}_{\text{11}}{X}_{11}$ replaced by ${\text{β}}_8{X}_8$	45.72	0.28	21,553.44	7.28
${\text{β}}_{11}{X}_{11}$ replaced by ${\text{β}}_9{X}_9$	42.16	0.42	21,549.89	3.73
${\text{β}}_{11}{X}_{11}$ replaced by ${\text{β}}_{10}{X}_{10}$	41.50	0.45	21,549.23	3.07
${\text{β}}_{11}{X}_{11}$ replaced by ${\text{β}}_{12}{X}_{12}$	41.12	0.47	21,548.84	2.68
${\text{β}}_{11}{X}_{11}$ replaced by ${\text{β}}_{13}{X}_{13}$	43.32	0.37	21,551.04	4.88

Abbreviation: AIC, Akaike's Information Criterion.

^aBirth weight z score or body mass index z score.

^bAIC is $2k-2\log \left(L\right)$ (35), where k is the number of parameters and L is the likelihood function.

^cModel 3, the final path analysis model after model reduction.

^dReplacement of the effect of body mass index at age 11 years on systolic blood pressure in the last equation in model 3 by the effect of body mass index at age 7 years on systolic blood pressure.