Competing Risk Regression Models for Epidemiologic Data

Abstract

Competing events can preclude the event of interest from occurring in epidemiologic data and can be analyzed by using extensions of survival analysis methods. In this paper, the authors outline 3 regression approaches for estimating 2 key quantities in competing risks analysis: the cause-specific relative hazard (_csRH) and the subdistribution relative hazard (_sdRH). They compare and contrast the structure of the risk sets and the interpretation of parameters obtained with these methods. They also demonstrate the use of these methods with data from the Women's Interagency HIV Study established in 1993, treating time to initiation of highly active antiretroviral therapy or to clinical disease progression as competing events. In our example, women with an injection drug use history were less likely than those without a history of injection drug use to initiate therapy prior to progression to acquired immunodeficiency syndrome or death by both measures of association (_csRH = 0.67, 95% confidence interval: 0.57, 0.80 and _sdRH = 0.60, 95% confidence interval: 0.50, 0.71). Moreover, the relative hazards for disease progression prior to treatment were elevated (_csRH = 1.71, 95% confidence interval: 1.37, 2.13 and _sdRH = 2.01, 95% confidence interval: 1.62, 2.51). Methods for competing risks should be used by epidemiologists, with the choice of method guided by the scientific question.

In time-to-event analyses, the occurrence of the event of interest is often precluded by another event. The canonical example is the study predictors of cause-specific mortality, whereby a death due to the primary cause of interest (e.g., cancer-related deaths) is precluded by death due to other causes. In this competing risks setting (1–3), individuals are observed from study entry to the occurrence of the event of interest, a competing event, or censoring. Competing risks are common to epidemiologic research (4–7), and recognition dates to the 1700s when Bernoulli estimated mortality rates (1, 8, 9).

The complement of the Kaplan-Meier survival curve may not appropriately estimate the cumulative incidence when competing events are censored (10–13). Both nonparametric (2, 10, 14, 15) and regression (8, 16, 17) methods exist for analyzing data with competing events. Although the nonparametric approaches have been well described, 2 widely used measures from regression approaches, the cause-specific relative hazard (_csRH) and the subdistribution relative hazard (_sdRH), have not been well described in the epidemiology literature (18).

The purpose of this paper is 3-fold. First, we provide intuition for the _csRH and _sdRH by considering the construction of risk sets and interpretation of the underlying hazard function. Second, we describe 3 different regression models for the analysis of epidemiologic data with competing risks. Third, we illustrate the use of these methods in an analysis that explores the association of injection drug use with the time to 2 competing outcomes in a cohort of human immunodeficiency virus (HIV)-infected women: initiation of combination antiretroviral therapy and the occurrence of acquired immunodeficiency syndrome (AIDS) or death prior to initiating combination antiretroviral therapy.

MATERIALS AND METHODS

Key measures in a competing risk framework

Five interrelated building blocks underpin standard (noncompeting) survival analysis: the time scale t (e.g., age, calendar time, disease duration, or study duration); the risk set; the hazard function h(t); the cumulative incidence function (CIF) F(t); and its complement, the survival function S(t) = 1 – F(t). In a competing risks framework, each of these components remains of central importance but modified, depending on how the competing event is handled. We consider an event of interest (event 1) and only 1 competing event (event 2), although one may extend to more events. We assume no measurement error, noninformative censoring, and no unmeasured confounding. Henceforth, T will be defined as the minimum time to either event 1 or event 2 (T = min(T₁, T₂, C), where T₁ and T₂ correspond to time to event 1 and event 2, respectively, and C corresponds to the censoring time).

A framework for competing risk regression

The regression approaches described below focus on 2 definitions of hazard, the cause-specific and the subdistribution hazards. The corresponding _csRH may be better suited for studying the etiology of diseases, whereas the _sdRH has use in predicting an individual's risk or allocating resources.

Consider an example. A group of diseased individuals are randomized to treatment A or treatment B, everyone is compliant to treatment protocols, and all are followed until either the disease is cured or individuals have an adverse event requiring discontinuation of treatment. The cumulative incidence for being cured may be estimated as 1 – the Kaplan-Meier product limit estimator stratified by treatment. Both curves will be essentially 1.0 by the end of follow-up, as everyone is followed to 1 of the 2 events. The shift in curves represents the etiologic association between treatment type and being cured, in that it reflects the relative change in the underlying hazard. However, one would not predict that the probability of being cured was 1.0 for either treatment by the end of follow-up, as we know that some individuals have the adverse event and must discontinue therapy. For prediction, one may require a curve that reflects the proportion cured by the end of follow-up. Additionally, if the _csRH_adverse > _csRH_cure ≥ 1.0 comparing treatment A versus treatment B, then the adverse event is occurring at a greater hazard rate in treatment group A. Thus, the proportion of individuals being cured would be different by treatment status by the end of follow-up even if the cure rates are the same. Therefore, the shift in these observed cumulative incidence curves should represent not only the etiologic association of treatment with being cured but also the influence of having a reduced number of individuals remaining at risk for being cured in group A due to a greater number of adverse events. The lower observed number of individuals being cured because of a greater proportion of adverse events may actually overpower the etiologic association, such that the observed cumulative incidence of being cured is no longer different between treatment groups. The nonparametric estimator for competing risks accounts for these issues. Similarly, the cause-specific and subdistribution hazard approaches reflect these 2 different kinds of comparison.

The cause-specific hazard

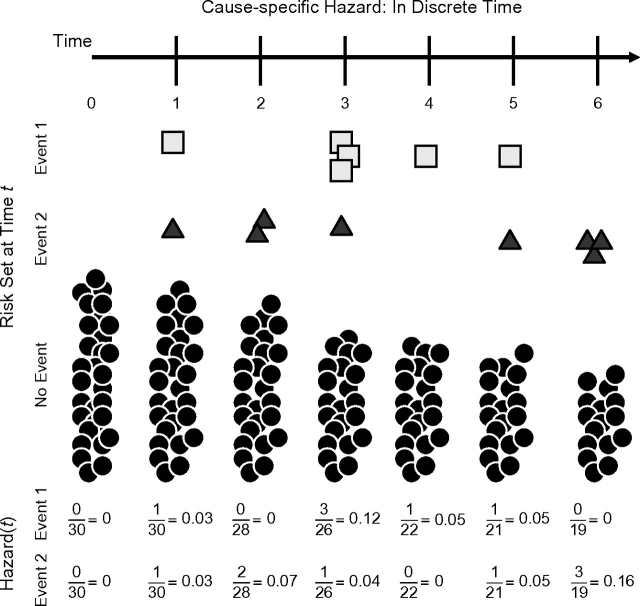
The manner in which risk sets are defined in standard survival analyses may be modified to allow for competing events. In standard survival analysis, the risk set is defined as the group of individuals that have not experienced the outcome and therefore are at risk for the event of interest at time t. Individuals who have a competing event can be removed from all later risk sets for the event of interest. Figure 1 illustrates this approach in discrete time. At time 0, there are 30 individuals at risk. At time 1, 1 individual has event 1, and another individual has event 2, such that the risk set for time 2 is now 28 = 30 –1_{event 1} – 1_{event 2}. Thus, individuals with an event 1 or event 2 prior to time t are excluded from the risk set at time t.

Figure 1.

Cause-specific hazard schematic. The risk set starts with 30 individuals (solid circles). Over time, individuals have either event 1 (square) or event 2 (triangle). As individuals have either event, they are removed from the remaining risk sets. The calculation for the cause-specific hazard is given at the bottom of the figure.

An estimate of the hazard for event 1 can be described in the discrete time setting as the number of individuals who experience the event divided by the number at risk at time t. For example, at time 3, this would be 3/26 = 0.12, which estimates the cause-specific hazard, which is formally defined as $h_j\left(t\right)=P(T=t,J=j|T\ge t)$, where J = j indicates whether event 1 (j = 1) or event 2 (j = 2) is being estimated.

The cause-specific hazard can be extended to continuous time (8, 19):

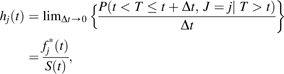(1)

where f_j^*(t) = P(T = t, J = j) is a “sub”-density function (“*” indicates an improper, i.e., “sub”-density function that integrates to <1), and S(t) reflects the net survival function of both events 1 and 2, that is, $S\left(t\right)=P(T>t)=\exp [-{\displaystyle {\int }_0^t{\displaystyle {\sum }_{j=1}^2{h}_j\left(u\right)du}}]=\exp [-{\displaystyle {\int }_0^{t}h\left(u\right)du]}$, where h(t) is the net hazard for having either event 1 or event 2 (8).

As described in the Web supplement posted on the Journal’s website (http://aje.oxfordjournals.org/), a likelihood function can be constructed from the cause-specific hazards, whereby individuals who experienced a competing event are treated as censored (8). Consequently, a proportional hazards model can be constructed for the cause-specific hazard:

(2)

where h_0j is the arbitrary baseline cause-specific hazard, and β_j, j = 1, 2 are the corresponding regression coefficients, where exp(β_j) = _csRH_j is interpretable as the relative change in the cause-specific hazard for the jth event corresponding to a 1-unit increase in the corresponding covariate. No assumptions of the relation between the competing outcomes are needed for estimation (2, 8). Estimation may be accomplished by using standard software. A proportional hazards model is constructed separately for each event type in which individuals who experience the competing event are treated as censored observations. Because the likelihood may be written such that the competing event is treated as a censored event, this proportional hazards model is exactly the same as what some investigators model when “ignoring” competing events. Alternatively, rather than separate models, a joint model could be used (20) (refer to Web supplement).

A Breslow estimator (21, 22) of the cumulative incidence proportion can be calculated by using the cause-specific hazard under the (untestable) assumption that the competing events are independent of each other (3, 18, 23–25). Models linking covariates to cause-specific hazards as measured by _csRH_j=1 provide a summary of how a covariate directly impacts the incidence without considering the effect of the competing event. Much has been written about how inferences from this approach need to be evaluated cautiously (8, 26), because the assumption of independent competing events is strongly needed to underpin the inference that the cause-specific hazard and corresponding cumulative incidence functions quantify the risk of the event in hypothetical populations where competing events are eliminated (8). Therefore, caution must be used in interpreting _csRH as an increase (decrease) in apparent risk; it is, however, valid to interpret it as a relative change in the cause-specific hazard rate.

The subdistribution hazard

In light of the strong assumption of independence between events to allow interpretation of the cause-specific cumulative incidence function (_csCIF), the competing risk literature has focused on an alternative measure of risk: the subdistribution cumulative incidence function (_sdCIF). This function is defined as the joint probability of an event prior to time t and that the event is of type j: F_j^*(t) = P(T < t, J = j). Although the _sdCIF may be estimated from the _csRH_j=1, extra steps are required as the _sdCIF is a function of the net survivor function and therefore directly impacted by the competing event (27, 28). The _sdCIF may be modeled directly.

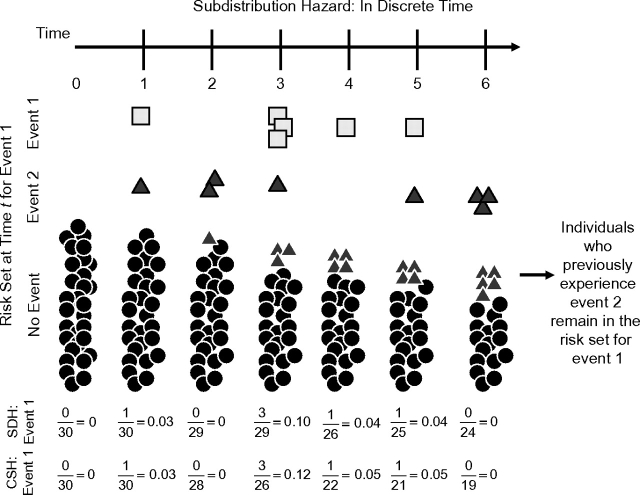
Interpretation of this measure can be understood by returning to the construction of risk sets and hazard functions. In contrast to the construction of risk sets that eliminate individuals who have the competing cause, risk sets were constructed so that they include both individuals without any event and those who have had the competing event. It may be counterintuitive to maintain individuals who had a competing event in the risk set. However, one can think of these individuals as a “placeholder” for the proportion of the population that cannot have the event of interest and place a constraint on this hazard function definition (16). Figure 2 illustrates this construction with the same population as in Figure 1. For example, one individual had the competing event at time 1 and is therefore maintained in the subsequent risk sets. Therefore, at t = 2, the risk set comprised 29 individuals; at t = 3, a total of 3 individuals by this time have previously experienced event 2 and are maintained in the risk set. With increasing t, the risk set comprised an increasing proportion of individuals who have had event 2.

Figure 2.

Subdistribution hazard schematic. The risk set starts with 30 individuals (solid circles). Over time, individuals have either event 1 (square) or event 2 (triangle). As individuals have the competing event (event 2, triangle), they are maintained in the risk set as triangles. Thus, over time, a greater proportion of the risk set becomes full of triangles that are individuals who have had the competing event prior to that time. The subdistribution hazard (SDH) for event 1 is given near the bottom of the figure along with the cause-specific hazard (CSH) for event 1 for comparison. Note that, because individuals are maintained in the risk set, the SDH tends to be lower than the CSH.

With this structure, a different hazard function is defined as the probability of the event given that an individual has survived up to time t without any event or has had the competing event prior to time t. This is the subdistribution hazard (16). For example at t = 3, the subdistribution hazard is 3/29 = 0.103, which is smaller than the cause-specific hazard of 0.12 because of the larger risk set.

For the discrete time setting, the subdistribution hazard is ${\text{λ}}_j\left(t\right)=P(T=t,J=j|T\ge t\mathrm{or}(T<t\mathrm{and}J\ne j))$. In continuous time, the subdistribution hazard is the following (16):

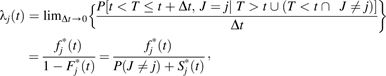(3)

where F_j^*(t) = P(T < t, J = j), S_j^*(t) = P(T > t, J = j), and 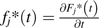are the subdistribution cumulative incidence, subsurvivor, and subdensity functions (note that P(J = j) = S_j^*(t) + F_j^*(t)).

An alternative proportional hazards model may be constructed from the subdistribution hazard, which is useful because the cause-specific hazard approach does not necessarily reflect what occurs with the _sdCIFs (16). This occurs because the _sdCIF is a function of the cause-specific hazards for both events 1 and 2 (29, 30) (Web supplement). The proportional subdistribution hazards model is then:

(4)

where λ_0j is the unspecified baseline subdistribution hazard. The proportionality assumption may be assessed by plotting the log(–log(1 – F_j^*(t)) against log(time) stratified by the covariate, where F_j^*(t) can be estimated from a nonparametric estimator for competing risks (2, 10, 14, 15). In the presence of noninformative censoring, it has been recommended to use a weighted score function to obtain an unbiased estimating equation from the partial likelihood (Web supplement) (16). This has been implemented in the CMPRSK library in the R statistical program.

The interpretation of _sdRH_j = exp(φ_j) is the relative change in the subdistribution hazard for a 1-unit increase in the corresponding covariate. The _sdRH_j is directly interpretable as a measure of association for the jth _sdCIF, and it is straightforward to estimate the subdistribution cumulative incidence by using a Breslow-type estimator to obtain the cumulative subdistribution hazard and evaluate 1 – exp(cumulative subdistribution hazard) (16).

Comparisons between _csRH and _sdRH

The relation between the _csRH_j=1 and _sdRH_j=1 is a function of the _csRH for the competing event (_csRH_j=2), the unspecified baseline cause-specific hazard for both events (h₀₁(t) and h₀₂(t)), and time (refer to Appendix):

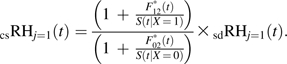(5)

Therefore, a situation in which the _csRH_j=1 = _sdRH_j=1 is when h₀₂ = 0. This also suggests that the _csRH_j=1 will be similar to _sdRH_j=1 when h₀₂ is small but that generally _csRH_j ≠ _sdRH_j. When _csRH_j=2 ≠ 1, the risk sets for the event of interest among exposed and unexposed individuals are modified differentially. When _csRH_j=2 > 1, a larger proportion of the risk set (for event J = 1) for exposed compared with unexposed individuals have had the competing event (and vice versa for _csRH_j=2 < 1). Consequently, the ratio between the subdistribution hazards for exposed and unexposed individuals for the event of interest will not be equivalent to the _csRH.

Given that the _csRH_j and _sdRH_j are generally different, how do we use these measures (Table 1)? In noncompeting risk settings, the impact of a high (low) relative hazard will directly translate to an increase (decrease) in cumulative incidence of the event for the exposed individuals as compared with unexposed individuals. In a competing risk framework, this is not necessarily true for the _csRH_j. The _csRH is a measure of association that does not necessarily directly translate into a measure of risk without the assumption of independence between the competing events. Without the assumption of independence or conducting extra steps to obtain the _sdCIF (Web supplement), the _csRH does not allow comparison of the cumulative incidence of the event in exposed versus unexposed individuals. Rather, the _csRH is a valid measure of the apparent effect of a covariate on the relative instantaneous hazard rate given that individuals have survived both events until time t. However, in that same instant, individuals may have a stronger (or weaker) relative hazard rate for the competing event.

Table 1.

Assumptions, Uses, and Advantages of 3 Different Regression Approaches to Modeling Competing Risks

	Approach
	Cause-specific Proportional Hazards Model	Subdistribution Proportional Hazards Model	Parametric Mixture Model
Model assumption	Assumes proportionality of the cause-specific hazard, as this model is exactly the same as conducting a regular proportional hazards model in which individuals with the competing event are censored at that time point.	Assumes that the subdistribution hazards are proportionala	Assumes that the investigator has correctly specified both the distribution for the event of interest and the competing event
Are these assumptions reasonable?	As with all proportional hazards models, the analyst should evaluate whether the proportionality assumption is met. In practice, this assumption is often violated.	The assumption that the subdistribution is proportional should be assessed.	Correctly specifying the distribution of events is difficult for any parametric model.
	Nevertheless, the investigator should acknowledge that there was some indication of nonproportionality and report the csRH as this is the weighted average over follow-up.	This can be done by assessing the residuals that are returned by the “crr” function in R against the unique failure times (16). This is analogous to examining the Schoenfeld residuals from a regular proportional hazards model.	The correct specification of the distribution may be made more tenable by utilizing a flexible distribution that can accommodate various shapes of the hazard function.
	Alternatively, violation of the proportional hazards assumption may be mitigated by including an interaction between variables and time to allow the csRH to vary over time.	Alternatively, proportionality may be assessed by evaluating the log(−log) transformation of the nonparametric cumulative incidence function estimators (2, 10, 14, 15) stratified by exposure variable. The step function curves should be separated by a constant difference.	A generalized gamma distribution is an example of a flexible distribution that can accommodate increasing, decreasing, arc-shaped- (increasing then decreasing), and bathtub-shaped (decreasing then increasing) hazard functions.
		Nevertheless, the investigator should acknowledge that there was some indication of nonproportionality and report the sdRH as this is the weighted average over follow-up.
		When the proportionality assumption is violated, this may be mitigated by including an interaction between variables and time.
What is the model useful for?
Measuring the association?	Yes, the csRH is a measure of association. It implies that, among any individuals who survive all events up to some unspecified time t, those with the exposure have a cause-specific hazard rate of csRH × the cause-specific hazard rate of those who do not have the exposure.	Yes, the sdRH is a measure of association. However, it is a measure of association that is due to both the association of the exposure at the event of interest and the possibly differential impact of competing events on the risk set for exposed and unexposed individuals.	Yes, both the csRH and sdRH are estimable.
Evaluating the risk of the event?	No, the csRH by itself cannot be used to predict whether the event will be observed. Whether the event will be observed is a function of both the csRH associated with the event of interest and the csRH associated with the competing event.	Yes, because the sdRH intrinsically accounts for the competing event by modifying the risk set at time t; a sdRH >1 indicates that those with exposure will be seen to have a quicker time to event in the study population. Similarly, a sdRH <1 indicates a longer time to event for those exposed.	Yes, in addition to the sdRH, the sdCIF is directly estimable.
	csRH >1 does not necessarily imply that the sdCIFexposed > the sdCIFunexposed and vice versa.	sdRH >1 does imply that the sdCIFexposed > the sdCIFunexposed and vice versa.
What is the model's advantage?	It measures the association of an exposure on the corresponding event in which the competing event contributes only by passively removing individuals from the risk set.	It measures the association of an exposure to the corresponding event in which the competing event actively contributes to the risk set.	The model can obtain the csRH, the sdRH, and the subdistribution cumulative incidence, as well as the cause-specific hazard and subdistribution hazards all as functions of time.
	The model does not have to correctly specify the unspecified baseline cause-specific hazard function.	The model does not have to correctly specify the unspecified baseline subdistribution hazard function.	The model does not require the assumption of proportional hazards over time.
			When correctly specified, parametric models generally tend to have more power than semi- or nonparametric models.

Abbreviations: _csRH, cause-specific relative hazard; _sdCIF, subdistribution of the cumulative incidence function; _sdRH, subdistribution relative hazard.

^aThe subdistribution proportional hazards model assumes that the transformation of the subdistribution cumulative incidence functions as log(−log) transformation results in a constant difference between curves (16).

In contrast, the _sdRH is useful for comparing the cumulative incidence for those with and without exposure because of the direct modeling of the _sdCIF. For instance, a situation could arise where the _csRH_j=1 = 1, suggesting no difference in the cause-specific hazard rate comparing exposed versus unexposed individuals. However, because the exposed individuals are more likely to have the competing event (_csRH_j=2 > 1), the _sdRH_j=1 will be <1 (Table 2) because of the differential modification of the risk sets as caused by the association between exposure and the competing event. This drives the subdistribution hazard lower for those with exposure relative to unexposed individuals, causing _sdRH_j=1 < 1. While _csRH_j=1 = 1 suggests no association, exposed individuals will be less likely to have the event because of the association of the exposure with the competing event. Therefore, the _csRH_j=1 directly measures the association of an exposure on event 1 as the competing event contributes only passively by removing individuals from the risk set, whereas the _sdRH_j=1 is a measure of association that reflects both the association of exposure with event 1 and the contribution of event 2 by actively maintaining individuals in the risk sets for exposed and unexposed individuals. Should the association of the exposure with event 1 be in direct opposition with the contribution of event 2, the _sdRH may be quite different from the _csRH (Table 2).

Table 2.

General Direction of the Time-averaged Subdistribution Relative Hazard for a Given Direction of the Time-averaged Cause-specific Relative Hazards for Both Events 1 and 2^a

csRH1	csRH2	sdRH1b	csRH1 Interpretationc	sdRH1 Interpretationd
<1	<1	>csRH1	Exposure associated with a decreased cause-specific hazard rate for event	Because exposure is associated with a decreased cause-specific hazard rate for the competing event, the sdRH1 is greater than what one would expect if the exposure were not associated with the competing event (e.g., csRH2 = 1), and therefore sdRH1 > csRH1.e
<1	>1	<csRH1	Exposure associated with a decreased cause-specific hazard rate for event	Because the exposure is associated with an increased cause-specific hazard rate for the competing event, the sdRH1 is less than what one would expect if the exposure were not associated with the competing event (e.g., csRH2 = 1), and therefore sdRH1 < csRH1.
>1	<1	>csRH1	Exposure associated with an increased cause-specific hazard rate for event	Because exposure is associated with a decreased cause-specific hazard rate for the competing event, the sdRH1 is greater than what one would expect if the exposure were not associated with the competing event (e.g., csRH2 = 1), and therefore sdRH1 > csRH1.
>1	>1	<csRH1	Exposure associated with an increased cause-specific hazard rate for event	Because the exposure is associated with an increased cause-specific hazard rate for the competing event, the sdRH1 is less than what one would expect if the exposure were not associated with the competing event (e.g., csRH2 = 1), and therefore sdRH1 < csRH1.f

Abbreviations: _csRH₁, cause-specific relative hazard for event 1; _csRH₂, cause-specific relative hazard for event 2; _sdRH₁, subdistribution relative hazard for event 1.

^aWe refer to the time-averaged relative hazards, as proportionality of the cause-specific hazards does not imply proportionality of the subdistribution hazards and vice versa. Refer to Latouche et al. (47) and Beyersmann and Schumacher (30) for further details.

^bThe exact magnitude of the difference between _csRH₁ and _sdRH₁ depends on the level of _csRH₁ and _csRH₂ and the baseline cause-specific hazard rate, h₀₁(t), and h₀₂(t).

^cThe _csRH₁ is whether or not the exposure has an association with the event of interest. It cannot be used to make inferences about the cumulative incidence in the presence of competing risks (e.g., P(T < t, J = j) without additional information regarding the _csRH₂ and the magnitude of the baseline cause-specific hazard rate for the competing event.

^dThe _sdRH₁ reflects how the exposure is associated with the event of interest by incorporating both the association between the exposure and the event of interest and the association of the exposure with the competing event (which influences the risk set).

^eNote that the _sdRH₁ could be >1 if both the association of the exposure with the competing event (_csRH₂) was strong enough and the baseline cause-specific hazard rate for the competing event is of great enough magnitude.

^fNote that the _sdRH₁ could be <1 if both the association of the exposure with the competing event (_csRH₂) was strong enough and the baseline cause-specific hazard rate for the competing event is of great enough magnitude.

A caveat when applying the _sdCIF to other populations is that the transportability of the estimate may be questionable if the distribution of the competing events differs from the original population. This is because the risk sets for exposed and unexposed individuals will be impacted differently by a change in the distribution of competing events.

A unified regression approach

The 2 primary models developed for estimating _csRH and _sdRH depend upon proportional hazard assumptions. Because equations 1 and 3 are not equivalent, a proportional cause-specific hazards model does not necessarily imply a proportional subdistribution hazards model (29, 30). Although time interactions could be included in the model to account for nonproportionality, this can complicate interpretation.

An alternative approach is to consider more general models that do not constrain any of the hazard functions to be proportional. A mixture of distributions for competing risks was proposed by Cox in 1959 (31) and was later expanded through decomposing the _sdCIF as follows (17):

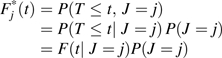(6)

and constructing likelihood contributions for the ith individual:

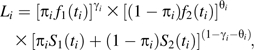(7)

where 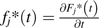for j = 1, 2 corresponds to a probability density function to model the jth event, S_j(t) is the corresponding survivor function P(T > t|J = j), π_i is the mixture probability P(J = 1), and γ_i and θ_i are indicator functions for J = 1 and J = 2, respectively.

Under this formulation, parametric distributions can be utilized to impose structure for f and π with parameters that can be linked to covariates. To model f (and S), a flexible parametric distribution, such as the generalized gamma distribution, can accommodate various shapes of the hazard function (32). A binary model can be constructed for the P(J = j) term to describe the occurrence for 2 events. Regression analysis can proceed by linking covariates to the parameters of these distributions (Web supplement).

This mixture model approach has a distinct advantage over other models: Both the cause-specific and subdistribution relative hazards _csRH_j and _sdRH_j may be derived and are not constrained to be constant over time. If a summary (over time) measure is desired, a time-weighted estimate can be constructed with confidence intervals obtained by bootstrap (33). Another advantage of the mixture model is that it is relatively easy to compare the subdistribution CIF, cause-specific hazards, or subdistribution hazards stratified by exposure and over time (34). Estimation of the parameters for the mixture model can be performed in SAS software by using the NLMIXED procedure and the log-likelihood function from equation 7.

Application

Prior studies have shown that HIV-infected individuals with past injection drug use are less likely to initiate effective therapy than those without (35–38) and are more likely to die in the era of highly active antiretroviral therapy (5, 38, 39). Yet, the comparison of treatment initiation by history of injection drug use when it has the potential to be the most effective (prior to AIDS or death) has not been undertaken.

Study population

The Women's Interagency HIV Study (WIHS) was established in August 1993 to investigate the impact of HIV infection on US women at 6 sites in New York (2 sites); Washington, DC; Los Angeles and San Francisco, California; and Chicago, Illinois. Details are provided elsewhere (40–43). In 1994–1995, 2,054 HIV-positive and 569 HIV-negative women were enrolled. Follow-up visits occur at 6-month intervals in which data are collected by structured interviews, physical examinations, and laboratory testing.

The study sample consisted of 1,164 women enrolled in WIHS, who were alive, infected with HIV, and free of clinical AIDS on December 6, 1995 (baseline), when the first protease inhibitor (saquinavir mesylate) was approved by the Federal Drug Administration. Women were followed until the first of the following: treatment initiation, AIDS diagnosis, death, or administrative censoring (September 28, 2006). Covariates included history of injection drug use at WIHS enrollment, whether an individual was African American, age, and CD4 nadir prior to baseline.

RESULTS

Individuals with and without an injection drug use history had similar nadir CD4 counts prior to baseline (Table 3). Women with an injection drug use history were more likely to be African American and older than those without an injection drug use history. Although the majority of women initiated treatment prior to clinical AIDS or death, this proportion was lower among those with a history of injection drug use. The proportion with AIDS or death prior to treatment was higher among those with injection drug use.

Table 3.

Characteristics for Women Enrolled in the Women's Interagency HIV Study on December 6, 1995, and Followed Through September 2006, United States

	No History of Injection Drug Use (n = 725)		History of Injection Drug Use (n  = 439)		Overall (N = 1,164)
	Median	Interquartile Range	Median	Interquartile Range	Median	Interquartile Range
Nadir CD4 count, no.	348	216–505	352	209–522	349	213–516
Age on December 6, 1995, years	33	29–39	40*	35–44	36	31–41
	No.	%	No.	%	No.	%
African American	399	55	273**	62	672	58
Initiated treatment prior to AIDS or death	469	65	210	48	679	58
AIDS or death prior to treatment	169	23	190	43	359	31

Abbreviations: AIDS, acquired immunodeficiency syndrome; HIV, human immunodeficiency virus.

*P < 0.001; **P = 0.017 for comparing those with and without a history of injection drug use.

Figure 3 shows both the estimated cause-specific and subdistribution cumulative incidences by outcome and injection drug use status. To illustrate the difference between the cause-specific and _sdCIFs, we estimated the _csCIF directly from the _csRH under the assumption of independence between events (Figure 3, A and C). However, the _sdCIF (Figure 3, B and D) can be estimated from the cause-specific proportional hazards model by taking extra steps (Web supplement) (27, 28). In addition, a nonparametric estimation of the subdistribution CIF was obtained by using an extension of the Kaplan-Meier methods to competing risks (2, 44). Regardless of the method (cause-specific proportional hazards model, subdistribution proportional hazards model, or mixture model) used for obtaining the subdistribution CIF, the estimated subdistributions were essentially equivalent to the extended Kaplan-Meier method for competing risks (P < 0.001 for both events comparing those with past injection drug use vs. those without) (2, 44).

Figure 3.

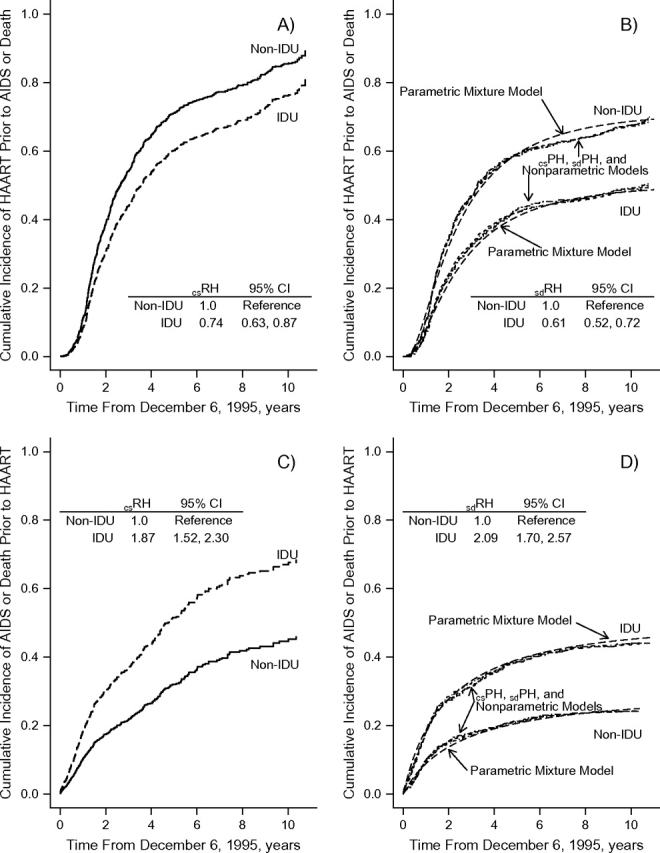
Cumulative incidence of treatment initiation prior to acquired immunodeficiency syndrome (AIDS) or death (A and B) and the cumulative incidence of AIDS or death prior to treatment (C and D) by injection drug use status and type of cumulative incidence (cause-specific, A and C; subdistribution, B and D; _csPH, from proportional cause-specific hazards model; _sdPH, from proportional subdistribution hazards model). The mixture model comprised a lognormal distribution for initiation of treatment and a generalized-gamma distribution for the time to AIDS or death prior to treatment initiation. CI, confidence interval; _csRH, cause-specific relative hazard; HAART, highly active antiretroviral therapy; IDU, injection drug use; _sdRH, subdistribution relative hazard.

The estimates of the _csRH and _sdRH from the semiparametric and parametric approaches are shown in Table 4 stratified by competing events. The parametric mixture model provided inferences essentially identical to the proportional hazards models. The _sdRH had a stronger association than the _csRH for both events. The _csRH_treatment was equal to 0.67; however, the _csRH_AIDS/death was 1.7. Therefore, as the subdistribution hazard maintains individuals who develop the competing event in the risk set (equation 3), this implies that individuals with an injection drug use history are maintained in the risk set in a greater proportion than those without a history of injection drug use. Thus, a greater relative change between the cause-specific and subdistribution hazards would be expected for those with an injection drug use history than for those without (i.e., a larger denominator among the injection drug use group because of a higher AIDS/death hazard rate). Therefore, the _sdRH_treatment should be less than the _csRH_treatment, which was observed (Table 4).

Table 4.

Effect of History of Injection Drug Use on the Proportion and Timing of Incident HIV Treatment Use and Incident AIDS or Death Among Women Within the Women's Interagency HIV Study, 1995–2006, United States^a

	History of Injection Drug Use Cause-specific Relative Hazard		History of Injection Drug Use Subdistribution Relative Hazard
	Estimate	95% Confidence Interval	Estimate	95% Confidence Interval
Time to treatment initiation prior to AIDS/death
Semiparametric proportional hazards modelb	0.67	0.57, 0.80	0.60	0.50, 0.71
Parametric mixture modelc	0.71	0.59, 0.85	0.60	0.50, 0.71
Time to AIDS or death prior to treatment initiation
Semiparametric proportional hazards modelb	1.71	1.37, 2.13	2.01	1.62, 2.51
Parametric mixture modelc	1.77	1.40, 2.27	2.02	1.62, 2.59

Abbreviations: AIDS, acquired immunodeficiency syndrome; HIV, human immunodeficiency virus.

^aModels are adjusted for age at study entry, race, and CD4 nadir prior to study entry; the CD4 nadir was included in the model to adjust for stage of disease in order to be able to appropriately compare those with and without a history of injection drug use.

^bSome indication of proportional hazards assumption may not hold; however, these differences were quantitative rather than qualitative (i.e., hazards do not cross).

^cA lognormal (for treatment) and generalized gamma (for AIDS/death) distribution was used for the parametric mixture model.

DISCUSSION

In this paper, we have discussed the 2 common methods for handling competing risks and their applications to regression settings. The _csRH and the _csCIF are familiar quantities because they reflect measures that are estimated when individuals with the competing event are censored. However, we have illustrated the utility of the subdistribution hazard and CIF as complementary measures of risk.

Should the _csRH_AIDS/death have been greater (e.g., 3.0), the arbitrary baseline hazard for AIDS/death > 0.2 (e.g., a constant 1.1) per year, and the observed _csRH_treatment = 0.67, then the _sdRH_treatment would have been lower than the 0.67. This would imply that, despite a direct association between injection drug use status and treatment initiation (_csRH_treatment = 0.67), individuals with an injection drug use (IDU) history were less likely to initiate treatment before disease progression (_sdCIF_IDU < _sdCIF_not-IDU as indicated by _sdRH_treatment < 1.0) and more likely to have HIV disease progression before therapy. However, the _csRH_treatment = 0.67 and the _csRH_AIDS/death = 1.71, which suggests that AIDS/death should contribute to an even lower _sdRH_treatment because those with past injection drug use had a higher cause-specific hazard rate for AIDS/death. The similarity of the _csRH_treatment and _sdRH_treatment implies that disease progression to AIDS/death did not greatly contribute to a further reduction in the association between injection drug use history and treatment initiation. This was due to the relatively low baseline hazard rate for AIDS/death; h₀₂(t) ranged from 0.157 to 0.224 per year. Thus, the _sdRH_treatment is only slightly stronger than that from the cause-specifc proportional hazards model (0.60 vs. 0.67, respectively). Beyersmann et al. (29) recently provide an alternative example where the difference between _csRH and _sdRH is large and they are in opposite directions.

The properties of the _csRH_j (no interpretation to _sdCIF without assumption) and _sdRH_j (translatable to _sdCIF) illustrate the circumstances in which the 2 measures of association may be most useful and therefore suggest a general guideline for use. The _csRH might be more applicable for studying the etiology of diseases, whereas the _sdRH might be more appropriate for predicting an individual's risk for an outcome or resource allocation. For example, the use of the antiretroviral drug abacavir has recently been associated with increased risk of myocardial infarction (45). Two competing questions can be framed: 1) Is the use of abacavir directly associated with myocardial infarction, and 2) regardless of the direct association, are individuals taking abacavir more likely to experience a myocardial infarction? For the first question, the _csRH may be more appropriate, as this measure will assess at any given time whether the individuals on abacavir have an increased instantaneous hazard rate for myocardial infarction among all individuals that have survived all events to this time point.

For the second question, the _sdRH is a better measure of association. This can be illustrated by assuming that abacavir is not directly associated with myocardial infarction (_csRH = 1 for association of abacavir with myocardial infarction). It remains possible that investigators may still expect a higher probability of myocardial infarction among those taking abacavir if individuals not on abacavir were more likely to die prior to a myocardial infarction. Consequently, the _sdRH for myocardial infarction would be >1 for those on abacavir, but it is by reducing mortality and keeping individuals alive to be able to experience a myocardial infarction. The latter knowledge may be useful in policy decisions.

We recognize that important issues such as left truncation and causality (46) as they pertain to competing risks have not been addressed here. Our goals were to describe and illustrate 2 common measures of association that may be used in the competing risk setting but that epidemiologists have avoided. The cause-specific hazard ratio and subdistribution hazard ratio are distinct, and the choice of approach should be driven by the scientific question. Future research should continue to explore the differences in approaches and expand the tools to understand and implement competing risk methods for epidemiologic data.

Glossary

Abbreviations

AIDS

acquired immunodeficiency syndrome

CIF

cumulative incidence function

_csCIF

cause-specific cumulative incidence function

_csRH

cause-specific relative hazard

HIV

human immunodeficiency virus

_sdCIF

subdistribution cumulative incidence function

_sdRH

subdistribution relative hazard

WIHS

Women's Interagency HIV Study

APPENDIX

This appendix further details the relation between the cause-specific hazard and the subdistribution hazard. Further details regarding the methods outlined within the main text may be found in the Web supplement data, which provide more rigorous details regarding the methods that may be useful for some readers but felt to be too technical such that the main points would be obscured to others. Additionally, the data used in the application are provided a long with code to implement competing risk analyses in R or SAS.

Relation between _csRH and _sdRH

Beyersmann et al. (29) noted that the _csRH is in good agreement with the _sdRH when there is no association of exposure and the competing event. To illustrate, let X be a binary exposure variable for 2 competing events. Let the _csRH(t) for event 1 and event 2 be equal to some constant, _csRH₁ and _csRH₂, respectively, and thus both events have proportional hazards across exposure status. Let the arbitrary baseline cause-specific hazard (i.e., when X = 0) for event 1 and event 2 be h₀₁(t) and h₀₂(t), respectively. Then, the hazards for those with X = 1 are h₁₁(t) = h₀₁(t) exp(βX) = h₀₁(t) × _csRH₁ and h₁₂(t) = h₀₂(t) exp(βX) = h₀₂(t) × _csRH₂ for events 1 and 2, respectively. Let λ₁(t) be the subdistribution hazard for event 1 and λ₀₁(t) and λ₁₁(t) be the subdistribution hazard for unexposed and exposed individuals, respectively. Beyersmann et al. (29) showed that the cause-specific hazard has the following general relation (not considering covariate X) with the subdistribution hazard for event 1:

(A1)

where $F_2^{\mathrm{*}}\left(t\right)$ is the subdistribution function for event 2, and S(t) is the net survival function. Thus, the cause-specific hazard for exposed individuals may be written as follows:

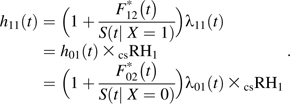(A2)

Thus, the _csRH₁ is as follows:

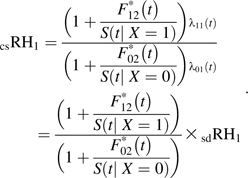(A3)

Note that the subdistribution equals the net survival multiplied by the cause-specific hazard (i.e., $F_{02}\left(t\right)={\displaystyle {\int }_0^{t}S\left(u|X=0\right)h_{02}\left(u\right)du\text{\hspace{0.17em}and\hspace{0.17em}}{F}_{12}\left(t\right)}={\displaystyle {\int }_0^{t}S\left(u|X=1\right)h_{12}\left(u\right)du}$). Thus, when h₀₂(t) is close to 0, the fractions within the parentheses in the numerator and in the denominator both tend toward 0 and _csRH₁ = _sdRH₁. Therefore, a low cause-specific hazard for the competing event can mitigate the effect of a large _csRH₂ that would contribute to the numerator in both the subdistribution, $F_{12}^{*}\left(t\right)$ and net survival among exposed individuals, S(t |X = 1). Additionally, Latouche et al. (47) showed through simulation the _csRH₁ ≈ _sdRH₁ when _csRH₂ = 1.