Abstract
A typical longitudinal study prospectively collects both repeated measures of a health status outcome as well as covariates that are used either as the primary predictor of interest or as important adjustment factors. In many situations, all covariates are measured on the entire study cohort. However, in some scenarios the primary covariates are time dependent yet may be ascertained retrospectively after completion of the study. One common example would be covariate measurements based on stored biological specimens such as blood plasma. While authors have previously proposed generalizations of the standard case–control design in which the clustered outcome measurements are used to selectively ascertain covariates (Neuhaus and Jewell, 1990) and therefore provide resource efficient collection of information, these designs do not appear to be commonly used. One potential barrier to the use of longitudinal outcome-dependent sampling designs would be the lack of a flexible class of likelihood-based analysis methods. With the relatively recent development of flexible and practical methods such as generalized linear mixed models (Breslow and Clayton, 1993) and marginalized models for categorical longitudinal data (see Heagerty and Zeger, 2000, for an overview), the class of likelihood-based methods is now sufficiently well developed to capture the major forms of longitudinal correlation found in biomedical repeated measures data. Therefore, the goal of this manuscript is to promote the consideration of outcome-dependent longitudinal sampling designs and to both outline and evaluate the basic conditional likelihood analysis allowing for valid statistical inference.
Keywords: Binary data, Longitudinal data analysis, Marginal models, Marginalized models, Outcome-dependent sampling, Time-dependent covariates
1. INTRODUCTION
We propose a retrospective, outcome-dependent sampling design for longitudinal binary response data when we are limited by the costs associated with exposure ascertainment. In this design, a subset of individuals from a cohort study are included in the outcome-dependent sample based on the values contained in their complete binary response vectors. We can properly account for the selective ascertainment with estimation based on maximum conditional likelihood, and we show that in realistic scientific settings we maintain nearly fully efficient estimates even when only a fraction of individuals from the original sample are included in the outcome-dependent sample.
Outcome-dependent (or biased) sampling is often used in epidemiological studies with binary response data. The case–control study (Anderson, 1972; Prentice and Pyke, 1979) is perhaps the most commonly used outcome-dependent sampling design, and from it many other designs have emerged. An outcome-dependent sampling design for correlated binary response data proposed by Neuhaus and Jewell (1990) samples individual clusters with probability based on the sum of components in the response vector. With this design and the assumption of an exchangeable within-cluster response dependence, certain regression parameters can be estimated with standard conditional logistic regression (CLR). The CLR approach implicitly removes clusters without response variation (e.g. outcome vector is all 0s or all 1s), and compared to estimation based on maximum likelihood of the generalized linear random intercept model, CLR has been shown to be efficient for parameters corresponding to covariates that vary predominantly within and not between clusters (Neuhaus and Lesperance, 1996; Neuhaus and Kalbfleisch, 1998). Outcome-dependent sampling schemes are designed to target covariate sampling at those participants with highly informative responses, and the work of Neuhaus and others makes clear that for time-varying covariate parameters with correlated response data, participants who do not experience response variation may be relatively uninformative.
Despite the work of Neuhaus and Jewell (1990), outcome-dependent sampling designs for repeated measures data do not appear to be commonly used. A major epidemiologic issue for the application of the design is the requirement that covariates must be able to be retrospectively ascertained. For any measurement that can only be collected in real time, such as a physical performance measure, the design cannot be used. However, with the recent instrumentation advances in molecular measurement technology (e.g. genotypes, protein signatures, and RNA expression) and the common storage of biological specimens, we feel that longitudinal outcome-dependent sampling designs warrant further consideration. We focus on 2 statistical variations of the original work of Neuhaus and Jewell: we discuss and evaluate conditional likelihood–based methods that permit quite flexible and computationally practical correlation model assumptions, and we focus on marginal regression models. We now comment on each of these aspects.
The original clustered data, conditional likelihood methods focused on a simple random intercept logistic regression model. Such a model conveniently allows use of standard CLR methods for analysis yet may be naively simple in terms of characterizing the correlation structure for longitudinal observations. Marginalized models (see Diggle and others, 2002, Section 11.3) are a relatively new and flexible class of models for correlated binary response data. They provide a fully parametric alternative to estimation with generalized estimating equations (Liang and Zeger, 1986) and a marginal model alternative to conditional generalized linear mixed models (GLMMs) (Stiratelli and others, 1984) or transition models. Furthermore, marginalized models for binary data now permit a flexible class of dependence models including random intercept (Heagerty, 1999), serial or Markov dependence (Heagerty, 2002), and mixed random intercept with serial dependence (Schildcrout and Heagerty, 2007). The flexibility in longitudinal dependence models allows selection of a valid likelihood that can properly characterize the common forms of longitudinal correlation encountered with serial binary data. The validity of the use of conditional likelihood for biased sampling critically depends on the proper specification of the full multivariate likelihood, and therefore, adequate flexibility is necessary to provide proper inference. Software for marginalized models is available as an R package and can be downloaded from http://faculty.washington.edu/heagerty.
Alternatively, one could consider conditionally specified GLMMs and the associated conditional likelihood analysis. GLMMs do allow generalization of the simple random intercept assumption by potentially allowing random slopes and/or autocorrelated serial processes in place of a (static) random intercept. In certain applications, the GLMM conditional regression coefficient may be of primary interest, while in other situations the marginal regression parameter may be of interest. Indeed, there is a large and sometimes contentious literature that compares and contrasts marginal and conditional approaches and it is not our goal to add to that discussion. We focus on marginalized models for 2 primary reasons: a sufficiently flexible class of correlation models have been developed and therefore correct likelihood specification is possible, and as opposed to GLMMs the regression parameter of interest has an interpretation (and value) that is separated from the dependence model assumptions.
We introduce the study design in Section 2 and discuss estimation with maximum conditional likelihood in Section 3. Operating characteristics of the design and associated estimators are explored in Section 4, and a strategy for study planning is proposed in Section 5. In Section 6, we illustrate the utility of the design in an analysis that examines the relationship between respiratory infections and short-term ambient ozone concentrations among children participating in the Children's Health Study (CHS; Peters and others, 1999a,b). A discussion follows in Section 7.
2. A LONGITUDINAL OUTCOME-DEPENDENT SAMPLING STUDY DESIGN
We propose an outcome-dependent sampling design for longitudinal binary response data, where the goal is efficient estimation of parameters for time-varying exposures that are expensive to measure. Though our interest is in longitudinal data, the results apply generally to correlated binary data. Considering individuals’ binary response vectors 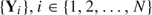 , from a prospective study, where i denotes participant, and
, from a prospective study, where i denotes participant, and 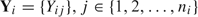 , we propose sampling only those participants who exhibit at least some response variation. If we let
, we propose sampling only those participants who exhibit at least some response variation. If we let 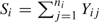 , we sample those for whom 0<Si < ni. Thus, we concentrate our limited resources on the exposure ascertainment of “responders” or those who we believe possess the vast majority of information toward estimating the regression target of inference.
, we sample those for whom 0<Si < ni. Thus, we concentrate our limited resources on the exposure ascertainment of “responders” or those who we believe possess the vast majority of information toward estimating the regression target of inference.
Anderson (1972) and Prentice and Pyke (1979) showed that we may use a prospective logistic regression model for case–control data to estimate parameters corresponding to log-odds ratios while ignoring the outcome-dependent sampling design. However, as discussed in Neuhaus and Jewell (1990) and Qaqish and others (1997), ignorance of the sampling mechanism is no longer possible for valid parameter estimation in the correlated data setting with cluster sampling. Toward estimating parameters with our approach, we modify the likelihood to acknowledge the ascertainment mechanism, and this allows valid estimation of all parameters.
3. ESTIMATION WITH MAXIMUM CONDITIONAL LIKELIHOOD
We now describe the conditional likelihood used to estimate regression parameters with our outcome-dependent sampling strategy. Let Nr denote the number of participants who exhibited at least some response variation during their observation period (e.g. all participants for whom 0<Si < ni). For participant i in the outcome-dependent sample, the joint multivariate distribution of Yi and Xi is 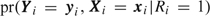 , where Ri is 1 if participant i is sampled and 0 otherwise. We factorize the joint distribution of the sampled participants prospectively in a manner similar to the way Prentice and Pyke (1979) did for univariate data,
, where Ri is 1 if participant i is sampled and 0 otherwise. We factorize the joint distribution of the sampled participants prospectively in a manner similar to the way Prentice and Pyke (1979) did for univariate data, 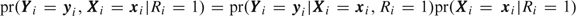 , and we base inference on the conditional probability,
, and we base inference on the conditional probability, 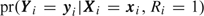 . Since Ri=1 corresponds to 0<Si < ni, the conditional likelihood for sampled participants is
. Since Ri=1 corresponds to 0<Si < ni, the conditional likelihood for sampled participants is
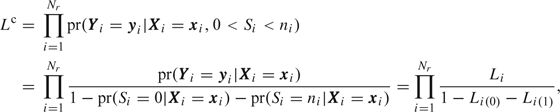 |
(3.1) |
where (1) Li, (2) Li(0), and (3) Li(1) correspond to participant i‘s contribution to the likelihood if simple random subsampling was done (1) in general, (2) if Si=0, and (3) if Si=ni. The denominator corrects for the ascertainment mechanism. Note that the conditional likelihood is a straightforward and computationally simple modification of the prospective likelihood (i.e. the correction requires additional evaluation of the terms Li(0) and Li(1)). Therefore, conditional likelihood computations are easily obtained provided the likelihood calculations for 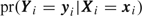 are available.
are available.
3.1. Likelihood factorization
In Section 3, we described the conditional likelihood used to estimate parameters with the proposed study design. While conditional maximum likelihood estimates for the outcome-dependent sample are consistent for the same quantities as maximum likelihood estimates for the original cohort, the statistics upon which we base inference are different. To gain insight into the scenarios under which our procedure is efficient, we use a likelihood factorization. We factorize the likelihood from the original cohort (L) into 2 components: (1) the conditional likelihood (Lc) and (2) a “summary” multinomial likelihood (Ls).
If we reorder participant identifiers so that participants iϵ{1, 2,…,Nr:Nr<N} exhibit response variation (e.g. 0<Si<ni), participants iϵ{Nr+1, …,N0:Nr+1≤N0 < N} exhibit no response variation with Si=0, and participants iϵ{N0+1,…, N} exhibit no response variation with Si=ni, then it can be shown that the likelihood for the parameters given the original cohort data, L, can be factorized as follows (see Appendix for details):
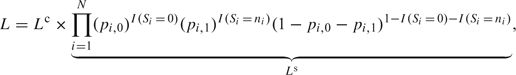 |
(3.2) |
where I(·) is 1 if · is true and 0 otherwise and Lc is the conditional likelihood based on the outcome-dependent sample. The contribution, Ls, is the likelihood for parameters in a trinomial summary distribution, where 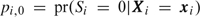 and
and 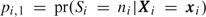 . If l, lc, and ls represent the associated log-likelihoods and θ is the parameter vector, then the log-likelihood is the sum l=lc+ls, the score vector is
. If l, lc, and ls represent the associated log-likelihoods and θ is the parameter vector, then the log-likelihood is the sum l=lc+ls, the score vector is 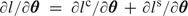 and the expected information matrix is
and the expected information matrix is 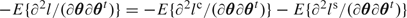
Information loss with our design occurs to the extent that the coarse summary indicators, I(Si=0), I(Si=ni), and 1−I(Si=0)−I(Si=ni), contain information about the parameters of interest. By drawing analogy to discussions of semi-individual–level studies (e.g. Sheppard, 2003), we expect the covariate series sum for each participant, 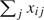 to be the key piece of information contained in xi for estimating model parameters from Ls. To demonstrate, let
to be the key piece of information contained in xi for estimating model parameters from Ls. To demonstrate, let 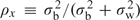 denote the intracluster correlation in covariate
denote the intracluster correlation in covariate 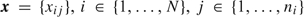 , where for equally sized clusters, σw2 is the mean within-participant variance in x and σb2 is the variance of participant-specific means. If ρx=0 and clusters are of equal size, then
, where for equally sized clusters, σw2 is the mean within-participant variance in x and σb2 is the variance of participant-specific means. If ρx=0 and clusters are of equal size, then 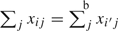 for all i≠i′, and we expect there to be little to no information about the regression parameter in Ls. Therefore, nearly all information in L may be contained in Lc. Alternatively, if ρx=1,
for all i≠i′, and we expect there to be little to no information about the regression parameter in Ls. Therefore, nearly all information in L may be contained in Lc. Alternatively, if ρx=1, 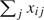 varies substantially from participant to participant, and the summary model may contain a large amount of information toward estimating the covariate parameter resulting in significant efficiency losses with the conditional likelihood approach. The value of ρx has been shown to impact operating characteristics of a number of estimators for correlated data models (e.g. Fitzmaurice, 1995; Mancl and Leroux, 1996; Schildcrout and Heagerty, 2005).
varies substantially from participant to participant, and the summary model may contain a large amount of information toward estimating the covariate parameter resulting in significant efficiency losses with the conditional likelihood approach. The value of ρx has been shown to impact operating characteristics of a number of estimators for correlated data models (e.g. Fitzmaurice, 1995; Mancl and Leroux, 1996; Schildcrout and Heagerty, 2005).
We now describe the information decomposition as a function of ρx graphically using profile likelihood surface plots. For illustration, we consider the first-order, marginalized transition model (Azzalini, 1994; Heagerty, 2002), and for each of ρx={0, 0.5, 1}, we simulated a single data set of N=400 individuals with ni=n=14 repeated measurements per individual. The data-generating model is given by
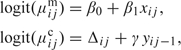 |
(3.3) |
where β0,β1,γ)=(−2.5, 0.5, 3.0) and xij is normally distributed. The value Δij links μijm and μijc, and for further discussion see Heagerty (2002). The original cohort log-likelihood (l), the conditional log-likelihood (lc), and summary log-likelihood (ls) were examined using a grid search on (β0, β1) values. Log-likelihood values represented by each grid point were calculated using profile likelihood by fixing the values of β0 and β1 and maximizing l and lc with respect to the nuisance dependence parameter γ. The ls value was taken to be the difference between the maximized l and lc values once their global maxima were aligned.
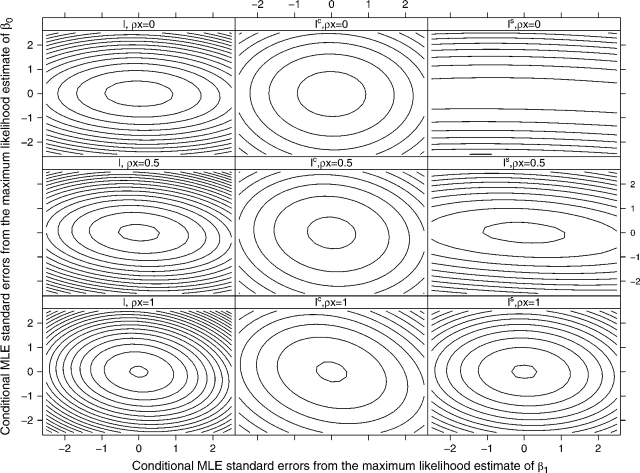
Figure 1 displays contours of the log-likelihood surfaces. The first, second, and third rows of these plots correspond to log-likelihood surfaces when ρx was set equal to 0, 0.5, and 1, respectively, and the columns represent l, lc, and ls from left to right. Contours are separated by 1-unit differences in maximized log-likelihood values, with β1 on the x-axis and β0 on the y-axis. The ranges of all axes for a given ρx value (within a row) were chosen to be 5 conditional maximum likelihood estimator standard errors wide. Recall that our primary interest is in estimates of β1.
Fig. 1.
Profile log-likelihood surface plots: A grid search was used for combinations of β0 and β1 values, and log-likelihoods were maximized with respect to the marginalized transition model dependence parameter γ. Panels on the left and center denote the original cohort log-likelihood surfaces and the outcome-dependent sample conditional log-likelihood surfaces, respectively. Both sets of plots have been centered at their maxima. The panels on the right represent the summary likelihood or the difference between the maximum likelihood and the conditional maximum likelihood surfaces. The top, middle, and bottom rows depict surfaces for which ρx values are equal to 0, 0.5, and 1, respectively. Each contour represents a log-likelihood value difference of 1, and the range (width and height) for all plots in the same row is 5 conditional maximum likelihood standard error estimates wide. 1
When ρx=0, ls (upper right panel) contained almost no information about β1, while lc and l contained approximately equal amounts of information (e.g. the curvature in the β1 direction was approximately equal in the upper left and upper center panels). However, lc contained far less information than l for estimating β0, as evidenced by the substantial difference in curvature in the β0 direction between the top center and top left panels. Equivalently, in ls there was significant curvature in the β0 direction (upper right panel).
In the second and third rows of this figure, we illustrate that ls curvature in the β1 direction grew with ρx (moving from the top right to lower right panels). Thus, as ρx increased from 0 to 1, proportionately less information about β1 from l was contained in lc.
Using the likelihood factorization, we have shown that the full likelihood is the product of the conditional likelihood and a summary likelihood. This allows a characterization of situations under which our selective ascertainment mechanism and conditional likelihood approach are relatively efficient. Our study design will likely be most efficient when ρx for the predictor of interest is close to zero. If it is not, substantial efficiency losses may be incurred and the proposed design would not be recommended. A more thorough examination is described in Section 4.
4. RELATIVE EFFICIENCY VERSUS A FULL COHORT ANALYSIS
Based on the results of Section 3.1, we presume that the utility of our study design depends highly on the distribution of the target covariates. To examine the impact that select characteristics of a data set have on the relative efficiency of maximum conditional likelihood estimators, we conducted a series of Monte Carlo calculations. We study the impact of (1) intracluster correlation in the covariate, x, ρxϵ{1, 0.5,0}; (2) number of participants, Nϵ{400, 4000}; (3) number of repeated measurements per participant, ni=nϵ{7, 14}; (4) degree of response dependence, γϵ{1.5, 3.0}; (5) covariate effect size, β1ϵ{0.15, 0.50}; and (6) variation in cluster size niϵ{14, U(5, 23)}. Calculations were based on the marginalized transition model described in Section 3.1.
Our primary interest was in the efficient estimation of β1. The intercept, β0, was set to a value that yielded approximately 50% of participants in the outcome-dependent sample. For the scenario with N=400 participants, average variances were calculated over 1000 replications, and with N=4000, 500 replications were used. Relative variance (RV) and relative root mean square error (RRMSE) are defined as 100 times the average variance and root mean square error estimates based on maximum likelihood using the original cohort divided by the average variance and root mean square error estimates based on maximum conditional likelihood using the outcome-dependent sample.
Table 1 shows the results from the relative efficiency study. Note that parameter estimates were approximately unbiased. Variance estimates (not shown) were also approximately unbiased, although a 5% bias was observed in the maximum conditional likelihood estimate of var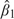 when ρx=1 and N=400. This may be due to relatively small sample size. For the intercept parameter, it is clear that estimates based on the outcome-dependent sample are far less efficient than those based on the original cohort analysis. The same is true for β1 when ρx=1. However, with proportionately more within-participant variation in the covariate, relative efficiency (as defined by RV and RRMSE) of the outcome-dependent sampling design increases, and when ρx=0, the efficiency is very high. This implies that 50% of participants who did not exhibit response variation were almost completely uninformative for estimating the time-varying covariate regression parameter. Even when ρx=0.5, RVs were nearly 75%, indicating that the “nonresponders” were relatively but not completely uninformative.
when ρx=1 and N=400. This may be due to relatively small sample size. For the intercept parameter, it is clear that estimates based on the outcome-dependent sample are far less efficient than those based on the original cohort analysis. The same is true for β1 when ρx=1. However, with proportionately more within-participant variation in the covariate, relative efficiency (as defined by RV and RRMSE) of the outcome-dependent sampling design increases, and when ρx=0, the efficiency is very high. This implies that 50% of participants who did not exhibit response variation were almost completely uninformative for estimating the time-varying covariate regression parameter. Even when ρx=0.5, RVs were nearly 75%, indicating that the “nonresponders” were relatively but not completely uninformative.
Table 1.
Percent bias in conditional maximum likelihood estimates based on the outcome-dependent sample (ODS) and maximum likelihood estimates based on the original cohort (OC), and the RVs and RRMSEs from the 2 approaches. Statistics are reported as percentages, and empirical variances (as opposed to average estimated variances) are used in calculations. RV and RRMSE are defined as 100 times the estimate based on the OC analysis divided by the estimate based on the ODS analysis. For N = 400 (N = 4000), we used 1000 (500) replicates
|
β0 |
β1 |
|||||||||||||
| Percent bias |
Relative efficiency |
Percent bias |
Relative efficiency |
|||||||||||
| N | ni | γ | ρx | β0 | β1 | Ave Nr | OC | ODS | RV | RRMSE | OC | ODS | RV | RRMSE |
| As a function of ρx | ||||||||||||||
| 4000 | 14 | 1.5 | 1 | − 2.75 | 0.15 | 2034 | 0 | 0 | 32 | 55 | − 1 | 0 | 37 | 60 |
| 0.5 | 2050 | 0 | 0 | 33 | 57 | − 1 | − 1 | 74 | 85 | |||||
| 0 | 2046 | 0 | 0 | 32 | 56 | 1 | 1 | 100 | 99 | |||||
| 400 | 14 | 1.5 | 1 | − 2.75 | 0.15 | 203 | 0 | 0 | 31 | 54 | − 1 | − 2 | 37 | 62 |
| 0.5 | 205 | 0 | 0 | 32 | 56 | 1 | 1 | 74 | 87 | |||||
| 0 | 204 | 0 | 0 | 32 | 59 | 0 | 1 | 99 | 100 | |||||
| As a function of ni, γ, β1 | ||||||||||||||
| 4000 | 14 | 1.5 | 0 | − 2.75 | 0.15 | 2046 | 0 | 0 | 32 | 56 | 1 | 1 | 100 | 99 |
| 0.5 | 2180 | 0 | 0 | 38 | 61 | 0 | 0 | 98 | 100 | |||||
| 4000 | 7 | 1.5 | 0 | − 2 | 0.15 | 1894 | 0 | 0 | 30 | 56 | 1 | 1 | 99 | 101 |
| 0.5 | 2015 | 0 | 0 | 34 | 61 | 0 | 0 | 95 | 97 | |||||
| 4000 | 14 | 3 | 0 | − 2.5 | 0.15 | 1782 | 0 | 0 | 30 | 54 | 0 | 0 | 99 | 100 |
| 0.5 | 1976 | 0 | 0 | 37 | 60 | 0 | 0 | 96 | 97 | |||||
| 4000 | 7 | 3 | 0 | − 1.75 | 0.15 | 1477 | 0 | − 1 | 26 | 47 | 0 | − 1 | 98 | 98 |
| 0.5 | 1685 | 0 | − 1 | 33 | 55 | 0 | 0 | 89 | 94 | |||||
| 400 | 14 | 1.5 | 0 | − 2.75 | 0.15 | 204 | 0 | 0 | 32 | 59 | 0 | 1 | 99 | 100 |
| 0.5 | 218 | 0 | 0 | 38 | 60 | 0 | 0 | 98 | 99 | |||||
| 400 | 7 | 1.5 | 0 | − 2 | 0.15 | 189 | 0 | 1 | 29 | 54 | 0 | 0 | 99 | 100 |
| 0.5 | 202 | 0 | 1 | 34 | 57 | 0 | 0 | 94 | 96 | |||||
| 400 | 14 | 3 | 0 | − 2.5 | 0.15 | 178 | 0 | 0 | 30 | 53 | 1 | 1 | 99 | 100 |
| 0.5 | 198 | 0 | 1 | 37 | 63 | 1 | 1 | 96 | 98 | |||||
| 400 | 7 | 3 | 0 | − 1.75 | 0.15 | 148 | 0 | 0 | 24 | 46 | 2 | 2 | 98 | 99 |
| 0.5 | 169 | 0 | 0 | 32 | 54 | 0 | 0 | 89 | 93 | |||||
| As a function of ni | ||||||||||||||
| 4000 | 14 | 3 | 0 | − 2.5 | 0.5 | 1976 | 0 | 0 | 37 | 60 | 0 | 0 | 96 | 97 |
| U(5, 23) | 1896 | 0 | 0 | 42 | 66 | 0 | 0 | 97 | 98 | |||||
| 400 | 14 | 3 | 0 | − 2.5 | 0.5 | 198 | 0 | 1 | 37 | 63 | 1 | 1 | 96 | 98 |
| U(5, 23) | 189 | 0 | 0 | 42 | 63 | 0 | 0 | 97 | 98 | |||||
The relative efficiency of our study design depended to a far lesser degree on the other design features studied, including sample size. There was some evidence that greater response dependence (larger γ values) along with larger β1 values led to slightly lower relative efficiency; however, the impact was small in comparison to the effect of ρx.
An important scenario under which the proposed design will be attractive is in the examination of a time-varying covariate by genotype or biomarker interaction. In this scenario, the exposure may be relatively easy to ascertain, but the genetic or biomarker measurement is costly. Again, we considered the first-order marginalized transition model, but with the following mean model:
For the time-varying exposure xij, ρx was set to 0, and I(Gi=1) was a binary value for the time-invariant group (or genotype) covariate. Our interest is in the parameters describing sensitivity to fluctuations in exposure (β1 and β3). The mean model parameters were fixed at the following values: β0=−2.75, β1=0.15, β2=1.25, β3=0.35, and the transition component γ was set to 3. We studied scenarios in which N equals 400 and 4000 participants in the original cohort and Gi=1 in one-fourth of participants. Results of our relative efficiency study were nearly identical for the N=4000 and N=400 cases. The rounded relative efficiencies of our design and analysis to the original cohort analysis for β0, β1, β2, and β3 were 35%, 100%, 52%, and 99%, respectively. These results were anticipated as again we find that efficiency is high for covariates that vary exclusively within participants and is low for those that vary exclusively between participants.
It is worth noting that because participants with Gi=1 had a greater predisposition for symptoms than those with Gi=0 (β2=1.25) and because they were more susceptible to the effects of xij (β3=0.35), they represented 36% of participants in the outcome-dependent samples on average as opposed to 25% in the original cohort (i.e. they were oversampled in the outcome-dependent sample). If the effect of Gi were such that they were undersampled, the relative efficiency of the interaction estimate may not be as impressive as we see in this example.
5. STUDY PLANNING/DESIGN FEASIBILITY
We have proposed a design for settings in which baseline covariates and longitudinal follow-up are available for all participants, but where we do not have measurement of a key exposure. During the planning phase of the study, it is possible to implement Monte Carlo techniques to examine the feasibility of obtaining relatively efficient inference using an outcome-dependent sampling design. Specifically, with the baseline and longitudinal data, we can compute the precision (or power) that would be expected if an outcome-dependent sampling design was adopted. In order to conduct such a sampling design evaluation, we need to presume a distribution for the not yet ascertained covariate and then randomly assign a realization from the covariate distribution given the baseline covariates and longitudinal data. For each such realization, we can then conduct both the full cohort and the outcome-dependent sample analyses and compare estimated standard errors. Replicating the approach and calculating average estimated variances allow study planners to consider whether the anticipated exposure effects and interactions are likely to be detected. Simulation under the null hypothesis is particularly straightforward since covariates can be drawn from their marginal distribution (conditional on baseline covariates). More computational work is necessary to simulate covariates under general effect sizes since the distribution of the covariates given the outcomes needs to be determined using both the conditional, [Yi|Xi], and the marginal covariate distribution, [Xi]. This general design evaluation approach can be used for a variety of presumed covariate distributions and anticipated effect sizes, and we discuss this further in context of an example in Section 6.1.
6. EXAMPLE: AIR POLLUTION EPIDEMIOLOGY
To illustrate a circumstance in which the proposed design could be implemented, we considered a subset of the children participating in the CHS. CHS aims to examine the chronic effects of air pollution on children residing in Southern California and details about this cohort, and the study design can be found in Peters and others (1999a,b). The data set we considered was provided by Professor Kiros Berhane and as stated by Berhane, “… is only intended to facilitate discussions on statistical methodology.” It pertains to 1600 selected fourth and seventh graders at 5 annual clinic visits from 1993 to 1997. Approximately, 300 of these participants were removed due to missingness of key exposures or inadequate follow-up.
The goal of our analysis was to examine the extent to which respiratory infections, assessed at the time of the 5 annual clinic visits for each participant, were related to short-term ozone concentrations (average of daytime ozone concentration the day of and the 3 days preceding the clinic visits). The respiratory infection outcome was binary and was ascertained at the time of each visit. Since ozone is a respiratory irritant, susceptible populations such as adolescents with asthma are thought to be particularly sensitive to its effects (see, e.g. Yu and others, 2000; Mortimer and others, 2002; Gent and others, 2003; Bell and others, 2005). Therefore, we consider a substudy that seeks to evaluate whether pollution-by-asthma status interactions appear to be significant in this population. In CHS, the asthma status was determined for all participants, and therefore, we can evaluate inference using the full cohort and using an outcome-dependent subsample for which asthma would be hypothetically ascertained were it not already available. Determination of patient comorbidity status is one example of a variable that may be moderately expensive to obtain due to diagnostic procedures and therefore represents a candidate covariate for the proposed design. A clinical diagnosis of asthma is based on a patient's symptoms, medical history, a comprehensive physical examination, and laboratory tests that measure pulmonary (lung) function. Thus, determination of asthma status requires a clinical visit with diagnostic evaluation and is potentially costly in terms of patient and family time and utilization of medical resources.
In many settings of air pollution epidemiology, ambient concentration effects on health outcomes are thought to be small while the potential for confounding associated with season is enormous. We acknowledged the potential impact of seasonal confounding in 2 ways. First, we included the 30-day average ozone concentrations in our regression models. Since ozone concentrations are highly associated with season, the adjustment should acknowledge a portion of seasonal effects. Second, we decomposed 4-day average concentration into between- and within-participant components and modeled them as separate terms. Specifically, for participant i at year j, ozone concentration, xij, was decomposed as follows: xij=(xij−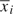 )+
)+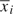 . The between-participant component,
. The between-participant component, 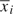 , which was participant i‘s average exposure across annual visits, hasρx=1, and the within-participant component xij−
, which was participant i‘s average exposure across annual visits, hasρx=1, and the within-participant component xij−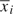 has ρx=0. Since these components are orthogonal to one another and seasonal confounding tends to operate at the between-participant level, parameter estimates for xij−
has ρx=0. Since these components are orthogonal to one another and seasonal confounding tends to operate at the between-participant level, parameter estimates for xij−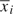 are likely to be less confounded by season. As discussed by Neuhaus and Kalbfleisch (1998), avoiding this decomposition and simply modeling xij implicitly imply that between-participant and within-participant effects are identical. Such an assumption may not be reasonable in a number of settings. In the present analysis, we are interested in the within-participant ozone concentration, xij−
are likely to be less confounded by season. As discussed by Neuhaus and Kalbfleisch (1998), avoiding this decomposition and simply modeling xij implicitly imply that between-participant and within-participant effects are identical. Such an assumption may not be reasonable in a number of settings. In the present analysis, we are interested in the within-participant ozone concentration, xij−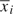 , and its interaction with the binary asthma status covariate.
, and its interaction with the binary asthma status covariate.
Characteristics of the study population for the original cohort and for the outcome-dependent sample are shown in Table 2. Of the 1286 participants who were in the original sample, 682 (53%) exhibited at least some response variation, so savings with the proposed design could be significant. The proportion of participants who had been diagnosed with asthma at baseline, which is assumed to be unknown at study conception, was similar between the 2 samples, as are most covariates. Since our conditional likelihood acknowledges the study design, it does not matter that there are more males in the original sample than in the outcome-dependent sample. However, we may anticipate that gender has an impact on the probability of respiratory infection.
Table 2.
Baseline characteristics of the study population in the original cohort (OC) and the outcome-dependent sample (ODS). The latter is a subset of the former, and binary covariates are shown as proportions. There were 2 cohorts in this study sample, fourth graders and seventh graders. We show the proportion in the seventh grade. We also display the 25th, 50th, and 75th percentiles of the 4-day average ozone concentrations across all observed values
| OC | ODS | |
| Number of subjects | 1286 | 682 |
| Number of observations | 5341 | 2886 |
| Proportion asthmatic at baseline | 0.23 | 0.24 |
| Proportion male | 0.50 | 0.44 |
| Proportion not white | 0.15 | 0.14 |
| Proportion with secondhand smoke exposure | 0.38 | 0.36 |
| Proportion in grade 7 | 0.34 | 0.37 |
| Ozone concentrations (ppb) | (35, 46, 61) | (34, 44, 58) |
Table 3 shows the results of the analysis. For illustration, we considered the marginalized transition and latent variable model (Schildcrout and Heagerty, 2007) which captures longitudinal response dependence using a Markov transition component as well as a random intercept. Parameter estimates are displayed for all covariates, and estimated, model-based standard errors are shown in parentheses. While not shown, robust standard errors (White, 1982) agreed closely with model-based standard errors. There appeared to be serial response dependence as the transition component parameter estimate 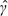 was approximately 0.6 using both approaches. However, long-range dependence appeared minimal as the variance component estimate,
was approximately 0.6 using both approaches. However, long-range dependence appeared minimal as the variance component estimate, 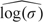 , was approximately −1.4. The existence of serial association is common in longitudinal data, and decaying dependence is not captured by assuming a simple random intercept–only model. With both modeling approaches, we would conclude that there is insufficient evidence to support an association between respiratory infections and short-term ozone concentrations irrespective of asthma status. Additionally, we cannot conclude that there is a difference between asthmatic and nonasthmatic children with respect to ozone sensitivity. However, it is clear that the proposed design performed as we had expected. For exclusively within-participant covariates (where ρx=0), there was very little information loss associated with the proposed design. Estimated standard errors for the main effect of within-participant ozone were 0.046 and 0.049 for the original cohort and the outcome-dependent sample–based analyses, respectively. Likewise, estimated standard errors were nearly identical for the estimated interaction with asthma status. As expected, our design was inefficient for participant-level covariate effects as evidenced by estimated standard errors which were nearly twice those obtained from the full cohort analysis.
, was approximately −1.4. The existence of serial association is common in longitudinal data, and decaying dependence is not captured by assuming a simple random intercept–only model. With both modeling approaches, we would conclude that there is insufficient evidence to support an association between respiratory infections and short-term ozone concentrations irrespective of asthma status. Additionally, we cannot conclude that there is a difference between asthmatic and nonasthmatic children with respect to ozone sensitivity. However, it is clear that the proposed design performed as we had expected. For exclusively within-participant covariates (where ρx=0), there was very little information loss associated with the proposed design. Estimated standard errors for the main effect of within-participant ozone were 0.046 and 0.049 for the original cohort and the outcome-dependent sample–based analyses, respectively. Likewise, estimated standard errors were nearly identical for the estimated interaction with asthma status. As expected, our design was inefficient for participant-level covariate effects as evidenced by estimated standard errors which were nearly twice those obtained from the full cohort analysis.
Table 3.
Analysis of the children participating in CHS. We show parameter estimates (standard errors) using maximum likelihood on the original cohort (OC) and maximum conditional likelihood on the outcome-dependent sample (ODS). The OC pertains to 1286 subjects, and the ODS pertains to the 698 subjects who exhibited response variation among all subjects. We also display the observed ρx for each covariate
| Covariate | ρx | OC | ODS |
| Intercept | 1 | − 1.235 (0.079) | − 1.476 (0.202) |
| Asthmatic | 1 | 0.112 (0.091) | 0.291 (0.182) |
| p = 0.15† | 0.110 | 0.225 | |
| p = 0.23† | 0.093 | 0.191 | |
| p = 0.30† | 0.085 | 0.175 | |
| Within-subject, 4-day average ozone (per 10 ppb) | 0 | − 0.007 (0.046) | 0.037 (0.049) |
| p = 0.15† | 0.045 | 0.047 | |
| p = 0.23† | 0.046 | 0.048 | |
| p = 0.30† | 0.047 | 0.049 | |
| Asthmatic × within-subject ozone | 0 | 0.037 (0.064) | 0.039 (0.061) |
| p = 0.15† | 0.077 | 0.076 | |
| p = 0.23† | 0.065 | 0.064 | |
| p = 0.30† | 0.060 | 0.059 | |
| Between-subject, 4-day average ozone (per 10 ppb) | 1 | 0.048 (0.057) | 0.113 (0.080) |
| Thirty-day average ozone (per 10 ppb) | 0.72 | − 0.165 (0.06) | − 0.231 (0.067) |
| Male | 1 | − 0.468 (0.079) | − 0.563 (0.171) |
| Noncaucasian | 1 | − 0.377 (0.116) | − 0.377 (0.245) |
| Grade 7 (versus grade 4) | 1 | 0.183 (0.081) | 0.008 (0.168) |
| Secondhand smoke exposure | 1 | − 0.039 (0.081) | 0.104 (0.167) |
| Dependence model parameters | |||
| γ | 0.603 (0.110) | 0.603 (0.115) | |
| log(σ) | − 1.427 (0.848) | − 1.427 (0.627) |
Standard error estimates from our feasibility check, where p is the presumed proportion of asthmatic children in the OC.
6.1. A retrospective look at study feasibility
As discussed in Section 5, prior to ascertaining asthma status on individuals, it may be advisable to use Monte Carlo techniques on assumed prevalences of being asthmatic along with the available data to examine the expected regression standard errors for key parameter estimates under both full cohort and outcome-dependent sampling. For the purpose of this exercise, we assumed 3 asthma status prevalences: p=0.15, p=0.23 (the actual value), and p=0.30. In Table 3, we display the square root of the average model-based variances (across 400 replicates) for key parameters. Note that estimated standard errors approximated the observed standard errors very well and suggested that the outcome-dependent sampling design would retain high efficiency for the target parameters. We believe that part of the reason the feasibility check performed as well as it did was due to the fact that there was no evidence in favor of the alternative hypothesis for the asthma status and the asthma status by ozone concentration interaction effects, and the null hypothesis was implicitly assumed in this feasibility check. Utilization of the general approach under specific alternative hypotheses would require additional computational work to obtain the necessary joint distribution of outcomes and covariates but would be appropriate in order to obtain power calculations.
7. DISCUSSION
We have introduced an outcome-dependent sampling design for longitudinal or correlated binary response data, where study resources are limited by the cost of exposure ascertainment. It is a special case of the design proposed by Neuhaus and Jewell (1990) which suggested to sample with probability proportional to the number of positive responses within the cluster. It may also be likened to the longitudinal data case–cohort design proposed by Pfeiffer and others (2005). By sampling those who exhibit response variation and by constructing a likelihood that conditions on the sampling design, we are able to estimate all parameters that can be estimated from the original cohort via maximum likelihood analysis. With properly specified dependence models, mean model parameter estimates were shown to be highly efficient for targets in which variation occurs exclusively within participant (e.g. ρx≈0). They are also highly efficient for group by time-varying covariate interactions.
We discussed our design in generality; however, in simulations and in the example we appealed to marginalized models rather than GLMMs. While the design and estimation strategy can be applied to both classes of models, one reason we chose the marginalized model approach is that, as opposed to GLMMs, mean model parameter interpretations do not rely on the specific dependence model choice. In the outcome-dependent sampling setting, this allows use of conditional likelihood estimation under alternative dependence model specifications in order to evaluate the sensitivity of inference to model assumptions without changing the interpretation (or value) of the true target regression parameter. Such flexibility can be important since the correct specification of the longitudinal data likelihood is required to ensure valid regression inference under the biased sampling.
In many studies, the time-varying target exposure is not mean balanced (e.g. ρx≠0). However, it is often reasonable to decompose the covariate into between- and within-participant components. This decomposition is discussed in Neuhaus and Kalbfleisch (1998). The advantage of avoiding this decomposition (e.g. increased power) is in the assumption that we are able to combine between- and within-participant covariate variations in order to estimate the corresponding parameter. In many circumstances, this assumption may not be reasonable due to unmeasured confounding and an induced regression model that contains the mean of the covariate (Palta and Yao, 1991). Even in air pollution epidemiology, where between- and within-participant health effects of air pollutants are thought to be reasonably close to one another, the potential for differential confounding at the between- versus within-participant level is substantial (see Sheppard, 2003). Thus, in many circumstances, this decomposition is reasonable, and in such cases, our study design is highly efficient.
With the growing availability of long-term cohort studies and electronic medical and hospital records, the retrospective construction of longitudinal studies is now relatively easy. We believe that our design and associated analysis procedure can be useful in a large number of such settings in which all the information needed for the analysis is available except for key exposures. By sampling only a fraction of the most informative participants, we may save a large amount in costs while losing very little information toward our estimation target.
FUNDING
This research was supported by grant HL 72966 from the National Heart Lung and Blood Institute.
Acknowledgments
Conflict of Interest: None declared.
Appendix
Likelihood decomposition
Let 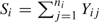 denote the sum of binary response for participant i, and assume that we reorder identification numbers so that participants iϵ{1, 2, …, Nr:Nr<N} exhibit response variation (e.g. 0<Si<ni), participants iϵ{Nr+1,…,N0:NR+1≤N0 < N} exhibit no response variation with Si=0, and participants iϵ{N0+1,…,N} exhibit no response variation with Si=ni. We factorize the original cohort likelihood, L, into the conditional likelihood, Lc, and the summary likelihood, Ls, as follows:
denote the sum of binary response for participant i, and assume that we reorder identification numbers so that participants iϵ{1, 2, …, Nr:Nr<N} exhibit response variation (e.g. 0<Si<ni), participants iϵ{Nr+1,…,N0:NR+1≤N0 < N} exhibit no response variation with Si=0, and participants iϵ{N0+1,…,N} exhibit no response variation with Si=ni. We factorize the original cohort likelihood, L, into the conditional likelihood, Lc, and the summary likelihood, Ls, as follows:
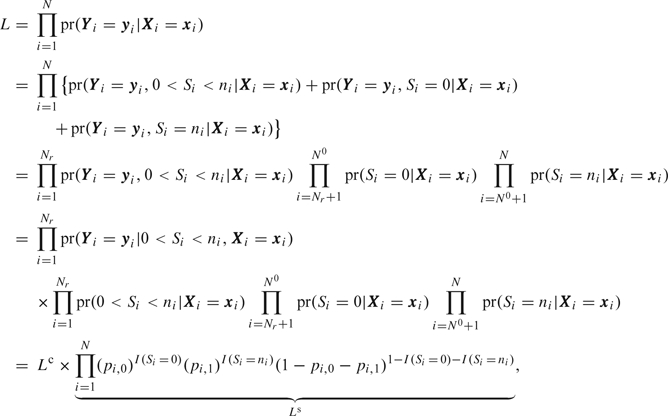 |
where Lc represents the conditional likelihood based on the subcohort that has been selectively ascertained. The contribution, Ls, is the likelihood for parameters in a trinomial summary distribution, and 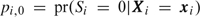 and
and 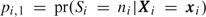 .
.
References
- Anderson JA. Separate sample logistic discrimination. Biometrika. 1972;59:19–35. [Google Scholar]
- Azzalini A. Logistic regression for autocorrelated data with application to repeated measures. Biometrika. 1994;81:767–775. [Google Scholar]
- Bell M, Dominici F, Samet J. A meta-analysis of time-series studies of ozone and mortality with comparison to the national morbidity, mortality, and air pollution study. Epidemiology. 2005;16:436–445. doi: 10.1097/01.ede.0000165817.40152.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 1993;88:9–25. [Google Scholar]
- Diggle P, Heagerty PJ, Liang K-Y, Zeger SL. Analysis of Longitudinal Data. New York: Oxford University Press; 2002. [Google Scholar]
- Fitzmaurice GM. A caveat concerning independence estimating equations with multivariate binary data. Biometrics. 1995;51:309–317. [PubMed] [Google Scholar]
- Gent J, Triche E, Holford T, Belanger K, Bracken M, Beckett W, Leaderer B. Association of low-level ozone and fine particles with respiratory symptoms in children with asthma. Journal of the American Statistical Association. 2003;290:1859–1867. doi: 10.1001/jama.290.14.1859. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ. Marginally specified logistic-normal models for longitudinal binary data. Biometrics. 1999;55:688–698. doi: 10.1111/j.0006-341x.1999.00688.x. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ. Marginalized transition models and likelihood inference for longitudinal categorical data. Biometrics. 2002;58:342–351. doi: 10.1111/j.0006-341x.2002.00342.x. [DOI] [PubMed] [Google Scholar]
- Heagerty PJ, Zeger SL. Marginalized multilevel models and likelihood inference (with comments and a rejoinder by the authors) Statistical Science. 2000;15:1–26. [Google Scholar]
- Liang K-Y, Zeger SL. Longitudinal data analysis using g linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- Mancl LA, Leroux BG. Efficiency of regression estimates for clustered data. Biometrics. 1996;52:500–511. [PubMed] [Google Scholar]
- Mortimer K, Neas L, Dockery D, Redline S, Tager I. The effect of air pollution on inner-city children with asthma. European Respiratory Journal. 2002;19:699–705. doi: 10.1183/09031936.02.00247102. [DOI] [PubMed] [Google Scholar]
- Neuhaus JM, Jewell NP. The effect of retrospective sampling on binary regression models for clustered data. Biometrics. 1990;46:977–990. [PubMed] [Google Scholar]
- Neuhaus JM, Kalbfleisch JD. Between- and within-cluster covariate effects in the analysis of clustered data. Biometrics. 1998;54:638–645. [PubMed] [Google Scholar]
- Neuhaus JM, Lesperance ML. Estimation efficiency in a binary mixed-effects model setting. Biometrika. 1996;83:441–446. [Google Scholar]
- Palta M, Yao T-J. Analysis of longitudinal data with unmeasured confounders. Biometrics. 1991;47:1355–1369. [PubMed] [Google Scholar]
- Peters JM, Avol E, Gauderman WJ, Linn WS, Navidi W, London SJ, Margolis H, Rappaport E, Vora H, Gong HJ. A study of twelve Southern California communities with differing levels and types of air pollution. II. Effects on pulmonary function. American Journal of Respiratory and Critical Care Medicine. 1999a;159:768–775. doi: 10.1164/ajrccm.159.3.9804144. and others. [DOI] [PubMed] [Google Scholar]
- Peters JM, Avol E, Navidi W, London SJ, Gauderman WJ, Lurmann F, Linn WS, Margolis H, Rappaport E, Gong H. A study of twelve Southern California communities with differing levels and types of air pollution. I. Prevalence of respiratory morbidity. American Journal of Respiratory and Critical Care Medicine. 1999b;159:760–767. doi: 10.1164/ajrccm.159.3.9804143. and others. [DOI] [PubMed] [Google Scholar]
- Pfeiffer R, Ryan L, Litonjua A, Pee D. A case-cohort design for assessing covariate effects in longitudinal studies. Biometrics. 2005;61:982–991. doi: 10.1111/j.1541-0420.2005.00364.x. [DOI] [PubMed] [Google Scholar]
- Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66:403–412. [Google Scholar]
- Qaqish BF, Zhou H, Cai J. On case-control sampling of clustered data. Biometrika. 1997;84:983–986. [Google Scholar]
- Schildcrout JS, Heagerty PJ. Regression analysis of longitudinal binary response data with time-dependent environmental covariates: bias and efficiency. Biostatistics. 2005;6:633–652. doi: 10.1093/biostatistics/kxi033. [DOI] [PubMed] [Google Scholar]
- Schildcrout JS, Heagerty PJ. Marginalized models for moderate to long series of longitudinal binary response data. Biometrics. 2007;63:322–331. doi: 10.1111/j.1541-0420.2006.00680.x. [DOI] [PubMed] [Google Scholar]
- Sheppard L. Insights on bias and information in group-level studies. Biostatistics. 2003;4:265–278. doi: 10.1093/biostatistics/4.2.265. [DOI] [PubMed] [Google Scholar]
- Stiratelli R, Laird N, Ware JH. Random-effects models for serial observations with binary response. Biometrics. 1984;40:961–971. [PubMed] [Google Scholar]
- White H. Maximum likelihood estimation of misspecified models. Econometrica. 1982;50:1–26. [Google Scholar]
- Yu O, Sheppard L, Lumley T, Koenig J, Shapiro G. Effects of ambient air pollution on symptoms of asthma in Seattle-area children enrolled in the CAMP study. Environmental Health Perspectives. 2000;108:1209–1214. doi: 10.1289/ehp.001081209. [DOI] [PMC free article] [PubMed] [Google Scholar]