The Central Sulcus: an Observer-Independent Characterization of Sulcal Landmarks and Depth Asymmetry

Abstract

Studies of the central sulcus (CS) often use observer-dependent procedures to assess CS morphology and sulcal landmarks. Here, we applied a novel method combining automated sulcus reconstruction, surface parameterization, and an observer-independent depth measurement to study the CS. This facilitated the quantitative assessment of the spatial position and intersubject variability of several sulcal landmarks. Sulcal depth profiles also allowed us to develop an algorithm for the clear identification of several landmarks, including the pli de passage fronto-pariétal moyen (PPFM), first described by Broca. Using this algorithm, the PPFM was identified in the majority of sulci, but exhibited limited spatial variability. This appears to support Cunningham's theory that this landmark may be a developmental remnant, and may argue against its role as a guide to the more variable somatotopic hand area. Sulcal depth profiles were also utilized to assess the influence of sex, handedness, and age on CS morphology. These profiles revealed leftward depth asymmetry in the superior extent of the CS of male subjects and near the midpoint of the CS in female subjects. Age correlations were performed for these asymmetries, and a significant correlation was seen only in the male subgroup.

Introduction

The central sulcus (CS) and other cerebral sulci have traditionally been studied using postmortem samples (Broca 1888; Campbell 1905; Cunningham 1905; White et al. 1997a). Recently, in vivo studies of the CS have been performed with the observer-dependent approach developed in postmortem studies, and this has furthered the understanding of the effects of handedness on CS morphology (Amunts et al. 1996) and the potential for somatotopic localization using sulcal features (Boling et al. 1999). However, this approach dictates that landmark features in the CS (e.g., points of greatest depth, curves or genua) be characterized by observer judgment. This has limited the ability of investigators to provide quantitative guidelines to CS landmark recognition that are generalizable to other studies. One well-known landmark, the “pli de passage fronto-pariétal moyen” (PPFM) (Broca 1888), manifests as an elevation in the floor of the sulcus at its midpoint, and is now thought to localize the somatopic hand area (White et al. 1997a; Boling et al. 1999). However, no quantitative guidelines exist for the recognition of the PPFM relative to other points in the CS.

In addition to sulcal landmarks, magnetic resonance imaging (MRI) studies have assessed the effects of handedness, age, and disease on CS morphology. The CS is well suited for these studies because it develops as early as the 20th week of fetal life (Chi et al. 1977), has several stable macroscopic features (see Fig. 1A), and predictably divides adjacent Brodmann areas (White et al. 1997a; Zilles et al. 1997). These features facilitate the study of normal and abnormal sulcal developmental (Blanton et al. 2001; Jackowski and Schultz 2005), the genetic control over sulcal shape (Lohmann et al. 1999; Le Goualher et al. 2000), and structure–function relationships in the primary sensorimotor cortex (Amunts et al. 1996). Although quantitative measures were applied in many of these studies, several of these investigations were based on time-intensive, observer-dependent approaches. For example, the effect of handedness on sulcal asymmetry has been studied through tracings of intrasulcal length on 2-dimensional images (Amunts et al. 1996; White et al. 1997b). Notably, 1 study has used semiautomated methods to assess CS morphology (Davatzikos and Bryan 2002), though manual contouring of the CS was required. However, this approach (Davatzikos and Bryan 2002) has the potential of capturing the 3-dimensional features of the sulcus and this approach is furthered in the present study.

Figure 1.

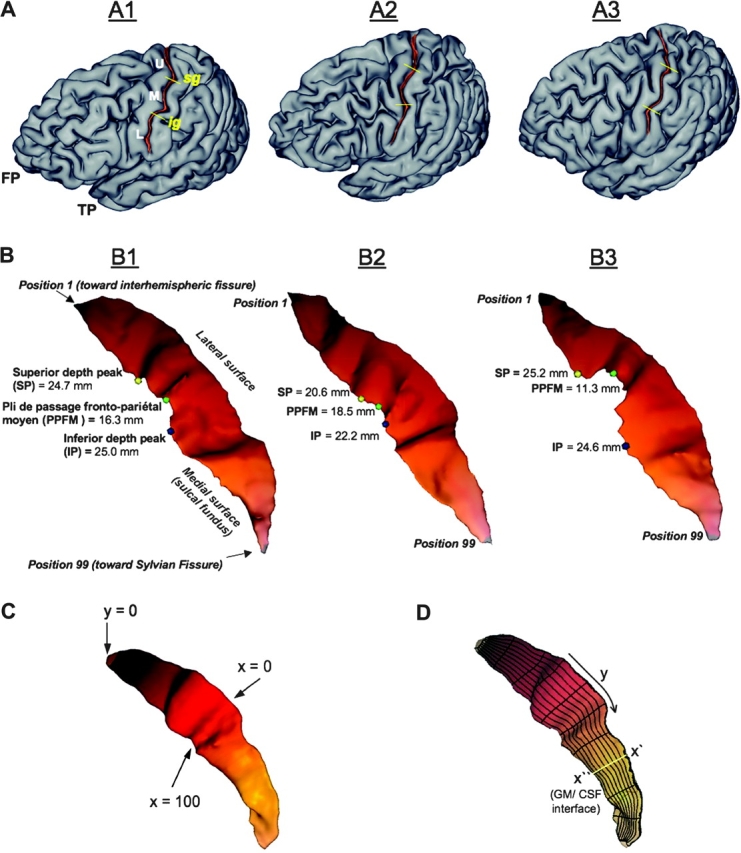
(A) Superficial appearance of the CS. Our observations agree with those of others (Symington and Crymble 1913; White et al. 1997a) that the superficial appearance of the sulcus is variable between subjects (A1; cf. A2 and A3). However, the CS of subject A1 is representative of classic descriptions (Cunningham 1892; Quain 1900; Campbell 1905). A1 demonstrates a case where the sulcus is divided into an upper (U), middle (M), and lower third (L) by 2 curves or genua (the frontal pole, FP, and temporal pole, TP, are marked for orientation). As described by Cunningham, the superior genu (SG) of the CS is “directed backward” (concave anteriorly) and the inferior genu (IG) “looks forward” (convex anteriorly) (Cunningham 1892, p. 166). Cunningham notes that the upper third (U) “inclines downwards and slightly backward,” the middle third (M) “bends suddenly forward and downward,” and the inferior third “proceeds very nearly vertically downwards” (Cunningham 1892, p. 166). The SG and IG are marked by yellow lines on 2 additional subjects to demonstrate the variability in their position. (B) Landmarks of the CS. The CS of subjects illustrated in A1–A3 have been extracted and their superior depth peak (SP, yellow circle), PPFM (green circle), and inferior depth peak (IP, blue circle) are marked. The depth is listed (in mm) next to the relevant position along the sulcus. Although several landmarks can be easily detected on visual inspection (e.g., the PPFM of B3), note that the overlaid landmarks were solely determined by applying a search algorithm to depth profiles (as demonstrated in Fig. 3 and discussed in Results). (C) Sulcal surface parameterization. A coordinate grid was generated on the surface of the sulcal mesh. (D) Depth measure. The sulcal depth profile was generated by fitting a cubic spline curve across y coordinate points sharing the same value at 99 positions along the length of the sulcus. The nonlinear-spline was fit across the sulcal mesh at each of 99 positions from the envelope of the brain (x′) to the GM/CSF interface (x″) at the sulcal fundus. An approximation of a cubic spline is indicated in (D) by the yellow line passing orthogonal to the long axis of the coordinate grid.

There were 2 aims in the present study relevant to CS morphology. The first aim was to apply an observer-independent measure of sulcal depth along the entire sulcal contour, treating depth along the CS as a continuous variable. This was accomplished using 3-dimensional surface parameterization following automated sulcal mesh reconstruction, a procedure that captures the complex topological features of cerebral sulci. In contrast, other recent CS morphology studies used intermittent data sampling, acquired data on intrasulcal length in 2 dimensions, or required manual sulcal contouring (Amunts et al. 1996, 2000; White et al. 1997b; Davatzikos and Bryan 2002). The method developed here allowed a CS depth profile to be generated, which facilitated quantitative CS landmark recognition (e.g., the PPFM) (see Fig. 1B). The second aim was to use the automated CS depth profile tool to evaluate the influence of handedness, sex, and age on CS asymmetry using a large sample with a wide age range (see Table 1). This is particularly relevant as there is disagreement in the literature regarding CS asymmetry in right-handed subjects and the effect of subject sex on sulcal morphology (Amunts et al. 1996, 2000; White et al. 1997b; Davatzikos and Bryan 2002).

Table 1.

Sample characteristics

Decade of life	n	Male	Female	EHI mean scores (Form 1 (SD)/Form 2 (SD)a)
21–30	8	4	4	100 (0)/92.5 (9.6)
31–40	11	6	5	100 (0)/92.2 (9.7)
41–50	8	4	4	100 (0)/95.6 (8.0)
51–60	7	4	3	100 (0)/96.0 (8.9)
61–70	12	5	7	98.9 (3.33)/100 (0)
>70	9	5	4	94.6 (11.4)/100 (0)

	N	Mean age (SD)b	EHI mean scores (Form 1 (SD)/Form 2 (SD)a)
Group	55	51.2 (18.5)	97.9 (6.7)/94.1 (8.7)
Male subgroup	27	51.6 (19.8)	95.4 (10.6)/92.2 (9.4)
Female subgroup	28	50.7 (17.5)	99.3 (2.9)/97.2 (6.5)

^aEHI scores were generated from 2 questionnaires using a similar scoring mechanism though with slight differences in the screening questions. Both questionnaires utilized a scoring mechanism based on 10 questions with maximum scores of either −100 (consistently left-handed) or +100 (consistent right-handed) (see Appendix B for detail). On both forms, scores > +40 are interpreted as right-handedness. Across all decades and in both sexes, subjects were strongly right handed (all means ≥ 92.2) according to both screening forms. All means are listed by Form 1 (SD)/Form 2 (SD). 26 subjects were screened with Form 1 and 29 subjects with Form 2.

^bGroup differences between male and female subgroups were assessed using a 2-tailed Student's t-test (unequal variance) for mean age, as well as for EHI mean scores (by form type). No significant differences were observed (all P ≥ 0.1).

Materials and Methods

Participants

Fifty-five healthy, right-handed individuals (27 men, 28 women) were participants in the study. Participant ages were uniformly distributed over a wide age range (21–89 years), with close age matching between male and female subgroups (see Table 1 for subject characteristics). Handedness testing was determined by the Edinburgh handedness inventory (EHI) (Oldfield 1971) (Table 1). All participants had at least a high school education. Imaging in the study was performed at the Research Imaging Center with the informed written consent of the participants and the approval of the Institutional Review Board at the University of Texas Health Science Center at San Antonio.

MRI Acquisition and Image Preprocessing

Images were acquired on a Siemens 3-T Trio MRI scanner with a high-resolution 8-channel head coil. T₁-weighted images were acquired using a retrospective motion correction protocol (Kochunov et al. 2006) at an isotropic resolution of 0.8 mm. Six full-resolution volumes were acquired using a 3-dimensional TurboFlash sequence with an adiabatic inversion contrast pulse. Images were aligned to the third volume and averaged. The scan parameters used were echo time/repetition time/inversion time = 3.04/2100/785 ms, flip angle = 130.

The image processing steps used in this study are detailed elsewhere (Kochunov et al. 2005; Cykowski et al. 2007) and are briefly summarized here. Nonbrain tissue was removed using the Brain Extraction Tool and radiofrequency inhomogeneities were corrected with the FAST algorithm (Smith et al. 2004). Images were globally, spatially normalized to the Talairach coordinate system using FSL FLIRT software with a 3-dimensional, 15-voxel wide sinc interpolation kernel (Smith et al. 2004). Processed images were imported into the BrainVISA (BV) sulcal extraction and identification “pipeline.” The BV pipeline reconstructed sulcal structures as the medial surfaces of 2 opposing gyral banks (see detailed review in Mangin et al. 2004). Reconstructed sulci spanned from the gray matter (GM)/cerebrospinal fluid (CSF) border at the most internal point of the sulcus to the envelope of the brain surface (Mangin et al. 2004). The brain envelope was determined from a morphological closing procedure on a mask of the brain that was generated from intensities in the T₁-weighted image (see Mangin et al. 2004, p. S132 for detail). The edges and end points of the reconstructed sulcus were determined using topological criteria (see Malandain et al. 1993; Mangin et al. 1995, 2004) and did not require manual specification. The top ridge of a sulcus corresponded to a series of points at the junction of the reconstructed sulcus and the brain envelope. Likewise, the bottom ridge of the sulcus was formed from a series of points at the fundus of the sulcus. Finally, the intersection of these top and bottom ridges formed the end points of the sulcus.

An automated sulcal-recognition algorithm assigned standard anatomical labels to these sulci using neural network-based pattern classifiers (Mangin et al. 2004). For the CS, the frequency of accurate recognition has been established as >96% (Mangin et al. 2004). The CS label was checked for errors and corrected as necessary according to standard anatomical convention (Ono et al. 1990).

Parameterization of the Sulcal Mesh Surface and Depth Measurement

Surface meshes of the reconstructed CS were parameterized to create a normalized x–y coordinate system on their surface (Coulon et al. 2006). The parameterization process was constrained by 3 features: the bottom ridge of the sulcal mesh (i.e., the sulcal fundus), the top ridge (i.e., at the brain envelope), and the end points of the sulcus where these top and bottom ridges joined. From these constraints, 2 coordinate fields (x and y) were extrapolated over the entire mesh surface. This extrapolation was performed by solving the heat equation on the surface, with the constraints behaving as constant heat sources (Coulon et al. 2006). This resulted in a smooth x–y coordinate system, with mesh surface points localized in respect to the features that were used as constraints. The coordinate system extended along the length of the CS from the superior (y = 0) to the inferior end of the sulcus (y = 100), and from the lateral (x = 0) to the medial edge of the sulcus (Fig. 1C). The heat equation provided a strong regularization of the coordinate field, so that if small defects on the mesh surface were present, these did not have a significant consequence on overall sulcal surface parameterization.

Depth was measured at 99 sulcal length positions (hereafter, “positions”) in a superior-to-inferior progression along the parameterized sulcal mesh surface. Position 1 was adjacent to the interhemispheric fissure and position 99 was adjacent to the Sylvian fissure (Fig. 1B). As depicted in Figure 1D, sulcal depth at each position was defined as the distance between paired points at the sulcal fundus (x″) and brain envelope (x′) that shared the same y coordinate. A nonlinear curve (a third order NURB) was fit between these paired mesh points at each of 99 positions (y = 0 and y = 100 at the tips of the sulcus were single points and therefore no depth could be measured). The advantage of spline interpolation in this process was that the fitting of the spline was robust against small defects on the mesh surface that might cause small distortions in the isolines generated during surface parameterization.

The length of the cubic spline curve was recorded as the depth at each position (using General Public License C++ code, http://www.geomtrictools.com). These depth values were smoothed with a mean filtering smoothing kernel (i.e., the average of the depth at 3 adjacent positions).

Intersubject Alignment

Two alignment procedures of sulcal depth values were initially performed. In the first approach, depth values between the left and right CS of each individual subject were aligned by the z-coordinate provided at each depth position using a linear least squares fitting method (intrasubject alignment). Following this, a linear least squares fitting method was used to align the left CS of all subjects by the z-coordinate of the depth position (intersubject alignment). The depth values at each position were averaged across subjects.

In the second alignment approach, the position of each depth measurement was aligned with the homologous position on the contralateral sulcus (i.e., left CS position 1 aligned with the right CS position 1, independent of their z-coordinate). Homologous position depth values were averaged across subjects (e.g., the depth at left CS position 1 was the mean of depths at left CS position 1 in all subjects, independent of the z-coordinates of individual subjects at this position). Comparing the standard error of the difference between left and right CS depth means, it was determined that mean error was lower in the second procedure (i.e., alignment by position) (mean error = 0.85 mm) than in the first procedure (i.e., alignment by z-coordinate) (mean error = 1.02 mm). Alignment of homologous positions along the sulcal length was therefore considered the most robust approach to prevent misalignment artifacts and was adopted for the remaining analysis. Therefore, the Talairach z-coordinates reported in the following sections of the study (i.e., Results and Discussion) are only approximations generated from the average of z-coordinates for any particular position along the sulcus.

Coefficient of Asymmetry

Coefficients of asymmetry (CAs) were used to provide a normalized measure of interhemispheric differences in sulcal depth. Homologous left and right position depth values were used to generate 99 CAs at each point along the mesh (1–99) according to a standard formula (Galaburda et al. 1987): (right depth − left depth)/(0.5 × (right depth + left depth)). Therefore, leftward asymmetry in mean depth at a particular position resulted in a negative value of the CA. CAs were averaged across the entire group, as well as male and female subgroups separately.

Statistical Analyses

A test of normality was applied for the distribution of CAs at each position using the Kolmogorov–Smirnov test with a Lilliefors correction (SPSS 2002). Values detected by this method were clearly outliers and were removed to reduce Type I error and prevent violations of the assumption of normality in the data (Zar 1996). The number of outliers totaled 104 of 5445 total CA values (n = 55, 99 CA points per subject), or 1.9% of all values. To test for the significance of CAs against the null distribution, a 1-sample t-test (2-tailed) was used to compare the mean CA at each position against a hypothesized null value (CA = 0.0). This comparison was made for the entire group of subjects, and the male and female subgroups. To test for differences between male and female groups at homologous positions, a 2-sample t-test (2-tailed, unequal variance) was utilized.

As a correction for multiple comparisons, Gaussian random field theory (RFT) was applied to the statistical maps. This approach was utilized because 1) the data were spatially continuous and 2) the mean filtering of depth values to smooth the data resulted in a greater spatial correlation between neighboring positions. The RFT approach allowed nondiscrete significant foci to be characterized in terms of their spatial relationship to one another so that clusters of significant adjacent positions could be determined (Friston et al. 1994). The critical threshold of adjacent positions (kα) was determined be 4 adjacent positions along the sulcus (using equations provided in Friston et al. 1994, 1996 and described in Appendix A).

Finally, global effects of age, hemisphere, and sex on mean sulcal depth were analyzed. Sex, decade of life, and hemisphere were entered as factors in the univariate General Linear Model using a Bonferroni correction (SPSS 2002). To further assess the effects of individual subject ages on mean sulcal depth, a linear correlation of individual subject age with mean sulcal depth was performed.

Results

Characterization of Sulcal Landmarks in the Depth Profile

Figure 2A,B illustrates how mean sulcal depth varies by position for the male and female subgroups. Importantly, the analyses here were performed by aligning the sulci of subjects by the position of the depth measurement. (Therefore, all Talairach z-coordinates reported here should only be considered an approximation to provide an additional reference system for reporting our results. They were generated by averaging the z-coordinate across all subjects for any particular position of a depth measurement.)

Figure 2.

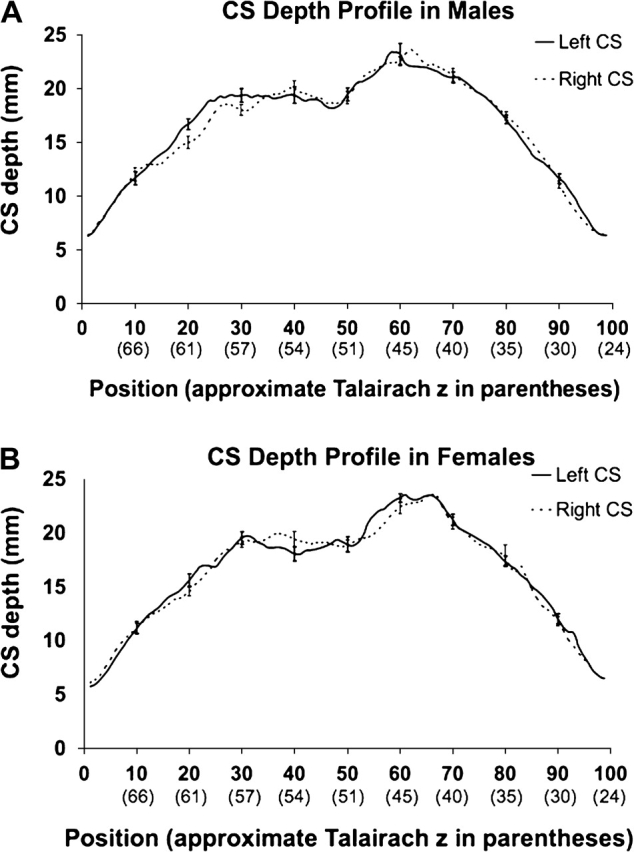
CS depth profiles in male and female subgroups. Sulcal depth profiles (±standard error bars) are shown for the male (2A) and female (2B) subgroups. Mean sulcal depth is plotted by both sulcal length position (bottom bold font). For additional reference, approximate Talairach z-coordinates are provided in parentheses below the numbered positions. It should be noted that values were aligned by position (not Talairach z-coordinate) for inter- and intrasubject comparisons (i.e., Talairach z-coordinates are for reference purposes only). Talairach coordinate points (at the sulcal fundus) are the mean z-coordinates across the entire subgroup (n = 27, male; n = 28, female) after alignment of sulci by position (see “Intersubject alignment” in Methods). Note that there is not an even spacing in both positions and Talairach z-coordinates. This is because absolute length is a function of x, y, and z. Therefore, the z-coordinate may change very slowly along contiguous positions where the sulcus bends (see Fig. 1B).

The CS depth profiles in both subgroups had steep slopes at the left end of the curve beginning at position 1 near the interhemispheric fissure. The profiles then reached a first depth peak (referred to hereafter as the “superior peak,” SP) as the profile moved inferiorly along the sulcus (Talairach z-coordinates of approximately 70–57 mm). From this first peak, depth values plateaued and remained elevated over the course of approximately 40 positions (Talairach z-coordinates of approximately 57–42 mm) in both subgroup profiles. At the right extremity of this plateau was a second depth peak closer to the Sylvian fissure (“inferior peak,” IP). From this second peak to the final position (closest to the Sylvian fissure) the slope was again steep as the CS became shallower (Talairach z-coordinates of approximately 42–24 mm). Finally, between the SP and IP a focal reduction in sulcal depth was apparent near the midpoint of the profile (hereafter, “PPFM”).

Analysis of the Superior Peak, Inferior Peak, and PPFM in CS Depth Profiles

A simple algorithm was devised to analyze the superior peak (SP), inferior peak (IP), and PPFM in individual subject depth profiles. The SP was determined to be the maximum depth value in the superior 50% of positions in the depth profile. The IP was recognized as the maximum depth value in the inferior 50% of the depth profile. Bounding the search with these markers, the PPFM was recognized as the minimum depth value between the SP and IP (see Fig. 3A). The position of the SP, IP, and PPFM is marked on Figure 3A, determined by the above criteria for the left CS of a single subject. 94.5% of left central sulci (n = 55) and 80% of the 55 right central sulci (n = 55) had depth profiles with a bimodal peak distribution as seen in Figures 2A,B and 3A. The majority of these profiles (77.9%) had an IP that was deeper than the SP (Fig. 3A).

Figure 3.

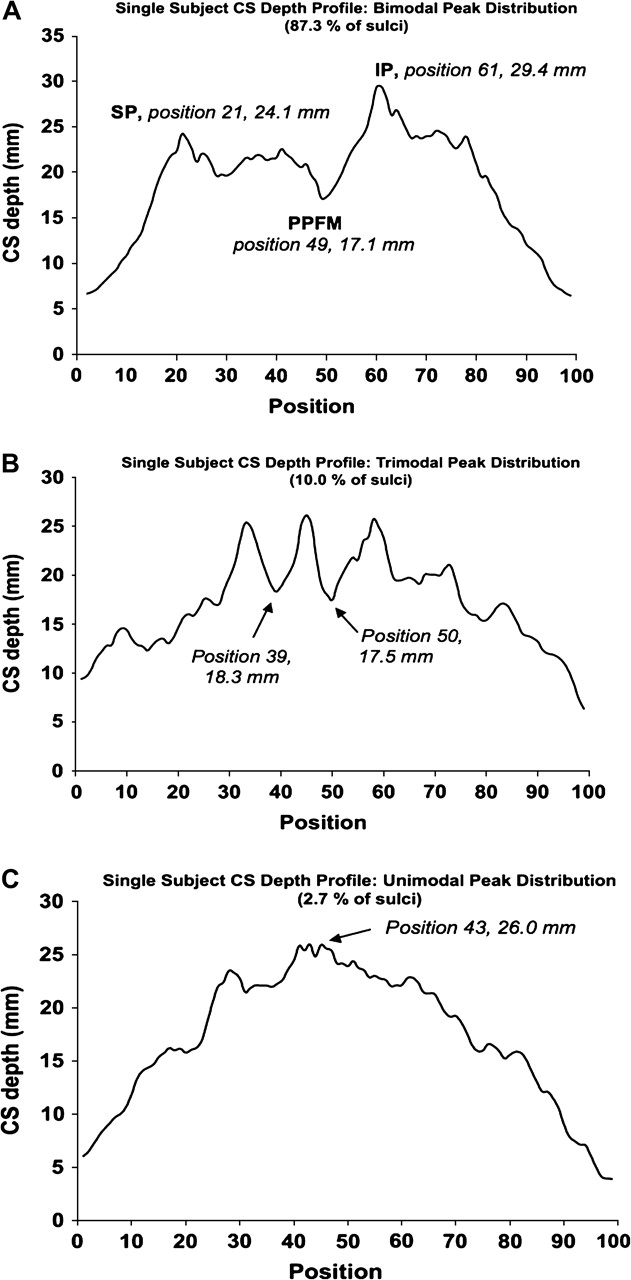
Patterns seen in individual sulcal depth profiles. Sulcal depth profiles of single sulci are shown that are representative of bimodal (A), trimodal (B), and unimodal (C) peak distributions. On the profile of a sulcus with a bimodal peak distribution, the superior peak (SP), PPFM, and inferior peak (IP) are labeled. A simple search algorithm determined the landmarks' position and depth (see Results for detail). The trimodal profile exemplifies a sulcus for which no PPFM was identified (2 shallow points of nearly equal depth between 3 surrounding peaks). The unimodal profile (C) was seen in only a few subjects. As our algorithm searched the 2 halves of the depth profile for distinct depth peaks, these cases were recognized as a single peak at the middle of the profile with no clear SP, IP, or PPFM.

Location and Depth of CS Landmarks and a Post Hoc Comparison by Sex and Side

Figure 4A displays the mean position and depth of the IP and SP, as well as the PPFM, for all sulci displaying these 3 features. The mean depth of IPs was 26.3 ± 3.6 mm for the left CS and 24.9 ± 2.9 mm for the right CS while the mean position of the IP was 61.5 ± 5.8 for the left CS and 61.7 ± 5.9 for the right CS. The mean depth of SPs was 23.3 ± 3.0 mm for the left CS and 22.7 ± 2.8 mm on the right, whereas the mean position of the SP was 34.1 ± 7.3 for the left CS and 37.2 ± 6.8 for the right CS. The mean depth of the PPFM was 16.3 ± 3.0 mm for the left CS and 17.0 ± 3.0 mm for the right CS, whereas the mean position of the PPFM was 46.4 ± 6.0 for the left CS and 46.3 ± 5.5 for the right CS. As an approximate percentage of sulcal length (from superior to inferior), this places the SP at 36% of the sulcal length, the PPFM at 47% of sulcal length, and the IP at 62% of sulcal length. Finally, mean sulcal depth for the entire group was 16.6 ± 1.3 mm for the left CS and 16.4 ± 1.2 mm for the right sulcus.

Figure 4.

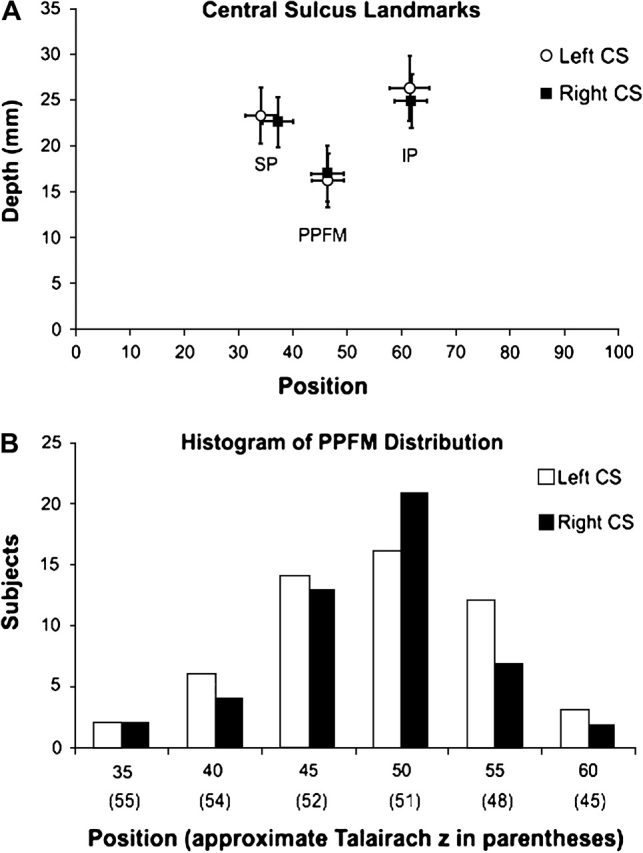
Distribution of CS landmarks. (A) The position and depth of the superior peak (SP), inferior peak (IP), and PPFM are shown for the left and right CS. The SD for both position and depth measures are shown for each point. Note that between sulci, the mean SP varies slightly by position and the IP varies slightly by depth. Though an interesting trend, these differences were not significant. (B) The distribution of the PPFM for both the left and right CS. The bin of positions (e.g., 45 is the bin of positions 41–45) is shown with the approximate Talairach coordinate in parentheses below.

A 2-tailed t-test with Bonferroni correction was used to compare the mean depth and position of each of these 3 features by subject sex (e.g., position and depth of left SP). No significant differences were seen in this comparison. Additionally, 2-tailed t-tests between the left and right CS for the depth and position of CS features in the entire group were performed. The uncorrected comparison of position for the SP was significant (t = 2.36, P = 0.02) (see Fig. 4A, “SP”). However, this did not meet the corrected significance threshold.

The Pli de Passage Fronto-Pariétal Moyen

A PPFM was detected in 96.4% of left central sulci and 89.1% of right central sulci in this study using the algorithm defined above (Fig. 3A). Figure 4B displays the histogram of PPFM distribution by position. 36.3% of all PPFMs were observed in the bin of positions from 46 to 50 (an approximate Talairach z-coordinate of 51 mm). As a percentage decrease in sulcal depth from the mean of the SP and IP, the PPFM represented an average 31.3 ± 12.6% drop (or 7.7 ± 3.5 mm) in sulcal depth from the mean depth of the SP and IP (see Fig. 4A).

Additional Patterns Observed in Sulcal Depth Profiles

As noted above, the majority of subjects displayed a bimodal depth peak distribution with the IP exceeding the SP. Likewise, 102 of 110 sulci had a clear local minimum (the PPFM) between these peaks. This typical distribution is exemplified by the depth profile of a single sulcus in Figure 3A. However, a small sample of sulci exhibited trimodal depth peak distributions (3.6% of left CS; 16.4% of right CS) with fewer still having a single depth peak (1.8% of left CS; 3.6% of right CS) (see Fig. 3B,C). In regard to superior and inferior peaks, the SP was observed to be greater in depth in 22.1% of subjects in contrast to the more typical pattern of a deeper IP. In several subjects with a trimodal peak distribution, there was still a clear local minimum found in searching between the most superior and inferior of the 3 peaks (see the Discussion section for a further discussion of trimodal peak distribution). In these cases, this location was considered the PPFM. Of the remaining 8 cases where no PPFM could reliably be identified, there were 2 patterns. In the first pattern, a trimodal distribution was seen with 2 local minima between peaks that were nearly identical in depth (5 subjects) (Fig. 3B). In the second pattern, a unimodal peak distribution was seen so that no PPFM could be identified (3 subjects) (Fig. 3C).

CS Depth Asymmetry

Sex Differences in Sulcal Depth Asymmetry

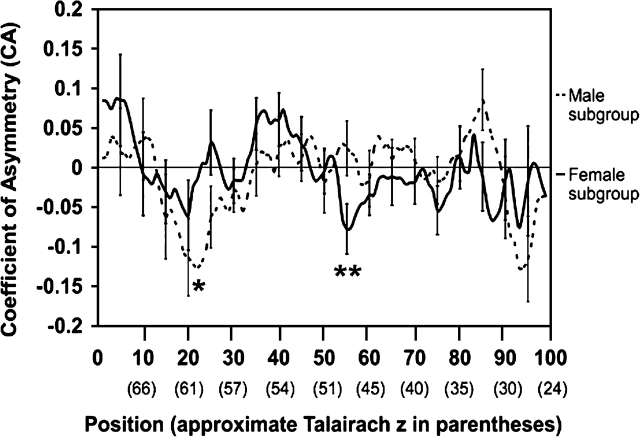
For the entire group, significant leftward depth asymmetry (following correction for multiple comparisons) was seen in the superior extent of the CS from positions 18–22 (maximum t value = 2.64; P ≤ 0.01) (Talairach z ≅ 60–63 mm). For the male subgroup, significant leftward depth asymmetry was seen in the superior extent of the sulcus from positions 19–24 (Talairach z ≅ 59–62 mm) (maximum t value = 2.83; P ≤ 0.008) (see Fig. 5). The female CA profile also revealed leftward sulcal asymmetry at these positions, but this did not reach significance (Fig. 5). However, in the female subject CA profile, significant leftward depth asymmetry was seen near the midpoint of the sulcus from positions 54–57 (Talairach z ≅ 48–50 mm; maximum t value = 2.5; P ≤ 0.02). A Student's t-test directly comparing male and female CA profiles at each homologous position yielded no significant differences.

Figure 5.

Significant findings in the CA for the male and female subgroups. CAs are plotted by position (with the approximate Talairach z-coordinate in parentheses below) as in Figure 2. Only points that were significant after correcting for multiple comparisons are noted. Significant leftward asymmetry was seen in the CA profiles at positions 18–22 (approximate Talairach z = 60–63 mm) in the group profile (not shown), positions 19–24 (approximate Talairach z = 59–62 mm) in the male subgroup (single asterisk), and positions 54–57 (approximate Talairach z = 48–50 mm) in the female subgroup (double asterisks). As noted in Figure 2, Talairach z-coordinates displayed are the mean the z-coordinate at the sulcal fundus for any particular position in the group (n = 55). CAs were determined as described in the methods (e.g., negative CA = leftward depth asymmetry).

CA Variance and Coefficient of Variation (V) in Depth

The greatest amount of variance in the CA was present in the upper and lower thirds of the CS. The mean variance of the CA was 0.06 for positions 0–30 (approximately corresponding to the upper third of the CS; see Fig. 1A) and positions 70–99 (approximately the lower third of the CS, Fig. 1A). In contrast, variance was much lower in the middle third of the CS (positions 30–70) with a mean CA variance of 0.03.

Using the SD of depth values to calculate a coefficient of variation (V) at all positions (Zar 1996), the left CS of the entire group had a range of V = 10.4% to 33.2% with a mean V across the sulcus of 19.3%. For the right CS, a similar range was seen with a range of V from 10.2% to 41.5% and a mean V across the sulcus of 18.4%. For both the left and right CS, the greatest values for V were seen across the upper and lower thirds of the sulcus. In contrast, across the plateau of the depth profile (see Fig. 2A,B; positions 30–70), the mean V was 16.6% for the left CS and 15.6% for the right CS.

Age Effects on Sulcal Depth Asymmetry

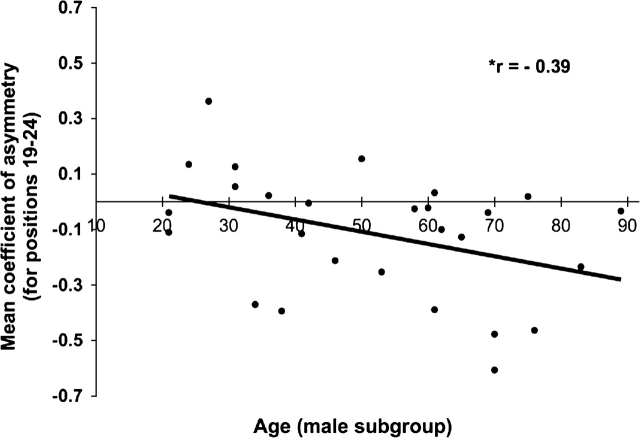
To further the analysis of sulcal asymmetry, a post hoc linear correlation of asymmetry and age was performed. The CA value used in the correlation was the mean of the significant range of positions in each CA profile. This linear correlation was performed using a 2-tailed hypothesis regarding the specific sample correlation coefficients. Only in the CA profile for male subjects was there a significant negative correlation (i.e., leftward asymmetry increased with age; P ≤ 0.05) with the mean of CA values over positions 19–24 (Talairach z ≅ 59 to 62 mm) (r = −0.39; P ≤ 0.05) (Fig. 6). The same linear correlations did not reach significance for the significant depth asymmetries seen in the entire group (r = −0.14; P ≥ 0.2; positions 18–22) or female subgroup (r = 0.29; P ≥ 0.1; positions 54–57).

Figure 6.

Age correlation of asymmetry in the male subgroup. Post hoc correlation of significant leftward asymmetry in the male subgroup (from positions 19 to 24). The asterisk indicates a 2-tailed P value ≤ 0.05 for the correlation coefficient r. No other significant age-related trends were noted for asymmetry or mean sulcal depth.

Effects of Sex, Hemisphere, and Age on Mean Sulcal Depth

No significant main effects of any factor on mean sulcal depth, or significant interactions between factors, were observed. Consistent with the nonsignificant effect of decade on mean sulcal depth, a linear correlation using individual subject ages with mean left and right CS depth was not significant (r = −0.15 for both the left and right sulci; P > 0.05).

Discussion

Several characteristic features of the central sulcus (CS) were revealed in the sulcal depth profiles of this study. The first feature was the presence of a superior peak (SP) near the junction of the upper and middle thirds of the CS (see Figs 1A and 3A). The second feature was an inferior peak (IP) located near the junction of the middle and lower thirds of the sulcus. Both the SP and IP were located in the vicinity of the somatotopic upper limb representation in the primary sensorimotor cortex by their approximate Talairach z-coordinates (Fox et al. 1985, 2004; Colebatch et al. 1991; Grafton et al. 1996; Alkadhi et al. 2002; Stippich et al. 2007). A third feature common to most sulci was that IP depth exceeded that of the SP (Fig. 3A). A final characteristic feature was the presence of a focal reduction in sulcal depth in the middle third of the sulcus, between these peaks. This focal depth reduction near the sulcal midpoint was detected with a simple algorithm and found in 96.4% of left central sulci and 89.1% of right central sulci. We consider this to be the “pli de passage fronto-pariétal moyen” (PPFM) described by Broca, Cunningham, and Campbell (Broca 1888; Cunningham 1892, 1905; Campbell 1905) and qualitatively evaluated in recent studies as well (White et al. 1997a; Boling et al. 1999; Boling and Olivier 2004). Surprisingly, the PPFM did not exhibit much positional variation (see Fig. 4A,B). Specifically, 36.3% of sulci had a PPFM within a group of 5 adjacent positions (41–45) corresponding to an approximate Talairach z-coordinate of 51 mm, with 62.7% of sulci exhibiting the PPFM within adjacent positions (41–50) corresponding to an approximate Talairach z of 51–52 mm.

Intrasubject comparisons of the depth profile also revealed significant leftward depth asymmetry, sex differences in the position of significant asymmetry, and age correlations of this asymmetry in male subjects. Leftward asymmetry of sulcal depth was seen in the entire group from positions 18–22 (Talairach z ≅ 60–63 mm) and in the male subgroup from positions 19–24 (Talairach z ≅ 59–62 mm). Female participants shared this leftward asymmetry in the superior extent of the CS, but this did not reach statistical significance (see Fig. 5). Additional sex differences in sulcal asymmetry included a leftward asymmetry seen only in the female subgroup at the midpoint of the sulcus from positions 54–57 (Talairach z ≅ 48–50 mm). The age distribution of study participants (21–89 years; see Table 1) allowed us to perform post hoc age correlations of these significant sulcal asymmetries. Significant age-correlated asymmetry was present only in the male subgroup. This may suggest the potential for experience-dependent plasticity in sulcal morphology (e.g., a result of more intensive usage of the dominant as compared to the nondominant hand). Notably, the greatest variance in depth asymmetry was noted at superior and inferior extremities of the CS. This is consistent with reports that those portions of the CS close to the interhemispheric fissure and Sylvian fissure display the most substantial positional variation between subjects (Zilles et al. 1997). These results were confirmed by assessing the coefficient of variation of the actual depth measure (i.e., variability in the measure was lowest across the plateau of the sulcal depth profile, Fig. 2A,B). The lowered variance toward the sulcal midpoint reduces the likelihood that outlier values influenced the position along this plateau of sulcal landmarks and the significant asymmetries reported here.

Characterization of CS Landmarks

The Pli de Passage Fronto-Pariétal Moyen

Paul Broca was the first to describe gyral passages connecting the frontal and parietal lobes in the vicinity of the CS. Two superficial passages (superior and inferior to the ends of the sulcus) were described as “deux plis de passage fronto-pariétal supérieur et inférieur” (Broca 1888, p. 764). Broca described a third passage as a “pli de passage fronto-pariétal moyen” (abbreviated “PPFM” here), a deeper passage across the floor of the CS that was constant and occasionally duplicated (Broca 1888, p. 778). Cunningham confirmed this observation of a “deep annectant gyrus” forming a “sunken bridge of connexion [sic]” (Cunningham 1905, p. 558), as did Campbell (Campbell 1905, p. 22). One modern examination of postmortem specimens confirmed that a focal elevation of the sulcal floor was present in 39 of 40 hemispheres (White et al. 1997a) and this was interpreted as an “anatomical hallmark of the hand (and wrist) representation” (White et al. 1997a, p. 29). This view was then extended by observer-dependent studies examining the spatial correlation between the PPFM and functional activity in the somatotopic hand area (Boling et al. 1999; Boling and Olivier 2004). One of these studies identified the PPFM using both 2-dimensional axial MR images and 3-dimensional surface reconstructions (examining the depths of the sulcus on 1 postmortem brain for confirmation) (Boling et al. 1999). Peak activations on positron emission tomography (PET) images within 10 mm of this observer-identified landmark were considered correct predictions of the somatotopic hand region (Boling et al. 1999).

In contrast with observer-dependent approaches, here we have defined the PPFM systematically by 1) developing an algorithm using a search of the depth profile for the lowest depth value between IP and SP, 2) characterizing the percent relative depth reduction (31.3 ± 12.6%) from the nearby IP and SP, and 3) expressing the spatial variability of the PPFM within the sulcus. With these criteria, the PPFM was found to be present in the majority of participants but exhibit limited spatial variability.

The present study cannot fully address whether the PPFM is a functional landmark (White et al. 1997a; Boling et al. 1999) or a remnant of sulcal development (Cunningham 1905). However, the quantitative characterization of PPFM placement may support Cunningham's original interpretation of this feature as a marker in the adult brain of fetal CS development (Cunningham 1905). Based on fetal studies, Cunningham described the CS as developing from 2 separate limbs (Campbell 1905; Cunningham 1905), though others report this only for nonhuman primates (Tamraz and Comair 2006). Nevertheless, Cunningham felt that the “deep annectant gyrus” elevating the sulcal fundus (the PPFM here) was the remnant of the union of these sulcal limbs. Two findings here support Cunningham's developmental interpretation. The first is that a PPFM could not clearly be identified in approximately 7% of sulci, slightly higher than previous qualitative estimates of its absence at 2.5% of hemispheres (White et al. 1997a). However, all subjects would have a somatotopic hand area. The second finding is that the PPFM has limited spatial variability, compared to the much broader distribution of the somatotopic hand area (see Fox et al. 2004). A histogram of PPFM distributions by position (Fig. 4B) revealed that positions 40–50 encompassed nearly two-thirds of PPFM locations. This range of positions would correspond to group Talairach averages of approximately 51–52 mm. That a potential developmental feature (e.g., the PPFM) might exhibit such limited variability in position is consistent with the original choice of the anterior commissure–posterior commissure (AC–PC) line for localization in the brain. Talairach and colleagues commented that the AC–PC line had a “relatively constant relationship to fairly well-defined telencephalic structures” because the AC was the axis around which the telencephalic vesicles developed (Talairach 1967, p. 40). In fact, the complete range of PPFM distributions was limited to approximate Talairach z-coordinates of 45–55 mm over the 102 sulci with this feature. In contrast, the control of specific portions of the distal upper limb (e.g., fingers, wrist) within the larger somatotopic upper limb representation is diffusely distributed (see review by Schieber 2001). As an example of this principle, 1 recent study looked at voluntary finger movement with PET and found that the center-of-mass of activity was distributed over Talairach z-coordinates from 34 to 60 mm (Fox et al. 2004). Though PPFM distributions seen here (see Fig. 4A,B) are within the somatotopic upper limb defined by functional imaging (Fox et al. 1985, 2004; Colebatch et al. 1991; Grafton et al. 1996; Alkadhi et al. 2002; Stippich et al. 2007), the limited spatial variance of the landmark compared with a more diffuse within-limb somatotopic representation may argue against a strict structure–function relationship.

One limitation of this interpretation is that we do not have sufficient functional imaging data on the participants of this study to determine the exact relationship between their somatotopic hand area and their PPFM (when present). Therefore, our estimates of functional activity in the hand area are derived from other studies. Additionally, our determination of CS landmarks was performed following sulcal alignment by position and not in Talairach coordinates (these are approximations as explained in the Methods). Both of these limitations mean that we cannot definitively exclude the possibility that the PPFM corresponds to the somatotopic hand area of the current study participants.

Sulcal Depth Peaks

The depth values reported here are consistent with those in previous postmortem studies using manual depth measures. The value of the IP (left CS = 26.3 ± 3.6 mm; right CS = 24.9 ± 2.9 mm) is consistent with estimates of maximal depth of cerebral sulci as 1 inch (25.3 mm) (Quain 1900) and the maximum depth seen in the CS in as 23–25 mm (Hrdlicka 1901). Likewise, the depth of the IP typically exceeding that of the SP is consistent with previous observations. Symington and Crymble observed that the elevation of the sulcal floor (i.e., the PPFM) was more easily detected from the steeper drop on its lateral (inferior here) aspect (toward the IP) (Symington and Crymble 1913, p. 330). The sulcal depth profiles seen here (Figs 2A,B and 3A) are consistent with this description. Finally, mean sulcal depth over the entire depth profile was 16.6 ± 1.3 mm for the left CS and 16.4 ± 1.2 mm for the right sulcus, a result comparable to other reports (Davatzikos and Bryan 2002; Tamraz and Comair 2006).

Other Depth Profile Patterns

The majority of central sulci in the participants of this study displayed a bimodal depth peak distribution (Fig. 3A). Typically, the IP exceeded the value of the SP and 102 of 110 sulci had a clear local minimum (the PPFM) between these peaks. Notably though, trimodal and unimodal depth peaks were observed in a small subset of participants (Fig. 3B,C). For CS with a single peak (unimodal), it was impossible to identify a PPFM using the guidelines proposed here. For CS with a trimodal peak, a local minimum value between the most superior and inferior peak was often still a clear feature of the depth profile. In these subjects we assigned this position as the center of the PPFM. In a few subjects with a trimodal depth distribution, 2 nearly equal shallow positions were found between the most superior and inferior depth peaks and therefore no PPFM was assigned (Fig. 3B). This finding of trimodal peaks in the sulcal depth profile is consistent with Broca's finding that the PPFM was doubled in few cases (Broca 1888, p. 778), thereby creating 3 depth peaks in the depth profiles of the current study.

CS Asymmetry

Leftward Sulcal Depth Asymmetry in Right-Handed Adults

Leftward asymmetry in the superior extent of the sulcus was significant in the CA profiles of the entire group and male subgroup (see Fig. 5). This offers support to an earlier study of intrasulcal length asymmetry (Amunts et al. 1996). That study found right-handed male subjects had a significant leftward asymmetry in CS depth, particularly in the superior extent (e.g., approximately z = 60–65 mm, Talairach) of the CS (Amunts et al. 1996). Amunts and colleagues also observed leftward asymmetry in the superior extent of the CS (also near z = 60 mm) in females. However, as in the present study, this asymmetry reached significance only in male participants.

There has been a disagreement in the literature regarding the relationship between handedness and CS asymmetry. Several studies have reported leftward asymmetry in intrasulcal length for right-handed subjects (Amunts et al. 1996, 2000), while others find no significant asymmetry related to handedness (White et al. 1997b) or even rightward sulcal depth asymmetry in right-handed subjects (Davatzikos and Bryan 2002). It should be noted that the study of White et al. (1997b) did not have handedness data available and this may explain the different conclusions drawn in that study. Additional studies have moved toward observer-independent depth measures, though the parameterized sulcal surfaces were derived from manually traced sulcal contours (Davatzikos and Bryan 2002). However, the rightward asymmetry in sulcal depth in right-handed subjects (Davatzikos and Bryan 2002) is a finding not reported in other studies and was not seen here. Nonetheless, we did find that alignment of depth measures by their position along the sulcus was the most robust approach (see Methods), as first presented by Davatzikos and Bryan (2002).

The CS asymmetry seen here in male participants is positioned near an overlapping region of the somatotopic proximal upper limb and lower limb representations and superior to the “hand area” (Fox et al. 1985, 2004; Colebatch et al. 1991; Grafton et al. 1996; Alkadhi et al. 2002; Stippich et al. 2007). Presumably though, this asymmetry is a consequence of an increase in the connectivity of left-hemispheric neural circuits and/or cortex dedicated to the coordination of the dominant limb. Indeed, the midpoint of the sulcus (closer to reports of the somatosensory hand area) is where the female subgroup showed significant leftward asymmetry in sulcal depths (centered at approximate Talairach z-coordinates of 48–50 mm). However, in the entire group and male subgroup depth profiles, it is intriguing that a functional difference (i.e., right-handedness) would present a focal anatomical asymmetry superior to the somatotopic distribution of that function. This may relate to the efficient coordination of movement sequences in the dominant limb exhibited about the proximal limb joints (Hammond 2002). Further, this asymmetry is likely related to GM thickness asymmetries in right-handed individuals. Luders and colleagues observed that cortical thickness in the left superior precentral gyrus was up to 15% greater than the right-sided homologue in 60 right-handed individuals (Luders et al. 2006). The greatest degree of leftward cortical thickness asymmetry was observed adjacent to the upper third of the sulcus (see Figure 1 in Luders et al. 2006a). An increase in GM thickness as observed in that study would likely deepen the adjacent portions of the left CS and may help to explain the leftward depth asymmetry seen here. Also consistent with the present result regarding leftward depth asymmetry in the superior extent of the CS, the degree of GM asymmetry in the study by Luders and colleagues was greatest in male subjects (Luders et al. 2006).

The lack of left-handed participants in the current study limits to our ability to relate these sulcal asymmetries directly to hand preference. However, a reversal of CS asymmetry (i.e., rightward depth asymmetry) has been observed in studies considering left-handed subjects (Amunts et al. 2000). The convergence of findings regarding right-handed subjects between the present study and those of Amunts et al. (1996, 2000) strengthens this indirect evidence that the CS asymmetry confirmed here is related to hand preference.

Sex Differences in CS Asymmetry

Male and female subjects had a leftward depth asymmetry in the superior extent of the sulcus, though this was significant only in the male subgroup. Likewise, only female subjects had a focal leftward asymmetry at the sulcal midpoint (see Fig. 5). In contrast with the male subgroup, the female subgroup did not have a significant age correlation of depth asymmetries. Amunts and colleagues observed nonsignificant leftward asymmetry in the superior extent of the CS in right-handed females, as well as at a z of 45 mm (near where the current study determined significant asymmetry was present) (see Figure 4, Amunts et al. 2000).

Sex differences in the anatomical and functional organization of the brain have been grouped into organizational effects and activational effects (Gorski 2000). Those effects that are organizational develop under the influence of sex hormones (e.g., estradiol) and sex chromosomes during development (Davies and Wilkinson 2006), and are permanent structural changes. Activational effects also develop under the influence of gonadal steroids (e.g., testosterone in the adult male brain), but these effects are reversible (e.g., following gonadectomy in an animal) (Gorski 2000). Studies of exogenous testosterone administration suggest activational effects on neuroanatomical features of both animal models (Brown and Bottjer 1993) and in human patients (Patwardhan et al. 2000). In light of theories of sex steroids exhibiting organizational and activational effects, it may be that this asymmetry at the midpoint of the CS in the female brain tends to be more organizational in nature than the CS asymmetry in males. In contrast, evidence that male subjects experience an activational effect on sulcal morphology is found in the age correlation of leftward asymmetry (Fig. 6). In addition, the findings here may relate to sex differences in motor system activity. Women have been reported to excel on tasks assessing finger dexterity through finger tapping (Kimura 1996). Functional MRI experiments have also demonstrated greater activity in the motor areas of men on a right-handed finger-tapping task, even in the absence of performance differences (Bell et al. 2006).

Age Correlation of Sulcal Asymmetry

One novel feature of the present study was the ability to correlate significant depth asymmetries with age over an approximately 70-year life span (see Table 1 and Fig. 6). Comparable studies of the CS have included primarily older individuals (White et al. 1997b; Davatzikos and Bryan 2002) or have had a narrower range of ages in participants (Amunts et al. 2000). Therefore, the increased leftward asymmetry with age in healthy male subjects (in the absence of special skill acquisition or practice) is a novel finding. A similar correlation was not seen for the female subgroup. This suggests that in male subjects, dynamic processes may underlie this focal leftward asymmetry near the somatotopic distribution of the proximal upper limb.

The finding of the present study that the asymmetry in the superior extent of the CS might be altered throughout the life span is consistent with other studies. Professional, male, right-handed keyboard players have been shown to exhibit less asymmetry in the CS than matched controls (Amunts et al. 1997). This symmetry was interpreted as a product of lifelong bimanual coordination in the male musician group (“training-induced plasticity”). Similar to the present correlation of sulcal asymmetry and age in males, the loss of regional leftward asymmetry was especially notable in the superior extent of the somatotopic upper limb representation (Amunts et al. 1997). Further, the depth of the CS in musicians significantly negatively correlated with the age the musicians began bimanual training (Amunts et al. 1997). This convergence of findings suggests that the unknown mechanical factors that drive sulcal asymmetry in the superior extent of the male CS sulcus are part of a lifelong remodeling process of the sulcus, and potentially, primary sensorimotor cortex structure.

One relevant point is that we did not find a significant relationship between age and mean CS depth. Some authors have reported trends of decreased sulcal depth and increased sulcal widening associated with the aging process (Kochunov et al. 2005; Rettmann et al. 2006). However, in a study of sulcal depth reductions with age, the CS was not a site where an age-correlated reduction in depth was seen (Rettmann et al. 2006). This bolsters the interpretation of our findings in the male subgroup as experience-dependent plasticity.

Study Limitations

One major limitation of the present study is that this analysis was cross-sectional, limiting the interpretation of correlation analyses. This is particularly important to note as a significant age correlation was seen in sulcal depth asymmetry in the male subgroup. Therefore, our age-correlation results must be interpreted with caution. Nonetheless, our findings are consistent with other cross-sectional studies in male subjects that suggest experience-dependent plasticity in sulcal morphology (Amunts et al. 1997).

The method of generating a CS depth profile developed here also needs to be repeated in longitudinal studies of sulcal anatomy. This will allow a test of measurement reliability using a repeated measures design. Additionally, further studies are needed to examine how useful the method is for sulci that have more complex topological features than the CS (e.g., the intraparietal sulcus).

Finally, our analysis revealed that the upper and lower thirds of the CS exhibit the greatest variability in sulcal depth and depth asymmetry. Incorporating these more variable areas of the CS into measures of CS morphology (e.g., sulcal shape) may confound studies that do not account for this fact. In particular, this should be noted in any future studies attempting to discern disease-related differences in sulcal structure or perform studies of the heritability of sulcal shape and depth. It may be that the most reliable points to study sulcal morphology in future studies is near to or along the plateau in the depth profile between the superior and inferior depth peaks (approximately the middle third of the sulcus).

Conclusions

In this study we developed a method to formulate CS depth profiles that treat sulcal depth as a continuous variable. This allowed us to characterize sulcal features (SP, PPFM, IP) for the first time in a quantitative manner that captured their spatial position and intersubject variability. This also allowed us to develop a simple algorithm for the clear in vivo identification of the PPFM based solely on the depth profile. An examination of the PPFM's frequency and limited spatial variability appears to support Cunningham's assertion of its developmental origins (Cunningham 1905). Though the effect of handedness on CS morphology has been disputed, our findings support a focal leftward asymmetry in CS depth. This asymmetry exists in 2 discrete locations (in the superior extent of the sulcus for males; near the midpoint of the sulcus in females). The findings also suggest that males exhibit more neuroplasticity in sulcal morphology, as evidenced by the age correlation of leftward asymmetry. Not only are the locations of significant asymmetry disparate in the male and female brain, but it also appears that the processes underlying the development and extent of that asymmetry may be different as well.

Funding

International Consortium for Brain Mapping grant from National Institute of Biomedical Imaging and Bioengineering (EB001955); National Institute of Mental Health (R01 MH078143); National Center for Research Resources grant for the Frederic C. Bartter General Clinical Research Center (M01 RR001346); National Institute of Biomedical Imaging and Bioengineering (K01 EB006395) to P.K.; and National Institute on Deafness and other Communication Disorders (F32 DC009116) to M.C.

Appendix A

The number of adjacent depth points in 1-dimension (the “critical region size,” or kα, in Friston et al. 1994) for a threshold (μ) of t-scores ≥ 2.0, P ≤ 0.05 was estimated using the actual voxel spacing between adjacent depth measures (to account for the smoothness in the data prior to mean filtering). Sulcal length was determined by fitting splines to the top and bottom ridges of the sulcus in >25% of the original sample (30 sulci, n = 15). The mean length of the sulcus (120.7 voxels at 0.8 mm spacing) was taken as the average of the bottom and top ridge lengths. This average sulcal length was divided by the number of depth positions generated (99) and multiplied by 3 (the size of the mean filter) to generate the full-width half max estimate (FWHM). Smoothness (W) was calculated from W = FWHM/√(4 log_e2) (see p. 212 in Friston et al. 1994). E{m}, E{n}, and E{N} were determined according to equations (4), (10), and (5) in Friston et al. (1994), respectively. The values of β and k (critical region size) were calculated as E{n^2/D} = 1/β and equation (14) in Friston et al. (1994), respectively.

Appendix B

EHI: Form 1 included 10 items asking the hand of preference for: writing, drawing, throwing, using scissors, using a toothbrush, using a screwdriver, using a spoon, using a key, using a hammer, and striking a match. Form 2 included 10 items asking the hand of preference for: writing, drawing, throwing, using scissors, using a toothbrush, using a knife, using a spoon, using a broom (upper hand), opening a box lid, and striking a match. Scores were slightly higher across all subjects screened with Form 1, as replies to the broom and box items on Form 2 were the most variable on either form (these generated more “no preference” and several “exclusively left” responses). Subjects were capable of answering the questions of preference as “exclusively right,” “exclusively left,” “usually right,” “usually left,” or “no preference.” Items marked as “exclusive” use of a hand scored as 2 in the appropriate column and a score of 1 was assigned to the appropriate column when a particular hand was preferred, but not to the exclusion of the other hand. Items where both hands were used were scored with a 1 in both the left and right hand columns. The score for all items was added for each column (left/right) and the difference between the 2 was taken (left-right). This difference between total left and right scores was divided by the cumulative total of both columns and multiplied by 100. The total possible score on the inventory ranged from −100 (strongly left handed) to +100 (strongly right handed). Subjects were classified as left-handed if the score was less than −40, right-handed if greater than +40, and ambidextrous between −40 and +40.