Abstract
With case-parent triads, one can estimate genotype relative risks by measuring the apparent overtransmission of susceptibility genotypes from parents to affected offspring. Results obtained using such designs, properly analyzed, resist both bias due to population structure and bias due to self-selection. Most diseases are not purely genetic, and environmental cofactors can also be important. In this paper, the authors describe how a polytomous logistic regression method previously developed for studying genetic effects on a quantitative trait can be used with case-parent data to study multiplicative gene-by-environment interaction. The idea is that if the joint effect of exposure and genotype on risk is submultiplicative or supermultiplicative, then, conditional on the parental genotypes, inheritance of a susceptibility genotype by affected offspring will appear to have been influenced by the offspring's exposure level. The authors' approach tolerates exposure-complicated genetic population structure, and simulations suggest power and Type I error rates comparable to those of competitors. With this approach, one can estimate the usual interaction parameters under a much less stringent assumption than gene-environment independence in the source population. Incompletely genotyped triads can contribute through an expectation-maximization algorithm. To illustrate, the authors consider polymorphisms in detoxification pathway genes and maternal smoking in relation to the birth defect oral cleft.
Keywords: case-control studies, epidemiologic methods, genetic epidemiology, genetic markers, genotype-environment interaction, logistic models
Family-based designs are of particular interest when studying diseases with onset early in life, such as asthma (1), autism, or birth defects. Investigators collect DNA from cases and their parents (producing a “triad”) in order to find genetic markers related to risk; one can also study maternally mediated genetic effects and parent-of-origin (imprinting) effects. Genotype relative risks can be estimated using a log-linear approach (2–5).
One can also use case-parent triads to study multiplicative gene-by-environment interactions for a dichotomous exposure or a categorical exposure (5, 6). Several other family-based approaches have been proposed, including the case-sibling design (7), the pseudosibling analysis (8), the family-based association test with interaction (FBAT-I) (9), and a method recently developed by Vansteelandt et al. (10).
While a case-only approach could also be used, its reliance on gene/environment independence in the source population should worry a careful investigator. A triad design tolerates a much weaker, within-family, independence assumption and enables assessment of genotype main effects. Thus, the case-parent design is both more robust and more informative than the case-only design.
Triad designs also offer advantages over the usual case-control design, which can be subject to self-selection, differential recall, and bias due to genetic population stratification, if subpopulations have a higher prevalence of the allele and a higher baseline risk of disease. The latter can bias interaction assessments if exposure prevalence also varies across subpopulations. By conditioning on parental genotypes, triad designs avoid bias due to these kinds of confounding. Even if parents self-select for their genes or for their affected child's exposures, self-selection will not produce bias unless the decision to participate is also influenced by which of their alleles they happened to pass on to their offspring.
Case-control designs applied to diseases with early-life onset also typically do not enable assessment of important potential confounders and contributors to risk, such as prenatal effects of the maternal genotype and imprinting effects. In addition, for a study of gene-by-environment interaction, family-based designs generally offer better power than would a case-control design for the same number of cases (6, 11). On the other hand, case-control designs, unlike family-based designs, enable estimation of the exposure effect in addition to the interaction effect. This important advantage can sometimes distort assessment of interaction, however, because misspecification of the main effect of a continuous exposure can cause bias.
In this paper, we describe how a method previously developed for studying genetic effects on a quantitative trait (12) can be used to assess gene-by-environment interaction involving continuous or categorical exposures. The method uses an approach we call quantitative polytomous logistic (QPL) (12). Suppose an autosomic diallelic marker, such as a single nucleotide polymorphism, is studied in case-parent triads and an exposure is measured for the cases. The exposure may be either that experienced via the mother during the pregnancy or one experienced later by the offspring. We show that the interaction assessed by QPL corresponds to the usual multiplicative interaction. To accommodate families with a missing genotype, we use an expectation-maximization algorithm (13).
The proposed approach requires conditional independence of the exposure and the offspring's genotype, given the parental genotypes, meaning that the exposure must not predict genetic transmissions from parents to offspring in the population at large, conditional on the parental genotypes. This assumption is much weaker than assuming independence of the exposure and genotypes in the population at large (as required with a case-only study), though it can be violated for genes that can influence exposure, such as genes governing alcohol metabolism.
We use simulations to compare the power and robustness of the proposed method with those of 2 other analytic approaches based on family data, the FBAT-I (9) and the quantitative transmission disequilibrium test (QTDT) (14), and also with the usual case-control (15) and case-only (16) approaches. To illustrate our proposed method, we test for gene-by-environment interaction between maternal smoking and polymorphisms in a gene involved in detoxification of smoking products, in a study of cleft lip/palate.
Some explanation for our application of the QTDT is needed. The QTDT uses a linear model in which the dependent variable is a quantitative trait, parental genotypes are included as covariates, and one tests for a predictive effect of the offspring genotype on the offspring trait. Here we simply replace the quantitative trait with an exposure—in effect testing whether, conditional on the parental genotypes, the inherited genotype predicts the exposure: Under a no-interaction null hypothesis, genotype and exposure should be independent. The method recently proposed by Vansteelandt et al. (10) uses a similar strategy. We do not simulate that method, however, because its current implementation does not permit saturation of the base model in genotype main effects, and thus the test built on it could often be invalid.
The case-sibling design will also not be considered further here, because for young-onset diseases many families will not have an unaffected offspring available; in addition, the exposure (particularly maternal exposures incurred during pregnancy) will tend to be overmatched in this context. The pseudosibling approach is also not considered, because for complete data it is virtually identical in performance to the polytomous logistic method we will describe, but unlike our approach it cannot readily accommodate incompletely genotyped persons.
METHODS
Proposed approach for complete data
Let C (equal to 0, 1, or 2) be the number of copies of the variant allele the child carries, with M and F being similarly defined for the mother and father, respectively. Let E denote the measured exposure. We assume mating symmetry in the source population so that for all m and f, Pr[M = m and F = f] = Pr[F = m and M = f]. The unordered pair of parental genotypes then defines 6 mating types, denoted as MF = {00, 01, 02, 11, 12, 22} (17).
Consider a multiplicative model for risk of a disease, D. Conditioning on the parental mating type, MF, to control confounding bias due to population stratification, and using C = 1 as the reference category, we write
| (1) |
In equation 1, I(C=0) and I(C=2) are indicator variables for families in which the affected offspring inherited 0 or 2 copies of the allele, respectively; the functions and allow logged relative risks to be functions of exposure. These functions are constants if there is no multiplicative interaction. Note that the main effect of exposure, hMF(e), can depend on parental mating type. For a rare disease, the estimates from model 1 (equation 1) correspond to estimates from a logistic model in a case-control design or a cohort-based analysis that adjusts for parental genotypes.
We can write the relative probabilities for offspring genotypes as a function of exposure given disease, making use of equation 1 and the assumption that Pr[C = c|MF,E = e] does not depend on E:
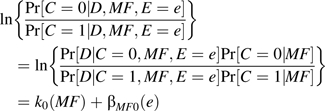 |
(2) |
and, similarly,
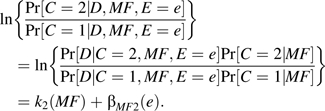 |
(3) |
The kc(MF) are constants defined by Mendelian inheritance as ln{Pr[C = c|MF]/Pr[C = 1|MF]} (18). The development leading to equations 2 and 3 demonstrates that the same interaction functions can be captured in a QPL model based on cases and parents as are in the prospective risk model (equation 1). There is no multiplicative interaction if and only if the functions are constants that do not depend on E.
For convenience when testing, the functions can be entered as linear in exposure, with the null hypothesis then corresponding to both coefficients being 0. One can use standard software (such as SAS or R) to fit a polytomous logistic model, which allows for the exposure effects by conditioning on family and allows for the genetic effects by incorporating intercept terms.
Practical details
QPL is implemented in the following way. To access the interaction, we model Pr(C = c|M = m, F = f, E = e, D), using logistic regression in SAS with a generalized logit function; the parental mating type and E are predictors. The model shown in Table 1 specifies a linear formulation for the interaction such that . Note that the 4 intercept parameters, , absorb both the Mendelian inheritance parameters defined above and genotype main effects. If interaction is detected, nonlinear functions of E can then be estimated. C = 1 is used as the reference category. Because we model case genotype conditionally on parental mating type, the sum of the probabilities is 1 within each mating type.
Table 1.
Probabilities Associated With the Gene-Environment Interaction Model (Polytomous Logistic)
| Parents (MF) | Offspring (C) | Probability (Pr(C|M,F,E,D)) |
| 00 | 0 | 1 |
| 02 | 1 | 1 |
| 22 | 2 | 1 |
| 01 | 0 | |
| 1 | ||
| 11 | 0 | |
| 1 | ||
| 2 | ||
| 12 | 1 | |
| 2 |
A test of gene-by-environment interaction should build from a model saturated in genetic effects by including all 4 of the genotype main-effect parameters (the 4 intercepts), to ensure a valid test of whether the environmental factor modifies those effects. Otherwise, exposure-involved population stratification can confound that assessment.
Using the polytomous logistic model, under the null hypothesis where the effects of E and genetic effects simply multiply, the transmission of the allele to cases will not appear to have been influenced by the exposure. The test is valid without assumptions either about the distribution of the exposure, E, or about the functional form of the dependence of risk on E. One can test the no-interaction null hypothesis using a likelihood ratio test statistic, which for adequate sample sizes is distributed under the null as approximately chi-squared with 2 degrees of freedom (df). One can also consider an alternative model in which allelic effects are monotonic in the interaction term (e.g., using R software) by constraining , which permits a 1-df trend test for interaction.
As seen in our previous work (12), the polytomous logistic model can be extended to include triads with missing parental genotype data, under the assumption that missingness is at random in the sense of Little and Rubin (19)—that is, missing genotypes are missing for reasons unrelated to the true missing genotype conditional on the observed data. The extended model makes use of information from all 6 mating types (not just the 3 with a heterozygous parent), through additional intercept parameters. Because the likelihood fully stratifies on parental genotypes, robustness against bias due to population stratification is preserved even when many genotypes are missing. In addition, an extension allowing multiple cases per family is possible (20).
Simulation methods
We used simulations to compare 5 alternative methods for assessing gene-by-environment interaction. For case-parent triad data, we considered 2 analytic approaches in addition to QPL: FBAT-I (9) is a nonparametric covariance-based analysis; the quantitative transmission approach was described above (14). The QTDT and QPL analyses produce either a 1-df test, based on constraining the interaction to be linear in the number of copies of the variant allele, or a 2-df test. FBAT-I produces a 1-df test only. Unlike QPL, both QTDT and FBAT-I are testing procedures, not estimation procedures, and FBAT-I is not readily able to handle incompletely genotyped triads. We also considered 2 less robust approaches: logistic regression applied to a case-control design, with as many controls as cases, and logistic regression applied to a case-only design.
For each scenario we simulated 1,000 data sets, each with 400 case families and 400 unrelated controls. The designs considered included differing numbers of persons: 400 (case-only), 800 (case-control), or 1,200 (triad methods). Triads were generated by sampling parental pairs (under scenarios with genetic population stratification, both parents came from the same subpopulation), generating a random child genotype based on Mendelian inheritance, and then generating exposure and disease status randomly, based on the presumed rare-disease risk model. Cases were retained until 400 families were generated. Simulated parents were ignored for the case-only analyses and the case-control analyses.
We assessed validity in the presence of population stratification under a no-interaction null hypothesis in the following way. We allowed 2 subpopulations of equal size, each having the diallelic gene in Hardy-Weinberg equilibrium. The allele frequencies differed between the 2 populations and across scenarios (Table 2). The proportion of unexposed persons also differed by subpopulation (Table 2), and we assigned exposures to the exposed persons by exponentiating a standard normal random variable and truncating the exposure at 6. The 1-copy and 2-copy genetic relative risks (relative to 0 copies) were unrelated to exposure (R1 = 1.15, R2 = 1.4).
Table 2.
Type I Error Rates for Tests of Interactiona
| % of Families With a Parent's Genotype Missing | Population Allele and Exposure Frequencies |
|||||
| Allele frequency in population 1: | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| Allele frequency in population 2: | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | |
| Frequency with E = 0 in population 1: | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | |
| Frequency with E = 0 in population 2: | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0 | QPL with 2 df | 0.098 | 0.054 | 0.051 | 0.059 | 0.061 |
| QTDT with 2 df | 0.05 | 0.04 | 0.05 | 0.06 | 0.05 | |
| Case-control with 2 df | 1 | 1 | 0.93 | 0.151 | 0.057 | |
| Case-only with 2 df | 1 | 0.999 | 0.626 | 0.101 | 0.061 | |
| QPL with 1 df | 0.05 | 0.047 | 0.054 | 0.056 | 0.054 | |
| FBAT-I (1 df) | 0.045 | 0.044 | 0.049 | 0.054 | 0.054 | |
| QTDT with 1 df | 0.04 | 0.04 | 0.05 | 0.06 | 0.05 | |
| Case-control with 1 df | 1 | 1 | 0.96 | 0.192 | 0.053 | |
| 25 | QPL with 2 df | 0.108 | 0.059 | 0.052 | 0.061 | 0.063 |
| QPL with 1 df | 0.053 | 0.041 | 0.057 | 0.056 | 0.063 | |
Abbreviations: FBAT-I, family-based association test with interaction; QPL, quantitative polytomous logistic; QTDT, quantitative transmission disequilibrium test.
Results are based on 1,000 simulations for each scenario of studies in a population subject to population stratification but with no interaction (rightmost column has no population stratification).
For non-null scenarios, we simulated data from a homogeneous population, using a range of susceptibility allele frequencies (from 0.1 to 0.5), to study statistical power. The exposure was generated as above, but with 30% of the population assigned as unexposed. As with the no-interaction scenario described above, the non-null scenarios were simulated with no main effect of exposure. The genetic relative risks for unexposed persons were R1 = 1.15 and R2 = 1.4, and the multiplicative interaction parameters were 1.2 and 1.5, per unit of exposure, for 1 and 2 copies of the variant allele, respectively. Expressed in terms of and (Table 1), these interaction parameters correspond to and , respectively. We also estimated the QPL power using the expectation-maximization algorithm (12, 13) when 25% of families had a parent missing.
Application to CYP2E1 and maternal smoking and risk of oral cleft
The cytochrome P-450 2E1 (CYP2E1) gene is involved in the metabolism of many tobacco-smoke products, including volatile nitrosamines and small organic chemicals such as benzene. Thus, variants in this gene plausibly influence fetal response to maternal smoking during pregnancy. We used data from 216 triads in which the offspring had an orofacial cleft to test for an interaction between a known variant in CYP2E1 (rs2249695) and the number of cigarettes the mother reported having smoked per day during pregnancy. The case-parent triads were recruited in Iowa, and details have been reported elsewhere (21).
RESULTS
For the null scenarios simulated (Table 2), both the 2-df and the 1-df QPL test demonstrated rejection rates consistent with for a sample size of 400 families and a minor allele frequency greater than 0.1 in each subpopulation. For lower allele frequencies, the 2-df QPL demonstrated inflated type I error, reflecting the fact that is not estimable when very few participants have 2 copies of the allele. For such scenarios, a 1-df test is advisable, although one should still saturate the base model in genotype effects. The 1-df QPL test performed well even when extreme allele frequencies and exposure prevalences in both subpopulations resulted in small numbers of informative families (see Table 2).
The standard case-control or case-only approaches displayed nominal type I error rates when there was no exposure-related population stratification (rightmost column of Table 2). For other scenarios, the case-control and case-only approaches had alarmingly elevated type I error rates (implying 95% confidence interval coverage well below 95%). By contrast, QPL performed well, with and without population stratification and regardless of whether or not genotype data were complete. FBAT-I and the QTDT also showed type I error rates consistent with the nominal.
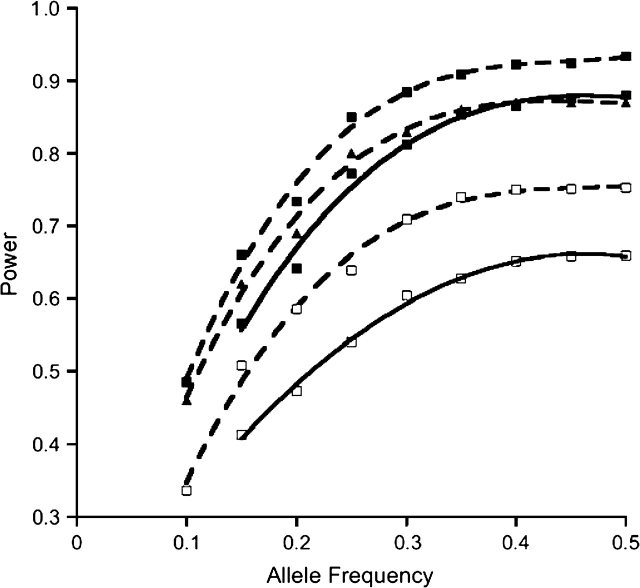
Compared with the case-control approach, the methods based on case-parent triads demonstrated better power when all were valid (Figure 1); as expected, QPL was much less powerful than the case-only approach (data not shown) when marginal gene-by-environment independence held for the population. Compared with other methods based on case-parent triads, the 1-df QPL demonstrated similar power (Figure 1) but the 2-df QPL was able to provide estimates for both interaction parameters, albeit with small bias using 400 families (Table 3). In addition, when used to augment QPL, the expectation-maximization algorithm was able to recover much of the lost power when 25% of families had a parent missing (Figure 2).
Figure 1.
Simulation-based estimated power of tests for interaction effects (level 0.05) at different allele frequencies. A 2-df test is denoted by a solid line and a 1-df test is denoted by a dashed line. The black squares represent the quantitative polytomous logistic (QPL) approach, the black triangles represent the quantitative transmission disequilibrium test (QTDT), and the white squares represent case-control analysis. Because of the inflated type I error rate at low allele frequencies for the 2-df QPL test, power for 2-df tests is shown starting from an allele frequency of 0.15. Power for the 2-df QTDT and the family-based association test with interaction was very similar to that for the QPL 1-df test and hence is not shown.
Table 3.
Estimates of the Interaction Parametersa
| % of Families With a Parent's Genotype Missing | Method | Interaction Being Estimated | Allele Frequency |
|||||||
| 0.2 |
0.3 |
0.4 |
0.5 |
|||||||
| RR | 95% CIb | RR | 95% CI | RR | 95% CI | RR | 95% CI | |||
| 0 | QPL | I1 | 1.21 | 1.20, 1.22 | 1.21 | 1.20, 1.22 | 1.22 | 1.21, 1.23 | 1.22 | 1.21, 1.23 |
| I2 | 1.53 | 1.52, 1.55 | 1.53 | 1.51, 1.54 | 1.53 | 1.51, 1.54 | 1.53 | 1.52, 1.55 | ||
| Case-control | I1 | 1.21 | 1.20, 1.22 | 1.21 | 1.20, 1.22 | 1.22 | 1.21, 1.22 | 1.21 | 1.20, 1.22 | |
| I2 | 1.65 | 1.62, 1.70 | 1.55 | 1.54, 1.57 | 1.54 | 1.52, 1.55 | 1.52 | 1.51, 1.54 | ||
| Case-only | I1 | 1.20 | 1.19, 1.21 | 1.20 | 1.19, 1.21 | 1.21 | 1.20, 1.22 | 1.21 | 1.20, 1.23 | |
| I2 | 1.51 | 1.49, 1.52 | 1.51 | 1.49, 1.52 | 1.51 | 1.49, 1.53 | 1.52 | 1.50, 1.54 | ||
| 25 | QPL | I1 | 1.21 | 1.20, 1.22 | 1.21 | 1.20, 1.22 | 1.22 | 1.21, 1.23 | 1.22 | 1.21, 1.23 |
| I2 | 1.53 | 1.51, 1.55 | 1.53 | 1.52, 1.54 | 1.53 | 1.51, 1.54 | 1.54 | 1.52, 1.55 | ||
Abbreviations: CI, confidence interval; QPL, quantitative polytomous logistic; RR, relative risk.
The interaction parameter values used for simulation were I1 = 1.2 and I2 = 1.5.
Confidence intervals were based on the empirical standard errors using 1,000 estimates from 1,000 simulations.
Figure 2.
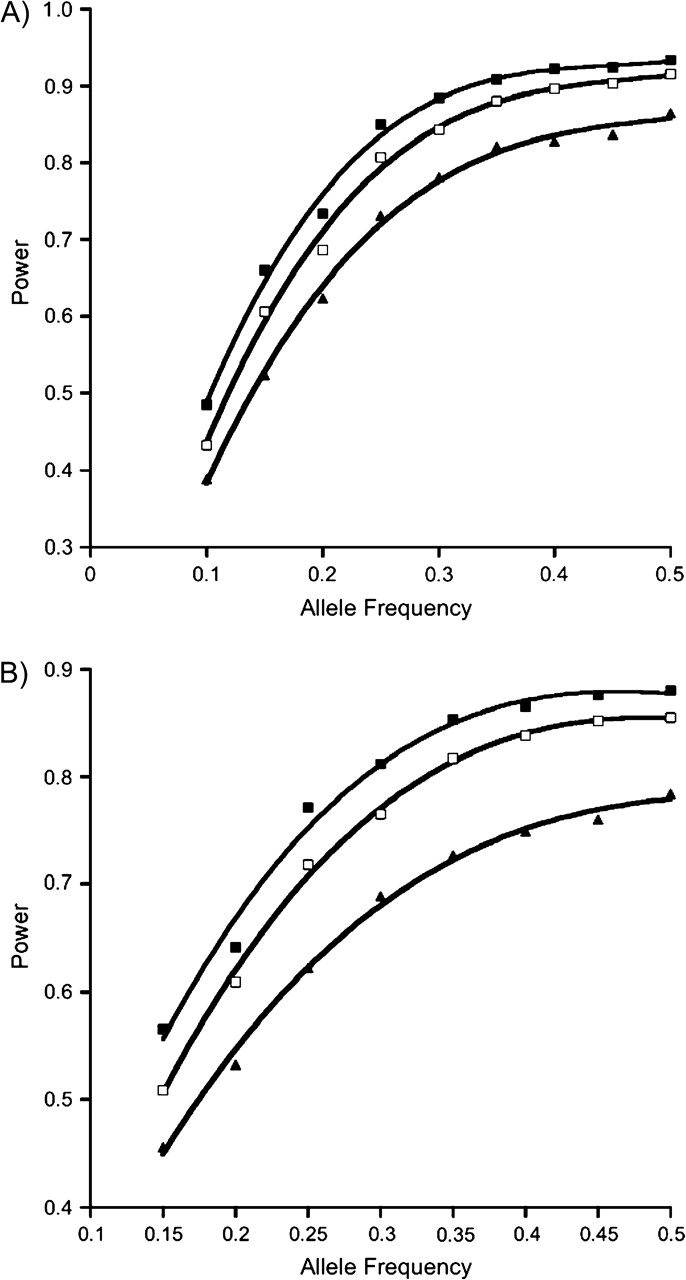
Power when 25% of families are missing genotype data on a parent. A) 1-df and B) 2-df tests. The black squares represent the quantitative polytomous logistic (QPL) approach with complete data, the open squares represent QPL using the expectation-maximization algorithm for missing data analysis, and the black triangles represent QPL using complete triads only when genotypes for 25% of fathers are missing. Because of the inflated type I error rate at low allele frequencies for the 2-df QPL gene-environment interaction test, the power of 2-df tests is shown starting from an allele frequency of 0.15.
Application to risk of oral cleft
The 2-df QPL test for interaction between the number of cigarettes the mother had smoked daily during pregnancy and a variant in the CYP2E1 gene produced a chi-squared value of 7.44 (P = 0.02), and the estimated interactions using C = 0 and E = 0 as the reference values were 1.05 and 1.2 (relative risks) for C = 1 and C = 2, respectively. The 1-df QPL test yielded a chi-squared value of 6.17 (P = 0.013). The estimated relative risks for the interactions were 1.06 and 1.12 (1.062 = 1.12). Thus, the ratio of the relative risks for oral cleft in a child with a copy of the variant allele compared with a child with no copies was estimated to increase by approximately 6% for each cigarette smoked per day.
DISCUSSION
The proposed polytomous logistic approach can be used with standard software to test gene-by-environment interaction based on case-parent triad data using only parents as controls. The QPL method was originally developed to identify genes related to a quantitative trait in studies of offspring and their parents (12). We have shown that the same mathematical structure applies to studies of affected persons and their parents, to allow one to assess the possible role of an inherited genotype in modifying the relative risk associated with an exposure. The proposed polytomous logistic model using case genotype as the outcome, conditional on parental genotypes and case exposure, was shown to correspond to the prospective multiplicative formulation for joint effects of genetic and environmental factors on risk of disease. The QPL method is flexible in that the exposure can be either continuous or categorical. QPL can also use partial information when 1 parent's genotype is missing. Moreover, we have illustrated that for a rare disease, the proposed method can offer both resistance to bias caused by exposure-related population stratification and improved power for detecting departures from multiplicative joint effects of genetic factors and exposures, as compared with a case-control approach. This demonstrated improved power of QPL did come in part at the cost of increasing the number of genotypes by 1.5-fold. Nonetheless, it still had a power advantage (Figure 1) when the comparison was made on a per-genotype basis (data not shown) by using 600 cases and controls.
QPL is also robust against self-selection and against misspecification of the dose-response for effects of the exposure. Despite these strengths, there is an important limitation: Designs that lack population-based controls are usually unable to estimate main effects of an exposure, and this limitation can severely constrain the interpretation of findings related to gene-by-environment interaction. In our example, smoking was already known to be a risk factor for clefting, but such prior knowledge will not always be available.
Based on simulations (also see our previous paper (12)), the power of the QPL method is comparable to that of 2 hypothesis-testing competitors for case-parent data, the parametric QTDT and the nonparametric FBAT-I. However, it offers important flexibility advantages in being able to accommodate maternal effects, parent-of-origin effects, and missing genotype data, through use of the expectation-maximization algorithm—issues not addressed by the other methods. Results of simulations for detecting interaction between an exposure and a parent-of-origin effect are detailed in the Appendix. Another method based on nuclear families is the pseudosibling method of Self et al. (8), later elaborated on by Cordell et al. (22) and Chatterjee et al. (23). For assessment of interaction, its likelihood (and inference about interaction) should be equivalent to that for QPL, once one saturates the models based on pseudosiblings for main effects of the inherited genotype. These pseudosibling approaches, however, offer no straightforward way to include incompletely genotyped triads.
The multinomial method proposed by Lim et al. (24) is similar to QPL but imposes additional constraints on the parental mating type frequencies and the genotype relative risks—constraints that can produce invalid tests. If there is population stratification or the locus under study is in linkage disequilibrium with a nearby susceptibility gene, the apparent main effects of genotype could vary across those parental genotype categories, invalidating a likelihood ratio test based on a potentially incorrect null model. In practice, even for a causative single nucleotide polymorphism, such a scenario is difficult to rule out, so the flexibility implied by using 4 intercept parameters becomes advantageous in practice.
SAS macros and R programs for carrying out the case-parent analyses are available on the Web site of one of the authors (C. R. W.) (http://www.niehs.nih.gov/research/atniehs/labs/bb/staff/weinberg/index.cfm#downloads). The macros are the same as those used for testing linkage and association between a marker and a quantitative trait. To implement QPL for gene-environment interaction, substitute the exposure for the trait variable.
Because of phenotypes expressed during pregnancy, the maternal genotype can be etiologically relevant, hence a potential confounder for effects of the offspring genotype. This issue is particularly a concern for diseases with onset early in life, such as a birth defect. One can take maternal effects into account in a straightforward way using a family-based design, whereas with traditional case-control approaches, a corresponding analysis would require studying the mother for each case and each control (25). While space does not permit consideration of maternal effects here, the QPL method has been extended to allow for them (26). For complete data, interactions between maternal effects and an exposure can be modeled by considering the mother to be the case and the father the control in a matched-pair case-control logistic analysis.
In summary, just as alleles that causally influence a quantitative trait will appear to have been transmitted from parents to offspring in a way that was influenced by the trait value, an exposure that interacts (in the multiplicative sense) with an allele in causing a disease outcome will appear to have had its transmission to affected offspring influenced by the value of that exposure. If we exploit this phenomenon, cases and their parents can tell us much, not only about genetic causal factors but also about exposures with relative risks modified by genetic cofactors.
Acknowledgments
Author affiliations: Department of Health Studies, Division of Biological Sciences, The University of Chicago, Chicago, Illinois (Emily O. Kistner); and Biostatistics Branch, National Institute of Environmental Health Sciences, Research Triangle Park, North Carolina (Min Shi, Clarice R. Weinberg).
This research was supported in part by the Intramural Research Program of the National Institutes of Health, National Institute of Environmental Health Sciences (grant Z01-ES04007-12).
The authors thank Dr. Jeffrey Murray for sharing the clefting genotype data and Drs. Sangmi Kim and David Umbach for their helpful comments.
Conflict of interest: none declared.
Glossary
Abbreviations
- CYP2E1
cytochrome P-450 2E1
- FBAT-I
family-based association test with interaction
- QPL
quantitative polytomous logistic
- QTDT
quantitative transmission disequilibrium test
APPENDIX
We carried out simulations to detect a pure interaction between an exposure and an imprinted gene. We assigned 30% of persons as unexposed and assigned exposures to the exposed persons by exponentiating a standard normal random variable and truncating the exposure at 6. For each scenario, we simulated 400 case-parent triads, with 1,000 simulated data sets per scenario. For analysis we used the method described previously by Kistner et al. (26), for which software is available, as described in that paper for the quantitative polytomous logistic method. The scenario we consider here is such that there are no genetic effects in the absence of exposure, whereas each 1-unit increment of exposure confers a relative risk of either 1.5 or 2.0 associated with inheritance of a copy from a particular parent, but there is no other genotype or exposure effect. The results, for both testing (power for a 0.05-level test) and estimation, are shown in the Appendix Table. Aside from the usual slight bias away from the null (as is often seen with logistic regression), the method performs reasonably well.
Appendix Table.
Power and estimation of gene-environment interaction tests with a gene subject to imprinting
| Frequency | Imprinting Interaction |
|||||
| 1.5 |
2 |
|||||
| Power | Imprinting |
Power | Imprinting |
|||
| RR | 95% CI | RR | 95% CI | |||
| 0.1 | 0.27 | 1.57 | 1.55, 1.60 | 0.64 | 2.10 | 2.06, 2.14 |
| 0.2 | 0.42 | 1.57 | 1.54, 1.59 | 0.84 | 2.08 | 2.05, 2.11 |
| 0.3 | 0.45 | 1.55 | 1.53, 1.57 | 0.92 | 2.10 | 2.07, 2.13 |
| 0.4 | 0.53 | 1.55 | 1.53, 1.57 | 0.97 | 2.09 | 2.06, 2.12 |
| 0.5 | 0.54 | 1.54 | 1.53, 1.56 | 0.99 | 2.12 | 2.09, 2.14 |
Abbreviations: CI, confidence interval; RR, relative risk.
References
- 1.Li H, Romieu I, Sienra-Monge JJ, et al. Genetic polymorphisms in arginase I and II and childhood asthma and atopy. J Allergy Clin Immunol. 2006;117(1):119–126. doi: 10.1016/j.jaci.2005.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wilcox AJ, Weinberg CR, Lie RT. Distinguishing the effects of maternal and offspring genes through studies of “case-parent triads”. Am J Epidemiol. 1998;148(9):893–901. doi: 10.1093/oxfordjournals.aje.a009715. [DOI] [PubMed] [Google Scholar]
- 3.Weinberg CR, Wilcox AJ, Lie RT. A log-linear approach to case-parent-triad data: assessing effects of disease genes that act either directly or through maternal effects and that may be subject to parental imprinting. Am J Hum Genet. 1998;62(4):969–978. doi: 10.1086/301802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Weinberg CR. Methods for detection of parent-of-origin effects in genetic studies of case-parents triads. Am J Hum Genet. 1999;65(1):229–235. doi: 10.1086/302466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Umbach DM, Weinberg CR. The use of case-parent triads to study joint effects of genotype and exposure. Am J Hum Genet. 2000;66(1):251–261. doi: 10.1086/302707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schaid DJ. Case-parents design for gene-environment interaction. Genet Epidemiol. 1999;16(3):261–273. doi: 10.1002/(SICI)1098-2272(1999)16:3<261::AID-GEPI3>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 7.Curtis D. Use of siblings as controls in case-control association studies. Ann Hum Genet. 1997;61(pt 4):319–333. doi: 10.1046/j.1469-1809.1998.6210089.x. [DOI] [PubMed] [Google Scholar]
- 8.Self SG, Longton G, Kopecky KJ, et al. On estimating HLA/disease association with application to a study of aplastic anemia. Biometrics. 1991;47(1):53–61. [PubMed] [Google Scholar]
- 9.Lake SL, Laird NM. Tests of gene-environment interaction for case-parent triads with general environmental exposures. Ann Hum Genet. 2004;68(pt 1):55–64. doi: 10.1046/j.1529-8817.2003.00073.x. [DOI] [PubMed] [Google Scholar]
- 10.Vansteelandt S, Demeo DL, Lasky-Su J, et al. Testing and estimating gene-environment interactions in family-based association studies. Biometrics. 2008;64(2):458–467. doi: 10.1111/j.1541-0420.2007.00925.x. [DOI] [PubMed] [Google Scholar]
- 11.Gauderman WJ. Sample size requirements for matched case-control studies of gene-environment interaction. Stat Med. 2002;21(1):35–50. doi: 10.1002/sim.973. [DOI] [PubMed] [Google Scholar]
- 12.Kistner EO, Weinberg CR. Method for using complete and incomplete trios to identify genes related to a quantitative trait. Genet Epidemiol. 2004;27(1):33–42. doi: 10.1002/gepi.20001. [DOI] [PubMed] [Google Scholar]
- 13.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B. 1977;39(1):1–38. [Google Scholar]
- 14.Gauderman WJ. Candidate gene association analysis for a quantitative trait, using parent-offspring trios. Genet Epidemiol. 2003;25(4):327–338. doi: 10.1002/gepi.10262. [DOI] [PubMed] [Google Scholar]
- 15.Rothman K, Greenland S. Modern Epidemiology. 2nd ed. Philadelphia, PA: Lippincott Williams & Wilkins; 1998. [Google Scholar]
- 16.Piegorsch WW, Weinberg CR, Taylor JA. Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat Med. 1994;13(2):153–162. doi: 10.1002/sim.4780130206. [DOI] [PubMed] [Google Scholar]
- 17.Schaid DJ, Sommer SS. Genotype relative risks: methods for design and analysis of candidate-gene association studies. Am J Hum Genet. 1993;53(5):1114–1126. [PMC free article] [PubMed] [Google Scholar]
- 18.Wheeler E, Cordell HJ. Quantitative trait association in parent offspring trios: extension of case/pseudocontrol method and comparison of prospective and retrospective approaches. Genet Epidemiol. 2007;31(8):813–833. doi: 10.1002/gepi.20243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Little RJ, Rubin DB. Statistical Analysis With Missing Data. New York, NY: John Wiley & Sons, Inc; 1987. [Google Scholar]
- 20.Kistner EO, Weinberg CR. A method for identifying genes related to a quantitative trait, incorporating multiple siblings and missing parents. Genet Epidemiol. 2005;29(2):155–165. doi: 10.1002/gepi.20084. [DOI] [PubMed] [Google Scholar]
- 21.Shi M, Christensen K, Weinberg CR, et al. Orofacial cleft risk is increased with maternal smoking and specific detoxification-gene variants. Am J Hum Genet. 2007;80(1):76–90. doi: 10.1086/510518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cordell HJ, Barratt BJ, Clayton DG. Case/pseudocontrol analysis in genetic association studies: a unified framework for detection of genotype and haplotype associations, gene-gene and gene-environment interactions, and parent-of-origin effects. Genet Epidemiol. 2004;26(3):167–185. doi: 10.1002/gepi.10307. [DOI] [PubMed] [Google Scholar]
- 23.Chatterjee N, Kalaylioglu Z, Carroll RJ. Exploiting gene-environment independence in family-based case-control studies: increased power for detecting associations, interactions and joint effects. Genet Epidemiol. 2005;28(2):138–156. doi: 10.1002/gepi.20049. [DOI] [PubMed] [Google Scholar]
- 24.Lim S, Beyene J, Greenwood CM. Continuous covariates in genetic association studies of case-parent triads: gene and gene-environment interaction effects, population stratification, and power analysis [electronic article] Stat Appl Genet Mol Biol. 2005;4(1) doi: 10.2202/1544-6115.1140. Article 20. [DOI] [PubMed] [Google Scholar]
- 25.Shi M, Umbach DM, Vermeulen SH, et al. Making the most of case-mother/control-mother studies. Am J Epidemiol. 2008;168(5):541–547. doi: 10.1093/aje/kwn149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kistner EO, Infante-Rivard C, Weinberg CR. A method for using incomplete triads to test maternally mediated genetic effects and parent-of-origin effects in relation to a quantitative trait. Am J Epidemiol. 2006;163(3):255–261. doi: 10.1093/aje/kwj030. [DOI] [PubMed] [Google Scholar]