Abstract
The fine spatial scales of the structures in the human brain represent an enormous challenge to the successful integration of information from different images for both within- and between-subject analysis. While many algorithms to register image pairs from the same subject exist, visual inspection shows that their accuracy and robustness to be suspect, particularly when there are strong intensity gradients and/or only part of the brain is imaged. This paper introduces a new algorithm called Boundary-Based Registration, or BBR. The novelty of BBR is that it treats the two images very differently. The reference image must be of sufficient resolution and quality to extract surfaces that separate tissue types. The input image is then aligned to the reference by maximizing the intensity gradient across tissue boundaries. Several lower quality images can be aligned through their alignment with the reference. Visual inspection and fMRI results show that BBR is more accurate than correlation ratio or normalized mutual information and is considerably more robust to even strong intensity inhomogeneities. BBR also excels at aligning partial brain images to whole brain images, a domain in which existing registration algorithms frequently fail. Even in the limit of registering a single slice, we show the BBR results to be robust and accurate.
INTRODUCTION
The fine spatial scales of the structures in the human brain represent an enormous challenge to the successful integration of information from different images. Cortex has a typical thickness of between 1 and 5mm (Fischl and Dale, 2000). Thalamic nuclei have spatial extents on the order of a few millimeters (Kandel, 2000). Cortex is also highly folded, meaning that points that are 20mm from each other as measured along the cortical surface can be within a few millimeters in three-dimensional space. This places stringent requirements on the accuracy and precision of algorithms for aligning images. Even a few millimeters of alignment error can cause a voxel in a tissue type in one image to be assigned to the wrong tissue type in another image. This challenge extends to several domains, including within-subject integration of images from a wide range of imaging modalities such as structural MRI, functional MRI (fMRI), arterial spin labeling (ASL), diffusion weighted imaging (DWI), positron emission tomography (PET), within-subject single-mode longitudinal analysis, and surface-based group analysis (Fischl et al., 1999).
Automatic within- and cross-modal registration has a long history of research in neuroimaging. The most prominent and widely used algorithms currently extant are Cross-Correlation (Collins et al., 1995), Mutual Information (MI; Maes et al., 1997; Maes et al., 1999; Wells et al., 1996), Normalized Mutual Information (NMI), and Correlation Ratio (CR; Roche et al., 1998). Surface-to-surface and shape registration (Borgefors, 1988) have also been used for multimodal registration; however, West (West et al., 1999) found that these were not as accurate as intensity-based techniques. The basic model used in CR is that an intensity value in one mode will have one, and only one, matching intensity value in the other mode. MI and NMI are similar to CR but less restrictive in that they attempt to sharpen the intensity joint histogram. For both methods, intensity mismatches are evidence for misregistration. Correspondence can be achieved by adjusting the registration parameters (i.e., translations, rotations, scalings, shears) until the best match (i.e., minimum cost) is achieved. Unfortunately, intensity inconsistencies can exist for other reasons, which may be mode-specific. For example, in a Blood-Oxygen-Dependent (BOLD) weighted image, the tissue outside of the brain often appears quite dark whereas it will be bright on an anatomical. The brain can be extracted from the anatomical image (Segonne et al., 2004), but the quality of the resulting registration will then be sensitive to the aggressiveness and quality of the extraction. Echo planar images (EPI) are also subject to B0 distortion in the form of non-linear metric distortion and intensity “drop out” (Jezzard and Balaban, 1995). In addition, coil sensitivity profiles and B1 inhomogeneity can create spatial intensity fluctuations. Coil sensitivity fluctuations can become extreme when surface coils are used as is often done when studying retinotopy with fMRI (Sereno et al., 1995). All these effects create inconsistencies in input intensity matching that are unrelated to the quality of alignment, but will be indistinguishable from alignment errors and thus can drive an alignment away from the true optimum.
In longitudinal analysis, in which the same subject is imaged over time in different scan sessions, cross-session alignment of the brain is well described by a rigid transformation, but there are significant non-rigid effects such as differences in jaw and tongue placement or head-neck angle. In theory, these can be accommodated by brain extraction, but, again, the resulting registration will be sensitive to differences in the extraction of the brain at different time points. Finally, we point out that some imaging modalities may not have full brain coverage. For example, the brain coverage in EPI must be reduced in order to reduce the slice thickness and maintain temporal resolution. Partial field-of-view (FoV) brain coverage creates enormous problems when attempting to register to a whole head
Recently, Saad (Saad et al., 2009) performed an extensive analysis comparing CR and MI and found that they had errors that could easily exceed 3mm. This led them to propose a new cost function optimized for T2*-T1 registration using a local Pearson correlation (LPC). LPC is a local method, meaning that the cost at each voxel is only dependent on the nearby voxels (roughly the 36 nearest neighbors). As part of the computation of the Pearson correlation, the mean intensity over a neighborhood is subtracted from the intensity at each voxel in the neighborhood. This is effectively a spatial high-pass filter and so enhances edges in both the input and reference images; the correlation is then computed over the neighborhood. Areas away from tissue boundaries should contribute little to the overall cost since these areas tend to have locally homogeneous intensities in both images which will be suppressed by the local mean removal. This means that the areas near the tissue boundaries will drive the cost function; in this way it is similar to BBR.
Like Saad, et al, we have also observed inaccuracies and sensitivities in the registrations found by CR and MI. In this paper, we propose a new algorithm based on the principle that the most salient registration cue is the contrast across a tissue boundary, and so we refer to it as Boundary-based Registration, or BBR. Unlike the methods reviewed above, BBR does not treat the two images as equal. One of the images (the “reference image”) must be a high-quality anatomical volume sufficient for extracting surfaces that separate brain structures and tissue types. The second image (the “input image”) can be any modality as long as it has tissue contrast. Alignment is achieved by maximizing the gradient of the input image intensity across the surface boundary. Intensity values in the anatomical image are not part of the cost function. If two or more input images need to be aligned, they can each be separately aligned to the reference with BBR. We emphasize that this is not a surface-to-surface registration like those described above. A surface is only extracted from one image, the high-quality anatomical; intensities are used from the second image. It is similar to LPC in that a local cost is computed from tissue boundaries. However, there are some differences in that BBR operates over a much smaller neighborhood (a few millimeters) and uses percent contrast instead of correlation coefficient. At the time this manuscript was being prepared, LPC had only recently been published, and so we have not had the chance to compare it to BBR directly.
We show that BBR yields superior accuracy compared to CR and NMI using blinded human raters as well as improved fMRI results. We then show that BBR is extremely robust to variations in its parameters and initialization, major fluctuations in image intensity inhomogeneity, and to partial brain images, even to the extent of accurately registering single slices, something for which most current registration methods fail. The software that implements BBR is publically distributed as part of the FreeSurfer (surfer.nmr.mgh.harvard.edu) software package.
METHODS
Cost Function Derivation
Our fundamental hypothesis in this research is that the quality of registration is best assessed by the magnitude and direction of the change of intensity across a tissue boundary. This is essentially what is done by a human when registering visually (see Figure 2), which motivates us to quantify goodness of alignment using boundary intensity gradients. In this work, the boundary we use is derived from an anatomical volume using a surface model. An anatomical surface model is one where a mesh of points, triangles and edges is used to define the boundary between different tissue types or structures. The mesh consists of a set of vertices and the neighborhood relations of each vertex. Each vertex has a coordinate in the 3D anatomical space that allows us to compute various geometric features of the boundary such as curvature and surface normal vectors. Though this method can be applied using the surface between any structures, we focus on the surface between cortex and adjoining white matter. We believe that cortex is best target for two reasons: (1) It is highly folded, allowing dense sampling of 3D space, and, (2) It is very thin (2.5mm on average; Fischl and Dale, 2000), implying that small alignment errors will generate large changes in the cost function. Despite the fact that we use the cortex as a target, we emphasize that the goal is to achieve good registration between the entire input volume and the entire anatomical volume, not just the locations along the cortex. However, for affine transformations, good cortical registration is sufficient to achieve good registration everywhere (assuming no non-linear distortion).
Figure 2.
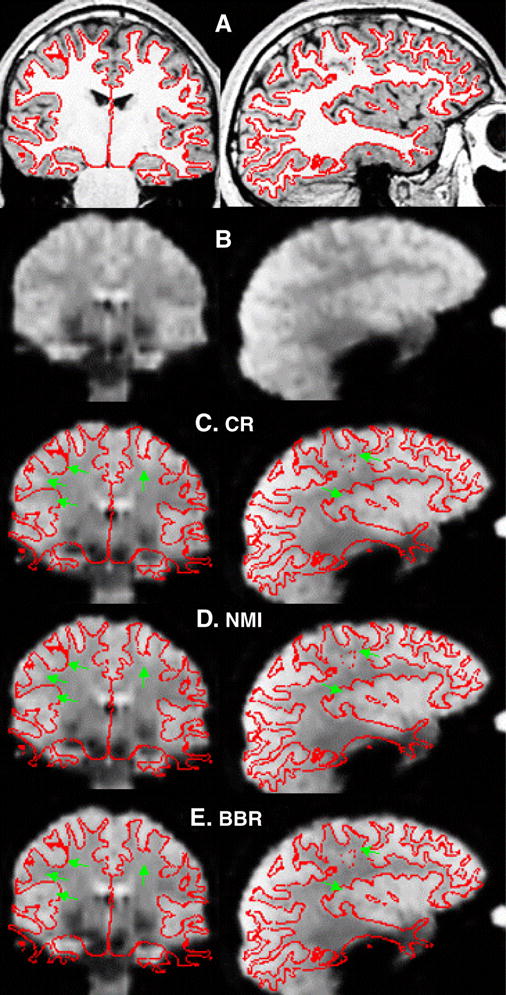
FreeSurfer manual registration tool (tkregister2), coronal and sagittal views. (A) T1-weighted anatomical with white surface. (B) T2*-weighted Functional. The cortex can be seen as bright patches against the darker white matter. (C–D) Functional with surface placed by the given registration technique. (C) CR. (D) NMI. (E). BBR. The green arrows are in the same place relative to the surface in each panel and indicate places where the registration in CR or NMI are inaccurate.
Several software programs exist to construct computational models of the cortical surface such as FreeSurfer (Dale et al., 1999; surfer.nmr.mgh.harvard.edu), Caret (Van Essen et al., 2001), BrainVISA (D. Riviere, 2003) and Brain Voyager (www.brainvoyager.com). In FreeSurfer, the cortical surface models include a representation of the surface between cortex and white matter (hereafter referred to as the “white surface”) as well as the outer surface of the brain (hereafter referred to as the “pial surface”); this allows an estimate of cortical thickness at each vertex. FreeSurfer also provides detailed labeling of both cortical and subcortical structures. This can be useful for excluding certain areas known to have problems in certain modes (e.g., orbital frontal cortex in EPI).
Let A be the 3D anatomical volume indexed by r (i.e., the intensity of A at point r is A(r)). Let E be the 3D input volume of the same subject indexed by p. Then some transform T exists such that p = T(r,θ) will bring the two volumes into registration where θ is the set of registration parameters. The input intensity value at anatomical location r for parameter set θ can be computed as E(T(r, θ)). We model T as an affine (12 degree-of-freedom (DOF)) transform (ie, 3 translations and 3 rotations, 3 scales, and 3 shears). The coordinate system is centered at the center of the anatomical volume, which puts it near the center of the brain. Transformations are applied in the order of translation, rotation, scaling, and shear, with translations measured in mm and rotations measured in degrees. By default, we use a rigid transform (6 DOFs) because we assume that both volumes are from the same subject; however, our software can handle as many as 12 DOFs. The problem, then, is to find T given all the issues discussed above.
A vertex V on the white surface will have a 3D location rV and surface normal nV (see Figure 1A). We can compute a location just inside the surface (i.e., in the white matter) as rwv = rV − Δwv*nV and just outside the surface (i.e., in the cortical gray matter) as rgv = rV +Δgv*nV, whereΔw and Δg are the white and gray matter projection distances, respectively, and may be vertex-dependent. For a given θ, these points can then be transformed to the input volume through T, ie, pwv(θ) = T(rwv, θ) and pgv(θ) = T(rgv, θ) in order to sample the intensity at these points given the set of registration parameters, i.e., the nominal white matter intensity would be wv=E(pwv(θ)), and the nominal gray matter intensity would be gv=E(pgv(θ)). We emphasize that gv and wv may or may not be in their respective tissue classes – that depends on the quality of the registration θ. If they are in their proper tissue classes, then we would expect the difference DV(θ) = gv−wv to be large and of a predictable sign (e.g., positive for BOLD). If they actually fell into the same tissue class, then we would expect the difference to be close to 0. This difference then becomes a measure of the quality of the registration at vertex V. If either gV or wV fall outside of the 3D FoV of E, then vertex V is excluded entirely from contributing to the final measure of goodness.
Figure 1.
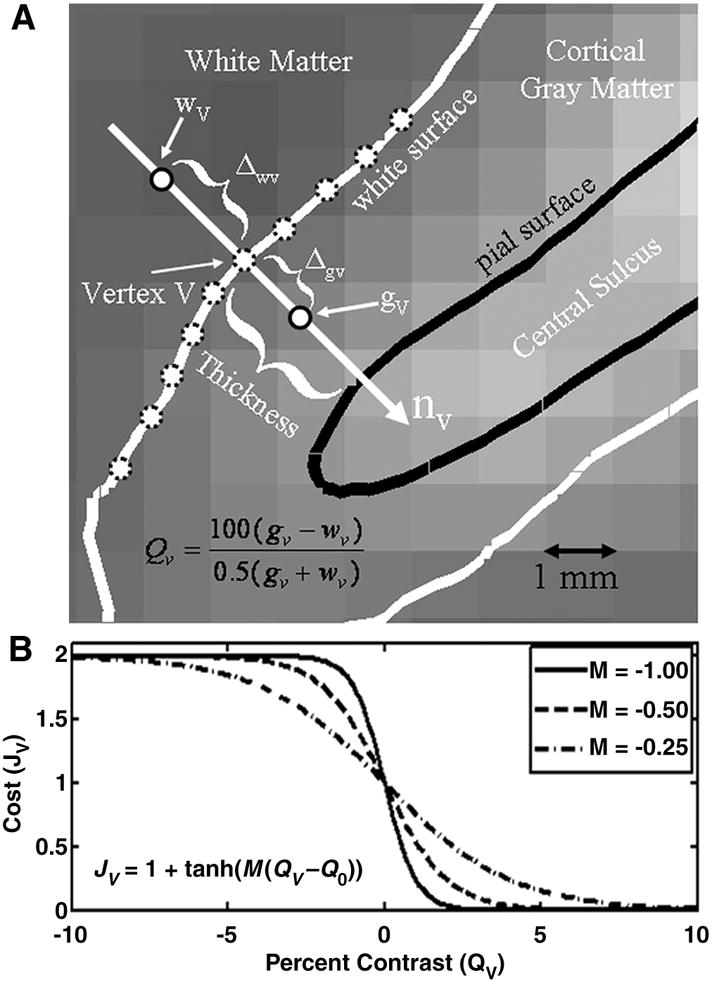
Diagram of how the BBR cost function is computed. (A) The gray scale background is a BOLD-weighted image approximately axially sliced through the central sulcus. The black line (“pial surface”) is the boundary between cortical gray matter and sulcal CSF. The white curve (“white surface”) is the boundary between cortical gray matter and white matter. The distance between the white and pial surfaces is the thickness, which is computed at each vertex V. The gray matter intensity at a vertex (gV) is computed at a fractional distance Δgv along the surface normal (nV) into cortex. The white matter intensity at a vertex (wV) is computed at an absolute distance Δwv along the surface normal (nV) into the white matter. The percent contrast at a vertex (QV, Equation 1) is then computed as the relative difference between the gray and white matter intensities. (B) Function that converts contrast into a cost, with large contrasts in the expected direction (positive for BOLD-weighted) having a low cost and those in the unexpected direction (negative) having a large but saturating cost.
One of the advantages to this method is that DV is mostly insensitive to spatial intensity inhomogeneities due to coil profiles or B1 inhomogeneities. These fluctuations are slowly varying over space, whereas DV is computed from points that are only a few millimeters apart. We also use a percent contrast measure at each vertex:
| (1) |
Using a percent contrast assures that bright regions do not get a larger weight than dark regions. We pass the percent contrast through a non-linearity (see Figure 1B) and sum over the surface to compute the final cost as given in the equation below:
| (2) |
where Q0 is an offset parameter, Mv is a slope parameter the sign of which is dependent upon the expected direction of contrast in the input image (positive for gray matter brighter than white), and hv is a weight for vertex V. Allowing the slope parameter to change with vertex can allow the modeling of contrast changes with anatomy. The tanh() function is motivated by the desire to have a smooth function with saturating non-linearity that reduces the weight for vertices that have a large contrast in the unexpected direction. In this way it is similar to the saturating cost functions used in robust statistics (Hampel, 1986). It also assures that vertices with a large direction of contrast in the expected direction have a low cost. We could have used a binarization (i.e., setting the cost to 0 if the direction of contrast is in the expected direction or 1 otherwise), but this would have made the cost function less smooth. We expect that most any function that meets these criteria would work, and we show that the final results are quite insensitive to parametric variations in the cost function. The total cost is summed over a (possible) subset B of vertices that fall within the 3D FoV of E. A subset allows for speed increases during an initialization phase and/or avoidance of problem regions. N is the total number of vertices participating; this might be less than the number of vertices in B if some vertices fell out of the 3D FoV of E.
By default, we use the following parameter settings: Q0=0; MV = +0.5 for modalities where we expect gray matter to be brighter than white matter (e.g., a T2-weighted MRI) and −0.5 for the reversed contrast; hV=1 for all vertices; Subset B: only vertices in cortex; the second and third optimization stages (below) sample every 100th vertex; the fourth and fifth sample every vertex. Δg and Δw are the distances from the gray/white junction that we sample the gray matter and white matter. Ideally, we want to push these as far apart as possible so as to avoid sampling the same voxel (easily possible at fMRI resolutions). However, if we sample the cortical gray matter too far away from the junction, we might miss it entirely. If we sample the white matter too far away from the junction, we might sample some other structure, although having access to the explicit surface models allows us to prevent this from happening. Since the gray matter thickness changes across cortex, we allow Δg to change with location (though it is certainly possible to fix it). By default we sample midway (Δg=0.5) between the white and pial surfaces. We set the default value of Δw=2mm independent of spatial location. Another advantage to separating these two points is that it will make the registration less sensitive to errors in surface placement during anatomical analysis. Given the values above, the surface could be off by +/−1mm, and gv and wv should still be located in their respective tissue types. Below, we show that the final registration is not very sensitive to even wide changes in these parameters. Finally, we use trilinear interpolation by default to assure smoothness in the cost function. If a vertex falls into an input image edge voxel, then nearest neighbor is used. We chose not to exclude edge voxels entirely as this would limit applications to those with 3 or more slices.
Handling B0 Distortion
B0 distortion is the geometric and intensity distortion caused by inhomogeneities in the main magnetic (B0) field caused predominantly by air-tissue interfaces in the scanner (Jezzard and Balaban, 1995). Acquisitions with long k-space readouts (such EPI) are most susceptible, and the B0 distortion tends to increase with an increase in resolution as this will usually increase the readout time. The metric distortion is non-linear and can be corrected through the use of a B0 map (Jezzard and Balaban, 1995). The intensity distortion (also called “dropout”) cannot be corrected. The metric and intensity distortions tend to occur in known anatomical locations (eg, orbital frontal, medial temporal gyrus, etc), and these areas are automatically labeled in FreeSurfer (Desikan et al., 2006). This gives us the ability to exclude them from the cost function. Note that these regions will still be aligned properly if the B0 distortion has been corrected, though the signal may be less useful due to dropout. If the B0 distortion has not been corrected, then these areas will be misregistered. We have built into our BBR implementation the ability to mask out the following regions: middle temporal gyrus, inferior temporal gyrus, temporal pole, fusiform gyrus, entorhinal, medial orbital frontal gyrus, caudal anterior cingulate gyrus, and rostral anterior cingulate gyrus. Below, we explore the effect that this has.
Optimization
Optimization is the process of finding the global cost minimum over the parameter space. No method except a costly, and possibly intractable, brute-force search can guarantee that the global optimum has been found. Registration methods typical rely on a course search over a wide range of parameter space followed by gradient descent to the optimum (Jenkinson et al., 2002). Suboptimal registrations can occur if the gradient descent gets trapped in a local minimum because the course search did not yield a starting point in the basin of the global minimum; the first two stages of the BBR optimization below are designed to avoid this problem. A local minimum may also be encountered because discontinuities exist near the global optimum (Jenkinson et al., 2002). This type of local minimum is avoided because, as we show, the BBR cost function is very smooth. The BBR optimization stages are:
-
Initialization. In this step we compute an initial registration that falls into the capture region, roughly within 7mm and 7° of the optimum (Figure 3). This can be accomplished in several ways:
The anatomical and input volumes were acquired in the same session, in which case the initial registration can be performed in scanner coordinates based purely on the geometry as long as the subject has not moved excessively between acquisitions.
The input volume is whole brain, in which case we use existing software that implements a global method (e.g., FSL/FLIRT or SPM/spm_coreg) to obtain an initial registration that will fall into the BBR capture region.
The input volume is partial brain or surface coil but a whole-brain volume was also acquired, in which case methods (a) and (b) can be combined. Note that any whole-brain volume is sufficient; it does not need to be an anatomical. If a surface coil is used, then the whole-brain should be acquired with the body coil.
If the above methods fail, the initial registration can be determined manually.
Coarse Search. Here we sample the cost function at 3 points along each parameter dimension to form a 6 dimensional grid in parameter space. The translations are sampled at −4, 0, and +4 mm and the rotations are sampled at −4, 0, and +4° for a total of 36 = 729 points; the point with the smallest cost is fed to the next step. This is done in order to extend the effective capture range of the algorithm, allowing datasets with large translations and rotations to be accurately registered. The surface is sampled every 100th vertex to speed computations (our typical surfaces have on the order of 150,000 vertices, so this still results in a dramatically over-determined problem with 1,500 data points and 6 unknowns). For problem data sets, the FoV and sampling resolution of this grid can be expanded at the cost of more computation time.
Gradient Descent I. The tolerance (see below) is set to 10−4 and the surface is sampled every 100th vertex to speed computations. The result is fed to the next stage.
Fine Search. Again, we sample the cost function at 3 points along each parameter dimension to form a 6 dimensional grid in parameter space. The translations are sampled at −0.1, 0, and +0.1 mm and the rotations are sampled at −0.1, 0, and +0.1° for a total of 36 = 729 points; the point with the smallest cost is fed to the next step. This is done for cases where the topography around the minimum is very flat. This step assures that the bowl will be approached from the best nearby position. The surface is sampled every vertex.
Gradient Descent II. The tolerance (see below) is set to 10−8 and the surface is sampled every vertex. If the registration is being done with more than 6 DOF, then the extra DOFs are optimized here. The previous steps use only 6 DOF.
Figure 3.
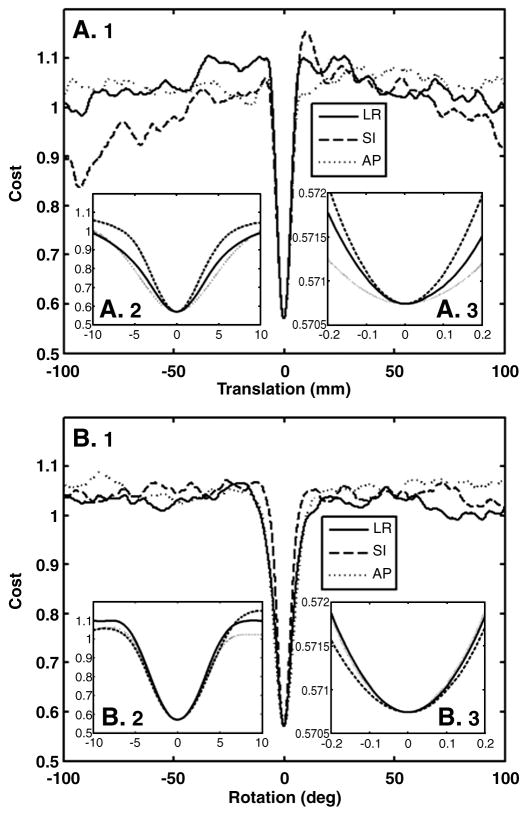
Cost function (Equation 2) when each of the 6 DOF is parametrically varied. (A) Translations in the left-right (LR), superior-inferior (SI), and anterior-posterior (AP) directions. (B) Rotations about each of those axes. Each panel shows a different scale: (1) +/−100mm, (2) +/−10mm, (3), +/−0.2mm. This shows that the minimum is global and that the cost function is extremely smooth, even at the sub-millimeter level.
The gradient descent is performed using a series of 1D minimizations (i.e., Powell’s method (Press et al., 1988)) as implemented in the VXL library (vxl.sourceforge.net)). The gradient descent has one parameter, the tolerance used to terminate the descent. The tolerance is the absolute difference in costs between successive steps divided by the average cost at those steps. The minimal tolerance achievable is constrained by the machine precision. In our tests, we found that setting the tolerance below 10−8 had no effect on a 64 bit machine.
Evaluation Criteria
In order to evaluate the accuracy of the BBR, we compare it to two other popular registration algorithms: CR and NMI. Except where noted, all algorithms are constrained to 6 DOF. Many neuroimaging software packages have implementations of CR and NMI, e.g., FSL (www.fmrib.ox.ac.uk/fsl); SPM (www.fil.ion.ucl.ac.uk/spm), AFNI (afni.nimh.nih.gov/afni), AIR (bishopw.loni.ucla.edu/AIR), and MINC (www.bic.mni.mcgill.ca/software). For our evaluations, we use the FSL implementation of CR (the FLIRT program), and the SPM implementation NMI (the spm_coreg program). These will be evaluated based on accuracy and robustness. Accuracy is judged based on visual inspection in which the raters are blinded to the registration algorithm identity, and ability to map fMRI activation to the surface. Robustness is assessed based on the ability of an algorithm to maintain a registration when the input image or the algorithm itself is changed in some way. The accuracy and robustness tests are performed on the same data set. Using the accuracy tests, we show that the accuracy of BBR equals or exceeds that of CR and NMI on whole-brain, artifact-free data. Using the robustness tests, we show that the BBR registration deviates little from the whole-brain result even under substantial changes to the data or to the implementation parameters. This implies that BBR remains accurate under these conditions. One way to measure accuracy is to know the ground truth under simulated conditions. While, it is not a simple matter to simulate metric and intensity distortion in MRI, some progress has been made in this area (Drobnjak et al., 2006; Xu et al., 2007). However, we have chosen to use a combination of visual inspection and consistency tests on real images.
Visual Inspection
we use the FreeSurfer interactive tool called “tkregister2” for visually inspecting (and possibly changing) a registration. The tool allows the anatomical and functional images to be displayed. The cortical surface can also be displayed on both images. Screen shots are shown in Figure 2. Panel A shows the T1-weighted anatomical with the white surface shown in red; notice how the white surface closely follows the gray/white boundary. Panel B shows a BOLD-weighted EPI image. While the cortical anatomy is blurry, it can clearly be seen. Panels C-E show the EPI with the white surface overlaid, where the EPI has been registered to the anatomical with the given method (C: CR; D: NMI, and E: BBR). The brighter patches in the EPI indicate gray matter (and/or cerebral spinal fluid (CSF)), whereas white matter appears darker. A good registration, then, is one where the red line closely follows the boundary of the bright patches. For each subject in the evaluation data set, the authors (DNG and BRF) ranked the three registrations. The raters were blinded as to the identity of each registration. The raters were also asked to make a subjective judgment as to whether the best registration was “acceptable”. Neither one of these measures gives an actual measurement as to how far off a registration is from “true”.
fMRI Activation
Activation in an fMRI experiment should appear in gray matter and so the amount of activation measured on the cortical surface can be used as a measure of the quality of the registration between the anatomical and the fMRI volumes. For a given registration, we sample the fMRI activation onto the surface and simply count the number of voxels above a threshold (p<.001); with the idea that the more voxels, the better the registration. Of course, some of those voxels will be false positives; however, the fMRI analysis we used (see below) includes temporal whitening so that the actual false positive rate should be close to the nominal rate of 0.1%. More importantly, we apply the registration after the analysis, so each registration will see the same false positive rate, and so false positives should not bias our ranking of methods. For more details, see fMRI analysis methods below.
Robustness
As mentioned above “robustness” is the ability of an algorithm to maintain a registration when the input image or the algorithm itself is changed in some way. The basic idea here is that there is only one optimum registration, and that the optimum should be invariant to initialization, image corruptions and a wide range of algorithm parameters. Note this makes no statement about whether the optimum is a good registration. To quantify the robustness, we need a measure of the difference between two registrations. For this we have chosen to use a measure we call the Average Absolute Distance (AAD); this is the distance that the cortical surface moves between the two sets of registrations parameters θ1 and θ2. The AAD is defined to be:
| (3) |
The AAD is measured in mm and gives us an easily interpretable metric for registration consistency. Note that this is not biased by the fact that we generate the cost function from the surface. The surface is simply a convenient way to sparsely sample the registration differences over the entire brain. This measure is similar to the measure introduced in (Jenkinson et al., 2002) in which a closed-form expression was used to compute the average RMS deviation between two registrations averaged over a sphere. However, AAD is computed over the actual cortical surface instead of a sphere and uses the absolute value instead of the square.
We propose several robustness tests:
Cost Function Parameter Manipulation (BBR only). The purpose of this test is to determine how sensitive the registration is to changes in the parameters of the cost function and the way algorithm is implemented. The parameters we perturbed are Q0, Mv, Δg, and Δw. We generate the first set of registration parameters (θ1) using the default parameters. When then change the cost function parameters and re-register the original volume, using the first registration as initialization, to generate the second set of parameters (θ2). We then compute the AAD between the two sets of registrations. Ideally, the AAD would be 0.
B0 Masking (BBR only): in this test, the first registration is generated using all cortical vertices on the surface. This registration seeds a second registration in which the vertices in the B0 regions described above are masked out (i.e., do no contribute to the cost function). The AAD is then computed between the two registrations.
Initialization Test (BBR only): in this test, we register a data set, then modify the resulting registration by translating and rotating it, and then use this modified registration as the initial starting point for Stages 2–5 to see how closely we return to the original registration. This simulates the case were Stage 1 is inaccurate. For each subject, we randomly selected 30 translations and rotations uniformly in the range of +/−10 mm and +/− 10° (i.e., all 6 registration parameters were simultaneously changed). The size of the “perturbation” was defined to be the maximum of these translations and rotations (measured in mm or degrees). The re-registration was deemed to have failed if it did not return to within 0.100mm AAD of its original location.
Reduced Field-of-View (FoV) Test: the first registration is generated from a whole-brain fMRI volume. The second registration is generated from the same volume after removing some number of slices from the top and bottom and using the first registration as initialization. These should generate exactly the same set of registration parameters. Thus we can measure the AAD as a function of the number of remaining slices. This simulates the case where data of interest is acquired with a reduced FoV, and a full FoV data set is acquired in the same scanning session to assist in registration
-
Intensity Inhomogeneity Test: the first registration is generated from the original fMRI volume. The bottom half of the slices are then discarded while the top half have their intensity scaled on a slice-by-slice basis. This situation simulates the case where a surface coil is used (which induces a sharp fall-off in intensity away from the coil). The initial whole-brain volume largely free from intensity inhomogeneity can be obtained using the body coil for reception (this is noisy but adequate). The coil profile is implemented as a half-cosine function:
where S is the slice number, Ns is the number of slices, and α is a control parameter (see Figure 6). For slices nearest the top of the brain (ie, low values of S), F is nearly 1 (no intensity distortion). For slices further away from the top, F drops off and reaches 0 when S=Ns. When α is 0, F=1 for all values of S (i.e., no distortion), as α increases to 1, the amount of drop off increases. Thus, we can measure the AAD as a function of α.
Surface Inaccuracy Test: in this test we evaluate how the BBR results change when a less accurate surface is used. For this we used the FMRIB’s Automated Segmentation Tool (FAST; Zhang et al., 2001) distributed with FSL. We used this program to segment the anatomical images into gray, white, and CSF, and then used FreeSurfer to generate a surface between white matter and the other tissue types. We then ran BBR with this surface, initializing with the registration from when the FreeSurfer surface was used. The AAD was then computed between these two registrations. Since this application only has one surface, we used an absolute gray matter projection distance of 2mm. Note that we are not trying to do a quantitative comparison between FreeSurfer and FAST, we simply want to generate reasonable surfaces that we do not expect to be as accurate as those generated by FreeSurfer.
Degree-of-Freedom Test: in this test we evaluate how the BBR registration changes when higher DOFs are used. We use the 6 DOF registration to seed the 9 (+scale) and 12 (+scale+shear) DOF optimizations, then measure the AAD between the pairs for all 18 subjects.
Figure 6.
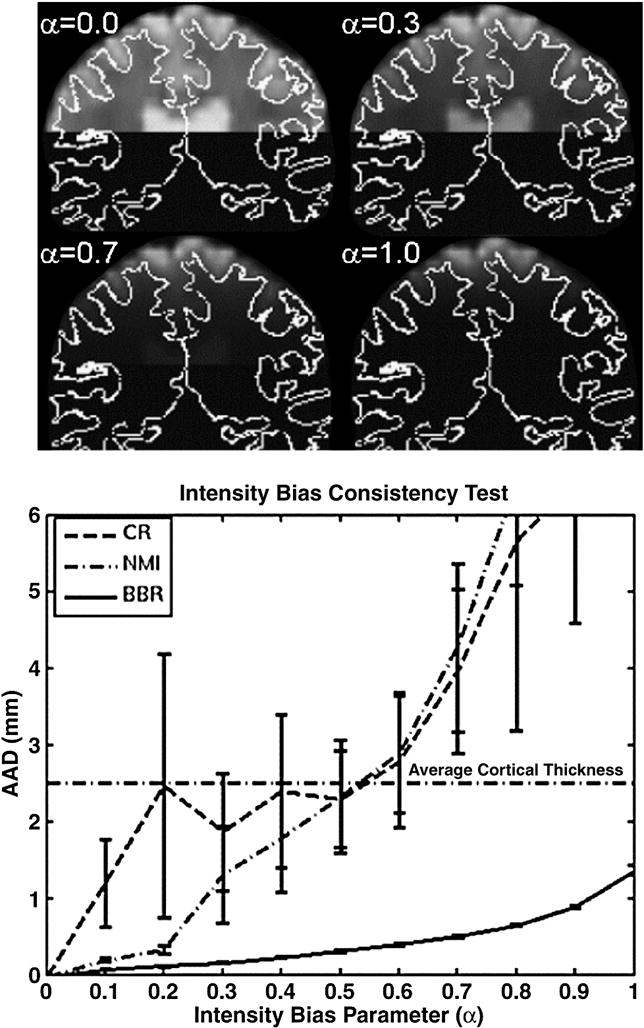
The top panel shows a coronal slice of the functional for four values of α in order to demonstrate how the intensity of each slice was attenuated using a half-cosine intensity bias model. The white curve is the gray/white boundary. For α=0, there is no bias; α=1 gives the maximum bias. Bottom panel shows how each method performed as the bias parameter was changed. The confidence intervals represent 1 standard error.
Evaluation Data Set, MRI Methods, and fMRI Analysis
The data set used to evaluate the registration method was collected as part of the Functional Biomedical Informatics Network (fBIRN, www.nbirn.net) East Coast Traveling Subjects (ECTS) pilot study. Eighteen subjects were each scanned at four sites undergoing both functional and anatomical protocols. This evaluation only deals with the data collected at MGH (Siemens 3T Tim-Trio with 12-channel head coil). A T1-weighted MP-RAGE volume was collected for each subject and analyzed in FreeSurfer to create the white and pial cortical surfaces and compute thickness and surface normal vectors at each vertex. Eight whole-brain fMRI data sets (TR=2000ms, TE=30ms, flip=77°, bandwidth=2298Hz/pixel, 30 slices, slice thickness 4mm skip 1mm, matrix size 64×64 at 220×220mm, 142 time points, sequential slice order) were acquired for each subject. Subjects performed a working memory task that consisted of four block types (1) Scrambled images, (2) Encode, (3) Distractor, (4) Probe. During Encode, subjects passively viewed line drawings which they were asked to remember. During the Distractor block, subjects were shown complex pictures and asked to respond with button press as to whether there was or was not a human face. During the Probe phase, subjects were shown pairs of line drawings, one of which they had seen during the Encode phase and asked to respond with a button press as to which drawing they had seen before. Each block lasted 16 sec. The middle time point of each run was used as the fMRI template for both registration and motion correction. The fMRI data were motion corrected using MCFLIRT and slice-time corrected using the FSL slicetimer program. The fMRI data were not spatially smoothed or otherwise interpolated as this would have made the results less sensitive to registration errors. The fMRI data were not corrected for B0 distortion. The fMRI time series analysis was performed using FEAT (Woolrich et al., 2001), modeling each block as a separate explanatory variable using the default gamma hemodynamic response model. The contrast between Probe and Scrambled blocks was thresholded at a voxel-wise threshold of p<.001 (uncorrected). This contrast yields robust activation across wide areas of the brain. Note that at this point, the thresholded map is still in the native functional space. The fMRI template was then registered to the anatomical using CR (FLIRT), NMI (spm_coreg), and BBR (with CR registration as initialization), all constrained to 6 DOF. For each registration method, the binarized activation map was sampled onto the cortical surface midway between the white and pial surfaces using nearest-neighbor interpolation (no attempt was made to exclude regions of high B0 distortion). The activation percentage was computed as the total number of positives divided by the number of vertices. This yielded 8 values for each subject. These were averaged to give 18 values for each method, and a paired permutation test was used to asses the significance of the differences between BBR, CR, and NMI.
RESULTS
Cost Function Smoothness, Optimality, and Capture Region
The cost function for 1D translations and rotations are shown in Figure 3 for a single subject; the 0-point is the location of the optimal solution (visually, the alignment looked very accurate). The cost function was evaluated by translating (Figure 3A) in each axis by +/−100mm in 0.010mm steps; this 200mm FoV was enough to encompass the entire brain in all dimensions. It was also evaluated by rotating about each axis by +/−100° in steps of 0.01° (Figure 3B). The three panels in Figures 3A and 3B show the behavior of the cost function at different scales around the optimum. There are two things to note about these results. First, the optimum is sharp and global – while there many local minima, none come close in cost at the true optimum; this is expected given the thin and highly folded nature of cortex. The actual cost at the optimum will depend on the average contrast between gray and white matter and so dependent on the modality and pulse sequence preparation. As this contrast drops, the cost at the optimum will rise. However, the cost far away from the optimum will always be around 1.0 regardless of the nature of the image. This is because, away from the optimum, the surface cuts randomly through the volume, and so the average contrast should be about 0, making the cost about 1.0 (see Figure 1, Panel B). While this suggests we can detect inaccurate registrations as those with costs “close” to 1.0, we cannot select a single cost threshold that will be good for all possible input images because of the dependence of the optimal cost on the actual contrast. However, once we do know what the expected contrast is, we can determine such a threshold. Note that costs near to or far from the optimum will not change much with intensity shading or partial brain FoV because we used a locally computed percent contrast. We explore this further below. The second thing to note about Figure 3 is that the cost function is extremely smooth, even at the scale of tens of microns and 100ths of a degree. The implication of this is that once the gradient descent starts inside the capture region, it is very likely to find the optimum. The capture range is quite sharp, about +/−5mm and +/−5°, though we expect this to be expanded by about 4mm and 4° due to the course search (Stage 2).
Visual Inspection Test
Figure 2 shows typical results for the three registration techniques. As discussed above, the accuracy is judged by how well the red line (white surface) approximates the boundary of the bright patches. Inaccuracies in registration are indicated by bright patches outside of the red line or dark patches inside the red line. Both CR (Panel 2C) and NMI (Panel 2D) have some problem areas indicated by the green arrows (these are in the same place relative to the red line in all three panels). There are extremely few locations in the BBR (Panel 2E) registration that are problematic. For reference, the AAD between BBR and CR for this data set was 3.74mm; the AAD was 2.86mm between BBR and NMI. Authors DNG and BRF rated the three registrations for each of the 18 subjects (blinded to registration algorithm, as noted above). The best registration was found to be “Acceptable” for all subjects. For both raters (DNG and BRF), BBR was rated best for all subjects; NMI received 17 second place rankings; CR received 1 second place. The only difference between the raters was the one CR case receiving a second place rating was different. The difference between BBR and CR was 4.895 mm AAD; the difference between BBR and NMI was 2.686 mm AAD. These are similar to the errors for CR and MI found by the raters in (Saad et al., 2009).
fMRI Activation Comparison
All methods achieved activation in excess of 13% of the cortical surface, averaged over all 18 subjects and 8 runs (BBR: 15.5%, NMI: 15.2%, CR: 13.9%). As discussed above, false positives will add about 0.1% and should not systematically bias any method since each method sees the same false positive rate. BBR increased the activation percentage over CR by about 12% (p<10−6). Each subject individually showed improvement, making the difference systematic and highly significant. BBR increased the activation percentage over NMI by only about 2% (p<.01). While modest, this difference was also systematic with 15/18 subject showing improvement. The significances quoted above were determined using a permutation test (Nichols and Holmes, 2001) with 1000000 iterations on the subject-wise difference between the activation percentages.
BBR Sensitivity to Starting Point
The starting point perturbation results are shown in Figure 4A. For perturbations below 5 (mm or degrees), all registrations were successful (i.e., AAD < 0.100mm). At a perturbation of 7, fewer than 5% failed (i.e., were caught in a local minimum). Figure 4B shows the mean cost of the successes and of the failures. One can see that there is a clear distinction between the two, meaning that failures can automatically be detected by evaluating the cost functional. This property is also evident from Figure 3, which shows that the costs at local minima are much higher than that at the optimum. The actual threshold needed to detect failures will be dependent on the contrast properties of the images being registered, so it will need to be computed from a representative set of data. This starting-point test is important because BBR must start within its basin of attraction of the global optimum to be successful. The initialization may be inaccurate due to inaccuracies in the Stage 1 technique (i.e., CR or NMI). For whole-brain data, we do not expect this to be likely from our experience, and (Saad et al., 2009) found that most of the CR and MI errors were no worse than 5mm.
Figure 4.
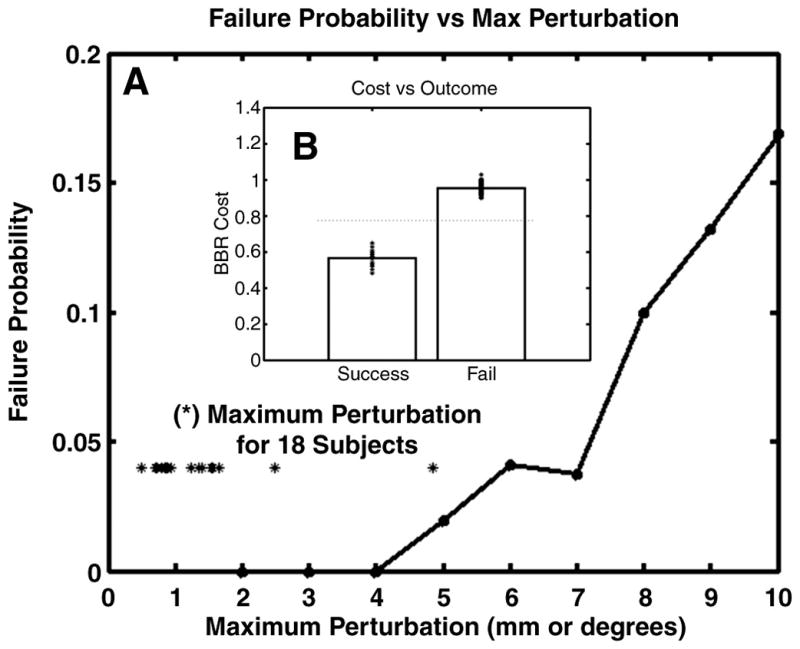
Robustness of BBR to random changes in initial position. Failure is defined as an inability to return to the original solution to within 0.100mm AAD. Panel A shows the probability of a failure as a function of maximum perturbation. The asterisks show the maximum perturbation for 18 subjects between their first fMRI run and their eighth within a scanning session. Panel B shows the value of the cost function for successes and failures (asterisks are individual data points) and demonstrates that the failures can be detected by a simple threshold.
If a partial FoV registration is being performed using a same-session whole-brain image as an intermediate step, then the subject may have moved between the acquisition of the whole- and partial-brain images. To get an idea of how big this motion might be in a real-world setting, we measured the maximum perturbation between the first and last fMRI runs for each of the 18 subjects (shown as asterisks in Figure 4A). Seventeen of the subjects were less than 3; the worst was 5, and none were failures. Based on these findings, we expect there to be very few cases where Stage 3 does not start in the capture region. When failures do occur, we expect to be able to automatically detect them.
BBR Sensitivity to Parametric Variation and B0 Masking
There are four parameters in the BBR cost function: (1) offset (Q0), (2) Slope (M), (3) Cortical Projection Distance (Δg), and (4) White Matter Projection Distance (Δw). The sensitivity to these parameters was tested by varying them individually over a range, re-registering, and seeing how much the registration changed (as measured with AAD). When the offset was varied from −2 to 5 (nominal 0), the worst AAD across all subjects was 0.400mm. When the slope was varied from 0.1 to 1 (nominal 0.5), the AAD for all subjects was less than 0.225mm. When the WM Projection Distance was varied from 0.1 to 4mm (nominal 2), the worst AAD was 0.425mm. When the Cortical Projection Distance was varied from 0.1 to 1 (nominal 0.5), the AAD was no worse than 0.300mm. This shows that the BBR solution is exceedinglyrobust with respect to wide changes in the parameters of the cost function, with the worst results across all subjects and parameter ranges being only 0.425mm. Including masking of B0 regions only changed the registration by an average of 0.200mm AAD with a maximum of 0.260mm AAD. In this case, masking out susceptibility regions had little effect, but this might not be the case in data sets where the B0 distortion is more extreme. To get an idea of the amount of B0 distortion in this data set, we used the FSL PRELUDE and FUGUE programs to compute the amount of voxel shift in various regions. In the medial orbital frontal regions, the shift was about 5mm (1.5 voxels); in inferior and medial temporal regions, the shift was about 3mm (.9 voxels).
Partial FoV Consistency Test
Figure 5 shows how the methods perform when the number of slices is systematically reduced. At full-brain (30 slices) and near full-brain coverage, the methods are similar in their ability to maintain consistency. However, as brain coverage drops, the performance of CR and NMI degrades considerably. At approximately half-brain coverage, the AAD is equal to the average human cortical thickness (2.5mm), meaning that cortical voxels in the functional images would likely not be mapped to cortex in the anatomical (or would be mapped to the wrong part of cortex). Below 4 slices, CR and NMI fail catastrophically. In contrast, BBR maintains AAD of better than 1mm down to 2 slices. Even using a single functional slice, the AAD is just above 1mm. In fact, 17 of the 18 subjects had better than 1mm AAD for a single slice. This is an important result because it is often the case that researchers need to acquire partial brain FoV in high-resolution fMRI applications (e.g., Duong et al., 2002; Hyde et al., 2001; Kirwan et al., 2007; Miller et al., 2006).
Figure 5.
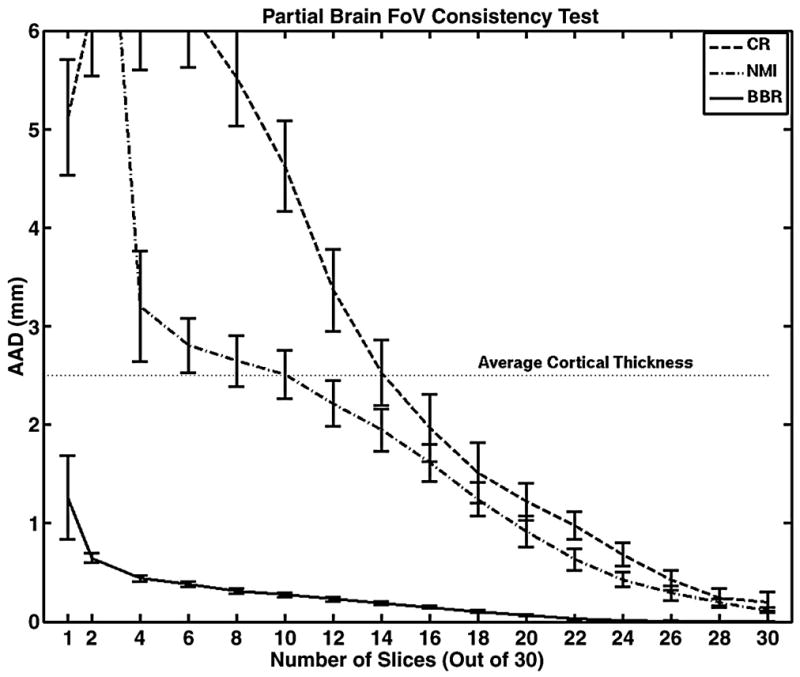
The effect of reducing the number of slices on the ability of each registration algorithm to stay at the same position found from the full-brain registration. BBR maintains very good repeatability, even down to one slice. The large error bar for BBR on the single slice is because 1 of the 18 subjects failed. The confidence intervals represent 1 standard error.
Intensity Bias Consistency Test
Figure 6 shows how the methods perform as increasing levels of intensity bias are applied. For all methods, the performance drops with more bias, but BBR clearly outperforms both CR and NMI. At α=0.5, CR and NMI have an AAD equal to the average cortical thickness, and beyond that level they begin to fail catastrophically. BBR maintains better than 1mm consistency all the way out to α=0.9.
Inaccurate Surface Test
Surfaces generated from the FAST segmentation had some regions of inaccuracy, particularly near the top of the head, the temporal lobes, and any place where a gyrus was very thin; however, the surface was fairly accurate through most of the brain. As mentioned above, this should not be construed as an evaluation or judgment of the FAST program; we simply used FAST to generate surfaces that are less accurate than FreeSurfer. The results show that use of the FAST surfaces had very little effect on the registration with an average AAD of 0.575 mm and worst case of 1.716 mm.
DOF Test
The average difference between 6 DOF and 9 DOF registrations was 1.237mm AAD. The scale changed by about 2 or 3 percent, which does not make a big difference at the center of the brain but can be as much as a few mm near the edge. It was very difficult to tell from visual inspection whether the scale was helping or hurting the final registration. The average difference between 6 DOF and 12 DOF was 1.315mm AAD; and the average difference between 9 DOF and 12 DOF was 0.281mm AAD. From this we conclude that 12 DOFs is probably not necessary, at least for this data set. It is not our purpose here to resolve the question as to what the appropriate number of DOFs is for registering within-subject, cross-modal images, rather we only want to measure the sensitivity of BBR to changes in DOF.
Computational Load
of the 18 subjects in the evaluation data set, none took more than 4 min to complete all stages of the 6 DOF registration on a 64-bit 2GHz XEON processor. This included the initialization stage using CR or NMI, which took about 30 sec by itself. The bulk of the time was spent in Stage 5. Thus BBR only added a few minutes to the total processing time. For 9 DOF, the time increased to only 6 min; for 12 DOF, the time was about 15 min. Note that the computational load only depends on the number of vertices on the surface; it is independent of the size or resolution of the input image. This does not take into account the amount of time needed to generate the surfaces, which can be as much as 30 hours if FreeSurfer is used. If one needs to have very accurate registration, then it is likely that one will need a very accurate model of the anatomy as well, and so generating the surfaces might not require any additional computational overhead. We also expect that BBR will perform well on surfaces of much lower quality. For example, the tests above showed very little deviation when less accurate FAST-based surfaces were used, and it only took FAST a few minutes to run.
Other Modalities
We have used BBR on several other modalities, including DWI, ex vivo T1, ASL, and B0 maps, which we report on qualitatively here. DWI: we used the low-b volume as the input (same that is used for motion correction). The low-b images of DWI scans have the same basic contrast and distortions as BOLD scans, and tend to be whole-brain and of higher resolution (ours had 2mm isotropic voxel size). Visual inspection showed a similar pattern to the BOLD, ie, CR and NMI performing well but BBR being a little more accurate. Ex vivo T1-weighted: our test images were very high resolution (80μm) acquisitions of single hemispheres suspended in fluid and were acquired using a special coil on a 7T system. This is a real challenge for CR and NMI, and they nearly always failed catastrophically. However, BBR performs very robustly and accurately. ASL: we have run BBR on both the tag and control images as well as on the difference images. Visually, the registrations look to have about the same accuracy as CR and NMI. Magnitude images from B0 maps: the amount of gray-white contrast in these images depends on the echo times at which they were acquired. The ones we evaluated were acquired at 3ms, which produced very little gray-white contrast BBR was still able to register them, but the performance as about the same as CR and NMI.
CONCLUSIONS
Accurate and robust alignment of brain images is critical for multimodal integration, surface-based intersubject analysis, longitudinal analysis, and pre-surgical planning. Due to the size of the brain structures involved, registration accuracy frequently needs to be better than 1mm. Our new alignment procedure, called Boundary-based Registration, or BBR, adjusts alignment by maximizing image contrast across tissue boundaries rather than matching intensities between two images or by matching surface shapes. One of the novelties of BBR is that it treats the two images asymmetrically: one must be a high-quality image with good anatomical contrast suitable for surface extraction; the other image (the “input image”) can be from any modality that has at least a minimal amount of gray/white contrast, e.g., BOLD fMRI, DTI, ASL, and PET; images from computed tomography (CT) would not be a candidate for BBR as there is usually no such contrast. The cost function is computed only from the intensities of the input image. If integration across two input images is needed, then they are both registered to the anatomical.
On whole-brain, artifact-free BOLD data, CR and NMI perform admirably, but BBR still systematically outperforms both. When the entire brain is not imaged or the images have large intensity biases, CR and NMI can fail catastrophically whereas BBR is consistent with the whole-brain, artifact-free result to within 1mm. BBR can even accurately align a single functional slice to the anatomical, which may facilitate some novel analysis techniques. The BBR cost function capture range is narrow (+/−5mm and +/−5°), which necessitates having a method to initialize registration in the correct basin of attraction. For this, we use existing implementations of CR or NMI, thus we see BBR as an augmentation of those procedures and not a full replacement. In the case where a partial brain FoV is needed, we recommend that the researcher also collect a fast whole-brain image in the same session, then use a CR or NMI whole-brain registration to seed the partial-brain BBR registration. BBR is also extremely robust to wide variations in its own parameters, and takes less than 4min to run.
The key ingredient to BBR’s performance is that it is based on a strong anatomical model derived from a high-quality structural image. This removes some of the burden from the (often) low-resolution cross-modal image. For example, it does not need to be skull-stripped and is insensitive to non-rigid effects such as jaw position, tongue position, head-neck orientation and differential image distortions. Using FreeSurfer’s automated cortical anatomical labeling, we can also exclude regions known to have intensity or distortion problems in the cross-modal images (e.g., B0 distortion regions in EPI). We have successfully used BBR for several difficult applications in our lab, including high-resolution ex vivo imaging. We freely distribute our implementation of BBR with FreeSurfer as the “bbregister” function. Finally, like (Saad et al., 2009), we strongly encourage researchers to visually inspect the quality of their registrations.
Acknowledgments
Support for this research was provided in part by the National Center for Research Resources (P41-RR14075, R01 RR16594-01A1, the NCRR BIRN Morphometric Project BIRN002, and Functional Imaging Biomedical Informatics Research Network (FBIRN) U24 RR021382), the National Institute for Biomedical Imaging and Bioengineering (R01 EB001550, R01EB006758), the National Institute for Neurological Disorders and Stroke (R01 NS052585-01) as well as the Mental Illness and Neuroscience Discovery (MIND) Institute, and is part of the National Alliance for Medical Image Computing (NAMIC), funded through the NIH Roadmap for Medical Research, Grant U54 EB005149. Additional support was provided by The Autism & Dyslexia Project funded by the Ellison Medical Foundation. We would also like to thank the FBIRN for setting up the cognitive fMRI tasks used in this manuscript.
References
- Borgefors G. Hierarchical chamfer matching: A parametric edge matching algorithm. IEEE Transactions on Pattern Analysis and Machine Intelligience. 1988;10:849–865. [Google Scholar]
- Collins D, Dai W, Peters T, Evans A. Automatic 3d model-based neuroanatomical segmentation. Human Brain Mapping. 1995;3:190–208. [Google Scholar]
- Riviere D, Jr, Cointepas Y, Papadopoulos-Orfanos D, Cachia A, Mangin J-F. A freely available anatomist/brainvisa package for structural morphometry of the cortical sulci. Proceedings of Human Brain Mapping; 2003. p. 934. [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis i: Segmentation and surface reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on mri scans into gyral based regions of interest. Neuroimage. 2006;31:968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Drobnjak I, Gavaghan D, Suli E, Pitt-Francis J, Jenkinson M. Development of a functional magnetic resonance imaging simulator for modeling realistic rigid-body motion artifacts. Magn Reson Med. 2006;56:364–380. doi: 10.1002/mrm.20939. [DOI] [PubMed] [Google Scholar]
- Duong TQ, Yacoub E, Adriany G, Hu X, Ugurbil K, Vaughan JT, Merkle H, Kim SG. High-resolution, spin-echo bold, and cbf fmri at 4 and 7 t. Magn Reson Med. 2002;48:589–593. doi: 10.1002/mrm.10252. [DOI] [PubMed] [Google Scholar]
- Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences. 2000;97:11044–11049. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RBH, Dale AM. High-resolution inter-subject averaging and a coordinate system for the cortical surface. Human Brain Mapping. 1999;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampel FR, Ronchetti Elvezio M, Rousseeuw Peter J, Stahel Werner A. Robust statistics - the approach based on influence functions. Wiley; New York: 1986. [Google Scholar]
- Hyde JS, Biswal BB, Jesmanowicz A. High-resolution fmri using multislice partial k-space gr-epi with cubic voxels. Magn Reson Med. 2001;46:114–125. doi: 10.1002/mrm.1166. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from bo field variations. Magn Reson Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- Kandel ER, Schwartz James H, Jessell Thomas M. Principles of neuroscience. 4. McGraw-Hill; 2000. [Google Scholar]
- Kirwan CB, Jones CK, Miller MI, Stark CE. High-resolution fmri investigation of the medial temporal lobe. Hum Brain Mapp. 2007;28:959–966. doi: 10.1002/hbm.20331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. 1997;16:187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- Maes F, Vandermeulen D, Suetens P. Comparative evaluation of multiresolution optimization strategies for multimodality image registration by maximization of mutual information. Med Image Anal. 1999;3:373–386. doi: 10.1016/s1361-8415(99)80030-9. [DOI] [PubMed] [Google Scholar]
- Miller KL, Smith SM, Jezzard P, Pauly JM. High-resolution fmri at 1.5t using balanced ssfp. Magn Reson Med. 2006;55:161–170. doi: 10.1002/mrm.20753. [DOI] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: A primer with examples. Human Brain Mapping. 2001;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical recipes in c: The art of scientific computing. Cambridge University Press; New York: 1988. [Google Scholar]
- Roche A, Malandain G, Pennec X, Ayache N. Lecture notes in computer science. Springer-Verlag; 1998. The correlation ratio as a new similarity measure for multimodal image registration; pp. 1115–1124. [Google Scholar]
- Saad ZS, Glen DR, Chen G, Beauchamp MS, Desai R, Cox RW. A new method for improving functional-to-structural mri alignment using local pearson correlation. Neuroimage. 2009;44:839–848. doi: 10.1016/j.neuroimage.2008.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segonne F, Dale AM, Busa E, Glessner M, Salat D, Hahn HK, Fischl B. A hybrid approach to the skull stripping problem in mri. Neuroimage. 2004;22:1060–1075. doi: 10.1016/j.neuroimage.2004.03.032. [DOI] [PubMed] [Google Scholar]
- Sereno MI, Dale AM, Reppas JB, Kwong KK, Belliveau JW, Brady TJ, Rosen BR, Tootell RBH. Borders of multiple visual areas in humans revealed by functional magnetic resonance imaging. Science. 1995;268:889–893. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Drury HA, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc. 2001;8:443–459. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells W, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Medical Image Analysis. 1996;1:35–52. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- West J, Fitzpatrick JM, Wang MY, Dawant BM, Maurer CR, Jr, Kessler RM, Maciunas RJ. Retrospective intermodality registration techniques for images of the head: Surface-based versus volume-based. IEEE Trans Med Imaging. 1999;18:144–150. doi: 10.1109/42.759119. [DOI] [PubMed] [Google Scholar]
- Woolrich M, Ripley B, Brady J, Smith S. Temporal autocorrelation in univariate linear modelling of fmri data. Neuroimage. 2001;14:1370–1386. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]
- Xu N, Fitzpatrick JM, Li Y, Dawant BM, Pickens DR, Morgan VL. Computer-generated fmri phantoms with motion-distortion interaction. Magn Reson Imaging. 2007;25:1376–1384. doi: 10.1016/j.mri.2007.03.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain mr images through hidden markov random field model and the expectation maximization algorithm. IEEE Transactions on Medical Imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]