Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2009 Aug 10;113(35):12148–12153. doi: 10.1021/jp9046962

Trans−cis Switching Mechanisms in Proline Analogues and Their Relevance for the Gating of the 5-HT3 Receptor

Claudio Melis 1,†, Giovanni Bussi 1,‡,§, Sarah C R Lummis 1,⊥, Carla Molteni 1,*,†
PMCID: PMC2733763  PMID: 19663504

Abstract

graphic file with name jp-2009-046962_0011.jpg

Trans−cis isomerization of a proline peptide bond is a potential mechanism to open the channel of the 5-HT3 receptor. Here, we have used the metadynamics method to theoretically explore such a mechanism. We have determined the free energy surfaces in aqueous solution of a series of dipeptides of proline analogues and evaluated the free energy difference between the cis and trans isomers. These theoretical results were then compared with data from mutagenesis experiments, in which the response of the 5-HT3 receptor was measured when the proline at the apex of the M2-M3 transmembrane domain loop was mutated. The strong correlation between the experimental and the theoretical data supports the existence of a trans−cis proline switch for opening the 5-HT3 receptor ion channel.

Introduction

Ligand-gated ion channels (LGICs) are multimeric membrane proteins that play an important role in fast synaptic transmission and in the modulation of cellular activity. They are involved in many neurological disorders, such as Alzheimer’s disease, anxiety, epilepsy, and learning and attention deficit, and are target sites for many drugs, including anesthetics and muscle relaxants.(1) LGICs exist in multiple conformations, of which the closed (inactive) and open (active) are the best-studied. The equilibrium between these two conformations is affected by the binding of an agonist, which stimulates the conformational change (gating) between the closed and the open states. Once the channel is open, ions can flow through the channel, altering the postsynaptic neuron membrane potential.

The 5-hydroxytryptamine 3 receptor (5-HT3R) is a member of the Cys-loop LGIC superfamily, which includes nicotinic acetylcholine (nACh), γ-aminobutyric acid (GABAA, GABAC), and glycine receptors.(2) These receptors are composed of five subunits arranged in a pentagonal array around a central pore. Each subunit has a large extracellular N-terminal domain, which contains the ligand binding site, a transmembrane domain, and an intracellular domain. The transmembrane domain is composed of four α-helices: M1, M2, M3 and M4; the M2 helix of each subunit lines the interior of the channel pore.

Mutagenesis experiments, in combination with various computational techniques, including homology modeling, ligand-docking, classical molecular dynamics, and first principle calculations, have supplied important information on the ligand-binding mechanism (see, e.g., refs (3−7)), but a clear atomistic picture of the successive gating mechanism is still missing. Data show that regions located at the interface of the extracellular and transmembrane domains are critical in linking binding with channel opening; these include the Cys-loop, the β1−β2 loop, and the M2−M3 loop.8−14

A model has been proposed for 5-HT3R gating whereby trans−cis isomerization of a specific proline (Pro308, alternatively labeled as Pro8*) at the apex of the M2−M3 loop would induce a conformational change in M2, resulting in a displacement of the hydrophobic girdle that occludes the pore and opening the channel.(15)

To examine the alleged switching role of proline in 5-HT3R and to provide atomistic insights to complement the mutagenesis experiments, we have performed a computational study of a proline dipeptide (N-acetylproline methylamide), the simplest model to study proline isomerization within a peptide, shown in Figure 1. We also investigated a range of dipeptides of the proline analogues that were studied experimentally.(15)

Figure 1.

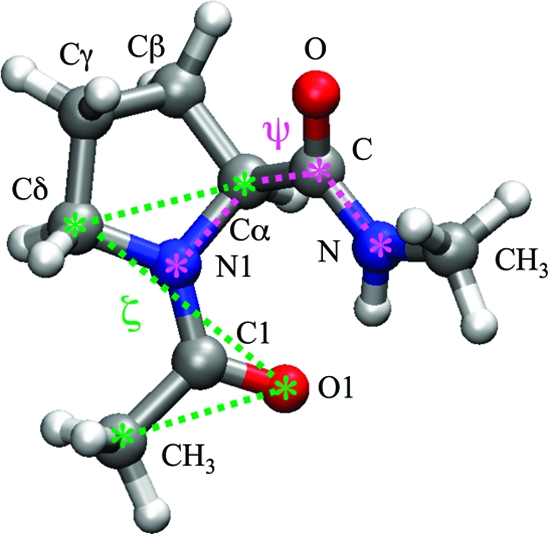
Figure 1

Open in a new tab

Proline dipeptide. The dihedral angles ζ and ψ are shown in green and magenta, respectively.

A number of previous studies of proline dipeptides have focused on single-point, total energy calculations by first principles methods in vacuo, for which the entropic contribution to the free energy was calculated within the harmonic approximation; when included, the solvent effects were evaluated implicitly.16−23 Here, using a classical force field scheme and the metadynamics method, we provide the free energy maps of the selected dipeptides and an evaluation of the free energy differences between the cis and trans isomers that takes into account the complexity of the basins of attraction without assumptions on their shape. At variance with previous free energy studies, we include the water solvent explicitly so as to quantify the effects of both intra- and intermolecular hydrogen bonds. Our study is relevant not only for the ligand-gated ion channels that have inspired it, but also for other biomolecules in which the trans−cis isomerization of the prolyl peptide bond plays an important role.(24) It provides a reference database for experiments, where the properties of proline analogues have been coherently calculated under the same conditions. Moreover, it can be easily extended to other proline analogues, pressure and temperature conditions, and solvents.

Methods

We created the initial structures of proline dipeptide and its analogues using the program Leap, contained in the Amber simulation package,(25) by terminating the proline analogues with the two groups acetamide (ACE) and N-methyl (NME). All the simulations were performed with the classical molecular dynamics AMBER(25) and ORAC(26) packages using the AMBER2003 force field.(27) We parametrized the nonstandard proline analogues by assigning to them partial charges from ab initio calculations; for consistency and for a better agreement with ab initio calculations in vacuo, we used ab initio partial charges also for Pro. Specifically, we calculated the ESP atomic partial charges(28) of Pro and its analogues at a density functional theory (DFT) level with the CPMD package,(29) using the PBE gradient-corrected xc-functional,(30) norm-conserving Martins−Troulliers pseudopotentials,(31) a kinetic energy cutoff for the wave function expansion in plane waves of 70 Ry, orthorhombic cells of size 15 × 14 × 14 A3, and the Hockney method for neglecting the electrostatic interactions between neighboring cells.(32) We determined the partial charges assigned to the force field for the trans isomer; however, we also calculated the DFT−ESP charges of proline dipeptide for the cis isomer and verified that the differences were small (mainly confined to the redistribution of charge between N and H in the NH group, whose total charge remained however very similar). Hence, the trans isomer charges are a good representation for all the conformers.

For the simulations in aqueous solution, we surrounded the dipeptides with 431 TIP3P water molecules(33) in a periodically repeated orthorhombic simulation cell. This was initially equilibrated at room temperature and atmospheric pressure using a time step of 0.5 fs for the molecular dynamic and evaluating the electrostatic contributions with particle mesh Ewald.(34) The volume of the cell was kept fixed at the equilibrated value during the metadynamics, and the temperature was controlled using the Nosé thermostat,(35) whereas in gas phase, we used a stochastic velocity rescaling.(36)

To assess the reliability of the AMBER2003 force field with the DFT−ESP charges for the description of the proline dipeptide trans−cis isomerization, we compared selected potential energy profiles in vacuo as a function of the torsional angles ζ (defined by the atoms CH3−O1−Cδ−Cα in Figure 1) and ψ (defined by N1−Cα−C−N), obtained with AMBER2003 and DFT calculations (Figure 3). The choice of these angles is discussed below. For the DFT calculations, we used the same protocol as for the ESP charges; each point corresponded to a geometry optimization at fixed ζ and ψ. The AMBER2003 force field qualitatively reproduces the location of the minima, maxima, and saddle points obtained with DFT and, most importantly for our study, the relative stability of the trans and cis isomers. Quantitatively, the differences in energy between the cis and trans absolute minima (ΔEc−t) were 2.4 kcal/mol with AMBER and 3.6 kcal/mol with DFT; the barriers were at ζ ∼ −90° and ψ ∼ 0° 15.3 kcal/mol with AMBER and 21.0 kcal/mol with DFT and, similarly, at ζ ∼ +90° and ψ ∼ 0° 15.7 kcal/mol with AMBER and 20.6 kcal/mol with DFT. The locations of our trans and cis minima and the corresponding ΔEt−c are in fairly good agreement with previously published DFT (B3LYP) and Hartree−Fock results.18,20 The larger error of the force field in the energy barrier with respect to the cis−trans energy difference is likely to be due to the relevance of electronic structure effects for the transition states in which the partial double bond character of the N1−C1 bond is broken. Although we were aware that the force field might not be able to capture subtle electronic structure effects, it was, indeed, able to reproduce the relevant features and allowed us to map the free energy surfaces (FES) in explicit solvent, a task that would be extremely computationally expensive with ab initio methods.

Figure 3.

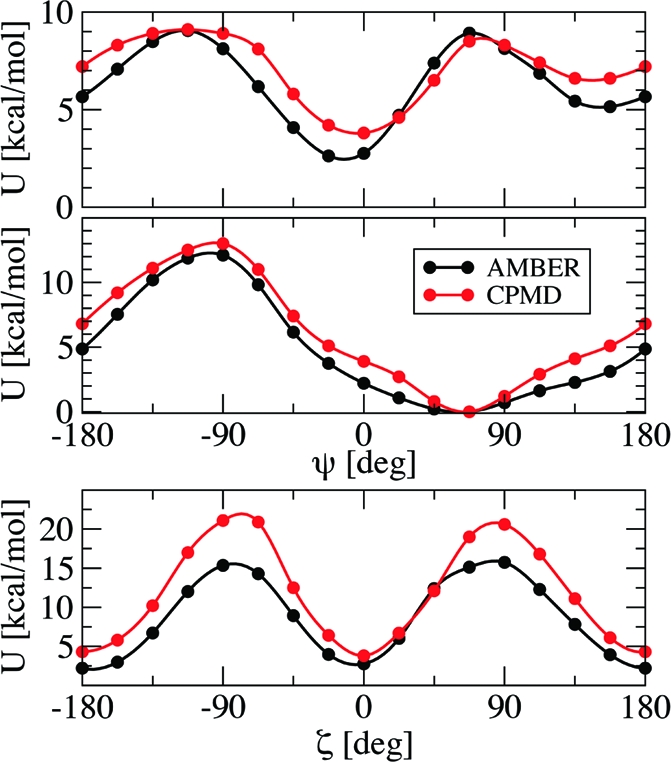
Figure 3

Open in a new tab

Potential energy profiles at selected values of ζ and ψ (in deg) obtained with DFT (red) and the AMBER2003 force field with DFT−ESP partial charges (black) for proline dipeptide in vacuo. The zero of the energy scale is set to the absolute minimum.

To evaluate the free energy surfaces, we used the metadynamics method, which is an efficient way to sample the free energy of complex polyatomic systems in the space of a few course-grained quantities (collective variables, CVs).(37) Metadynamics works by adding a history-dependent potential, built as a sum of Gaussians, whose role is to discourage the system from revisiting regions in the CV space already visited, thus accelerating rare events involving barrier crossing. When metadynamics is used with properly chosen collective variables, it provides an unbiased estimate of the free energy surface.38,39 However, the efficiency of the metadynamics method strongly depends on which collective variables are chosen as reaction coordinates for a particular mechanism.

In the case of Pro trans−cis isomerization, the most intuitive choice of CV is the imide torsional angle ω (Cα−N1−C1−CH3 in Figure 1), which is equal to 180° for the trans and to 0° for the cis isomer. However, during the isomerization, this angle is coupled to the out-of-plane deformation (pyramidalization) of the imide nitrogen, described by the improper dihedral angle η (C1−Cα−N1−Cδ): this should also be specified in addition to ω to unambiguously identify the saddle points. Alternatively, Fischer et al.(40) proposed the use of the improper dihedral angle ζ (CH3−O1−Cδ−Cα), which at the same time takes into account both the trans−cis isomerization and the nitrogen pyramidalization. Similarly to ω, ζ = 0° for the cis isomer and ζ = 180° for the trans isomer; at variance from ω, ζ is around ± 90° at the saddle points, independently on the nitrogen pyramidalization, thus effectively removing the need to specify η.

In our metadynamics calculations, we used as CVs ζ and also the torsional angle ψ (N1−Cα−C−N), which describes the orientation of the C-terminal amide. This is important because both experimental(41) and theoretical(40) studies have shown that the proline trans−cis isomerization is affected by the interaction between the C-terminal group and either the lone pair of the imide nitrogen (N1) or the imide carbonyl oxygen (O1). These interactions may, in fact, lower the torsional barrier by decreasing the double bond character of the bond between N1 and C1 in a process of autocatalysis.

We performed metadynamics simulations at room temperature. We built the history-dependent potential by summing up Gaussians of width 9° and height W = 0.07 kcal/mol, with a stride of τ = 400 fs. We then estimated the free energy from the negative of the history-dependent potential at the end of the simulation. Converged free energies required about 40 000 Gaussians each, for a simulated time of 16 ns. To accelerate the free energy calculations, we adopted the multiple walker scheme, which allows an efficient parallelization of the method.(42) As discussed in refs (38) and (39), the statistical error on the estimated free energy depends on the rate, W/τ. Our parameters were relatively conservative and allowed us to obtain accurate evaluations of the free energy profiles. The statistical errors were lower than 0.2 kcal/mol for the simulations in vacuo and lower than 0.3 kcal/mol for the simulations in aqueous solution. We further decreased the error by taking the average of the history-dependent potential over the last 4 ns of simulation.(43)

Results

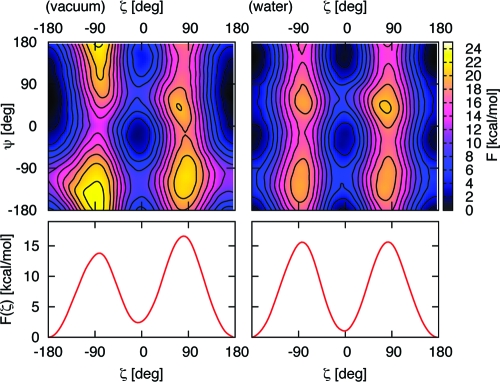
In Figure 4, we show the free energy maps as a function of ζ and ψ for proline dipeptide in vacuo and aqueous solution; the zero in each graph is the absolute minimum. We obtained the free energy difference in vacuo between the cis and trans isomers by integrating over the relevant regions so as to account for the different shapes of the basin of attractions. Our calculated value (2.4 ± 0.2 kcal/mol) is in good agreement with previously published DFT B3LYP/6-31G+d(d) and B3LYP/6-311++G(d,p) calculations, in which vibrational frequencies were calculated for the stationary points in the gas phase and then used to compute free energies.18,20

Figure 4.

Figure 4

Open in a new tab

Top: free energy maps at room temperature for proline dipeptide in vacuo (left) and water (right) as a function of the dihedral angles ζ and ψ. Bottom: the corresponding free energy profile integrated over ψ. The zero of the energy scale is set at the absolute minimum, and the spacing between lines is 0.2 kcal/mol.

In vacuo, the trans global minimum at ζ ∼ 180° and ψ ∼ 60° corresponds to a configuration with an intramolecular hydrogen bond between the NH group and O1. The cis isomer has two minima; no intramolecular hydrogen bonds were possible in this configuration; hence, the trans−cis isomerization disrupts the intramolecular hydrogen bond within the dipeptide. The presence of intramolecular hydrogen bonds was highly affected by the environment. In vacuo, the NH···O hydrogen bond occurred for 43% of the trans configurations (defined as −90° < ζ < 90°), with ψ ranging from 0° to 90°; in water, its occurrence was reduced to 16%. This was due to the competition between the formation of the intramolecular hydrogen bond and that of intermolecular hydrogen bonds with the water molecules. Specifically, O and O1 each formed, on average, 2.1 and 1.9 hydrogen bonds with water. N1 did not form any hydrogen bonds with water, whereas N formed only 0.8 hydrogen bonds (0.1 as acceptor and 0.7 as donor). These averages were evaluated for any value of ζ; restricting the averages to the trans isomer gave almost identical values (2.0 and 1.9 hydrogen bonds between water molecules and O and O1, respectively).

The influence of the solvent is clearly reflected in the FES, where the unique trans minimum basin in vacuo is substituted by a pair of trans minima in water, at ψ ∼ 145° and −25°, as shown in Figure 4. Hence, in water, the trans basin is more similar to the cis one, where no intramolecular hydrogen bonds can be formed. Because of the importance of the intermolecular hydrogen bonds, it is essential that explicit water molecules were included in the simulations.

We calculated a free energy difference between the cis and trans isomers in water equal to 1.0 kcal/mol; with an error of ±0.3 kcal/mol, this is in good agreement with experiments, which estimates 0.6 kcal/mol.23,44 The reduction of the cis−trans free energy difference in aqueous with respect to that in vacuo is in line with DFT/B3LYP and implicit solvent calculations.18,20 The isomerization barrier, obtained from the FES profiles integrated over ψ (Figure 4) increased from 13.8 kcal/mol in vacuo to 15.6 kcal/mol in aqueous solution, thus confirming the mechanism of autocatalysis determined by the presence of the intramolecular hydrogen bond.18,20

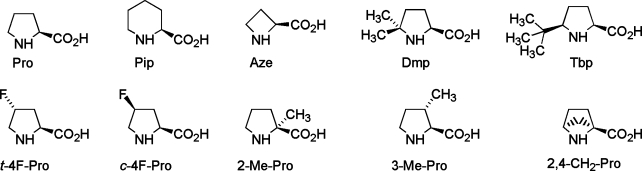
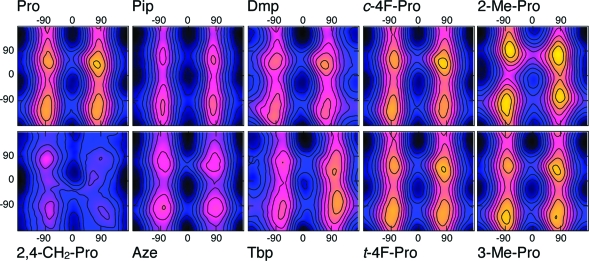
Although the environment in the ion channel is much more complex, we expect that simulations of the trans−cis proline switch in water represent a realistic environment. In fact, the M2−M3 loop, where Pro308 is situated, has been shown to be solvent-accessible in a variety of Cys-loop receptors.45,46 Hence, we believe that the studies in aqueous solution are a good representation of the in vivo situation. We therefore investigated the proline analogues (Figure 2), which have been experimentally studied in the 5-HT3R15, in aqueous solution. These analogues exhibit various ring features and preference for either of the two isomers.(47) The corresponding free energy maps are shown in Figure 5, where, as in Figure 4, the zero of the scale is aligned with the absolute minimum of each FES. The cis−trans free energy differences with respect to Pro and the lowest isomerization barriers are shown in Table 1. All proline analogues favored the trans isomers, except Dmp and Tbp, which favored the cis.

Figure 2.

Figure 2

Open in a new tab

The proline analogues considered in this study.

Figure 5.

Figure 5

Open in a new tab

Free energy maps at room temperature of the proline dipeptide analogues in aqueous solution as a function of the dihedral angles ξ (horizontal, in deg) and ψ (vertical, in deg). The spacing between lines is 0.2 kcal/mol. The free energy scale is as in Figure 4.

Table 1. Free Energy Difference between the Cis and Trans Isomers (ΔFc−t), Variation of ΔFc−t with Respect to Pro (ΔΔFc−t) and Isomerization Barriers for Proline Dipeptide and Its Analogues in Watera.

  ΔFc−t, (kcal/mol) ΔΔFc−t, (kcal/mol) barrier t → c, (kcal/mol)
Pro 1.1 0.0 15.6
Pip 0.9 −0.2 12.7
Aze 0.4 −0.7 11.7
Dmp −2.6 −3.7 10.0
Tbp −2.2 −3.3 10.2
t-4F-Pro 0.6 −0.5 15.6
c-4F-Pro 1.2 0.1 15.6
2-Me-Pro 3.2 2.1 13.8
3-Me-Pro 0.5 −0.6 15.4
2,4-CH2-Pro 2.1 1.0 6.4
Open in a new tab
a

The isomerisation barrier is the smallest between the two calculated for clockwise and counterclockwise trans−cis isomerisation.

In Pip and Aze, the size of the ring was, respectively, increased and decreased as compared to Pro; the relative stability of the cis and trans configurations was very similar in Pip and Pro, whereas the cis stability was slightly increased in Aze. Dmp and Tbp favored the cis isomer. In Dmp, the steric interaction between the two methyl groups added to Cδ and the ACE methyl group disfavored the trans isomer. In Tbp, the steric interaction between the bulky tert-butyl group attached to Cδ and the ACE group also disfavored the trans isomer; however, the distance between the three methyl groups in the tert-butyl and the ACE methyl group was larger than for Dmp, resulting in a weaker interaction and a reduced destabilization of the trans. Both the isomerization barriers of Dmp and Tbp were substantially lower than that of Pro.

The relative trans−cis stabilities of the fluoroprolines were also similar to that of Pro, with t-4F-Pro slightly stabilizing the cis more than both Pro and c-4F-Pro; in aqueous solution, the fluorine atoms in both residues formed hydrogen bonds with water molecules, which neutralized the main effects of their presence on the ring. Specifically, the fluorine atom acted as acceptor for, on average, 0.9 hydrogen bonds with water in the t-4F-Pro simulation and 0.7 in the c-4F-Pro simulation. The isomerization barriers were similar to that of Pro.

2-Me-Pro favored the trans isomer, due to the methyl group attached to Cα, which sterically interacted with the ACE methyl group, disfavoring the cis configuration. The addition of a methyl group to Cβ, as in the 3-Me-Pro, did not significantly affect the cis preference with respect to Pro because it is farther away from the isomerization bond. In addition, 2,4-CH2-Pro favored the trans isomer due to the steric interaction between the ACE methyl group and the methylene group attached to Cα and Cδ; the presence of the methylene group substantially decreased the isomerization barrier with respect to Pro.

Evaluation of the hydrogen bonds formed during the metadynamics for all the proline analogues revealed strong similarity to Pro, with averages for the number of hydrogen bonds between water molecules and O1, O, NH, and N1 ranging from 1.9 to 2.2, from 1.6 to 1.8, from 0.5 to 0.9, and from 0.0 to 0.1, respectively. The percentages of occurrence of the intramolecular hydrogen bond were also not dissimilar from that of Pro, ranging from 12% for Pip to 20% for c-4F-Pro. This indicates that the effect of the solvent for the proline analogues was as crucial as it was for Pro.

Discussion and Conclusions

A trans−cis isomerization of a proline peptide bond is an attractive mechanism to change protein conformation and has been shown to be important in the function of several proteins. The data we present here support previous studies that show that such a mechanism can open the pore of the 5-HT3 receptor.(15) The comparison between the relative free energies of the cis and trans isomers of a range of proline analogue dipeptides and those inferred from the relative EC50s of the 5-HT3 receptor activation allowed us to isolate the isomerization of the proline peptide bond from all the other concurrent events that occur when 5-HT binds to this receptor and lead to channel gating. The strong correlation we found supports the proposal that trans−cis isomerization is, indeed, a realistic switching mechanism.

In the previous published experimental paper,(15) the cis−trans free energy differences correlated with the experimental EC50s were obtained from the literature for a range of different peptides at different experimental conditions,48−50 and the comparison was done only for a subset of the investigated proline analogues. Here, we evaluated the relative cis−trans free energy difference for all the experimentally investigated proline analogues, including those resulting in nonfunctional channels, using the same model system under the same conditions. Hence, we considered our data more accurate and consistent. The theoretical protocol that we have developed can be easily extended to other residues and conditions so as to provide a reference database for future experimental measurements done in the same spirit of those by Lummis et al.(15) in other proteins or involving other prolines.

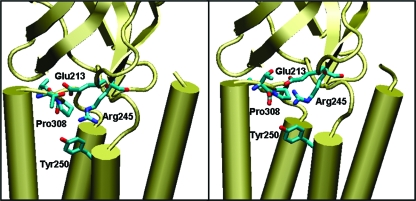
Our simulations also revealed specific interactions within the dipeptides and with the solvent that explain the free energy profiles, thus providing additional information on the atomistic details of the isomerization mechanisms. In particular, the isomerization from trans to cis disrupted the hydrogen bond between the residues immediately preceding and following Pro308 (specifically, between the NH group of NME and the O1 atom of ACE). Such a hydrogen bond, which was present in the trans isomer both in vacuo and in solution in different percentages, was, in fact, absent in the cis. This absence is likely to be mirrored in the M2−M3 loop of 5-HT3R. Through preliminary calculations on extended peptides mimicking the M2−M3 loop, we verified that the hydrogen bond between the threonine and leucine that sandwich Pro308 was, indeed, broken during the trans−cis isomerization; the occurrence of another hydrogen bond between this threonine and another threonine in the M2−M3 loop also decreased substantially during the isomerization: modifications in the interaction network might facilitate the movement of the M2 helix leading to the opening of the channel. Indeed, the trans−cis proline isomerization has the potential to bring many changes in the interactions with surrounding residues in the 5-HT3 receptor, as can be inferred in Figure 7. Here, Pro308 is shown in its trans and cis forms, together with nearby residues in homology models for the 5-HT3 receptor. Pro308 and the two adjacent residues Thr307 and Leu309, highlighted with sticks, are in the M2−M3 loop; Glu213 is in the F loop; Arg245 is at the boundary between the extracellular and the transmembrane domain; and Tyr250 is at the start of the M1 helix. These homology models were generated using MODELLER 6v2(51) as previously described,(3) with the extracellular domain based on the crystal structure of the acetylcholine binding protein (AChBP) at 2.7 Å resolution (PDB ID: 1I9B(52)) and the transmembrane domain on the structure of the nACh receptor at 4 Å resolution (PDB ID: 2BG9(53)).

Figure 7.

Figure 7

Open in a new tab

Homology models of the 5-HT3 receptors where Pro308, in the trans (left) and cis (right) configurations, and selected surrounding residues are shown explicitly. Pro308 and the adjacent residues Thr207 and Leu209 are in the M2−M3 loop, Glu213 is in the F loop, Arg245 is at the boundary between the extracellular and the transmembrane domains, and Tyr250 is at the start of the M1 helix.

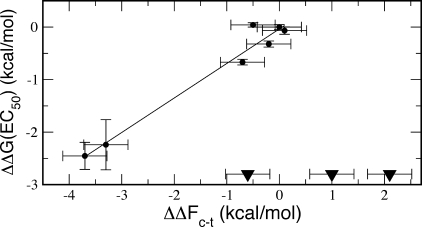
The cis−trans free energy differences relative to proline, when plotted against those obtained from the EC50 values (Figure 6), cluster mainly around two regions for the proline analogues that behave similarly to proline (Pip, Aze, t-4F-Pro and c-4F-Pro) and those with a clear preference for the cis isomer (Tbp and Dmp). They reveal a correlation coefficient of 0.98, similar to the experimental data previously reported(15) and indicating a tight relationship between the population of cis and trans isomers and the receptor response. The slope of the best fit, however, is different: from our theoretical data, it is m = 0.66, whereas the previous value was m = 1.(15) The latter suggests that the equilibrium between closed and open channels is purely due to the equilibrium between trans and cis Pro308, but the new data suggest the relationship may be more complex and possibly nonlinear. A linear relationship in fact would also predict that all analogues, including 2-Me-Pro and 2,4-CH2-Pro would be functional, with EC50s significantly less than the maximum concentration that has been tested.

Figure 6.

Figure 6

Open in a new tab

Correlation between cis−trans free energy differences from the metadynamics simulations and from experimental data (EC50s) on the activation of 5-HT3R;(15) the data for the mutants corresponding to functional channels are indicated as circles; those corresponding to nonfunctional channels (hence with no available EC50), with triangles.

This does not, however, mean that the original hypothesis is incorrect. For example, the observed differences could be due to the inaccuracy in the empirical force field, which cannot capture subtle electronic effects that can alter quantitatively, rather than qualitatively, the isomer population. The channel environment, which was absent in our calculations, is also likely to play an important role in triggering and catalyzing the isomerization so as to reconcile the observed gating time scale with that inferred from the isomerization barrier. In particular, there could be steric hindrance effects that might prevent isomerization paths allowed in water, such as in the case of 3-Me-Pro, which does not behave in the dipeptide much differently from proline, but in the experiments produced a nonfunctional channel.

In summary, using classical molecular dynamics combined with state-of-the-art metadynamics, we have characterized the free energy surfaces of a series of proline dipeptide analogues as the simplest model of trans−cis proline switch and deduced information about the relative stability of their trans and cis conformers. Although a number of issues, which would benefit from simulations of more complex systems, remain open, the excellent correlation between our calculated free energy difference and those deduced from the experimental EC50s support the idea of a switching role for Pro308 for the gating of 5-HT3R.

Acknowledgments

We thank Francesco L. Gervasio, Davide Branduardi, and Michele Parrinello (ETH Zurich, CH) for useful discussion on the metadynamics technique. C. Melis and C. Molteni acknowledge the EPSRC Life Science Interface programme (Grant no. EP/E014505/1). C. Melis and G. Bussi thank the London Thomas Young Centre for Theory and Simulation of Materials for junior research fellowships for collaborative visits. S. C. R. Lummis is a Wellcome Trust Senior Research Fellow in Basic Biomedical Science.

References

  1. Lester H. A.; Dibas M. I.; Dahan D. S.; Leite J. F.; Dougherty D. A. Trends. Neurosci. 2004, 27, 329. [DOI] [PubMed] [Google Scholar]
  2. Reeves D. C.; Lummis S. C. R. Mol. Membr. Biol. 2002, 19, 11. [DOI] [PubMed] [Google Scholar]
  3. Reeves D. C.; Sayed M. F. R.; Chau P. L.; Price K. L.; Lummis S. C. R. Biophys. J. 2003, 84, 2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Lummis S. C. R.; Beene D. L.; Harrison N. J.; Lester H. A.; Dougherty D. A. Chem. Biol. 2005, 12, 993. [DOI] [PubMed] [Google Scholar]
  5. Melis C.; Chau P. L.; Price K. L.; Lummis S. C. R.; Molteni C. J. Phys. Chem. B. 2006, 110, 26313. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Melis C.; Lummis S. C. R.; Molteni C. Biophys. J. 2008, 95, 4115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Beene D. L.; Brandt G. S.; Zhong W. G.; Zacharias N. M.; Lester H. A.; Dougherty D. A. Biochemistry 2002, 41, 10262. [DOI] [PubMed] [Google Scholar]
  8. Absalom N. L.; Lewis T. M.; Schofield P. R. Exp. Physiol. 2004, 89, 145. [DOI] [PubMed] [Google Scholar]
  9. Miyazawa A.; Fujiyoshi Y.; Unwin N. Nature 2003, 423, 949. [DOI] [PubMed] [Google Scholar]
  10. Kash T. L.; Jenkins A.; Kelley J. C.; Trudell J. R.; Harrison N. L. Nature 2003, 421, 272. [DOI] [PubMed] [Google Scholar]
  11. Bouzat C.; Gumilar F.; Spitzmaul G.; Wang H. L.; Rayes D.; Hansen S. B.; Taylor P.; Sine S. M. Nature 2004, 430, 896. [DOI] [PubMed] [Google Scholar]
  12. Absalom N. L.; Lewis T. M.; Kaplan W.; Pierce K. D.; Schofield P. R. J. Biol. Chem. 2003, 278, 50151. [DOI] [PubMed] [Google Scholar]
  13. Hilf R. J. C.; Dutzler R. Nature 2009, 457, 115. [DOI] [PubMed] [Google Scholar]
  14. Bocquet N.; Nury H.; Baaden M.; Le Poupon C.; Changeux J.-P.; Delarue M.; Corringer P.-J. Nature 2009, 457, 111. [DOI] [PubMed] [Google Scholar]
  15. Lummis S. C. R.; Beene D. L.; Lee L. W.; Lester H. A.; Broadhurst R. W.; Dougherty D. A. Nature 2005, 438, 248. [DOI] [PubMed] [Google Scholar]
  16. Improta R.; Benzi C.; Barone V. J. Am. Chem. Soc. 2001, 123, 12568. [DOI] [PubMed] [Google Scholar]
  17. DeRider M. L.; Wilkens S. J.; Waddell M. J.; Bretscher L. E.; Weinhold F.; Raines R. T.; Markley J. L. J. Am. Chem. Soc. 2002, 124, 2497. [DOI] [PubMed] [Google Scholar]
  18. Kang Y. K. J. Mol. Struct.: THEOCHEM 2004, 675, 37. [Google Scholar]
  19. Song I. K.; Kang Y. K. J. Phys. Chem. B 2005, 109, 16982. [DOI] [PubMed] [Google Scholar]
  20. Kang Y. K. J. Phys. Chem. B 2006, 110, 21338. [DOI] [PubMed] [Google Scholar]
  21. Jhon J. S.; Kang Y. K. J. Phys. Chem. B 2007, 111, 3496. [DOI] [PubMed] [Google Scholar]
  22. Hamelberg D.; Shen T.; McCammon J. A. J. Am. Chem. Soc. 2005, 127, 1969. [DOI] [PubMed] [Google Scholar]
  23. Beausoleil E.; Lubell W. D. J. Am. Chem. Soc. 1996, 118, 12902. [Google Scholar]
  24. Leone V.; Lattanzi G.; Molteni C.; Carloni P. PLoS Comp. Biol. 2009, 5, e1000309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Case D. A.; Cheatham T. E. III; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. J. Comput. Chem. 2005, 26, 1668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Procacci P.; Darden T. A.; Paci E.; Marchi M. J. Comput. Chem. 1997, 18, 1848. [Google Scholar]
  27. Ponder J. W.; Case D. A. Protein Simulations, Adv. Protein Chem. 2003, 66, 27. [DOI] [PubMed] [Google Scholar]
  28. Singh U. C.; Kollman P. A. J. Comput. Chem. 1984, 5, 129. [Google Scholar]
  29. CPMD, http://www.cpmd.org/, Copyright IBM Corp 1990−2009, Copyright MPI für Festkörperforshung Stuttgart, 1997−2001.
  30. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865. [DOI] [PubMed] [Google Scholar]
  31. Troullier N.; Martins J. L. Phys. Rev. B 1991, 43, 1993. [DOI] [PubMed] [Google Scholar]
  32. Hockney R. W. Methods Comput. Phys. 1970, 9, 136. [Google Scholar]
  33. Jorgensen W. L.; Chandrasekhar J.; Madura J.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79, 926. [Google Scholar]
  34. Darden T.; York D.; Pederson L. J. Chem. Phys. 1993, 98, 10089. [Google Scholar]
  35. Nosé S. J. Chem. Phys. 1984, 81, 511. [Google Scholar]
  36. Bussi G.; Donadio D.; Parrinello M. J. Chem. Phys. 2007, 126, 014101. [DOI] [PubMed] [Google Scholar]
  37. Laio A.; Parrinello M. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 12562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Laio A.; Rodriguez-Fortea A.; Gervasio F. L.; Ceccarelli M.; Parrinello M. J. Phys. Chem. B 2005, 109, 6714. [DOI] [PubMed] [Google Scholar]
  39. Bussi G.; Laio A.; Parrinello M. Phys. Rev. Lett. 2006, 96, 090601. [DOI] [PubMed] [Google Scholar]
  40. Fischer S.; Dunbrack R. L., Jr.; Karplus M. J. Am. Chem. Soc. 1994, 116, 11931. [Google Scholar]
  41. Cox C.; Young V. G.; Lectka T. J. Am. Chem. Soc. 1997, 119, 2307. [Google Scholar]
  42. Raiteri P.; Laio A.; Gervasio F. L.; Micheletti C.; Parrinello M. J. Phys. Chem. B 2006, 110, 3533. [DOI] [PubMed] [Google Scholar]
  43. Micheletti C.; Laio A.; Parrinello M. Phys. Rev. Lett. 2004, 92, 170601. [DOI] [PubMed] [Google Scholar]
  44. Taylor C. M.; Hardré R.; Edwards P. J. B.; Park J. H. Org. Lett. 2003, 5, 4413. [DOI] [PubMed] [Google Scholar]
  45. Lynch J. W.; Han N. L. R.; Haddrill J.; Pierce K. D.; Schofield P. R. J. Neurosci. 2001, 21, 2589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Bera A. K.; Chatav M.; Akabas M. H. J. Biol. Chem. 2002, 277, 43002. [DOI] [PubMed] [Google Scholar]
  47. Dugave C.; Demange L. Chem. Rev. 2003, 103, 2475. [DOI] [PubMed] [Google Scholar]
  48. Kern D.; Schutkowski M.; Drakenberg T. J. Am. Chem. Soc. 1997, 119, 8403. [Google Scholar]
  49. An S. S. A.; Lester C. C.; Peng J. L.; Li Y. J.; Rothwarf D. M.; Welker E.; Thannhauser T. W.; Zhang L. S.; Tam J. P.; Scheraga H. A. J. Am. Chem. Soc. 1999, 121, 11558. [Google Scholar]
  50. Halab L.; Lubell W. D. J. Org. Chem. 1999, 64, 3312. [DOI] [PubMed] [Google Scholar]
  51. Eswar N.; Marti-Renom M. A.; Webb B.; Madhusudhan M. S.; Eramian D.; Shen M.; Pieper U.; Sali A.. Curr. Prot. Bioinf. 2006, Chapter 5, Unit 5.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Brejc K.; van Dijk W. J.; Klaassen R. V.; Schuurmans M.; van Der Oost J.; Smit A. B.; Sixma T. K. Nature 2001, 411, 269. [DOI] [PubMed] [Google Scholar]
  53. Unwin N. J. Mol. Biol. 2005, 346, 967. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES