Adaptive Control of Saccades via Internal Feedback

Abstract

Ballistic movements like saccades require the brain to generate motor commands without the benefit of sensory feedback. Despite this, saccades are remarkably accurate. Theory suggests that this accuracy arises because the brain relies on an internal forward model that monitors the motor commands, predicts their sensory consequences, and corrects eye trajectory midflight. If control of saccades relies on a forward model, then the forward model should adapt whenever its predictions fail to match sensory feedback at the end of the movement. Using optimal feedback control theory, we predicted how this adaptation should alter saccade trajectories. We trained subjects on a paradigm in which the horizontal target jumped vertically during the saccade. With training, the final position of the saccade moved toward the second target. However, saccades became increasingly curved, i.e., suboptimal, as oculomotor commands were corrected on-line to steer the eye toward the second target. The adaptive response had two components: (1) the motor commands that initiated the saccades changed slowly, aiming the saccade closer to the jumped target. The adaptation of these earliest motor commands displayed little forgetting during the rest periods. (2) Late in saccade trajectory, another adaptive response steered it still closer to the jumped target, producing curvature. Adaptation of these late motor commands showed near-complete forgetting during the rest periods. The two components adapted at different timescales, with the late-acting component displaying much faster rates. It appears that in controlling saccades, the brain relies on an internal feedback that has the characteristics of a fast-adapting forward model.

Introduction

Our motor commands are strongly influenced by feedback. Theory suggest that this feedback takes two forms: an external feedback through the sensory system, and an internal feedback that predicts the sensory consequences of motor commands through forward models (Wolpert et al., 1995). In actions such as reaching, walking, and speech that are heavily influenced by external feedback from one or more sensory modalities (Houde and Jordan, 2002; Vaziri et al., 2006), internal prediction and external feedback are combined to adjust the motor output in real time, making it exceedingly difficult to isolate the effects of forward models. An exception to this constraint is the saccade: rapid eye movements that redirect the fovea toward targets of interest. Typical saccades are too brief for visual feedback to influence saccade trajectory. Furthermore, proprioceptive signals from the eyes do not play any significant role in controlling saccade trajectories (Keller and Robinson, 1971; Guthrie et al., 1983). Thus, to ensure accuracy, the brain may “steer” the saccades by relying on an internal estimate of the state of the eye (e.g., position, velocity), derived from an efferent copy of ongoing motor commands (Robinson, 1975; Optican, 2005). Support for this idea comes from the observation that both natural (Quaia et al., 2000) and drug-induced (Jurgens et al., 1981) variability of saccade velocity and duration have little influence on saccade amplitude. That is, variability of motor commands that initiate saccades may be partially corrected via an internal feedback process that relies on efferent copy.

Here, we conjectured that if a forward model exists in the saccadic system, then it should be able to adapt in response to persistent discrepancy between the observed and predicted sensory states. Experimentally, such discrepancy, or error, can be artificially induced by moving the target of a saccade intrasaccadically, so that at saccade termination the eye fails to land on target. Although it is well known that such error drives saccade adaptation (Hopp and Fuchs, 2004), we hypothesize that saccade adaptation is led by adaptation of the forward model. In particular, if the motor commands that move the eyes rely on this forward model, then its adaptation should leave its signature on saccade trajectories.

To predict what these trajectory changes might look like, we used stochastic optimal feedback control theory (Todorov, 2005) to model saccades. In this framework, given the estimated state of the eyes with respect to the target, motor commands are generated to minimize some cost. One component of the cost may be a measure of endpoint variability (Harris and Wolpert, 1998, 2006). Another component may be the value that the brain assigns to the visual stimulus, because rewarded stimuli tend to produce faster saccades (Takikawa et al., 2002). A balance between these factors nicely reproduces the velocities and durations that one typically observes in saccades to stationary targets. Here, we used this framework to make a number of predictions about how trajectories might change if the forward model that provides state estimation were to adapt to endpoint errors caused by intrasaccadic motion of the target. The theoretical predictions were particularly dramatic when the intrasaccadic target jump was perpendicular to the initial direction of the target. We used this “cross-axis” adaptation paradigm (Deubel, 1987; Frens and Van Opstal, 1994; Noto et al., 1999) to test the hypothesis that motor commands that produce saccades are fundamentally dependent on a forward model.

Materials and Methods

We used a directional scleral search coil system (Skalar Medical, Delft, The Netherlands) to record horizontal and vertical eye movements at 1000 Hz from either the right or the left eye (Robinson, 1963). Subjects sat in a dark room facing a vertical screen on which light-emitting diodes (LEDs) were presented. The seat and head position of the subject was adjusted using a laser projector so that the midpoint between the subject's eyes was at the center of the magnetic field and aligned to the LED located at the center of the vertical target screen (0°, 0°). Bite bars were used to minimize head movements.

Experimental paradigm for cross-axis adaptation.

Each experiment consisted of four blocks: oblique control trials, preadaptation catch trials, adaptation trials interspersed with catch trials, and postadaptation catch trials (Fig. 1A). We will explain each block below.

Figure 1.

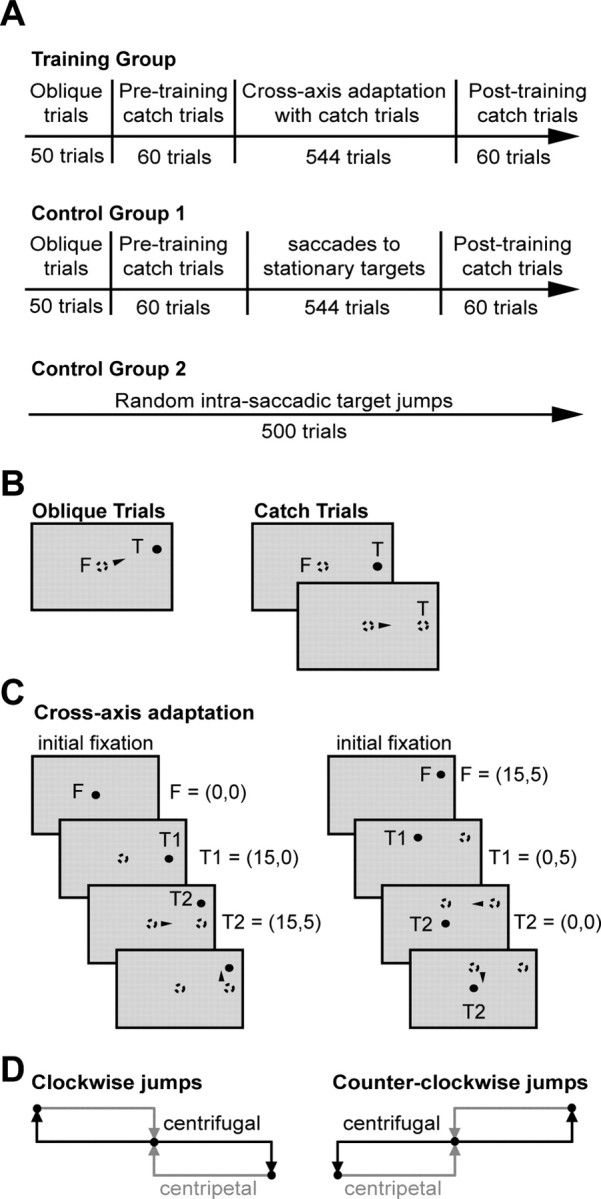
Experimental paradigm. A, Chronology of the experiments. B, Target presentation sequence for oblique and catch trials. In oblique trials, targets were displayed randomly 15° lateral to the center LED and 0, 1, 2, 3, or 5° above (in the first quadrant) or below (in the third quadrant) the meridian. Each trial began with fixation (F) at the center LED (0°, 0°) for a random interval of 1–2 s, after which the center LED was extinguished and the target LED was turned on for 1 s. In catch trials, the target disappears at saccade onset. C, Target presentation sequence for a pair of adaptation trials during a counterclockwise adaptation experiment. Filled circles indicate currently illuminated LEDs, and open circles indicate previously illuminated LEDs. Arrowheads indicate when a saccade began. D, Target configurations for clockwise and counterclockwise cross-axis saccade adaptation experiments.

Targets for oblique trials and adaptation trials lay either in the first and third quadrants or in the second and fourth quadrants of the visual space, depending on whether the target jump under investigation was in the counterclockwise or clockwise direction (Fig. 1D). Figure 1B illustrates oblique control trials for the counterclockwise adaptation experiment. The oblique trials consisted of two sets: 25 trials to five targets located in the first quadrant, five repetitions to each target, followed by another 25 trials to five targets located in the third quadrant, also five repetitions to each target. Target appearance within the set was random. The target locations were 15° lateral to the center LED and 0, 1, 2, 3, or 5° above (in the first quadrant) or below (in the third quadrant) the meridian. Each trial began with fixation at the center LED (0°, 0°) for a random interval of 1–2 s, after which the center LED was extinguished and the target LED was turned on for 1 s. The intertrial interval was 500 ms. During clockwise adaptation experiments, targets were presented in the second and fourth quadrants 15° lateral to the center with vertical eccentricities of 0, 2, 3, 4, and 5°.

In a catch trial, the target LED was displayed, but after saccade initiation, it was extinguished so that the saccade would complete in darkness. The catch trial block contained 60 trials (Fig. 1B). On odd-numbered trials, the center fixation LED was turned on for a random period of 1–2 s; a target then appeared 15° to either the left or the right. This target LED was extinguished when the subject began to saccade (gaze moved outside of a 2° window surrounding the center fixation). The fixation target was turned back on 750 ms later. This relit target then became the fixation LED for the next trial. Thus, the odd-numbered catch trials were all centrifugal and began at the center LED, whereas the even-numbered catch trials were all centripetal and began at ±15° lateral to the center. These centrifugal and centripetal trial pairs were repeated 15 times on each side of the center LED randomly during the catch trial block.

Trials in the adaptation block were organized in centrifugal–centripetal pairs. During a counterclockwise adaptation experiment (Fig. 1C), odd trials began with fixation at the center LED for 1–2 s. A target 15° to the left or the right of the center then appeared (T1). As soon as the subject began to saccade, the target jumped 5° vertically to a new location (T2). The jump direction was consistently counterclockwise to the orientation of T1, i.e., when T1 was at (15°, 0°), T2 was at (15°, 5°), and when T1 was at (−15°, 0°), T2 was at (−15°, −5°). The T2 LED was on for 1 s and then continued to stay on to serve as the fixation point for the centripetal–even trial. T1 for these even trials were at either (0°, 5°) or (0°, −5°). Once the saccade toward T1 (primary saccade) began, T1 jumped to (0°, 0°). Each of the two possible centrifugal–centripetal trial pairs was presented 15 times within an adaptation set.

Four catch trial pairs were randomly interspersed among the adaptation trials during training. Altogether, an adaptation set consisted of 60 adaptation trials and 8 catch trials. The adaptation set was repeated eight times, and a short break (15 s to 1 min) was given between sets.

In the clockwise adaptation experiment, targets jumped clockwise vertically from the meridian to the second and fourth quadrants of visual space (Fig. 1D). All other aspects of the training block were identical to those for the counterclockwise experiment. Because we found no significant differences in saccade endpoints and chord slopes between the clockwise and counterclockwise adaptation experiments, the data for the two adaptation groups were combined.

During adaptation, the primary saccade to T1 was always followed by a secondary, “catch-up” saccade that brought the eyes to T2. The data presented here represent characteristics of only the primary saccade.

Control experiment 1: effect of fatigue on saccade dynamics.

As we will show, the predicted change in the adaptation experiment was development of curved saccades. However, in addition to this, we saw other changes in the saccade's trajectory, notably a strong pattern of change in peak velocities. Therefore, a control experiment was performed to determine which of the changes that we had seen in the first experiment was an adaptive response to the intrasaccadic target jumps. The trial structure was identical to the adaptation experiment: targets traced the same “figure-eight” configuration as shown in Figure 1C either in a clockwise (n = 6) or counterclockwise (n = 6) design (three of these subjects performed both designs; their two datasets were averaged before group analysis). In the control experiment, there were 544 trials in the main session, exactly the same as in the adaptation experiment. Whereas in the adaptation experiment, the two targets in each trial (T1 and T2) transitioned intrasaccadically, in the control experiment, T1 and T2 transitioned without an intrasaccadic jump. That is, T1 was shown first, and after completion of the saccade to T1, T2 was displayed. T1 remained lit for a random period of 800–1500 ms (mean, 1150 ms), long enough for the saccade to be completed. After T1 was extinguished, T2 was displayed for 600 ms and continued to stay on as the fixation LED for the next trial. In this way, the total number of saccades (both horizontal and vertical), the total distance covered by the saccades, and the total duration of this control experiment closely matched the adaptation experiment. We used the horizontal saccade from fixation to T1 to make direct comparison with the primary saccades in the adaptation experiment.

Control experiment 2: random target jump experiment.

Another control experiment was conducted to determine whether the brain could use visual information during the intrasaccadic target jump to alter saccade trajectory. This control experiment consisted of a block of 500 target jump trials; no other trial types were given. During each trial, the target T1 jumped either up or down in random. Trials were organized in two groups: leftward and rightward sets. Trials in the leftward sets began with fixation at (25°, 0°). On any one trial, T1 could be 15, 25, 30, 45, or 50° to the left of fixation. As soon as the subject's eye left the 2° fixation window, T1 disappeared and a target (T2) appeared either directly above or below T1 at −10, −5, 0, 5, or 10°. Each leftward set consisted of 50 trials, with each of the 25 possible T1–T2 combinations appearing twice. Trials of the rightward sets began with fixation at (−25°, 0°) and had symmetrical target configurations as the leftward trials. Both types of target sets were repeated five times, resulting in a total of 500 trials. Only trials in which T1 was 15° in magnitude were used as control for the adaptation experiment.

Subjects.

Subjects were recruited from the Johns Hopkins medical community. Seven subjects (including authors H.C., W.J., and D.Z.) performed the cross-axis adaptation experiments twice: clockwise adaptation paradigm on one day and counterclockwise adaptation paradigm on another day. The order in which the two paradigms were given was counterbalanced across subjects. Four additional subjects (including author R.S.) performed only one of the two paradigms (two subjects performed the clockwise paradigm, and two subjects performed the counterclockwise paradigm). Data from all 11 subjects were pooled in the analysis. Nine subjects participated in the first control study (including authors H.C., D.Z., and R.S.). Seven subjects participated in the second control study (including authors W.J. and D.Z.). All subjects gave written consent to protocols approved by the Johns Hopkins Institution Review Board.

Modeling the saccadic system using stochastic optimal feedback control.

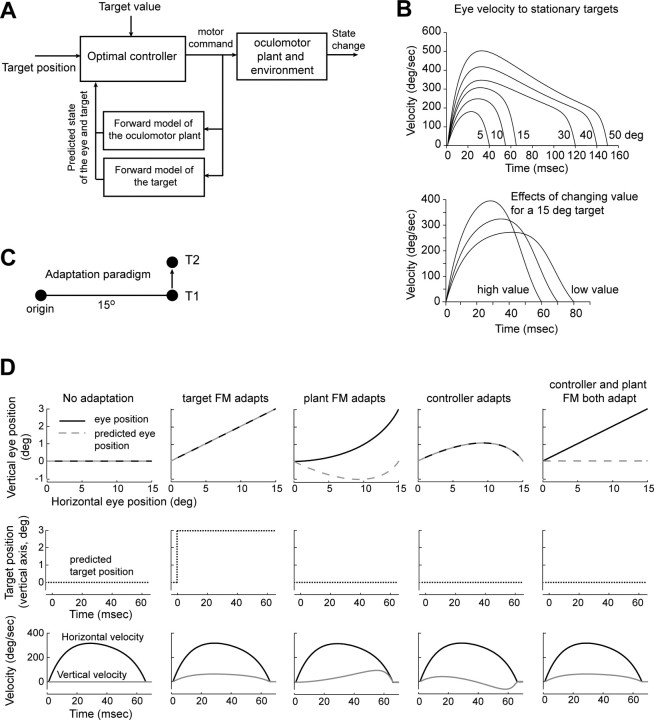
The purpose of our modeling was to help predict the changes that should take place in saccade trajectories if a forward model were to adapt. This was a two-step process: first, we produced a control system that could generate saccade trajectories that resembled typical eye movements of healthy subjects. Previous work had accomplished this using open-loop stochastic optimal control (Harris and Wolpert, 1998, 2006). Here, however, we assumed that saccades were aided by an internal feedback loop (i.e., closed loop) that used efference copy of ongoing motor commands to predict the moment-to-moment sensory states of the eye. The solution to this problem can be found using stochastic feedback optimal control theory. Second, we considered how the errors that resulted from intrasaccadic motion of the target might cause adaptation in our control system.

The schematic in Figure 2A provides the building blocks of our model. We modeled the oculomotor plant with a linear set of discrete, second-order equations:

where x^(t) = [e_x, ė_x, e_y, ė_y, r_x, r_y]^T is the two-dimensional state of the eye at time t (position and velocity) augmented by state of the target, r = [r_x, r_y]. The reason why it is important to include the position of the target as part of the state vector is that in an intrasaccadic target jump experiment, the state of the target is causally linked to the state of the eyes (because the target jumps when the eyes move a certain amount). The motor command is represented by u^(t) = [u_x, u_y]^T, and ε^(t) is a vector random variable representing signal-dependent noise. This noise has an SD that grows with the size of the motor command. As suggested by Todorov (2005), we can write ε^(t) in terms of normally distributed scalar random variables φ₁ and φ₂, each with zero mean and variance one:

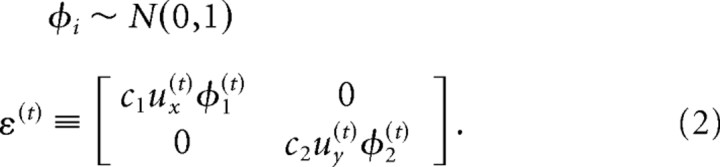By defining

we see that ε^(t) = Σ_iC_iu^(t)φ_i^(t), which has var[ε^(t)] = Σ_iC_iu^(t)u^(t)TC_i^T. Therefore, the SD of the noise grows linearly with the size of the motor command, a property called signal-dependent noise. This representation of noise allows us to rewrite Equation 1 as a function of a normally distributed noise φ_i:

Equation 4 is a discrete time representation of the system, with matrices A and B having dimensions of 6 × 6 and 6 × 2. We computed these matrices as follows: we began in continuous time with a second-order linear model of the eye plant with time constants of 224 and 13 ms (Robinson, 1986). In continuous time, matrices A and B are 4 × 4 and 4 × 2. We then transformed the equations to discrete time using a time step of 1 ms using exact solutions to the linear differential equations afforded by matrix exponentials, and then augmented their dimensions to include state of the target. The resulting matrices are given in supplemental material (available at www.jneurosci.org).

Figure 2.

An optimal feedback control model of saccades. A, Schematic of the controller. B, Velocity profiles for typical saccades produced by the controller for various amplitudes. Each target has a position as well as a value. The top plot displays saccade velocities for a value α of 0.03 (Eq. 5). The bottom plot shows how the saccade velocity changes for a 15° target when the value of the target becomes smaller or larger (α = 0.0085, 0.015, and 0.03). C, Cross-axis saccade adaptation paradigm. While fixating the origin, target T1 is lit. As soon as the saccade begins, T1 is extinguished and T2 is lit. D, Comparisons of various implementations of cross-axis saccade adaptation. FM, Forward model. The teaching signal that guides adaptation is the retinal error at the end of the saccade. For the middle three columns, we assumed that endpoint errors are interpreted by the brain as inaccuracies in the control signals that generated the eye movements. This control signal depends on two structures: a controller and a forward model. If both structures adapt, then saccades will be straight to T2, despite the fact that the learner believes the eyes to be at T1. If the controller is the only structure that adapts, then saccades will show an initial vertical component, but then curve back toward T1 (because of the corrections imposed by the internal feedback from the FM). If the FM adapts but the controller does not, then the curvature will be toward T2. The curvature is again caused by the FM. Finally, it is possible that the brain interprets the errors as a jump in the position of the visual target (right-most column). In this case, the trajectories will be straight.

The next step was to formulate the optimal feedback controller. Because analytical solutions to stochastic optimal feedback control are only possible for quadratic cost functions, we defined the following cost at time t for time step Δt:

The first term reflects our desire to bring the eyes to the position of the visual stimulus. The terms in this matrix penalize the distance between the eye position and the stimulus position as well as the saccade velocity from some time p onward (p is thus interpreted as the desired duration planned by the oculomotor plant; see below). The matrix R (2 × 2) specifies a motor cost. This cost penalizes motor commands (because noise in the motor commands grows with the size). Finally, the term α is simply a cost per unit time. This parameter penalizes movement duration, encouraging movements to terminate as soon as possible (Harris and Wolpert, 2006). Therefore, the term α reflects the value (or importance) that we assign to completing the task.

According to Equation 5, the specific trajectory of a saccade results from balancing two costs: if we perform a slow movement, motor costs will be small, but we accrue costs associated with the passage of time. If we move fast, we will reduce the costs associated with time passage, but incur large motor costs. A movement duration that minimizes the balance of these two costs is an optimum movement. In our model, the duration of a saccade is dependent on the value that the brain assigns to the stimulus, i.e., α. Given a target value, one solves the optimization problem by picking a movement end time p, finding the control policy that minimizes the total cost from time 0 to time p, computing the resulting total cost, and then repeating the procedure for a different p until one finds the movement end time that has the minimum total cost. The total cost for a given p is written as follows:

This is a constraint minimization problem, where the constraint is Equation 4. The result is a linear feedback control law of the following form:

where the optimal control policy, G^(t), is a time-dependent feedback gain applied to estimated state x̂^(t). By inserting the expected value of Equation 7 into Equation 5, one can compute the total cost J_p. Next, one searches among the various candidate movement end times and finds the one that has the minimum total cost.

For a given movement end time p, the procedure for finding the control policy Equation 7 has been shown by Todorov (2005). Briefly, G^(t) is found as follows: set W_x^(p) = Q^(p) and W_e^(p) = 0 for the last time step, then compute recursively backward in time:

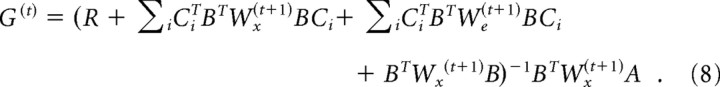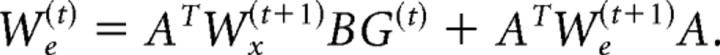Step-by-step derivations are available at R.S.'s web-based course notes on Learning Theory, lectures on optimal control. The only user-defined parameter in the system is the signal-dependent noise matrix C and the ratio of the stimulus value Q to the constant motor cost R. We used the values c₁ = c₂ = 0.02 because they produced trajectories that resembled empirical data (Fig. 2B). We used Q/R = 5 × 10⁵H(t − p), where H(t) is the Heaviside step function, thereby making the assumption that there is no cost for not being at the target before the desired saccade duration p. Finally, α = 0.03 yielded realistic saccade durations given a target eccentricity.

The forward model's function is to estimate future sensory states based on an efferent copy of the motor commands:

The accuracy of its estimation depends on the accuracy of its model of the oculomotor plant dynamics (Â and B̂). Together, Equations 7 and 9 describe the internal feedback control loop, through which the control policy guides the saccade trajectory toward its goal in an optimal manner.

The credit assignment problem of saccade adaptation.

During the saccade, the forward model predicted the state of the target r̂^(t) and the eye ê^(t). No sensory feedback was available during the saccade, but at saccade termination, sensory feedback y⁽ⁿ⁾ reported retinal error, i.e.,

If the sensory feedback was different than expected, i.e., y⁽ⁿ⁾ ≠ ŷ⁽ⁿ⁾, then the system faced a credit assignment problem: did the target move, or did the eye behave differently than expected? If the credit was assigned to the target, then the forward model should learn that contingent on the motor commands, the target is changing position. We simulated this by having the forward model remap the target position at saccade onset. If the credit is assigned to the motor commands that moved the eye, then the forward model should learn to change its model of eye dynamics. We simulated this by changing the forward model's parameter B̂ so that the horizontal and the vertical saccade systems were coupled. Specifically, with adaptation, small but increasing amplitude of vertical eye movements were produced in addition to horizontal movements in response to horizontal motor commands, thereby reducing the endpoint errors that one observes in cross-axis adaptation. These ideas are detailed in the supplemental material (available at www.jneurosci.org).

Results

Predictions of optimal control theory

Figure 2A provides a schematic of the feedback controller that we used to simulate generation of saccades. Given a visual target and the internal value that the controller assigns to that target, the controller generates the initial motor commands based on the current state of the eye. These motor commands minimize a specific cost (Harris and Wolpert, 2006) that balances the need to arrive at the target as soon as possible (specified by the value of the target) with the need to minimize variability (specified by the signal-dependent noise in the motor commands). While the commands are taking effect, the forward model uses a copy of the commands to estimate the moment-by-moment sensory state of the eye, which in turn is used by the controller to generate the subsequent motor commands. This process continues until the eye reaches the target. The resulting trajectories for various targets are displayed in Figure 2B. These saccades indeed resembled the highly stereotypical trajectories observed in normal subjects.

There are two types of “internal models” in this framework. The controller uses an internal model of the oculomotor plant to optimize its motor commands. Given this model, it tries to produce a sequence of motor commands that minimize costs. (In earlier literature, the controller might be called an “inverse model”.) The forward model, however, also uses an internal model to estimate how those commands change the state of the plant. Only when the forward model of the eye plant and the controller's model of the eye both match the actual dynamics of the oculomotor plant does the system produce optimal saccades (Fig. 2B).

In a typical saccade adaptation paradigm, the target of the saccade is jumped intrasaccadically such that the saccade terminates with an error. Because these experiments are performed in complete darkness, the cause of this error is ambiguous to the brain: it could have been caused by an unexpected change in the dynamics of the eye plant or by movement of the target. As a result, the forward model needs to estimate both the state of the eyes and the state of the target (because neither can be sensed during a movement). In response to an endpoint error, the saccadic system could adapt its model of the oculomotor plant, its representation of the target, or perhaps both. If the brain interprets the error as being caused by the motion of the target, then the target should be remapped at saccade onset. If, on the other hand, the brain interprets the error as being caused by a change in the oculomotor plant, then both the controller and the forward model need to learn from the error.

Suppose that the errors are interpreted as a change in the oculomotor plant. If the controller and the forward model adapted their internal representations of the oculomotor plant at the same rate, training would cause saccades to terminate closer to T2 (Fig. 2D). In this case, saccades would remain optimal, i.e., straight. However, if errors caused a faster change in the forward model than the controller (or vice versa), then the motor commands would no longer be optimum. As a result, saccades would become curved. For example, if the forward model adapts faster than the controller, then the imbalance would produce saccades that curve toward T2. On the other hand, if the controller adapts faster than the forward model, then the imbalance would produce saccades that curve toward T1.

Suppose that the endpoint error is interpreted as an intrasaccadic motion of the target. In this case, there is no need for adaptation in the internal models of the oculomotor plant. Rather, the brain simply needs to remap the observed target to a new location. The result is a saccade that remains optimal, that is, straight.

In summary, the theoretical prediction of this framework is that depending on how the brain interprets the endpoint errors, the adaptation will leave a specific signature on saccade trajectories. In particular, rapid adaptation of the forward model of the eye plant should cause curvature toward T2.

Adaptation to an intrasaccadic target jump

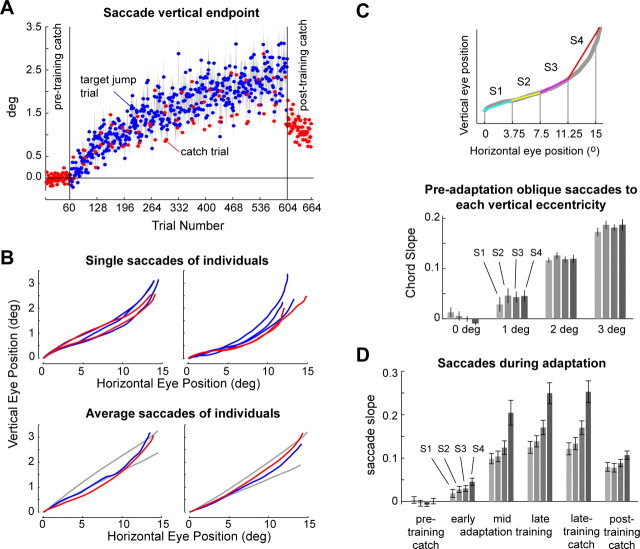
Eleven subjects trained in the cross-axis paradigm. The training included adaptation trials (in which T1 jumped to T2) (Fig. 1C), as well as catch trials (in which T1 was simply extinguished at the onset of the saccade and the movement ended in complete darkness) (Fig. 1B). We quantified adaptation by tracking the vertical amplitude of the primary saccade. By the final adaptation trials, the primary saccades had achieved 2.4° vertical amplitude, or 48% (mean of last 10% of the trials; median, 46%; SEM, 4%) of the 5° target jump (Fig. 3A). Saccade endpoints were indistinguishable between adaptation trials and catch trials.

Figure 3.

Adaptation in response to intrasaccadic target jump. A, Vertical endpoint of saccades during adaptation trials and postadaptation catch trials. Gray shading indicates SEM for each trial (n = 11 subjects). B, Saccades from two representative subjects. Top row, Primary saccade trajectories of the last three adaptation trials (blue) and the last two catch trials (red). Bottom row, Average primary saccade position in the last 10% of adaptation trials and the catch trials in the same trial range, overlaid on average trajectories to preadaptation control trials to oblique targets at (15°, 2°) (gray) and (15°, 3°) (gray). C, Top, Quantifying trajectory curvature. Each primary saccade trajectory was divided into four segments (four chords), and the slopes of the chords were labeled. Curvature is represented as relative change in slope from initial segment (white; S1) of the saccade to the final segment (black; S4). Bottom, Average preadaptation oblique saccades to each vertical eccentricity. Error bars represent SEM (n = 11). Before adaptation, oblique trials showed no tendency toward curvature (comparison of S2, S3, and S4 slopes with S1, p > 0.2 for all cases). D, During adaptation, S4 became increasingly larger than S1. S4 is significantly greater than S3 during the early, middle, and late 10% adaptation trials (48 trials each) at p = 0.002, p = 0.0003, and p = 0.000003 (1-tailed paired t test). “Late-training catch” refers to the 10 catch trials given during the last one-third of the adaptation block. S4 is significantly greater than S3 in the late-training and posttraining catch trials at p = 0.0002 and p = 0.002, respectively. Error bars represent SEM (n = 11).

As training progressed, saccades became curved (Fig. 3B). To quantify curvature, we divided each primary saccade into four equal segments along the horizontal direction and then measured the slope of the line extending the ends of each segment (chord). The chord slopes are labeled as S1, S2, S3, and S4 (Fig. 3C, inset). Because saccades to oblique targets of large vertical eccentricity can be curved (Smit and Van Gisbergen, 1990), it is important to determine whether the curvature we observed was specific to adaptation. Figure 3C displays average chord slopes across subjects during oblique trials to targets with vertical eccentricities of 0, 1, 2, or 3°. The oblique saccades to targets at 2 and 3° are particularly relevant because during adaptation, the maximum vertical extent of the saccades was ∼2.5° (Fig. 3A). The chord slopes of these oblique saccades were indistinguishable from a straight line.

Figure 3D displays average chord slopes across subjects during the adaptation blocks. Before training began, saccades to horizontal targets were straight. During adaptation, all four chord slopes increased, but at different rates: from the first to the last chord, the slopes rose progressively faster, with S4 increasing the fastest. In fact, S4 became significantly different from all other chord slopes within the first 50 adaptation trials (S4 was significantly greater than S3 during the first, middle, and last 10% adaptation trials at p < 0.005 for all comparisons, one-tailed paired t test). S4 was twice the size of S1 at the end of the training (mean S4/S1 ratio, 2.1). At the end of adaptation, S1 reached an average value of 0.12 ± 0.01 (SEM). If this initial slope was maintained throughout the saccade, i.e., if the saccades were straight, then the saccade would have reached a vertical extent of 1.8°. Therefore, the change in S1 accounted for 75% of the entire adaptive response of 2.4° vertical eccentricity. The rest of the adaptive response (0.6°, or 25%) was a result of the curvature, which occurred late in the movement, but helped increase the vertical eccentricity and reduce the endpoint errors.

Figure 3D also shows the average chord slopes during catch trials in the last third of the adaptation block. The slopes of the catch trials had essentially identical profiles as the late training trials. That is, the trajectory was the same whether or not there was an intrasaccadic target jump, indicating that curvature was not caused by an intrasaccadic visual input. In a separate control study (control experiment 2), in which target jumps were random (T1 had an equal chance of jumping up or down during the initial saccade), we found that the primary saccades showed no detectable curvature or bias in their endpoint toward the direction of the target jump (supplemental material, available at www.jneurosci.org). Together with the catch trials in the main adaptation experiment, this control experiment showed that intrasaccadic target jumps were neither necessary nor sufficient to cause curvature. Rather, curvature was produced only when endpoint errors for a given saccade target were consistent.

After the last set of adaptation trials, we presented a block of trials in which every target was a catch trial. Our objective was to measure how quickly the motor memory decayed when endpoint errors were no longer available to support adaptation. Here, S1, which had increased slowly during adaptation, showed a small decline. In contrast, S4, which had shown a large increase during adaptation (and had resulted in curvature), now showed a large decline.

In summary, cross-axis adaptation resulted in curved saccades, suggesting that motor commands that arrived late in the saccade's trajectory benefited from an adaptive process that learned faster than the motor commands that initiated the saccade. This is consistent with a system in which the fast adaptive mechanism is in the forward model (Fig. 2D).

Multiple timescales of change in saccade curvature

In our experiment, primary saccades were made at a rate of approximately once per 2.5 s (2.69 ± 0.28 s) to 68 sequential visual targets. After each set of trials, subjects rested by closing their eyes for 15–60 s. An inspection of the trial-by-trial changes in saccade slopes revealed a remarkable pattern. During each adaptation set, S1 gradually increased. However, S4 increased more rapidly (Fig. 4A), resulting in curvature. During the short rest period between sets, S4 that had rapidly increased now showed near-complete forgetting, whereas S1 showed little or no change. As a result, saccades that had become curved by the end of a training set were nearly straight after the brief rest period. To quantify this, for each subject and each set break we compared slopes of the two saccades made before the break with those of the two saccades made after the break. The resulting distribution of between-set change in S1 had a mean that was not different from zero (p = 0.88), suggesting that S1 did not show forgetting between sets. In contrast, the between-set change in S4 was strongly negative (p < 0.001), suggesting that the short break produced rapid forgetting in S4. This implied that saccades became curved during each adaptation set, but then S4 forgetting during the rest period caused loss of saccade curvature as the new set begun. To quantify this, in Figure 4B we plotted the curvature (S4 − S1) of the first two and last two saccades of each set. In five of nine sets, the saccades at the beginning of the set had slopes that were not different from a straight line (curvature not significantly different from zero). However, curvature of the last two saccades was significantly greater than zero for eight of nine sets.

Figure 4.

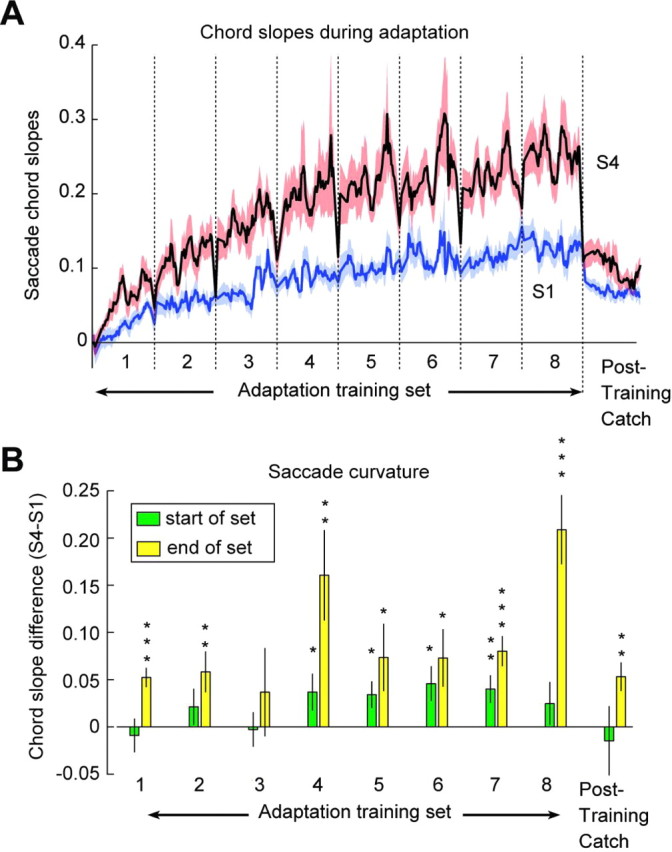
The multiple timescales of adaptation. A, Moving average of the time course of S1 and S4 during adaptation (480 trials) and posttraining catch trials (60 trials). To highlight the rapid changes at the start of each set, we used a variable bin width (bw): bw = 2 trials for the first two trials in each set, bw = 4 for the next four trials, and bw = 6 for the rest of the set. Red and blue shaded areas represent SEM (n = 11). B, Curvature (chord slope S4 − S1) at the start and end of each set. The bin size is two saccades. Saccades that initiate each set have generally smaller curvature than saccades that complete the set. Eight of nine sets end with saccades that are curved (*p < 0.05; **p < 0.01; ***p < 0.001). Error bars represent SEM (n = 11).

If we consider S1 as a proxy for motor commands that initiated the saccade, then these commands adapted slowly in response to the endpoint errors and showed little or no forgetting during the short set breaks. The postadaptation catch trials were a particularly revealing indicator of the process of adaptation, because during these trials, the errors were no longer available. Without an error to drive and sustain adaptation, memory of adapted behavior should decay to its baseline state (Smith et al., 2006). Indeed, we observed that during the postadaptation catch trials, S1 slowly decayed toward zero (Fig. 4A).

We may consider S4 as a proxy for motor commands that occurred later in the saccade trajectory, at a time when internal feedback could impose a greater influence. Unlike S1, S4 displayed multiple timescales of change: it showed a gradual increase across sets; a rapid forgetting during the rest period between sets; a rapid “relearning” soon after the set began; and finally, a rapid decline in the postadaptation catch trials.

Therefore, it is possible that two separate mechanisms were responsible for the changes that occurred in saccade trajectories. The mechanism that produced the motor commands that initiated the saccade learned slowly and forgot slowly. The mechanism that acted later in saccade trajectory learned more quickly and displayed strong forgetting with short passage of time.

Trajectory changes as a result of stimulus repetition

Although our computational model suggested that there may be curvature in the adapted saccades, it also predicted that adaptation should produce little or no change in saccade durations (Fig. 2D). This is because duration is strongly related to the expected value of the visual stimulus. Unless this value changes, the modeled trajectories will not exhibit significant changes in saccade durations. However, the data presented a strikingly different picture. Figure 5,A and B, presents the peak horizontal velocity and durations of the saccades during the entire experiment. Despite the fact that primary saccades were made at a rate of less than once per 2.5 s, the peak velocities steadily decreased and then recovered almost completely after the short break between the sets (Fig. 5A). Similarly, saccade durations increased in each set and then dropped after each short set break. These patterns of change clearly exhibited two timescales: a slow timescale that gradually decreased peak horizontal velocities from the first set to the last set and a fast timescale that allowed them to recover after each set break.

Figure 5.

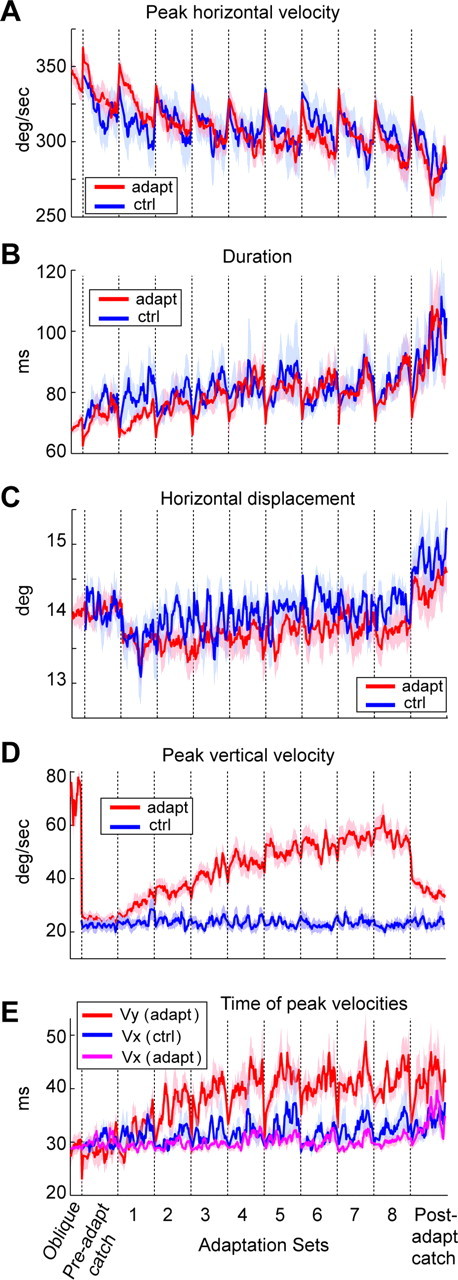
Trial-dependent changes in saccade trajectories that were unrelated to adaptation. A, Saccade peak horizontal velocities. In both the control and the adaptation groups, the horizontal velocities showed a set structure suggesting a fatigue-like process in the horizontal motor commands that initiated the movements. B, Saccade durations. In both groups, saccade durations increased with a set structure consistent with a process that was highly correlated to the change in peak velocities (within-subject covariance between peak horizontal velocity and duration was significant at p < 10⁻⁵ for all subjects). C, Saccade horizontal amplitudes. Despite the reductions in peak horizontal velocity, horizontal amplitudes generally remained unchanged. D, Peak vertical velocity. In the adaptation group, endpoint errors induced changes in the vertical motor commands. These changes, as reflected by the peak vertical velocity, were specific to the adaptation group and did not exhibit the fatigue-like effects that we saw in the horizontal motor commands. Our noise level for saccade velocities is ∼22°/s. Therefore, the vertical component velocities shown in the control trials as well as the preadaptation catch trials reflect noise. Note the value for the control oblique saccades at the far left of the figure. E, Timing of the peak velocities in the horizontal (x) and vertical (y) directions for the adaptation experiment, and timing of peak horizontal velocity during the control experiment (timing of the peak vertical velocity was omitted because it was at noise levels). In the adaptation group, when horizontal velocity declined in each set, the adaptive response via internal feedback was an increase in the vertical motor command, resulting in a shift of the peak vertical velocity. Data in all panels are moving averages: fixed bin width (8) for oblique trial set and variable bin widths (Fig. 4A) for all other sets. Shades represent SEM.

To determine whether these changes were related to our adaptation paradigm, we performed a control study in which subjects were presented with the same sequence of visual stimuli (control group 1, intertrial interval of 2.43 ± 0.38 s). However, the targets remained stationary. The two groups exhibited nearly identical changes in peak horizontal velocity and duration (Fig. 5A,B). Therefore, these changes were unrelated to the endpoint errors.

The trial-by-trial covariance between saccade horizontal velocities and durations was highly significant for each subject in both groups (p < 10⁻⁵ for each subject). The average correlation was −0.60 ± 0.009 and −0.63 ± 0.027 (mean ± variance) for the adaptation and control groups. Indeed, it appeared that the variability in the motor commands that initiated the saccade, as reflected in the variability in peak velocities, was partially compensated by motor commands that stretched the saccade in time. As a result, the horizontal position of the saccade endpoints remained immune to the variability in peak velocities (Fig. 5C) (adaptation group, correlation between peak velocity and duration, r = 0.059; p > 0.1).

What were the changes that were specifically an adaptive response to the endpoint errors? By comparing the trajectories, it became clear that the horizontal component of the trajectories was essentially identical in the two groups. The only difference was in the vertical axis: the control group never produced vertical saccade velocities that rose above noise levels (Fig. 5D). In contrast, the peak vertical speed climbed steadily in the adaptation group. Therefore, only the changes along the vertical axis were specific to adaptation.

What caused the curvature? An important clue was the timing of the peak vertical velocities (Fig. 5E). In each set, peak vertical velocity shifted increasingly later in the movement compared with the peak horizontal velocity. This difference between the timing of the peak horizontal and vertical velocities induced curvature. If we view the timing of the peak vertical velocity as a proxy for the timing of the motor commands that moved the eyes vertically, Figure 5E illustrates that these vertical motor commands occurred late with respect to the motor commands that moved the eyes horizontally. The late arrival of these vertical motor commands caused curvature.

Discussion

Our experiments produced three main findings. (1) When a horizontal visual target predictably jumped vertically, motor commands that initiated the saccades (S1) slowly learned from endpoint error. This adaptation exhibited little forgetting during the set breaks, and slow forgetting when the error feedback was clamped to zero during postadaptation catch trials. (2) Later in the saccade's trajectory, another adaptive component (S4) “steered” the saccades closer to the jumped target, resulting in curvature. These late-arriving motor commands exhibited a faster timescale of adaptation, learning quickly from endpoint errors and forgetting quickly (e.g., during the short set breaks, or during the catch trials). The curvature is consistent with a model of saccade control in which a fast adaptive process monitors the efference copy and corrects the movements as they are produced. (3) Saccade repetition produced reductions in the peak horizontal velocities, i.e., the horizontal component of the motor commands that initiated the saccades became smaller as saccades repeated. However, these reductions did not result in a corresponding reduction in horizontal displacement of the eyes, because saccade durations were increased in lockstep with the reductions in peak horizontal velocity. These changes were present in both the adaptive group and a control group in which targets remained stationary. Therefore, saccade trajectories of healthy people changed in response to two different factors: endpoint errors and stimulus repetition.

Response to stimulus repetition

A number of investigators have noted that when subjects make saccades to a sequence of visual stimuli, velocities tend to decline (Fuchs and Binder, 1983; Straube et al., 1997). This effect is not attributable to fatigue in the extraocular muscles (in our case, saccades were at a very low rate with intertrial interval >2 s), but is probably of neural origin, related to the motivational state of the subject.

How could motivational states affect saccade trajectory? A key feature of our experiment was the repetitive nature of the stimuli. Sensory neurons that encode some particular attribute of a stimulus show progressively smaller responses when that attribute is repeated (Miller and Desimone, 1994; Kohn and Movshon, 2003). For example, repeated display of a visual stimulus in the receptive field of a cell in the superior colliculus will produce reduced discharge (Boehnke et al., 2007). This effect is termed “repetition suppression” (Dinstein et al., 2007). In the optimal control framework, planning of any action takes into account the value associated with the stimulus: the movement is slower toward a stimulus that has a lower value. Indeed, when one varies the amount of reward associated with a visual stimulus, saccade velocities are faster for stimuli with higher expected reward (Takikawa et al., 2002). It is possible that when a visual stimulus repeats, the internal value that the brain associates with it becomes smaller. If our speculation regarding a link between target repetition and reduced value is accurate, then the striking changes in peak horizontal velocities that we observed suggest that there is a highly structured change in the value associated with a repeating stimulus. This would imply that some of the variability in motor commands that initiate a saccade is attributable not to random noise, but to changes in the internal value that the subject assigns to that movement.

Response to movement errors

Optimal control allows one to consider how saccade trajectories might change in response to intrasaccadic motion of a visual target. When the target jumps, there is a discrepancy between the observed sensory state at the end of the saccade and the predicted state. This should drive adaptation in the forward model. Two kinds of predictions may be made by the forward model: it could predict how the state of the target changes as motor commands begin moving the eyes, and it could predict how the state of the eye changes as a consequence of the same motor commands. The endpoint error can produce a change in both of these predictions. Depending on how the error is interpreted, the result might be a straight saccade to the remapped location of the target, or curvature. We observed that saccades tended to be relatively straight at the start of each adaptation set, but then quickly became curved as trials continued in that set. Curvature was a direct result of the fact that the motor commands that produced vertical motion of the eyes arrived late in the saccade's trajectory (Fig. 5E). This result suggests that saccades are controlled by an internal feedback process that monitors motor commands and corrects them as they are generated.

Changes in S1 accounted for 75% of the total adaptive response. Therefore, curvature was not a dominant factor in the overall adaptive response. Indeed, changes in S1 occurred gradually but displayed little or no forgetting during the set breaks, whereas changes in S4 occurred rapidly and displayed large forgetting during the set breaks. This raises the possibility that these two components of the adaptive response were caused by two separate mechanisms.

Although curvature was an adaptive response to endpoint errors (because it did not occur in either of the two control groups), it exhibited trial-to-trial temporal characteristics (Fig. 4A) that were strikingly similar to trajectory changes associated with stimulus repetition (Fig. 5A). When peak velocities were high, duration was short, and saccades were generally straight. When peak velocities decline, durations increased, and saccades became curved.

One possibility is that as a stimulus repeated, its value declined, resulting in smaller motor commands that initiated the saccade. An internal feedback process monitored these commands and issued corrective horizontal motor commands later in the saccade's trajectory, increasing its duration. When there were persistent endpoint errors, this internal feedback process adapted by learning to produce motor commands that moved the eyes vertically, reducing endpoint errors. The next time that the stimulus afforded a movement that began with a smaller than usual horizontal motor commands, the internal feedback was again engaged to compensate. However, because this internal feedback had adapted, it produced compensation in the horizontal as well as in the vertical directions. Because the timing of its compensatory response was late in the saccade's trajectory, the result was curvature (Fig. 5E).

Is there evidence that the internal feedback pathway that compensates for a “fatigue” is also responsible for adaptation to endpoint errors? The cerebellum is known to be critical for many aspects of saccade control and adaptation (Hopp and Fuchs, 2004; Girard and Berthoz, 2005). It appears that changes in Purkinje cell simple spike population activity during compensation for saccadic fatigue is consistent with changes that occur during short-term saccade adaptation (Catz et al., 2006). Barash et al. (1999) observed that when monkeys with cerebellar damage performed hundreds of saccades to a repeating stimulus, saccade amplitudes gradually declined. In separate sessions, the same animals were unable to adapt to an intrasaccadic target jump. In contrast, healthy animals maintained saccade amplitudes in response to a repeating stimulus and adapted to the target jump. These results combined with our observations suggest that a forward model in the cerebellum may not only be responsible for some of the adaptation in response to endpoint errors, but is fundamentally part of the control system that attempts to compensate for “fatigue.”

Adaptive internal feedback and the cerebellum

The idea of an adapting forward model may also explain some of the data in traditional in-axis adaptation paradigms. In a gain–decrease study by Fitzgibbon et al. (1986), the peak velocity of the adapting saccades did not conform to the “main sequence” relationship: the peak velocity was larger than expected for the length of the saccade. This is consistent with an internal feedback control process that adapted to the endpoint errors, stopping the saccade earlier than expected from the peak velocities. A similar process may account for the increased durations observed in the gain–increase study of Straube and Deubel (1995).

In our block diagram, we assumed that the forward model could predict both the state of the target and the state of the eyes. If we imagine that this forward model is in the cerebellum, we can speculate about the pathways that express these two state predictions. The cerebellum exerts its influence on saccades via two pathways leaving the caudal fastigial nucleus (cFN). The short pathway projects directly to the brainstem neurons that generate the premotor saccade commands, called the saccade pulse generator (PG). The long pathway ascends via the thalamus to various cortical eye fields, which then could influence the superior colliculus and the PG. The superior colliculus likely issues the feedforward saccadic commands that produce S1. The adaptation of S1 may depend on the long pathway involving the cortex. Recently, it has been shown that neurons in the superior colliculus show changes correlated with saccade adaptation (Takeichi et al., 2007). Gaymard et al. (2001) observed reduced saccade adaptation in patients with lesions in the cerebellar thalamus. They suggested that the thalamus relayed adaptation-related information from the cerebellum to cerebral cortical oculomotor areas. The remapping of the target (changes in S1) might occur through this long pathway.

Several lines of work suggest that the superior colliculus–cerebellar–brainstem side loop, or the short pathway leaving cFN, may contribute to S4. Because of its direct projection to the PG, the cFN can strongly influence saccadic control, as revealed by lesion (Vilis and Hore, 1981; Robinson et al., 1993; Iwamoto and Yoshida, 2002) and inactivation (Robinson et al., 2002; Goffart et al., 2004) studies. In particular, unilateral muscimol injections in the cFN causes saccade trajectories to curve toward the lesioned side (Robinson et al., 1993). Furthermore, both the cFN and dorsal cerebellar vermis are essential for saccade adaptation (Takagi et al., 1998; Barash et al., 1999; Robinson et al., 2002). Indeed, cFN neurons show changes in discharge that correlate with saccade adaptation (Scudder and McGee, 2003), and inhibitory burst neurons (IBNs) within the PG show changes in activity that correlate with saccade adaptation and likely reflect activity in cFN neurons that project directly to IBNs (Kojima et al., 2008). The curvature might be a result of rapid adaptation in this pathway.

The projections from the superior colliculus to the cerebellum may provide the efference copy necessary for on-line control for saccade trajectory. Adaptive changes in saccade amplitude are already reflected in the superior colliculus (Takeichi et al., 2007) and in the nucleus reticularis tegmenti pontis (Takeichi et al., 2005), both sources of input to the cerebellum. Together, the superior colliculus–cerebellar–brainstem side loop seems important for steering saccade trajectories midflight (Optican and Quaia, 2002; Optican, 2005). This side loop is a likely substrate for carrying out the computations required by the forward model of the oculomotor plant.

In summary, control of saccades depends on an adaptive internal feedback that has the characteristics of a forward model. When the visual target is displaced intrasaccadically in the cross-axis paradigm, the internal feedback adapts to endpoint errors and corrects the oculomotor commands as they are generated, resulting in curvature. When the visual target remains stationary, the internal feedback still plays a fundamental role by compensating for the variability in motor commands that initiate a saccade. A significant source of this variability may be a changing motivational state of the subject.