Abstract
The mistranslation-induced protein misfolding hypothesis predicts that selection should prefer high-fidelity codons at sites at which translation errors are structurally disruptive and lead to protein misfolding and aggregation. To test this hypothesis, we analyzed the relationship between codon usage bias and protein structure in the genomes of four model organisms, Escherichia coli, yeast, fly, and mouse. Using both the Mantel–Haenszel procedure, which applies to categorical data, and a newly developed association test for continuous variables, we find that translationally optimal codons associate with buried residues and also with residues at sites where mutations lead to large changes in free energy (ΔΔG). In each species, only a subset of all amino acids show this signal, but most amino acids show the signal in at least one species. By repeating the analysis on a reduced data set that excludes interdomain linkers, we show that our results are not caused by an association of rare codons with solvent-accessible linker regions. Finally, we find that our results depend weakly on expression level; the association between optimal codons and buried sites exists at all expression levels, but increases in strength as expression level increases.
Keywords: codon usage bias, optimal codon, protein structure, protein evolution, translational accuracy selection
Introduction
Synonymous mutations are usually referred to as “silent,” but increasing evidence shows that they experience significant selection pressures in a wide range of organisms. For example, selection on synonymous sites has been linked to transcription, splicing, DNA secondary structure, and messenger RNA secondary structure and stability (Xia 1996, Vinogradov 2003, Chamary and Hurst 2005a, 2005b; Hoede et al. 2006, Parmley et al. 2006, Warnecke and Hurst 2007, Stoletzki 2008). The strongest selection pressure on synonymous sites, at least in microbes, seems to be selection for translational efficiency. This pressure causes highly expressed genes to be encoded predominantly by codons corresponding to highly abundant transfer RNAs (tRNAs). It has been observed in bacteria, plants, yeast, fly, worm, and even mammals (Ikemura 1981, Ikemura1985, Sharpetal1986, AkashiEyre-Walker1998, Duret2002, UrrutiaHurst2003, Comeron2004, Wrightetal2004, LavnerKotlar2005).
Selection for translational efficiency may reflect selection for rapid translation (speed selection), selection for translation with high fidelity (accuracy selection), or both. Akashi (1994) argued that selection for translational accuracy should lead to inhomogeneous codon usage within genes. More important sites (i.e., sites that are less robust to translation errors) should be more frequently encoded by codons with high fidelity than other sites. Akashi (1994) found such a signal in Drosophila. Later, others found similar results in Escherichia coli, yeast, worm, and mammals (Stoletzki and Eyre-Walker 2007, Drummond and Wilke 2008).
Akashi (1994) suggested to classify sites as important or not depending on whether they are conserved at the amino acid level in an orthologous sequence. But although there is good evidence that evolutionary conservation reflects functional (Lichtarge et al. 1996) and structural (Koshi and Goldstein 1995, Mirny and Shakhnovich 1999, Mirny and Shakhnovich 2001a, 2001b; Schueler-Furman and Baker 2003) constraints, multiple other factors influence evolutionary conservation as well. Among them are the divergence time between orthologous sequences, the background rate of amino acid substitutions (which can vary over several orders of magnitude among genes within the same organism), mutational biases, and random chance. Moreover, the relative frequency of mutations at sites with different biochemical properties (e.g., solvent accessibility) changes with sequence divergence (Sasidharan and Chothia 2007). Ultimately, instead of linking codon usage bias to conserved or variable sites, we would like to link codon usage bias to sites with specific biochemical properties. In line with this reasoning, Akashi (1994) carried out a second analysis in which he showed that preferred codon usage was increased in putative zink finger and homeodomain regions of transcription factors.
Motivated by Drummond and Wilke's (2008) hypothesis that translational accuracy selection minimizes the misfolding of mistranslated proteins, we test here whether translationally optimal codons are associated with structurally sensitive sites, that is, sites at which translation errors are particularly likely to cause misfolding. We focus on residues’ solvent accessibility because substitutions in the solvent-shielded core of proteins tend to be particularly disruptive (Matthews 1993, Tokuriki et al. 2007). As a second measure of structural sensitivity, we use computationally predicted changes in free energy upon mutation (ΔΔG values).
We consider four model organisms, E. coli, Saccharomyces cerevisiae, Drosophila melanogaster, and Mus musculus. We define translationally optimal codons as those that are overrepresented in highly expressed genes and address the following questions: 1) Are optimal codons more likely to encode residues in the core of proteins or on the surface? 2) Is such an association a general characteristic for all amino acids or does it depend on the type of amino acid encoded? 3) Are the results affected by gene expression level? 4) Are the results affected by an excess of rare codons in interdomain linkers? 5) Are optimal codons more likely to occur at sites for which computational modeling predicts that amino acid substitutions are particularly disruptive?
Materials and Methods
Structural Data
To match gene sequences to protein structures, we used the GTOP (Genomes TO Protein structures and functions) database (Kawabata et al. 2002). We saved a match in the database for further calculation if its region of similarity was longer than 80% of the protein length and its sequence identity was larger than 40% of the sequence in the Protein Data Bank (PDB). This process yielded 822, 403, 947, and 1464 matches in E. coli, S. cerevisiae, D. melanogaster, and M. musculus, respectively.
For each protein with a match, we obtained the corresponding 3D crystal structure from the PDB. For every match, we retained only the specific matching peptide chain. After aligning the gene sequence and the sequence from the crystal structure with MUSCLE (Edgar 2004), we calculated the percent solvent-accessible surface area for each aligned residue with the DSSP program (Kabsch and Sander 1983). We normalized these results by the reference surface areas of an extended Gly-X-Gly peptide (Creighton 1992). We considered residues with less than 25% relative solvent accessibility as buried. Because we discarded all but the matching peptide chain, residues involved in protein–protein interfaces were considered as exposed for the purpose of our study.
We used the Rosetta ΔΔG module (Kortemme and Baker 2002, Kortemmeetal2004) to estimate the change in the free energy gap, ΔΔG, for all 19 possible single-point amino acid substitutions at each site. Although most mutations are destabilizing (ΔΔG > 0 kcal/mol) (Tokuriki et al. 2007), proteins are often quite mutationally robust (Markiewicz et al. 1994, Guo et al. 2004, Bloom et al. 2005, Bloom, Drummond, et al. 2006) and only approximately 20% of all mutations are significantly destabilizing (ΔΔG > 2.0 kcal/mol) (Tokuriki et al. 2007). We considered mutations with ΔΔG > 3.0 kcal/mol as strongly destabilizing mutations and calculated the “structural importance” of a site as its fraction of strongly destabilizing mutations.
Because the protein sequences in our data set are not always 100% identical to the sequences of the structure homologs in PDB (see fig. S1), we tested the effect of sequence dissimilarity on our structural data (solvent accessibility and structural importance). We collected 58 groups of structure homologs from the PDB-REPRDB database (Noguchi et al. 2001, NoguchiAkiyama2003), which is a database of representative protein chains selected from the PDB. Each group of structure homologs contained one representative protein and three homologs with sequence identity to the representative protein between 80% and 100%, between 60% and 80%, and between 40% and 60%, respectively. We used the following criteria to collect groups of structure homologs: We only included structures for which we found at least one homolog in each sequence-identity interval. If there was more than one homolog falling into one sequence-identity bin, we retained only the homolog with the lowest sequence identity to the representative protein. This choice made our test more conservative. For each group, we calculated the correlation between the solvent accessibility of the representative protein and its homologs and the correlation between the structural importance of the representative protein and its homologs, respectively. We found that both solvent accessibility and structural importance tended to correlate strongly among homologous proteins, but the correlation coefficient decreased with decreasing sequence identity (see fig. S2). For solvent accessibility, the median Spearman correlation coefficient ranged from 0.964 (80%–100% identity) to 0.871 (40%–60% identity), and for structural importance, it ranged from 0.797 (80%–100% identity) to 0.626 (40%–60% identity).
We obtained protein domain boundary information from the CATH domain structure database (http://www. cathdb.info/) (Orengo et al. 1997, Greene et al. 2007). We defined domain linkers to be regions that are centered at CATH domain boundaries and extend at least 10 residues in both directions. Loops (continuous peptides composed of residues with DSSP classes S, T, and “-”), which neighbor on or overlap this region were also considered as parts of domain linkers. Finally, we considered both termini of the protein as domain boundaries. These criteria are strict and yield a conservative analysis of nonlinker regions.
Genomic Data
We obtained genomic sequences from the following sources: the Comprehensive Microbial Resource (http://cmr.tigr.org/cmr.tigr.org/) for E. coli, the Saccharomyces Genome Database (ftp://genome-ftp.stanford.edu/) for S. cerevisiae, the Eisen Lab (http://rana.lbl.gov/drosophila/) for D. melanogaster, and Ensembl (http://www.ensembl.org/) for M. musculus.
We designated as evolutionarily conserved all sites at which the amino acid was unchanged compared with the orthologous gene in a closely related species. We used the following orthologs: For E. coli, we obtained orthologs between E. coli and Salmonella typhimurium from the Comprehensive Microbial Resource. For yeast, we obtained orthologs between S. cerevisiae and Saccharomyces bayanus from the Saccharomyces Genome Database. For fly, we obtained orthologs between D. melanogaster and Drosophila yakuba from the Drosophila 12-genome project AAAWiki at http://rana.lbl.gov/drosophila/. For mouse, we obtained orthologs between M. musculus and Rattus norvegicus from Biomart through the Ensembl Homology track. We aligned each pair of orthologs at the peptide level using MUSCLE (Edgar 2004).
Expression Data
We used previously published expression data for each species: For E. coli, we obtained gene expression levels measured in messenger RNAs per cell from Covert et al. (2004); for S. cerevisiae, we used expression data from Holstege et al. (1998); for D. melanogaster, we used as expression level the geometric mean of expression data from different tissues obtained by Stolc et al. (2004); and for M. musculus, we measured expression level as the breadth of expression among different tissues (Su et al. 2004). After combining the expression data with the structural data, we ended up with 698, 384, 123, and 569 genes for E. coli, S. cerevisiae, D. melanogaster, and M. musculus, respectively.
Inferring Optimal Codons
To identify which codons are translationally optimal in each species, we compared the codon usage pattern between the gene groups showing the lowest 5% and highest 5% expression level in each species. We defined codons as “optimal” if they showed a statistically significant increase in frequency in the highly expressed group, as determined by a chi-square test. We defined codon optimality (Copt) as the odds ratio of codon usage between highly and lowly expressed groups, calculated separately for each codon:
| (1) |
Here, nhigh and nlow are the observed numbers of the codon in the highly and lowly expressed groups, respectively, and Nhigh and Nlow are the observed numbers of the corresponding amino acid in the highly and lowly expressed groups, respectively.
Statistical Tests of Association
We used two different methods to test for association, one using categorical variables and one using continuous variables. For pairs of categorical variables (e.g., optimal vs. nonoptimal codons and buried vs. exposed sites), we stratified the data by gene and synonymous codon family within each gene and constructed a separate 2×2 contingency table for each stratum. We then combined either the tables for all genes and a given codon family or the tables for all genes and all codon families into an overall analysis using the Mantel–Haenszel procedure (Mantel and Haenszel 1959, Mantel1963). The null hypothesis in this analysis assumes that the status of the site (e.g., buried or exposed) is independent of the codon type in any given stratum. Because the Mantel–Haenszel procedure yields undefined results on contingency tables whose sum of all four entries is less than 2 (i.e., 0 or 1), we excluded all such tables from the analyses.
For pairs of continuous variables (e.g., codon optimality and solvent accessibility), we also stratified the data by gene and synonymous codon family within each gene. Then, for each stratum, we separately calculated the Pearson correlation coefficient between the two variables. As test statistic, we used the mean of the correlation coefficients over all strata. We calculated the sampling distribution by randomly reshuffling, separately for each gene, synonymous codons among sites with identical amino acid, and recalculating all correlation coefficients. We generated 1,000 resampled sequences for each gene.
We carried out all statistical analyses using the software R (R Development Core Team 2008). In the analyses of individual amino acids, we corrected for multiple testing using the false discovery rate method of Benjamini and Hochberg (1995), as implemented in the R function p.adjust().
Results
Optimal Codons are Preferred at Buried Sites
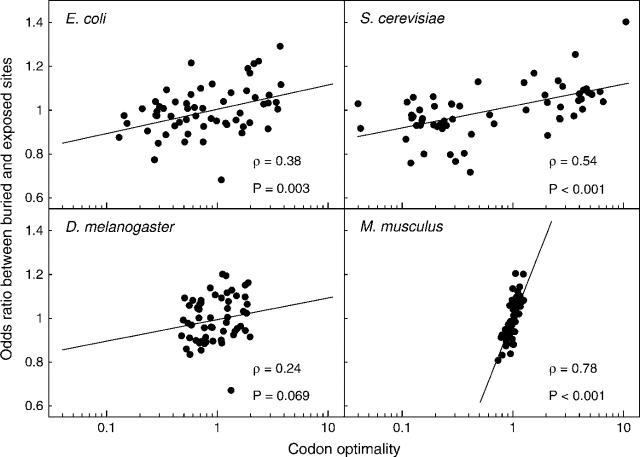
We first assessed whether there was any relationship between a codon's tendency to be preferentially used in highly expressed genes and the same codon's tendency to be preferentially used at buried sites. We calculated 2 odds ratios each for 59 codons (excluding ATG for Met, TGG for Trp, and three stop codons). The first odds ratio, which we refer to as codon optimality (Copt, see Materials and Methods), measures whether the codon is preferred in highly expressed genes compared with all other codons encoding the same amino acid. The second odds ratio, which we denote by Oburied, measures whether the codon is preferred at buried sites compared with all other codons encoding the same amino acid. To control for confounding effects of differing amino acid usage among genes, we calculated Oburied by first constructing 2×2 contingency tables of codon usage within each gene (see table 1 for an example) and then using the Mantel–Haenszel procedure (Mantel and Haenszel 1959, Mantel 1963) to combine the odds ratios for each individual contingency table into an overall odds ratio Oburied. We list the values of Copt and Oburied for each codon in table S1. In all species except fly, we found a significant positive correlation between Copt and Oburied (Spearman's ρ = 0.38,P = 0.003 for E. coli; ρ = 0.54,P < 0.001 for S. cerevisiae; ρ = 0.24,P = 0.069 for D. melanogaster; and ρ = 0.78,P≪0.001 for M. musculus; see also fig. 1).
Table 1.
Example of a 2×2 Contingency Table for Codon ACT in One Particular Gene in Escherichia coli
| Codon | Buried Sites | Exposed Sites |
| ACT | 15 | 5 |
| ACC, ACA, ACG | 3 | 6 |
NOTE.—Codon ACT encodes amino acid Thr. The other three non-ACT codons encoding Thr are ACC, ACA, and ACG. The odds ratio of ACT usage between buried and exposed sites is (15/5)/(3/6) = 6 for this contingency table. Because there is one table of ACT per gene, we applied the Mantel–Haenszel procedure to calculate the joint odds ratio of use frequency between buried and exposed sites for all genes.
FIG. 1.—
Odds ratio Oburied versus codon optimality Copt. With the exception of fly, all organisms show a significant correlation between these two quantities.
The correlation between Copt and Oburied reveals that there is an association between codon usage and protein structure. To determine whether this correlation is consistent across all amino acids or if different amino acids have different trends, we carried out a similar statistical test on each amino acid separately. We inferred a set of optimal codons for each species (see Materials and Methods and table S2). For each gene, we then constructed separate 2×2 contingency tables for the 18 amino acids encoded by at least two codons (see table 2 for an example). For each of these 18 amino acids, we calculated a joint odds ratio (Ojoint) of optimal codon usage between buried and exposed sites using the Mantel–Haenszel procedure. A value of Ojoint greater than 1 signifies a preference for optimal codons at buried sites (and nonoptimal codons at exposed sites).
Table 2.
Example of a 2×2 Contingency Table for Amino Acid Thr in One Particular Gene in Escherichia coli
| Codon | Buried Sites | Exposed Sites | |
| Optimal | ACT, ACC | 16 | 6 |
| Nonoptimal | ACA, ACG | 2 | 5 |
NOTE.—Codons ACT and ACC are optimal codons for amino acid Thr in E. coli (see table S2). The odds ratio of optimal codon usage between buried and exposed sites is (16/6)/(2/5) = 6.67 for this contingency table. Because there is one table of Thr per one gene, we applied the Mantel–Haenszel procedure to calculate the joint odds ratio for all tables of Thr across all genes.
We found that 13 of 18 amino acids showed, in at least one species, a significant preference for optimal codons at buried residues (table 3). Unexpectedly, in E. coli, 2 of these 13 amino acids (Ala and Val) showed a significant preference for optimal codons at exposed residues. The remaining codons (Cys, Glu, His, Pro, and Tyr) showed no significant preference for optimal codons to be buried or exposed in any of the four species tested. Of a total of 72 association tests, 23 showed a significant preference for buried optimal codons, whereas only 2 showed a significant preference for exposed optimal codons.
Table 3.
Odds Ratio of Optimal Codon Usage between Buried and Exposed Sites
| Escherichia coli | Saccharomyces cerevisiae | Drosophila melanogaster | Mus musculus | |||||
| Amino Acid | Whole | Nonlinker | Whole | Nonlinker | Whole | Nonlinker | Whole | Nonlinker |
| Ala | 0.92* | 0.93 | 1.06 | 1.06 | 1.13*** | 1.15**(*) | — | — |
| Arg | 1.01 | 0.97 | 1.19(*) | 1.05 | 0.96 | 0.96 | 1.15*** | 1.17*** |
| Asn | 1.29*** | 1.25*** | 1.07 | 1.16(*) | 1.10(*) | 1.12(*) | 1.14*** | 1.22*** |
| Asp | 1.06 | 1.08 | 0.89(*) | 0.86(*) | 0.93(*) | 0.89*(*) | 1.09** | 1.14*** |
| Cys | 0.99 | 0.99 | 1.19 | 1.30 | 0.96 | 0.91 | — | — |
| Gln | 1.17**(*) | 1.26*** | 1.04 | 0.99 | 1.04 | 0.93 | 1.21*** | 1.34*** |
| Glu | 1.08 | 1.10 | 1.05 | 1.09 | 1.02 | 1.07 | 1.05 | 1.03 |
| Gly | 1.06 | 1.08 | 1.42*** | 1.29*** | 0.98 | 0.92(*) | 1.09*** | 1.09** |
| His | 1.03 | 1.07 | 0.97 | 1.08 | 0.94 | 0.88 | 1.07 | 1.06 |
| Ile | 1.03 | 1.03 | 1.17(*) | 1.27(*) | 1.14**(*) | 1.19**(*) | 1.07* | 1.12* |
| Leu | 1.11**(*) | 1.08 | 1.10 | 1.18(**) | 1.15*** | 1.15**(*) | 1.07** | 1.11**(*) |
| Lys | — | — | 1.07 | 1.07 | 0.92(*) | 0.91 | 1.08* | 1.15**(*) |
| Phe | 1.01 | 0.98 | 1.07 | 1.06 | 1.16** | 1.10 | 1.05 | 1.08 |
| Pro | 1.03 | 1.06 | 1.09 | 1.08 | 1.08(*) | 1.09 | 0.98 | 1.00 |
| Ser | 1.36*** | 1.41*** | 1.25*** | 1.27*** | 1.01 | 1.04 | 1.22*** | 1.32*** |
| Thr | 1.17*** | 1.15*(*) | 1.00 | 1.02 | 1.06 | 1.03 | 1.13*** | 1.12** |
| Tyr | 0.92 | 0.86 | 1.09 | 1.08 | 0.94 | 0.89 | — | — |
| Val | 0.88*** | 0.89* | 1.10 | 1.20(*) | 1.16*** | 1.14*(*) | 1.09**(*) | 1.14*** |
| Overall | 1.06*** | 1.07*** | 1.10*** | 1.11*** | 1.04*** | 1.03** | 1.10*** | 1.13*** |
NOTE.—Significance levels in parentheses disappear after correction for multiple testing.Whole, odds ratio for whole protein sequences; nonlinker, odds ratio for sequences without domain boundary region; —, no optimal codon.
*P < 0.05; **P < 0.01; ***P < 0.001.
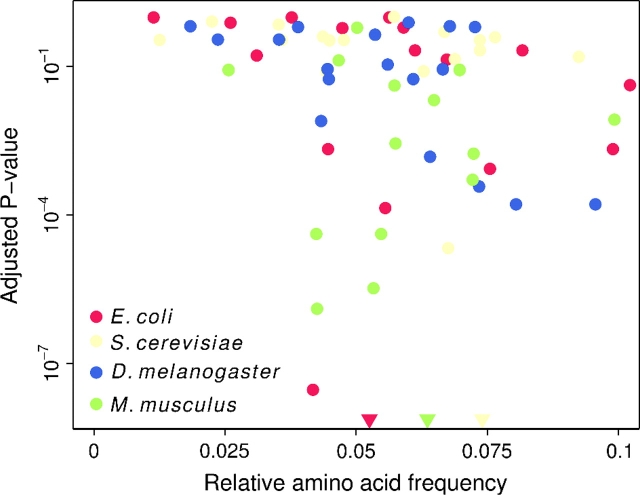
Why did some amino acids show a signal and others did not? We found no clear pattern related to amino acid biochemistry, such as polarity or volume. Most amino acids showed a signal in at least one species. Instead, we found that amino acid frequency was the best predictor of a significant association between codon optimality and solvent exposure. We observed a negative correlation between the significance level (P value after correction for multiple testing) from the Mantel–Haenszel test and the relative amino acid frequency (Spearman's ρ = − 0.33,P = 0.007, data of all four species pooled; see also fig. 2). This finding suggests that the absence of a significant association for some amino acids is likely caused by lack of statistical power rather than by a specific biochemical mechanism.
FIG 2.—
Mantel–Haenszel P value as a function of relative use frequency of each amino acid. The P value is adjusted for multiple testing (Benjamini and Hochberg 1995). Triangles indicate three data points that fall below the bottom of the graph.
For each species, we also used the Mantel–Haenszel procedure to combine all 2 × 2 contingency tables for all genes and all amino acids into a single overall odds ratio. This analysis corresponds to Drummond and Wilke (2008)‘s analysis but using buried sites instead of evolutionary conserved sites. We found a statistically significant association between optimal codons and buried sites in all species (table 3). These results were not strongly dependent on solvent-accessibility cutoff used to identify buried residues (table S3).
To control for evolutionary conservation, we tested for an association between optimal codons and buried sites considering only evolutionarily conserved residues in each species. The results remained largely unchanged from the results including all residues (table S4).
Because many ribosomal proteins contain natively unstructured regions, which assume their structure only upon binding other parts of the ribosome, we also repeated the association test on a data set excluding all ribosomal proteins. Our full data set contained 40 ribosomal proteins in E. coli, 29 in yeast, 22 in fly, and 14 in mouse. The results remained largely unchanged after excluding these genes (table S5).
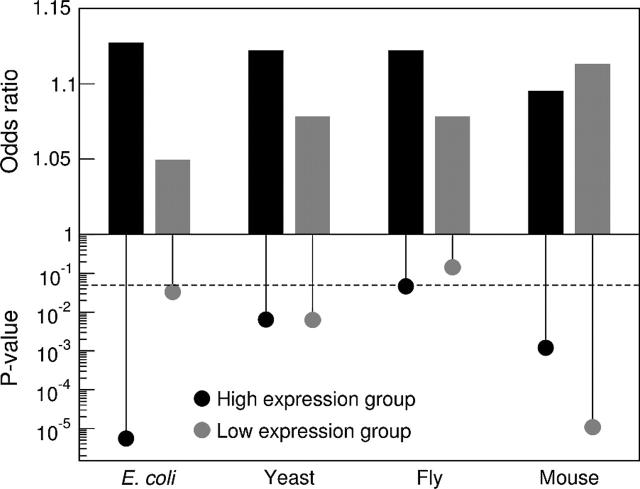
To determine if the association between optimal codons and buried sites was affected by expression level, we calculated the overall odds ratio separately for the highest (top 25%) and lowest (bottom 25%) expressed genes (see fig. 3). In all species except mouse, the overall odds ratio for the highest expressed genes tended to be higher than the one for the lowest expressed genes. However, with the exception of fly, which had the smallest sample size, the overall odds ratio was significantly larger than 1.0 even for genes with low expression level. Thus, highly expressed genes seem to show a stronger association between optimal codons and buried sites than genes with low expression level, but even the latter genes do show a significant association. This result mirrors the general observation that evolutionary constraints appear to increase with gene expression level (Duret and Mouchiroud 2000, Pal et al. 2001, Lemos et al. 2005, Drummond et al. 2006, Wolf et al. 2006, Eames and Kortemme 2007, Drummond and Wilke 2008).
FIG 3.—
The overall joint odds ratio Ojoint and the corresponding P value for the 25% highest and lowest expressed genes in all organisms. The dashed line denotes the significance level of α = 0.05.
Codon Optimality Correlates Negatively with Solvent Accessibility
The Mantel–Haenszel procedure properly controls for potentially confounding effects of differing codon or amino acid usage frequencies among genes. Its main drawback is that it requires categorical data, such as a classification of all residues into buried or exposed, or of all codons into optimal or nonoptimal. Solvent accessibility and codon optimality are continuous quantities, and by forcing them into dichotomous categories, we may be losing statistical power.
We devised a new statistical test in the spirit of the Mantel–Haenszel procedure but that made use of the specific values of codon optimality and solvent accessibility for each residue. For each amino acid in each gene, we separately calculated the Pearson correlation coefficient between the codon optimality of all codons encoding this amino acid and the solvent accessibility of the amino acid in the 3D protein structure. As test statistic, we used the mean of all these correlation coefficients. We calculated the sampling distribution of this statistic by randomly permuting synonymous codons within each gene (see Materials and Methods). We then carried out one-tailed tests. Our alternative hypothesis was that the mean correlation coefficient should be more negative than expected by chance if optimal codons associate with low solvent accessibility.
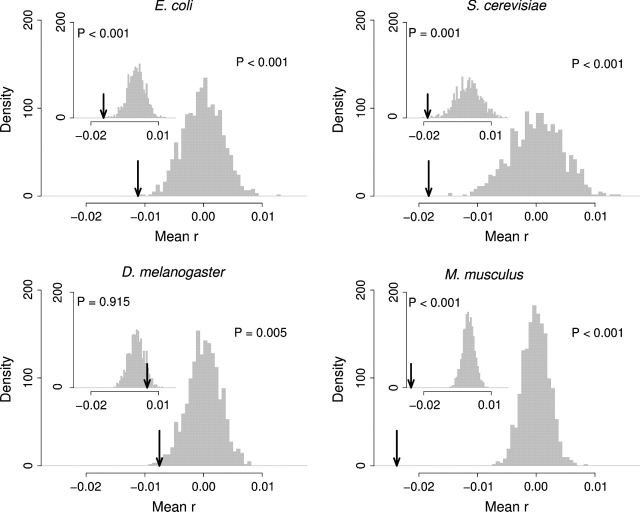
When we combined the correlation coefficients for all amino acids, we found that, for all organisms, we could reject the null hypothesis of no significant association between codon optimality and solvent accessibility. We found P < 0.001 for E. coli, P < 0.001 for yeast, P = 0.005 for fly, and P < 0.001 for mouse (fig. 4). The analysis for individual amino acids largely mirrored our Mantel–Haenszel results (fig. S3). However, the statistical power of the association test on continuous variables seemed to be generally lower than that of the Mantel–Haenszel procedure. In general, if we found a significant result with the association test on continuous variables, we also found it in the Mantel–Haenszel procedure, but the reverse was not true in all cases.
FIG 4.—
Test for association between codon optimality and solvent accessibility. The black arrows indicate the mean correlation coefficient between these two quantities over all amino acids and all genes. The gray histograms show the sampling distribution of the same quantity under the null hypothesis of no association. The main figure of each panel shows the results for complete genes, and the inset shows the results when interdomain linker regions are excluded.
The advantage of the association test on continuous variables is that we could employ it also for amino acids for which we could not clearly identify optimal codons. These amino acids include Lys for E. coli and Cys, Ala, and Tyr for mouse. Of these four, Cys in E. coli showed a marginally significant result and Ala in mouse showed a strongly significant result (fig. S3).
Codon Optimality Correlates with Structural Importance
So far, we tested for an association between optimal codons and buried sites. Our reasoning was that mutations at buried sites are more disruptive than mutations at exposed sites and that therefore buried sites should be more sensitive to translation errors. An alternative, and more direct, way of assessing whether a site is sensitive to mutation is to determine the distribution of free energy changes (ΔΔG values) that substitutions at this site effect. Mutations with negative ΔΔG stabilize the protein fold and should typically not have deleterious effects. Mutations with a small positive ΔΔG are mildly destabilizing. Whether such mutations will be disruptive or not is hard to predict. But once ΔΔG exceeds 2–3 kcal/mol, the mutation is almost certainly disruptive. Thus, as a measure of a site's sensitivity to substitutions, we calculated ΔΔG values for all 19 possible amino acid substitutions at that site and then determined the fraction of these substitutions with ΔΔG > 3.0 kcal/mol. We refer to this fraction as the “structural importance” of the site because it assesses the likelihood that a mutation at this site is structurally disruptive.
Our hypothesis was that if selection for translational accuracy acts to minimize mistranslation-induced protein misfolding then sites with higher structural importance should associate with more optimal codons and vice versa. By classifying sites at which at least two mutations had ΔΔG > 3.0 kcal/mol as important sites and all other sites as unimportant sites, we could employ the Mantel–Haenszel procedure to determine whether optimal codons associated with structurally important sites. Our results were similar to our previous results considering buried and exposed sites. In all organisms, the overall joint odds ratio was significantly larger than 1.0 (table S6). Our results for individual amino acids were also largely consistent with those obtained for buried/exposed sites, but there were some differences. For example, Glu in E. coli and Cys in yeast showed a significant association between optimal codons and structurally important sites but not between optimal codons and buried sites. By contrast, in fly and mouse, we mostly found the opposite result that several amino acids showed a significant association between optimal codons and buried sites but not between optimal codons and structurally important sites.
We also carried out the test of association between continuous variables. Because we expected codon optimality to increase with structural importance, we calculated one-tailed P values for the right tail of the sampling distribution of the mean correlation coefficient. We found a significant association between optimal codons and structurally important sites in yeast (P < 0.001) and mouse (P < 0.001) but not in E. coli (P = 0.230) or fly (P = 0.230) (fig. S4). When considering the results for individual amino acids (fig. S5), we found again that they largely agreed with those of the Mantel–Haenszel procedure on the same data (table S6) but that the association test on continuous variables seemed to be overall less powerful. However, there were a few notable exceptions. Gln in mouse showed a highly significant association when considering continuous variables but no association under the Mantel–Haenszel procedure. For Ser in fly, optimal codons seemed to associate with structurally unimportant sites when considering continuous variables (a right-tailed P value of 1 corresponds to a left-tailed P value of < 0.001), but we found no such signal under the Mantel–Haenszel procedure.
Nonrandom Pattern in Nonlinker Regions
Thanaraj and Argos (1996b) reported that nonoptimal codons are overrepresented in linker regions between domains. Because linker regions are generally solvent exposed and less sensitive to amino acid substitutions, an excess of nonoptimal codons in these regions could lead to an apparent excess of optimal codons at buried or structurally important sites. To exclude the possibility that our results are caused by abundant nonoptimal codons in interdomain linkers, we repeated all our analyses but excluded linker regions (see Materials and Methods). The new results were largely unchanged from the previous ones. Tables 3 and S6 and figures 4 and S4 show a side-by-side comparisons of the same results for entire proteins and proteins with interdomain linkers excluded. Figures S6 and S7 show the same analyses as figures S3 and S5, respectively, but with interdomain linkers excluded. There were some cases in which results disappeared, for example, in table 3 for Leu and Ala in E. coli and for Phe in fly. Yet by and large, we could confirm that even when we excluded interdomain linker regions, we found a significant association between optimal codons and either buried sites or structurally important sites.
DISCUSSION
We examined the relationship between codon usage bias and protein structure in the genomes of four model organisms. We found that optimal codons tend to be associated with buried sites. In E. coli, yeast, and fly, the association was stronger in highly expressed genes than in genes with low expression level. The effect was present in most codon families in at least one organism. We found no clear relationship between the biophysical properties of the encoded amino acids and the presence or absence of an association between optimal codons and buried sites. Instead, the best predictor for a significant association was amino acid frequency. We also found that optimal codons tend to be associated with sites for which computational modeling predicts that substitutions are destabilizing.
This study is not the first to provide evidence that codon usage bias is affected by protein structure; previous studies include Thanaraj and Argos (1996a), Orešič and Shalloway (1998), Xie and Ding (1998), Orešič et al. (2003), and Gu et al. (2004). However, many of the previous studies suffer from statistical limitations such as not correcting for multiple testing or not controling for confounding effects of amino acid usage frequencies. Most previous studies suggest that the relationship between protein structure and codon usage bias is rather limited. For example, in a study of E. coli and human, Orešič and Shalloway (1998) found only a single codon each that associated with structural features of the encoded proteins. In human, this codon is GAU, and it is preferred at the N termini of α-helices. Most previous studies focused on protein secondary structure, whereas the structural features we considered here were solvent accessibility and structural importance (i.e., ΔΔG values). We believe that we found a comparatively strong and pervasive signal in part because of this choice. The extent to which mutations tend to disrupt protein folding and function depends only weakly on secondary structure and much more strongly on solvent accessibility (Goldman et al. 1998, Bustamante et al. 2000, Dean et al. 2002, Bloom, Labthavikul, et al. 2006).
What is the biophysical mechanism that links codon usage bias to protein structure? Experimental work has focused on the hypothesis that ribosome kinetics may affect protein folding (Komar et al. 1999, Cortazzoetal2002, Goymer 2007, Komar2007, Kimchi-Sarfatyetal2007). A cluster of suboptimal codons might stall the ribosome and as a consequence either facilitate or disrupt cotranslational folding. Thanaraj and Argos (1996b) argued that rare codons associate with interdomain linkers because the slowdown of the ribosome when translating these linker regions would allow the individual domains to fold independently. Yet more recently, Widmann et al. (2008) showed that evolutionarily conserved (and thus presumably important) rare codons are not restricted to interdomain linker regions. To verify that our results were not caused by an excess of rare codons in solvent-exposed linker regions, we redid our analysis on a restricted data set that excluded all interdomain linker regions. We again found an association between optimal codons and structurally sensitive sites. Thus, although nonoptimal codons may or may not be preferred in interdomain linker regions, our results are not caused by the codon usage in these linkers.
Most previous work has focused on the interplay between translation and folding kinetics, but translation fidelity may be as important or more so in shaping synonymous codon usage. According to the mistranslation-induced misfolding hypothesis (Drummond and Wilke 2008), selection for translational accuracy should lead to an excess of high-fidelity codons at sites at which translation errors would be particularly destabilizing. Our results are broadly consistent with this hypothesis, even though our evidence is only indirect. Few studies have attempted the direct measurement of codon fidelity under translation or of the propensity of mutations at different sites to cause misfolding. Thus, we had no comprehensive data set for either of these quantities and had to use proxies for both.
We equated high-fidelity codons with optimal codons and identified as optimal those codons that were significantly more frequent in highly expressed genes than in genes with low expression level. Because the sets of optimal codons we determined in this way were largely consistent with sets of optimal codons determined by counts of tRNA genes (Ikemura 1985, Moriyama and Powell 1997, Man and Pilpel 2007, Drummond and Wilke 2008), we believe that our optimal codons are by and large the high-fidelity codons of the respective organism. However, we cannot be certain that we correctly identified high-fidelity codons in all cases. In fact, for the two amino acids for which optimal codons were associated with exposed sites in our analysis (Ala and Val in E. coli), the codons we determined to be optimal may be of low fidelity. One issue that may arise in this context is that of speed-accuracy tradeoffs. The most rapidly translated codon may not be the most accurately translated one or vice versa because speed should be determined primarily by the absolute number of tRNA copies in a cell, whereas accuracy should depend on the relative abundance of the cognate tRNA compared with competing tRNAs. If an organism experiences both selection for translation speed and translational accuracy then it is possible that the most rapidly translated codon is the most abundant one in highly expressed genes but that the most accurately translated codon is preferred at sites at which translation errors need to be avoided.
Our analysis also assumes that all genes in an organism have the same optimal codons. This assumption may be violated if tRNA pools vary substantially over time or among tissues in multicellular organisms. Such differences have indeed been reported (Dong et al. 1996, Dittmar et al. 2006), but they do not appear to be large enough to invalidate our approach. Nevertheless, a future study could try to obtain more accurate, gene-specific codon optimality values.
As a measure of the extent to which translation errors at a site may lead to misfolding, we used two quantities, the solvent-accessible surface area and the site's structural importance as measured by the computationally predicted stability effects (ΔΔG values) of mutations at that site. Both of these quantities can be calculated only if an accurate 3D crystal structure is available. Because the number of crystal structures for proteins of a specific organism remains limited, we augmented our data sets with crystal structures from homologous proteins. Consequently, for many genes in our data sets, solvent accessible surface areas and ΔΔG values are only estimates. To assess how reliable these estimates are, we carried out a controlled analysis of how these quantities change with decreasing sequence identity among homologs. We found that both remain highly predictive even if the homologs have diverged substantially (fig. S2). We also found that solvent-accessible surface area is generally more conserved among homologs than ΔΔG values are.
We predicted ΔΔG values using the default energy function of the Rosetta ΔΔG module. This energy function was not necessarily optimized for the wide range of different protein structures to which we applied it. However, because we were using the ΔΔG predictions only to find sites at which substitutions have large disruptive effects, such as would be caused by steric clashes of the side chains, the ΔΔG predictions should be reasonably accurate nevertheless.
Previous works (Akashi 1994, Stoletzki and Eyre-Walker 2007, Drummond and Wilke 2008) studied selection for translational accuracy using the categorical Mantel–Haenszel procedure and we followed the same strategy here. But because the quantities we studied are not inherently categorical, we also devised an association test on continuous variables based on stratified correlation coefficients. The two statistical procedures yielded overall similar results, but the test on continuous variables seemed to be less powerful. Yet, this test has several advantages that make it worthy to pursue. First, the results of the categorical test depend on the arbitrary choice by which continuous variables are classified into categories. For example, we designated sites as buried if their relative solvent accessibility fell below a 25% cutoff. A different choice of cutoff led to somewhat (if only slightly) different results (table S3). The test on continuous variables does not suffer from this problem. Second, according to the criterion we chose to identify optimal codons, we could not select optimal codons for a few amino acids in some species. Thus, we had to exclude these amino acids from the categorical analysis but could include them in the continuous analysis.
The overall odds ratios we obtained from the Mantel–Haenszel procedure are of comparable magnitude, but generally somewhat smaller, than the odds ratios measuring the association between optimal codons and evolutionarily conserved sites (table 1 in Drummond and Wilke 2008). The biggest deviation arises in fly where we found an odds ratio of 1.04, whereas Drummond and Wilke (2008) found 1.36. Some of these differences are likely caused by the limitations on quality and quantity of structural data. Fly in particular had the lowest fraction of closely matching crystal structures (fig. S1). An alternative explanation for the smaller odds ratios in our study could be that a significant proportion of sites under translational accuracy selection are functionally important rather than structurally important and that the criterion of evolutionary conservation accurately identifies these sites. Future work could try to disentangle structural and functional constraints by assembling a data set of proteins for which structurally important sites are known and then testing whether optimal codons associate more strongly with structurally important sites, functionally important sites, or possibly the joint set of both structurally and functionally important sites.
SUPPLEMENTARY MATERIAL
Supplementary tables S1–S6 and figures S1–S7 are available online as supplementary material at Molecular Biology and Evolution (http://www.mbe.oxfordjournals. org/).
Acknowledgments
We would like to thank D. Allan Drummond for stimulating discussions. This work was supported in part by NIH grant R01 AI065960. The University of Texas provided computing resources.
References
- Akashi H. Synonymous codon usage in Drosophila melanogaster: natural selection and translational accuracy. Genetics. 1994;136:927–935. doi: 10.1093/genetics/136.3.927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akashi H, Eyre-Walker A. Translational selection and molecular evolution. Curr Opin Genet Dev. 1998;8:688–693. doi: 10.1016/s0959-437x(98)80038-5. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Series B. 1995;57:289–300. [Google Scholar]
- Bloom JD, Drummond DA, Arnold FH, Wilke CO. Structural determinants of the rate of protein evolution in yeast. Mol Biol Evol. 2006;23:1751–1761. doi: 10.1093/molbev/msl040. [DOI] [PubMed] [Google Scholar]
- Bloom JD, Labthavikul ST, Otey CR, Arnold FH. Protein stability promotes evolvability. Proc Natl Acad Sci USA. 2006;103:5869–5874. doi: 10.1073/pnas.0510098103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloom JD, Silberg JJ, Wilke CO, Drummond DA, Adami C, Arnold FH. Thermodynamic prediction of protein neutrality. Proc Natl Acad Sci USA. 2005;102:606–611. doi: 10.1073/pnas.0406744102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante CD, Townsend JP, Hartl DL. Solvent accessibility and purifying selection within proteins of Escherichia coli and Salmonella enterica. Mol Biol Evol. 2000;17:301–308. doi: 10.1093/oxfordjournals.molbev.a026310. [DOI] [PubMed] [Google Scholar]
- Chamary JV, Hurst LD. Biased codon usage near intron-exon junctions: selection on splicing enhancers, splice-site recognition or something else? Trends Genet. 2005a;21:256–259. doi: 10.1016/j.tig.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Chamary JV, Hurst LD. Evidence for selection on synonymous mutations affecting stability of mRNA secondary structure in mammals. Genome Biol. 2005b;6:R75. doi: 10.1186/gb-2005-6-9-r75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeron JM. Selective and mutational patterns associated with gene expression in humans: influences on synonymous composition and intron presence. Genetics. 2004;167:1293–1304. doi: 10.1534/genetics.104.026351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortazzo P, Cervenansky C, Marin M, Reiss C, Ehrlich R, Deana A. Silent mutations affect in vivo protein folding in Escherichia coli. Biochem Biophys Res Commun. 2002;293:537–541. doi: 10.1016/S0006-291X(02)00226-7. [DOI] [PubMed] [Google Scholar]
- Covert MW, Knight EM, Reed JL, Herrgard MJ, Palsson BO. Integrating high-throughput and computational data elucidates bacterial networks. Nature. 2004;429:92–96. doi: 10.1038/nature02456. [DOI] [PubMed] [Google Scholar]
- Creighton TE. Proteins: structures and molecular properties. In: York New., editor. Freeman; 1992. 2. [Google Scholar]
- Dean AM, Neuhauser C, Grenier E, Golding GB. The pattern of amino acid replacements in α/β-barrels. Mol Biol Evol. 2002;19:1846–1864. doi: 10.1093/oxfordjournals.molbev.a004009. [DOI] [PubMed] [Google Scholar]
- Dittmar KA, Goodenbour JM, Pan T. Tissue-specific differences in human transfer RNA expression. PLoS Genet. 2:e221. 2006 doi: 10.1371/journal.pgen.0020221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong HJ, Nilsson L, Kurland CG. Co-variation of tRNA abundance and codon usage in Escherichia coli at different growth rates. J Mol Biol. 1996;260:649–663. doi: 10.1006/jmbi.1996.0428. [DOI] [PubMed] [Google Scholar]
- Drummond DA, Raval A, Wilke CO. A single determinant dominates the rate of yeast protein evolution. Mol Biol Evol. 2006;23:327–337. doi: 10.1093/molbev/msj038. [DOI] [PubMed] [Google Scholar]
- Drummond DA, Wilke CO. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell. 2008;134:341–352. doi: 10.1016/j.cell.2008.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duret L. Evolution of synonymous codon usage in metazoans. Curr Opin Genet Dev. 2002;12:640–649. doi: 10.1016/s0959-437x(02)00353-2. [DOI] [PubMed] [Google Scholar]
- Duret L, Mouchiroud D. Determinants of substitution rates in mammalian genes: expression pattern affects selection intensity but not mutation rate. Mol Biol Evol. 2000;17:68–74. doi: 10.1093/oxfordjournals.molbev.a026239. [DOI] [PubMed] [Google Scholar]
- Eames M, Kortemme T. Structural mapping of protein interactions reveals differences in evolutionary pressures correlated to mRNA level and protein abundance. Structure. 2007;15:1442–1451. doi: 10.1016/j.str.2007.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar RC. Muscle: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman N, Thorne JL, Jones DT. Assessing the impact of secondary structure and solvent accessibility on protein evolution. Genetics. 1998;149:445–458. doi: 10.1093/genetics/149.1.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goymer P. Synonymous mutations break their silence. Nat Rev Genet. 2007;8:92. [Google Scholar]
- Greene LH, Lewis TE, Addou S, et al. The CATH domain structure database: new protocols and classification levels give a more comprehensive resource for exploring evolution. Nucleic Acids Res. 14 co-authors. 2007;35:D291–D297. doi: 10.1093/nar/gkl959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu W, Zhou T, Ma J, Sun X, Lu Z. The relationship between synonymous codon usage and protein structure in Escherichia coli and Homo sapiens. Biosystems. 2004;73:89–97. doi: 10.1016/j.biosystems.2003.10.001. [DOI] [PubMed] [Google Scholar]
- Guo HH, Choe J, Loeb LA. Protein tolerance to random amino acid change. Proc Natl Acad Sci USA. 2004;101:9205–9210. doi: 10.1073/pnas.0403255101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoede C, Denamur E, Tenaillon O. Selection acts on DNA secondary structures to decrease transcriptional mutagenesis. PLoS Genetics. 2:e176. 2006 doi: 10.1371/journal.pgen.0020176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holstege FCP, Jennings E, Wyrick JJ, Lee TI, Hengartner CJ, Green MR, Golub TR, Lander ES, Young RA. Dissecting the regulatory circuitry of a eukaryotic genome. Cell. 1998;95:717–728. doi: 10.1016/s0092-8674(00)81641-4. [DOI] [PubMed] [Google Scholar]
- Ikemura T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the E. coli translational system. J Mol Biol. 1981;151:389–409. doi: 10.1016/0022-2836(81)90003-6. [DOI] [PubMed] [Google Scholar]
- Ikemura T. Codon usage and tRNA content in unicellular and multicellular organisms. Mol Biol Evol. 1985;2:13–34. doi: 10.1093/oxfordjournals.molbev.a040335. [DOI] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Kawabata T, Fukuchi S, Homma K, Ota M, Araki J, Ito T, Ichiyoshi N, Nishikawa K. GTOP: a database of protein structures predicted from genome sequence. Nucleic Acids Res. 2002;30:294–298. doi: 10.1093/nar/30.1.294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimchi-Sarfaty C, Oh JM, Kim IW, Sauna ZE, Calcagno AM, Ambudkar SV, Gottesman MM. A “silent” polymorphism in the mdr1 gene changes substrate specificity. Science. 2007;315:525–528. doi: 10.1126/science.1135308. [DOI] [PubMed] [Google Scholar]
- Komar AA. SNPs, silent but not invisible. Science. 2007;315:466–467. doi: 10.1126/science.1138239. [DOI] [PubMed] [Google Scholar]
- Komar AA, Lesnik T, Reiss C. Synonymous codon substitutions affect ribosome traffic and protein folding during in vitro translation. FEBS Lett. 1999;462:387–391. doi: 10.1016/s0014-5793(99)01566-5. [DOI] [PubMed] [Google Scholar]
- Kortemme T, Baker D. A simple physical model for binding energy hot spots in protein-protein complexes. Proc Natl Acad Sci USA. 2002;99:14116–14121. doi: 10.1073/pnas.202485799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kortemme T, Kim DE, Baker D. Computational alanine scanning of protein-protein interfaces. Science STKE. 219:l2. 2004 doi: 10.1126/stke.2192004pl2. [DOI] [PubMed] [Google Scholar]
- Koshi JM, Goldstein RA. Context-dependent optimal substitution matrices. Protein Eng. 1995;8:641–645. doi: 10.1093/protein/8.7.641. [DOI] [PubMed] [Google Scholar]
- Lavner Y, Kotlar D. Codon bias as a factor in regulating expression via translation rate in the human genome. Gene. 2005;345:127–138. doi: 10.1016/j.gene.2004.11.035. [DOI] [PubMed] [Google Scholar]
- Lemos B, Bettencourt BR, Meiklejohn CD, Hartl DL. Evolution of proteins and gene expression levels are coupled in Drosophila and are independently associated with mRNA abundance, protein length, and number of protein-protein interactions. Mol Biol Evol. 2005;22:1345–1354. doi: 10.1093/molbev/msi122. [DOI] [PubMed] [Google Scholar]
- Lichtarge O, Bourne HR, Cohen FE. An evolutionary trace method defines binding surfaces common to protein families. J Mol Biol. 1996;257:342–358. doi: 10.1006/jmbi.1996.0167. [DOI] [PubMed] [Google Scholar]
- Man O, Pilpel Y. Differential translation efficiency of orthologous genes is involved in phenotypic divergence of yeast species. Nat Genet. 2007;39:415–421. doi: 10.1038/ng1967. [DOI] [PubMed] [Google Scholar]
- Mantel N. Chi-square tests with one degree of freedom; extensions of the Mantel-Haenszel procedure. J Am Stat Assoc. 1963;58:690–700. [Google Scholar]
- Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst. 1959;22:719–748. [PubMed] [Google Scholar]
- Markiewicz P, Kleina LG, Cruz C, Ehret S, Miller JH. Genetic studies of the lac repressor. xiv. analysis of 4000 altered Escherichia coli lac repressors reveals essential and non-essential residues, as well as “spacers” which do not require a specific sequence. J Mol Biol. 1994;240:421–433. doi: 10.1006/jmbi.1994.1458. [DOI] [PubMed] [Google Scholar]
- Matthews BW. Structural and genetic analysis of protein stability. Annu Rev Biochem. 1993;62:139–160. doi: 10.1146/annurev.bi.62.070193.001035. [DOI] [PubMed] [Google Scholar]
- Mirny LA, Shakhnovich EI. Universally conserved positions in protein folds: reading evolutionary signals about stability, folding kinetics and function. J Mol Biol. 1999;291:177–196. doi: 10.1006/jmbi.1999.2911. [DOI] [PubMed] [Google Scholar]
- Mirny LA, Shakhnovich EI. Evolutionary conservation of the folding nucleus. J Mol Biol. 2001a;308:123–129. doi: 10.1006/jmbi.2001.4602. [DOI] [PubMed] [Google Scholar]
- Mirny LA, Shakhnovich EI. Protein folding theory: from lattice to all-atom models. Annu Rev Biophys Biomol Struct. 2001b;30:361–396. doi: 10.1146/annurev.biophys.30.1.361. [DOI] [PubMed] [Google Scholar]
- Moriyama EN, Powell JR. Codon usage bias and tRNA abundance in Drosophila. J Mol Evol. 1997;45:514–523. doi: 10.1007/pl00006256. [DOI] [PubMed] [Google Scholar]
- Noguchi T, Akiyama Y. PDB-REPRDB: a database of representative protein chains from the Protein Data Bank (PDB) in 2003. Nucleic Acids Res. 2003;31:492–493. doi: 10.1093/nar/gkg022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noguchi T, Matsuda H, Akiyama Y. PDB-REPRDB: a database of representative protein chains from the Protein Data Bank (PDB) Nucleic Acids Res. 2001;29:219–220. doi: 10.1093/nar/29.1.219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orengo CA, Michie AD, Jones DT, Swindells MB, Thornton JM. CATH: a hierarchic classification of protein domain structures. Structure. 1997;5:1093–1108. doi: 10.1016/s0969-2126(97)00260-8. [DOI] [PubMed] [Google Scholar]
- Orešič M, Dehn M, Korenblum D, Shalloway D. Tracing specific synonymous codon-secondary structure correlations through evolution. J Mol Evol. 2003;56:473–484. doi: 10.1007/s00239-002-2418-x. [DOI] [PubMed] [Google Scholar]
- Orešič M, Shalloway D. Specific correlations between relative synonymous codon usage and protein secondary structure. J Mol Biol. 1998;281:31–48. doi: 10.1006/jmbi.1998.1921. [DOI] [PubMed] [Google Scholar]
- Pal C, Papp B, Hurst LD. Highly expressed genes in yeast evolve slowly. Genetics. 2001;158:927–931. doi: 10.1093/genetics/158.2.927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmley J, Chamary J, Hurst L. Evidence for purifying selection against synonymous mutations in mammalian exonic splicing enhancers. Mol Biol Evol. 2006;23:301–309. doi: 10.1093/molbev/msj035. [DOI] [PubMed] [Google Scholar]
- R Development Core Team a language and environment for statistical computing. Vienna (Austria): R Foundation for Statistical Computing. ISBN 3-900051-07-0. 2008 R. [Google Scholar]
- Sasidharan R, Chothia C. The selection of acceptable protein mutations. Proc Natl Acad Sci USA. 2007;104:10080–10085. doi: 10.1073/pnas.0703737104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schueler-Furman O, Baker D. Conserved residue clustering and protein structure prediction. Proteins. 2003;52:225–235. doi: 10.1002/prot.10365. [DOI] [PubMed] [Google Scholar]
- Sharp PM, Tuohy T, Mosurski K. Codon usage in yeast: cluster analysis clearly differentiates highly and lowly expressed genes. Nucleic Acids Res. 1986;14:5125–5143. doi: 10.1093/nar/14.13.5125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stolc V, Gauhar Z, Mason C, et al. 12 co-authors. A gene expression map for the euchromatic genome of Drosophila melanogaster. Science. 2004;306:655–660. doi: 10.1126/science.1101312. [DOI] [PubMed] [Google Scholar]
- Stoletzki N. Conflicting selection pressures on synonymous codon use in yeast suggest selection on mRNA secondary structures. BMC Evol Biol. 2008;8:224. doi: 10.1186/1471-2148-8-224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoletzki N, Eyre-Walker A. Synonymous codon usage in Escherichia coli: selection for translational accuracy. Mol Biol Evol. 2007;24:374–381. doi: 10.1093/molbev/msl166. [DOI] [PubMed] [Google Scholar]
- Su AI, Wiltshire T, Batalov S, et al. 13 co-authors. A gene atlas of the mouse and human protein-encoding transcriptomes. Proc Natl Acad Sci USA. 2004;101:6062–6067. doi: 10.1073/pnas.0400782101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thanaraj TA, Argos P. Protein secondary structural types are differentially coded on messenger RNA. Protein Sci. 1996a;5:1973–1983. doi: 10.1002/pro.5560051003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thanaraj TA, Argos P. Ribosome-mediated translational pause and protein domain organization. Protein Sci. 1996b;5:1594–1612. doi: 10.1002/pro.5560050814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokuriki N, Stricher F, Schymkowitz J, Serrano L, Tawfik DS. The stability effects of protein mutations appear to be universally distributed. J Mol Biol. 2007;369:1318–1332. doi: 10.1016/j.jmb.2007.03.069. [DOI] [PubMed] [Google Scholar]
- Urrutia AO, Hurst LD. The signature of selection mediated by expression on human genes. Genome Res. 2003;13:2260–2264. doi: 10.1101/gr.641103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinogradov AE. DNA helix: the importance of being GC-rich. Nucleic Acids Res. 2003;31:1838–1844. doi: 10.1093/nar/gkg296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warnecke T, Hurst LD. Evidence for a trade-off between translational efficiency and splicing regulation in determining synonymous codon sauge in Drosophila melanogaster. Mol Biol Evol. 2007;24:2755–2762. doi: 10.1093/molbev/msm210. [DOI] [PubMed] [Google Scholar]
- Widmann M, Clairo M, Dippon J, Pleiss J. Analysis of the distribution of functionally relevant rare codons. BMC Genomics. 2008;9:207. doi: 10.1186/1471-2164-9-207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf YI, Carmel L, Koonin EV. Unifying measures of gene function and evolution. Proc Biol Sci. 2006;273:1507–1515. doi: 10.1098/rspb.2006.3472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright SI, Yau CB, Looseley M, Meyers BC. Effects of gene expression on molecular evolution in Arabidopsis thaliana and Arabidopsis lyrata. Mol Biol Evol. 2004;21:1719–1726. doi: 10.1093/molbev/msh191. [DOI] [PubMed] [Google Scholar]
- Xia X. Maximizing transcription efficiency causes codon usage bias. Genetics. 1996;144:1309–1320. doi: 10.1093/genetics/144.3.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie T, Ding D. The relationship between synonymous codon usage and protein structure. FEBS Lett. 1998;434:93–96. doi: 10.1016/s0014-5793(98)00955-7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.