A fast randomized algorithm for overdetermined linear least-squares regression

Abstract

We introduce a randomized algorithm for overdetermined linear least-squares regression. Given an arbitrary full-rank m × n matrix A with m ≥ n, any m × 1 vector b, and any positive real number ε, the procedure computes an n × 1 vector x such that x minimizes the Euclidean norm ‖Ax − b‖ to relative precision ε. The algorithm typically requires 𝒪((log(n)+log(1/ε))mn+n³) floating-point operations. This cost is less than the 𝒪(mn²) required by the classical schemes based on QR-decompositions or bidiagonalization. We present several numerical examples illustrating the performance of the algorithm.

Least-squares fitting has permeated the sciences and engineering after its introduction over two centuries ago (see, for example, ref. 1 for a brief historical review). Linear least-squares regression is fundamental in the analysis of data, such as that generated from biology, econometrics, engineering, physics, and many other technical disciplines.

Perhaps the most commonly encountered formulation of linear least-squares regression involves a full-rank m × n matrix A and an m × 1 column vector b, with m ≥ n; the task is to find an n × 1 column vector x such that the Euclidean norm ‖Ax − b‖ is minimized. Classical algorithms using QR-decompositions or bidiagonalization require

floating-point operations in order to compute x (see, for example, ref. 1 or Chapter 5 in ref. 2). The present article introduces a randomized algorithm that, given any positive real number ε, computes a vector x minimizing ‖Ax − b‖ to relative precision ε, that is, the algorithm produces a vector x such that

This algorithm typically requires

operations. When n is sufficiently large and m is much greater than n (that is, the regression is highly overdetermined), then the cost in Eq. 3 is less than the cost in Eq. 1. Furthermore, in the numerical experiments of Numerical Results, the algorithm of the present article runs substantially faster than the standard methods based on QR-decompositions.

The method of the present article is an extension of the methods introduced in refs. 3–5. Their algorithms and ours have similar costs; however, for the computation of x minimizing ‖Ax − b‖ to relative precision ε, the earlier algorithms involve costs proportional to 1/ε, whereas the algorithm of the present paper involves a cost proportional to log(1/ε) (see Eq. 3 above).

The present article describes algorithms optimized for the case when the entries of A and b are complex valued. Needless to say, real-valued versions of our schemes are similar. This article has the following structure: The first section sets the notation. The second section discusses a randomized linear transformation which can be applied rapidly to arbitrary vectors. The third section provides the relevant mathematical apparatus. The fourth section describes the algorithm of the present article. The fifth section illustrates the performance of the algorithm via several numerical examples. The sixth section draws conclusions and proposes directions for future work.

Notation

In this section, we set notational conventions employed throughout the present article.

We denote an identity matrix by Eq. 1. We consider the entries of all vectors and matrices in this article to be complex valued. For any vector x, we define ‖x‖ to be the Euclidean (l²) norm of x. For any matrix A, we define A* to be the adjoint of A, and we define the norm ‖A‖ of A to be the spectral (l²-operator) norm of A, that is, ‖A‖ is the greatest singular value of A. We define the condition number of A to be the l² condition number of A, that is, the greatest singular value of A divided by the least singular value of A. If A has at least as many rows as columns, then the condition number of A is given by the expression

For any positive integers m and n with m ≥ n, and any m × n matrix A, we will be using the singular value decomposition of A in the form

where U is an m × n matrix whose columns are orthonormal, V is an n × n matrix whose columns are orthonormal, and Σ is a diagonal n × n matrix whose entries are all nonnegative. We abbreviate “singular value decomposition” to “SVD” and “independent, identically distributed” to “i.i.d.”

For any positive integer m, we define the discrete Fourier transform F^(m) to be the complex m × m matrix with the entries

for j,k = 1,2,…,m−1,m, where $i=\sqrt{-1}$ and e = exp(1); if the size m is clear from the context, then we omit the superscript in F^(m), denoting the discrete Fourier transform by simply F.

Preliminaries

In this section, we discuss a subsampled randomized Fourier transform. Refs. 3–6 introduced a similar transform for similar purposes.

For any positive integers l and m with l ≤ m, we define the l × m SRFT to be the l × m random matrix

where G and H are defined as follows.

In Eq. 7, G is the l × m random matrix given by the formula

where S is the l × m matrix whose entries are all zeros, aside from a single 1 in column s_j of row j for j = 1,2,…,l−1,l, where s₁, s₂, …,s_l−1, s_l are i.i.d. integer random variables, each distributed uniformly over {1, 2, …, m−1, m}; moreover, F is the m × m discrete Fourier transform, and D is the diagonal m × m matrix whose diagonal entries d₁, d₂, …, d_m−1, d_m are i.i.d. complex random variables, each distributed uniformly over the unit circle. (In our numerical implementations, we drew s₁, s₂, …, s_l−1, s_l from {1, 2, …, m − 1, m} without replacement, instead of using i.i.d. draws.)

In Eq. 7, H is the m × m random matrix given by the formula

where Π and Π̃ are m × m permutation matrices chosen independently and uniformly at random, and Z and Z̃ are diagonal m × m matrices whose diagonal entries ζ₁, ζ₂, …, ζ_m−1, ζ_m and ζ̃₁,ζ̃₂,…,ζ̃_m−1,ζ̃_m are i.i.d. complex random variables, each distributed uniformly over the unit circle; furthermore, Θ and Θ̃ are the m × m matrices defined via the formulae

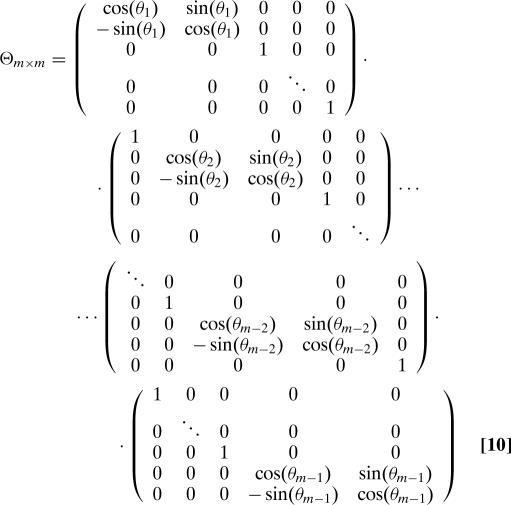and (the same as Eq. 10, but with tildes)

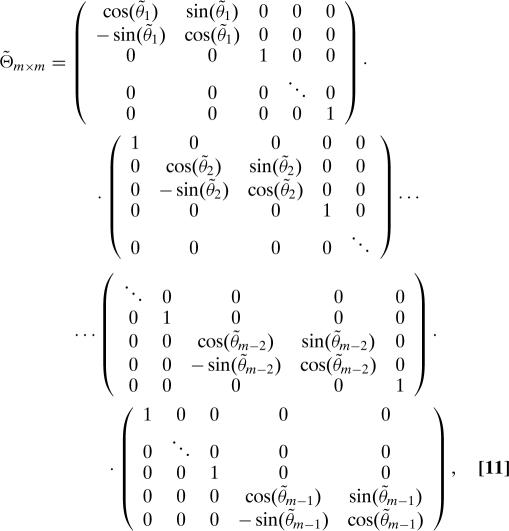where θ₁,θ₂,…,θ_m−2,θ_m−1,θ̃₁,θ̃₂…,θ̃_m−2,θ̃_m−1 are i.i.d. real random variables drawn uniformly from [0,2π]. We observe that Θ, Θ̃, Π, Π̃, Z, and Z̃ are all unitary, and so H is also unitary.

We call the transform T an “SRFT” for lack of a better term.

Remark 1. Our earlier articles, refs. 7 and 8, omitted the matrix H in the definition of the SRFT (Eq. 7). Numerical experiments indicate that including H improves the performance of the algorithm of the present article on sparse matrices.

The following lemma is similar to the subspace Johnson–Lindenstrauss lemma (Corollary 11) of ref. 4, and is proven (in a slightly different form) as Lemma 4.4 of ref. 8. The lemma provides a highly probable upper bound on the condition number of the product of the l × m matrix G defined in Eq. 8 and an independent m × n matrix U whose columns are orthonormal, assuming that l is less than m and is sufficiently greater than n².

Lemma 1. Suppose that α and β are real numbers >1, and l, m, and n are positive integers, such that

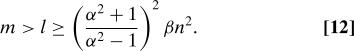Suppose further that G is the l × m random matrix defined in Eq.8. Suppose in addition that U is an m × n random matrix whose columns are orthonormal, and that U is independent of G.

Then, the condition number of GU is at most α with probability at least $1-\frac{1}{\beta }$.

The following corollary of Lemma 1 follows immediately from the fact that the random matrix H defined in Eq. 9 is unitary and independent of the random matrix G defined in Eq. 8. The corollary provides a highly probable upper bound on the condition number of the l × m SRFT (defined in Eq. 7) applied to an m × n matrix U whose columns are orthonormal, assuming that l is less than m and is sufficiently greater than n².

Corollary 1. Suppose that α and β are real numbers greater than 1, and l, m, and n are positive integers, such that Eq.12 holds. Suppose further that T is the l × m SRFT defined in Eq.7. Suppose in addition that U is an m × n matrix whose columns are orthonormal.

Then, the condition number of TU is at most α with probability at least $1-\frac{1}{\beta }$.

The following lemma states that, if A is an m × n matrix, b is an m × 1 vector, and T is the l × m SRFT defined in Eq. 7, then, with high probability, an n × 1 vector z minimizing ‖TAz − Tb‖ also minimizes ‖Az − b‖ to within a reasonably small factor. Whereas solving Az ≈ b in the least-squares sense involves m simultaneous linear equations, solving TAz ≈ Tb involves just l simultaneous equations. This lemma is modeled after similar results in refs. 3–5, and is proven (in a slightly different form) as Lemma 4.8 of ref. 8.

Lemma 2. Suppose that α and β are real numbers >1, and l, m, and n are positive integers, such that

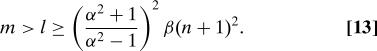Suppose further that T is the l × m SRFT defined in Eq.7. Suppose in addition that A is an m × n matrix, and b is an m × 1 vector. Suppose finally that z is an n × 1 vector minimizing the quantity

Then,

with probability at least $1-\frac{1}{\beta }$.

Mathematical Apparatus

In this section, we prove a theorem that (in conjunction with Corollary 1) guarantees that the algorithm of the present article is fast.

In the proof of Theorem 1 below, we will need the following technical lemma.

Lemma 3. Suppose that l, m, and n are positive integers such that m ≥ l ≥ n. Suppose further that A is an m × n matrix, and that the SVD of A is

where U is an m × n matrix whose columns are orthonormal, V is an n × n matrix whose columns are orthonormal, and Σ is a diagonal n × n matrix whose entries are all nonnegative. Suppose in addition that T is an l × m matrix, and that the SVD of the l × n matrix TU is

Then, there exist an n × n matrix P, and an l × n matrix Q whose columns are orthonormal, such that

Furthermore, if P is any n × n matrix, and Q is any l × n matrix whose columns are orthonormal, such that P and Q satisfy Eq.18, then

if, in addition, the matrices A and TU both have full rank (rank n), then there exists a unitary n × n matrix W such that

Proof: An example of matrices P and Q satisfying Eq. 18 such that the columns of Q are orthonormal is P=Σ̃Ṽ*ΣV* and Q = Ũ.

We now assume that P is any n × n matrix, and Q is any l × n matrix whose columns are orthonormal, such that P and Q satisfy Eq. 18. Combining Eqs. 18, 16, and 17 yields

Combining Eq. 21 and the fact that the columns of Q are orthonormal (so that Q*Q = 1) yields Eq. 19.

For the remainder of the proof, we assume that the matrices A and TU both have full rank. To establish Eq. 20, we demonstrate that the column spans of Q and Ũ are the same. It then follows from the fact that the columns of Q are an orthonormal basis for this column span, as are the columns of Ũ, that there exists a unitary n × n matrix W satisfying Eq. 20. We now complete the proof by showing that

Obviously, it follows from Eq. 21 that

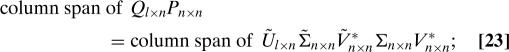we will simplify both sides of Eq. 23, in order to obtain Eq. 22.

It follows from the assumption that A and TU both have full rank that the matrices Σ and Σ̃ in the SVDs in Eqs. 16 and 17 are nonsingular, and so (as the unitary matrices V and Ṽ are also nonsingular)

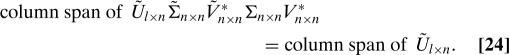Combining Eqs. 23, 24, and the fact that the column span of Ũ is n-dimensional (after all, the n columns of Ũ are orthonormal) yields that the column span of QP is n-dimensional. Combining this fact, the fact that the column span of QP is a subspace of the column span of Q, and the fact that the column span of Q is n-dimensional (after all, the n columns of Q are orthonormal) yields

Combining Eqs. 23, 24, and 25 yields Eq. 22, completing the proof.

The following theorem states that, given an m × n matrix A, the condition number of a certain preconditioned version of A corresponding to an l × m matrix T is equal to the condition number of TU, where U is an m × n matrix of orthonormal left singular vectors of A.

Theorem 1. Suppose that l, m, and n are positive integers such that m ≥ l ≥ n. Suppose further that A is a full-rank m × n matrix, and that the SVD of A is

Suppose in addition that T is an l × m matrix such that the l × n matrix TU has full rank.

Then, there exist an n × n matrix P, and an l × n matrix Q whose columns are orthonormal, such that

Furthermore, if P is any n × n matrix, and Q is any l × n matrix whose columns are orthonormal, such that P and Q satisfy Eq.27, then the condition numbers of AP⁻¹ and TU are equal.

Proof: Lemma 3 guarantees the existence of matrices P and Q satisfying Eq. 27 such that the columns of Q are orthonormal.

For the remainder of the proof, we assume that P is an n × n matrix, and Q is an l × n matrix whose columns are orthonormal, such that P and Q satisfy Eq. 27. Combining Eq. 19, Eq. 20, and the fact that the columns of Q are orthonormal (so that Q*Q = 1) yields

where W is the matrix from Eq. 20, and Σ̃ and Ṽ are the matrices from the SVD in Eq. 17. Combining Eq. 26, Eq. 28, and the fact that V, Ṽ, and W are unitary yields

Combining Eq. 29, the fact that Ṽ and W are unitary, the fact that the columns of U are orthonormal (so that U*U = 1), and the fact that Σ̃ is diagonal yields

and

Combining Eqs. 4, 30, and 31, and the SVD in Eq. 17 yields that the condition numbers of AP⁻¹ and TU are equal, completing the proof.

The Algorithm

In this section, we describe the algorithm of the present article, giving details about its implementation and computational costs.

Description of the Algorithm.

Suppose that m and n are positive integers with m ≥ n, A is a full-rank m × n matrix, and b is an m × 1 column vector. In this subsection, we describe a procedure for the computation of an n × 1 column vector x such that x minimizes ‖Ax − b‖ to arbitrarily high precision.

Rather than directly calculating the vector x minimizing ‖Ax − b‖, we will first calculate the vector y minimizing ‖Cy − b‖, where C = AP⁻¹ and y = Px, with an appropriate choice of an n × n matrix P; the matrix P is known as a preconditioning matrix. With an appropriate choice of P, the condition number of C is reasonably small, and so an iterative solver such as the conjugate gradient method will require only a few iterations in order to obtain y minimizing ‖Cy − b‖ to high precision. Once we have calculated y, we obtain x via the formula x = P⁻¹y.

To construct the preconditioning matrix P, we compute E = TA, where T is the l × m SRFT defined in Eq. 7, with m ≥ l ≥ n. We then form a pivoted QR-decomposition of E, computing an l × n matrix Q whose columns are orthonormal, an upper-triangular n × n matrix R, and an n × n permutation matrix Π, such that E = QR Π. We use the product P = RΠ as the preconditioning matrix. Fortuitously, because this matrix P is the product of an upper-triangular matrix and a permutation matrix, we can apply P⁻¹ or (P⁻¹)* to any arbitrary vector rapidly, without calculating the entries of P⁻¹ explicitly.

The condition number of C = AP⁻¹ is reasonably small with very high probability whenever l is sufficiently greater than n, due to Theorem 1 and Corollary 1; moreover, numerical experiments reported in Numerical Results suggest that the condition number of C is practically always less than 3 or so when l = 4n. Therefore, when l is sufficiently greater than n, the conjugate gradient method requires only a few iterations in order to compute y minimizing ‖Cy − b‖ to high precision; furthermore, the conjugate gradient method requires only applications of A, A*, P⁻¹, and (P⁻¹)* to vectors, and all of these matrices are readily available for application to vectors. Once we have calculated y, we obtain x minimizing ‖Ax − b‖ via the formula x = P⁻¹y.

There is a natural choice for the starting vector of the conjugate gradient iterations. Combining the fact that E = TA with Eqs. 14 and 15 yields that, with high probability, the n × 1 vector z minimizing ‖Ez − Tb‖ also minimizes ‖Az − b‖ to within a factor of 3, provided that l is sufficiently greater than n (in practice, l = 4n is sufficient). Thus, z is a good choice for the starting vector of the iterations. Moreover, combining the facts that E = QP and that the columns of Q are orthonormal yields that z = P⁻¹Q*Tb, providing a convenient means of computing z.

In summary, if ε is any specified positive real number, we can compute an n × 1 column vector x such that x minimizes ‖Ax − b‖ to relative precision ε, via the following five steps:

1. Compute E = TA, where T is the l × m SRFT defined in Eq. 7, with m ≥ l ≥ n. (See, for example, Subsection 3.3 of ref. 8 for details on applying the SRFT rapidly.)

2. Form a pivoted QR-decomposition of E from Step 1, computing an l × n matrix Q whose columns are orthonormal, an upper-triangular n × n matrix R, and an n × n permutation matrix Π, such that E = QR Π. (See, for example, Chapter 5 in ref. 2 for details on computing such a pivoted QR-decomposition.)

3. Compute the n × 1 column vector z = P⁻¹ (Q*(Tb)), where T is the l × m SRFT defined in Eq. 7, Q is the l × n matrix from Step 2 whose columns are orthonormal, and P = RΠ; R and Π are the upper-triangular and permutation matrices from Step 2. (See, for example, Subsection 3.3 of ref. 8 for details on applying the SRFT rapidly.)

4. Compute an n × 1 column vector y which minimizes ‖AP⁻¹y − b‖ to relative precision ε, via the preconditioned conjugate gradient iterations, where P = RΠ is the preconditioning matrix; R and Π are the upper-triangular and permutation matrices from Step 2. Use z from Step 3 as the starting vector. (See, for example, Algorithm 7.4.3 in ref. 1 for details on the preconditioned conjugate gradient iterations for linear least-squares problems.)

5. Compute x = P⁻¹y, where y is the vector from Step 4, and again P = RΠ; R and Π are the upper-triangular and permutation matrices from Step 2.

Cost.

In this subsection, we estimate the number of floating-point operations required by each step of the algorithm of the preceding subsection.

We denote by k the condition number of the preconditioned matrix AP⁻¹. The five steps of the algorithm incur the following costs:

1. Applying T to every column of A costs 𝒪(mnlog(l)).

2. Computing the pivoted QR-decomposition of E costs 𝒪(n²l).

3. Applying T to b costs 𝒪(mlog(l)). Applying Q* to Tb costs 𝒪(nl). Applying P⁻¹ = Π⁻¹ R⁻¹ to Q*Tb costs 𝒪(n²).

4. When l ≥ 4n², Eq. 15 guarantees with high probability that the vector z has a residual ‖Az − b‖ that is no greater than 3 times the minimum possible. When started with such a vector, the preconditioned conjugate gradient algorithm requires 𝒪(klog(1/ε)) iterations in order to improve the relative precision of the residual to ε (see, for example, formula 7.4.7 in ref. 1). Applying A and A* a total of 𝒪(klog(1/ε)) times costs 𝒪(mnklog(1/ε)). Applying P⁻¹ and (P⁻¹)* a total of 𝒪(klog(1/ε)) times costs 𝒪(n²klog(1/ε)). These costs dominate the costs of the remaining computations in the preconditioned conjugate gradient iterations.

5. Applying P⁻¹ = Π⁻¹ R⁻¹ to y costs 𝒪(n²).

Summing up the costs in the five steps above, we see that the cost of the entire algorithm is

The condition number k of the preconditioned matrix AP⁻¹ can be made arbitrarily close to 1, by choosing l sufficiently large. According to Theorem 1 and Corollary 1, choosing l ≥ 4n² guarantees that k is at most 3, with high probability.

Remark 2. Currently, our estimates require that l be at least 4n² in order to ensure with high probability that k is at most 3 and that the residual ‖Az − b‖ is no greater than three times the minimum possible. However, our numerical experiments indicate that it is not necessary for l to be as large as 4n² (though it is sufficient). Indeed, in all of our tests, choosing l = 4n produced a condition number k less than 3 and a residual ‖Az − b‖ no greater than three times the minimum possible residual. With l = 4n and k ≤ 3, the cost in Eq.32 becomes

Numerical Results

In this section, we describe the results of several numerical tests of the algorithm of the present article.

We use the algorithm to compute an n × 1 vector x such that x minimizes ‖Ax − b‖ to high precision, where b is an m × 1 unit vector, and A is the m × n matrix defined via the formula

in all experiments described below, U is obtained by applying the Gram–Schmidt process to the columns of an m × n matrix whose entries are i.i.d. centered complex Gaussian random variables, V is obtained by applying the Gram–Schmidt process to the columns of an n × n matrix whose entries are i.i.d. centered complex Gaussian random variables, and Σ is a diagonal n × n matrix, with the diagonal entries

for k = 1,2, …, n − 1,n. Clearly, the condition number k_A of A is

The m × 1 unit vector b is defined via the formula

where w is a random m × 1 unit vector orthogonal to the column span of A, and Ay is a vector from the column span of A such that ‖b‖ = 1.

We implemented the algorithm in Fortran 77 in double-precision arithmetic, and used the Lahey/Fujitsu Express v6.2 compiler. We used one core of a 1.86 GHz Intel Centrino Core Duo microprocessor with 1 GB of RAM. For the direct computations, we used the classical algorithm for pivoted QR-decompositions based on plane (Householder) reflections (see, for example, Chapter 5 in ref. 2).

Table 1 displays timing results with m = 32768 for various values of n; Table 2 displays the corresponding errors. Table 3 displays timing results with n = 256 for various values of m; Table 4 displays the corresponding errors.

Table 1.

Timings

m	n	l	t0	t	t0/t
32768	64	256	.14E1	.13E1	1.1
32768	128	512	.55E1	.27E1	2.0
32768	256	1024	.22E2	.59E1	3.7
32768	512	2048	.89E2	.15E2	5.7

Table 2.

Condition numbers after preconditioning and accuracies

m	n	l	k	i	εrel
32768	64	256	2.7	14	.120E—15
32768	128	512	2.9	14	.132E—15
32768	256	1024	2.9	14	.429E—15
32768	512	2048	2.9	13	.115E—14

Table 3.

Timings

m	n	l	t0	t	t0/t
2048	256	1024	.12E1	.71E0	1.6
4096	256	1024	.25E1	.94E0	2.6
8192	256	1024	.51E1	.14E1	3.5
16384	256	1024	.10E2	.26E1	4.1
32768	256	1024	.22E2	.50E1	4.4
65536	256	1024	.49E2	.11E2	4.4

Table 4.

Condition numbers after preconditioning and accuracies

m	n	l	k	i	εrel
2048	256	1024	2.2	4	.326E—10
4096	256	1024	2.6	5	.364E—10
8192	256	1024	2.7	6	.160E—10
16384	256	1024	2.8	7	.599E—11
32768	256	1024	2.9	8	.502E—11
65536	256	1024	2.9	8	.177E—11

The headings of the tables are as follows:

• m is the number of rows in the matrix A, as well as the length of the vector b, in ‖Ax − b‖.

• n is the number of columns in the matrix A, as well as the length of the vector x, in ‖Ax − b‖.

• l is the number of rows in the matrix T used in Steps 1 and 3 of the procedure in Description of the Algorithm.

• t₀ is the time in seconds required by the direct, classical algorithm.

• t is the time in seconds required by the algorithm of the present article.

• t₀/t is the factor by which the algorithm of the present article is faster than the classical algorithm.

• k is the condition number of AP⁻¹, the preconditioned version of the matrix A.

• i is the number of iterations required by the preconditioned conjugate gradient method to yield the requested precision ε_rel of 0.5E–14 or better in Table 2, and 0.5E–10 or better in Table 4.

• ε_rel is defined via the formula

  

  where k_A is the condition number of A given in Eq. 36, δ = |Ax − b‖ (x is the solution vector produced by the randomized algorithm), and

  

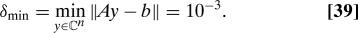
Remark 3. Standard perturbation theory shows that ε_relis the appropriately normalized measure of the precision produced by the algorithm; see, for example, formula 1.4.27 in ref.1.

The values for ε_rel and i reported in the tables are the worst (maximum) values encountered during 10 independent randomized trials of the algorithm, as applied to the same matrix A and vector b. The values for t reported in the tables are the average values over 10 independent randomized trials. None of the quantities reported in the tables varied significantly over repeated randomized trials.

The following observations can be made from the examples reported here, and from our more extensive experiments:

1. When m = 32768, n = 512, and the condition number of A is 10⁶, the randomized algorithm runs over five times faster than the classical algorithm based on plane (Householder) reflections, even at full double precision.

2. As observed in Remark 2, our choice l = 4n seems to ensure that the condition number k of the preconditioned matrix is at most 3. More generally, k seems to be smaller than a function of the ratio l/n.

3. The algorithm of the present article produces high precision at reasonably low cost.

Conclusions and Generalizations

This article provides a fast algorithm for overdetermined linear least-squares regression. If the matrices A and A* from the regression involving ‖Ax − b‖ can be applied sufficiently rapidly to arbitrary vectors, then the algorithm of the present article can be accelerated further. Moreover, the methods developed here for overdetermined regression extend to underdetermined regression.

The theoretical bounds in Lemma 1, Corollary 1, and Lemma 2 should be considered preliminary. Our numerical experiments indicate that the algorithm of the present article performs better than our estimates guarantee. Furthermore, there is nothing magical about the subsampled randomized Fourier transform defined in Eq. 7. In our experience, several other similar transforms appear to work at least as well, and we are investigating these alternatives (see, for example, ref. 9).