CONTEXT-SPECIFIC GENE REGULATIONS IN CANCER GENE EXPRESSION DATA

Abstract

Learning or inferring networks of genomic regulation specific to a cellular state, such as a subtype of tumor, can yield insight above and beyond that resulting from network learning-techniques which do not acknowledge the adaptive nature of the cellular system. In this study we show that Cellular Context Mining, which is based on a mathematical model of contextual genomic regulation, produces gene regulatory networks (GRNs) from steady-state expression microarray data which are specific to the varying cellular contexts hidden in the data; we show that these GRNs not only model gene interactions, but that they are also readily annotated with context-specific genomic information. We propose that these context-specific GRNs provide advantages over other techniques, such as clustering and Bayesian networks, when applied to gene expression data of cancer patients.

1. Introduction

Under normal conditions, a cell maintains a specific state by tightly controlling various molecules using a variety of regulatory mechanisms. In the face of environmental changes, a cell adjusts its regulatory mechanisms accordingly. Mutation or other types of damage that alter these regulatory mechanisms may erode this control and cause the cell to transition into another state significantly different from the prior normal state [5]. If the normal state is taken to be “healthy” and the altered state is taken to be “tumor”, for example, the regulatory functions must have been altered in significant ways to arrive at the “tumor” state. Since the way the system interprets and acts upon certain inputs is altered, we say that there is a change in cellular context.

Although, a tumor state of the cell is different from normal, the continuing proliferation and survival of cancer shows that such a state is indeed steady and maintained by complex regulatory behavior, albeit behavior different from the regulation maintaining the normal state. If one can learn from the contextual information which regulating mechanisms differ from context to context, then one can potentially discover the mechanisms that initiate and maintain complex, hard to treat diseases, such as cancer.

High throughput data collection methods, including gene expression microarrays, provide vast amount of data to study various aspects of cellular processes. Many methods and techniques exist to discern and model the regulatory behavior of cells, and each certainly has distinct advantages and disadvantages. For instance, traditional clustering approaches like k-means or hierarchical clustering can help group samples or genes, revealing possible novel subtypes of diseases or subclasses of molecular functions. Bayesian networks have been employed as models of genomic regulation; however they inherently assume homogeneity of samples and thus cannot model different “cellular contexts,” a serious limitation in disease like cancer that are not homogeneous.

In this paper, we will first describe a mathematical model of contextual genomic regulation [2], then a method based upon that model to identify cellular contexts [8], and also a method to construct context-specific gene regulatory networks. We apply the context mining method to gene expression data collected from a broad spectrum of cancer patients to reveal the modular and context-specific structure of gene regulatory networks hidden within the data. Finally, we conclude with the future direction of our work.

2. Methods

2.1. Mathematical Model for Contextual Genomic Regulation

It is important to select a mathematical model of a cell’s regulatory activity that accounts for regulation which very actively adjusts to differing internal and external environmental factors. Rather than models which infer connections between single genes, or between genes and phenotypes, we wish to select a model which can find subsets of samples where it is possible to attribute the states of all the members of a set of controlled genes to a single gene, or to a small set of regulatory genes which have expression properties that could be the source of control.

Recently, Dougherty et al. [2] introduced a mathematical model to approximate contextual genomic regulation. Formally, the model assumes there are m sets, G₁, G₂, …, G_m, of driver genes and m corresponding sets, S₁, S₂, …, S_m, of driven genes. For each set of driven genes S_j, there is a corresponding set G_j of driver genes regulating their behavior. G₁, G₂, …, G_m are not necessarily disjoint, neither are S₁, S₂, …, S_m necessarily disjoint; thus some driver gene may regulate more than one driven set, and some driven gene may be regulated by more than one driver gene set.

Two parameters are essential to the definition of the Contextual Genomic Regulation model. To define these parameters, consider a single set of driver genes G and its driven set of regulated genes S. For the set of drivers, still assuming a binary model (without loss of generality), there exists a state vector Y = (Y₁, Y₂, …, Y_q) where Y_k gives the value of g_k ∈ G. Let regulation by the driver genes be such that for a state y of the driver gene state vector Y (for G), when Y = y, all genes in S take on the value 1 with high probability.

Without loss of generality, let y be the state in which all members of Y have the value 1, denoted by 1; we will consider two situations for G, namely the situation where Y = 1 and the situation where Y ≠ 1. Similarly to Y for G, let X = (X₁, X₂, …, X_r) be the state vector for S where X_k gives the value of s_k ∈ S. In the first case, where Y = 1, although the driver is ON, there may be other regulatory activities within the context affecting the driven genes. For any driven gene s_k ∈ S, the conditional probability of s_k being ON is stated

$$P(X_k=1|\mathbf{Y}=\mathbf{1})=1-{\mathrm{\delta }}_k$$ (1)

where δ_k depends on the extent that contextual effects diminish the influence of the driver on the driven gene k. Hence, we refer to δ as the interference parameter. Now if Y ≠ 1, then the probability that some driven state X_k = 1 depends on contextual effects alone and not the effects of drivers is given by

$$P(X_k=1|\mathbf{Y}\ne \mathbf{1})={\eta }_k$$ (2)

where η_k depends on the extent that contextual effects outside of the drivers activate the driven genes. Hence, we refer to η_k as the crosstalk parameter. Further considerations of the model, including prediction accuracy and error representation are left to the original paper from Dougherty et al [2].

2.2. Identification of Cellular Contexts

Based on the above model, a cellular context is taken to be a set of genes, one or more of which function as drivers and the others as driven genes, which exhibit consistent transcriptional behavior across a subset of samples. Kim et al.[8] have proposed an algorithm to identify cellular contexts in gene expression data called Cellular Context Mining (CCM), where the genes in a context have significantly low interference and crosstalk values across the samples in the context. One major step in CCM, known as in-silico conditioning, is designed to be similar to a biologist manipulating the status of a gene or conditioning cells in an experiment with techniques including ectopic expression or gene silencing. With in-silico conditioning, the conditioning and the observations are not performed manually as the data is collected, but rather computationally after the data has been collected, hence the name. In this paper, we only consider a single gene driver at a time for conditioning, although the model allows for more. Each conditioning of a gene G_i (driver) on a value Y_i = y_i yields a subset of samples M_i within which a set of genes S_i = {g_i(1), … g_i(k)} appears to be tightly regulated, so a cellular context, therefore, is defined as C_i = { G_i, Y_i, S_i, M_i }. A re-sampling approach is used to determine the most statistically significant contexts represented in the data. Note that each context defines regulatory relationships G_i → g ∈ S_i, specific to M_i with G_i (driver) conditioned on a value Y_i = y_i. These implicit relationships lead to the construction of context specific regulatory networks.

The advantage of the context mining method is that it is built upon a biologically-inspired mathematical model, which gives strong meaning to the direction of the edges, i.e. one driver gene controlling another. Also, cellular context mining identifies each context with a corresponding driver gene and a set of samples, thereby ensuring the identification of a unique and statistically significant cellular context.

2.3. Context-Specific Gene Regulatory Networks

This study asserts that the gene regulatory networks (GRNs) produced by cellular context mining exhibit biological advantages absent in related techniques. We first note that driver g_j in the context C_j might be driven by a g_i in another context C_i. The chaining of such regulatory relationships g_i → g_j, in addition to implicit driver-driven relationships g_i → g ∈ S_i, results in an interesting graphical structure, representing relationships between contexts. We call this a context-specific gene regulatory network (GRN) as each regulatory relationship g_i → g ∈ S_i is specific to corresponding subset of samples, M_i.

A context-specific GRN differs from other representations not in its graphical structure, but by the fact that contexts connected to one another in a network differ in their sample composition. Formally, a context-specific GRN H is a pair H = (V, E), where V is a set of gene-representing vertices and E is a set of edges oriented from genes designated as drivers to genes designated as driven; thus H is a directed graph structure, though not necessarily acyclic, since a driven gene in one context may be a driver in another.

Again, note that each edge e_i* is specific to only its corresponding subset of samples, M_i, where e_i* refers to g_i → g ∈ S_i. This study shows that not only do context-specific GRNs report verifiable (and possibly novel) relationships between genes, but moreover the overall network structure groups itself into biologically meaningful and readily annotated context clusters. We applied this technique to the Target Now (TN) data set, which includes gene expression profiles of 146 patients with refractory cancer. Amalgamation of identified cellular contexts yielded a context-based network structure. Biological annotation according to sample composition of context clusters and literature verification of gene-disease relevance was carried out. This is unique among network learning techniques, which we illustrate with a comparison to Bayesian network approaches.

2.4. Bayesian Network Analysis

The Bayesian network model is a popular tool for modeling GRNs. Here, we used a hybrid algorithm of hierarchical clustering and order restriction (H CORE) [7] and sparse candidate (SC) [4] to learn genome-wide Bayesian network structures from a dataset. To compensate for the inadequate amount of observed data, we applied a k-fold bootstrapping in learning GRN with Bayesian network learning. The process of learning a GRN with bootstrapped learning of Bayesian networks can be described as follows.

With the dataset D, we built K subsets D₁, D₂, …, D_K by randomly selecting (k-1)/k proportion (for example, 90% if k = 10) of samples from D. We applied the hybrid algorithm of H-CORE and SC to learn a Bayesian network structure H_i from each D_i, and built K Bayesian network structures. The likelihood of an edge g_i → g_j to be in the final GRN H_BN was evaluated as follows:

$$L(g_i\to g_j)=\frac{{\displaystyle \sum _{\forall H_l\text{with}{g}_i\to g_j}\text{Pr}(H_l|{\mathit{D}}_l)}}{{\displaystyle \sum _{k=1}^K\text{Pr}(H_k|{\mathit{D}}_k)}}$$ (3)

We built the final GRN H_BN only with the edges having likelihood L larger than 0.5.

3. Results

3.1. Target Now Dataset

In applying the method described above, we used the gene expression profile of the Target Now (TN) study (http://www.targetnow.com). The motivation of the Target Now study is to determine whether patients with refractory cancer, who had not received a benefit from the standard types of treatment, could derive benefit from therapy with a drug not normally used for their particular form of cancer. The therapeutic to apply is one that has activity against a gene target that is found to be altered in that patient’s cancer. The cancer patients contributing to the TN study all have late stages cancer. Late stage cancer is very frequently de-differentiated, having lost a great deal of the specialized functions present in the tissue from which it arose. Due to this biological simplification of the system, those genes whose abundance is found to be altered from the normal tissue of origin and whose change of abundance is found in other refractory cancers (of the same type or of different types) may be representatives of changes that are necessary to support a particular molecular subtype of cancer.

The TN dataset, which consists of 17,085 unique probes from 146 patients with different types of refractory cancer, was used to learn context-specific GRNs. The dataset was pre-filtered based on transcription activity of each gene across the samples to be reduced to only 4,000 probes. The distribution of the 146 samples between different cancer tumor types is listed in Table 1.

Table 1.

Target Now Dataset Sample Distribution with the number of samples associated with different cancer tumor types.

Pancreas	20	Colon	7	Brain	4	Cervical	3	Esophagus	2
Ovarian	19	Kidney	6	Lung	4	Gallbladder	3	Skin	2
Melanoma	18	Salivary	6	Adipose	3	Rectal	3	T Cell	2
Breast	16	Adrenal	5	Bladder	3	Stomach	3	Thyroid	2

Single Sample: Appendix, Cartilage, Chondrosarcoma, Eccrine Adenocarcinoma, Glioma, Gastric, Ileum, Lymphoma, Monocytes, Prostate, Uterus, Rhabdomyosarcoma, Synovial Cell Sarcoma, Skeletal Muscle, Testicular

3.2. Context Clusters

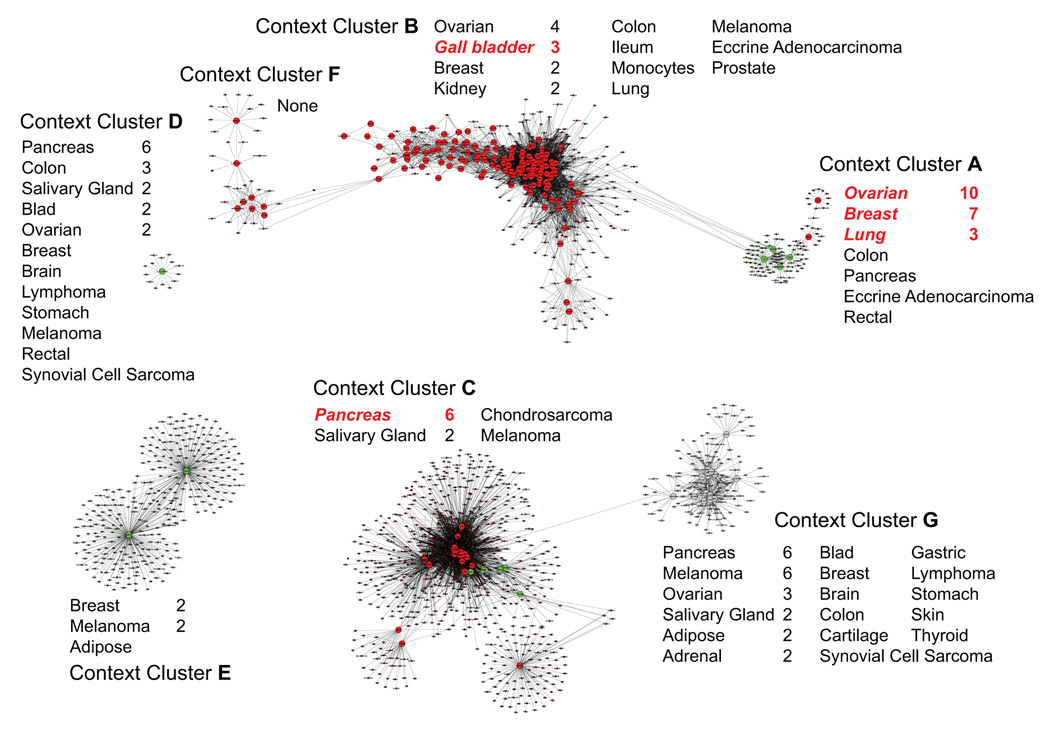
Running the context mining algorithm with a strict statistical significance threshold resulted in 205 contexts with p-value < 0.0004. Using these contexts, the method described to create context specific GRNs yielded a directed graph with 1,790 vertices (genes) and 9,566 edges (regulatory relationships), as shown in Figure 1 (in Sect. 3.3). This graph had an interesting property of being systematically fragmented into four separate context clusters, which were identified by locating the weakly connected components^‡ in the graph.

Figure 1.

Context-clusters and context-specific GRNs – each context cluster is annotated with the corresponding set of samples and highlights significantly enriched tumor types in red. See Table 1 for cancer tumor sample distribution in the dataset. In the graph itself, red vertices represent over-expressed genes, green under-expressed, and grey neither under- nor over-expressed. Edges are oriented from driver genes (large vertices) to driven genes (small vertices).

These context clusters provide a useful approach to interpreting the contexts found by the context mining algorithm. The clusters typically display significant overlaps among their subsets of samples. This is due to complex inter-connections among drivers that result from particular common cellular processes being shared among them. Forming context clusters readily reveals these common cellular contexts on the basis of their more densely connected components.

When investigating four separate context clusters, we noticed the two largest context clusters consisted of densely connected parts loosely bound to one another. Seeking to further characterize the data on the basis of very dense connectivity, we investigated the connections within the two largest context clusters. In Figure 1, bottom right, we segregated the first large cluster into context clusters C and G. Context cluster G is easily separable as all its genes are neither under- nor over-expressed (unlike C), and only one edge exists between the context clusters C and G (C drives a gene also driven by G). These characteristics convinced us that C and G should be analyzed as separate context clusters. The weak connection may have been rooted in tissue of origin similarity, as between them they account for two-thirds of the pancreatic samples in the data with six members in each. Next, we segregated the top large cluster in Figure 1 into context clusters A, B and F. All driver-to-driver edges between A and B are oriented from A to B, implying a hierarchical regulatory relationship from A to B. Also, like C and G, their connection in the graph is explained by the fact that both A and B represent significant numbers of both breast and ovarian tumor types. Context clusters B and F share four edges, two involve genes driven by drivers in both B and F. The two remaining edges are both directed from F to drivers in B, indicating again a possible hierarchical regulatory relationship between the two.

On the basis of density of connection and directionality of control, we resolved the four original context clusters into seven biologically separable ones. Each of these seven context clusters are visible in Figure 1 and have the associated tumor types next to them. Enriched tumor types are highlighted in red and the numbers next to all tumor types correspond to the number of samples distinguished as significant by the scoring function (Equation 4, discussed in next section). See Table 1 for sample information about the dataset’s sample composition.

3.3. Enrichment Calculations

3.3.1. Sample Association to Context Cluster

As a context cluster is a set of cellular contexts connected to one another through inter-context regulation, it would be informative to associate a set of samples to each context cluster based on its strength of association with the member contexts. Sample association to context clusters also allows annotation of the context cluster as a partial representative of cancer type. Since one context cluster is comprised of potentially many contexts, each representing a particular subset of biological samples, it is of interest which of those samples appears in more than one context in the context cluster. Samples were scored on the basis of occurrence within the context, over all the contexts found in the context cluster. A sample s, given a context cluster C consisting of m contexts {C₁, C₂,…, C_m}, would have the scoring:

$$\text{SAS}(\mathrm{s},C)=\sqrt[m]{{\displaystyle \prod _{i=1}^m{f}_i(s),}}\text{where}{f}_i(s)=\{\begin{array}{cc}\raisebox{1ex}{$k_i$}\!\left/ \!\raisebox{-1ex}{$N$}\right.,& s\in C_i\\ 1,& \text{otherwise}\end{array}$$ (4)

where k_i is number of samples within context C_i and N is the total number of samples in the gene expression data. The sample which occurs in all contexts of the context cluster would then have the least score, and the sample which is not present in any of the contexts will have a score of 1. The samples with score less than 0.5 were associated to corresponding context cluster. Using only the selected samples, the distributions and tumor types were calculated across all context clusters. Figure 1 depicts the tumor types having nonzero sample counts corresponding to each context cluster.

3.3.2. Tumor Type Enrichment

After sample association to specific context cluster, each cluster was subjected to a statistical test for enrichment of specific types of tumors. The Yates corrected chi square test for significance was applied (as numbers were less than 5) to each tumor type-context cluster pair. Some of the significant results are summarized below in Table 2. Figure 1 highlights (in red) the tumor type considered enriched within the corresponding context cluster.

Table 2.

Chi-square enrichment test p-values of tumor types in different context clusters

Context Cluster A		Context Cluster B		Context Cluster C
Tumor Type	p-value	Tumor Type	p-value	Tumor Type	p-value
Ovarian	2.3E-05	Gallbladder	1.6E-04	Pancreas	8.2E-05
Breast	0.0057
Lung	0.012

Intriguingly, context cluster A showed significant tumor enrichment of ovarian cancer, breast cancer and lung cancer. A literature survey shows breast cancer drugs are being used in the treatment of lung cancer [11], because of vital role of estrogen in lung development and subsequently cancer pathway.

Conventional approaches such as clustering and Bayesian network learning provide some ability to observe sample enrichment, but they do so in ways that do not exploit the association of particular expression behaviors in subsets of the samples to the fullest extent. Since clustering and Bayesian network learning implicitly assume that the observed data is from a single distribution, their results are always diluted approximations relative to results that assume the observed data to have come from various different distributions and evaluate them in appropriate isolation.

We compared our method to some conventional clustering algorithms, i.e. hierarchical clustering and k-means clustering using similarity metrics of correlation and Euclidean distance, in Cluster version 3.0 [3], to group samples with similar gene expression profiles together. We were able to verify that in cases where a similar number of clusters (six or seven) were identified by conventional methods, the conventional clusters display significant overlap (ranging from 40% to 90% overlap) with context clusters in terms of samples (and thus tumor type enrichment). Conventional clustering algorithms do not however provide a quantitative evaluation with which to isolate vital gene markers or describe the genes’ activity for the subtype of disease described by the sample subset. The context cluster approach has a distinct advantage of extracting relevant genes pertaining to the particular disease type.

Some examples of known gene interactions and relationships to diseases within context clusters were verified through a literature survey. Context cluster A involved breast cancer, ovarian cancer and lung cancer, and included genes such as TNFRSF1A, which is known to promote breast cancer [10]; CD74, usually expressed in ovarian and lung cancers, is being considered as a target for Multiple Myeloma treatment therapy [1]; HLA-DM, its expression when combined with that of HLA-DR, is considered to influence breast tumor progression and patient outcome [9]. Context cluster C, related to pancreatic cancer, contained GP2, a protein specifically expressed in pancreatic acinar cells and considered as a diagnostic marker in animals [6].

3.4. Comparison of Context Mining and Bayesian Network Analysis

Context clusters (A ~ G) were compared to H_BN, which is the result from the Bayesian network analysis. H_BN was composed of many subgraphs (H_CCs), which were connected components, and the top 32 large H_CCs were chosen as the target of comparison. The degree of overlap was evaluated for each pair (context cluster, H_CC) using the geometric mean of common gene ratios for the context cluster and the H_CC. A pair with a degree of overlap larger than 0.162 was determined to share a significant amount of genes after considering the empirical distribution of the degree of overlap. To figure out the difference between two results, enrichment analyses for GO terms were conducted for every context cluster and every H_CC using GoMiner [12].

Figure 2 shows the comparison between context mining and Bayesian network analysis. The comparison revealed that there are 10 H_CCs with a significant number of shared genes with at least one context cluster (Shared = {H_CC,₁, H_CC,₂, H_CC,₃, H_CC,₇, H_CC,₁₆, H_CC,₁₇, H_CC,₁₉, H_CC,₂₆, H_CC,₃₀, H_CC,₃₂}). When H_CCs in Shared were subject to GO term enrichment analysis, most of such H_CCs did not have any enriched GO term (8 of 10). On the contrary, other H_CCs with no significantly shared genes (NonShared) were often enriched with GO terms (19 of 22). The reason can be as follows: Bayesian network learning assumes that the observed data is from a single distribution, and is therefore trying to capture information consistent across all samples in the observed data. On the contrary, context mining captures information consistent in subset of samples. If a H_CC shares significant amount of genes with a context cluster, it means that significant portion of information in H_CC is consistent only in some subset of samples. This is a bias from the viewpoint of Bayesian network learning, because H_CC was built with a bias toward the process of capturing information consistent across all samples. For this reason, the shared genes in a H_CC may have inconsistent information with those unshared genes in the H_CC, eventually make it hard for H_CC to have enriched GO terms. The conventional Bayesian network learning is therefore not an optimum choice for identifying context-specific information from some subset of samples.

Figure 2.

The left table shows the degree of overlap for each pair of a context cluster (A ~ G) and a subgraph (H_CC,1 ~ H_CC,32) from Bayesian network analysis. A shaded cell in the table represents the pair with significantly shared genes. A shaded context cluster or a H_CC has at least one enriched GO term while non-shaded one has no enriched GO term. The right graph shows the portion of H_CCs with enriched GO terms for H_CCs with significantly shared genes (Shared) and H_CCs with no significantly shared genes (NonShared).

From this comparison and the tumor enrichment studies of context clusters in previous sections, we show that the context-specific GRN has a novel ability to represent context-specific information from subset of samples while conventional approaches assuming the entire sample set to be from single distribution have much more difficult time recognizing this kind of behavior.

4. Conclusions

This paper presents a novel approach to generate context clusters, i.e. disease pertinent (cancer tumor type in case of Target Now dataset), specific Gene Regulatory Networks using cellular contexts through the context mining algorithm. This study asserts that these gene regulatory networks (GRNs) produced by cellular context mining exhibit biological advantages absent in related techniques. The mapping of inter and intra context edges provides a resultant graph, which consists of context clusters, densely connected components, found to have interesting properties such as specific cancer tumor type enrichment (used for context cluster annotation) and occurrence of genes relevant to the annotated disease. Comparison of this approach with conventional clustering algorithms demonstrated its advantage for relevant gene subset identification. When compared with Bayesian network analysis, we noted that context clusters can capture regulatory relationships specific to subset of samples while conventional Bayesian network learning rarely captures meaningful context-specific information.

We are currently working on multi-variate in-silico conditioning in the context mining and incorporation of clinical annotation (if available) for learning and prediction purposes, in addition to the analysis of larger data sets available in NIH/GEO, Oncomine and EBI/ArrayExpress gene expression data repository.