Scaffold Topologies I: Exhaustive Enumeration up to 8 Rings

Abstract

Mapping the chemical space of small organic molecules is approached from a theoretical graph theory viewpoint, in an effort to begin the systematic exploration of molecular topologies. We present an algorithm for exhaustive generation of scaffold topologies with up to 8 rings, and an efficient comparison method for graphs within this class. This method uses the return index, a topological invariant derived from the adjacency matrix of the graph, as defined below. Furthermore, we describe an algorithm that verifies the adequacy of the comparison method. Applications of this method for chemical space exploration in the context of drug discovery are discussed. The key result is a unique characterization of scaffold topologies, which may lead to more efficient ways to query large chemical databases.

Introduction

The question of how vast is the chemical space of small organic molecules (CSSM) has been addressed in several ways — all of them related to in silico technologies, such as virtual chemical library enumeration starting from known lists of reagents. For example, the effort of enumerating all derivatives of n-hexane, from mono- to 14-substituted hexanes, starting from a list of 150 substituents, exceeds 10²⁹ unique structures¹. Although most of these hexane derivatives might be, to date, synthetically inaccessible, a small number of building blocks can lead to an unlimited number of possibilities, as witnessed in living systems: Twenty-two proteinogenic amino acids and five nucleotides combine to form large arrays of proteins and nucleic acids, respectively. Representatives of all the “tangible” chemicals² (in the order of 100 million physical compounds) can be collected and catalogued; and starting from such a database one could, in theory, expand into the space of virtual chemistry. However, there is currently no approach that would enable the systematic exploration of this chemical space. Indeed, most methods explore only the limited space covered by (a) known chemical reactions and (b) available/known chemical reagents. The question of how large this chemical space really is has relevance if one considers that adequate sampling² is required, should one desire to query biological endpoints using a diverse set of small molecules. To date, the CSSM has been systematically mapped for organic molecules with 11 or less main atoms and molecular weight less than 160 Daltons³. Eliminating constrained structures, the total number of chemicals produced was approximately 44 million. A chemical database of synthetically feasible structures is available at http://www.dcb.unibe.ch/groups/reymond/. In another study⁴, orderly generation was used to produce all possible single-bonded carbon graphs ranging from a maximum of 20 atoms and 2 rings to 13 atoms and 8 rings. A total of about 1.45 billion graphs were generated⁵, but this effort was never completed. Thus, the process of exhaustively mapping the CSSM is far from trivial, even when the effort is restricted to graph-reduced scaffolds.

In this paper, we map the CSSM for all molecules containing 8 or fewer independent rings and any number of atoms, by systematically exploring the topologies that can be present in the CSSM at the graph level, i.e., carbon-based single-bond scaffolds only. The exploration of scaffolds is critical, since with few exceptions, medicinal chemistry-based drugs contain scaffolds. We reduce the discussion of scaffolds to their corresponding topologies, a description of the connected ring structure of a class of scaffolds. In this paper, we show how the complete set of scaffold topologies (up to a given size) may be algorithmically generated and uniquely characterized. The space of possible scaffolds may be partitioned by topology class so that the union of topology classes is precisely the space of possible scaffolds. We present results for the population of topologies in systems up to and including 8 rings. In a paired paper⁶ we examine a number of chemical databases, some large and general, some smaller and more biologically oriented, for the properties of their topologies. We compare the results with the complete coverage developed here for molecules with up to and including 8 rings.

Basic concepts

A graph, G, sometimes called a pseudograph⁷, is a collection of nodes and edges such that each edge connects exactly two not-necessarily distinct nodes. Denote the set of nodes by V (G) = {v₁,v₂, … ,v_n}. A walk is a sequence of contiguous edges, or equivalently, a sequence of connected nodes, from v_i to v_j, and a path is a walk in which each node is traversed at most once. A cycle is a path starting and ending at v_i. In a connected graph, any two distinct nodes are connected by at least one path. All graphs we consider in this analysis are connected graphs. A graph may be described by any of its corresponding adjacency matrices. An adjacency matrix of a graph, A , is a symmetric matrix, where each entry (a_ij) counts the edges connecting v_i and v_j. A graph with n nodes may be described by any of up to n! adjacency matrices of size n × n which are equivalent up to permutation of indices. These matrices are considered isomorphic. The degree of node v_i is its row (or equivalently, column) sum, which describes the number of edge-segments incident to node $v_i:\text{deg}(v_i)={\displaystyle {\sum }_{j=1}^n{a}_{\mathit{\text{ij}}}}$. Each edge has two terminal segments and an edge with both terminal segments incident to a node v_i is called a loop and increments deg(v_i) by two. A node of degree k is called a k-node and l edges connecting the same pair of nodes are called an l-edge. A graph with multiple edges between the same nodes but without loops is called a multigraph, while a graph without multiple edges or loops is called a simple graph⁷. The problem of deciding if there exists a relabeling of indices that makes the adjacency matrices of two given graphs coincide is called the graph isomorphism problem⁸. In general, the recognition of the isomorphism of simple graphs with bounded valences can be carried out in polynomial time⁹ and of all graphs in moderately exponential time, $O\left(e^{\sqrt{n\text{log}n}}\right)$ where n is the number of nodes in the graph.

In this discussion, a scaffold topology or, topology, is a connected graph with the minimal number of nodes and corresponding edges required to fully describe its ring structure. We limit this analysis to topologies with a maximum nodal degree of four, corresponding to the valence of neutral carbon. Except for the graph consisting of exactly one ring (one node with a loop), topologies contain nodes exclusively of degrees 3 and 4. The one-ring graph is referred to as an isolated loop.

A scaffold, in this context, is a chemical graph composed solely of rings and optional linking linear structures. All branches of a scaffold terminate in a ring. This description is functionally equivalent to the one found in Koch et al.¹⁰ and Bemis and Murcko¹¹ (where it is called a molecular framework). We prefer the terms scaffold and scaffold topology to emphasize its theoretical, chemistry-free nature. At this level, the objects contain only topological information, as defined above. A molecule with its corresponding scaffold and topology is shown in Figure 1. We limit this discussion to scaffolds containing only single-bonds and a maximum atomic valence of four. Any such scaffold may be constructed from exactly one topology by distributing 2-nodes along its edges, expanding each edge in the topology into a chain of one or more edges. To describe the space of carbon-based single-bond scaffolds with, say, 25 atoms, let n_d = 25 − n, the number of 2-nodes to distribute in a graph with n nodes and e edges. Then a sharp upper bound for the number of scaffolds, n_scaffolds, that may exist in each (n, e) topology class is $n_{\mathit{\text{scaffolds}}}\le \left(\begin{array}{c}e+n_d-1\\ n_d\end{array}\right)$ with equality if and only if there are no equivalent edges in the topology. Two edges, e_i and e_j, are considered equivalent if the graphs resulting from attaching an isolated loop to each of e_i and e_j, respectively (as seen in Figure 3 (case 3)), differ only by permutation of indices.

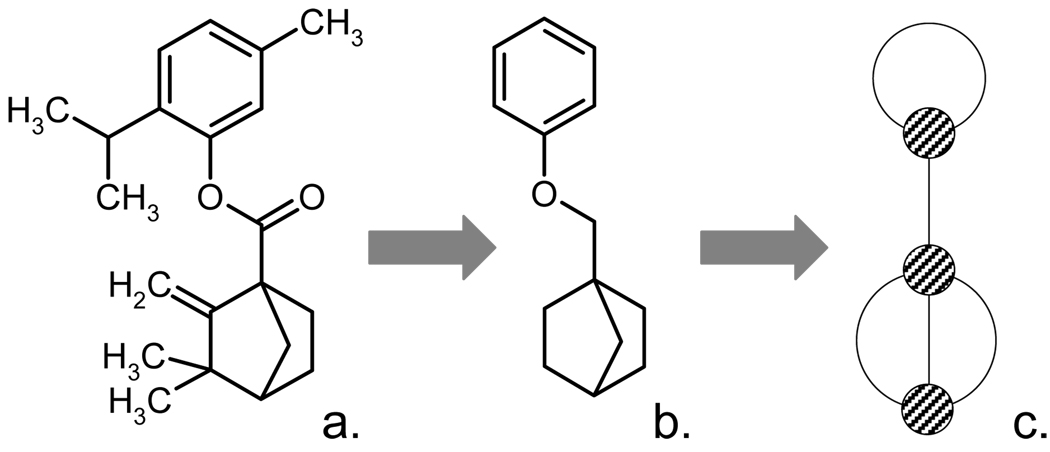
Figure 1.

a. (5-methyl-2-propan-2-yl-phenyl) 3,3-dimethyl-2-methylidene-bicyclo[2.2.1]heptane-1-carboxylate. b. The scaffold corresponding to this molecule. c. The topology corresponding to this scaffold.

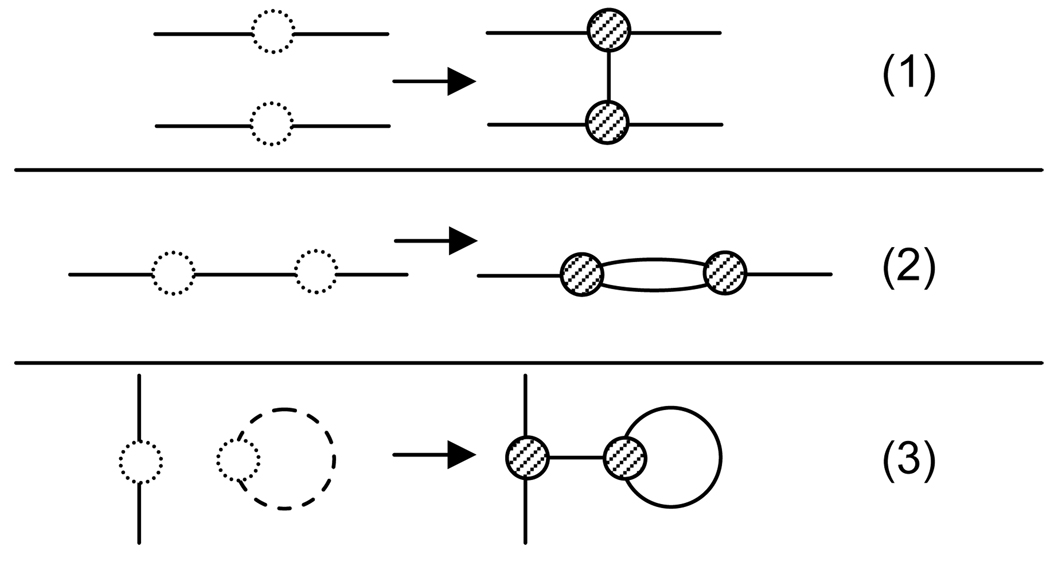
Figure 3.

Three operations to increment r by one and N₃ by two.

Let n denote total number of nodes in a graph, and N_k denote the number of k-nodes. Summing over nodal degrees: $n={\displaystyle \sum _{k\ge 1}{N}_k}$.

For scaffolds, n = N₂ + N₃ + N₄ and for topologies with 4 ≥ n ≥ 3, n = N₃ + N₄.

Let e count the total number of edges in a graph, then $2e={\displaystyle \sum _{k\ge 1}{\mathit{\text{kN}}}_k}$.

For scaffolds, 2e = 2N₂+ 3N₃ + 4N₄ and for topologies with 4 ≥ n ≥ 3, 2e = 3N₃ + 4N₄.

The number of independent rings, referred to in this analysis as the number of rings, is equivalent to Cauchy’s nullity, μ = r = e − n + 1.

For topologies with 4 ≥ n ≥ 3, r = N₄ + N₃/2 + 1. Holding N₄ constant, N₃ increments by two as r increments by one.

Generating topologies

All topologies with r rings and j 4-nodes may be generated by at least one topology with r rings and j-1 4-nodes by “fusing” together a pair of connected 3-nodes into a single 4-node in an otherwise identical graph.

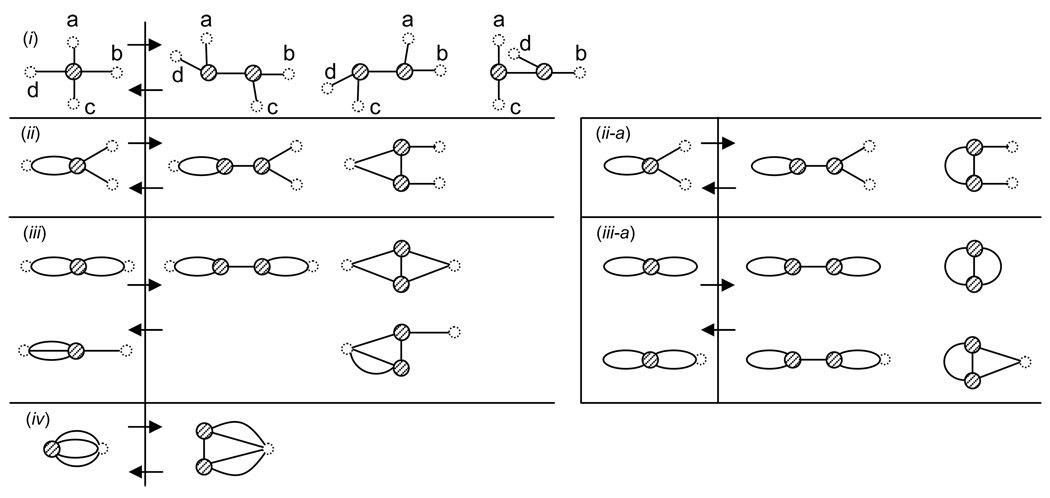
A 4-node without any loops may connect to:

1. 4 distinct nodes by 1-edges

2. 3 distinct nodes: two by 1-edges and one by a 2-edge

3. 2 distinct nodes by 2-edges, or one by a 1-edge and one by a 3-edge

4. 1 distinct node by one 4-edge

A 4-node with loops may connect to:

• (ii-a) 2 distinct nodes by 1-edges and one loop

• (iii-a) 1 distinct node by a 2-edge and one loop, or 2 loops

In case (i), the 4-node may be constructed three ways. In cases (ii), (ii-a), (iii) with 2-edges, and (iii-a), the 4-node may be constructed two ways. In case (iii) with a 3-edge and case (iv), the 4-nodes may be constructed one way.

See Figure 2.

Figure 2.

The correspondence between 4-nodes and pairs of connected 3-nodes.

Denote the family of topologies with r rings, N₃ 3-nodes and N₄ 4-nodes by (r, N₃, N₄). For a particular r and N₄, we may generate all topologies in (r, N₃, N₄) from the family (r , N₃ + 2 , N₄−1), 1 ≤ N₄ ≤ r−1, where N₃ = 2(r − N₄ − 1).

As a topology is the reduced form of a family of scaffolds, where the corresponding scaffolds may break up any edge in a topology into a chain of contiguous edges, we may consider edge-i in a topology to contain any number of “virtual” 2-nodes, u_i,k, i = 1, 2, …, e; k = 1, 2, …; that is, in a graph with n nodes, an edge may be added by connecting u_i,k to u_j,l which then acquire degree three and become v_n+1 and v_n+2, respectively.

There are three ways to increment the number of 3-nodes in a topology holding N₄ constant: (r, N₃, N₄) ↦ (r+1, N₃ + 2, N₄), where N₄ = r − N₃/2−1

1. connecting u_I,kto u_j,l, i≠j

2. connecting u_i,kto u_i,l

3. connecting u_i,kto u_loop, where u_loop denotes the 2-node of an isolated loop (the isolated loop may also be considered “virtual” until it is connected to the topology via an edge).

See Figure 3.

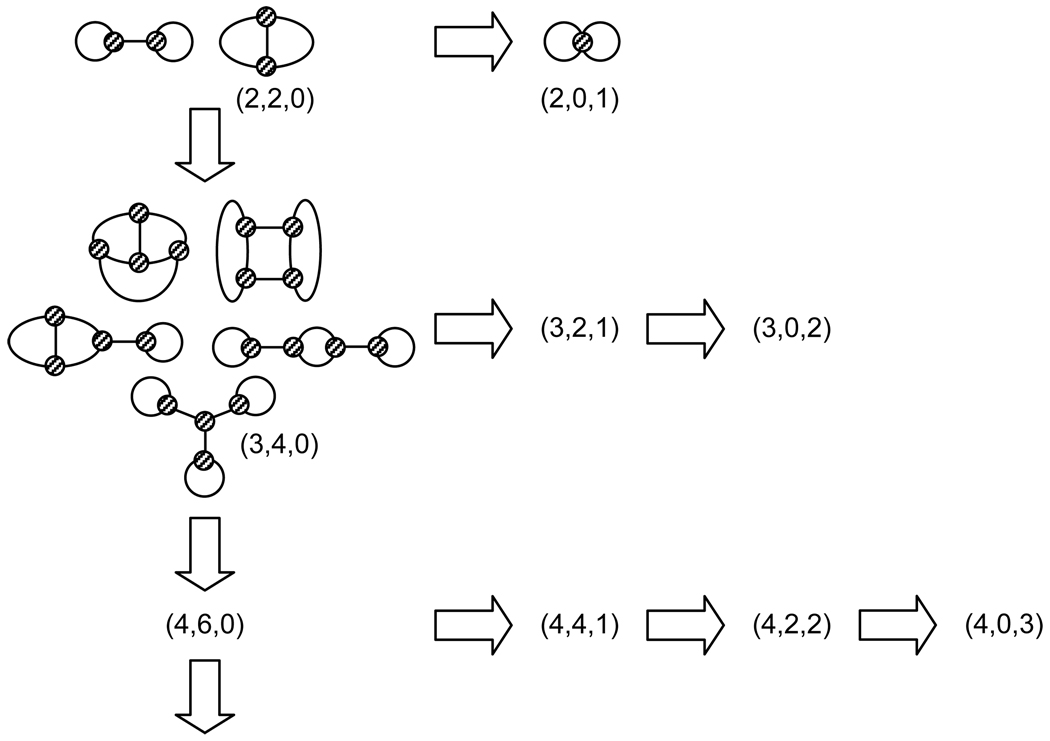
With these three operations to increment r by one, e by three and N₃ by two, and a single operation to decrement N₃ by two and e by one, and increment N₄ by one, we may generate all topologies with a given number of rings by starting with any complete family of topologies containing only 3-nodes: (r, 2(r− 1), 0). We choose to start with the two topologies in (2, 2, 0). See Figure 4.

Figure 4.

Schematic diagram of generation scheme showing all graphs in (2, 2, 0), (2, 0, 1) and (3, 4, 0)

The completeness of the generation scheme follows from the following two observations:

1. If in a graph with N₃ 3-nodes and N₄ 4-nodes and thus r= N₃/2+ N₄+1 rings, we replace one 4-node by two 3-nodes by following any of the steps in Fig. 2 from left to right, there results a graph with N₄−1 4-nodes and N₃+2 3-nodes, the same number of rings and one less edge

2. In a graph containing only 3-nodes, there are only three ways to remove an edge, given by the reverse of each of the steps shown in Fig. 3. Hence, if we consider any graph containing N₃ 3-nodes and zero 4-nodes, and thus r= N₃/2+1 rings, and we remove any edge by the reverse of moves of type 3(1) or 3(2) such that the graph remains connected and also remove the resulting 2-nodes, or if we remove a loop, its associated node, and the node connected to it (the reverse move of 3(3)), we end up with a graph with N₃−2 3-nodes, and consequently r−1 rings (and 3 fewer edges)

Now, if we assume that we have all possible graphs with N₃ 3-nodes and zero 4-nodes, it follows from observation (2) above that we will get all possible graphs with N₃+2 3-nodes and zero 4-nodes (and r+1 rings). Beginning with all possible graphs with two 3-nodes (the two graphs shown in Fig. 4), it follows by induction that we may generate all possible graphs with arbitrary (but even) numbers N₃ of 3-nodes and zero 4-nodes (and thus r= N₃/2+1 rings). And, following observation (1), if we assume that we have all possible graphs with N₃ 3-nodes and N₄ 4-nodes and r= N₃/2+ N₄+1 rings, then we may get all possible graphs of N₃−2 3-nodes and N₄+1 4-nodes by following all possible moves shown in Fig. 2 from right to left. This process may be repeated until we generate all possible graphs with zero 3-nodes and r-1 4-nodes.

Return-Index

The algorithm described above generates all possible topologies, but due to symmetries generates many topologies more than once. To enumerate the complete collection of distinct topologies, we compare each topology with the members of its (r, N₃, N₄) class. As mentioned previously, a graph with n nodes has up to n! associated adjacency matrices, considered isomorphic. It is possible to avoid comparing n! matrix permutations, as would be required to determine isomorphism from adjacency matrices directly. Several algorithms exist for solving the graph isomorphism problem efficiently for different categories of graphs, among which McKay’s package nauty¹² is considered state-of-the-art for both exhaustive generation and solution of the isomorphism problem¹³. The most relevant algorithms in nauty for our purpose are GENG, which may produce an exhaustive enumeration of simple graphs that may include up to one loop per vertex but not multiedges, LABELG, which produces a canonical labeling of all simple graphs of the type generated by GENG, and MULTIG, which can generate all possible distinct multigraphs corresponding to a given simple graph with no loops and test them for isomorphism (but does not produce a canonical labeling). Since pseudographs with both loops and multiedges are not allowed¹², one would need to include 2-nodes, then prune the graphs thus generated, removing all 2-nodes and discarding equivalent graphs. Although it could be possible to use this approach with some effort, it would result in huge numbers of redundant structures that would have to be generated, pruned and compared. There have been other attempts to separate pseudographs into equivalence classes via a labeling scheme and then explore the corresponding chemical space. Lipkus¹⁴ classifies the CSSM with a trio of topological descriptors, while Xu and Johnson^15,16 used molecular equivalence numbers, which produce finer-grained classes than our topologies, but the method was potentially subject to classification noise.

These considerations led us to seek a direct approach, one that would work for the scaffold topology type graphs considered here. In general, a graph may be associated with a diverse set of topological invariants that are independent of the specific indexing. Such invariants which both possess discriminating power and can be computed in polynomial time may help reduce the isomorphism problem. Different types of invariants have been introduced by various authors (see, e.g., Ivanciuc et al.¹⁷ and the references therein). One such set of invariants are the eigenvalues of the adjacency matrix, the spectrum of the graph¹⁸. It is well known that the spectrum of a graph does not fully discriminate between graphs, in that isospectral but nonisomorphic graphs do exist¹⁹. For our purposes, we were able to arrive at a simple, discriminating method for comparing scaffold topologies with up to 8 rings that can be carried out in polynomial, O(n₃ ) time, as well as a unique characterization for such graphs, by introducing the ordered return-index.

Let a k-walk denote a walk of length k. It is well known⁷ that the entries of A^k, $(a_{\mathit{\text{ij}}}^{(k)})$ contain the number of k-walks from v_i to v_j. In particular, $(a_{\mathit{\text{ii}}}^{(k)})$ contains the number of return-walks, starting and ending at v_i. We construct the return-index, R, an n × n matrix whose columns, R^(k), contain the diagonal entries of, A^k $(a_{\mathit{\text{jj}}}^{(k)})$, j = 1, 2, …, n. In practice, R is constructed by taking the powers of A´, the adjacency matrix with all entries on the main diagonal set to zero. No information is lost as all nodes in A are of degree 3 or 4, and subtracting off loops leaves affected nodes with degree zero, one, or two, respectively, distinguishing them from other nodes in the topology. The degree is zero in exactly one case, depicted in Figure 4, where the single node with two loops is the only member of the family (2, 0, 1). The first column of R (return-walks of length one) does not contain any distinguishing information, and is replaced with the number of 1-nodes each respective node has as first-order neighbors in A´, in a linear-time algorithm. The full calculation of R is a cubic-time algorithm. Each column of A (or A´) has at most four entries, and the calculation of each power is at most 4n² operations. Since we need to calculate n−1 powers, the total operations count is of the order of n³.

The rows of R, each of which contains information with respect to a particular node of A´, may be sorted in descending numerical order. The row R´ corresponding to node v_i is its return-string. The ordered matrix, R´, may be used to compare graphs. It is clear that two graphs with different return-indices are not isomorphic. It is not true in general that two graphs with the same ordered return-index are necessarily isomorphic. We demonstrated by exhaustive pairwise comparison that for topology graphs of up to and including 8 rings, the ordered return index fully distinguishes non-isomorphic graphs (data not shown). These topologies can be queried interactively at the UNM Biocomputing website²⁰.

Verification of the Ordered Return-Index

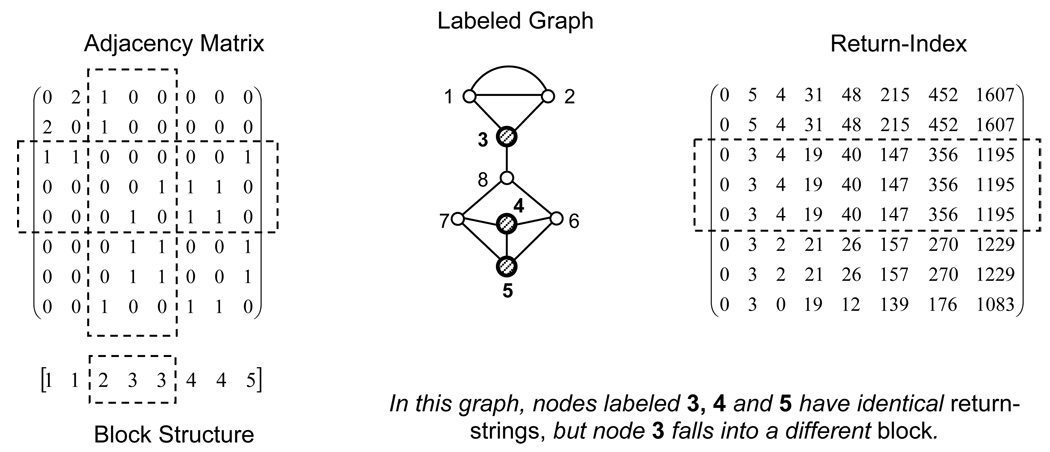
To verify that R´ fully discriminates topologies up to a certain size, we ran the generation algorithm, comparing topologies by R´. Where R´ matched another previously generated topology in the corresponding (r, N₃, N₄) class, adjacency matrices were compared using all possibly equivalent graph labelings until we found a match. The determination of possibly equivalent labelings is described below. In all cases where the return-indices of two graphs matched, some permutation (labeling) of the adjacency matrices matched as well. In order to reduce the number of permutations and comparisons, the graphs are first assigned a semi-canonical numbering with respect to the return-string corresponding to each node. The graph is then labeled in terms of “blocks” where each block contains nodes with the same return-string. We implement the following recursive algorithm:

1. For each node, form a neighbor-list specifying to which blocks its first-order neighbors belong.

2. Reorder nodes within existing blocks according to the neighbor-lists

3. Relabel the graph with a new set of blocks separating previous blocks by neighbor-lists.

4. If any new blocks were created in (3), and there are less than n blocks, return to (1).

This algorithm is guaranteed to terminate in less than n steps as the number of blocks cannot exceed the number of nodes. The block structure is the final list of blocks corresponding to the reordered list of nodes; by construction, the block structure is arranged in ascending numerical order. The members of each block in the final block-structure are called topologically equivalent nodes. Two isomorphic graphs must have the same block-structure. In comparing adjacency matrices, graphs are first relabeled in terms of their block-structure. Only indices falling within the same blocks need be permuted in order to find a match between matrices. An example of topologically inequivalent nodes with the same return-string is shown in Figure 5.

Figure 5.

Example of topologically inequivalent nodes with same return-string.

A useful byproduct of having established that the ordered return index has discriminatory power when applied to scaffold topologies with up to 8 rings, is the unique characterization for such graphs. Indeed, if we tag each such graph with its ordered return index, we have shown that identical ordered return indices imply isomorphism. The actual proof of this fact still requires permutation and comparison, since the method does not result in a canonical labeling of the nodes of a pseudograph, but rather a division of the nodes of a graph into topologically descriptive subclasses. Thus, the non-isomorphism of two graphs with distinct ordered return indices is automatic. In order to establish adequacy of the return index for determining isomorphism in case of identical ordered return-indices, we need to compare all possible reindexings of topologically equivalent nodes. This process, although much reduced relative to a full comparison of all permutations, can still be daunting. However, once carried out for all possible topologies of up to 8 rings, we found that the ordered return index is indeed adequate to distinguish all such topologies. Having established this, we have thus reduced the problem of detecting graph isomorphism of scaffold topologies, i.e. pseudographs of valence three or four with eight or fewer rings to the simple, polynomial time computation of the ordered return index and the linear time comparison of the indices of two graphs.

Counterexamples with more than 8 rings

The return index, even without the additional discrimination provided by the neighbor ranking, has at least the same discriminating power as the spectrum. This is a consequence of the fact that a matrix satisfies its own characteristic polynomial (Cayley-Hamilton theorem²¹). Thus, if the characteristic polynomial is given by

$$p(\lambda )={\lambda }^n+p_{n-1}{\lambda }^{n-1}+\cdots +p_1\lambda +p_0$$

then, since P(A) = 0 , it follows that

$$a_{\mathit{\text{ii}}}^{(n)}+p_{n-1}{a}_{\mathit{\text{ii}}}^{(n-1)}+\cdots +p_1{a}_{\mathit{\text{ii}}}+p_0=0,i=1,\cdots ,n$$

so that the coefficients of the characteristic polynomial can be determined completely from the entries of the return index matrix R, since there are n equations in the n quantities p _i i , =1,…,n, Thus, graphs with the same return index have the same characteristic polynomials and are therefore isospectral.

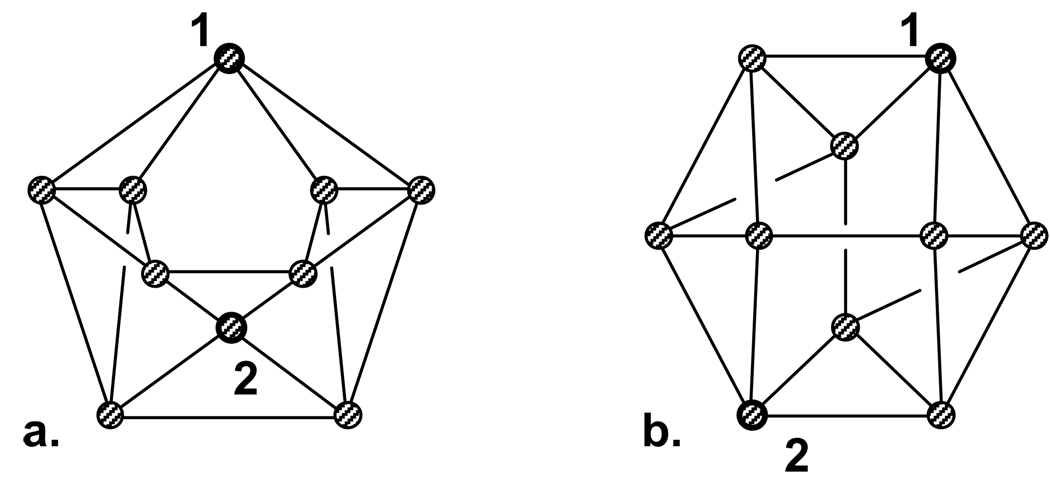
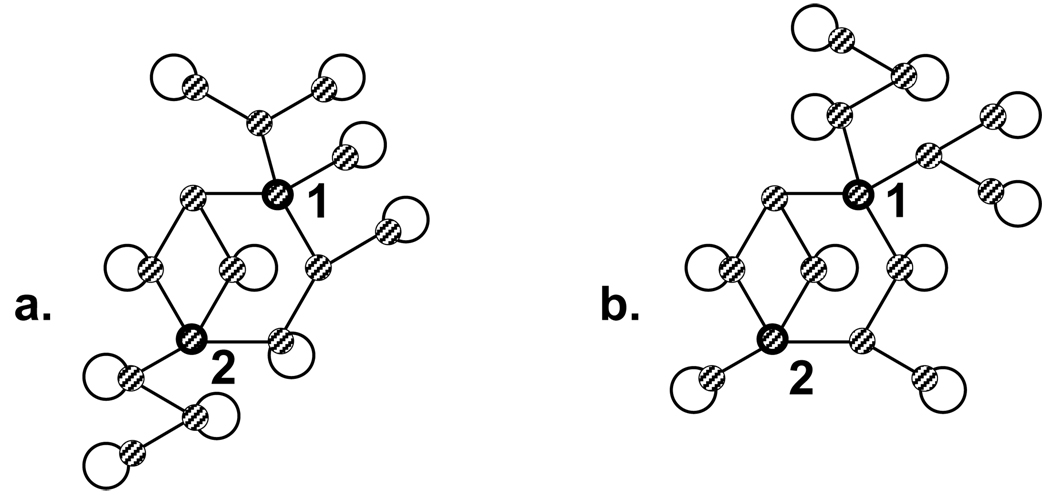
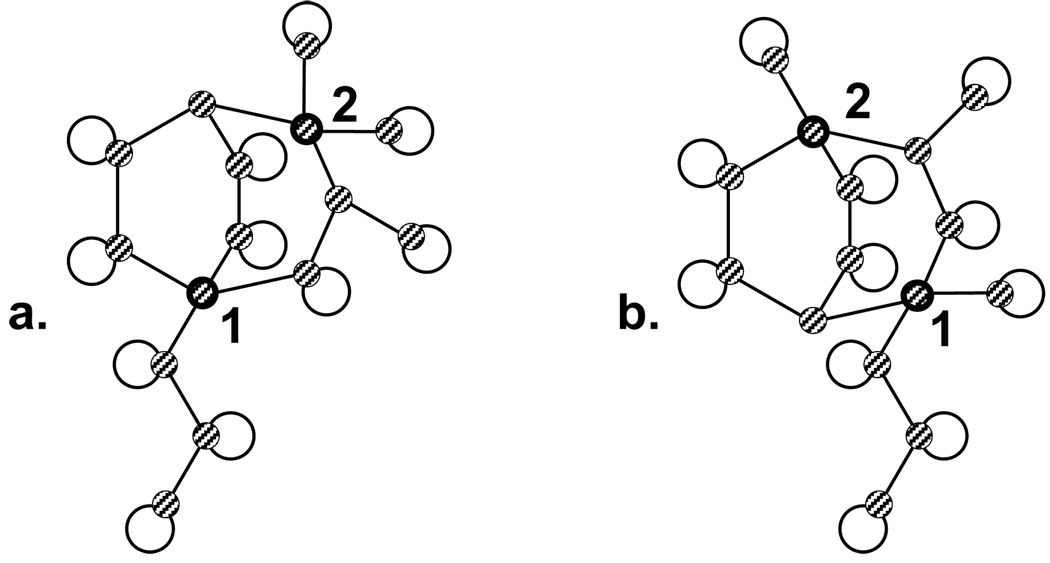
The following three pairs of topologies are not differentiated by the return-index, if it is calculated without replacing the first column of R with 1-node neighbor information; with that modification, the third pair is distinguished. The topologies in the first pair, with 11 rings, found among various examples on isospectral graphs in Cvetkovič et al.¹⁹, have identical return-indices but different block structures (Figure 6). The topologies in the second pair, with 12 rings, have identical return-indices and block structures (Figure 7). These graphs are not isomorphic, as can be shown by permutation of indices within blocks of topologically equivalent nodes, or by the observation that there is no node in graph (a) with the same branching structure as that of node (1) in graph (b). The topologies in the third pair, with 13 rings, have identical return indices but different block structures (Figure 8). All three pairs of graphs contain a pair of nodes with equivalent return-strings, but which fall into different blocks in at least one of the two graphs in the pair. We have not determined whether there are any counterexamples with 9 or 10 rings.

Figure 6.

In graph (a), nodes labeled 1 and 2 have identical return-strings, but fall into different blocks. In graph (b), nodes labeled 1 and 2 have identical return-strings, and fall into the same block. Graphs (a) and (b) have identical return-indices but different block structures.

Figure 7.

In both graphs (a) and (b), nodes labeled 1 and 2 have identical return-strings, but fall into different blocks. Graphs (a) and (b) have identical return-indices and block structures, but are not isomorphic.

Figure 8.

In both graphs (a) and (b), nodes labeled 1 and 2 have identical return-strings, but fall into different blocks. Graphs (a) and (b) have identical return-indices, but they have different respective block structures. With the return-index modified to contain the number of 1-node neighbors instead of return-walks of length one, graphs (a) and (b) are fully distinguished without comparing block-structures.

Results and Conclusions

In this paper, we described a method and an algorithm for the systematic generation of topologies with up to, and including 8 rings, and an efficient (cubic time) algorithm for comparing these graphs to determine isomorphism. Furthermore, we produced a unique characterization for scaffold topology pseudographs with up to 8 rings. A practical application of this result follows: If all small molecules (up to 8 rings) in a given chemical database are tagged by the ordered return index characterizing their topologies (an operation that only needs to be performed once for any given database), then the problem of deciding if a given molecule is present in the database can be quickly reduced by querying only those database entries with the same topology. This renders database searching more efficient, in particular since most chemical collections now exceed 10⁷ unique chemicals.

The total numbers of topologies in each class of (r, N₃, N₄) are summarized in Table 1 and shown in Figure 8. A lower bound for the number of unique topologies in (9, 16, 0) is 204,637. We have not confirmed whether the return-index is adequate to distinguish between topologies with 9 or 10 rings, and we have found counterexamples for which the return index supplemented with only nearest neighbor loop information fails for 11 and 12 rings.

Table 1.

Total number of distinct topologies up to and including 8 rings.

						N3
		0	2	4	6	8	10	12	14	total
	1	1								1
	2	1	2							3
	3	2	5	5						12
r	4	4	22	30	17					73
	5	10	88	228	193	71				590
	6	28	430	1,655	2,457	1,496	388			6,454
	7	97	2,242	12,905	28,301	28,649	13,343	2,592		88,129
	8	359	13,239	105,188	326,761	483,124	365,994	136,666	21,096	1,452,427

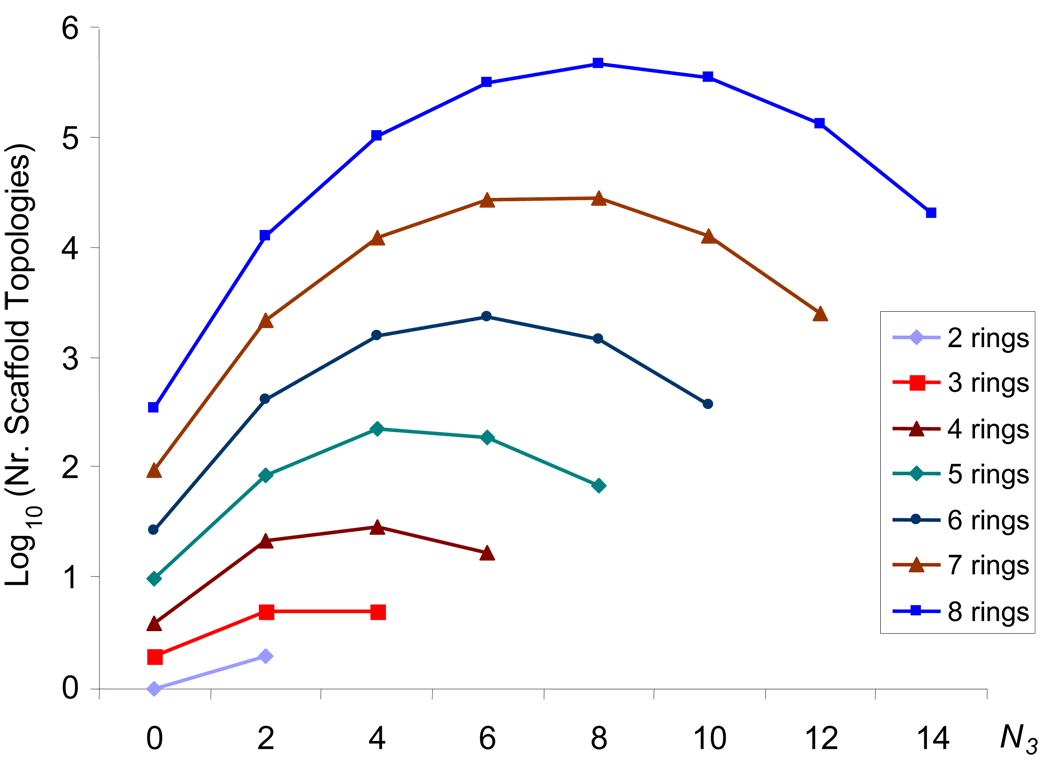
The population density of the topological scaffold space is higher at the mid-level combination of 3-nodes and 4-nodes for any given number of rings (Fig. 9). The shape of the population density curves is similar to that of the binomial coefficients. This is in notable contrast to the population densities of topologies found in the chemical databases discussed in a paired paper³. Those chemical databases show higher populations for topologies containing not more that one 4-node.

Figure 9.

Total number of distinct topologies with 2 through 8 rings, plotted as a function of N₃.

We note that the number of possible scaffold topologies for up to 6 rings is slightly over 7,000, and dramatically increases with higher ring numbers. Moreover, the number of non-planar topologies grows with the number of rings: While there are no non-planar scaffold topologies with 2 or 3 rings and exactly one with 4, the number grows to roughly 10% of the total for 8 rings. In an accompanying paper, we present the topological scaffold space occupancy (distribution) for a diverse set of chemical databases⁶. The probability of finding existing molecules for a given scaffold topology decreases rapidly for higher ring numbers. Additionally, there are exactly 44 molecules, belonging to 12 distinct non-planar topology classes, found in the entire merged database we considered⁶ (planarity was determined using the routine PLANARG of nauty¹²).

Since this is a complete enumeration of all the possible scaffold topologies, we anticipate that the use of this system can become standard for rapid queries of ultra-large databases. Furthermore, this system can provide a basis for the systematic topological classification of organic small molecules, and serve as a first step to the complete mapping of topological chemical space.