Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Aug 25.
Published in final edited form as: J Biomech. 2009 Jul 25;42(12):1996–1999. doi: 10.1016/j.jbiomech.2009.05.024

Comparison of Two Methods for Calculating the Frictional Properties of Articular Cartilage Using a Simple Pendulum and Intact Mouse Knee Joints

Elizabeth I Drewniak 1, Gregory D Jay 2, Braden C Fleming 1, Joseph J Crisco 1
PMCID: PMC2734508  NIHMSID: NIHMS132734  PMID: 19632680

Abstract

In attempts to better understand the etiology of osteoarthritis, a debilitating joint disease that results in the degeneration of articular cartilage in synovial joints, researchers have focused on joint tribology, the study of joint friction, lubrication, and wear. Several different approaches have been used to investigate the frictional properties of articular cartilage. In this study, we examined two analysis methods for calculating the coefficient of friction (μ) using a simple pendulum system and BL6 murine knee joints (n=10) as the fulcrum. A Stanton linear decay model (Lin μ) and an exponential model that accounts for viscous damping (Exp μ) were fit to the decaying pendulum oscillations. Root mean square error (RMSE), asymptotic standard error (ASE), and coefficient of variation (CV) were calculated to evaluate the fit and measurement precision of each model. This investigation demonstrated that while Lin μ was more repeatable, based on CV (5.0% for Lin μ; 18% for Exp μ), Exp μ provided a better fitting model, based on RMSE (0.165° for Exp μ; 0.391° for Lin μ) and ASE (0.033 for Exp μ; 0.185 for Lin μ), and had a significantly lower coefficient of friction value (0.022±0.007 for Exp μ; 0.042±0.016 for Lin μ) (p=0.001). This study details the use of a simple pendulum for examining cartilage properties in situ that will have applications investigating cartilage mechanics in a variety of species. The Exp μ model provided a more accurate fit to the experimental data for predicting the frictional properties of intact joints in pendulum systems.

Keywords: coefficient of friction, pendulum, viscous damping, articular cartilage

1. Introduction

Osteoarthritis is a common degenerative joint disease that can be characterized by the gradual loss of articular cartilage (AC) within synovial joints such as the knee. In a healthy state, AC is a relatively smooth tissue that covers articulating surfaces, distributes loads, decreases stresses on contact areas, and allows for motion of two surfaces while minimizing friction and wear. In attempts to better understand how and why cartilage becomes osteoarthritic, many researchers have investigated the coefficient of friction (μ) of AC using a variety of methods, including whole joints in pendulums (Crisco, Blume, Teeple, Fleming, & Jay, 2007; Jay, et al., 2007; Jones, 1936; Stanton, 1923; Teeple, et al., 2007; Wright & Dowson, 1976), cartilage plugs with custom-built apparatuses (Caligaris & Ateshian, 2008; Forster & Fisher, 1996; Gleghorn, Jones, Flannery, & Bonassar, 2007; Krishnan, Mariner, & Ateshian, 2005; Linn, 1967; Schmidt & Sah, 2007; Tanaka, et al., 2004; Wright & Dowson, 1976), and atomic force microscopy (AFM) (Coles, et al., 2008; Park, Costa, & Ateshian, 2004).

Cartilage plugs are extremely useful in the study of the mechanical properties of AC; however, they pose challenges when using small animal models, including mice. Despite their small size, murine models have many benefits, including transgenic capabilities related to the development and homeostasis of AC. A study by Jay et al. (2007) investigated the frictional properties of Prg4 mutant mice using a simple pendulum system. Like Jay et al.’s study, the present study examines the frictional properties of mouse knee cartilage using a pendulum, but there were some differences between the two studies, including pendulum weight, resting angle, range of motion, and data analysis. Of note, the method described herein allows for collection of three-dimensional (3-D) joint motion and automated data processing.

A recent study examined two mathematical models for calculating μ: a Stanton linear decay model (Lin μ) and an exponential decay model (Exp μ) that accounts for viscous damping caused by extra-articular structures (Crisco, et al., 2007) The objective of the present study was to compare these two models for calculating μ using experimental data collected and processed with an automated approach. This objective was accomplished using a simple pendulum system and BL6 mouse knees.

2. Methods

Using procedures approved by the RIH Animal Welfare Committee, hind limbs from 10-week-old BL6 mice (n = 10) were excised and flash frozen with liquid nitrogen post-euthanasia. Specimens were stored at −80°C for 1–7 weeks. Pilot data showed no differences between μ of AC from fresh and frozen knee joints. On the day of testing, specimens were thawed and the skin, musculature, and supporting connective tissue were dissected away, leaving the joint capsule intact. The proximal femur and distal tibia were rigidly embedded in square, 6.25 mm-wide brass tubes with a urethane-potting compound (Smooth-ON, Easton, PA). The pendulum arm, weighing approximately 50 grams (~2x’s body weight) was fit to the tube encasing the femur. The tube encasing the tibia was rigidly fixed with four set screws to a platform designed to place the resting angle of the knee at ~70° when the pendulum was in equilibrium. This resting angle was chosen following analysis of small rodent kinematic studies (Fischer & Blickhan, 2006; Fischer, Schilling, Schmidt, Haarhaus, & Witte, 2002). Four reflective markers were attached to both the pendulum arm and to the base of apparatus (Figure 1). The pendulum was rotated to place the knee joint at an initial offset angle of ~12°, released, and allowed to oscillate freely. Five trials were collected for each knee. Pendulum motion was tracked in 3-D at 100 Hz (VICON, Centennial, CO.) with rotational accuracy of better than 0.05° and translational accuracy of better than 0.06 mm. Oscillation data was then processed with Visual3D software (C-Motion, Inc., Germantown, MD) and custom MATLAB (MathWorks, Inc., Natick, MA) code to determine the peak amplitude of each cycle of oscillation.

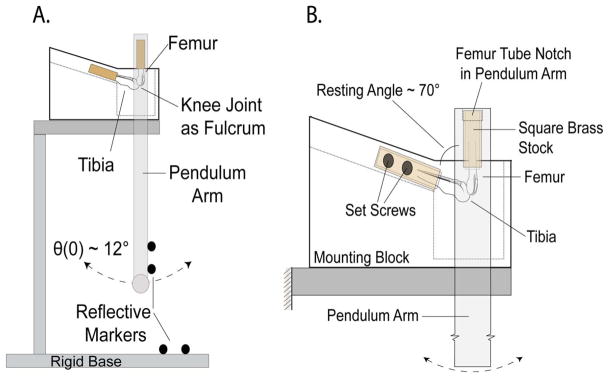
Figure 1.

Figure 1

Open in a new tab

Figure 1A. Schematic of simple pendulum system used for amplitude decay data collection. The pendulum arm was fixed to the proximal end of the femur and the tibia was rigidly mounted to a base platform. Four reflective markers were attached to both the pendulum arm and to the base (not all markers shown) for 3-D motion tracking. The arm was set to an initial angle of ~12°, released, and allowed to oscillate freely until damping out completely. B. Close-up schematic of the knee joint mount. Both limbs were embedded in square 6.25 mm tubing with a urethane-potting compound and secured into the apparatus at a resting angle of 70°. The tibia was fixed to the base with four set screws (two on each side of the limb). The proximal end of the tube-fitted femur fit into a square notch cut into the pendulum arm.

Two models for computing μ were fit to the experimental peak amplitude data using custom MATLAB code. The Stanton μ model provided a linear fit (Lin μ), while the second model fit the experimental data with an exponential curve (Exp μ) that included a calculation for viscous damping (c) (Crisco, et al., 2007). The goodness of fit of each model was described using the root mean square error (RMSE). The asymptotic standard error (ASE) was calculated to determine the uncertainty of the curve-fitted parameters relative to each model. The Lin μ, Exp μ, and c values were determined for each specimen by averaging over the five trials. Mean (±SD) μ values for each model were then calculated across all specimens. The measurement precision of each model in estimating μ was quantified using coefficient of variation analysis (CV). The reliability of each model was quantified with an intra-class correlation coefficient (ICC). The RMSE, ASE, CV, Lin μ and Exp μ values were evaluated for statistical differences with a Mann-Whitney Rank Sum Test (SigmaStat3.5, Systat Software, Inc., San Jose, CA). A significant value of p<0.05 was set a priori.

3. Results

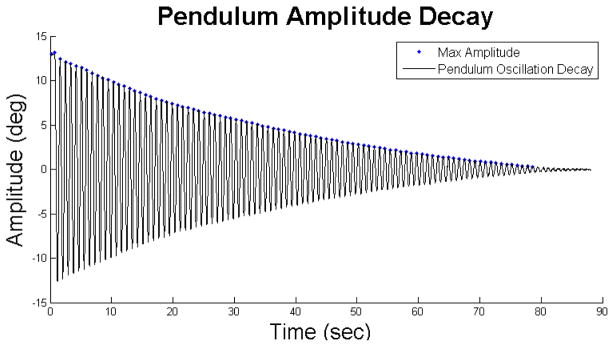
With an initial offset angle of 12±1°, the BL6 knees oscillated for 78±25 cycles before damping brought the pendulum to equilibrium (Figure 2). In all trials, the decay in peak amplitude was curvilinear when plotted as a function of cycle number. The frequency of the pendulum motion was approximately 1Hz.

Figure 2.

Figure 2

Open in a new tab

Representative plot of pendulum oscillation decay starting with initial release of the pendulum arm through damping out of the system. Points denote the maximum amplitude of each cycle.

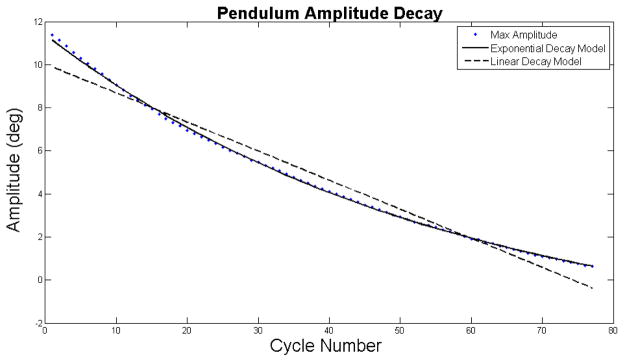
Exp μ provided a significantly (p<0.001) closer fit to the experimental data (Figure 3) than Lin μ with overall average RMSE values of 0.17°±0.062 and 0.40°±0.14, respectively. The ASE for Exp μ was significantly lower (p<0.001) than that of Lin μ, 0.033 and 0.185, respectively. The μ values predicted by Exp μ (0.022±0.007) were significantly less than the μ values predicted by Lin μ (0.042±0.016). The range of Exp μ values was 0.016–0.037, while the range of Lin μ was 0.031–0.080. CV of μ for Exp μ was 18% and 5.0% for Lin μ. The ICC for Lin μ was 0.975, while the ICC for Exp μ was 0.708. The value of viscous damping predicted by Exp μ was 2.969×10−5 ± 3.409×10−5 kg*m2/s.

Figure 3.

Figure 3

Open in a new tab

Representative plot of the Lin μ (dashed line) and Exp μ (solid line), which accounts for viscous damping fit to the maximum amplitudes points for each cycle. The Exp μ model provided a much closer fit to the experimental data with a RMSE of 0.078° and an ASE of 0.033°, versus the Lin μ RMSE of 0.55° and ASE of 0.185°

4. Discussion

We modeled the decay of oscillations of a simple pendulum with intact BL6 mouse knees as the fulcrum using two models, Lin μ and Exp μ. The use of a pendulum provides a simple, cost-effective method for measuring the μ of the AC of intact murine knee joints, while allowing for unconstrained motion with compressive loads that emulate in vivo conditions. While there are benefits with a pendulum system, there are also limitations. The calculated values represent the entire articular surface and joint, including capsular ligaments and synovium. Both models neglect aerodynamic drag created by the pendulum apparatus. Like this study, Jay et al. (2007) used a pendulum with a mouse knee joint serving as the fulcrum of the system and each specimen consisted of a mouse hind limb with an intact knee capsule. While Jay et al. calculate μ within the midpoint of joint oscillation, our models compute μ using the entire oscillation data. This difference in data processing method may account for the differences in calculated μ values we observed, which were higher than that of Jay et al.

Cartilage plugs are useful for studying the frictional properties of AC without the influence of intra-capsular ligaments and surrounding tissues. However, transgenic mice provide valuable opportunities for the study of chondroprotection within an intact joint. Obtaining cartilage plugs from murine joints is currently not a feasible option. The μ values computed with this approach were higher than those obtained with cartilage plug methods; however, they were within the range μ values from studies investigating whole joints (Barnett & Cobbold, 1962; McCutchen, 1962; Roberts, Unsworth, & Mian, 1982; Teeple, et al., 2008; Teeple, et al., 2007; Unsworth, Dowson, & Wright, 1975).

The two methods for computing μ of AC yielded significantly different results. Based on the calculated CV and ICC values, the Lin μ model had increased measurement precision and reliability, likely providing a more useful tool for detecting subtle differences among experimental groups. Additionally, a majority of studies that have investigated the frictional properties of articular cartilage with pendulums and whole joints have used the Stanton model, making it useful for drawing comparisons with other values in literature (Charnley, 1960; McCutchen, 1962; Stanton, 1923; Tanaka, et al., 2005; Tanaka, et al., 2004; Teeple, et al., 2007; Unsworth, et al., 1975; Wright & Dowson, 1976). Conversely, Exp μ provided a better fit to the experimental data, based on RMSE and ASE, especially noting that the amplitude decay was curvilinear. Exp μ also accounts for viscous damping, and significantly lower μ values.

Acknowledgments

The authors would like to acknowledge their funding sources: NIH AR050180, NIH P20-RRO24484, RIH Orthopaedic Foundation, Inc., and University Orthopedics, Inc. Thank you to VICON for use of cameras and software for motion capture. Thank you to Jason Machan, PhD for help with statistical analysis. The authors also thank: Michael Rainbow, Evan Leventhal, and Chung-Ja Cha, PhD for their assistance.

Footnotes

Conflict of Interest Statement

The authors of this manuscript have nothing to disclose/no conflicts of interest.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Barnett CH, Cobbold AF. Lubrication within living joints. The Journal of Bone and Joint Surgery. 1962;44B (3):662–674. [Google Scholar]
  2. Caligaris M, Ateshian GA. Effects of sustained interstitial fluid pressurization under migrating contact area, and boundary lubrication by synovial fluid, on cartilage friction. Osteoarthritis and Cartilage. 2008;16 (10):1220–1227. doi: 10.1016/j.joca.2008.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Charnley J. The lubrication of animal joints in relation to surgical reconstruction by arthroplasty. Annals of the Rheumatic Diseases. 1960;19:10–19. doi: 10.1136/ard.19.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Coles JM, Blum JJ, Jay GD, Darling EM, Guilak F, Zauscher S. In situ friction measurement on murine cartilage by atomic force microscopy. Journal of Biomechanics. 2008;41 (3):541–548. doi: 10.1016/j.jbiomech.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Crisco JJ, Blume J, Teeple E, Fleming BC, Jay GD. Assuming exponential decay by incorporating viscous damping improves the prediction of the coefficient of friction in pendulum tests of whole articular joints. Proceedings of the Institution of Mechanical Engineers [H] 2007;221 (3):325–333. doi: 10.1243/09544119JEIM248. [DOI] [PubMed] [Google Scholar]
  6. Fischer MS, Blickhan R. The tri-segmented limbs of therian mammals: kinematics, dynamics, and self-stabilization: a review. Journal of Experimental Zoology. 2006;305A (11):935–952. doi: 10.1002/jez.a.333. [DOI] [PubMed] [Google Scholar]
  7. Fischer MS, Schilling N, Schmidt M, Haarhaus D, Witte H. Basic limb kinematics of small therian mammals. The Journal of Experimental Biology. 2002;205 (Pt 9):1315–1338. doi: 10.1242/jeb.205.9.1315. [DOI] [PubMed] [Google Scholar]
  8. Forster H, Fisher J. The influence of loading time and lubricant on the friction of articular cartilage. Proceedings of the Institution of Mechanical Engineers [H] 1996;210 (2):109–119. doi: 10.1243/PIME_PROC_1996_210_399_02. [DOI] [PubMed] [Google Scholar]
  9. Gleghorn JP, Jones AR, Flannery CR, Bonassar LJ. Boundary mode frictional properties of engineered cartilaginous tissues. European Cells & Materials Journal. 2007;14:20–28. doi: 10.22203/ecm.v014a02. [DOI] [PubMed] [Google Scholar]
  10. Jay GD, Torres JR, Rhee DK, Helminen HJ, Hytinnen MM, Cha CJ. Association between friction and wear in diarthrodial joints lacking lubricin. Arthritis & Rheumatism. 2007;56 (11):3662–3669. doi: 10.1002/art.22974. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jones ES. Joint Lubrication. The Lancet. 1936;230:1043–1044. [Google Scholar]
  12. Krishnan R, Mariner EN, Ateshian GA. Effect of dynamic loading on the frictional response of bovine articular cartilage. Journal of Biomechanics. 2005;38 (8):1665–1673. doi: 10.1016/j.jbiomech.2004.07.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Linn FC. Lubrication of animal joints. I. The arthrotripsometer. Journal of Bone and Joint Surgery American. 1967;49 (6):1079–1098. [PubMed] [Google Scholar]
  14. McCutchen CW. The frictional properties of animal joints. Wear. 1962;5:1. [Google Scholar]
  15. Park S, Costa KD, Ateshian GA. Microscale frictional response of bovine articular cartilage from atomic force microscopy. Journal of Biomechanics. 2004;37 (11):1679–1687. doi: 10.1016/j.jbiomech.2004.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Roberts BJ, Unsworth A, Mian N. Modes of lubrication in human hip joints. Annals of the Rheumatic Diseases. 1982;41 (3):217–224. doi: 10.1136/ard.41.3.217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Schmidt TA, Sah RL. Effect of synovial fluid on boundary lubrication of articular cartilage. Osteoarthritis and Cartilage. 2007;15 (1):35–47. doi: 10.1016/j.joca.2006.06.005. [DOI] [PubMed] [Google Scholar]
  18. Stanton TE. Boundary lubrication in engineering practice. Engineer. 1923;135:678–680. [Google Scholar]
  19. Tanaka E, Iwabe T, Dalla-Bona DA, Kawai N, van Eijden T, Tanaka M, Kitagawa S, Takata T, Tanne K. The effect of experimental cartilage damage and impairment and restoration of synovial lubrication on friction in the temporomandibular joint. Journal of Orofacial Pain. 2005;19 (4):331–336. [PubMed] [Google Scholar]
  20. Tanaka E, Kawai N, Tanaka M, Todoh M, van Eijden T, Hanaoka K, et al. The frictional coefficient of the temporomandibular joint and its dependency on the magnitude and duration of joint loading. Journal of Dental Research. 2004;83 (5):404–407. doi: 10.1177/154405910408300510. [DOI] [PubMed] [Google Scholar]
  21. Teeple E, Elsaid KA, Fleming BC, Jay GD, Aslani K, Crisco JJ, Mechrefe AP. Coefficients of friction, lubricin, and cartilage damage in the anterior cruciate ligament-deficient guinea pig knee. Journal of Orthopaedic Research. 2008;26 (2):231–237. doi: 10.1002/jor.20492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Teeple E, Fleming BC, Mechrefe AP, Crisco JJ, Brady MF, Jay GD. Frictional properties of Hartley guinea pig knees with and without proteolytic disruption of the articular surfaces. Osteoarthritis and Cartilage. 2007;15 (3):309–315. doi: 10.1016/j.joca.2006.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Unsworth A, Dowson D, Wright V. Some new evidence on human joint lubrication. Annals of the Rheumatic Diseases. 1975;34 (4):277–285. doi: 10.1136/ard.34.4.277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Wright V, Dowson D. Lubrication and cartilage. Journal of Anatomy. 1976;121 (Pt 1):107–118. [PMC free article] [PubMed] [Google Scholar]

RESOURCES