Abstract
Correctly selecting appropriate actions in an uncertain environment requires gathering experience about the available actions by sampling them over several trials. Recent findings suggest that the human rostral cingulate zone (RCZ) is important for the integration of extended action–outcome associations across multiple trials and in coding the subjective value of each action. During functional magnetic resonance imaging, healthy volunteers performed two versions of a probabilistic reversal learning task with high (HP) or low (LP) reward probabilities that required them to integrate action–outcome relations over lower or higher numbers of trials, respectively. In the HP session, subjects needed fewer trials to adjust their behavior in response to a reversal of response–reward contingencies. Similarly, the learning rate derived from a reinforcement learning model was higher in the HP condition. This was accompanied by a stronger response of the RCZ to negative feedback upon reversals in the HP condition. Furthermore, RCZ activity related to negative reward prediction errors varied as a function of the learning rate, which determines to what extent the prediction error is used to update action values. These data show that RCZ responses vary as a function of the information content provided by the environment. The more likely a negative event indicates the need for behavioral adaptations, the more prominent is the response of the RCZ. Thus, both the window of trials over which reinforcement information is integrated and adjustment of action values in the RCZ covary with the stochastics of the environment.
Introduction
Surviving in a changing environment requires constant evaluation of action outcomes. If an action leads to an unfavorable outcome, behavior needs to be adjusted. The dorsal anterior cingulate cortex (dACC) has been implicated in using feedback information to guide behavior (Shima and Tanji, 1998; Swick and Turken, 2002; Matsumoto et al., 2003, 2007; Ridderinkhof et al., 2004; Walton et al., 2004; Williams et al., 2004; Amiez et al., 2006). In humans, the rostral cingulate zone (RCZ), the putative homolog of the monkey rostral cingulate motor area (rCMA), is particularly responsive to performance errors and negative feedback in a variety of tasks (Ullsperger and von Cramon, 2001, 2003, 2004; Gehring and Willoughby, 2002; Kerns et al., 2004). Neurons in the monkey rCMA respond to reward reduction, and muscimol deactivation of the rCMA impaired the animals' performance in a reversal learning task (Shima and Tanji, 1998). More recently, Kennerley et al. (2006) showed that monkeys with lesions to the rostral cingulate sulcus were not impaired in adapting their behavior after negative feedback in a response reversal learning task. However, lesioned animals used only the outcome of the most recent trials to guide behavior and frequently reverted back to the previously successful action. From this behavioral pattern, the idea evolved that the dACC/RCZ, rather than detecting the occurrence of single negative events, is involved in generating a history of action outcomes across multiple trials. In agreement with this, we recently observed that the response of the RCZ to negative feedback varied as a function of the number of preceding negative feedback trials (Jocham et al., 2009). Behrens et al. (2007) showed that activity in the RCZ covaried with subjects' estimate of the “volatility” of the environment. They argue that RCZ activity reflects the salience of each outcome for future actions.
For real-life decisions, such integration over several trials is necessary, because reinforcement is usually available in a probabilistic, rather than deterministic manner. For example, when preferring route A over route B on your way to work, you may know that choice of neither route will avoid a traffic jam in all occasions. However, from experience you estimate that the chances of not getting into a jam are 80% for A and only 30% for B. Therefore, the information carried by single events is insufficient to guide decisions. We hypothesized that, if this integrative function is supported by the dACC/RCZ, then the response of this region to negative feedback should covary with the information content of the feedback. When low information content requires accumulation of negative outcomes over several trials before adjusting behavior, single negative feedback should evoke only a weak response. In contrast, if the informativity of feedback is high and thus a negative event is likely to indicate the need for a behavioral adjustment, a strong dACC/RCZ response and pronounced adjustment of action values should be evoked.
We tested this hypothesis by scanning human volunteers using functional magnetic resonance imaging (fMRI) while they performed a probabilistic reversal learning task on two different sessions. The information content carried by the feedback was manipulated by the stochastics of the reinforcement schedule: the correct stimulus was reinforced in either 90% [high probability (HP)] or 75% [low probability (LP)] of the trials.
Materials and Methods
Participants.
Twenty-two Caucasian subjects (12 females) participated in the study. One female subject had to be excluded due to excessive head motion on one of the two sessions. Thus, the final sample consisted of 11 female and 10 male subjects, aged 21–35 years (24.6 mean ± 0.76 SEM). All subjects gave written informed consent before fMRI measurements. The study was performed according to the Declaration of Helsinki.
Experimental design.
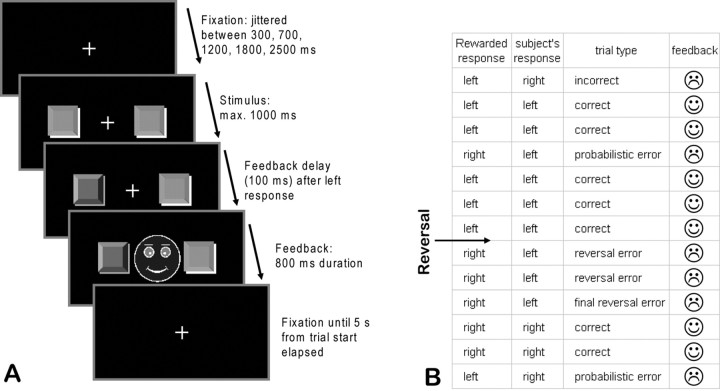
We used a probabilistic response reversal task (Cools et al., 2002). On each trial, subjects were required to choose between two identical stimuli, which consisted of two symbolic square buttons of the same color to the left and right of a central fixation cross. Subjects had to indicate their response with the index finger of the left or right hand. Subjects performed the task twice on two separate sessions separated by a minimum of 1 d (17.1 mean ± 5.39 SEM). In the HP session, one of the two responses (left or right) was rewarded in 90% of the trials, while in the remaining 10% of trials, the other response was rewarded. Reward allocation to one of the two responses was thus mutually exclusive. In the LP session, the reward ratio was 75% to 25%. The order of sessions was counterbalanced across subjects. After a randomly jittered block length of 18–24 trials, the reward contingencies reversed, and the other response was now rewarded with the respective probability. Note that this reversal learning task is entirely response based, implementing a reversal in response–reward mapping. This is in contrast to the task used by Cools et al. (2002), which implements a reversal in the stimulus–reward mapping. Participants were instructed to switch to the other response only when they were sure that the rule had changed. In both sessions, subjects underwent 19 blocks (and thus 18 contingency reversals), totaling 382 trials. Mean trial duration was 5 s. Additionally, 46 null events of the same duration were randomly interspersed with the experimental trials. During null events, only the fixation cross was presented. Each session lasted ∼36 min. On each trial (Fig. 1A), a central fixation cross was presented, followed by presentation of the two stimuli after a variable interval (randomly jittered between 300, 700, 1200, 1800, and 2500 ms). The two stimuli remained on the screen until the subject made a response or after 1000 ms had elapsed. After a response was made, the corresponding symbolic button on the screen was depressed to mark the subject's choice. Feedback consisted of a smiling face for correct responses and a frowning face for incorrect responses. If no response was made within a 1000 ms response window, a face with a question mark was presented. Feedback was presented centrally between the two stimuli with a delay of 100 ms after the response and remained on screen for 800 ms. After feedback offset, only the fixation cross remained on the screen until the end of the trial. For each positive feedback, participants received 0.01 euros (EUR). The cumulative reward was paid at the end of the experiment. As expected from the different reward schedule, subjects earned more money in the HP (mean 2.96 EUR ± 0.03 SEM) than in the LP (mean 2.13 EUR ± 0.02 SEM) session. Before scanning on the first session, subjects underwent a 30-trial training session to get familiarized with the concept of probabilistic errors (Cools et al., 2002).
Figure 1.
A, Sequence of stimulus events within a trial of the probabilistic reversal learning task. Following selection of one of the two stimuli, the choice was visualized to the subject by depression and darkening of the respective button on the screen. This was followed after 100 ms by positive or negative feedback, according to the task schedule. B, Example of a sequence of trials and the categorization of the trials according to the subject's response and the feedback obtained.
Reinforcement learning model.
There are many different variants of reinforcement learning models (Sutton and Barto, 1998). We used a simple Q-learning model (Watkins and Dayan, 1992) to obtain trial-by-trial measures of reward prediction error and decision certainty, parameters that are not directly observable in subjects' behavior. In this model, the two possible actions, i.e., choosing the left or right response, are assigned an action value QL(t) and QR(t), respectively. Q values are then updated on each trial by the deviation of the actual from the expected outcome:
α is the learning rate that scales the impact of the prediction error. δ is the prediction error, which is computed as follows:
where r is the reward, which is either 1 (reward available for choosing the left option) or 0 (reward available for choosing the alternative option). Values for QR(t) are calculated in analogy. Since in our task, reward allocation to the two responses is mutually exclusive, we designed our reinforcement learning model to update on each trial the Q values for both the chosen and the nonchosen option. This reflects the situation that upon every feedback, subjects gain information about both possible responses. Q values for the left and right responses were initialized with 0.5.
Subjects' choices were then modeled using softmax action selection (Sutton and Barto, 1998). On each trial, the probability of the model for choosing response L is as follows:
and the probability for choosing R is calculated analogously. The parameter β is the so-called temperature that reflects the subject's bias toward either exploratory (i.e., random choice of one response) or exploitatory (i.e., choice of the response with the highest Q value) behavior.
Decision certainty was determined as the absolute difference between the probabilities of the model for choosing the left or right response (Klein et al., 2007):
The model was fitted to subjects' behavior by searching the values for the parameters α and β that resulted in the best model fit. Iterations were run across both parameters from 0.01 to 1 with a step size of 0.01 (i.e., both α and β can take values from 0.01 to 1). The best-fitting parameters are those that yield the highest log likelihood estimate (LLE) (Frank et al., 2007) and therefore are most predictive of subjects' actual behavior:
where PC,t is the probability of the model to make the choice C that was actually made by the subject on trial t. The prediction error for the chosen response was derived on a trial-by-trial basis and subsequently used as a regressor in the fMRI analyses as described below. Additionally, the learning rates obtained for each subject in each of the two conditions were used as a covariate in the second-level analyses of prediction error-related activity.
Stochastics of the reward environment.
To obtain a formal measure that shows that the information content is lower in the LP than in the HP condition, we calculated the entropy (Mitchell, 1997) of the two reward schedules. Specifically, for a number of C consecutive trials, the entropy E is as follows:
where A and B are the number of trials in which the left and right response was rewarded, respectively. We calculated and subsequently averaged E for a sliding window of C = 6 trials moving along all trials of the experiment. Note that E can take on values between 0 and 1. Entropy is maximal when informativity is lowest, which in our context means that the left and right response are each rewarded in 50% of the trials within the sliding window. Furthermore, we also analyzed whether subjects' behavior was more random in the LP than in the HP condition. Therefore we calculated the behavioral entropy according to Equation 6, using for A and B the number of left and right choices of the subject, respectively.
Image acquisition.
Data acquisition was performed at 3 T on a Siemens Magnetom Trio equipped with an eight-channel phased array head coil. Thirty slices (3 mm thickness, 3 − 3 × 3 mm voxel size, 0.3 mm interslice gap) were obtained in an interleaved manner parallel to the anterior commissure–posterior commissure line using a single-shot gradient echo-planar imaging (EPI) sequence (repetition time: 2000 ms; echo time: 30 ms; bandwidth: 116 kHz; flip angle: 90°; 64 × 64 pixel matrix; field of view: 192 mm) sensitive to blood-oxygen level-dependent (BOLD) contrast. To improve the localization of activations, a high-resolution brain image (three-dimensional reference dataset) was recorded from each participant in a separate session using a modified driven equilibrium Fourier transform sequence.
Image processing and analysis.
Analysis of fMRI data was performed using FSL (FMRIB's Software Library) (Smith et al., 2004). Functional data were motion corrected using rigid-body registration to the central volume (Jenkinson et al., 2002). Low-frequency signals were removed using a Gaussian-weighted lines 1/100 Hz high-pass filter. Spatial smoothing was applied using a Gaussian filter with 7 mm full width at half maximum. Slice-time acquisition differences were corrected using Hanning-windowed sinc interpolation. Registration of the EPI images with the high-resolution brain images and normalization into standard (MNI) space was performed using affine registration (Jenkinson and Smith, 2001). A general linear model was fitted into prewhitened data space to account for local autocorrelations (Woolrich et al., 2001). Analysis I aimed at investigating effects of negative and positive feedback in general. Analysis II considered negative feedback in relation to reversals in task contingencies and behavioral changes. For analysis I, negative and positive feedback were modeled at feedback onset, and the contrast between negative and positive feedback (ALLNEG − ALLPOS) was assessed. For analysis II, a different trial classification was used, similar to the one used by Cools et al. (2002): negative feedback that was delivered following a correct response due to the probabilistic task schedule was termed a probabilistic error. When task contingencies reversed and subjects received negative feedback because they still responded to the previously correct stimulus, this was called a reversal error (REVERR), but only if those errors were not followed by a change of behavior on the subsequent trial. In contrast, reversal errors that were followed by a switch to the then correct response on the next trial were considered to be final reversal errors (FINREVERR) (Fig. 1B). All positive feedback trials were grouped together. To analyze prediction error-related signals, separate regressors were set up that contained the onsets (modeled to feedback onset) and the trial-by-trial amplitude of the prediction error (obtained from the computational model). For all analyses, the regressors were convolved with a synthetic hemodynamic response function (double gamma function) and its first derivative. For group analyses, individual contrast images derived from contrast between parameter estimates for the different events and those derived from the computational parameters, were entered into a second-level mixed-effects analysis (Woolrich et al., 2004), for which a general linear model was fit to estimate the group mean effect of the regressors. Analyses were first performed separately for the HP and LP sessions to detect patterns of activation. Subsequently, paired t tests were performed to assess differences in brain activity between the two conditions.
The following contrasts were calculated and assessed within and between the two groups: for the effects of negative feedback in general, the contrast ALLNEG − ALLPOS was analyzed. To investigate activity on error trials that was specific to reversals, we compared final reversal errors with positive feedback trials (FINREVERR − ALLPOS). To analyze the effects of negative feedback due to task rule reversal without a subsequent change in behavior, we contrasted reversal errors with positive feedback (REVERR − ALLPOS). Based on our own previous findings (Jocham et al., 2009) and those from Kennerley et al. (2006), we furthermore predicted that activity to negative feedback would be higher when this was preceded by another negative feedback trial (NEG + 1) than when it was the first negative feedback (NEG + 0) after positive feedback trials. The contrast (NEG + 1) − (NEG + 0) was calculated and compared between conditions. Time courses of the hemodynamic response function to NEG + 0 and NEG + 1 trials were extracted from a region of interest in the RCZ (derived from the between-condition comparison of the contrast NEG + 1 vs NEG + 0, MNI x = −6, y = 39, z = 29) using PEATE (Perl Event-Related Average Time course extraction), a companion tool to FSL (http://www.jonaskaplan.com/peate/peate-cocoa.html). Unlike in a previous study (Jocham et al., 2009), BOLD responses for NEG + 2 trials could only be calculated for the LP condition because three successive negative feedback trials rarely occurred in the HP condition. Results are reported on the whole-brain level with a significance level of p < 0.001 uncorrected and a minimum cluster size of five contiguous voxels, unless stated differently.
Persistence of behavioral adaptation.
To investigate postreversal behavior in more detail, we analyzed to what extent subjects sustained their new response after a reversal due to a change in task contingency. Specifically, we analyzed the eight trials following a final reversal error and analyzed, for all 18 blocks, the proportion of trials after reversal in which subjects maintained the newly correct response before they switched back to the (now) incorrect response.
Statistical analyses.
The number of reversal errors was defined by the number of trials it took subjects to switch to the alternative response after a change in reward contingencies, summed over all 18 reversals. The total number of switches between the two response options was also counted over the entire experimental session. Given our clear a priori predictions, behavioral and computational data were tested for differences between conditions using one-tailed paired t tests. The trial-by-trial parameter certainty derived from the model was plotted beginning from the third trial before a contingency reversal up to the 10th trial after a reversal (averaged across the 18 reversals) and analyzed using a two-factorial ANOVA with trial (14 time points) and condition (two conditions) as factors. When appropriate, post hoc paired t tests were used to identify significant differences between conditions at individual time points. A p value <0.05 was considered statistically significant.
Results
Behavioral and computational data
As expected, subjects committed more reversal errors in the LP than in the HP condition (p < 0.001). Across all 18 reversals the total number of reversal errors was (mean ± SEM) 41.10 ± 1.69 in the HP condition and 61.19 ± 4.18 in the LP condition. The average number of reversal errors committed per reversal was 2.31 ± 0.088 and 3.53 ± 0.227 for the HP and LP conditions, respectively (supplemental Fig. S1A, available at www.jneurosci.org as supplemental material). Furthermore, subjects switched between the two response alternatives significantly more often in the LP condition (total number of switches: 39.81 ± 3.96) than in the HP condition (total number of switches: 27.05 ± 3.31, p < 0.001) (supplemental Fig. S1B, available at www.jneurosci.org as supplemental material). This increased switching was due to an increased occurrence of switching after receiving negative feedback (lose–shift behavior) in the LP (35.95 ± 3.71) compared with the HP condition (22.24 ± 1.68, p < 0.001). In contrast, the incidence of switching after receiving positive feedback (win–shift behavior) did not differ between conditions (HP: 4.81 ± 1.78; LP: 3.86 ± 1.04; p > 0.29). We also analyzed whether the order in which subjects underwent the HP and LP session affected their behavior. None of the behavioral measures differed as a function of the order of testing (all p values >0.150).
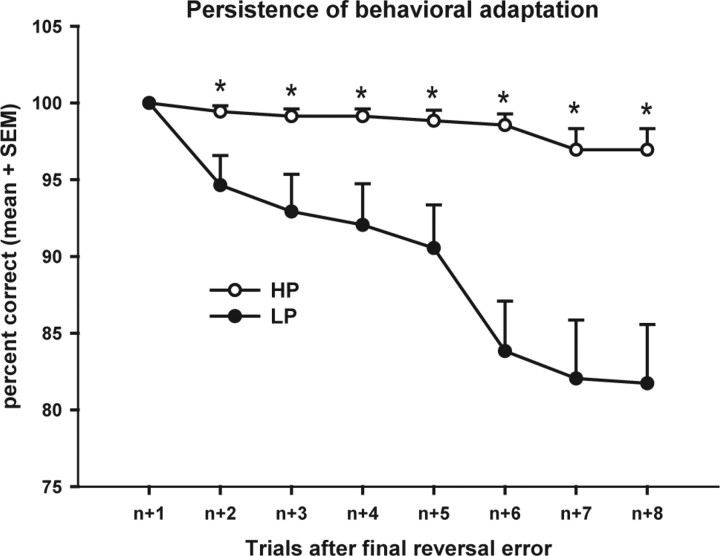
Figure 2 shows that, in the LP condition, with increasing number of trials after the final reversal error the likelihood decreased that subjects maintain the newly correct response. In the HP condition, in contrast, subjects' performance was still close to 100% even on the eighth trial after the final reversal error. Two-way ANOVA with trial (eight trials) and condition (two conditions) as factors revealed an effect of trial (F(7,140) = 21.704, p < 0.001) and condition (F(1,20) = 14.775, p = 0.001) and a trial × condition interaction (F(7,140) = 17.193, p < 0.001). Post hoc t test showed that subjects' likelihood to maintain the newly correct response was higher in the HP condition at all time points (p values <0.015) following the first trial after the final reversal error (here, by definition, each subject has a score of 100%). This reduced propensity of subjects in the LP condition to maintain the new response was most likely due to the increased number of negative feedback trials that subjects encountered in this condition (two-way ANOVA: effect of condition: F(1,21) = 14.531, p = 0.001, post hoc t test: p values <0.002 at all time points).
Figure 2.
Persistence of behavioral adaptations for the two conditions. Shown on the x-axis is the number of trials after a successful reversal of behavior, i.e., trial n + 1 is the trial immediately following the final reversal error. The values on the y-axis are the percentage of the 18 reversals, in which the subjects maintain this newly correct response on trials n + 1 to n + 8. *p < 0.02.
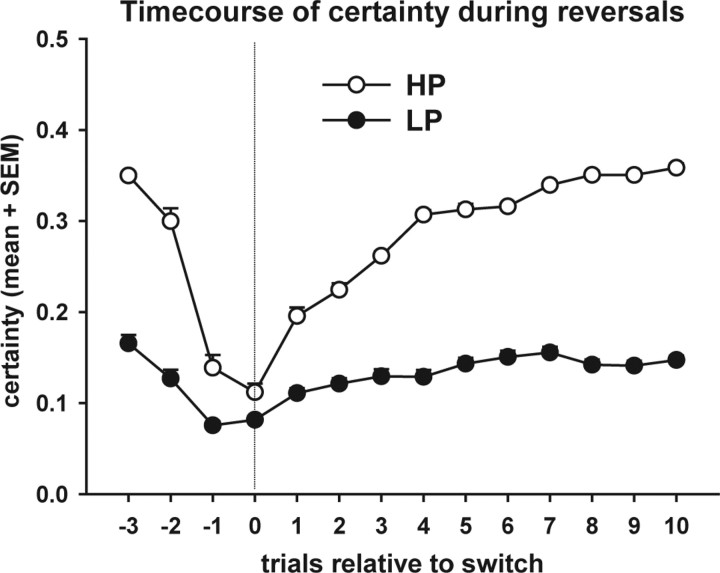
The learning rate α derived from the computational model was higher in the HP condition (0.2967 ± 0.0107) than in the LP condition (0.1662 ± 0.0121, p < 0.001) (supplemental Fig. S2A, available at www.jneurosci.org as supplemental material). In contrast, the temperature β, although numerically lower in the LP condition, did not differ significantly between the two conditions (p = 0.145) (supplemental Fig. S2B, available at www.jneurosci.org as supplemental material). Decision certainty was markedly lower in the LP (0.1387 ± 0.0058) than in the HP condition (0.3032 ± 0.003, p < 0.001) (supplemental Fig. S2C, available at www.jneurosci.org as supplemental material). Analysis of the course of decision certainty around the reversals shows that in the HP condition, subjects rapidly regained the level of certainty they had before the reversal, while subjects in the LP condition required more trials to reach the prereversal level again (which overall was lower in the LP condition) (Fig. 3). Two-way ANOVA revealed an effect of trial (F(13,260) = 195.21, p < 0.001), an effect of condition (F(1,20) = 613.9, p < 0.001), and a trial × condition interaction (F(13,260) = 67.78, p < 0.001) on decision certainty. Post hoc tests revealed that decision certainty was lower in the LP than in the HP condition in all of the analyzed trials (p values <0.002).
Figure 3.
Time course of the trial-by-trial decision certainty, plotted relative to rule reversals (averaged across all 18 reversals). Trial 0 is the trial at which the alternative response is selected for the first time following a rule reversal. Subjects in the HP condition rapidly regain prereversal levels of certainty while this takes longer in the LP condition. In the LP condition, certainty generally remains at a lower level than in the HP condition (p < 0.05 at all time points).
The mean magnitude of the positive prediction error was significantly higher in the LP (0.376454 ± 0.006287) than in the HP condition (0.1830596 ± 0.002823, p < 0.001). The mean magnitude of the negative prediction error in contrast was significantly higher in the HP (−0.787217 ± 0.009232) than in the LP condition (−0.636685 ± 0.006745, p < 0.001).
Analysis of the entropy of the reward environment, i.e., the reinforcement schedules of the HP and the LP condition, revealed a higher level of entropy in the LP condition (Table 1). This formal measure thus shows that the variation in reward allocation to the two response options is higher in the LP condition, rendering the overall information context in this condition less stable. Furthermore, not only the reward schedule, but also subjects' behavior, was characterized by a significantly higher level of entropy (p < 0.001) in the LP condition (Table 1).
Table 1.
Mean entropy of the reinforcement schedule (environmental entropy) and of subjects' choices (behavioral entropy) for the HP and LP conditions
| Environmental entropy | Behavioral entropy | |
|---|---|---|
| HP | 0.509 ± 0.0189 | 0.23779 ± 0.0117 |
| LP | 0.8302 ± 0.0099 | 0.61756 ± 0.0123 |
Both environmental and behavioral entropy are higher in the LP condition.
Imaging data
Negative feedback (ALLNEG − ALLPOS) induced significant signal change in the RCZ and in the lateral PFC in both conditions. In the LP condition, lateral PFC activation was restricted to the right hemisphere, while it was observed bilaterally in the HP condition (supplemental Fig. S3, available at www.jneurosci.org as supplemental material). Furthermore, in the HP condition, there was increased BOLD signal in response to negative feedback in the posterior cingulate cortex. Importantly, the response of the RCZ to negative feedback in general did not differ between conditions.
Reversal-related activity (FINREVERR − ALLPOS) was found in the RCZ and the bilateral middle frontal gyrus in both conditions. In the HP condition, there was additional activation in the pregenual BA 32 and bilaterally in the inferior parietal lobule (the latter was observed only on the right side in the LP condition). See supplemental Table S1 (available at www.jneurosci.org as supplemental material) for a complete list of activated brain regions in this contrast. Reversal-related activity in the RCZ did not differ between conditions. Only in the right dorsal postcentral sulcus, activity was higher in the HP than in the LP condition. Activity induced by reversal errors not followed by a switch (REVERR − ALLPOS) was found in similar regions as in the contrast FINREVERR − ALLPOS (for a complete list of activated brain regions, refer to supplemental Table S2, available at www.jneurosci.org as supplemental material). These included the RCZ, the middle frontal gyrus, and the bilateral inferior parietal lobule in both conditions (Fig. 4). In agreement with our hypothesis, paired t test revealed that reversal errors elicited a stronger effect in the RCZ (MNI x = 6, y = 34, z = 31, 1764 mm3) and bilaterally in the lateral prefrontal cortex (MNI x = 45, y = 31, z = 31, 1266 mm3 and x = −44, y = 27, z = 22, 1214 mm3) in the HP than in the LP condition (Fig. 4).
Figure 4.
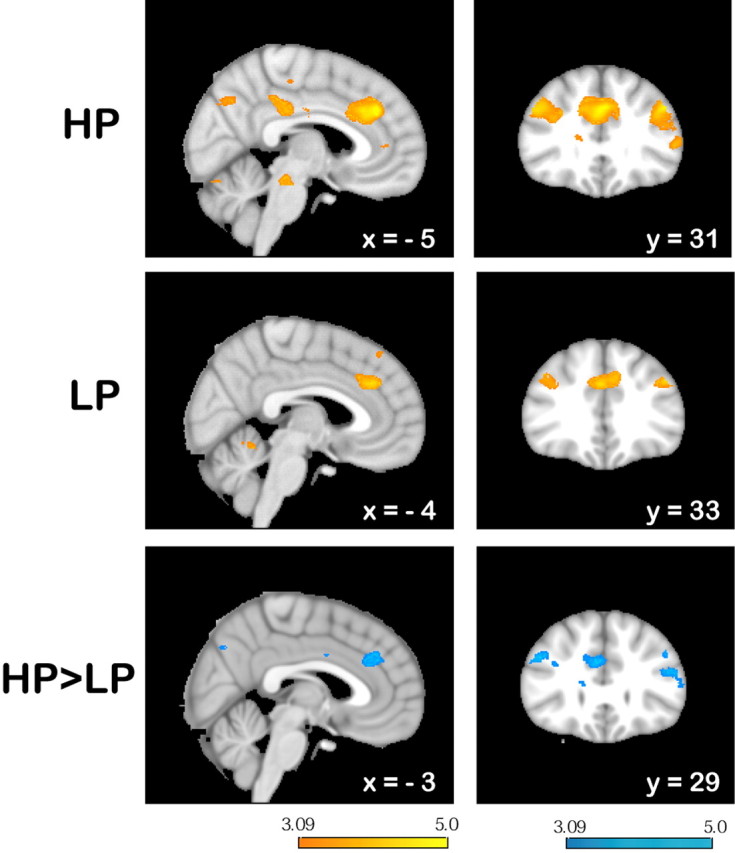
Signal change in response to reversal errors (REVERR − ALLPOS) superimposed on the MNI template brain. In both conditions (HP: top row; LP: middle row), there was increased activity in the RCZ (left) and in the lateral prefrontal cortex (right). Both the response of the RCZ and the lateral prefrontal cortex were more pronounced in the HP than in the LP condition. The color bars indicate z-scores. See supplemental Table S2 (available at www.jneurosci.org as supplemental material) for a comprehensive list of all activations.
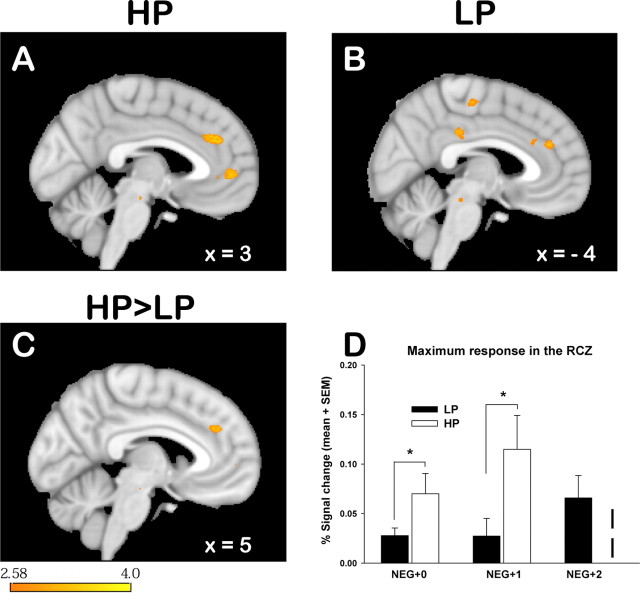
Signals that correlated with positive reward prediction errors were found in the medial orbitofrontal cortex and in the posterior cingulate cortex in both conditions. Negative prediction error signals were found in the HP condition in the RCZ (Fig. 5A), the posterior cingulate cortex, and a large part of the bilateral middle frontal gyrus. Similarly, in the LP condition, negative prediction error signals were also observed in the RCZ (Fig. 5B) and in the middle frontal gyrus; the latter, however, was only found in the right hemisphere. Comparisons between the two conditions showed that the correlation of the negative prediction error with RCZ activity was more pronounced in the HP than in the LP condition (MNI x = 5, y = 22, z = 27, 137 mm3) (Fig. 5C). The degree to which the prediction error is used to update the action value (the Q value of the reinforcement learning model) is determined by the learning rate α. We assumed that RCZ activity represents the degree to which action values are updated. Therefore, we hypothesized that the increased correlation of RCZ activity with negative prediction errors is driven by the learning rate (which scales the impact of the prediction error). To show this, we conducted the second-level comparison between the HP and LP conditions again, this time using each subject's learning rate as a covariate. This abolished the difference between the two conditions, thus showing that the different correlation is mediated by the learning rate. Furthermore, to show more directly that RCZ activity is related to updating of action values, prediction error regressors from each subject were multiplied with the individual subject's learning rate. This again yielded a strong correlation with RCZ activity. Additionally, just like for the second-level parametric analysis, which takes the learning rate into account, the correlation here did not differ between the HP and LP conditions either.
Figure 5.
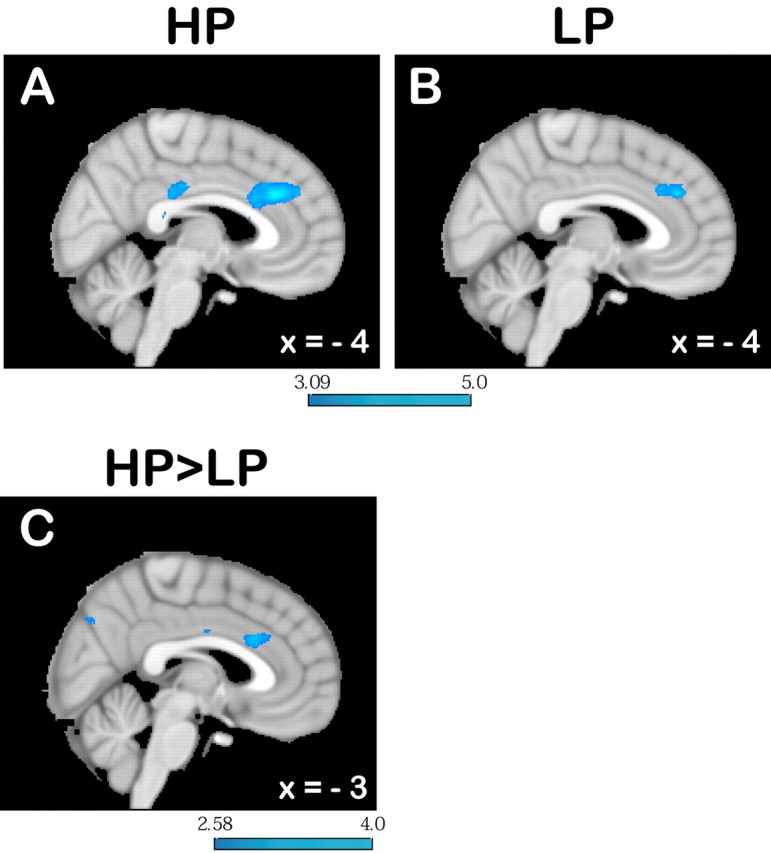
Signal change related to negative prediction errors derived from a reinforcement learning model. A, B, There was marked signal increase in response to negative prediction errors in the RCZ in both the HP (A) and LP (B) conditions. This effect was more pronounced in the HP than in the LP condition. For illustration of the extent of the HP-LP difference, the image in C is thresholded at p < 0.005. The color bar indicates z-scores.
Analysis of the contrast NEG + 1 (negative feedback preceded by a trial with negative feedback) versus NEG + 0 (negative feedback preceded by a trial with positive feedback) revealed increased BOLD response in the RCZ for NEG + 1 compared with NEG + 0 trials in both conditions. However, in the LP condition, the extent of activation was below the required cluster threshold; therefore, results are shown at p < 0.005 in Figure 6[HP: MNI x = −7, y = 35, z = 29, 402 mm3 (Fig. 6A); LP: MNI x = 4, y = 39, z = 24, 37 mm3 (Fig. 6B)]. Consistent with our hypothesis, this effect was more pronounced in the HP condition (MNI x = −4, y = 39, z = 29, 305 mm3, p < 0.005) (Fig. 6C). We extracted time courses of hemodynamic activity from a sphere with 3 mm radius centered at the peak coordinate of the between-condition difference and calculated the base-to-peak amplitudes of the BOLD response for NEG + 0 and NEG + 1 trials. Paired t test showed that in NEG + 1, but also already in NEG + 0, the amplitudes were markedly higher in the HP than in the LP condition (p < 0.04 and p < 0.01, for NEG + 0 and NEG + 1, respectively) (Fig. 6D).
Figure 6.
Signal change in the RCZ in response to negative feedback depended on whether a trial with negative feedback was preceded by another trial with negative feedback (NEG + 1) or not (NEG + 0). A, B, The contrast NEG + 1 versus NEG + 0 showed increased activity in the RCZ in both the HP (A) and LP (B) conditions at p < 0.005. C, This effect was more pronounced in the HP than in the LP condition at p < 0.005. Time courses of hemodynamic activity were extracted from a 3 mm sphere centered on the peak coordinate of the contrast shown in A at MNI x = −6, y = 39, z = 29. D, Base-to-peak amplitudes were calculated as the difference from baseline (mean from −4 s to event onset) to peak (mean from the time points 4–8 seconds after event onset). *p < 0.05, one-tailed. The amplitudes for NEG + 2 trials could only be calculated for the LP condition, because many subjects in the HP condition hardly ever encountered three consecutive negative feedback trials. The color bar indicates z-scores.
Discussion
The purpose of the present experiment was to create two experimental environments that require subjects to integrate action outcomes over different numbers of trials. Our results indicate that subjects indeed had to integrate over a higher number of trials in the LP than in the HP condition, as is evident by the increased number of reversal errors. In accordance with this, the learning rate derived from a Q-learning algorithm was higher for the HP than for the LP condition, consistent with a more rapid adaptation to the environment in the HP condition. These results demonstrate that subjects in the LP condition rely less on the individual feedback they receive in one trial, but integrate outcome information over more trials. This reduced impact of single action outcomes was mirrored by the diminished impact of reversal-related negative feedback on RCZ activity: when subjects received negative feedback due to a change of task contingencies, this evoked a stronger RCZ response in the HP than in the LP condition. Furthermore, as was previously shown (Jocham et al., 2009), the response of the RCZ to negative feedback increased from the first to the second successive negative feedback. Again, this increase was steeper in the HP condition. Importantly, the response of the RCZ to the final reversal error, i.e., the time at which subjects have collected enough information to be certain that the task contingencies have reversed, did not differ between conditions. Furthermore, the response of the RCZ to negative feedback in general was not different between conditions either. The overall network of brain regions we found to be activated upon reversals included the RCZ, lateral prefrontal cortex, and lateral parietal cortex. This is consistent with previous studies (Cools et al., 2002; Kringelbach and Rolls, 2003; Budhani et al., 2007; Cohen et al., 2007; Mitchell et al., 2008; Jocham et al., 2009).
The increased number of reversal errors and the lower learning rate in the LP condition reflect the fact that subjects have to widen the window of trials across which they integrate action outcomes. Still, even though subjects took more trials in the LP condition to reverse to the newly correct choice, they did not attain the same level of certainty. Furthermore subjects showed an increased amount of overall switching between the response alternatives in the LP condition. Information content of feedback can formally be described by the outcome entropy of the reinforcement schedule (Eq. 6), which is higher in the LP condition. Since entropy is inversely related to information content, this indicates lower information content in the LP condition. As can be expected from the increased overall occurrence of switching behavior in the LP condition, not only the entropy of the reinforcement schedule, but also behavioral entropy, was higher in this condition.
Our findings show similarities to those by Behrens et al. (2007), who showed that subjects' estimate of the environment's “volatility” correlated with fMRI signal in the RCZ. In their study, subjects performed two sessions, one in which no reversal of contingencies occurred and one in which contingencies reversed every 30–40 trials (stable reward rate in both environments). This is different to our experiment, where the frequency of rule reversals is the same for both conditions but the reward rates differ (HP vs LP). Thus, rather than “volatility” caused by rule reversals, it is the “reliability” of the feedback that drives the differences in our study. Our data show that negative feedback is encoded in the RCZ in adaptation to the reward environment, i.e., the reliability of the feedback. When individual events contain less behaviorally relevant information, RCZ responses to negative feedback are diminished, and prominent responses are only evoked when evidence in favor of a change in the environment accumulates. Responses of the RCZ to negative feedback are thus dependent on the outcome of previous trials, as has already been demonstrated (Jocham et al., 2009). Therefore, using a different approach than Behrens et al. (2007), we provide additional support for the concept that RCZ activity reflects the degree to which subjects use the information they obtain to guide future decisions. Both approaches therefore seem to converge to the same conclusion on RCZ function: its activity is related to updating of action values.
How does the RCZ accomplish the widening or narrowing of the window of trials across which reinforcement information has to be integrated—or in other words, how are different environmental statistics transformed into more or less pronounced responses of the RCZ to negative feedback? The RCZ is anatomically well positioned to integrate actions and outcomes. On the one hand, this area is closely interconnected with the motor system. The monkey CMA projects to and receives afferents from primary and secondary motor cortices (Morecraft and Van Hoesen, 1992; Bates and Goldman-Rakic, 1993; Picard and Strick, 1996; Hatanaka et al., 2003). The CMA also projects to the striatum (Takada et al., 2001), and there are direct projections to motor neurons of the spinal cord (He et al., 1995). On the other hand, information regarding the valence of outcomes is conveyed to the CMA from the amygdala and orbitofrontal cortex (Barbas and De Olmos, 1990; Ongür and Price, 2000). Through the constant integration of actions with their outcomes, the RCZ might be trained to enhance or decrease the response to negative feedback, depending on whether behavioral adaptations had been successful or not. In case of the LP condition, the environment is rather “noisy,” as is evident by the increased entropy of the reinforcement schedule, and negative feedback on rule reversals (i.e., the signal needed to guide behavior) is not as salient as in the HP condition and thus is less likely to evoke a significant RCZ response.
Another aspect of the present study is that we found pronounced responses of the RCZ to a computational model-derived negative prediction error signal. While a large body of literature exists on signals relating to positive reward prediction errors, in particular in the striatum (McClure et al., 2003; O'Doherty, 2004; O'Doherty et al., 2004; Ramnani et al., 2004; Abler et al., 2006; Menon et al., 2007), signals related to negative reward prediction errors have been largely neglected. It is noteworthy that, in our present study, negative prediction errors engaged the RCZ to a higher degree in the HP than in the LP condition, thus paralleling our findings from reversal-related activity to negative feedback. This difference in the strength of correlations between conditions demonstrates that the negative prediction error is not the sole factor that drives RCZ activity. In fact, adding the learning rate as a covariate, the difference between the conditions disappeared. This suggests that it is not the prediction error alone, but rather the prediction error scaled by the learning rate that is encoded in the RCZ. The product of learning rate and prediction error represents the value on the right side of Equation 1 that is added to the current Q value, i.e., the term that determines the extent to which the action value is updated. This finding is consistent with a recent study by Behrens et al. (2007) showing a correlation between the individual learning rate and RCZ activity.
It is puzzling that, on the one hand, RCZ activity to negative feedback increased with the number of preceding negative feedback trials, while, on the other hand, RCZ activity also covaried with negative reward prediction errors. Since negative prediction errors become smaller upon every successive negative feedback, this appears contradictory. However, our data suggest that RCZ activity is not driven by negative prediction errors alone, but instead is correlated with the updating of action values, i.e., the product of prediction error and learning rate. A disadvantage of the current model might be that one single learning rate was fitted for each subject, which remains constant throughout the course of the experiment. Addressing the issue of a dynamic learning rate remains a challenge for future modeling studies.
While reinforcement learning models assume an implicit process, it is well conceivable that subjects also made use of declarative/explicit strategies. Implicit and explicit strategies may well work in parallel to allow optimal decision making. On the basis of the present data, it cannot be determined to which extent subjects made use of either of the two. However, in our opinion, this does not object the interpretation that the learning rate and the response of the RCZ depend both on the outcome of previous trials and on the stochastics of the reward environment.
It is also conceivable that subjects based their estimate of whether or not a reversal had occurred on calculations of point probability. However, point probabilities would converge to a similar result as feedback integration over trials: a single negative feedback is more likely to indicate a reversal in the HP than in the LP condition and therefore can be seen as more informative. Thus, calculation of point probabilities might be one possible cognitive process that dictates the differential search window and updating of action values. The increased entropy in the LP condition, of both reward environment and behavior, supports this interpretation.
Together, the results of the present study show that the response of the RCZ to negative feedback varies as a function of the environmental context. The more stochastic, and therefore, the less reliable the environment becomes, the less pronounced are the responses of the RCZ to single negative events. Behaviorally, this is paralleled by a longer period of trials across which action–outcome associations are integrated and an increase in the number of errors committed before reversing. Furthermore, signals related to negative reward prediction errors also diminish with lower learning rates, i.e., decreasing reliability of the feedback. The responsivity of the RCZ is thus related to changing environmental stochastics, and action values are adjusted to allow optimal adaptation to reversing reward contingencies.
Footnotes
J.N. was supported by a grant from the National Institutes of Health (R01 MH74457). We are very thankful to Tim Behrens for his support in estimating volatility in our task and for valuable discussions.
References
- Abler B, Walter H, Erk S, Kammerer H, Spitzer M. Prediction error as a linear function of reward probability is coded in human nucleus accumbens. Neuroimage. 2006;31:790–795. doi: 10.1016/j.neuroimage.2006.01.001. [DOI] [PubMed] [Google Scholar]
- Amiez C, Joseph JP, Procyk E. Reward encoding in the monkey anterior cingulate cortex. Cereb Cortex. 2006;16:1040–1055. doi: 10.1093/cercor/bhj046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbas H, De Olmos J. Projections from the amygdala to basoventral and mediodorsal prefrontal regions in the rhesus monkey. J Comp Neurol. 1990;300:549–571. doi: 10.1002/cne.903000409. [DOI] [PubMed] [Google Scholar]
- Bates JF, Goldman-Rakic PS. Prefrontal connections of medial motor areas in the rhesus monkey. J Comp Neurol. 1993;336:211–228. doi: 10.1002/cne.903360205. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Woolrich MW, Walton ME, Rushworth MF. Learning the value of information in an uncertain world. Nat Neurosci. 2007;10:1214–1221. doi: 10.1038/nn1954. [DOI] [PubMed] [Google Scholar]
- Budhani S, Marsh AA, Pine DS, Blair RJ. Neural correlates of response reversal: considering acquisition. Neuroimage. 2007;34:1754–1765. doi: 10.1016/j.neuroimage.2006.08.060. [DOI] [PubMed] [Google Scholar]
- Cohen MX, Krohn-Grimberghe A, Elger CE, Weber B. Dopamine gene predicts the brain's response to dopaminergic drug. Eur J Neurosci. 2007;26:3652–3660. doi: 10.1111/j.1460-9568.2007.05947.x. [DOI] [PubMed] [Google Scholar]
- Cools R, Clark L, Owen AM, Robbins TW. Defining the neural mechanisms of probabilistic reversal learning using event-related functional magnetic resonance imaging. J Neurosci. 2002;22:4563–4567. doi: 10.1523/JNEUROSCI.22-11-04563.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Moustafa AA, Haughey HM, Curran T, Hutchison KE. Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proc Natl Acad Sci U S A. 2007;104:16311–16316. doi: 10.1073/pnas.0706111104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gehring WJ, Willoughby AR. The medial frontal cortex and the rapid processing of monetary gains and losses. Science. 2002;295:2279–2282. doi: 10.1126/science.1066893. [DOI] [PubMed] [Google Scholar]
- Hatanaka N, Tokuno H, Hamada I, Inase M, Ito Y, Imanishi M, Hasegawa N, Akazawa T, Nambu A, Takada M. Thalamocortical and intracortical connections of monkey cingulate motor areas. J Comp Neurol. 2003;462:121–138. doi: 10.1002/cne.10720. [DOI] [PubMed] [Google Scholar]
- He SQ, Dum RP, Strick PL. Topographic organization of corticospinal projections from the frontal lobe: motor areas on the medial surface of the hemisphere. J Neurosci. 1995;15:3284–3306. doi: 10.1523/JNEUROSCI.15-05-03284.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jocham G, Klein TA, Neumann J, von Cramon DY, Reuter M, Ullsperger M. Dopamine DRD2 polymorphism alters reversal learning and associated neural activity. J Neurosci. 2009;29:3695–3704. doi: 10.1523/JNEUROSCI.5195-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennerley SW, Walton ME, Behrens TE, Buckley MJ, Rushworth MF. Optimal decision making and the anterior cingulate cortex. Nat Neurosci. 2006;9:940–947. doi: 10.1038/nn1724. [DOI] [PubMed] [Google Scholar]
- Kerns JG, Cohen JD, MacDonald AW, 3rd, Cho RY, Stenger VA, Carter CS. Anterior cingulate conflict monitoring and adjustments in control. Science. 2004;303:1023–1026. doi: 10.1126/science.1089910. [DOI] [PubMed] [Google Scholar]
- Klein TA, Neumann J, Reuter M, Hennig J, von Cramon DY, Ullsperger M. Genetically determined differences in learning from errors. Science. 2007;318:1642–1645. doi: 10.1126/science.1145044. [DOI] [PubMed] [Google Scholar]
- Kringelbach ML, Rolls ET. Neural correlates of rapid reversal learning in a simple model of human social interaction. Neuroimage. 2003;20:1371–1383. doi: 10.1016/S1053-8119(03)00393-8. [DOI] [PubMed] [Google Scholar]
- Matsumoto K, Suzuki W, Tanaka K. Neuronal correlates of goal-based motor selection in the prefrontal cortex. Science. 2003;301:229–232. doi: 10.1126/science.1084204. [DOI] [PubMed] [Google Scholar]
- Matsumoto M, Matsumoto K, Abe H, Tanaka K. Medial prefrontal cell activity signaling prediction errors of action values. Nat Neurosci. 2007;10:647–656. doi: 10.1038/nn1890. [DOI] [PubMed] [Google Scholar]
- McClure SM, Berns GS, Montague PR. Temporal prediction errors in a passive learning task activate human striatum. Neuron. 2003;38:339–346. doi: 10.1016/s0896-6273(03)00154-5. [DOI] [PubMed] [Google Scholar]
- Menon M, Jensen J, Vitcu I, Graff-Guerrero A, Crawley A, Smith MA, Kapur S. Temporal difference modeling of the blood-oxygen level dependent response during aversive conditioning in humans: effects of dopaminergic modulation. Biol Psychiatry. 2007;62:765–772. doi: 10.1016/j.biopsych.2006.10.020. [DOI] [PubMed] [Google Scholar]
- Mitchell DG, Rhodes RA, Pine DS, Blair RJ. The contribution of ventrolateral and dorsolateral prefrontal cortex to response reversal. Behav Brain Res. 2008;187:80–87. doi: 10.1016/j.bbr.2007.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell T. New York: McGraw-Hill; 1997. Machine learning. [Google Scholar]
- Morecraft RJ, Van Hoesen GW. Cingulate input to the primary and supplementary motor cortices in the rhesus monkey: evidence for somatotopy in areas 24c and 23c. J Comp Neurol. 1992;322:471–489. doi: 10.1002/cne.903220403. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP. Reward representations and reward-related learning in the human brain: insights from neuroimaging. Curr Opin Neurobiol. 2004;14:769–776. doi: 10.1016/j.conb.2004.10.016. [DOI] [PubMed] [Google Scholar]
- O'Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304:452–454. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- Ongür D, Price JL. The organization of networks within the orbital and medial prefrontal cortex of rats, monkeys and humans. Cereb Cortex. 2000;10:206–219. doi: 10.1093/cercor/10.3.206. [DOI] [PubMed] [Google Scholar]
- Picard N, Strick PL. Motor areas of the medial wall: a review of their location and functional activation. Cereb Cortex. 1996;6:342–353. doi: 10.1093/cercor/6.3.342. [DOI] [PubMed] [Google Scholar]
- Ramnani N, Elliott R, Athwal BS, Passingham RE. Prediction error for free monetary reward in the human prefrontal cortex. Neuroimage. 2004;23:777–786. doi: 10.1016/j.neuroimage.2004.07.028. [DOI] [PubMed] [Google Scholar]
- Ridderinkhof KR, Ullsperger M, Crone EA, Nieuwenhuis S. The role of the medial frontal cortex in cognitive control. Science. 2004;306:443–447. doi: 10.1126/science.1100301. [DOI] [PubMed] [Google Scholar]
- Shima K, Tanji J. Role for cingulate motor area cells in voluntary movement selection based on reward. Science. 1998;282:1335–1338. doi: 10.1126/science.282.5392.1335. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(Suppl 1):S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Cambridge, MA: MIT; 1998. Reinforcement learning: an introduction. [Google Scholar]
- Swick D, Turken AU. Dissociation between conflict detection and error monitoring in the human anterior cingulate cortex. Proc Natl Acad Sci U S A. 2002;99:16354–16359. doi: 10.1073/pnas.252521499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takada M, Tokuno H, Hamada I, Inase M, Ito Y, Imanishi M, Hasegawa N, Akazawa T, Hatanaka N, Nambu A. Organization of inputs from cingulate motor areas to basal ganglia in macaque monkey. Eur J Neurosci. 2001;14:1633–1650. doi: 10.1046/j.0953-816x.2001.01789.x. [DOI] [PubMed] [Google Scholar]
- Ullsperger M, von Cramon DY. Subprocesses of performance monitoring: a dissociation of error processing and response competition revealed by event-related fMRI and ERPs. Neuroimage. 2001;14:1387–1401. doi: 10.1006/nimg.2001.0935. [DOI] [PubMed] [Google Scholar]
- Ullsperger M, von Cramon DY. Error monitoring using external feedback: specific roles of the habenular complex, the reward system, and the cingulate motor area revealed by functional magnetic resonance imaging. J Neurosci. 2003;23:4308–4314. doi: 10.1523/JNEUROSCI.23-10-04308.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullsperger M, von Cramon DY. Neuroimaging of performance monitoring: error detection and beyond. Cortex. 2004;40:593–604. doi: 10.1016/s0010-9452(08)70155-2. [DOI] [PubMed] [Google Scholar]
- Walton ME, Devlin JT, Rushworth MF. Interactions between decision making and performance monitoring within prefrontal cortex. Nat Neurosci. 2004;7:1259–1265. doi: 10.1038/nn1339. [DOI] [PubMed] [Google Scholar]
- Watkins CJCH, Dayan P. Q-learning. Machine Learning. 1992;8:279–292. [Google Scholar]
- Williams ZM, Bush G, Rauch SL, Cosgrove GR, Eskandar EN. Human anterior cingulate neurons and the integration of monetary reward with motor responses. Nat Neurosci. 2004;7:1370–1375. doi: 10.1038/nn1354. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Ripley BD, Brady M, Smith SM. Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage. 2001;14:1370–1386. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Behrens TE, Beckmann CF, Jenkinson M, Smith SM. Multilevel linear modelling for FMRI group analysis using Bayesian inference. Neuroimage. 2004;21:1732–1747. doi: 10.1016/j.neuroimage.2003.12.023. [DOI] [PubMed] [Google Scholar]