Highly Fluorescent Noble Metal Quantum Dots

Abstract

Highly fluorescent, water-soluble, few-atom noble metal quantum dots have been created that behave as multi-electron artificial atoms with discrete, size-tunable electronic transitions throughout the visible and near IR. These “molecular metals” exhibit highly polarizable transitions and scale in size according to the simple relation, E_fermi/N^1/3, predicted by the free electron model of metallic behavior. This simple scaling indicates that fluorescence arises from intraband transitions of free electrons and that these conduction electron transitions are the low number limit of the plasmon – the collective dipole oscillations occurring when a continuous density of states is reached. Providing the “missing link” between atomic and nanoparticle behavior in noble metals, these emissive, water-soluble Au nanoclusters open new opportunities for biological labels, energy transfer pairs, and light emitting sources in nanoscale optoelectronics.

INTRODUCTION

While high conductivity and beautiful surface luster are generally accepted as the characteristics of bulk noble metals (1–4), the study of few-atom metal clusters has attracted great interest because they bridge the properties of isolated atoms to nanoparticles and even to the bulk (5–10). Nanoscale metals are roughly classified into three size domains: large nanoparticles, small nanoparticles, and clusters, corresponding to three different characteristic length scales (1, 11). Optical responses of large metal nanoparticles (R>λ) to external electromagnetic fields are simply dependent on their sizes, free electron density, and, therefore, their nearly bulk-like dielectric function relative to that of the surrounding medium, and they can be quantitatively described with Mie theory (1). When particle size approaches the electron mean free path (~50 nm for gold and silver) (11), the dielectric function and refractive indices become strongly size dependent, but when properly incorporated, Mie theory still provides an adequate description (1, 11). Eventually, when particle size becomes comparable to the third characteristic length - the Fermi wavelength of an electron (i.e. de Broglie’s wavelength of an electron at the Fermi energy, or ~0.5 nm for gold and silver) (2, 12, 13), optical, electronic, and chemical properties of metal clusters are dramatically different from the other two size regimes. In this smallest size regime, metal clusters become “molecular species” (14–16), and discrete states with strong fluorescence can be observed (6, 9, 10, 17–22). It is these molecule-like properties of such highly polarizable, few atom metal clusters that is the primary topic of this review.

Our goal has been to explore and exploit the high polarizability and free electron scalings of molecular-scale metal clusters in the condensed phase. While nicely demonstrated in the gas phase for alkali metals (23–27), Au (28–30) and Ag clusters (31–33) offer not only the opportunity for maintaining metallic properties in aqueous solutions, but also great promise as a new class of biolabels. Much fundamental and applied work continues in our laboratory and in others (34–38) on these materials due to their exciting optical properties. While Ag nanoclusters hold great potential as robust optical materials, the atom to bulk transition in aqueous Au nanoclusters, as revealed by their size-dependent photophysics is the primary focus of this review. Providing the “missing link” between atomic and nanoparticle behavior in noble metals, these highly fluorescent Au nanoclusters smoothly link the optical and electronic structure transitions from atoms to nanoparticles with observable free electron behavior and likely serve as a guide in understanding the even brighter emission from Ag nanoclusters.

FREE ELECTRON MODEL

In 1900, Drude successfully explained the electrical and thermal conductivities of metals by modifying the kinetic theory of gases to account for the greatly increased electron densities and interactions of metals (1, 11). Drude’s modifications were: (1) The interactions of a given electron with other particles are neglected between collisions. (2) Electron-electron scattering is neglected. (3) Electrons experience a collision probability per unit time of 1/τ, where τ is the interval between two successive collisions. Consequently, the Drude model considers the valence electrons of metals to be free electrons due to strong electron screening effects. These free electrons are delocalized in bulk metals and do not belong to any specific metal atoms. As a result, free electrons move in the constant potential field provided by the positively charged cores. The total Hamiltonian of free electrons in a metal can be written as the sum of “noninteracting” Hamiltonians of free electrons (i.e. the “one particle” approximation). Although the free electron model was originally proposed based on the kinetic theory of gases, the dramatic difference between these two systems is that the energy levels are not quantized in a gas while they are quantized in metals due to the Pauli exclusion principle (11, 39). Therefore, a simple particle in a box model can be used to describe the energies of the free electrons in few-nm and smaller metals,

$$E_n=\frac{n^2{h}^2}{8m{L}^2}$$ [1]

in which n is the principal quantum number, E_n is the energy of a quantized level, L is the size of the metal, m is electron mass, and h is Planck’s constant. This simple model sheds light on how the free electrons pile up in metals, as governed by level multiplicities within this approximately harmonic confinement potential at small cluster size (11, 39). The topmost filled level corresponds to the highest electron energy of a given metal, called the Fermi energy E_f, which is independent of the metal size.

On all size scales the displacement of free electrons in an electric field gives rise to polarization changes at the nanoparticle surface with a linear restoring force between electrons and positive charges (1). Differences in size-dependent optical response mainly arise from the change in the number of free electrons. When metal nanoparticle sizes become much smaller than the electron mean free path, both the absorption frequency and linewidth have simple size dependences and are quantitatively related to inverse particle radius, R⁻¹ (40). Consequently, when metal nanoparticle size approaches the Fermi wavelength, the continuous band structures of metals break up into discrete energy levels. In 1964, Kubo produced quantitative predictions of the electronic structure of very small metal clusters based on the recognition that quasi-continuous electron energy states of bulk metals become discrete on the few-atom scale (12). The energy level spacing between adjacent levels for a N-atom particle is on the order of E_f/N, where E_f is the Fermi energy of the bulk metal. The relative difference between the energy level spacing and thermal energy has become a criterion to distinguish metallic from nonmetallic behavior (41). If the energy level spacings are smaller than k_BT, thermal energy can create mobile electron-hole pairs in the metals, and current can flow. However, if energy level spacings are much larger than available thermal energy, the free electrons in the metal clusters are confined to discrete energy levels. Thus, the metal clusters are often considered to be nonmetallic, even though they may exhibit free electron scaling behavior. Although Kubo et al. predicted some properties of metal cluster electronic structure, quantitative correlation of electronic structures with the number of metal atoms was not elucidated until 1984 (25).

OPTICAL RESPONSE OF ALKALI METAL CLUSTERS AND THE JELLIUM MODEL

Knight and co-workers observed a periodic pattern of intense peaks in the mass spectra of sodium clusters, indicating that Na_N clusters with N=2,8,18,20,40,58 have greater stability than do others (25). These magic numbers can be rationalized with a simple quantum mechanical model – the jellium model, which originates from nuclear physics (23, 25, 27, 40). Due to strong electron screening effects, valence electrons of noble metal atoms are considered free electrons after neglecting electron-electron and electron-ion interactions. In this model, a metal cluster is modeled by uniform, positively charged spheres with electronic shells filled with free electrons. These free electrons are provided by the valence electrons of the individual metal atoms forming the clusters which delocalize and form orbitals surrounding the positively charged core. Distinct from electronic structure of single atoms, cluster electron density is independent of the number of free electrons in the metal clusters, similar to the nuclear shell model (40). However, analogous to single atoms, free electrons in metal clusters are also delocalized in electronic shells surrounding the atoms and subject to the Pauli exclusion principle. Like the free electrons in larger (i.e. plasmon-supporting) nanoparticles, these electrons experience a linear restoring force modeled by Hooke’s law, such that the quantized shells can be described by a simple 3D harmonic oscillator (23, 25, 27, 40). Due to the nature of the cluster spherical potential, the solutions of the Schrödinger equation are very similar to and directly mapable onto those of single atoms. Although jellium orbitals are labeled similarly to atomic orbitals, the principal quantum number n of jellium orbitals is related to the n_atom of atomic orbitals by n = n_atom−l, where l is the angular momentum quantum number (40). In this nuclear shell model, angular momentum is not restricted by the principal quantum number n. As a result, 1s, 1p, 1d, 2s, 1f, 2p, … are used in the electronic structure of alkali clusters because of potential surface differences between clusters and atoms. For example, an electron in hydrogen atom is in a Coulomb (r⁻¹) potential, while an electron in a metal cluster is in an approximately harmonic (r²) potential. For a given shell n (40), the magic numbers, N_o, for the familiar r⁻¹ potential are given by

$$N_0=\frac{2}{3}n(n+\frac{1}{2})(n+1)$$ [2]

with 2, 10, 28…, corresponding to 1s, 2s, 2p, 3s, 3p, 3d, …. electronic shells, while the magic numbers for the harmonic oscillator are 2, 8, 20, 40, …, corresponding to 1s, 1p, 1d, 2s, 1f, 2p, … electronic shells according to

$$N_0=\frac{1}{3}(n+1)(n+2)(n+3)$$ [3]

The harmonic energy level spacing ω₀ in a spherical harmonic oscillator potential is dependent on the Wigner-Seitz radius r_s and the number N of free electrons in the clusters,

$$\hslash {\omega }_0=3.61•\frac{{\hslash }^2}{2\mu r_s^2}{(N)}^{-\frac{1}{3}}$$ [4]

Fundamentally, this jellium model is the Drude free electron model and contains the same assumptions. The magic sizes observed in jellium clusters are due to the complete filling of the different valence shells. Due to the similarity in electronic structure between metal clusters and single atoms, these metal clusters are often referred to as “multi-electron” artificial atoms (23, 25, 27, 40), and are reasonably well-approximated by a many-particles-in-a-box model, in which increasing box size also increases the ground state energy level and gives an effective R⁻¹ (inverse cluster radius) scaling of transition energy. Deviations from spherical symmetry of the free electron distribution further split these levels and have been incorporated in Clemenger’s original descriptions (23, 42).

Since free electrons are piled up in metal clusters with constant electron density, Fermi energies of “free electron” metals only depend on the electron density (ρ₀) or the Wigner-Seitz radius (r_s) of the metals

$$E_f=\frac{p_f^2}{2\mu }=\frac{{(3{\pi }^2{\rho }_0)}^{2/3}{\hslash }^2}{2\mu }={(\frac{9\pi }{4r_s})}^{\frac{2}{3}}\frac{{\hslash }^2}{2\mu }$$ [5]

By combining equations 4 and 5, a very simple relation of frequency, particle radius, and Fermi energy can be derived (23, 25, 27, 30, 40)

$$\hslash {\omega }_0\cong E_f{(N)}^{-\frac{1}{3}}=E_f{r}_s/R$$ [6]

This simple relation explains how the electronic structures of metallic clusters scale with the number of free electrons, and has been confirmed by many gas phase studies that clearly indicate strong size-dependent transitions from single electron intraband resonances to collective plasmon oscillation in few atom metal clusters (1, 2, 24–27, 43, 44). These studies typically photodissociate the clusters, however, and do not probe the lowest lying transitions.

ABSORPTION AND EMISSION OF NOBLE METAL CLUSTERS

Obviously, if one desires to maintain highly polarizable metallic properties in aqueous solvents, the alkali metals must be avoided. The noble metals (Au, Ag, and Cu) are all excellent conductors, and each has a single unpaired electron in their valence s-orbitals that generate the free electrons of the bulk conduction band. Their greatly improved chemical stability relative to the alkali metals make them promising candidates for creating highly polarizable molecular-scale metals with strong optical responses in aqueous media. While such sub-nm nanoclusters are too small to have the continuous density of states (DOS) necessary to support a “plasmon” characteristic of larger free electron metal nanoparticles (1, 44), the jellium model predicts that both nanoparticle plasmon widths and nanocluster transition energies of true free electron metals should scale with inverse cluster radius (40). As gas phase photodissociation experiments are unable to probe the lowest energy transitions (1), the size-dependent behavior of gold and the development of the plasmon remain poorly understood (1, 7, 9, 45–47).

Since optical and electronic properties of metal clusters are determined by their electronic structure, it is very important to understand how the electronic structure changes with size in this smallest size regime. On the molecular scale, 5d electrons of gold clusters are more tightly bound to the nucleus than 6s electrons are, thereby producing a large energy gap between the s and d bands. Consequently, conductance of few-atom gold clusters is solely determined by the conduction band structure built up by 6s valence electrons (48). Within this framework, our goal has been to utilize highly polarizable Au, Ag, and Cu cluster fluorescence in the condensed phase to not only create new water-soluble emitters, but also understand the atom to nanoparticle transition in these metals. While Cu produces highly emissive species (30), it oxidizes too readily. Ag nanoclusters offer great potential as ultrabright fluorescent (30–32) and Raman-active (33) labels, but require proper scaffold design to fully realize their promise while tempering their tendency to aggregate. While much effort is currently devoted to Ag (31–33), Au shows similar size scalings with increased stability and excellent optical properties of its own (28–30). Thus, the creation of new types of fluorescent gold clusters with high quantum yields and tunable emission will not only shed light on the fundamental question of how the electronic structures of gold clusters change with size, but also offers the opportunity to develop a new generation of small and biocompatible fluorophores as biological labels (28) or as optoelectronic emitters (49–51).

FLUORESCENT GOLD NANOCLUSTERS

Marcus and Schwentner first reported that gold dimers yield UV and visible emission in 1987 (52). Harbich et al. used a similar method to prepare Au₂ and Au₃ embedded in argon matrices and studied their UV and visible photophysics at low temperature (21, 53, 54). Collings et al. also investigated the gas phase visible and UV absorption spectra of gold clusters Au_N (N=7,9,11,13) using photodepletion spectroscopy (55–57). Similar to Ag, a pronounced odd-even alternation in the mass spectra of gold clusters was observed in Au cluster stability (56).

Gold clusters are highly stable under ambient conditions. Exhibiting absorptions between 1.6 and 4.0 eV, Schmid and coworkers created solution-phase Au_11, Au₁₃, and Au₅₅ (58–63). Au₅₅ is especially interesting because of its remarkable chemical stability. The extraordinary stability of Au₅₅ is due to its almost perfect close-packed cuboctahedral structure (58). Other gold clusters such as Au₁₃ and Au₁₄₇ are also quite stable because they have closed atomic shells. This “chemical selection” in the solution phase avoids having an arbitrary number of atoms in a particle which combined with electronic magic cluster effects, determine the magic sizes of gold clusters under ambient conditions (58, 64). The optical spectra of Au₅₅ appear to be rather structureless, neither showing a collective excitation resonance nor exhibiting distinct absorption bands known from few-atom clusters, possibly bridging the transition from discrete energy levels to collective oscillations (58, 62, 63, 65, 66) which become apparent in ~2-nm diameter Au nanoparticles (1, 44).

Fluorescence has also been reported from Au clusters in the solution phase. In 1998, Wilcoxon et al. reported blue emission at 440 nm from small gold nanoparticles (diameter < 2.5 nm) (67), however, due to the heterogeneity of the solution, the exact size of emissive species was undetermined. Near IR emission was also reported from glutathione encapsulated Au ₂₈ clusters (9) and from tiopronin-capped ~1-nm Au species (68–75), both in aqueous solution. Compared to well-studied alkali clusters (24, 25), the size-dependent electronic structure of these noble metals remained poorly understood, yet a framework (9, 23, 76) for linking nanoparticle and cluster optical properties through free electron scalings was in place. Advantageously, on the molecular scale, the d electrons have little perturbation on the conduction band structure of few-atom gold clusters (48), implying that the free electron model should apply to these molecular metals.

EXCITATION AND EMISSION SPECTRA OF FLUORESCENT GOLD CLUSTERS

Emissive Au nanoclusters have been prepared in a variety of scaffolds. In order to allow Au-Au interactions to dominate, we employed –OH and –NH₂ terminated poly(amidoamine) (PAMAM) dendrimers to concentrate and initiate the formation of few-atom nanoclusters. Much effort by other labs has shown the ability of water-soluble PAMAM to form reasonably monodisperse Au and Ag nanoparticles in aqueous solution (77–80). Alkanethiol scaffolds have also been utilized to produce similarly fluorescent Au nanoclusters in organic solvents with similar results (30). Detailed synthetic procedures have been reported (28, 30), but the simple adjustment of Au:PAMAM molar ratios biases the distribution toward one of several emitters identified throughout the visible and near IR. Figure 1 shows a fluorescence image and discrete excitation and emission spectra of different dendrimer encapsulated gold clusters in aqueous solutions. By adjusting the molar ratio between gold ions from 1:1 to 1:15, both excitation and emission energies of observed fluorescent species can be tuned from the UV to the near IR. Analogous to producing large nanoparticles within PAMAM hosts (77), both the relative Au:PAMAM concentration and the dendrimer generation enable optimization of the desired nanocluster emission color in solution. Interestingly, the PAMAM scaffold stabilizes different nanocluster sizes and yields orders of magnitude higher fluorescence quantum yields than does glutathione, for example (9).

Figure 1.

Figure 1. a. Excitation (dashed) and emission (solid) spectra of different gold nanoclusters. Emission from the longest wavelength sample was limited by the detector response. Excitation and emission maxima shift to longer wavelength with increasing initial Au concentrations, suggesting that increasing nanocluster size leads to lower energy emission.

Figure 1. b. Emission from the three shortest wavelength emitting gold nanocluster solutions (from left to right) under long-wavelength UV lamp irradiation (366nm). The leftmost solution appears slightly bluer, but similar in color to Au₈ (center) due to the color sensitivity of the human eye. Green emission appears weaker due to inefficient excitation at 366 nm.

SIZE DETERMINATION OF FLUORESCENT GOLD CLUSTERS

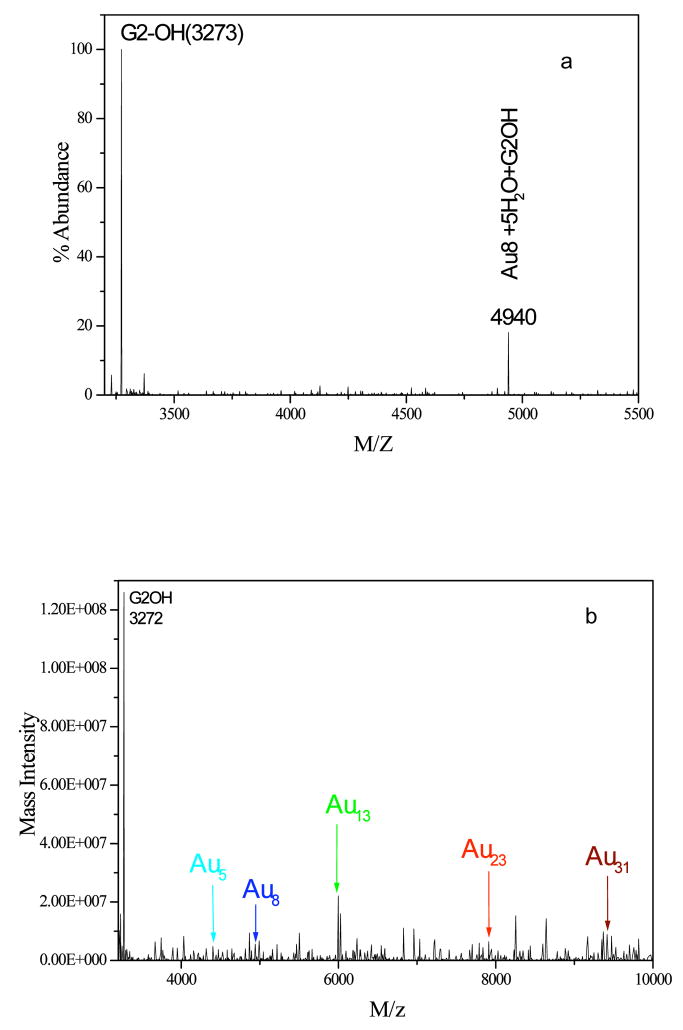
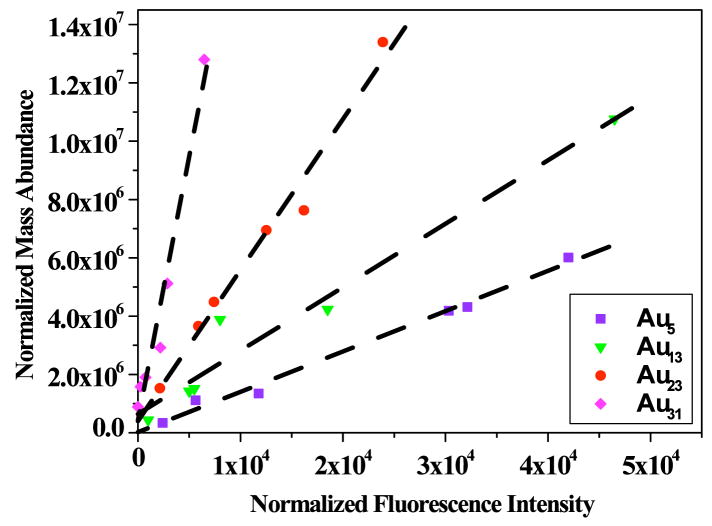
The well-defined dendrimer structure enables analysis of encapsulated nanocluster sizes with electrospray ionization (ESI) mass spectrometry. As shown in Figure 2a, Au₈ is the dominant Au-containing species in the blue emitting solutions and its abundance linearly correlates with fluorescence intensity. In accord with stable nanoclusters having 8 valence electrons (one from each Au atom) (81), this dominant nanocluster is confirmed to be in the overall neutral oxidation state as even 100-fold excess of highly reducing BH ₄- does not alter the nanodot fluorescence. Confirmed through expected shifts relative to the dendrimer parent peak upon dissolution in D₂O instead of H₂O, five molecules of water were also found to be associated with the hydrophilic PAMAM dendrimer-Au complex. While five waters appears to be the favored number, smaller peaks corresponding to Au₈ with other numbers of water molecules ranging from one to six were also observed in the mass spectra of other similarly prepared samples. The peaks containing Au₈ were only observed in fluorescent Au nanocluster solutions, and the fluorescence intensities of differently prepared solutions are directly proportional to relative abundances of Au₈ nanocluster peaks alone, indicating that the efficient blue emission results from Au₈ nanodots. In the mass spectroscopic studies of other different-color fluorescent gold nanocluster solutions, many peaks appear in the mass spectra from a combination of fragmentation and non-fluorescent products (Figure 2b). Consequently, to determine each fluorescent nanocluster size, each fluorescent solution was assayed through correlation of electrospray mass spectrometry abundances and fluorescence intensity at each wavelength. In each case, there was a one-to-one correspondence between only one specific peak in the mass spectrum and a specific fluorescent transition. In other words, only one mass peak exhibited a linear correlation with each fluorescence peak, thereby enabling direct determination of each fluorescent nanocluster size (Figure 3). This enabled direct assignment of the UV (Au₅), green (Au₁₃), red (Au₂₃), and near IR (Au ₃₁) emitting species each encapsulated within the PAMAM scaffold (“Au nanodots”) (28).

Figure 2.

Figure 2. a. ESI mass spectrum of G2-OH PAMAM encapsulated gold nanodots. PAMAM-Au₈ mass spectrum (theoretical m/z of dendrimer G2-OH (3272) encapsulated Au₈ and 5H₂O is 4939)

Figure 2. b. Other identified Au nanocluster species observed in a typical mass spectrum of a fluorescent gold cluster solution.

Figure 3.

Fluorescent nanocluster size determinations. Correlations of mass spec abundance with each fluorescence transition intensity observed in Figure 1A over many samples yield linear correlations of only a single species with each fluorescence transition. In addition to separately identified Au₈, nanocluster sizes (emission maxima) were determined to be Au₅ (385 nm), Au₁₃ (510 nm), Au₂₃ (760 nm), and Au₃₁ (866 nm) through linear correlation of mass abundance and fluorescence intensity at each emission maximum.

CORRELATION OF GOLD CLUSTER SIZE AND ITS EMISSION

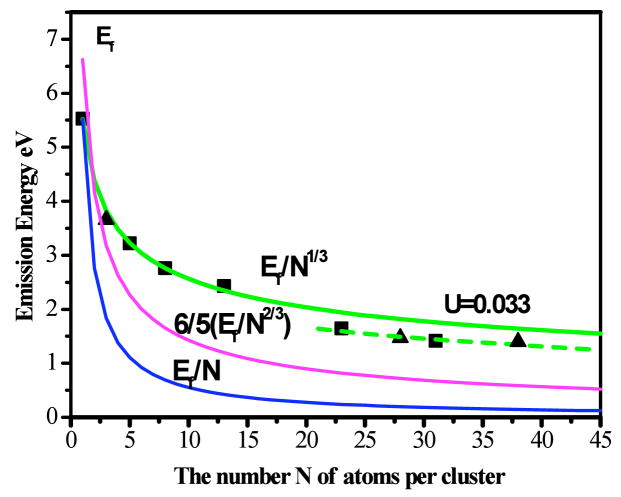
The dependence of emission energy on the number of atoms, N, in each gold nanocluster (Figure 4) is quantitatively fit for the smallest nanoclusters with no adjustable parameters by the simple scaling relation of E_Fermi/N^1/3, in which E_Fermi is the Fermi energy of bulk gold (23, 25, 42). For a spherical cluster, the radius, R, is equal to r_s•N^1/3, in which r_s is the Wigner-Seitz radius and N is the number of atoms per cluster. Identical to that for gas phase alkali metal nanocluster electronic absorption (27, 44), the transition energy scaling with inverse cluster radius indicates that electronic structure is solely determined by the Au nanocluster free electron density and nanocluster size. Analogous to the protoplasmonic transitions in gas phase alkali clusters (26, 44), our observations suggest that the free electron shell-filling model corresponds exactly to the spherical jellium approximation – the simplest model for explaining delocalized, free conduction electron behavior relative to the atomic cluster core, and an excellent basic model explaining plasmon absorption in large nanoparticles (23, 25, 42).

Figure 4.

Correlation of the number of atoms, N, per cluster with emission energy. Emission energy decreases with increasing number of atoms. The correlation of emission energy with N is quantitatively fit with E_fermi/N^1/3, as predicted by the jellium model (1, 2). When N is equal to 1, the energy of valence electron is equal to Fermi energy because the valence electron is at the HOMO level. Emission energies of Au₂₃ and Au₃₁ exhibit slight deviations from the E_fermi/N^1/3 scaling. Consistent with the narrow excitation and emission spectra, the potential confining the free electrons flattens slightly for Au₂₃ and Au₃₁, with anharmonicity parameter U=0.033 (42). The experimental values for the emission energies of Au₃ (82), Au₂₈ (9)and Au₃₈ (71) are 3.66, 1.55, and 1.44 eV respectively (represented by ▲), which are all consistent with the observed scaling relations. Kubo’s predicted model E_f/N (12) and the square potential box model (6/5E_f/N^2/3 (1) are also shown in the figure. Obviously these models can not accurately fit the emission energy scalings of the gold clusters.

Observation of this simple energy scaling E_Fermi/N^1/3 from fluorescent gold clusters offers clear and direct experimental evidence of the discrete nature of the excited state in noble metal clusters, and the evolution from discrete intraband transitions of the free electrons to the plasmon of large nanoparticles in the condensed phase. The jellium E_Fermi/N^1/3 energy scaling law accurately describes the size-dependent electronic structure and relative electronic transitions of the small clusters. These quantum-confined protoplasmonic transitions of the free conduction electrons suggest nearly spherical electronic nanocluster structures with electrons bound by an approximately harmonic potential in three dimensions. While a harmonic potential would give a R⁻² electronic transition energy dependence for a single electron in the conduction band, the degeneracy in filling the delocalized nanocluster energy level shells (1s, 1p, 1d, 2s, 1f, 2p, …), and the size-independent electron density for the given material yield an effective R⁻¹ dependence on cluster size (2, 23), further demonstrating the metallic origin of these Au nanocluster fluorescent transitions. Recent reports of Au₃ (82) and Au₄ (83) cluster emission demonstrate UV emission for each Au cluster which are within only a few percent of the jellium-predicted transition energy for each size. This suggests that metallic behavior persists even to three Au atoms, resulting from the oscillation of free electrons in a roughly spherical electronic nanocluster structure bound by an approximately harmonic potential in three dimensions.

Consideration of the effective single particle potential as a three-dimensional harmonic oscillator turns out to be very good approximation for small metal clusters (i.e. N<20). However, for larger clusters, Clemenger found that a small anharmonic distortion term is required due to the deformation of the potential well (42). As a result, the effective single particle Hamiltonian for electrons with mass m is

$$H=-\frac{p^2}{2m}+\frac{m{{\omega }_0}^2{q}^2}{2}-Uh{\omega }_0[l^2-n(n+3)/6)]$$ [7]

, in which p and q are single electron momentum and coordinate operators, l is the angular momentum, n is the shell number, and U is the distortion parameter. The third term accounts for the shape change of the potential surface as a function of size (schematized in Figure 5). Consequently, the transition energy spacing for larger metal clusters are given by (42)

Figure 5.

Schematic of size-dependent surface potentials of gold clusters on different size scales. For the smallest gold clusters (Au₃ to Au₁₃), cluster emission energies can be well fit with the energy scaling law E_fermi/N^1/3, where N is the number of atoms in each cluster, indicating that electronic structure transitions of these small gold clusters are well-described by a spherical harmonic potential. With increasing size, small anharmonicities distort the potential well, which at larger sizes gradually distorts into a Woods-Saxon potential surface (42), and eventually becomes a square well potential characteristic of electrons in large metal nanoparticles (1).

$$\mathrm{\Delta }{E}_{\mathit{emission}}=\frac{E_f}{N^{1/3}}[1-U(l_e^2-l_g^2-\frac{n+2}{3})]$$ [8]

, in which l_e and l_g are the angular momenta of the excited and ground states, respectively. Indeed, the distortion of surface potential well is observed from the larger fluorescent gold clusters (N=23 and 31). Electron screening increases and the potential bounding each electron flattens, thereby slightly increasing the anharmonicity. Figure 4 shows that the potential confining free electrons in larger gold clusters Au₂₃ and Au₃₁ flattens only slightly, indicated by an anharmonicity distortion parameter (23, 42) of U~0.033 based on equation 8. Even the HOMO-LUMO gaps from gas phase Au₂₀ (84) and water soluble Au₁₁ (85) and Au₂₈ (9) lie close to the same curves and are consistent with our results (Figure 4). Similarly, Au₃₈ reported by Murray’s group gives IR emission with maximum energy at 1.41 eV (71) which is about a 3% deviation from the jellium value (1.48 eV), further suggesting the distortion parameter (U=0.033) remains constant even at particle sizes as large as 38 atoms. While this free electron scaling nicely models the transition energies of all observed Au species, it does not explain why we only observed these specific cluster sizes. Our correlation of mass spectrometry abundance with fluorescence intensity over many samples only enables identification of fluorescent species (i.e. we cannot uniquely identify size-dependent properties of non-fluorescent species). Additionally, while Au₈ is a magic cluster due to favorable electronic considerations, Au₅, Au₁₃, Au₂₃, and Au₃₁ have some degree of stability due to atomic arrangements (40). While only magic cluster sizes correspond to shell closings (42), the approximately spherical electronic structure indicated by the scaling with inverse cluster radius shows that these nanomaterials are indeed “multi-electron artificial atoms” (2, 86, 87). In contrast to predictions of planarity for gas phase Au_{N≤ 7} nanoclusters (88), the PAMAM-encapsulated nanocluster geometries must be approximately spherical to yield the observed scaling, as has been directly observed when Au nanoclusters are measured in the condensed phase (89).

PHOTOPHYSICAL PROPERTIES OF FLUORESCENT GOLD CLUSTERS

The detailed photophysical properties of different water-soluble gold nanoclusters (Table 1) indicate that these Au nanodots behave as not only quantum-confined, but also molecular and size-tunable fluorophores. The high quantum yields are comparable to the best water-soluble emitters currently available, ranging from 70% for UV-emitting Au₅ to ~10% for Au₃₁ in the near IR. In contrast to larger semiconductor nanocrystals, dendrimer encapsulated gold clusters have well-defined excitation and emission spectra while requiring neither complicated high temperature syntheses with toxic precursors nor difficult overcoating with surface passivation and solubilization chemistry for applicablity as biolabels. In order to maintain the Au-Au interactions, however, no specific chelation chemistry to bind and stabilize the nanocluster as a whole is present, thereby conferring very little specificity in nanocluster creation.

Table 1.

Photophysical properties of PAMAM-encapsulated gold nanoclusters in water

Gold Cluster	Excitation (FWHM) eV	Emission (FWHM) eV	Quantum Yield %	Lifetime ns	Intrinsic decay rate(×109 GHz)
Au5	3.76 (0.42)	3.22 (0.45)	70	3.5	0.2
Au8	3.22 (0.54)	2.72 (0.55)	42	7.5	0.056
Au13	2.86 (0.38)	2.43 (0.41)	25	5.2	0.048
Au23	1.85 (0.21)	1.65 (0.26)	15	3.6	0.042
Au31	1.62 (0.20)	1.41 (0.10)	10	-	-

As gold nanoclusters are too small to have the continuous density of states and plasmon absorptions characteristic of larger nanoparticles (>2 nm) (29, 90), the transition energy instead of the plasmon absorption width should scale with inverse cluster radius. While there is great debate regarding size-induced metal to insulator transitions and the nature/lack of plasmon absorption in few-atom metal nanoclusters (2, 23, 45, 91), the size-dependent scaling of excitation and emission energies with E_Fermi/N^1/3 (Figure 4) directly indicates that free electron behavior begins in Au_N as small as N=3 (28, 82, 83). Such free electron protoplasmonic intraband absorption and fluorescence give rise to discrete size-dependent Au transitions throughout the visible beginning at the few-atom size scale. As nanocluster size increases further, transition energies decrease with the increasing density of states, thereby forcing energy level spacings to eventually become comparable to available thermal energy. This relaxes the angular momentum selection rules as single electron states become less well defined in favor of the effectively continuous density of states characteristic of plasmon absorption within nanoparticles and bulk metals. As a result, nanoparticle absorption is mainly due to collective oscillations of free electrons, and its plasmon absorption width is solely dependent on its relaxation constant that is proportional to (1/R) (1, 28). Absorption, of course, is governed by k(N), the size-dependent imaginary part of the refractive index, n′(N)=n(N)+ik(N), while plasmon width results from the imaginary portion of the dielectric constant, ε(N)= ε₁(N)+ iε₂(N). Because ε(N)=n′(N)² for non-magnetic materials, ε(N) = [n(N)]² − [k(N)]² + 2i·n(N)·k(N) and the portion governing the plasmon width is simply ε₂(N) = 2·n(N)·k(N), and is linearly dependent on k(N). Any size dependence in absorption is directly related to the imaginary portion of the dielectric constant which governs plasmon width, thereby connecting the atomic and nanoparticle limits. Consequently, by directly probing the lowest energy absorptions and emissions, these studies connect nanocluster transition energies, both of which scale with inverse particle radius (R⁻¹ or, equivalently, N^−1/3). With increasing size and decreasing transition energy, confinement switches from being relative to the Fermi wavelength (yielding discrete size-dependent optical transitions) to being relative to the electron mean free path (yielding plasmon widths that scale with the free electron DOS and the imaginary dielectric constant). Both regimes scale with inverse cluster radius as the delocalized free electron states giving rise to nanocluster fluorescence become sufficiently dense at larger sizes that they enable the Au nanoparticle plasmon absorptions and generate the characteristic N^−1/3 scaling of the plasmon width. Consequently, the size dependent transition frequencies of our water soluble Au nanoclusters are the small size limit of the plasmon absorption within bulk metals and provide a smooth connection between atomic and metallic behavior with true protoplasmonic fluorescence that is well-described at all sizes by the spherical jellium model (26).

PHOTON ANTIBUNCHING FROM FLUORESCENT GOLD CLUSTERS

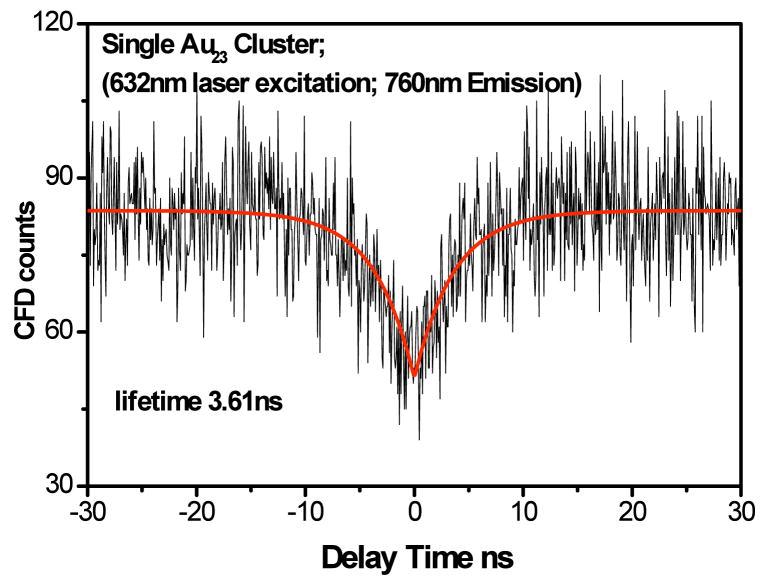
Although discrete optical transitions and their correlation with size suggest that these gold nanodots are “multi-electron” artificial atoms, direct optical evidence for these artificial atoms as single quantum systems is still lacking. Single metal atoms are certainly individual quantum systems capable of yielding antibunched photons, however, metal nanoparticles exhibit collective oscillations of free electrons under light excitation and produce bunched photons. Such plasmon scattering results from the continuous band structure of metal nanoparticles (1, 87) and prevents observation of non-classical photon correlations. The discrete electronic structures of gold clusters should provide a unique opportunity to observe this photon antibunching behavior from few-atom metal clusters. Measurement of photon correlations from single Au₂₃ clusters was performed by equally splitting emission from a single Au₂₃ cluster onto two single-photon-sensitive detectors as described for other systems (33, 92–94). For true single quantum systems, a dip in the photon pair distribution should be observed at zero time delay between the two detectors, indicating reduced probability of two photons being simultaneously emitted. This dip at zero interphoton arrival delay is indeed observed for Au₂₃ (Figure 6), showing that gold clusters behave as true multi-electron artificial atoms.

Figure 6.

Antibunched fluorescence from a single Au₂₃ cluster, excited at 632.8 nm. Photons arriving at each of two detectors show a decreased probability of two photons arriving simultaneously (at zero interphoton delay). The rise time of the antibunched signal matches the Au₂₃ lifetime in Table 1.

SCAFFOLD DEPENDENCE OF EMISSION

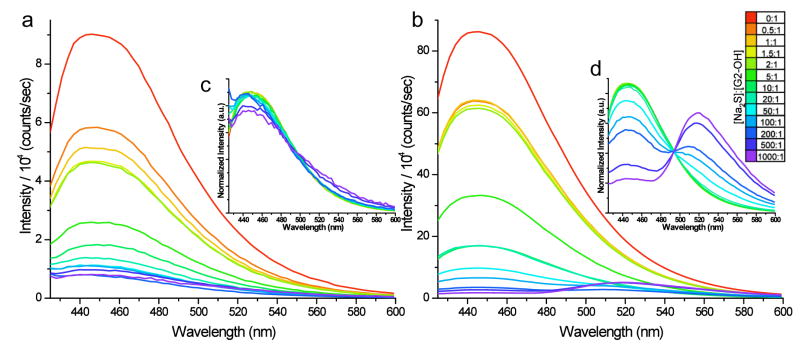
Although there are no chromophores in PAMAM-OH, blue emission at 450 nm has recently been reported from these OH-terminated PAMAM dendrimers after oxidation with persulfate, leading to the suggestion that Au³⁺ similarly oxidizes PAMAM to yield a non-auric fluorophore with similar emission to that which we reported for Au₈ (95). While NH₂-terminated PAMAM yielded gold clusters with indistinguishable fluorescence properties compared to clusters in PAMAM-OH, it failed to produce a fluorescent product upon similar persulfate oxidation, as similarly reported in Ref. (95). Furthermore, although addition of Na₂S quenched the emission of both PAMAM-OH encapsulated Au₈ and persulfate-oxidized PAMAM-OH prepared according to Ref. (95), the resulting species displayed distinctly different emission spectra, thereby clearly distinguishing these species (Figure 7). Au nanodot emission is simply quenched with addition of Na₂S without spectral changes until 500-fold excess of Na₂S is added. Conversely, oxidized PAMAM-OH emission spectra exhibit a new green peak at only ~20 fold excess of Na₂S. PAMAM concentrations are the same in the two samples, and the Au:PAMAM ratio is 1:1 for our Au₈ sample. Only at very large excess Na₂S concentrations do we see any evidence of the residual PAMAM-derived emission being quenched in the Au nanodot sample, with the Au₈ emission being quenched first. This clearly indicates that while there is some small background fluorescence in our Au₈-PAMAM conjugates, the strong oxidized PAMAM emission reported by others (95) is not an appropriate control for the emission we report. While the emission indeed appears quite similar, it behaves differently, and the Au₈ emission energy falls nearly perfectly on the jellium scaling curve. Furthermore, we have synthesized octadecanethiol capped fluorescent gold clusters with slow NaBH₄-reduction in chloroform/ethanol solution (30). Similar excitation and emission peaks were observed from the emissive alkanethiol-capped Au species created through this method. Not only was strong blue emission at 455 nm observed from octadecanethiol encapsulated gold clusters (similar to Au₈ emission), but emission from these gold clusters can also be tuned from blue to near IR with very similar spectra to the PAMAM-encapsulated species we observed (Figure 8). Because of uncertainty in the number of ligands per cluster and the organic solvents used, clean mass spectra are difficult to obtain, thereby making assignment of each species difficult, but comparison with our PAMAM-encapsulated Au nanocluster data provides strong support for similarly sized emissive species.

Figure 7.

Emission spectra (excitation at 375 nm) of aqueous PAMAM dendrimer (a) encapsulating NaBH₄-reduced gold nanoclusters and (b) treated with persulfate with increasing additions of Na₂S (red curve to violet curve). Insets (c) and (d) show spectra (a) and (b), respectively, normalized to equal integrated intensity. The persulfate-treated samples show the creation of a green-emitting species apparent at as little as a 20-fold excess of Na₂S, while all but the two final Au-containing samples (500- and 1000-fold excess of Na₂S) show no change in peak shape.

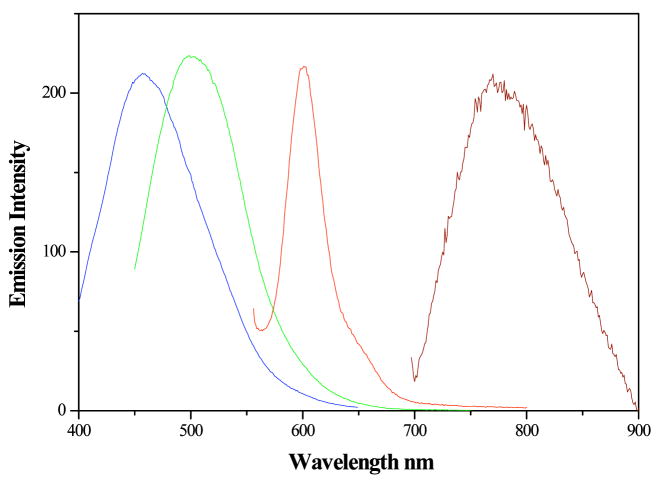
Figure 8.

Emission spectra of octadecanethiol encapsulated gold nanoclusters in chloroform. Blue (455-nm) emitting gold clusters with maximum excitation at 365 nm. Green (510 nm) emitting gold clusters with maximum excitation at 430 nm. Red (600 nm) emitting gold clusters with maximum excitation at 586 nm. IR (776 nm) emitting gold clusters with maximum excitation at 650 nm. These excitation and emission spectra closely match those in PAMAM scaffolds.

SUMMARY POINTS

1. Metallic several atom gold multi-electron artificial atoms have been created in aqueous solution that exhibit size-tunable high quantum yield fluorescence from the UV to the near IR.

2. These sub-nm gold clusters exhibit free electron scalings characteristic of metallic behavior down to as small as 3-atom clusters.

3. Observed protoplasmic fluorescence arises from intraband transitions of the free electrons that smoothly link atomic and nanoparticle limits in condensed phase gold nanoclusters.

4. Fluorescent gold species can be created in a variety of scaffolds and is independent of any scaffold-centered emission.

5. Bright highly polarizable noble metal nanoclusters of silver and copper also give bright emission and hold great promise as ultrabright, biocompatible biolabels and light emitting sources in nanoscale electronics (96).

6. Greater chemical specificity in scaffold design should be incorporated to improve yield, purity, and overall stability for use as future biolabels.

7. Discrete excitation and emission, strong antibunched emission, and high quantum yields suggest that these noble metal nanoclusters may nicely complement larger semiconductor quantum dots in a variety of applications.

Acronyms List

DOS

density of states

ESI

electrospray ionization

PAMAM

poly(amidoamine)

PAMAM-OH

hydroxyl-terminated PAMAM

PAMAM-NH₂

amine-terminated PAMAM