Synchronized moving aperture radiation therapy (SMART): superimposing tumor motion on IMRT MLC leaf sequences under realistic delivery conditions

Abstract

Synchronized moving aperture radiation therapy (SMART) has been proposed to account for tumor motions during radiotherapy in prior work. The basic idea of SMART is to synchronize the moving radiation beam aperture formed by a dynamic multileaf collimator (DMLC) with the tumor motion induced by respiration. In this paper, a two-dimensional (2D) superimposing leaf sequencing method is presented for SMART. A leaf sequence optimization strategy was generated to assure the SMART delivery under realistic delivery conditions. The study of delivery performance using the Varian LINAC and the Millennium DMLC showed that clinical factors such as collimator angle, dose rate, initial phase and machine tolerance affect the delivery accuracy and efficiency. An in-house leaf sequencing software was developed to implement the 2D superimposing leaf sequencing method and optimize the motion-corrected leaf sequence under realistic clinical conditions. The analysis of dynamic log (Dynalog) files showed that optimization of the leaf sequence for various clinical factors can avoid beam hold-offs which break the synchronization of SMART and fail the SMART dose delivery. Through comparison between the simulated delivered fluence map and the planed fluence map, it was shown that the motion-corrected leaf sequence can greatly reduce the dose error.

1. Introduction

Respiratory tumor and organ motion is one of the main challenges for accurate dose delivery in radiotherapy. The respiratory motion may cause the actual delivered dose to be different from the planed dose, especially in intensity-modulated radiation therapy (IMRT) where the interplay effect may introduce hot and cold spots inside the target volume (Yang et al 1997, Yu et al 1998, Bortfeld et al 2002, Jiang et al 2003, Chui et al 2003).

Various techniques have been developed to account for the respiratory motion in dose delivery, including breath-hold, respiratory gating and tumor-tracking techniques. Breath-hold techniques include the deep-inspiration breath-hold (DIBH) technique and the active breathing control (ABC) technique. In the DIBH method, dose is delivered when patients achieve the maximum inspiration (Hanley et al 1999, Rosenzweig et al 2000), while in the ABC method, a spirometer is used to force patients to hold their breath at a pre-defined lung volume (Wong et al 1999). Breath-hold techniques may not be appropriate for lung cancer patients with poor pulmonary function since it is hard for them to tolerate a long breath-holding time. Respiratory gating techniques have been widely studied and used in clinical practice (e.g., Jiang (2006)). During gated delivery, a particular portion of the breathing cycle is selected as a pre-defined ‘gating window’, and the radiation beam will be turned on only when the patient's breathing signal is within the gating window. Tumor tracking techniques include the real-time tracking delivery methods and the synchronized delivery methods. In the real-time tracking delivery methods, moving targets are monitored during treatment, and the radiation beam is continuously adapted to track the targets in real time (e.g., Keall et al (2001), Murphy (2004)). In the synchronized delivery methods, the motion of a target is acquired before the treatment and is used to synchronize the motion of the radiation beam during the treatment (Neicu et al 2003).

The synchronized moving aperture radiation therapy (SMART) is one of the synchronized delivery methods (Neicu et al 2003). In SMART, data of tumor motion are collected, and the motion pattern is described by the average tumor trajectory (ATT) before the treatment. During the treatment, a dynamic multileaf collimator (DMLC) is used to synchronize the radiation beam to the moving targets based on the ATT. The synchronization between the beam motion and the tumor motion is critical to the accuracy of dose delivery. In order to achieve the synchronization in SMART, a regular tumor motion has to be ensured, and the radiation beam must have sufficient tracking capability. The ATT and breathing coach were studied to obtain regular tumor trajectories (Neicu et al 2003, 2006). The capability of the DMLC in tumor tracking delivery was investigated (Keall et al 2001, Wijesooriya et al 2005, McMahon et al 2007). DMLC leaf sequencing methods for a moving target were theoretically studied (Papiez 2004, Papiez and Rangaraj 2005, Webb 2005, McQuaid and Webb 2006, Tacke et al 2007, Rangaraj et al 2008).

In this study, we investigated how to improve the DMLC tracking performance in the implement of SMART. A two-dimensional superimposing method was applied in DMLC leaf sequencing and studied under realistic delivery conditions. DMLC-related clinical parameters such as dose rate, collimator angle, gantry angle, initial phase and machine tolerance were studied for the accuracy and efficiency of synchronized dose delivery.

2. Materials and methods

2.1. 2D superimposing leaf sequencing method

The proposed superimposing leaf sequencing method is to modify leaf sequences by superimposing tumor motion onto leaf sequences generated for a static target. The modified leaf sequences can be used to track a moving target and deliver the expected fluence map to a moving target.

The idea of the 2D superimposing method is to superimpose the two-dimensional tumor motion projected in the beam's eye view (BEV) onto the original DMLC leaf sequences, which are planned for a static target. The DMLC coordinate is defined in figure 1. Along the y-axis, there are total n rows of leaves, and there are two leaves at each row, the left and right leaves. Each leaf can only move along the x-axis. For a leaf at the y-axis position of y_L, its x-axis position at time t is defined as x_L,Left(t, y_L) for a left leaf, and x_L,Right(t, y_L) for a right leaf. Since the same superimposing method applies to both left and right leaves, without loss of generality, we will not distinguish the left and right leaves in the following discussion.

Figure 1.

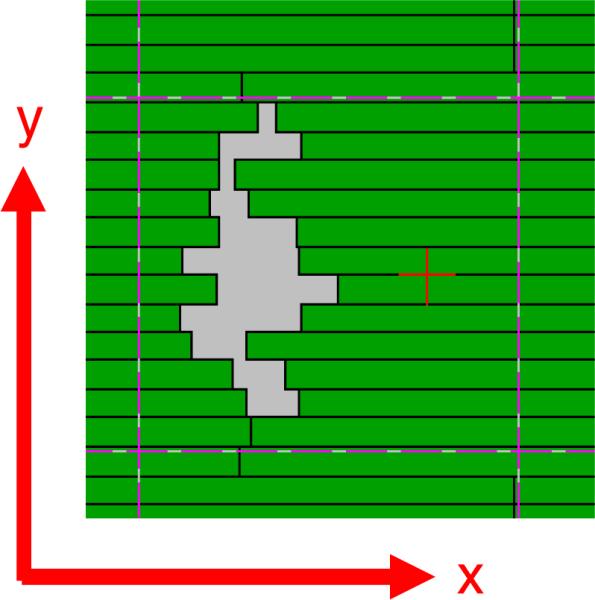
DMLC coordinate.

The 2D superimposing method includes two steps. First, the tumor motion in the y-axis direction is superimposed onto the original leaf sequences in the y-axis direction. Assume the original leaf position to be y_L, and the tumor displacement along the y-axis from the static position at time t to be Δy_T (t). Then, the new leaf position will be

$$y_L^{\prime }=y_L+\Delta y_T\left(t\right).$$ (1)

After superimposing the tumor motion in the y-axis onto the leaf sequence, the next step is to calculate the new leaf velocity to compensate the effect of tumor motion in the x-axis. Assume the original leaf position along the x-axis at time t to be x_L(t, y_L), and the tumor displacement along the x-axis from the static position at time t to be x_T (t). By superimposing the tumor displacement Δx_T (t) onto the original leaf position x_L(t, y_L), the new leaf position is defined as follows:

$$x_L(t,y_L^{\prime })=x_L(t,y_L)+\Delta x_T\left(t\right),$$ (2)

where $y_L^{\prime }$ is the y-axis position of new leaf position as defined in equation (1).

Since the DMLC has a maximum speed limitation, in order to identify factors affecting leaf speed, the velocity of MLC leaf is derived from equations (1) and (2). Taking derivatives on both side of equation (2) with respect to time t, we obtain

$$\frac{\partial x_L(t,y_L^{\prime })}{\partial t}+\frac{\partial x_L(t,y_L^{\prime })}{\partial y_L^{\prime }}\frac{\partial y_L^{\prime }}{\partial t}=\frac{\partial x_L(t,y_L)}{\partial t}+\frac{\partial \Delta x_T\left(t\right)}{\partial t},$$ (3)

where

• $\frac{\partial x_L(t,y_L^{\prime })}{\partial t}=v_L(t,y_L^{\prime })$ is the x-axis velocity of leaf at the y-axis position of $y_L^{\prime }$ at time t,

• $\frac{\partial x_L(t,y_L^{\prime })}{\partial y_L^{\prime }}=\frac{\partial x_L(t,y_L)}{\partial y_L}$ represents the impact of tumor motion along the y-axis to the leaf position along the x-axis,

• $\frac{\partial y_L^{\prime }}{\partial t}=\frac{\partial \Delta y_T\left(t\right)}{\partial t}=v_{T,y}\left(t\right)$ is the tumor velocity along the y-axis at time t by taking derivative on both sides of equation (1),

• $\frac{\partial x_L(t,y_L)}{\partial t}=v_L(t,y_L)$ is the x-axis velocity of leaf at the y-axis position of y_L at time t, and

• $\frac{\partial \Delta x_T\left(t\right)}{\partial t}=v_{T,x}\left(t\right)$ is the tumor velocity along the x-axis at time t.

Thus, the new leaf velocity after compensating the effect of tumor motion can be expressed as

$$v_L(t,y_L^{\prime })=v_L(t,y_L)+v_{T,x}\left(t\right)-\frac{\partial x_L(t,y_L)}{\partial y_L}\times v_{T,y}\left(t\right).$$ (4)

In the DMLC, the new leaf velocity after compensating the effect of tumor motion should be less than the DMLC maximum speed to ensure a successful synchronized dose delivery. Various clinical parameters of dose delivery will be discussed in the following section to satisfy this requirement.

2.2. Leaf sequence optimization under realistic delivery conditions

In SMART delivery, the synchronization between the beam motion and the tumor motion is critical to the accuracy of dose delivery. When the radiation beam is held off during the treatment, such synchronization will be broken, and thus dosimetric error will be introduced. Under realistic delivery conditions, the leaf sequence needs to be optimized to eliminate the occurrence of beam hold-offs in order to achieve high delivery accuracy.

When the planned leaf speed exceeds a certain DMLC speed limit, the radiation beam will be held off. To avoid the occurrence of beam hold-offs, the planned leaf speed needs to be controlled within such speed limits. Factors that affect leaf speed can be identified from equation (4). The first item in the right side, i.e., the original leaf velocity v_L(t, y_L), can be reduced by decreasing the dose rate. For the same fluence modulation, the leaf velocity is inversely proportional to the delivery time. And for a given amount of dose, the total delivery time is inversely proportional to dose rate. Thus the leaf velocity is proportional to the dose rate. The last two items in the right side can be affected by the collimator angle and the initial breathing phase when delivery starts. The collimator angle determines tumor motions sub-partition along the x-direction and the y-direction of a collimator. Since a typical tumor trajectory is close to an oval shape, the decrease of x-direction motion will cause the increase of y-direction motion, and vice versa. Due to the high dose conformality in IMRT treatment, a small amount of target displacement along the y-direction may be translated to a large amount of leaf displacement along the x-direction. Through the comparison of effects caused by the x-direction and y-direction motions, it was found that increasing the x-direction tumor motion and decreasing the y-direction tumor motion can reduce the combined effects of the last two items in equation (4) on the leaf velocity. Since the initial phase is the phase of the respiratory cycle when dose delivery starts, the selection of initial phase affects the start point of the tumor trajectory.

The problem of beam hold-offs may also be caused by the limitation of machine tolerance, which defines the tolerance of the difference between the planned leaf end position and the actual one. During dose delivery, LINAC communicates with the DMLC to check the leaf position in each self-checking cycle of 0.055 s, which is the communication delay between the LINAC and the DMLC. If the position difference between the planned leaf end position and the actual one is greater than the predefined tolerance, the LINAC will turn off the radiation beam until the position differences of all leaves are within the tolerance. In existence of communication delay, an effective limiting velocity, instead of the maximum mechanical leaf speed, is used as the leaf speed limit to ensure that the position difference between the planned leaf end position and the actual one at the end of delay time is within the machine tolerance (Litzenberg et al 2002). Practically, the maximum leaf speed should be less than the effective limiting velocity in order to deliver leaf sequences without beam hold-offs. The effective limiting velocity which is associated with the machine tolerance is defined as follows:

$$V_{\text{eff}}=\frac{X_{\text{tol}}}{\alpha t_{\text{delay}}},$$ (5)

where V_eff is the effective limiting velocity, X_tol is the machine tolerance, t_delay is the delay time between the DMLC controller and the LINAC, and α is a machine-dependent factor to account for the variation of delay time during dose delivery and was set to be 1.8 in our study. Leaves with speeds less than V_eff can move to the planed leaf position within the machine tolerance in the delay time, and thus avoid beam hold-offs.

The leaf velocity greater than the effective limiting velocity is called the over-limit leaf velocity. The percentage of over-limit leaf velocity (POLV) is defined as follows:

$$\mathrm{POLV}=\frac{\sum _{i=1}^N{W}_i}{N},$$

where N is the number of control points of leaf sequences, and W_i is a weighting factor as defined as follows:

$$W_i=\{\begin{array}{ccc}\hfill 0\hfill & \hfill \text{if}\hfill & \hfill V_i<V_{\text{eff}},\hfill \\ \hfill 1\hfill & \hfill \text{if}\hfill & \hfill V_i<V_{\text{eff}},\hfill \end{array}\phantom{\}}$$

where V_i is the leaf velocity at every control point of the leaf sequence.

Beam hold-offs are affected not only by the number of over-limit velocities, but also by the magnitude of those over-limit velocities. For a larger over-limit velocity, it takes the machine to hold off a longer period of time for the leaf to reach the expected position. Therefore, POLV is not an appropriate index to evaluate the severity of beam hold-offs. To complement the limitation of POLV, another index, the weighted average leaf speed (WALS), is proposed to evaluate the severity of beam hold-offs. The WALS is defined as follows:

$$\mathrm{WALS}=\frac{\sum _{i=1}^N{W}_i{V}_i∕V_{\text{eff}}}{N}.$$ (6)

The WALS is an unitless ratio. As shown in equation (6), the WALS is an averaged over-limit velocity relative to the effective limiting velocity, and can accurately capture the severity of beam hold-offs. A lower WALS value means a lower percentage of interruption time. WALS=0 means that there are no beam-offs. The WALS will be used in this paper as an index to optimize clinical parameters to prevent beam hold-offs.

In order to optimize the motion-corrected leaf sequences to eliminate the occurrence of beam hold-offs, an in-house software was developed to automatically re-optimize the leaf sequence under realistic delivery conditions. There are three steps to calculate the motion-corrected leaf sequence: collimator angle setting, initial phase selection and dose rate adjustment.

Step 1. Collimator angle setting

First the motion-corrected leaf sequences are generated by superimposing tumor motion onto the original leaf sequence with various collimator angles. Based on leaf velocities of the motion-corrected leaf sequences, a range of acceptable collimator angles will be obtained. If the preset collimator angle is out of the range, the original plan needs to be adjusted to satisfy the accepted range of collimator angles.

Step 2. Initial phase selection

After the collimator angle is fixed, the motion-corrected leaf sequence will be calculated for various initial phases in order to identify the optimal initial phase to obtain the lowest leaf speed and thus reduce the possibility of beam hold-offs.

Step 3. Dose rate adjustment

Since the reducing dose rate increases the treatment time and thus decreases the efficiency of dose delivery, a high dose rate is desired to achieve efficient and accurate dose delivery. In this step, the dose rate is decreased until the maximum leaf speed is less than the effective limiting velocity for the selected machine tolerance.

2.3. Experiments

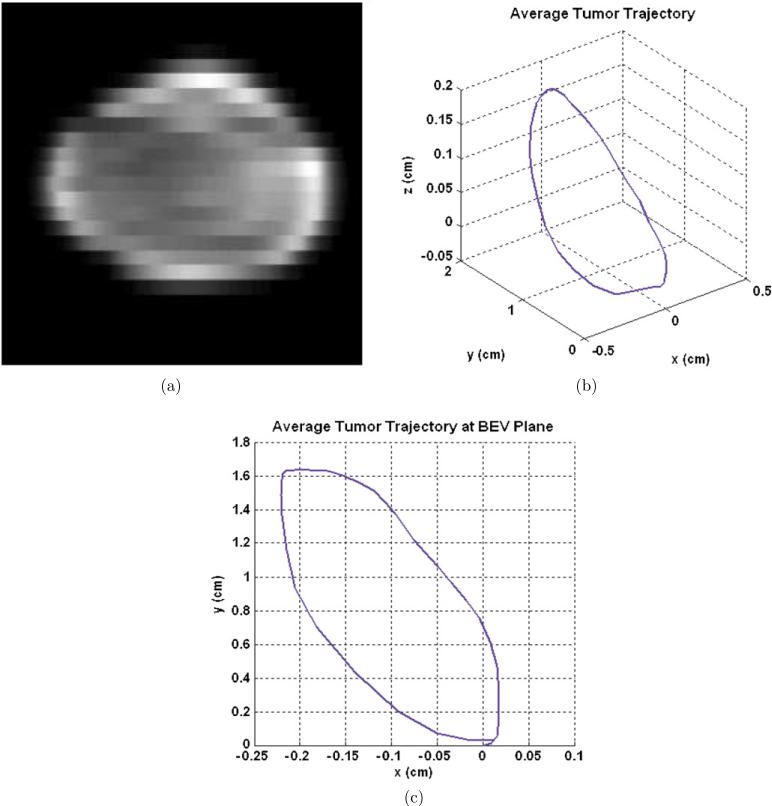
The implementation of the 2D superimposing method is limited by the hardware constraints of the DMLC. In this study, the delivery accuracy of SMART was improved by finding the optimal settings of clinical factors for the motion-corrected leaf sequence. Collimator angle, initial phase, dose rate and machine tolerance were studied. First, an IMRT treatment plan was generated for the exhale phase of a patient's 4D CT data, and the expected fluence map is shown in figure 2(a). The tumor motion information was obtained from the ATT. The ATT was calculated by averaging the tumor motion over several breathing cycles and is shown in figure 2(b) (Neicu et al 2003). Then the ATT was projected to the BEV plane with a gantry angle of 180° in the Varian coordinate as shown in figure 2(c). To avoid beam interruption, the sliding window leaf sequence with 240 control points was exported. The maximum leaf speed used for the original leaf sequences was set at 2.5 cm s⁻¹. The dose rate of original leaf sequences was set at 600 MU min⁻¹, and the space of control points was set at 0.5 MU.

Figure 2.

(a) Expected fluence map, (b) averaged tumor trajectory (ATT) and (c) ATT projection at the beam's eye view (BEV) plane.

The original leaf sequence of a static target was delivered by the Varian 2100 CD with the Millenium 120-leaf DMLC with the following initial settings: collimator angle of 180°, initial phase of 0°, dose rate of 600 MU min⁻¹ and machine tolerance of 2 mm. After dose delivery, the dynamic log (Dynalog) files were exported and the fluence map was simulated from DMLC Dynalog files for the moving targets and is shown in figure 3(a). The difference between the planed and the delivered fluence map is shown in figure 3(b).

Figure 3.

Experiment results of the original leaf sequence without motion correction: (a) delivered fluence map and (b) difference between the expected and delivered fluences from figure 2(a) and figure 3(a), respectively.

An in-house software applied the 2D superimposing method to superimpose the tumor motion from the ATT onto the original leaf sequences in order to correct the motion effect. First, the motion-corrected sequences generated with a collimator angle of 180°, an initial phase of 0° and a dose rate of 600 MU min⁻¹ were delivered with a machine tolerance of 2 mm. Then four experiments were performed to study the performance of SMART delivery under realistic delivery conditions.

Experiment 1 (collimator angle)

In order to study the effect of collimator angle on leaf velocity, the motion-corrected leaf sequence was recalculated with a collimator angle of every 10° from 0° to 180°. After the WALS of motion-corrected leaf sequences with different collimator angles was calculated, an optimal collimator angle was selected to reduce the leaf velocity.

Experiment 2 (initial phase)

After the optimal collimator angle was determined, each phase of every 10° from 0° to 360° was selected as the initial phase to calculate motion-corrected leaf sequences. Then an optimal initial phase was selected based on the calculation of WALS.

Experiment 3 (dose rate)

After the collimator angle and the initial phase were selected, the motion-corrected leaf sequence was calculated with a dose rate of 600 MU min⁻¹, 500 MU min⁻¹, 400 MU min⁻¹, 300 MU min⁻¹, 200 MU min⁻¹ and 100 MU min⁻¹, respectively, and delivered with a machine tolerance of 2 mm.

Experiment 4 (machine tolerance)

For each motion-corrected leaf sequence with a dose rate of 100 MU min⁻¹, 200 MU min⁻¹, 300 MU min⁻¹ and 400 MU min⁻¹, the leaf sequence was delivered with four different machine tolerances of 2 mm, 3 mm, 4 mm and 5 mm.

The motion-corrected leaf sequences with different settings of collimator angle, initial phase, dose rate and machine tolerance were executed by the Millenium 120-leaf DMLC, and the dose was delivered by the Varian 2100 CD LINAC. After dose delivery, the Dynalog files generated by the DMLC were exported to analyze the performance of dose delivery.

3. Results

In the following, the effect of different clinical parameters is discussed and the overall delivery performance is presented.

3.1. Effect of collimator angle

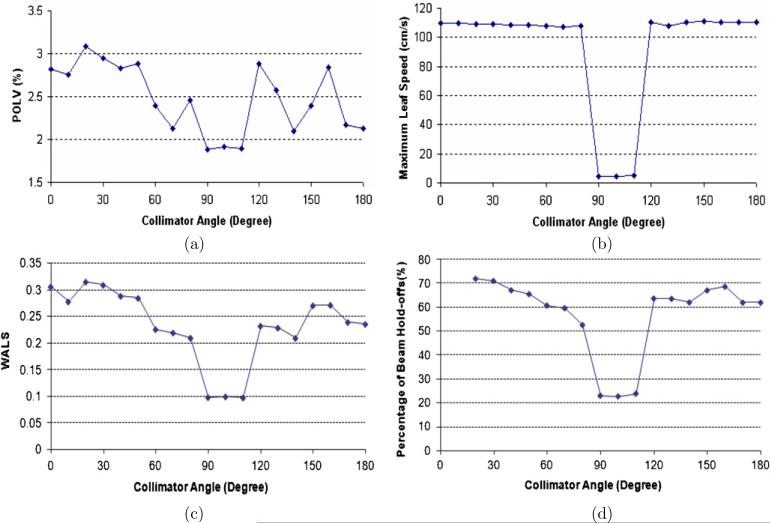
The collimator angle is one of the major reasons which affect leaf velocities, and needs to be fixed before leaf sequencing. For leaf sequences with different collimator angles, the POLV, maximum leaf speed and WALS were calculated and shown in figure 4. From the analysis of Dynalog files exported after dose delivery, the percentage of time with beam hold-offs was measured and shown in figure 4(d). As expected, it is observed in figure 4 that the WALS gives the best estimate of the percentage of time with beam interruption. For this reason, we will not show plots of the POLV and maximum leaf speed in the following discussion for other clinical parameters. Based on the WALS, an acceptable range of collimator angles can be determined. As shown in figure 4(c), the range in this case is from 90° to 110°.

Figure 4.

Results for different collimator angles: (a) percentage of over-limit leaf velocities (POLV), (b) maximum leaf velocities, (c) weighted average leaf speed (WALS) and (d) percentage of time with beam hold-offs.

3.2. Effect of initial phase

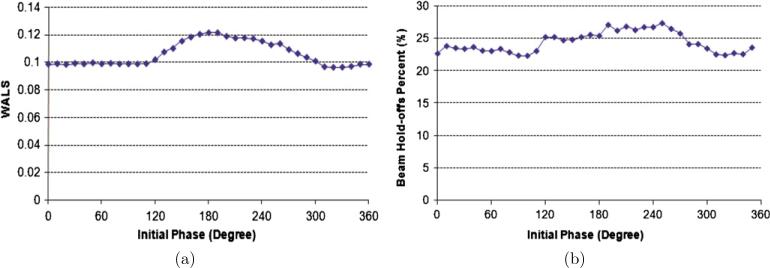
The initial phase was the second factor to be optimized in order to decrease leaf velocities. The WALS of motion-corrected leaf sequences with different initial phases is shown in figure 5(a). The percentage time with beam hold-offs delivered by these leaf sequences was measured and shown in figure 5(b). As expected, the curve of percentage time with beam hold-offs has the similar trend as that of the WALS, indicating that the WALS is a good indicator of the severity of beam hold-offs. Due to the high value of WALS between 120° and 310°, an initial phase in that range should be avoided. In this paper, an initial phase of 320° was selected in the following analysis.

Figure 5.

Results for different initial phases: (a) weighted average leaf speed and (b) percentage of time with beam hold-offs.

3.3. Effect of dose rate

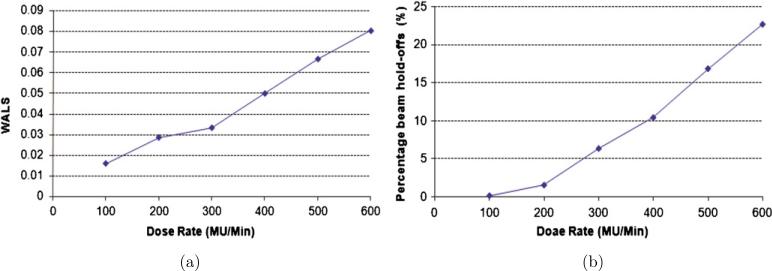
Dose rate is another major factor that affects leaf velocities. With a selected collimator angle of 90° and an initial phase of 320°, the motion-corrected leaf sequences were calculated for every 100 MU min⁻¹ from 100 MU min⁻¹ to 600 MU min⁻¹. Then, the WALS was calculated for the motion-corrected leaf sequences at each dose rate, and is shown in figure 6(a). After the leaf sequences were delivered, the percentage of beam interruption time was measured, and is shown in figure 6(b). It is observed from figure 6 that the WALS and the percentage of time with beam hold-offs decrease as the dose rate decreases. Although a lower dose rate can reduce the universal leaf velocities, it also increases the treatment time. Therefore, when beam hold-offs can be avoided, a higher dose rate is desired to increase the efficiency of dose delivery. It is shown in figure 6(a) that with a machine tolerance of 2 mm, the WALS is greater than 0 at any dose rate. A different machine tolerance will be selected in the next step to increase the dose rate without causing beam hold-offs.

Figure 6.

Results for different dose rates: (a) weighted average leaf speed and (b) percentage of time with beam hold-offs.

3.4. Effect of machine tolerance

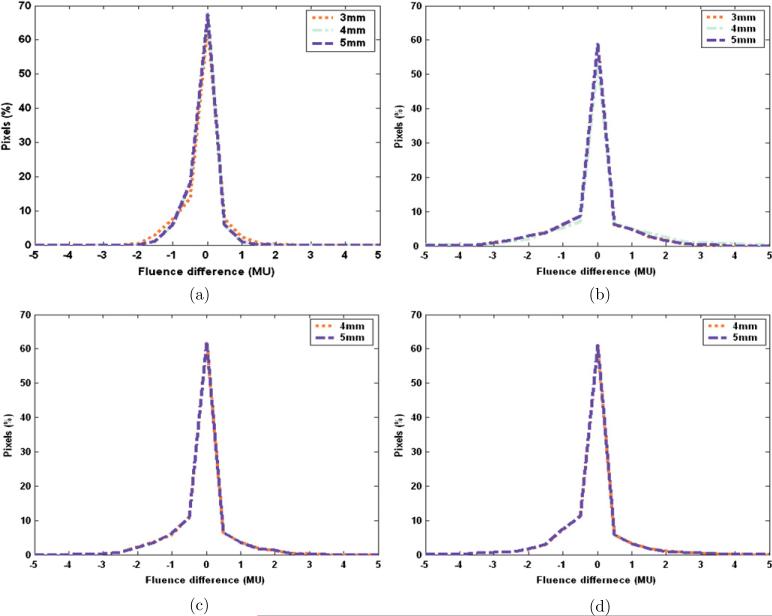
It is clear that increasing machine tolerance will reduce the possibility of beam hold-offs. However, a higher machine tolerance may reduce the accuracy of dose delivery. In order to study the effect of machine tolerance on the accuracy of dose delivery, the motion-corrected leaf sequences were delivered with different machine tolerances. The distributions of fluence difference for leaf sequences with different dose rates and machine tolerances are shown in figure 7, where only leaf sequences without beam hold-offs are displayed. It is observed in figure 7 that only slight difference exits between different machine tolerance settings regarding the fluence difference. Therefore, a machine tolerance of 5 mm, which is the maximum machine tolerance, was selected in order to reduce the possibility of beam hold-offs.

Figure 7.

Distributions of fluence difference at different dose rates and machine tolerances: (a) dose rate of 100 MU min⁻¹, machine tolerance of 5 mm, 4 mm and 3 mm; (b) dose rate of 200 MU min⁻¹, machine tolerance of 5 mm, 4 mm and 3 mm; (c) dose rate of 300 MU min⁻¹, machine tolerance of 5 mm and 4 mm; (d) dose rate of 400 MU min⁻¹, machine tolerance of 5mmand4mm.

Then, the WALS of motion-corrected leaf sequences obtained in section 3.3 was recalculated. With a new machine tolerance of 5 mm, the WALS was reduced to 0.045 at a dose rate of 600 MU min⁻¹, and 0 at a dose rate of 400 MU min⁻¹ or less. After the delivery of motion-corrected leaf sequences with a new machine tolerance of 5 mm, the exported Dynalog files showed that there was no beam hold-offs occurred for a dose rate of 400 MU min⁻¹ or less, which is consistent with the calculation of WALS.

3.5. Delivery performance

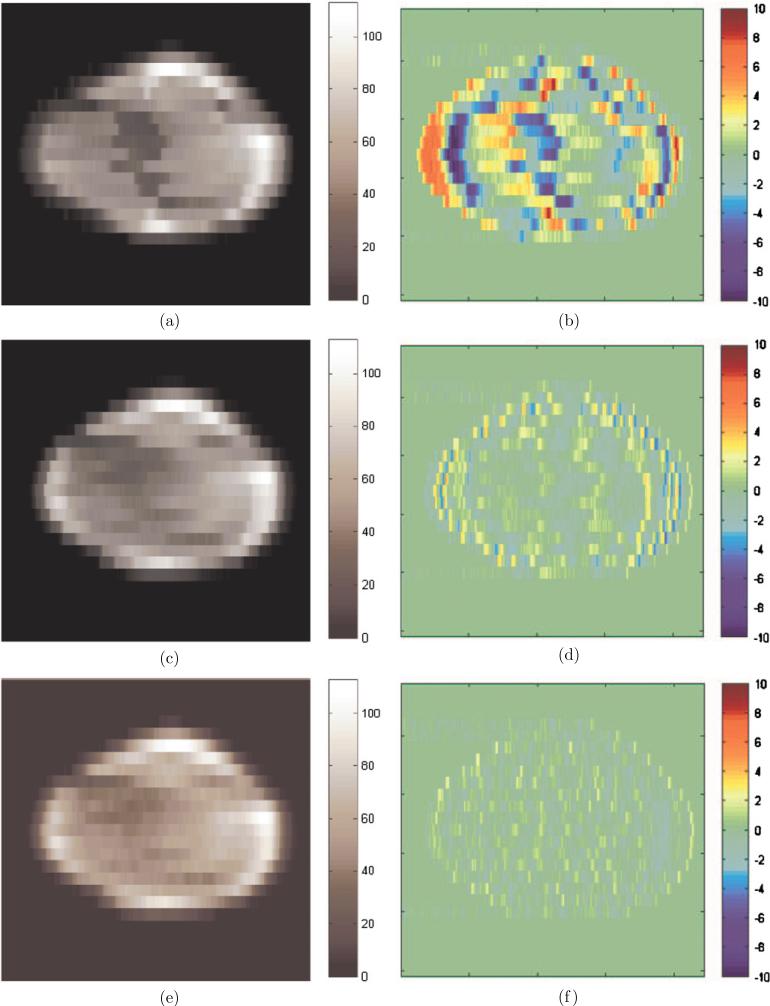
The delivered fluence maps with motion-corrected leaf sequences were simulated from Dynalog files through an in-house software and are shown in figures 8(a), (c), (e), and the fluence differences between delivered dose and planned dose were calculated and are shown in figures 8(b), (d) and (f).

Figure 8.

Delivered fluence maps (a), (c), (e) and fluence differences (b), (d), (f) with motion-corrected leaf sequences under different settings of clinical parameters: (a), (b) collimator angle 180°, initial phase 0°, dose rate 600MU min⁻¹ and machine tolerance 2 mm; (c), (d) collimator angle 90°, initial phase 320°, dose rate 400MU min⁻¹ and machine tolerance 5 mm; (e), (f) collimator angle 90°, initial phase 320°, dose rate 100MU min⁻¹ and machine tolerance 3 mm.

In figures 8(a) and (b), the leaf sequence was motion corrected, but was not optimized for realistic delivery conditions. The leaf sequence was calculated with a collimator angle of 180°, an initial phase of 0°, a dose rate of 600 MU min⁻¹ and a machine tolerance of 2 mm. These clinical parameters were the same as those of original leaf sequence without motion correction as shown in figure 3. The maximum fluence difference in figure 3 is around ±33 MU, which is ±30% of the expected value. In figure 8(b), the maximum fluence difference is around ±10 MU, which is ±9% of the expected value. It is clear that dose error was significantly reduced by motion-corrected leaf sequences. It is also observed that the area of dose error over ±2% was decreased around five times after the leaf sequences were motion corrected. However, it was shown from the exported Dynalog files that with non-optimum clinical parameters there was about 65% of delivery time when beam hold-offs occurred during delivery.

In order to avoid beam hold-offs, motion-corrected leaf sequences were optimized with respect to clinical parameters, including the collimator angle, initial phase, dose rate and machine tolerance. The optimal collimator angle was set at 90° and the optimal initial phase was set at 320°. The delivered fluence map of the optimized leaf sequence with a high dose rate of 400 MU min⁻¹ and a loose machine tolerance of 5 mm is shown in figure 8(c). And the delivered fluence map of the optimized leaf sequence with a low dose rate of 100 MU min⁻¹ and a tight machine tolerance of 3 mm is shown in figure 8(e). The difference between these two delivered fluence maps and the expected fluence map are shown in figures 8(d) and (f), respectively. After dose delivery, the exported Dynalog files showed that there were no beam hold-offs in both cases. By eliminating beam hold-offs, the maximum dose error was further reduced to ±5% and ±3.5% as shown in figures 8(d) and (f), respectively. Through the comparison between figures 8(d), (f) and 8(b), it is also observed that the area of dose error over ±2% was further reduced around six times after the motion-corrected leaf sequences were optimized under the realistic delivery conditions.

Although the dose error in figure 8(f) with low dose rate and tight machine tolerance was slightly lower than that in figure 8(e) with high dose rate and loose machine tolerance, the dose error of ±5% in figure 8(f) is already clinically acceptable. As explained in section 3.3, a lower dose rate increases the delivery time and thus decreases the delivery efficiency. In this example, the delivery time in figures 8(e), (f) was three times longer than that in figures 8(c), (d). Therefore, the delivery conditions used in figures 8(c), (d) were selected as the optimal clinical parameters in this example.

4. Discussion

The superimposing method is one of leaf sequencing techniques to account for the dose error caused by tumor motion during treatment delivery. Compared to other leaf sequencing techniques, the superimposing method is easy to implement. However, in the clinical implementation of the superimposing method, the delivery performance is affected by beam hold-offs, where the requested leaf velocities are beyond the machine constraints, since the occurrence of beam hold-offs breaks the synchronization between the DMLC and targets.

To avoid beam hold-offs, leaf velocities of motion-corrected leaf sequences were studied. Equation (4) of the 2D superimposing method provides a guidance to optimize motion-corrected leaf sequences under realistic clinical conditions. Clinical factors such as collimator angle, initial phase, dose rate and machine tolerance were studied. An optimization index, the WALS, was introduced to evaluate the severity of beam hold-offs. When WALS equal to zero, beam hold-offs can be totally avoided. The measurement of beam hold-off time is consistent with the calculation of WALS.

The collimator angle is the first factor to be optimized since the change of collimator angle will cause the re-calculation of original leaf sequences. It was noted that in the example discussed in section 3.1, when the collimator angle was set to be between 90° and 110°, the direction of leaf motion was aligned with the major direction of tumor motion, which was around 100° as shown in figure 2(b). However, in general, aligning the direction of leaf motion with the major direction of tumor motion may not necessarily achieve the optimal collimator angle regarding beam hold-offs. First, it may be very difficult, if not impossible, to define the major direction of tumor motion, for example, for an irregular tumor trajectory or a circular tumor trajectory. Second, for those tumor trajectories with major and minor motion directions, the optimal collimator angle is affected by multiple factors, for example, the expected fluence map and the tumor motion components along both the x- and y-directions of the DMLC, and may not be the same as the major direction of tumor motion. Comprehensive understanding of the impact of such factors on the optimal collimator angle is beyond the scope of this paper. Due to such complexity, there is no simple approach which we know to determine the optimal collimator angle regarding beam hold-offs. The approach presented in this paper can identify the range of optimal collimator angle through the iterative calculation of WALS at different collimator angles.

After the optimal collimator angle and initial phase are determined, the dose rate and machine tolerance need to be considered together to optimize leaf sequences. In SMART, a regular tumor motion is assumed and the synchronization between the tumor motion and the DMLC motion needs to be ensured during the treatment. The treatment will be terminated if desynchronization occurs, which may caused by irregular tumor motion or beam hold-offs. The possibility of having irregular tumor motion increases when the treatment time increases. Therefore, a high dose rate is desired to reduce the possibility of irregular tumor motion. However, as discussed in section 3.3, a high dose rate increases the universal leaf velocities, and may cause beam hold-offs. Then, machine tolerance needs to be increased to reduce beam hold-offs. In our example, the study of delivered fluence maps with different machine tolerances showed that the dose error was acceptable with a maximum machine tolerance of 5 mm. So using a loose machine tolerance to keep a high dose rate is feasible when delivering dose to moving targets.

From experiment results discussed in section 3, it was shown that leaf velocities were reduced after the motion-corrected leaf sequences were optimized under realistic delivery conditions. The reduced leaf velocities avoided beam hold-offs, and thus improved the DMLC performance during treatment. Besides the example shown in section 3, another three original leaf sequences were studied with five different tumor trajectories. In all cases, the optimized clinical parameters were identified for motion-corrected leaf sequences generated by the superimposing method, the synchronization was ensured during treatment, and the performance of SMART dose delivery was improved through the optimized leaf sequences.

5. Conclusion

In this work, SMART delivery by the DMLC was studied to reduce the motion-related dose error. A 2D superimposing method was developed and used to modify the original leaf sequence to generate motion-corrected leaf sequences for SMART. By performing the motion-corrected leaf sequences, DMLC motion was synchronized with tumor motion. The study of leaf velocities and beam hold-offs showed that the actual DMLC based dose delivery is affected by DMLC mechanical constraints. Eliminating beam hold-offs ensures the synchronization between the leaf motion and the tumor motion. To avoid beam hold-offs, the maximum leaf velocity should be less than the effective limiting velocity. The leaf velocity can be adjusted by the settings of clinical parameters such as collimator angle, initial phase and dose rate. Also the selection of machine tolerance can avoid beam hold-offs. Through the comparison between the delivered fluence map and the planed fluence map, it was shown that the optimized leaf sequences can significantly reduce the dose error caused by tumor motion during the DMLC-based IMRT dose delivery.