Computer-based Studies of Diffusion through Stomata of Different Architecture

Abstract

Background and Aims

The influence of stomatal architecture on stomatal conductance and on the developing concentration gradient was explored quantitatively by comparing diffusion rates of water vapour and CO₂ occurring in a set of three-dimensional stoma models. The influence on diffusion of an internal cuticle, a sunken stoma, a partially closed stoma and of substomatal chambers of two different sizes was considered.

Methods

The study was performed by using a commercial computer program based on the Finite Element Method which allows for the simulation of diffusion in three dimensions. By using this method, diffusion was generated by prescribed gas concentrations at the boundaries of the substomatal chamber and outside of the leaf. The program calculates the distribution of gas concentrations over the entire model space.

Key Results

Locating the stomatal pore at the bottom of a stomatal antechamber with a depth of 20 µm decreased the conductance significantly (at roughly about 30 %). The humidity directly above the stomatal pore is significantly higher with the stomatal antechamber present. Lining the walls of the substomatal chamber with an internal cuticle which suppresses evaporation had an even stronger effect by reducing the conductance to 60 % of the original value. The study corroborates therefore the results of former studies that water will evaporate preferentially at sites in the immediate vicinity to the stomatal pore if no internal cuticle is present. The conductance decrease affects only water vapour and not CO₂. Increasing the substomatal chamber increases CO₂ uptake, whereas transpiration increases if an internal cuticle is present.

Conclusions

Variation of stomatal structure may, with unchanged pore size and depth, profoundly affect gas exchange and the pathways of liquid water inside the leaf. Equations for calculation of stomatal conductance which are solely based on stomatal density and pore depth and size can significantly overestimate stomatal conductance.

INTRODUCTION

The diffusive conductance of a leaf is mainly dependent on boundary layer and stomatal conductance (or resistance). There are various approaches for modelling the regulation of stomatal conductance as a response to environmental and physiological factors (e.g. Farquhar and Wong, 1984; Ball et al., 1987; Leuning, 1990; Collatz et al., 1991; Buckley et al., 2003). These models consider the plant control mechanisms of actual pore size. Besides the instantaneous pore size, stomatal conductance is dependent on various structural features, such as stomatal density, pore shape and depth, and the degree of interference between adjacent stomata. Theoretical approaches for calculating stomatal conductance are based on these parameters (Brown and Escombe, 1900; Parlange and Waggoner, 1970; Lushnikov et al., 1994). The size of the substomatal chamber also influences stomatal conductance. It was found for a simple cylindrical model that the rate of water vapour flux decreases until the substomatal chamber reaches the size of a few pore radii (Pickard, 1981). Larger sizes which are usually realized for real stomata can promote CO₂ uptake (Pickard, 1982). By applying the equation of Parlange and Waggoner (1970) to an elongated slit, Van Gardingen et al. (1989) achieved very good agreement between calculated and measured conductance for Avena fatua after determining the actual stomatal pore sizes by Cryo-SEM.

Stomatal architecture, however, shows a large variability among plants and many features are interpreted as influencing stomatal conductance. For example, sunken stomata, seated at the bottom of a recess termed the stomatal antechamber (Napp-Zinn, 1973) or stomata located in crypts or grooves (housing more than one stoma; Napp-Zinn, 1973) are considered as xeromorphic properties decreasing stomatal conductance (Lösch et al., 1982; Larcher, 2003). Lösch et al. (1982) compared the transpiration rates of two shrub species, Eriobotrya japonica and Nerium oleander. He suggested that the lower conductance of E. japonica might be due to the dense hair covering the abaxial leaf surfaces which possibly decreases conductance more effectively than the sunken stomata of N. oleander. Another feature which is expected to decrease the conductance are stomatal wax plugs which are especially common in conifers (and which often also have sunken stomata). Brodribb and Hill (1997) reported that stomatal wax plugs decrease leaf conductance significantly. They interpreted wax plugs, however, not as an adaptation to drought, but as a means to prevent the formation of a water film over the stomatal pore during rain or mist (Brodribb and Hill, 1997). On the contrary, Feild et al. (1998) found that stomatal plugs of Drimys winteri lead to a minor resistance increase of about 8 %.

Internal cuticles are also expected to influence stomatal diffusion. Cuticular substances which cover mesophyll cell walls adjacent to intercellular air spaces were found in a number of different species (Scott, 1948; Norris and Bukovac, 1968; Wullschleger and Oosterhuis, 1989; Pesacreta and Hasenstein, 1999). The extent of the internal cuticle differs for different species and is also subject to controversial discussion (Pesacreta and Hasenstein, 1999). The efficiency of an internal cuticle as an evaporative barrier is unclear. It is usually much thinner than the external cuticle, but no conclusion can be drawn from the thickness of the internal cuticle to its capacity to prevent water loss (Pesacreta and Hasenstein, 1999). Since there is evidence that evaporation is strongest close to the stoma if no evaporative barrier exists (Tyree and Yianoulis, 1980; Pickard, 1981; Yianoulis and Tyree, 1984), any decrease of evaporation in the vicinity of the stomatal pore should influence diffusion. Cuticle-free areas on the inner walls of guard cells of several tree species were interpreted as sites of strong evaporation which were involved in the humidity response of the stomata (Appleby and Davies, 1983).

The model approaches mentioned so far are based on different simplifications of the stomatal structure. They describe diffusion through channels with elliptic or circular cross-section (Parlange and Waggoner, 1970; Lushnikov et al., 1994) or diffusion through circular pores located above a substomatal chamber which is hemispherical or cylindrical (Tyree and Yianoulis, 1980; Pickard, 1981, 1982; Yianoulis and Tyree, 1984). In all these cases, the pore aperture was located at the same level as the epidermis. In some models, a stomatal channel was not integrated. If the models included a substomatal chamber, then evaporation was allowed at the entire chamber wall. One model variation of Pickard (1981) included an internal cuticle leading to a significant reduction of conductance. It was, however, located at the ceiling around the stomatal pore which lacked a stomatal channel. The simplifications depended on the aspects considered and were necessary if a mathematical–analytical approach was applied. A numerical study which considered gasesous exchange through a stoma whose geometry is based on Pinus sylvestris and which included an antechamber and a substomatal cavity (both cylindric) was performed by Vesala et al. (1995, 1996). They found that gas exchange is insensitive to moderate variations of size and shape of the sub-stomatal cavity.

In this contribution, diffusion in different stomata with a stomatal channel located above a substomatal chamber is simulated in order to explore the quantitative influence of the position of the pore, the presence of an internal cuticle and the size of the substomatal chamber on conductance. This is accomplished by applying a computer simulation approach based on the Finite Element (FE) method. This method allows for the consideration of physical processes occurring in complex structures which are represented by a mesh consisting of defined geometrical entities, such as triangular or quadrilateral elements. Diffusion of both water vapour and CO₂ is considered for six different stoma models. The stoma models differ with respect to location of the pore (sunken versus non-sunken), the presence of an internal cuticle which restricts evaporation inside the substomatal chamber and the size of the chamber. The modelling approach focuses on diffusion through a single stoma only, i.e. the boundary layer above the leaf or interference between adjacent stomata are not considered.

MATERIALS AND METHODS

Model technique

The process of diffusion, according to Fick's law, reads for three dimensions as [J = diffusional flux, D = diffusion coefficient, C = concentration, grad = differential operator (M/Mx, M/My, M/Mz)]:

1

This differential equation can be solved only for simple geometric problems, such as circular or elliptic pores or capillaries. It is, however, possible to consider diffusion in more complex three-dimensional structures by using numerical methods, such as the FE method. Due to availability of high amounts of computer resources nowadays it is possible to treat three-dimensional FE models with a high spatial resolution on common PCs. In this contribution, the commercial FE-based program FIDAP 8·7 (Fluent Inc., Lebanon, USA) was applied. FIDAP is a CFD (Computational Fluid Dynamics) program which also includes a diffusion module.

FE is a numerical approach to the solution of differential equations (Zienkiewicz and Taylor, 1989). By using this method, the considered continuum (the continuous space) is divided into a number of elements with prescribed geometry, usually triangular or quadrilateral elements, which are interconnected at their nodes. The aim is to transform the differential equations describing the continuum into a system of algebraic equations describing the behaviour of the interconnected discrete elements. The system of algebraic equations is then solved by iterative numeric procedures for the population of elements which compose the considered geometry. Each change in geometry requires the construction of a new mesh, whereas changes in non-geometrical model components (such as the diffusion coefficient) are simply achieved by changing the input parameters. The results are calculated for the steady state.

The procedure of creating and running a model consists of several steps. Firstly, the desired mesh is created by using an appropriate model generator program. Then the physical problem together with its solution routines is defined. After running the solution module of the program, a data file with the results at each element node is available. Successful application of FE requires the construction of a grid or mesh which shows a certain minimum density of elements. This minimum density is obtained by subsequently increasing the number of elements until the calculated results do not change significantly.

The FE models

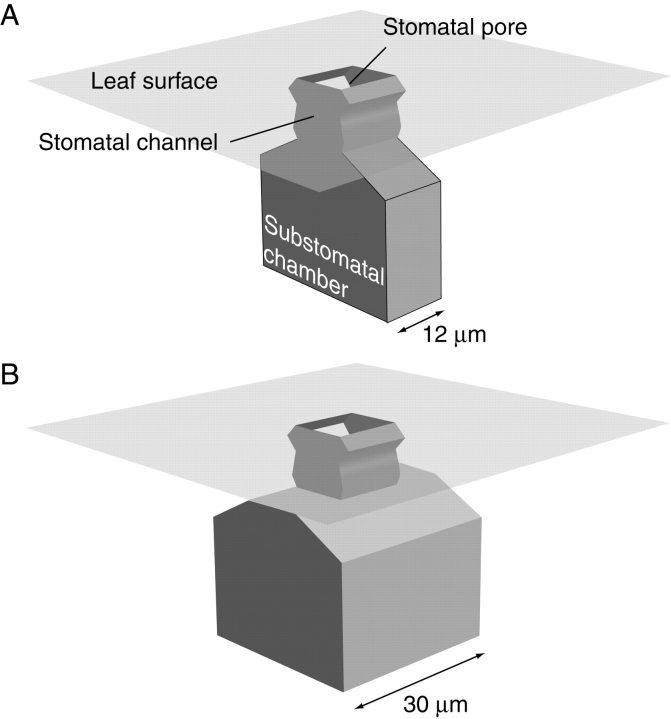
Each of the stomatal variations considered represents an FE model. The six different models are summarized in Table 1. The basic three-dimensional geometry BASIC model is depicted in Fig. 1. It consists of a stomatal channel which connects leaf surface and substomatal chamber. The stomatal pore size shows a broad range of variation in plants. In a survey concerning stomatal dimensions by Napp-Zinn (1973), a range of 7·5–36·5 µm is given as a characteristic magnitude of common pore lengths. Various examples of taxa with stomatal pore lengths of this size can also be found in Metcalfe and Chalk (1979). Much larger sizes occur but these represent the extreme values. A standard pore size of 12 × 10 µm = 120 µm² was chosen for the model, because this value appears to lie within the typical range found for mesophytic plants. All models show this pore size, with the exception of one model (CLOS). Here the pore is partially closed with a pore area of 48 µm² (12 × 4 µm) in order to test the correctness of the model. A value of 10 µm was chosen for the length of the channel ( = stomatal pore depth) for all models. This value appears to lie within the typical range for channel depths (Metcalfe and Chalk, 1979). SUNK represents a model of a sunken stoma. Here, the stomatal pore is seated at the bottom of a stomatal antechamber. The antechamber is 20 µm deep with an area of 12 × 30 µm = 360 µm². A cross-sectional view (perpendicular to the pore) of the different models is provided in Fig. 2 which also shows the evaporative sites of the models (see below).

Table 1.

Summary of the different models

	BASIC	INTERN	CLOS	SUNK	CHAM	CHAINT
Pore area (μm2)	120	120	48	120	120	120
Internal cuticle	No	Yes	No	No	No	Yes
Chamber length (μm)*	12	12	12	12	32	32
Sunken stoma	No	No	No	Yes	No	No
Transpiration (%)	100	59·5	46·1	71·3	98·6	74·5
CO2 influx (%)	100	100	52·9	75·8	124·2	124·2

The features which were varied are provided for each model.

Also shown are the differences in the fluxes of water vapour and CO₂, expressed as percentage values of the flux rates of the BASIC model.

*Chamber dimension parallel to the long axis of the stomatal pore.

Fig. 1.

Basic geometry of the three-dimensional model with a smaller (A) and a larger (B) substomatal chamber. It includes a stomatal porus which is connected to the chamber by a stomatal channel. The model also comprises an air layer adjacent to the leaf surface which has a thickness of 35 µm. The dimension of the pore is 10 × 12 µm, the depth of the channel amounts to 10 µm. The smaller substomatal chamber has a length of 12 µm and the length of the larger chamber amounts to 30 µm. For the other model dimensions see text and the cross-sectional representations in Fig. 2.

Fig. 2.

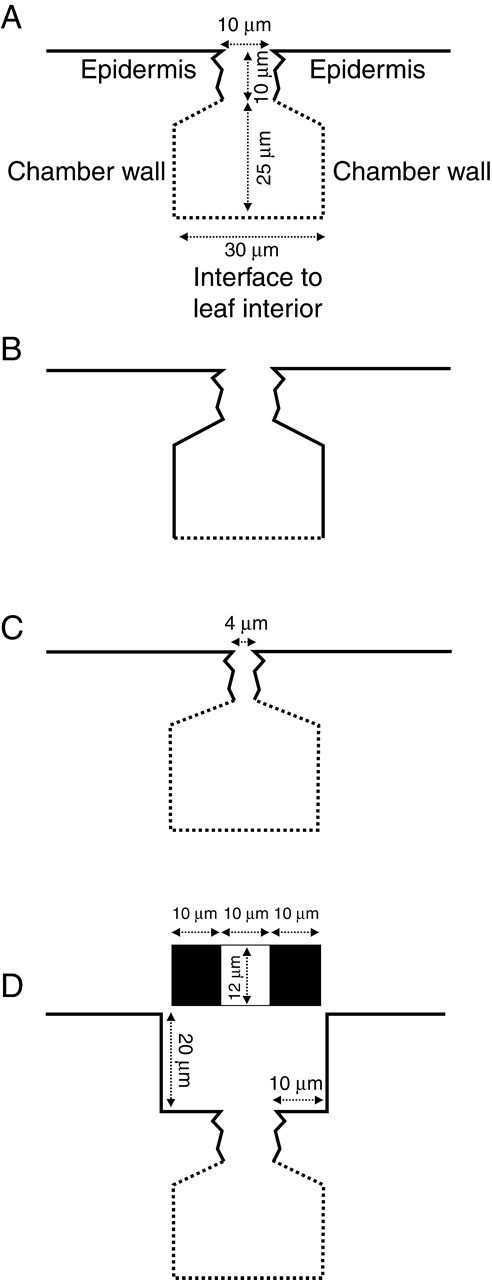
The different models, depicted in cross-sectional view (cut plane perpendicular to the pore, at the centre of the models). Continuous lines represent non-evaporative sites; dotted lines, sources of water vapour. The bottom of the substomatal chamber represents the interface to the leaf interior. It also represents the sink for CO₂. The model dimensions are indicated. The stomatal pore has a length of 12 µm and a width of 10 µm for all models, with the exception of the CLOS model (see below). The CHAM and CHAINT models with the larger substomatal chamber are not shown, because the substomatal chamber is increased in the direction perpendicular to the cross-section (see text). They therefore show the same cross-sectional views as BASIC and INTERN. The outlines of both models are shown in Fig. 1. (A) The basic BASIC model; (B) the INTERN model, with the substomatal chamber walls being covered with an internal cuticle; (C) the partially closed CLOS model (pore dimension: 4 × 12 µm); (D) model of a sunken stoma. The stoma is located at the bottom of an antechamber with a depth of 20 µm. The area of the antechamber amounts to 12 × 30 µm. The location of the pore at the bottom of the chamber is depicted as top view above the cross-section with the white rectangle representing the outline of the pore and the black rectangles, the bottom parts of the antechamber.

The substomatal chamber has a funnel-shaped geometry (with the stem of the funnel representing the lower side of guard cells) with a length (dimension perpendicular to the pore) of 25 µm. The width (dimension perpendicular to the long axis of the stoma) amounts to 30 µm and the depth (dimension parallel to the long axis of the stoma) amounts to 12 µm (see Figs 1 and 2). Size and shape of the substomatal chamber differs among plant taxa. The actual chamber size and shape was chosen, because only simple hemispherical or cylindrical shapes were considered so far and, according to the results of Pickard (1981, 1982), the chamber size shows no significant effect on water vapour diffusion once a chamber length and width of about twice the pore width is achieved. Two models, CHAM and CHAINT, are equipped with a larger substomatal chamber, and are also depicted in Fig. 1. In these models, the depth of the substomatal chamber amounts to 30 µm.

Additionally, the evaporative sites were varied. Figure 2 shows the evaporative and non-evaporative sites ( = covered by an internal cuticle). In the BASIC, CLOS, SUNK and CHAM models, only the stomatal channel is covered by an internal cuticle completely suppressing evaporation. All other internal parts of the model are sources of water vapour of a defined concentration (for the assignments of water vapour concentrations see below). In the INTERN and CHAINT models, the internal cuticle covers the lateral walls of the substomatal chamber (see Fig. 2).

Physical parameters

For the model calculations, a temperature of 20 °C is chosen. No temperature gradient is included and the diffusional constants for water vapour (2·42 10⁻⁵ m² s⁻¹) and CO₂ (1·5 10⁻⁵ m² s⁻¹) at 20 °C were applied. The model does not take into account temperature gradients which alter the absolute concentrations of water vapour for a certain relative humidity. Results obtained by model calculations performed by Yianoulis and Tyree (1984) indicated that evaporation at the leaf interior leads to cooling effects which decrease the temperature of the evaporating sites to about 0·1–0·4 °C. These alter the concentration gradients slightly but do not change the overall diffusion pattern. The external concentration of water vapour amounts to 50 % relative humidity. A relative humidity of 99 % is assigned to the evaporative sites (Farquhar and Raschke, 1978). This value is also assigned to the bottom of the substomatal chamber for all models.

The external CO₂ concentration is defined to amount to 360 ppm. The CO₂ sink created by photosynthesis is represented by a CO₂ concentration at the bottom of the substomatal chamber, defined as 70 % of the external value (=250 ppm). Only the bottom of the substomatal chamber is equipped with this CO₂ sink, because the assimilating tissues can be far away from stomata (e.g. the palisade parenchyma in the case of hypostomatous leaves). The model includes only the substomatal chamber close to the stomatal channel and not its continuations into the intercellular air spaces between the assimilating cells.

The ratio of 0·7 between internal and external CO₂ was chosen as sink strength because values from 0·6–0·8 are commonly observed for many species under optimum conditions (e.g. Franks and Farquhar, 1999). The detailed patterns of the CO₂ gradient within a leaf are much more complex (Parkhurst, 1994; Aalto and Juurola, 2002). This is, however, not the subject of the present contribution and the assigned boundary condition of 250 ppm CO₂ fulfils only the function of generating diffusive CO₂ influx into the model stoma. The program calculates the spatial distribution of gas concentrations within the model space for the steady state. From the concentration patterns, the diffusional fluxes out of and into the stoma are calculated.

According to Vesala (1998) who considered the effects of forced convection (wind) on mass transfer in the leaf boundary layer region, stomatal interference under windy conditions can affect stomatal water vapour diffusion. The effect depends on leaf size and wind velocity (Vesala, 1998). Wind does not significantly influence the diffusion through one single stoma. The present study therefore does not consider the effects of air movements which become essential for the next higher level of leaf gas exchange (i.e. a population of stomata interacting with their specific diffusive properties).

RESULTS

Concentration gradients

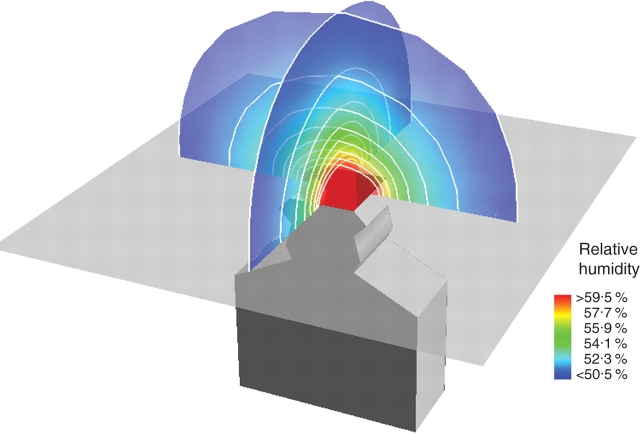
The expected cup-shaped concentration gradients above the stomatal pore developed for both water vapour and CO₂. The contours of water vapour concentration for the model BASIC are plotted in Fig. 3. A steep gradient for water vapour developed within the stomatal channel (see Fig. 4A). In the substomatal chamber, the relative humidity is close to 99 % relative humidity. For CO₂, a steep concentration gradient is also present along the stomatal channel (see Fig. 4B). The CO₂ gradient in the substomatal chamber is, however, much stronger than the water vapour gradient (see Fig. 4A, B). This is to be expected since CO₂ has to move from the pore to the chamber floor. The bulging out of the concentration contours at both pore openings of a stoma is included as ‘end correction’ in equations describing diffusion through a single stoma, because it increases the effective pore depth (Nobel, 1991). For water vapour, the effect at the internal pore is minimal due to the very low gradient at this site.

Fig. 3.

Spatial pattern of water vapour concentration above the pore of the BASIC model. To allow for visibility of the arrangement of the concentration contours, their cup-shaped arrangement is depicted at two co-ordinate planes intersecting each other at the centre of the stomatal pore.

Fig. 4.

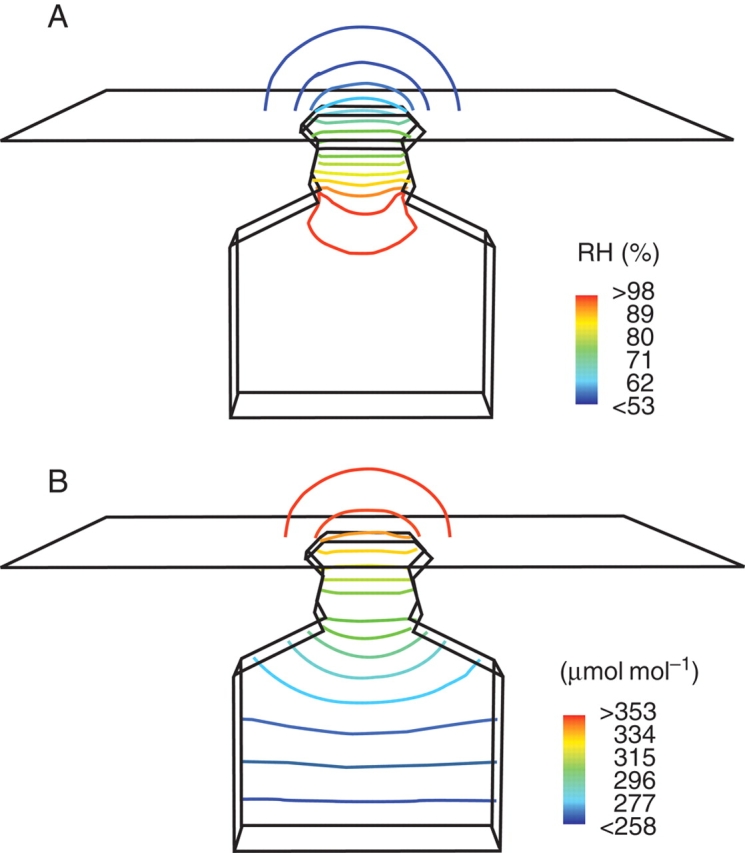
Concentration gradient inside the model BASIC, plotted as contour lines into a cut plane of the model: (A) contour lines of water vapour, (B) contour lines of CO₂.

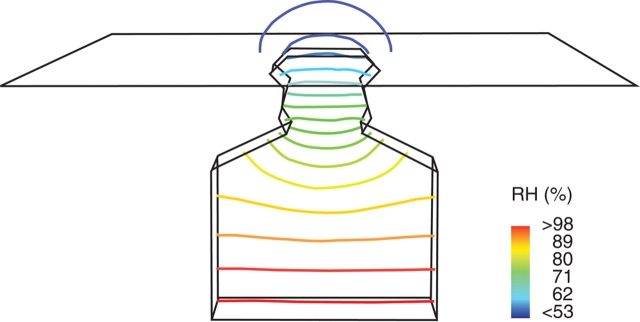
In the case of the INTERN model which restricts the water vapour source to the chamber floor, a significant water vapour gradient also developed along the substomatal chamber (Fig. 5). Inside the substomatal chamber of INTERN, significantly lower humidity values are present compared with BASIC. Egorov and Karphushkin (1988) reported leaf internal humidity values of 90–95 %, which correspond roughly with the humidity levels inside the substomatal chamber of INTERN. For the SUNK model, the concentration contours outside of the leaf show a cup-shaped gradient in the cavity above the stomatal pore which gradually straightens out and becomes cup-shaped again above the cavity opening (data not shown).

Fig. 5.

Concentration gradient of water vapour inside the stomatal model INTERN (model with internal cuticle lining the sides of the substomatal chamber), plotted as contour lines into a cut plane of the model.

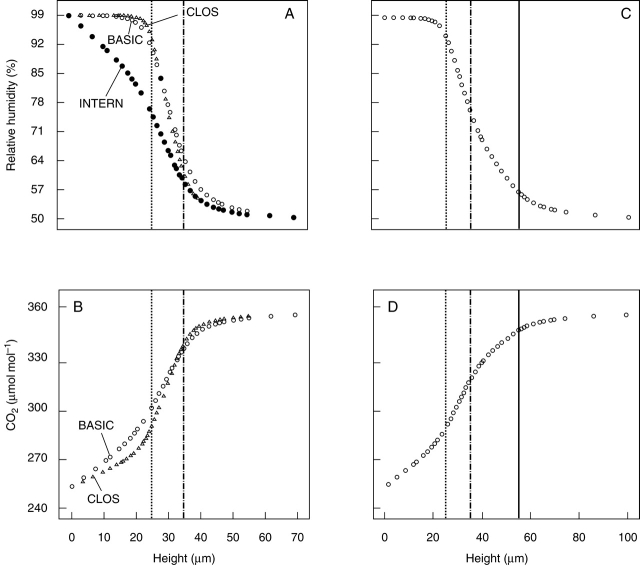
The gradients of H₂O and CO₂ are summarized for several models in Fig. 6 by plotting the concentration values from the bottom of the model to its top (maximum height = 70 µm for BASIC, INTERN and CLOS models and 100 µm for the SUNK model) at the location of the centre point of the pore. The steep concentration gradient for both water vapour and CO₂ along the stomatal channel is illustrated for all structures. Furthermore, the plots demonstrate the different shapes of the concentration gradients of water vapour and CO₂ below the stomatal channel in the case of the BASIC, CLOS and SUNK models. The flat water vapour gradient along the substomatal chamber in these models shows that water vapour diffusing into the channel originated preferentially from sites closest to the internal pore. In the INTERN model, which restricts both the water vapour source and the CO₂ sink to the bottom of the model, a significant water vapour gradient similar to the CO₂ gradient also developed along the substomatal chamber.

Fig. 6.

The gradients of water vapour and CO₂ depicted for the BASIC, INTERN, CLOS and SUNK models. The concentration values are plotted against the height, from the bottom of each model to its top, at the centre point of the porus. The maximum height amounts to 70 µm for BASIC, INTERN and CLOS models and to 100 µm for the SUNK model. (A) Concentration gradient of water vapour for BASIC (open circles), INTERN (filled circles) and CLOS (triangles) models. (B) Concentration gradient of CO₂ for BASIC (open circles) and CLOS (triangles) models. The INTERN model is not included in this graph since it shows a gradient of CO₂ which is identical to the BASIC model. (C) Concentration gradient of water vapour for the SUNK model. (D) Concentration gradient of CO₂ for the SUNK model. Dotted line, internal pore of stomatal chamber; broken line, external pore of stomatal channel; solid line, external orifice of stomatal antechamber.

Decreasing of the pore area by partial closure in model CLOS caused a slightly higher gradient above the pore for water vapour and below the pore for CO₂. For SUNK, the depression of the stomatal pore resulted in the continuation of the channel gradient along the antechamber which increases the diffusion resistance. This also leads to a higher humidity level directly above the pore.

Fluxes of water vapour and CO₂

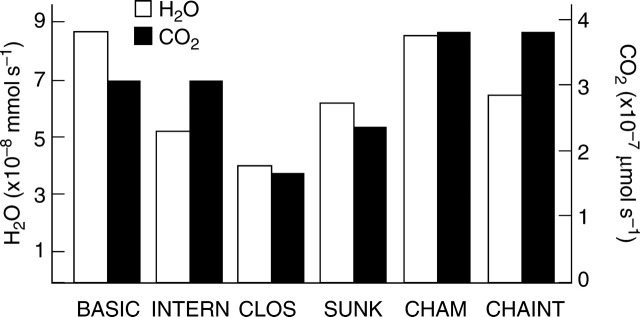
The flux rates (mmol s⁻¹ for water vapour, and μmol s⁻¹ for CO₂) per stoma are depicted in Fig. 7. The standard BASIC model attains a water vapour flux of about 8·5 10⁻⁸ mmol s⁻¹ and a CO₂ flux of about 3 10⁻⁷ µmol s⁻¹. The elimination of water vapour sources in the immediate vicinity of the pore by the internal cuticle in the INTERN structure leads to a considerable decrease in water vapour flux amounting to 5 10⁻⁸ mmol s⁻¹ or to about 59 % of the BASIC model. In the case of CO₂, the flux rates are identical for both BASIC and INTERN since the internal cuticle only affects water vapour. Table 1 provides the flux rates of all model structures as percentage values of the rates attained by the BASIC model (defined as 100 %).

Fig. 7.

Diffusional fluxes of the different models, plotted as histogram.

Decreasing the stomatal pore area from 120 µm² to 48 µm² in the CLOS model leads to a water vapour flux of 4 10⁻⁸ mmol s⁻¹ and to a CO₂ flux of 1·6 10⁻⁷ µmol s⁻¹. The fact that the decreases in gas fluxes (amounting to 46 % for water vapour and to 52 % for CO₂ compared with the rates of model BASIC) are less than the decrease in pore area (pore area of SUNK = 40 % of the pore area of the BASIC model) is caused by the circumstance that the pore closure in CLOS is attained by decreasing pore width. This means that the ratio between pore length and pore width and thus pore geometry changes during closing which has an additional effect on conductance (Parlange and Waggoner, 1970). The small difference in the decrease of the flux rates between water vapour and CO₂ is probably due to the different distributions of sinks and sources for the two gases. Since water vapour diffuses towards the internal pore from all sides, whereas CO₂ has to move from the bottom through the whole substomatal chamber, a decrease of the stomatal pore size promotes especially the internal gradient of CO₂.

For the sunken stoma model SUNK, the additional gradient residing inside the stomatal antechamber decreased the flux rates of both water vapour and CO₂ significantly. The flux rate amounts to about 6 10⁻⁸ mmol s⁻¹ for water vapour and to 2 10⁻⁷ µmol s⁻¹ for CO₂. The presence of the antechamber resulted therefore in a conductance decrease of about 30 % for both gases. The diffusional flux of water vapour is, however, higher than for the INTERN model (equipped with an internal cuticle).

Enlarging the substomatal chamber in the CHAM model had no substantial influence on water vapour outflux (Fig. 7 and Table 1). CO₂ influx, however, increased by about 24 % (Fig. 1 and Table 1). This is in accordance with the findings of Pickard (1981) who stated that increasing the substomatal chamber size of more than about twice the pore width causes no further significant reduction of transpiration, but should promote CO₂ uptake. The reason for the increase in CO₂ influx is that an enlargement of the substomatal chamber size means an increase of the chamber bottom size and therefore of the CO₂ sink. The CHAINT model shows the same substomatal chamber size as CHAM, but with an internal cuticle. The diffusional CO₂ influx is identical for both CHAM and CHAINT models (see Fig. 7 and Table 1). The water vapour flux decreases for CHAINT (compared with CHAM) as expected. The transpiration is 6·4 10⁻⁸ mmol s⁻¹ for CHAINT, which amounts to about 75 % of the transpiration of the CHAM model structure. The reduction in transpiration achieved with an internal cuticle and a larger substomatal chamber (CHAM compared with CHAINT) is therefore lower than with an internal cuticle added to a smaller substomatal chamber (BASIC compared with INTERN) (see Fig. 7 and Table 1).

DISCUSSION

Sunken stomata are usually interpreted as reducing transpiration. The introduction of an antechamber resulted in a significant reduction in stomatal conductance for the models considered (Fig. 7). There are many types of arrangements which are more complex than the simple antechamber considered here. For example, the stomata in Nerium oleander or in Banksia are arranged in stomatal crypts filled with hairs (Metcalfe and Chalk, 1979; Lösch, 1982). In conifers, the sunken stomata are often additionally capped by a stomatal plug (Napp-Zinn, 1966). It is to be expected that these kinds of crypts offer a larger resistance to diffusion. However, not only transpiration is decreased by stomatal crypts but also CO₂ influx. Sunken stomata therefore also affect assimilation. Feild et al. (1998) remark that a‘… major conceptual problem with the idea of regulating water loss by a large, fixed resistance in the stomatal porus is that CO₂ uptake would be reduced as well’. Despite the circumstance that both conductance to water vapour and CO₂ are decreased, stomatal antechambers or crypts are probably beneficial for the plant. Feild et al. (1998) suggest that the stomatal plugs of Drimys winteri decrease wettability of the leaf surface in order to maintain gas exchange and therefore photosynthesis during rain or mist by preventing the formation of a water film covering the stomata. Also Sequoia sempervirens growing in fog-inundated regions shows sunken and plugged stomata (Burgess and Dawson, 2004).

Whereas the protection of stomata from the formation of a water film is clearly conceivable as the main function of stomatal crypts in the case of humid and foggy environments, this appears to be less reasonable for arid habitats. Here, sunken stomata or stomata arranged in crypts may be beneficial as an adaptation to drought. Besides decreasing stomatal conductance (which also decreases the rate of the CO₂ influx), it may be speculated that another benefit is the creation of special microclimatic conditions, i.e. higher humidity directly above the stomatal pore. For the simple antechamber arrangement considered in this study, the relative humidity above the pore amounts to about 75 %, whereas it amounts to about 63 % for the non-sunken basic model (Fig. 6). A more elaborate construction, e.g. a stomatal crypt housing more than one stoma and equipped with hairs restricting diffusion further, would achieve a much stronger effect, especially under the conditions of a thin boundary layer. This microclimate of higher humidity would possibly allow the stomatal pore to be open for much longer time intervals than if the pore were exposed to the lower humidity level at the leaf surface. In fact, Feild et al. (1998) observed in the case of stomatal plugs in Drimys winteri that these structures are able to prevent stomatal closure, and it was speculated that this phenomenon is possibly due to high levels of humidity at the stomatal pore.

Whereas the depression of a stomatal pore below the leaf surface resulted in a general decrease in the conductance of the stoma, the lining of the substomatal chamber with an internal cuticle mainly affected water vapour (Fig. 7). This is due to the circumstance that water obviously evaporates preferentially in the direct vicinity of the pore, whereas CO₂ drawdown occurs over the whole mesophyll. The phenomenon of intense evaporation close to the stomatal porus is termed as peristomatal transpiration (Lange et al., 1971; Maier-Maercker, 1983). It is suggested that the sensitivity of guard cells to vapour pressure difference in many plant species is correlated with peristomatal transpiration acting as a ‘humidity sensor’ (Lange et al., 1971; Wullschleger and Oosterhuis, 1989; Bunce, 1996; Kerstiens, 1996; Maier-Maercker, 1998). Indications of peristomatal transpiration were also found in some former studies: it was demonstrated by both theoretical approaches (Rand, 1977; Tyree and Yianoulis, 1980; Pickard, 1981) and an experimental model (Meidner, 1976) that the largest amount of water vapour leaving a stoma stems from locations near to the stomatal pore if no evaporation barrier is present. The existence of a significant amount of peristomatal transpiration was questioned by Boyer (1985) and by Nonami et al. (1990). In both contributions, the important role of an internal cuticle acting as an evaporation barrier suppressing peristomatal transpiration was emphasized.

There are several reports and debates about the existence of an internal cuticle (Scott, 1948; Norris and Bukovac, 1968; Wullschleger and Oosterhuis, 1989; Nonami et al., 1990; Jeffree, 1996; Pesacreta and Hasenstein, 1999). The main problem is that it is not clear whether this layer (if present) represents a barrier to evaporation. The internal cuticle is reported to be much thinner than the external cuticle (Nonami et al, 1990; Pesacreta and Hasenstein, 1999). This does not, however, necessarily mean that the internal cuticle does not act as a barrier for water vapour. The permeability of a cuticle for water vapour is strongly dependent on its chemical nature (Schreiber et al., 1996). The higher thickness of external cuticles may also be related to mechanical functions or to prevent abrasion (Kerstiens, 1996; Wiedemann and Neinhuis, 1998). In fact, Wullschleger and Oosterhuis (1989) ascribed the insensitivity of the stomata of Gossypium hirsutum to vapour pressure difference to be caused by the presence of an internal cuticle preventing peristomatal transpiration. In the internal cuticles which line the guard cells of Ulmus glabra, perforations were found which were interpreted as evaporating sites in the cell walls in order to perceive high vapour pressure difference (Appleby and Davies, 1983). The results of Nonami et al. (1990) for Tradescantia virginiana indicate that the internal cuticle represents a significant barrier to evaporation.

The substantial effect of the internal cuticle on water vapour diffusion exceeded the decrease in diffusion caused by the stomatal antechamber (Fig. 7). A significant effect of an internal cuticle was also found by Pickard (1981) for a cylindrical model of a substomatal chamber. In this model, the cuticle was located on the underside of the epidermis surrounding the pore which lacked a stomatal channel. An extensive internal cuticle may thus be considered as a suitable device to decrease conductance of water vapour without affecting photosynthesis. The evaporative sites are then forced back into the leaf interior with implications for the pathways of liquid water and water vapour inside a leaf.

In the present study, the internal cuticle also had implications for the effect of substomatal chamber size on transpiration. Enlarging the rectangular substomatal chamber of the present models by increasing the chamber depth did not lead to a significant decrease in transpiration (Fig. 7). In the case of the cylindrical model considered by Pickard (1981), transpiration decreased until the chamber radius amounted to about twice the pore radius. For the smaller rectangular model chamber of the present study, the optimum size was therefore already attained. In a subsequent analysis, Pickard (1982) pointed out that further enlargement of the chamber should promote CO₂ uptake. In the present study, the models with the larger substomatal chambers in fact showed a significantly higher CO₂ influx than the models with the smaller chambers (Fig. 7). The obvious reason for the increase in CO₂ influx is that the cross-sectional area of the diffusion pathway into the leaf interior is larger in the case of the larger substomatal chambers. Contrary to the results of Pickard (1981), however, the model combining a larger substomatal chamber with an internal cuticle showed a higher transpiration than the model with internal cuticle and a smaller substomatal chamber (Fig. 7). This is probably due to the structural differences between the present models and the model of Pickard (1981). In the latter model, the stoma consisted of a circular pore in the ceiling of a cylindrical chamber. The internal cuticle was modelled as a layer covering the internal side of the ceiling around the pore opening. In the present study, the internal cuticle covered the walls of the substomatal chamber. Expanding a substomatal chamber whose walls are covered with an internal cuticle has a promoting effect on both water vapour and on CO₂ diffusion since for both gases the cross-sectional area available for diffusion is increased.

In summary, stomatal structure can have a profound influence on gas conductance, the developing concentration gradients and on the location of the evaporating sites. Precise knowledge concerning concentration gradients in the vicinity of the stomatal pore and within the leaf is significant for analysing stomatal pore width regulation. This is also of high relevance for topics interrelated with water movements inside leaves, such as determination of leaf hydraulic conductance by various methods (Sack et al., 2002), observed correlations between stomatal traits, such as pore area, and hydraulic leaf conductance (Sack and Holbrook, 2006) or distribution of isotopes over the leaf (Barbour and Farquhar, 2003). Numerical simulation of gas diffusion represents a suitable tool for gaining information about the interrelationship between stomatal structure, gas exchange and evaporation inside a leaf and which is expected to improve our knowledge about the functional role of stomatal features.