Do we Underestimate the Importance of Leaf Size in Plant Economics? Disproportional Scaling of Support Costs Within the Spectrum of Leaf Physiognomy

Abstract

Background

Broad scaling relationships between leaf size and function do not take into account that leaves of different size may contain different fractions of support in petiole and mid-rib.

Methods

The fractions of leaf biomass in petiole, mid-rib and lamina, and the differences in chemistry and structure among mid-ribs, petioles and laminas were investigated in 122 species of contrasting leaf size, life form and climatic distribution to determine the extent to which differences in support modify whole-lamina and whole-leaf structural and chemical characteristics, and the extent to which size-dependent support investments are affected by plant life form and site climate.

Key Results

For the entire data set, leaf fresh mass varied over five orders of magnitude. The percentage of dry mass in mid-rib increased strongly with lamina size, reaching more than 40 % in the largest laminas. The whole-leaf percentage of mid-rib and petiole increased with leaf size, and the overall support investment was more than 60 % in the largest leaves. Fractional support investments were generally larger in herbaceous than in woody species and tended to be lower in Mediterranean than in cool temperate and tropical plants. Mid-ribs and petioles had lower N and C percentages, and lower dry to fresh mass ratio, but greater density (mass per unit volume) than laminas. N percentage of lamina without mid-rib was up to 40 % higher in the largest leaves than the total-lamina (lamina and mid-rib) N percentage, and up to 60 % higher than whole-leaf N percentage, while lamina density calculated without mid-rib was up to 80 % less than that with the mid-rib. For all leaf compartments, N percentage was negatively associated with density and dry to fresh mass ratio, while C percentage was positively linked to these characteristics, reflecting the overall inverse scaling between structural and physiological characteristics. However, the correlations between N and C percentages and structural characteristics differed among mid-ribs, petioles and laminas, implying that the mass-weighted average leaf N and C percentage, density, and dry to fresh mass ratio can have different functional values depending on the importance of within-leaf support investments.

Conclusions

These data demonstrate that variation in leaf size is associated with major changes in within-leaf support investments and in large modifications in integrated leaf chemical and structural characteristics. These size-dependent alterations can importantly affect general leaf structure vs. function scaling relationships. These data further demonstrate important life-form effects on and climatic differentiation in foliage support costs.

INTRODUCTION

There is intense interest in general scaling relationships between foliage structure, chemistry and physiological characteristics (Reich and Oleksyn, 2004; Wright et al., 2004; He et al., 2006) as well as in scaling of plant physiological activity and chemistry with size (Westoby and Wright, 2003; Niklas et al., 2005; Niklas, 2006; Reich et al., 2006). Leaf size is a basic foliage physiognomic characteristic, and numerous studies have tried to explain the prominent variation in leaf size at the global scale. Characteristic correlations between leaf size and climate have been employed to gain insight into adaptive modifications in leaf size (Grubb, 1977; Tanner, 1980; Givnish, 1984; Medina, 1984; Royer et al., 2005). In particular, increases in leaf size in warmer and more humid habitats have frequently been demonstrated (Grubb, 1977; Tanner, 1980; Givnish, 1984; Medina, 1984; Royer et al., 2005). These studies are in agreement with predictions from simulation experiments suggesting that variations in leaf size along the climatic gradients result from greater evaporative demand of larger leaves due to enhanced thickness of the boundary layer for energy and gaseous exchange (for a comprehensive review see Gates, 1980).

In addition to energy balance, optimization of overall biomass investment in support can be a selection pressure causing diversification in leaf size (Givnish, 1986, 1987). Larger leaves allow the plants to gain height more rapidly because less woody branches (Givnish, 1978,b, 1984) and lower twig biomass are required to support larger than smaller leaves (Westoby and Wright, 2003; Pickup et al., 2005; Sun et al., 2006; Wright et al., 2006). However, larger leaves need longer petioles to avoid self-shading (Takenaka, 1994; Pearcy et al., 2005). Support requirements also increase disproportionately with the length of cantilevered structures (Gere and Timoshenko, 1997). Due to the economics of light interception and biomechanical requirements, increases in leaf size are often bound to enhanced biomass investment in petiole, and may also bring about larger fractional biomass allocation in mid-rib (Givnish, 1984; Niinemets et al., 2006; Niinemets and Sack, 2006). Leaf size is generally thought to have no direct effect on foliage physiological activity (Givnish and Vermeij, 1976; Gates, 1980; Ackerly and Reich, 1999; Ackerly et al., 2002). However, disproportionately greater biomass investments in vasculature and sclerenchyma in larger leaves for efficient exposure of laminas to solar radiation and for effective water transport to mesophyll cells can result in lower biomass fractions in mesophyll and, accordingly, in lower mass-based photosynthesis rates (Poorter and Evans, 1998; Garnier et al., 1999). As photosynthetic capacity scales with stomatal conductance (Schulze et al., 1994; Reich et al., 1999), effective water transport capacity may be especially relevant in leaves with greater photosynthetic potential, suggesting that there are inherent trade-offs between photosynthetic capacity and leaf size.

There are broad interspecific relationships between foliar structural attributes such as leaf dry mass per unit area, nitrogen percentage, dry to fresh mass ratio, leaf density and foliage photosynthetic capacity per unit dry mass (Reich et al., 1997; Niinemets, 1999b; Wright et al., 2004) and relative growth rate (Reich, 1998). Yet, any integrated whole-leaf trait is a mass-weighted average of the trait values for support and photosynthetic tissues. There is evidence that dry to fresh mass ratios and N percentages of leaf laminas and leaf support tissues are correlated (Niinemets, 1999a; Niinemets and Kull, 1999), but it is not clear whether the elemental composition, dry to fresh mass ratio, density and dry mass per unit area scale in the same way for structural and photosynthetic tissues. Support tissues and mesophyll have different air space volumes, and also consist of cells with different lumen diameter and wall thickness, and of cells with different nitrogen cost (Roderick et al., 1999a), suggesting that scaling relations between chemical and structural characteristics may be different for support tissues and lamina. For leaves with a larger fraction of biomass in support, significant differences in scaling of foliage chemical and structural characteristics can modify the fundamental relationships between foliage integrated structural and chemical characteristics and potential photosynthetic activity. This evidence collectively suggests that scaling relations between foliage integrated structural and physiological traits can importantly differ between small- and large-leaved species.

In a previous study with 44 temperate species, a strong scaling of foliage support costs with leaf size was observed, and it was shown that this scaling significantly affected the distribution of leaf nitrogen among structural and physiological compartments, and thereby whole-leaf N percentage (Niinemets et al., 2006). That study, with a limited number of species, is used here as a springboard to test a general hypothesis that the scaling relationships between structural and chemical characteristics differ among support and functional tissues for an extended set of species with strongly varying architecture and chemical composition from cool temperate, Mediterranean and tropical ecosystems. The density, dry to fresh mass ratio and chemical composition were further determined separately for petiole, mid-rib and the rest of the lamina, and the overall role of variations in the fraction of support investments on major whole-leaf integrated characteristics was assessed. Because herbs are photosynthetically more active, in particular, on a unit mass basis (Hikosaka et al., 1998; Ellsworth et al., 2004), and accordingly require greater vascular capacities for water conduction, it was further hypothesized that leaves of equivalent size have larger fractional biomass investments in mid-rib and petiole in herbs than in woody species.

As leaf water availability can be only moderately enhanced by increased biomass investment in veins when soil is very dry, plants have developed highly effective physiological mechanisms for maintenance of leaf water status in highly seasonal water-stress-prone environments (Flexas and Medrano, 2002; Medrano et al., 2002). In water-limited environments, cell walls of lamina are thicker and often strongly lignified (Niinemets, 2001; Niinemets and Sack, 2006), implying that self-support of lamina can significantly rely on lamina cells (‘non-specific’ support) in addition to vasculature. Given this, it was further suggested that plants from Mediterranean and warm temperate climates that keep leaves throughout severe seasonal water stress periods have lower fractional biomass investments in mid-rib and petiole than plants from cool temperate and tropical wet climates where such seasonal water stress events are absent or less severe.

MATERIALS AND METHODS

Study sites and sample species

For the study, leaves of 122 vascular plant species were collected from two sites with temperate moderately continental climate in Estonia and from four sites with Mediterranean climate in Spain during the growing seasons of 2000–2003 (see Appendix for list of species and sample sites). The primary goal in species selection was to achieve a wide range of leaves with contrasting size and shape (Appendix). In Estonia, 35 species were sampled from large gaps in a broadleaved deciduous forest in Ülenurme (58°18′N, 26°42′E, elevation 60 m) (for details of sampling site see Niinemets et al., 2006), and 30 species were sampled from field (19) and greenhouse (11, Appendix) collections of the Botanical Garden of the University of Tartu (58°22′N, 26°43′E, elevation 20 m). In Spain, eight species were sampled from the Giardino Botanico Reale, Madrid (40°25′N, 3°40′W, elevation 600 m), 12 species from parks close to the Centro de Ciencias Medioambientales, CSIC, Madrid (40°27′N, 3°42′W, elevation 600 m), 37 species from parks and surroundings of Malaga (36°43′N, 4°25′W, elevation 10–30 m) and three species from the Alcornocales Natural Park, Sierra del Aljibe, Cádiz province (Sierra del Cabrito, Llanos del Juncal area, 36°20′N, 5°30′W, elevation 300–600 m). Subtropical and tropical plants sampled from the greenhouse were grown in conditions approximating the climate in the native sites as closely as possible.

Forty-four species sampled were non-native in their sampling locations (Appendix). Of these, ten were of South American, 16 of Asian, three of South African, three of European, two of North American, one interspecific hybrid of Asian and North American origin (Platanus hybrida Brot.), one of New Zealand origin and one species of Australian origin (Appendix). The species were divided between three climate classes depending on origin: cool temperate, Mediterranean/warm-temperate and sub-tropical/tropical (Appendix). Although this led to pooling of sites in some cases, environmental differences between the three climatic groups were much larger than the differences in climate between the sites within a specific climatic group.

Of all species, 50 were woody and 72 herbaceous, 39 had evergreen foliage, while 83 were deciduous or annuals. Twelve species had compound leaves. In the analysis here, we consider a leaflet of a compound leaf as a functional analogue of a leaf in simple-leaved species. This is because the leaflet is a biomechanical analogue of a simple leaf, while an entire compound leaf is a biomechanical analogue of a branch in simple-leaved species. It has previously been demonstrated that within-leaf support requirements are larger for intact compound leaves than for simple leaves of given fresh mass and area (Niinemets et al., 2006). This difference is mainly because rachises of compound leaves are generally sparsely foliated compared with non-dissected laminas of simple leaves, resulting in effectively longer lever arms and greater biomass costs for mechanical stability (Niinemets, 1998; Niinemets et al., 2006).

Foliage sampling and structural analyses

Fully mature leaves were taken from the upper canopy of a given plant for detailed structural and chemical analyses. The leaves sampled were exposed to more than 25 % of the incident irradiance. On average, 3·07 ± 0·26 (1–5) representative leaves were sampled per species (altogether 375 leaves). The collected leaves were immediately enclosed in plastic bags with wet filter paper and transported to the laboratory for further analyses.

In the laboratory, lamina and petiole were separated and their lengths were determined. Images of leaves after pressing the leaf flat were taken with a Nikon Coolpix 990 camera equipped with Tele Converter TC-E2 2× (Nikon Corporation, Tokyo, Japan). Objects of known area were photographed together with the leaves to determine an appropriate pixel to centimetre conversion ratio for every picture. Petiole diameters were measured in two perpendicular directions at the base and at the apex with digital precision callipers (Mitutoyo CD-15DC, Mitutoyo Ltd, Hampshire, UK). Lamina thickness in several locations between the major veins was also measured with the callipers.

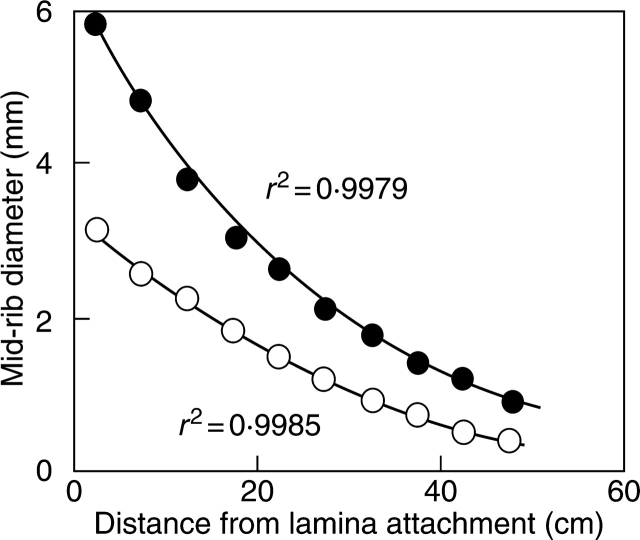
For 44 species sampled in Estonia from Ülenurme forest and the Botanical Garden of the University of Tartu (Appendix), lamina and mid-rib (central major leaf vein running from leaf base to leaf tip) were immediately separated by a razor blade. Due to strong tapering of mid-rib from base to apex (see Fig. 2 for a sample relationship), separation of lamina and mid-rib became increasingly inexact towards the apex. To avoid inclusion of pieces of lamina in mid-rib fraction, the mid-rib was separated from the lamina base towards the apex to a point where the apical diameter was >0·1–0·2 mm (for a discussion see Givnish, 1986). This threshold diameter resulted in sampling of >90 % of total mid-rib length.

Fig. 1.

Changes in mid-rib diameter with the distance from lamina attachment for a sample leaf of the tropical herb species Musa basjoo Sieb. et Zucc. Mid-rib diameter was measured in two perpendicular directions. Closed symbols denote the mid-rib diameter as faced from above (parallel to lamina plane) and open symbols the diameter perpendicular to the lamina plane. Total lamina length was 55·2 cm. Mid-rib between 0 and 50 cm could be reliably separated from the rest of the lamina, while separation of mid-rib between 50 and 55·2 cm was unreliable due to strong tapering of the mid-rib. Third-order polynomial regressions were fitted to the data to predict the diameters of the remaining part of the mid-rib, and calculate the total volume of the mid-rib. Fresh and dry mass of the entire mid-rib were further calculated using the average density and dry to fresh mass ratio for the entire mid-rib. For this sample leaf, the missing part of the mid-rib was predicted to comprise 0·3 % of the total mid-rib dry mass.

For the remaining species, lamina was cut into 1–5-cm (depending on the overall length of the lamina) segments from the base towards the apex to determine the distribution of lamina mass and characterize leaf shape quantitatively. Mid-rib was separated from every lamina strip, and mid-rib diameter was measured in two perpendicular directions for every separate piece. Again, a threshold diameter to separate mid-rib from lamina in specific lamina segments was 0·1–0·2 mm.

Fresh mass of petiole, pieces of lamina and mid-rib, or entire lamina and mid-rib was determined immediately after finishing these measurements, and dry mass after oven-drying for at least 48 h at 75 °C. Dry to fresh mass ratios (D) of specific leaf fractions were determined.

Leaf structural characteristics

UTHSCSA Imagetool 2·00alpha (C. D. Wilcox, S. B. Dove, W. D. McDavid and D. B. Greer, Department of Dental Diagnostic Science, The University of Texas Health Science Center, San Antonio, TX, USA; ddsdx.uthscsa.edu) was used to measure projected leaf area (A_LT). Petiole length and apical and basal diameters were used to calculate petiole projected area (A_P), and petiole dry mass per unit area (σ_P) was calculated. Petiole volume (V_P) was further computed from the petiole diameters and petiole length approximating petiole to a frustum of a cone with elliptical cross-section. Petiole density (ρ_P) was calculated as the ratio of petiole dry mass to V_P.

As with the petiole, mid-rib projected area (A_R) and density were determined. Leaf area without mid-rib was determined from A_LT − A_R. For 78 species, in which mid-rib had been dissected into 1–5-cm strips, mid-rib area and volume were found separately for every piece, allowing us to enhance the precision of mid-rib volume and area determinations. Because mid-rib parts with a diameter less than 0·1–0·2 mm could not be reliably separated from the rest of the lamina, polynomial regressions were developed (r² > 0·95, in most cases nearly 0·99) between mid-rib diameter and the distance from leaf base using the existing mid-rib parts (see Fig. 1). These polynomial regressions were employed to predict the diameter of the mid-rib for the pieces, in which mid-rib was not separated from the lamina. Again, the mid-rib diameters in two perpendicular directions were used to calculate the volume and projected area of mid-rib in specific lamina pieces. The dry mass of missing mid-rip pieces was found by using an average mid-rib density and the piece volume, and fresh mass by using an average mid-rib dry to fresh mass ratio. These data of missing mid-rib parts were further employed to calculate corrected whole lamina and mid-rib dry and fresh masses. However, due to strong tapering of mid-ribs towards the apex, this correction increased mid-rib dry mass on average only by 1·31 ± 0·20 % (0–15 %). Given this relatively minor correction, no attempt was made to correct the mid-rib dry masses for the 44 species, in which leaves were not dissected and mid-rib tapering could not be determined. Because >90 % overall mid-rib length was sampled in these species, it is suggested that the underestimation of ‘true’ mid-rib dry mass was small. All statistical correlations and comparisons between the groups were qualitatively identical for entire data set and for a truncated data set including only corrected mid-rib and lamina dry masses.

Dry masses of mid-rib (M_R), lamina without mid-rib (M_L) and petiole (M_P) were used to calculate the fraction of mid-rib in lamina [F^R_TL = M_R/(M_L + M_R)], and the fractions of mid-rib [F^R_WL = M_R/(M_L + M_R + M_P)] and petiole [F^P = M_P/(M_L + M_R + M_P)] in whole leaf. Total leaf fractional investment in support within the leaf was computed as F^R_WL + F_P.

Lamina dry mass per unit area without mid-rib (σ_L) was calculated as M_L/(A_LT − A_R) and with mid-rib (σ_LT) as (M_L + M_R)/A_LT. σ_L and σ_LT were divided by lamina thickness to obtain an estimate of lamina density without mid-rib (ρ_L) and with mid-rib (ρ_LT). Absolute difference between lamina density without (‘true’ density of lamina tissues) and with mid-rib was found as ρ_L − ρ_LT and relative difference in density as (ρ_L − ρ_LT)/ρ_L.

Chemical analyses

Nitrogen and carbon percentages of lamina without mid-rib (N_L and C_L), petiole (N_P and C_P) and mid-rib (N_R and C_R) were estimated gas chromatographically after combustion of the sample at >1000 °C in oxygen with a Perkin Elmer series II CHNS/O Analyser 2400 (Perkin Elmer Life and Analytical Sciences, Inc., Boston, MA, USA). C/N analyses were performed separately for mid-rib, petiole and rest of the lamina for every leaf, except for the smallest leaves, in which petioles and mid-ribs of different specimens of the same species were pooled for the analysis. Overall, more than 1200 C/N analyses were conducted.

Because proteins are rich in carbon (53·5 %, Vertregt and Penning de Vries, 1987), differences in C percentage between different leaf fractions may partly result from differences in protein content. To account for changes in C percentage because of proteins, we calculate the protein-free leaf C percentage (C^S) for every leaf fraction as:

1

where C is the carbon and N the N percentage for either the mid-rib, rest of the lamina or petiole, and the coefficient 6·25 converts N content to protein content (Vertregt and Penning de Vries, 1987; Niinemets and Tamm, 2005). This equation assumes that all leaf N is in organic form, but a significant part of total leaf N may be present as nitrate, in particular, in fertilized plants (Poorter et al., 1990). Although the C percentage of structural polysaccharides that form the major part of leaf carbon is around 40 %, overall leaf C percentage may be less due to certain mineral content in the leaves. In the present study, the lowest leaf C percentages were around 25 % (see Fig. 4B). To avoid possible bias in C^S values due to potentially high nitrate contents, species with a C^S value in any of leaf fractions below 25 % were not used in calculation of average C^S values.

Fig. 4.

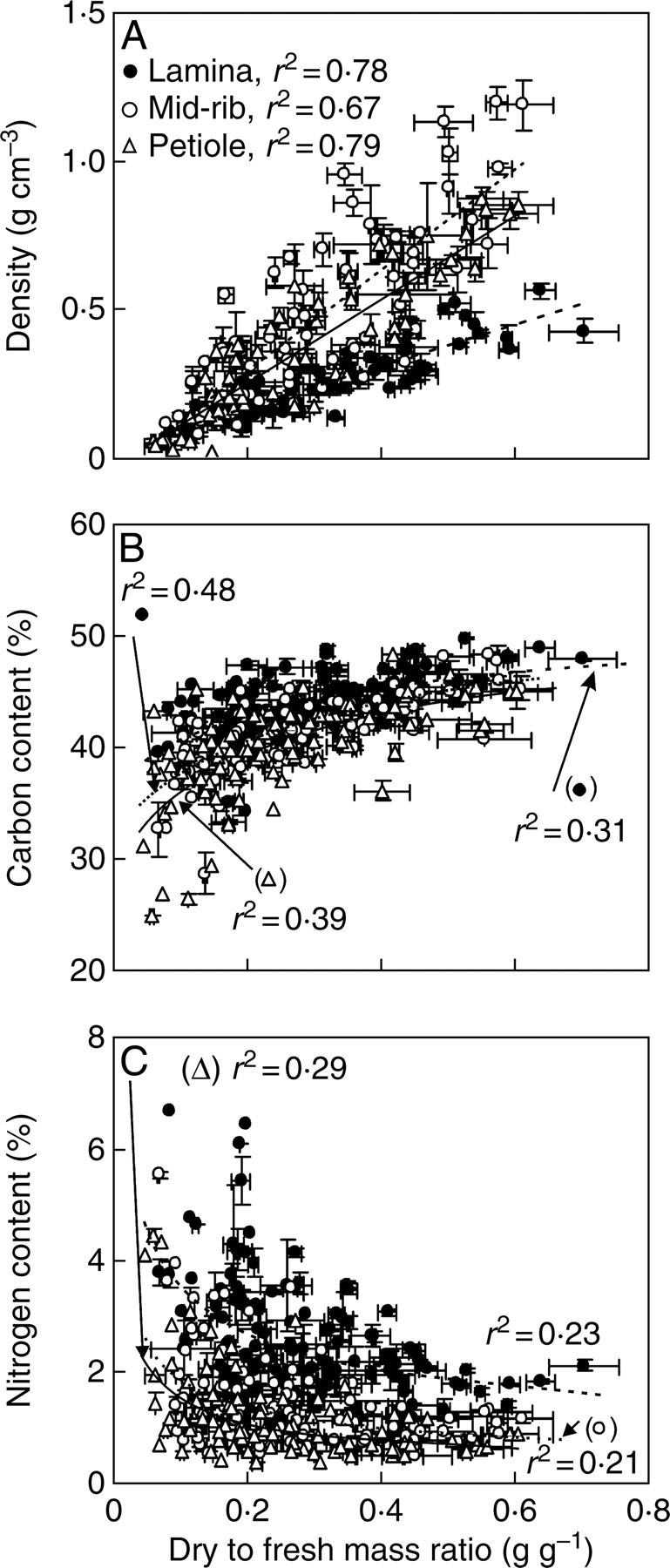
Density (A), and carbon (B) and nitrogen (C) percentages of lamina without mid-rib (dashed line), mid-rib (dotted line) and petiole (solid line) in relation to dry to fresh mass ratio of these leaf fractions. Data presentation and species as in Fig. 3. Linear (A) or non-linear regressions in the form y = ax^b were fitted to the data. All regressions are significant at P < 0·001.

The mass-weighted lamina N percentage (N_LT) was further found as:

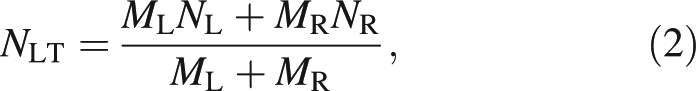2

and the mass-weighted whole-leaf N percentage (N_WL) as:

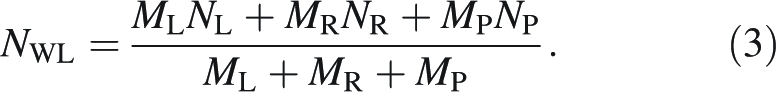3

Analogously, mass-weighted whole-lamina (C_LT) and whole-leaf (C_WL) C percentages were calculated. The fraction of whole-leaf N in mid-rib (F^N_R) was calculated as:

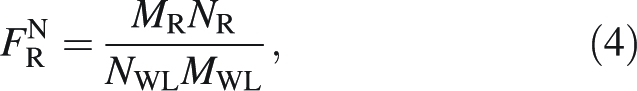4

where M_WL is the sum of M_R, M_L and M_P. The fractions of whole-leaf N in lamina, and petiole and in overall support as well as the corresponding fractions of leaf carbon were computed in an analogous manner.

The absolute difference in N percentage between lamina without mid-rib and total lamina was found as N_L − N_LT and the relative difference, R^N_LT, as:

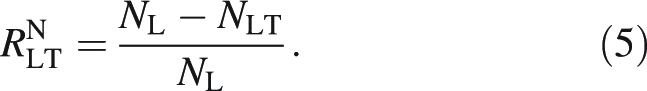5

The absolute difference in N percentage between lamina without mid-rib and total leaf was found as N_L − N_WL and the relative difference, R^N_LW, as:

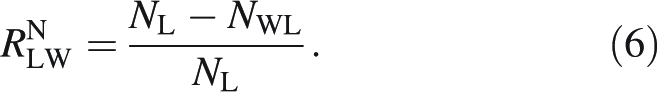6

Analogously, absolute and relative differences were found for C percentage.

Leaf size estimates

Leaf size can be quantified as leaf area, volume, dry and fresh mass. All these size estimates describe different aspects of leaf functioning. Leaf area characterizes leaf energy balance, and leaf area and fresh mass characterize leaf biomechanical efficiency and mechanical load, while dry mass estimates leaf construction cost, and volume provides an estimate of leaf space requirements, in particular for leaves with thick foliage elements with complex three-dimensional cross-section geometry. In our study, all four estimates of leaf size were available. All the size estimates were highly correlated with explained variances (r²) of log–log allometric relationships always larger than 0·93 (P < 0·001; Fig. 2 for correlations between leaf volume, dry and fresh mass and leaf area).

Fig. 2.

Leaf area (A), dry (B) and fresh mass (C) in relation to leaf volume in all studied species. The inset in (B) demonstrates the correlation between leaf density (dry mass per unit volume) and leaf volume (y = 0·251x⁻¹⁸², r² = 0·44). Leaf size estimates refer to whole leaf, i.e. lamina with mid-rib and petiole. Log–log-transformed data were fitted by standardized major axis regressions using SMATR 2·0 (SMATR, Standardised Major Axis Tests & Routines by D. Falster, D. Warton & I. Wright, http://www.bio.mq.edu.au/ecology/SMATR) (for details see Warton et al., 2006). All regressions are significant at P < 0·001. 95 % confidence intervals for the scaling exponent (regression slope in log–log axes) were 0·802 and 0·886 for A, 0·798 and 0·891 for B, and 0·935 and 0·999 for C.

The scaling exponent b of allometric relationships in the form of y = ax^b provides information on the size-dependent modification of foliage characteristics. When b is 1·0, the scaling is isometric, i.e. both regression variables change in direct proportion to each other. We fitted the log–log-transformed data by standardized major axis regression using SMATR 2·0 (Standardised Major Axis Tests & Routines by D. Falster, D. Warton and I. Wright; http://www.bio.mq.edu.au/ecology/SMATR) (for details see Warton et al., 2006). In the present data set, the correlations between volume and fresh mass (Fig. 2C) and area and dry mass (b = 0·93 with 95 % confidence intervals of 0·88 and 0·99) were close to isometric. In contrast, the scaling exponent was less than one for leaf area vs. volume (Fig. 2A), leaf dry mass vs. volume (Fig. 2B), leaf dry mass vs. fresh mass (b = 0·91 with 95 % confidence intervals of 0·87 and 0·95), and area vs. fresh mass (b = 0·84 with 95 % intervals of 0·80 and 0·89), implying allometric scaling. In fact, the ratios of leaf dry mass per unit volume (density) decreased with increasing volume (inset in Fig. 2B), and analogous negative correlations were observed between leaf fresh mass and leaf dry to fresh mass ratio (r² = 0·18, P < 0·001) and leaf fresh mass per unit area scaled positively with fresh leaf mass (r² = 0·32, P < 0·001). However, even though the scaling exponent was less than one for the area vs. volume relationship (Fig. 2A), the ratio of leaf volume to area (leaf thickness) was poorly associated with leaf volume (r² = 0·02).

Although the scaling relationships between different foliage size estimates were in several cases allometric, all relationships with leaf support investments and structural and chemical characteristics were qualitatively identical when any of the four different size estimates was used as explanatory variable. As we were primarily interested in size-dependent modifications in support costs, and because static load on support elements scales with fresh mass, the fractional support investments are demonstrated in relation to lamina and whole leaf fresh mass. In addition, while the correlations were analogous with log-transformed lamina and whole-leaf dry mass and with log-transformed projected area, the fraction of explained variance was always lower if dry mass (e.g. for Fig. 3, average r² = 0·31 for all four relationships) or area (average r² = 0·29 for the same relationships in Fig. 3) were used as explanatory variables (average r² = 0·37 for the relationships with fresh mass in Fig. 3).

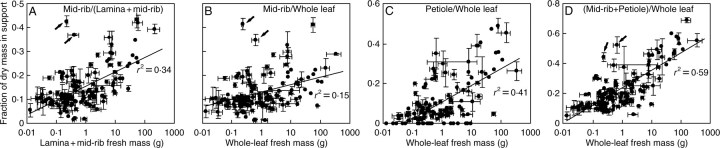
Fig. 3.

The fraction of dry mass in support within leaf lamina (A) in relation to total lamina (lamina and mid-rib) fresh mass, and the contributions of mid-rib (B) and petiole (C) to total support fraction (D) within the leaf in relation to total leaf fresh mass in 122 species of contrasting leaf size and structure (see Appendix for species list). Error bars indicate ± s.e. Data were fitted by linear regressions (see Table 3A for regression equations). Arrows denote two species with strongly dissected leaves [Leontodon taraxacoides (Vill.) Merat. and Taraxacum officinale G. H. Weber ex Wiggers] that, at given leaf size, had larger fractional biomass investments in mid-rib and overall biomass investment in support than the rest of the data. Regression equations were very similar without these outlying observations, but r² values were remarkably greater (r² = 0·43 for A, r² = 0·22 for B, r² = 0·43 for C, and r² = 0·64 for D). All regressions are significant at P < 0·001.

Data analysis

The experimental unit in the present study is species, and mean values with standard errors of the mean (s.e.) of all characteristics were calculated for every species. Linear and non-linear regression analyses were employed to examine the statistical relationships between foliage structural and chemical characteristics, and leaf size and investment in support. Paired sample t-tests were employed to compare the percentages of N and C, and integrated structural characteristics such as dry mass per unit area and density among mid-rib, petiole and lamina. ANCOVA analyses that assume linear relationships were employed to compare the statistical relationships among different leaf compartments and fractional biomass investments between herbaceous and woody plants and among different climatic groups. A separate-slope ANCOVA model that includes an interaction term was used first to compare the slopes. Whenever the interaction term was found not to differ among the groups, the model was refitted using a common slope model to compare the intercepts. Lamina and whole-leaf size estimates were log-transformed before all statistical analyses. In ANCOVA analyses, dry to fresh mass ratio was log-transformed to linearize the relationships in cases where regression analyses suggested a non-linear dependence. ANOVA analysis was used to compare the average values of leaf structural and chemical characteristics between different life forms and climatic groups. All statistical tests were considered significant at P < 0·05.

RESULTS

Size-dependent support investments within lamina and within the whole leaf

Fresh mass of leaves (or leaflets in compound-leaved species) spanned more than four orders of magnitude (0·0129–318 g). The fraction of mid-rib in lamina [F^R_TL = M_R/(M_L + M_R); see Table 1 for definition of all symbols] scaled positively with whole-lamina fresh mass (M^F_LT). Up to 45 % of total lamina biomass was invested in mid-rib in the largest leaves (Fig. 3A; see Table 2 for the range and average). The whole-leaf fractions of mid-rib [F^R_WL = M_R/(M_L + M_R + M_P); Fig. 3B] and petiole [F_P = M_P/(M_L + M_R + M_P); Fig. 3C] and total within-leaf support investment (F^R_WL + F_P; Fig. 3D) also correlated positively with whole-leaf fresh mass (M^F_WL). However, the relationship of total within-leaf support investment with M^F_WL was stronger (Fig. 3D) than the correlations of either F^R_WL or F^P with M^F_WL (cf. Figs 3B, C and Fig. 3D). In these correlations, Leontodon taraxacoides and Taraxacum officinale with strongly dissected leaves had larger support investments at a given leaf size than the rest of the data (Fig. 3). Nevertheless, all relationships were qualitatively identical with and without these outlying observations (Fig. 3).

Table 1.

Definition of acronyms and subscripts^* used

Acronym (unit)	Definition
A (m2)	Projected area
C (%)	Carbon percentage (content per dry mass)
CS (%)	Protein-free carbon percentage (eqn 1)
D (g g−1)	Dry to fresh mass ratio
FC (g g−1)	Carbon mass fraction
FN (g g−1)	Nitrogen mass fraction
FP (g g−1)	Petiole dry mass fraction in whole leaf
FR (g g−1)	Mid-rib dry mass fraction (either in lamina, FRTL, or in whole leaf, FRWL)
M (g)	Dry mass
MF (g)	Fresh mass
N (%)	Nitrogen percentage (dry mass basis)
RCLT	Relative difference in carbon percentage between lamina without mid-rib (CL) and lamina with mid-rib (CLT) (as for N in eqn 5)
RCLW	Relative difference in carbon percentage between lamina without mid-rib (NL) and whole leaf (CWL) (as for N in eqn 6)
RNLT	Relative difference in nitrogen percentage between lamina without mid-rib (NL) and lamina with mid-rib (NLT) (eqn 5)
RNLW	Relative difference in nitrogen percentage between lamina without mid-rib (NL) and whole leaf (NWL) (eqn 6)
V (m3)	Volume
ρ (g cm–3)	Density (mass per unit volume)
σ (g m–2)	Dry mass per unit area

*The main symbols may be followed by a leaf-fraction-specific subscript as follows: WL, whole leaf (mid-rib, lamina, petiole); TL, whole lamina (mid-rib with lamina); L, lamina without mid-rib; P, petiole; R, mid-rib.

Table 2.

Average (±s.e.) and minimum and maximum values of structural and chemical characteristics of different foliage fractions for 122 species of contrasting leaf size and structure (see Appendix for species list)

	Leaf fraction†
Characteristic*	Mid-rib	Lamina	Mid-rib + lamina‡	Petiole§
N percentage (%)	1·42 ± 0·09 (0·46–5·46)	2·56 ± 0·10 (1·00–6·59)	2·37 ± 0·09 (0·96–5·9)	1·18 ± 0·08 (0·34–4·44)
C percentage (%)	41·00 ± 0·34 (28·6–48·2)	43·63 ± 0·27 (32·4–49·5)	43·26 ± 0·27 (31·3–49·1)	40·05 ± 0·44 (24·9–48·1)
Structural C percentage (%)	40·14 ± 0·33 (25·6–47·8)	41·80 ± 0·35 (27·3–49·0)	41·46 ± 0·36 (26·8–48·6)	39·42 ± 0·44 (23·0–47·0)
Fraction of total biomass (g g–1)	0·129 ± 0·007 (0·012–0·41)	0·762 ± 0·013 (0·30–0·95)	0·891 ± 0·011 (0·51–1·0)	0·109 ± 0·011 (0·0–0·49)
Fraction of total leaf N (g g–1)	0·0796 ± 0·005 (0·0064–0·39)	0·860 ± 0·009 (0·52–0·99)	0·940 ± 0·007 (0·63–1·0)	0·0714 ± 0·008 (0·0–0·38)
Fraction of total leaf C (g g–1)	0·123 ± 0·007 (0·012–0·41)	0·774 ± 0·013 (0·32–0·98)	0·897 ± 0·011 (0·49–1·0)	0·123 ± 0·013 (0·0–0·51)
Dry to fresh mass ratio (g g–1)	0·264 ± 0·012 (0·067–0·60)	0·284 ± 0·012 (0·066–0·69)	0·276 ± 0·012 (0·067–0·68)	0·249 ± 0·014 (0·046–0·60)
Density (g cm–3)	0·461 ± 0·034 (0·078–1·19)	0·246 ± 0·013 (0·090–0·56)	0·277 ± 0·013 (0·097–0·60)	0·361 ± 0·030 (0·024–0·87)
Dry mass per unit area (g m–2)	339 ± 24 (82·7–887)	53·9 ± 3·2 (12·9–170)	62·2 ± 3·4 (13·7–197)	525 ± 35 (45–1700)

* Structural C percentage (‘protein-fee’ C) was calculated by eqn (1), and eqn (3) provides a sample relationship to calculate the fractions of N and C in different leaf compartments.

† All characteristics are significantly different among different leaf compartments at P < 0·001 according to paired sample t-tests, except for the fractions of total leaf carbon in mid-rib and petiole (P > 0·6) and dry to fresh mass ratios of petiole and mid-rib that differ at P = 0·004.

‡ Mid-rib + lamina characteristics are mass-weighted averages of mid-rib and lamina without mid-rib (see eqn 2 for sample calculations).

§ Average C, N and structural C percentages and dry to fresh mass ratio, density and dry mass per unit area are only calculated for leaves with petioles (33 species did not have petioles; see Appendix).

Life-form and climatic differences in fractional support investments

For various estimates of fractional support costs, ANCOVA analyses demonstrated that the slopes of the regressions in the form y = a + bLn(fresh mass) were not different between herbaceous and woody species (Table 3A). However, for F^R_TL vs. M^F_TL and F^R_WL + F^P vs. M^F_WL relationships, the intercept was larger for herbaceous than for woody species (Table 3A). Overall, the relationships were more scattered in woody species.

Table 3.

Comparison of the relationships of fractional biomass in support with fresh mass of lamina and mid-rib (M^F_TL) and fresh mass of whole leaf (M^F_WL): parameters of the regressions in the form y = a + bLn(x)

A: Life form differences
		Regression characteristics†
Relationship*	Group	n	a	b	r2
FRTL vs. MFTL	All	122	0·156	0·0255	0·34
	Herbaceous	72	0·281A	0·0169A	0·38
	Woody	50	0·128B	0·0145A	0·20
FRWL vs. MFWL	All	122	0·130	0·0138	0·15
	Herbaceous	72	0·140A	0·0151A	0·17
	Woody	50	0·115A	0·0069A	0·07‡
FP vs. MFWL	All	122	0·111	0·0363	0·41
	Herbaceous	72	0·122A	0·0369A	0·40
	Woody	50	0·0929A	0·0306A	0·39
FP + FRWL vs. MFWL	All	122	0·240	0·0505	0·59
	Herbaceous	72	0·259A	0·0525A	0·61
	Woody	50	0·206B	0·0377A	0·51
B: Climatic differences
		Regression characteristics
Relationship	Group§	n	a	b	r2
FRTL vs. MFTL	Temperate	46	0·160A	0·0288A	0·48
	Mediterranean	52	0·151A	0·0190A	0·14
	Tropics	24	0·129B	0·0344A	0·42
FRWL vs. MFWL	Temperate	46	0·121B	0·0146A	0·26
	Mediterranean	52	0·136A	0·0122A	0·08
	Tropics	24	0·120B	0·0186A	0·16
FP vs. MFWL	Temperate	46	0·148A	0·0421A	0·59
	Mediterranean	52	0·081B	0·0197A	0·16
	Tropics	24	0·075B	0·0435A	0·31
FP + FRWL vs. MFWL	Temperate	46	0·265A	0·0568A	0·74
	Mediterranean	52	0·218	0·0295B	0·23
	Tropics	24	0·196B	0·0622A	0·62

* F^R_TL, fraction of mid-rib biomass in lamina; F^R_WL, fraction of mid-rib biomass in whole leaf; F^P, fraction of petiole biomass in whole leaf, F^P + F^R_WL, total whole leaf biomass in support.

^† Regression coefficients with the same upper-case letter are not significantly different from each other according to ANCOVA analyses (separate slope analysis with an interaction term followed by a common slope analysis that lacks the interaction term). When the slopes were statistically different (significant interaction term), ANCOVA analysis was completed as the common slope test to separate the regression elevations is not meaningful in such a case (Sokal and Rohlf, 1995).

^‡ All r² values are at least significant at P < 0·05, except the regression with r² = 0·07 (P = 0·06).

^§ Mediterranean species group refers to Mediterranean and warm/temperate vegetation, temperate group to cool temperate plants and tropics group to subtropical and tropical species (see Appendix).

In all cases, the slopes of fractional biomass investment vs. fresh mass tended to be lower for Mediterranean/warm temperate than for cool temperate and tropical plants. However, only the slope of F^R_WL + F^P vs. M^F_WL was significantly lower in the Mediterranean than in the other two groups (Table 3B). The intercepts of these relations were in several cases highest in cool temperate plants, except for the intercept of F^R_WL vs. M^F_WL relationship, which was greatest in the Mediterranean species group (Table 3B).

Lamina density was lower for herbaceous species (average ± s.e. = 0·238 ± 0·015 g cm⁻³) than in woody species (0·315 ± 0·018 g cm⁻³, P < 0·001 for the difference between the means), and higher for Mediterranean/warm temperate (0·269 ± 0·015 g cm⁻³) and cool temperate species (0·243 ± 0·011 g cm⁻³) than in tropical species (0·183 ± 0·018 g cm⁻³, P < 0·03 for difference between the means). Lamina density was negatively related to F^R_TL (for all data pooled, r² = 0·14, P < 0·01 for non-linear regression in the form y = ax^b) and to F^R_WL + F^P (r² = 0·25, P < 0·001), indicating that plants with structurally more robust lamina had lower biomass investments in support.

Differences in chemistry and structure among mid-ribs, laminas and petioles

According to paired t-tests, average values of all chemical and structural characteristics differed at P < 0·001 among mid-ribs, laminas and petioles, except for the average fraction of total leaf C in mid-rib and petiole (P > 0·6) and for the average dry to fresh mass ratio of mid-rib and petiole that differed at P = 0·004 (Table 2). Average N percentage was always larger for lamina, followed by mid-rib and petiole (Table 2). Lamina also had larger average bulk carbon content than either mid-rib or petiole (Table 2). The difference in average structural C percentage (eqn 1) between leaf compartments was smaller than the difference in bulk leaf C percentage (Table 2), suggesting that higher lamina bulk C percentage partly resulted from high content of carbon-rich proteins (53·5 % carbon in proteins vs. average carbon content of different leaf compartments of 40–44 %, Table 2, eqn 1). The distribution of leaf carbon among leaf compartments (eqn 4) largely reflected the distribution of dry mass, but due to larger differences in N percentage, the average fraction of total N in lamina was significantly larger than the fraction of total biomass in lamina (Table 2). Chemical characteristics were strongly and positively correlated for leaf compartments, e.g. for N percentages, r² = 0·74 for lamina vs. mid-rib, r² = 0·73 for lamina vs. petiole, and r² = 0·85 for mid-rib vs. petiole (P < 0·001 for all). Analogous correlations were observed for C percentages (r² > 0·47, P < 0·001 for all).

Dry to fresh mass ratio (D) was highest for laminas followed by mid-ribs and petioles. Mid-ribs and petioles had significantly larger dry mass per unit area and density than laminas (Table 2). For the 122 species studied, these three structural characteristics varied for every leaf compartment by more than an order of magnitude. The greatest variation, 36–37-fold, was found for petiole dry mass per unit area and density. This large range of variation was due to low density and dry mass per unit area in species with hollow petioles such as Arctium tomentosum, Ligularia wilsoniana, Cirsium oleraceum, Cucurbita pepo, Heracleum sosnowskyi and Tussilago farfara. Variation in petiole dry to fresh mass ratio was only 13-fold, supporting this suggestion.

Structural characteristics for different leaf compartments were generally strongly correlated among leaf fractions, e.g. r² > 0·81 for dry to fresh mass ratio and r² > 0·41 for density (P < 0·001 for all), but the correlation between dry mass per unit area of lamina vs. mid-rib was weak (r² = 0·03, P < 0·05).

Density (Fig. 4A) and C percentage (Fig. 4B) of different leaf compartments were positively correlated with D, while the correlation between N percentage and D was negative (Fig. 4C). ANCOVA analyses that assume linear correlations were employed to test for the differences in these relations among different leaf compartments. The slope of density versus D was lower for laminas than for petioles and mid-ribs (P < 0·001), but at a given D, mid-ribs had higher density than petioles (P < 0·01, Fig. 4A). The slopes of carbon and N percentage vs. log(D) (D was log-transformed to linearize the relationships) were not different among different leaf compartments (P > 0·07 for carbon and P > 0·7 for N percentage). At a given log(D), carbon (Fig. 4B) and nitrogen (Fig. 4C) percentages were higher for laminas (P < 0·001), while the elemental percentages did not differ among petioles and mid-ribs (P > 0·07).

Influence of support investments on integrated leaf chemical and structural characteristics

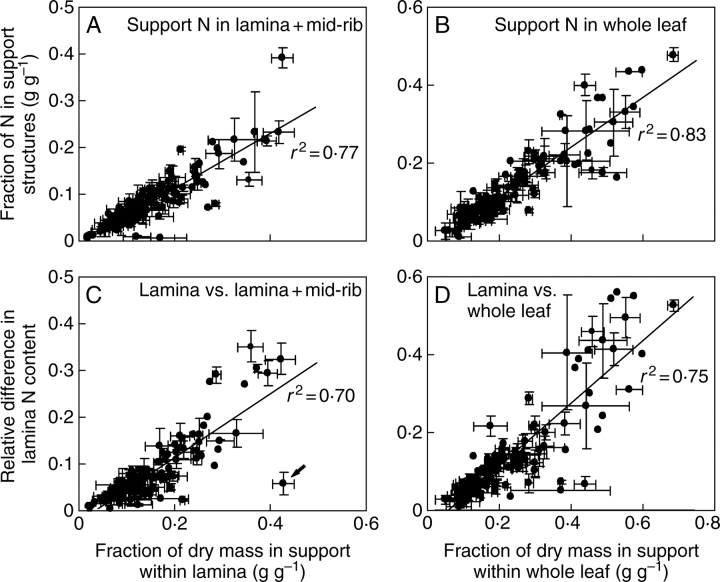
The fraction of whole-lamina N (Fig. 5A, eqn 4) and whole-leaf N (Fig. 5B) in support scaled positively with the fraction of dry mass in support. Although the slope of these relationships was significantly less than 1·0 (0·59 for Fig. 5A and 0·63 for Fig. 5B) due to lower N percentage of the support structures relative to entire leaf (Table 2), up to 40 % of lamina N was in mid-rib, and up to 50 % of whole-leaf N was invested in support (Fig. 5A, B).

Fig. 5.

The fractions of whole-lamina N in support biomass (eqn 4) vs. the fraction of dry mass in support within the lamina, i.e. mid-rib/(lamina with mid-rib) (A), the fraction of whole-leaf N in support biomass in relation to the fraction of support biomass within the leaf (B), and the relative difference in N percentage between lamina without mid-rib (N_L) and entire lamina N_LT (R^N_LT, eqn 5) in relation to the fraction of dry mass in support within lamina (C), and the relative difference [R^N_LW = (N_L – N_WL)/N_L] in N percentage between lamina without mid-rib and whole leaf (R^N_LW, eqn 6) (D). Data presentation and fitting for 122 species as in Fig. 3. All regressions are significant at P < 0·001. The arrow on panel C denotes an outlying observation for Leontodon taraxacoides that had a large fraction of biomass in support, but a relatively small difference in N percentage between mid-rib (2·72 ± 0·03 %) and the rest of the lamina (3·11 ± 0·13 %). The explained variance was improved by removing this outlying observation (r² = 0·77), but the slope and intercept of the regression equation were marginally modified (data not shown).

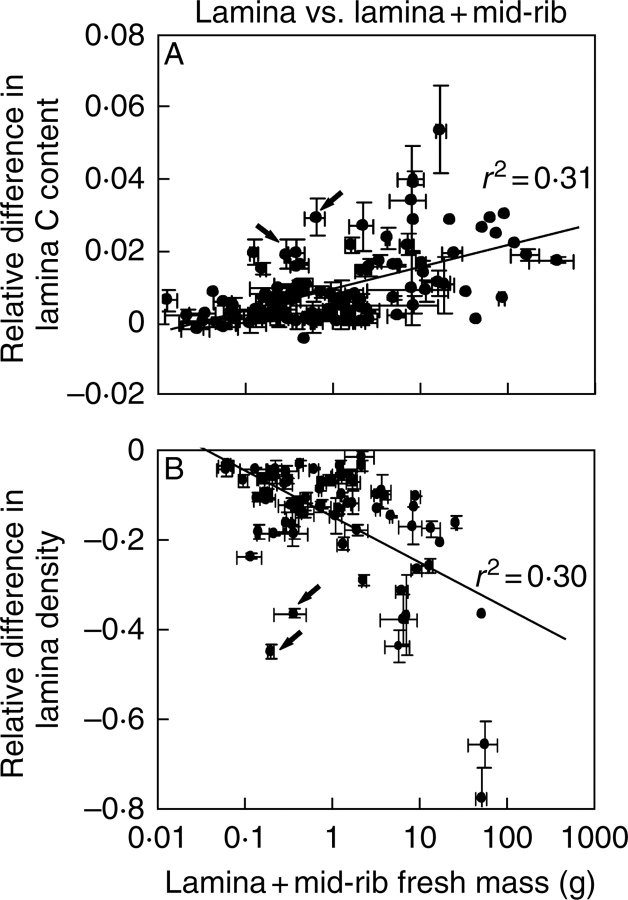
Absolute differences in lamina without mid-rib (N_L) and whole-lamina (N_LT) N percentage (N_L − N_LT), and lamina without mid-rib and whole-leaf (N_WL) N percentage (N_L − N_WL) scaled positively with the fractional investment in support (r² = 0·66 for N_L − N_LT vs. the fraction of lamina in mid-rib and r² = 0·73 for N_L − N_WL versus the fraction of support within the entire leaf, P < 0·001 for both). Analogously, the relative differences, R_LT (eqn 5, Fig. 5C) and R_LW (eqn 6, Fig. 5D), scaled positively with the fractional investment in support. Both relative (Fig. 6A) and absolute (r² = 0·37) differences in N percentage between lamina without mid-rib and entire lamina scaled positively with lamina fresh mass. The relative (Fig. 6B) and absolute (r² = 0·50) difference between lamina and whole-leaf N percentage increased with increasing whole-leaf fresh mass. Overall, lamina N percentage was up to 0·4-fold lower (on average ± s.e., 0·078 ± 0·007) due to mid-rib, and whole-leaf N percentage was up to 0·6-fold less (on average 0·142 ± 0·012) due to support structures (Fig. 6A, B). In absolute terms, support structures decreased whole-lamina N percentage up to 1·1 % (on average ± s.e. = 0·194 ± 0·018 %) and whole-leaf N percentage up to 1·8 % (0·330 ± 0·032 %).

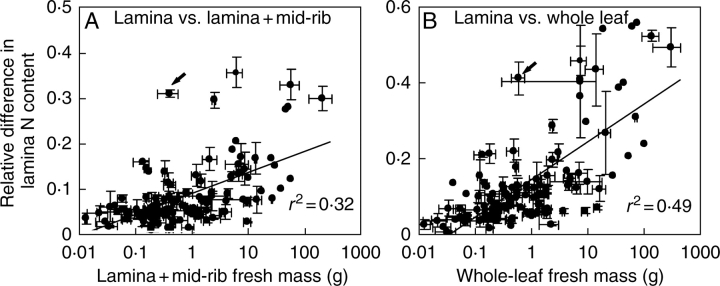
Fig. 6.

The relative differences in N percentage between lamina without mid-rib and lamina with mid-rib in relation to whole-lamina (lamina and mid-rib) fresh mass (A), and the corresponding differences in N percentage between lamina without mid-rib and whole-leaf (B) in relation to whole-leaf fresh mass. Data presentation and fitting for 122 species as in Fig. 3. Relative differences are defined in Fig. 4. All regressions are significant at P < 0·001. The arrows denote outlying observations for Leontodon taraxacoides (Fig. 3). The explained variances without this outlying observation were r² = 0·37 for A and r² = 0·52 for B.

Due to lower C percentage of support structures (Table 2), entire lamina and whole-leaf C percentages were also lower than the C percentage of lamina without mid-rib (e.g. Fig. 7A), but the relative difference was at most approx. 0·05 (average ± s.e. = 0·0092 ± 0·0009) for entire lamina (Fig. 7A) and 0·13 (0·0180 ± 0·0021) for the whole leaf. The absolute difference was at most 2·1 % for entire lamina and 6·7 % for whole leaf.

Fig. 7.

The relative differences in C percentage (A) and density (B) between lamina without mid-rib and lamina with mid-rib in relation to whole-lamina fresh mass. The relative difference in C percentage between lamina without mid-rib (C_L) and entire lamina (C_LT) is given as (C_L – C_LT)/C_L, and the relative difference between the density of lamina calculated without mid-rib (ρ_L) and with mid-rib (ρ_LT) as (ρ_L – ρ_LT)/ρ_L. Data presentation and fitting as in Fig. 3. All regressions are significant at P < 0·001. The arrows denote outlying observations for Leontodon taraxacoides and Taraxacum officinale that at a given leaf size had larger fractions of biomass in support than the rest of the data (Fig. 3). Fitting the data without these outlying observations improved the explained variance somewhat (r² = 0·34 for A and r² = 0·39 for B), but only slightly altered the regression slope and intercept (data not shown).

Because of the higher density of support tissues, lamina density was up to 0·8-fold larger when calculated with mid-rib than without mid-rib (average ± s.e. relative difference was −0·151 ± 0·015; Fig. 7B).

DISCUSSION

Leaf-size-dependent variation in support costs

For 122 vascular plant species investigated, four different leaf size estimates varied by 4–5 orders of magnitude (Fig. 1). This extensive variation in leaf size was accompanied by strong variation in the fractional leaf biomass investment in mid-rib, petiole and total support (Fig. 3). According to basic mechanical theory, bending moment of a cantilevered beam increases with the cube of its length as the mass becomes located further from the axis of bending (Gere and Timoshenko, 1997). Thus, larger leaves are expected to require disproportionately greater fractions of biomass in support to counterbalance the bending moments exerted by leaf elements. Within-leaf support costs have been examined only for a few species, but the available evidence generally agrees with larger fractional investment of biomass in support in larger leaves (Givnish, 1984; Niinemets et al., 2004; Niinemets and Sack, 2006). In the data reported by Givnish (1984) and Niinemets (2006), the fraction of total lamina biomass in mid-rib was 10–25 % in the largest leaves. The present study demonstrates that mid-rib can comprise nearly half of total lamina biomass in the largest leaves as well as in strongly dissected leaves (Fig. 3A) and further underlines that support biomass forms a major leaf fraction.

At a given lamina size, strongly dissected leaves were apparently outliers (Fig. 3A). However, larger support investment in such leaves is in agreement with the lower contribution of lamina tissues to the overall leaf rigidity in dissected laminas (Givnish, 1978a). Apart from strongly dissected leaves, there was still a considerable scatter in basic scaling of lamina size and fraction in support. Given that leaf light interception efficiency increases with increasing investment in support (Brites and Valladares, 2005), we suggest that variation in support investments of leaves of any given size can be associated with modified light interception efficiency (self-shading, lamina angle, etc.).

According to previous studies, the fraction of total leaf biomass in petiole also generally scales positively with leaf size (Niinemets et al., 2004; Niinemets and Sack, 2006), but not always (Niinemets and Sack, 2006). In fact, whole-leaf fractions of total biomass in mid-rib (Fig. 3B) and in petiole (Fig. 3C) considered separately were less strongly associated with leaf size than the sum of the two (Fig. 3D). This indicates that plants cannot maximize the investment in both petiole and mid-rib simultaneously. While larger leaves appear to require less stemwood xylem for support than smaller leaves (Pickup et al., 2005), nearly 70 % of total biomass was invested in support within large leaves (Fig. 3D). Thus, lower stemwood costs of large leaves may be offset by enhanced within-leaf support costs. These data collectively suggest that requirements for mechanical support may limit the maximum leaf size.

Apart from biomechanics, lower boundary-layer conductance for heat transfer in larger leaves (Gates, 1980) also implies potentially higher leaf temperatures and greater evaporative demands at equivalent incident radiation flux. Thus, enhanced investment in veins may be required to achieve a high latent heat loss via enhanced transpiration. There is conclusive evidence that leaf hydraulic conductance scales with leaf evaporative demand (Brodribb et al., 2002; Sack et al., 2003; Sack and Tyree, 2005), and some data indicate that leaf size can be partly determined by leaf hydrology (Zwieniecki et al., 2004a, b). However, the latter observations have not been confirmed for interspecific data sets (Sack et al., 2003), suggesting that the linkage between leaf hydrology and size is indirect.

Life-form and climate effects on support costs

Herbaceous species have lower dry mass per unit area and leaf life span, and higher mass-based photosynthetic capacities than woody species (Ellsworth et al., 2004; Wright et al., 2004; Shipley et al., 2005). As there is also a strong general relationship between photosynthetic capacity and stomatal conductance to water vapour (for a review see Schulze et al., 1994), it is suggested that at equivalent leaf size, greater fractional investment in support is needed in herbaceous species to supply physiologically more active leaves with water. This hypothesis was supported both for within-lamina fractional biomass investments and for total fraction of support biomass within the entire leaf (significant intercept differences between herbs and woody plants in Table 3A). Of course, longer living leaves of woody species that had greater lamina density in the present study may contain a larger fraction of biomass in cell walls (non-specific support), implying that the overall investment in support may be similar in herbs and woody species. However, an important difference between support biomass investment in veins and cell walls is that enhanced cell-wall thickening can result in stronger internal CO₂ diffusion limitations and reduction of foliage photosynthetic rates of all cells in the lamina (Terashima et al., 2005), while modification in support biomass distribution between lamina and veins should not necessarily affect photosynthetic capacity of interveinal areas.

Leaf structural characteristics are significantly affected by site climate; in particular, leaf laminas are tougher with thicker and more lignified cell walls in drier environments (Niinemets, 2001; Wright et al., 2005). We further hypothesized that Mediterranean species that support leaves throughout extensive water stress periods have lower fractional biomass investment in vasculature because these species are characterized by low photosynthetic capacities and also because physiological adjustments constitute a more effective way to cope with water stress than additional vein formation. In the present study, Mediterranean/warm temperate species had higher lamina density than species from wet tropical environments, but similar density as cool/temperate species. There was evidence that total fractional support costs changed less plastically with leaf size in Mediterranean species, resulting in a lower fraction of support biomass in larger leaves. Overall, the support mass fractions were negatively associated with lamina density, indicating that there is a general negative relationship between lamina toughness (‘non-specific’ support) and biomass investment in specialized support structures. As there are very few species with long-living large leaves, enhanced investment simultaneously in vasculature and cell walls may not constitute a viable strategy.

Reduction of leaf size in stressful environments has been explained on the basis of leaf boundary-layer conductance for heat and gaseous transport (see Introduction). However, leaf size may also decline due to overall carbon limitation in stressful environments, making construction of large leaves with extensive vascular and cell-wall fractions overtly expensive. Further studies including a more complete coverage of species from different climates and functional types are needed to test the hypothesis that certain leaf size and longevity combinations depend on overall availability of support biomass and the distribution of the support biomass between vasculature and cell walls.

Differences in chemistry and structural characteristics between lamina, mid-rib and petiole

Within every leaf compartment, N percentage, dry to fresh mass ratio, density and dry mass per unit area varied almost an order of magnitude, while C percentages varied approx. two-fold (Table 2). This extensive variation occurred in a correlative manner such that greater N percentage was associated with lower density and lower dry to fresh mass ratio, while C percentage was positively linked to density and dry to fresh mass ratio (Fig. 4). N percentage of a specific foliage compartment is a proxy of its protein percentage, and accordingly, overall physiological activity, while density, dry to fresh mass ratio and C percentage provide an estimate of the fractional investment in cell walls (Garnier and Laurent, 1994; Garnier et al., 1999; Roderick et al., 1999b). Thus, the relationships depicted in Fig. 4 reflect general reverse correlations between functional activity of plant organs and the fraction of cell walls in the foliage (Garnier and Laurent, 1994; Garnier et al., 1999; Roderick et al., 1999b). Correlations of C percentage with density and dry to fresh mass ratio further imply that in denser foliage, cell walls contain more carbon-rich chemicals such as lignin [63·3 % carbon according to the structure of lignin proposed by Nimz (1974) vs. 44·4 % carbon in cellulose] (Niinemets et al., 2005; Poorter et al., 2006).

Higher N percentage and lower density of lamina relative to mid-ribs and petioles is in accordance with greater physiological activity of leaf lamina. Photosynthetic activity of support structures is roughly one order of magnitude less than that of leaf laminas (Niinemets, 1999a; Schmidt et al., 2000; Hibberd and Quick, 2001; Wittmann et al., 2001). However, lamina had a greater C percentage and higher dry to fresh mass ratio than the support structures (Table 2). Lower C percentages of support elements than those of lamina have also been observed in previous studies (Niinemets, 1998, 1999a; Niinemets and Kull, 1999). However, differences in C percentage not only reflect differences in structural compounds but also differences in carbon-rich physiologically active compounds such as proteins (53·5 % carbon). Differences in structural C percentage (eqn 1) between lamina and support structures were much smaller than differences in total leaf C percentage (Table 2). In addition, minerals such as calcium and magnesium are tightly associated with structural polysaccharide matrix, and the overall percentage of bound minerals increases with increasing structural C percentage (Demarty et al., 1984; Niinemets and Tamm, 2005). Higher mineral percentage can explain slightly lower ‘structural’ C percentage in petioles and mid-ribs than in the lamina without mid-rib [see Poorter (1994) for a discussion of the role of minerals on leaf carbon content]. Despite lower total C percentage, structural carbohydrate percentage can still be greater in support structures than in laminas because of differences in protein percentage and minerals (Niinemets, 1999a).

Dry to fresh mass ratio of lamina was also higher than that of mid-ribs and petioles (Table 2), consistent with previous observations (Niinemets, 1999a; Niinemets and Kull, 1999). Lower dry to fresh mass ratio of support structures may be indicative of large water-filled vessels in mid-ribs and petioles (Fisher and Larson, 1983; Niklas, 1991). Although the presence of extensive water-filled vascular elements leads to low dry to fresh mass ratios, the average tissue density may still be high due to thick cell walls, low intercellular air space and extensive cell-wall lignification.

Differences in chemical composition among foliage compartments (see above) and different plant compartments (Chapin, 1989; Poorter and Villar, 1997) have been frequently observed. An important outcome of the present study is that due to differences in chemical composition and architecture among foliage compartments, correlations between chemical and structural characteristics vary among lamina, mid-rib and petiole (Fig. 4). Thus, diversity in function also leads to different scaling of chemical and structural characteristics among laminas and support elements. Previously, tissue-specific scaling relations have been demonstrated for biomechanical characteristics (Niklas, 1993).

Leaves of different size have contrasting integrated characteristics

Broad general scaling relations between foliage structural, chemical and physiological traits have been reported across the globe (Wright et al., 2004), and global variation in foliage nutrient percentages has been analysed (Reich and Oleksyn, 2004; Han et al., 2005; Reich, 2005). In particular, foliage photosynthetic capacity per mass (A_mass) increases with increasing foliage N percentage and decreases with increasing leaf dry mass per unit area and increasing leaf longevity, reflecting the overall compromise between structural and functional tissues within the leaf (Wright et al., 2004). In addition, foliage N percentage tends to increase with decreasing average annual temperature (Han et al., 2005; Reich, 2005). Gradients in leaf size from tropical rain forest to deserts and temperate forests have been described in numerous studies (Grubb, 1977; Tanner, 1980; Medina, 1984), but the potential significance of variations in leaf size on A_mass has not been considered in current photosynthesis scaling relations, except with regard to the direct effects of leaf size on foliar energy balance. The present analysis demonstrates that size-dependent variations in support investments significantly affect integrated foliage characteristics such as total N percentage, dry to fresh mass ratio and density (Figs 5–7). As support structures are less N-rich than the lamina, the fraction of N in support structures is lower than the fraction of biomass in support. However, within the lamina, up to 40 % of N may be in mid-rib (commonly 10–20 %, Fig. 5A) and within the leaf up to 50 % of N may be in petiole and mid-rib (commonly 15–30 %, Fig. 5B). As a result, the difference in N percentage between lamina with and without mid-rib and lamina and whole leaf directly scale with fractional biomass investments in support (Fig. 5C, D). As the fraction of biomass in support scales with leaf size (Fig. 3), the difference in N percentage also scales with leaf size (Fig. 6A, B). In the largest leaves, lamina N percentage without mid-rib may even differ more than 40 % relative to total lamina N percentage, and more than 60 % relative to whole leaf N percentage (Figs 5 and 6).

This evidence suggests that size-dependent scaling of fractional biomass investments in support may provide an important explanation for variation of foliage photosynthetic capacities of coexisting species that possess similar dry mass per unit area and leaf longevity, but different fractions of support due to differences in size. For instance, leaf photosynthetic capacity can vary more than an order of magnitude at given leaf dry mass per unit area and longevity in global-scale relationships (Wright et al., 2004; He et al., 2006). Whether this variability is associated with leaf size awaits further testing.

There are further strong allometric relationships between total plant leaf mass and total leaf nitrogen in leaves (Niklas et al., 2005; Niklas, 2006). Based on data from 131 vascular plant species, Niklas et al. (2005) suggested that scaling of nitrogen with leaf mass is isometric (i.e. the scaling exponent is close to 1·0), suggesting that N percentage does not scale with leaf mass. However, this conclusion was based on a species set in which the variability in leaf size was moderate. The current findings indicate that scaling exponents different from 1·0 are necessary when plant canopies composed of leaves with widely varying size are compared. As leaf size tends to increase from colder to warmer environments in humid sites (Grubb, 1977; Tanner, 1980; Medina, 1984), average temperature-driven decline in N percentage observed at a global scale (Han et al., 2005; Reich, 2005) may arise from larger fractions of support biomass in warmer humid sites.

A major influence of leaf size on whole-lamina and whole-leaf integrated characteristics has important methodological implications. As a rule, leaf density is determined as a ratio of whole-lamina dry mass per unit area and leaf thickness, the latter commonly being measured in interveinal leaf locations. However, veins have different structure than the rest of the lamina, and accounting for mid-rib area and dry mass can alter the estimations of density by as much as 80 % (Fig. 7B). Using certain foliage structural characteristics as surrogates of others, e.g. foliage fresh mass to area ratio as an estimate of foliage thickness (Vile et al., 2005), assumes that the leaves are homogeneous. However, scaling relations between dry to fresh mass ratio and density differ between lamina and mid-rib, implying that the whole-lamina integrated traits cannot simply be converted to each other. For example, a given value of leaf density may correspond to different values of whole-lamina dry to fresh mass ratio depending on the fraction of support tissues.

From a photosynthetic perspective, only interveinal areas are generally enclosed in typical clip-on gas-exchange cuvettes during photosynthesis measurements, especially when measurements are conducted in large leaves. At the same time, foliage chemical characteristics as well as integrated structural variables such as dry to fresh mass ratio are estimated for the entire lamina or entire leaf. In addition, destructive harvests of foliar biomass or litter-trap sampling to determine foliage photosynthesis potentials from N percentage and/or structural variables and make inferences for entire canopy or ecosystem carbon gain potentials generally do not separate petiole and lamina biomass, and mid-ribs from the rest of the lamina. As the current analysis suggests, this can lead to a significant bias in large-scale comparisons, especially when sites supporting species with large leaves exhibiting emergent protruding veins are compared with small-leaved vegetation.

CONCLUSIONS

Economics of support gives an additional dimension to interpretations of global variation patterns in leaf size. The present analysis suggests that differences in leaf size can significantly alter whole-lamina and whole-leaf integrated chemical and structural characteristics, and thereby modify general scaling relationships between plant structure, chemistry and function. The results further indicate that size-dependent scaling of leaf support investments significantly depends on plant life form and climate. Important size-dependent variation in support investments need to be considered in interpreting general scaling relationships between leaf physiology, structure and chemistry.

APPENDIX

Appendix.

Information for species and leaf characteristics for 122 species collected from different European sites

Species1	Family	Sampling site	Climate12	Life form	Evergreen12	Has petioles12	Compound-leaved12	Leaf shape	Venation	Margin	Lamina dissection
Acanthus spinosus L.10	Acanthaceae	58°22′N, 26°43′E	M	Herb	N	Y	N	Ovate/lanceolate	Pinnate	Serrate	Pinnatisect
Acer campestre L.10	Aceraceae	40°27′N, 3°42′W	M	Tree	N	Y	N	Cordate	Palmate	Smooth	Palmatifid
Acer platanoides L.10	Aceraceae	58°22′N, 26°43′E	CT	Tree	N	Y	N	Ovate/orbicular	Palmate	Smooth	Palmatifid
Acer pseudoplatanus L.10	Aceraceae	36°43′N, 4°25′W	M	Tree	N	Y	N	Oval/orbicular	Palmate	Smooth	Palmatifid
Aegopodium podagraria L.	Apiaceae	58°18′N, 26°42′E	CT	Herb	N	N	Y	Ovate	Pinnate	Serrate	Entire
Angelica sylvestris L.	Apiaceae	58°22′N, 26°43′E	CT	Herb	N	N	Y	Ovate	Pinnate	Serrate	Entire
Anthriscus sylvestris (L.) Hoffm.	Apiaceae	58°18′N, 26°42′E	CT	Herb	N	N	Y	Ovate	Pinnate	Serrate	Entire
Anthurium hookeri Kunth.10	Araceae	58°22′N, 26°43′E2,3	T	Herb	Y	Y	N	Obovate	Pinnate	Smooth	Entire
Anthurium hybridum Hort. ex Engl.10	Araceae	58°22′N, 26°43′E2,3	T	Herb	Y	Y	N	Cordate	Pinnate	Smooth	Entire
Arbutus unedo L.10	Ericaceae	40°27′N, 3°42′W	M	Shrub/tree	Y	Y	N	Obovate	Pinnate	Serrate	Entire
Arctium tomentosum Mill.	Compositae	58°22′N, 26°43′E	CT	Herb	N	Y	N	Cordate	Pinnate	Serrate	Entire
Armoracia rusticana (Lam.) Gaertn., Mey. et Scherb.	Brassicaceae	58°22′N, 26°43′E	CT	Herb	N	Y	N	Elliptic	Pinnate	Serrate	Entire
Arundo donax L.10	Poaceae	36°43′N, 4°25′W4	T	Grass	Y	N	N	Linear/ensifrom	Parallel	Smooth	Entire
Asarum europaeum L.	Aristolochiaceae	58°18′N, 26°42′E	CT	Herb	Y	Y	N	Reniform	Parallel/pinnate	Smooth	Entire
Aspidistra elatior L.10	Liliaceae	40°25′N, 3°40′W4	T	Herb	Y	Y	N	Elliptic/linear	Parallel	Smooth	Entire
Aster sp.10	Compositae	36°43′N, 4°25′W	M	Herb	N	Y	N	Ovate	Pinnate	Smooth	Entire
Avena sterilis L.10	Poaceae	36°43′N, 4°25′W	M	Grass	N	N	N	Linear/ensifrom	Parallel	Smooth	Entire
Bougainvillea glabra Choisy10	Nyctaginaceae	36°43′N, 4°25′W3	T	Shrub/vine	Y	Y	N	Ovate	Pinnate	Smooth	Entire
Brugmansia arborea (L.) Lagerh.10	Solanaceae	58°22′N, 26°43′E2,3	T	Tree	N	Y	N	Cordate	Pinnate	Smooth	Entire
Canna × generalis Bailey (pro sp.)10	Cannaceae	36°43′N, 4°25′W3	T	Herb	Y	N	N	Elliptic/linear	Parallel	Smooth	Entire
Carduncellus caeruleus (L.) C. Presl.10	Compositae	36°43′N, 4°25′W	M	Herb	N	N	N	Ovate	Parallel/pinnate	Serrate	Entire
Ceanothus thyrsiflorus Eschsch.10	Rhamnaceae	36°43′N, 4°25′W5	M	Shrub	Y	Y	N	Oval/obovate	Parallel/pinnate	Smooth	Entire
Celastrus orbiculatus Thunb.10	Celastraceae	36°43′N, 4°25′W4	M	Woody vine	N	Y	N	Orbicular	Pinnate	Serrate	Entire
Celtis australis L.10	Ulmaceae	36°43′N, 4°25′W	M	Tree	N	Y	N	Ovate	Pinnate	Serrate	Entire
Cercis siliquastrum L.10	Fabaceae	40°27′N, 3°42′W	M	Shrub/tree	N	Y	N	Orbicular	Pinnate	Smooth	Entire
Chrysanthemum sp.10	Compositae	36°43′N, 4°25′W4	M	Herb	N	N	N	Ovate	Pinnate	Serrate	Pinnatisect
Cirsium oleraceum (L.) Scop.	Compositae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Ovate	Pinnate	Serrate	Pinnatisect
Cistus ladanifer L.10	Cistaceae	40°27′N, 3°42′W	M	Shrub	Y	N	N	Elliptic/linear	Pinnate	Smooth	Entire
Convallaria majalis L.	Liliaceae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Elliptic	Parallel	Smooth	Entire
Convolvulus arvensis L.10	Convolvulaceae	36°43′N, 4°25′W	M	Herbaceous vine	N	Y	N	Cordate	Pinnate	Smooth	Entire
Corylus avellana L.	Corylaceae	58°18′N, 26°42′E	CT	Shrub	N	Y	N	Oval/obovate	Pinnate	Serrate	Entire
Corynocarpus laevigata J.R. Forst. & G. Forst10	Corynocarpaceae	40°25′N, 3°40′W8	M	Shrub/tree	Y	Y	N	Obovate	Pinnate	Smooth	Entire
Crepis paludosa (L.) Moench	Compositae	58°18′N, 26°42′E	CT	Herb	N	N	N	Obovate	Pinnate	Serrate	Entire
Cucurbita pepo L.	Cucurbitaceae	58°22′N, 26°43′E3	T	Herb	N	Y	N	Orbicular	Palmate	Smooth
Cyphomandra betacea (Cav.) Sendtn.10	Solanaceae	58°22′N, 26°43′E2,3	M	Shrub/tree	Y	Y	N	Ovate	Pinnate	Smooth	Entire
Dioscorea esculenta (Lour.) Burkhill.10	Dioscoreaceae	58°22′N, 26°43′E2,3	T	Herb	Y	Y	N	Cordate	Parallel	Smooth	Entire
Dittrichia viscosa (L.) W. Greuter10	Compositae	36°43′N, 4°25′W	M	Herb	Y	N	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Echinops sphaerocephalus L.	Compositae	58°22′N, 26°43′E7	M	Herb	N	Y	N	Ovate	Pinnate	Serrate	Pinnatisect
Elaeagnus angustifolia L.10	Elaeagnaceae	36°43′N, 4°25′W	M	Shrub	Y	Y	N	Ovate	Pinnate	Smooth	Entire
Epilobium montanum L.	Onagraceae	58°18′N, 26°42′E	CT	Herb	N	N	N	Ovate	Pinnate	Smooth	Entire
Eriobotrya japonica (Thunb.) Lindl.10	Rosaceae	40°27′N, 3°42′W4	M	Tree	Y	Y	N	Elliptic	Pinnate	Smooth	Entire
Eucalyptus camaldulensis Dehnh.10	Myrtaceae	40°27′N, 3°42′W9	M	Tree	Y	Y	N	Falcate/lanceolate	Pinnate	Smooth	Entire
Fagopyrum esculentum Moench10	Polygonaceae	36°43′N, 4°25′W	M	Herb	N	Y	N	Cordate	Pinnate	Smooth	Entire
Fragaria vesca L.	Rosaceae	58°18′N, 26°42′E	CT	Herb	N	N	Y	Oval	Pinnate	Serrate	Entire
Fraxinus excelsior L.	Oleaceae	58°18′N, 26°42′E	CT	Tree	N	N	Y	Elliptic	Pinnate	Serrate	Entire
Geranium molle L.10	Geraniaceae	36°43′N, 4°25′W	M	Herb	N	Y	N	Orbicular	Palmate	Serrate/crenate	Entire
Geranium palustre L.	Geraniaceae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Ovate	Palmate	Serrate	Palmisect
Hedera helix L.10	Araliaceae	58°22′N, 26°43′E	M	Woody vine	Y	Y	N	Elliptic/lobate	Palmate	Smooth	Palmatifid
Hedychium coccineum Buch.-Ham.10	Zingiberaceae	40°25′N, 3°40′W4	T	Herb	Y	Y	N	Elliptic/ovate	Parallel	Smooth	Entire
Hedychium gardnerianum Shepard ex. Ker. Kawl.10	Zingiberaceae	40°25′N, 3°40′W4	T	Herb	Y	N	N	Ovate/elliptic	Parallel	Smooth	Entire
Helianthus annuus L.	Compositae	58°22′N, 26°43′E5	M	Herb	N	Y	N	Cordate	Palmate	Smooth	Entire
Hepatica nobilis Gars.	Ranunculaceae	58°18′N, 26°42′E	CT	Herb	Y	Y	Y	Orbicular	Palmate	Smooth	Palmisect
Heracleum sosnowskyi Manden.	Apiaceae	58°22′N, 26°43′E7	CT	Herb	N	Y	N	Orbicular/ovate	Palmate	Serrate	Pinnatisect
Hibiscus rosa-sinensis L.10	Malvaceae	36°43′N, 4°25′W4	T	Shrub	Y	Y	N	Ovate	Pinnate	Serrate	Entire
Hippophae rhamnoides L.10	Elaeagnaceae	36°43′N, 4°25′W4	M	Shrub/tree	N	N	N	Linear	Pinnate	Smooth	Entire
Lactuca serriola L.10	Compositae	36°43′N, 4°25′W	M	Herb	N	N	N	Obovate/oblong	Pinnate	Serrate	Pinnatifid
Lamium galeobdolon (L.) L.	Labiatae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Ovate	Pinnate	Serrate	Entire
Leontodon taraxacoides (Vill.) Merat10	Compositae	36°43′N, 4°25′W	M	Herb	N	Y	N	Obovate/oblanceolate	Pinnate	Serrate	Pinnatifid
Ligularia wilsoniana (Hemsl.) Greenm.	Compositae	58°22′N, 26°43′E4	CT	Herb	N	Y	N	Cordate	Pinnate	Serrate	Entire
Lonicera xylosteum L.	Caprifoliaceae	58°18′N, 26°42′E	CT	Shrub	N	Y	N	Ovate	Pinnate	Smooth	Entire
Magnolia kobus DC.10	Magnoliaceae	58°22′N, 26°43′E2,4	M	Shrub/tree	N	Y	N	Obovate	Pinnate	Smooth	Entire
Maianthemum bifolium (L.) Schmidt	Liliaceae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Cordate	Parallel	Smooth	Entire
Malva parviflora L.10	Malvaceae	36°43′N, 4°25′W	M	Herb	N	Y	N	Orbicular	Palmate	Serrate	Palmatifid
Melampyrum nemorosum L.10	Scrophulariaceae	58°18′N, 26°42′E	CT	Herb	N	N	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Monstera deliciosa Liebm.10	Araceae	58°22′N, 26°43′E2,4	T	Woody vine	Y	Y	N	Ovate/orbicular	Pinnate	Smooth	Pinnatisect
Musa basjoo Sieb. et Zucc.10	Musaceae	40°25′N, 3°40′W4	T	Herb	Y	N	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Musa × paradisiaca L.10	Musaceae	58°22′N, 26°43′E2,4	T	Herb	Y	Y	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Myrtus communis L.10	Myrtaceae	36°20′N, 5°30′W	M	Shrub	Y	Y	N	Elliptic	Pinnate	Smooth	Entire
Nerium oleander L.10	Apocynaceae	36°43′N, 4°25′W	M	Shrub/tree	Y	Y	N	Elliptic/linear	Pinnate	Smooth	Entire
Olea europaea L.10	Oleaceae	40°27′N, 3°42′W	M	Tree	Y	Y	N	Elliptic	Pinnate	Smooth	Entire
Oxalis acetosella L.	Oxalidaceae	58°18′N, 26°42′E	CT	Herb	Y/N	N	Y	Obovate/reniform	Parallel	Smooth	Entire
Padus avium Mill.	Rosaceae	58°18′N, 26°42′E	CT	Tree	N	Y	N	Elliptic	Pinnate	Serrate	Entire
Paris quadrifola L.	Liliaceae	58°18′N, 26°42′E	CT	Herb	N	N	Y	Elliptic	Parallel	Smooth	Entire
Passiflora coriacea Juss.10	Passifloraceae	58°22′N, 26°43′E2,3	T	Woody vine	Y	Y	N	Reniform	Pinnate	Smooth	Entire
Pelargonium sp.10	Geraniaceae	40°25′N, 3°40′W6	T	Herb	N	Y	N	Orbicular/ovate	Palmate	Serrate	Entire
Pelargonium × hybridum (L.) Aiton10	Geraniaceae	36°43′N, 4°25′W6	T	Herb	N	Y	N	Orbicular	Palmate	Serrate	Palmatifid
Phalaris minor Retz.10	Poaceae	36°43′N, 4°25′W	M	Grass	N	N	N	Linear/ensifrom	Parallel	Smooth	Entire
Phlomis purpurea L.10	Labiatae	36°43′N, 4°25′W	M	Shrub	Y	Y	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Phragmites communis Trin.10	Poaceae	58°22′N, 26°43′E	CT	Grass	N	N	N	Linear/ensifrom	Parallel	Smooth	Entire
Picris echioides L.10	Compositae	36°43′N, 4°25′W	M	Herb	N	N	N	Ovate/oblanceolate	Pinnate	Serrate	Entire
Pisonia silvatica Standl.10	Nyctaginaceae	40°25′N, 3°40′W3	T	Tree	Y	Y	N	Elliptic	Pinnate	Smooth	Entire
Pittosporum tobira (Thunb.) Ait.10	Pittosporaceae	40°27′N, 3°42′W4	M	Shrub	Y	Y	N	Obovate	Pinnate	Smooth	Entire
Plantago lagopus L.10	Plantaginaceae	36°43′N, 4°25′W	M	Herb	N	Y	N	Elliptic/ovate/linear	Parallel	Smooth	Entire
Platanus hybrida Brot.10	Platanaceae	36°43′N, 4°25′W4,5	M	Tree	N	Y	N	Cordate	Palmate	Smooth	Palmatifid
Polygonatum multiflorum (L.) All.	Liliaceae	58°18′N, 26°42′E	CT	Herb	N	N	N	Oval	Parallel	Smooth	Entire
Polygonum cuspidatum Sieb. et Zucc.	Polygonaceae	58°22′N, 26°43′E4	CT	Herb	N	Y	N	Ovate	Pinnate	Smooth	Entire
Populus alba L.10	Salicaceae	36°43′N, 4°25′W	M	Tree	N	Y	N	Oval/obovate	Pinnate	Serrate	Pinnatifid
Populus tremula L.	Salicaceae	58°18′N, 26°42′E	CT	Tree	N	Y	N	Orbicular	Pinnate	Serrate	Entire
Prunella vulgaris L.	Labiatae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Ovate	Pinnate	Smooth	Entire
Prunus laurocerasus L.10	Rosaceae	40°27′N, 3°42′W	M	Shrub	Y	Y	N	Obovate	Pinnate	Serrate	Entire
Psoralea bituminosa L.10	Fabaceae	36°43′N, 4°25′W	M	Herb	N	Y	Y	Ovate	Pinnate	Smooth	Entire
Quercus canariensis Willd.10	Fagaceae	36°20′N, 5°30′W	M	Tree	N	Y	N	Obovate (lyrate)	Pinnate	Smooth	Pinnatifid
Quercus robur L.10	Fagaceae	58°22′N, 26°43′E	CT	Tree	N	Y	N	Obovate (lyrate)	Pinnate	Smooth	Pinnatifid
Quercus suber L.10	Fagaceae	36°20′N, 5°30′W	M	Tree	Y	Y	N	Elliptic/ovate	Pinnate	Smooth	Entire
Ranunculus cassubicus L.	Ranunculaceae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Reniform	Palmate	Serrate	Entire
Rheum raphonticum L.	Polygonaceae	58°22′N, 26°43′E4	CT	Herb	N	Y	N	Cordate	Pinnate	Crenate	Entire
Rheum rhabarbarum L.10	Polygonaceae	58°22′N, 26°43′E7	CT	Herb	N	Y	N	Cordate	Palmate	Crenate	Entire
Ribes alpinum L.	Grossulariaceae	58°18′N, 26°42′E	CT	Shrub	N	Y	N	Ovate	Palmate	Serrate	Palmisect
Ribes nigrum L.	Grossulariaceae	58°18′N, 26°42′E	CT	Shrub	N	Y	N	Ovate	Palmate	Serrate	Palmisect
Ribes rubrum L.10	Grossulariaceae	36°43′N, 4°25′W	M	Shrub	N	Y	N	Ovate	Palmate	Serrate	Palmitifid
Ricinus communis L.10	Euphorbiaceae	36°43′N, 4°25′W4	T	Shrub	N	Y	N	Orbicular	Palmate	Serrate	Palmatisect
Rubus idaeus L.	Rosaceae	58°18′N, 26°42′E	CT	Shrub	N	N	Y	Ovate	Pinnate	Serrate	Entire
Rubus saxatilis L.	Rosaceae	58°18′N, 26°42′E	CT	Herb	N	N	Y	Ovate	Pinnate	Serrate	Entire
Rumex crispus L.	Polygonaceae	58°22′N, 26°43′E	CT	Herb	N	Y	N	Elliptic	Pinnate	Crenate	Entire
Sanchezia nobilis Hook.10	Acanthaceae	58°22′N, 26°43′E2,3	T	Shrub	Y	Y	N	Elliptic	Pinnate	Smooth	Entire
Scorpiurus sulcatus L.10	Fabaceae	36°43′N, 4°25′W	M	Herb	N	N	N	Obovate/oblanceolate	Parallel	Smooth	Entire
Scutellaria costaricana H. Wendl.10	Labiatae	36°43′N, 4°25′W3	T	Herb	N	Y	N	Ovate	Parallel	Serrate	Entire
Solanum nigrum L.10	Solanaceae	36°43′N, 4°25′W	M	Herb	N	Y	N	Ovate	Pinnate	Smooth	Entire
Sorbus aucuparia L.	Rosaceae	58°18′N, 26°42′E	CT	Tree	N	N	Y	Elliptic	Pinnate	Serrate	Entire
Stellaria holostea L.	Caryophyllaceae	58°18′N, 26°42′E	CT	Herb	N	N	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Strelitzia reginae Banks.10	Strelitziaceae	40°25′N, 3°40′W6	T	Herb	Y	Y	N	Ovate/lanceolate	Pinnate	Smooth	Entire
Syringa vulgaris L.10	Oleaceae	40°27′N, 3°42′W	M	Shrub	N	Y	N	Cordate	Pinnate	Smooth	Entire
Taraxacum officinale G. H. Weber ex Wiggers10	Compositae	58°22′N, 26°43′E	CT	Herb	N	Y	N	Obovate/oblanceolate	Pinnate	Serrate	Pinnatisect
Tradescantia fluminensis Matuda10	Commelinaceae	58°22′N, 26°43′E2,3	T	Herb	Y	N	N	Ovate	Parallel	Smooth	Entire
Triticum aestivum L.10	Poaceae	36°43′N, 4°25′W	M	Grass	N	N	N	Linear/ensifrom	Parallel	Smooth	Entire
Tussilago farfara L.	Compositae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Cordate	Palmate	Serrate	Entire
Ulmus glabra L.10	Ulmaceae	58°22′N, 26°43′E	CT	Tree	N	N	N	Ovate	Pinnate	Serrate	Entire
Verbascum nigrum L.	Scrophulariaceae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Ovate	Pinnate	Serrate	Entire
Veronica chamaedrys L.	Scrophulariaceae	58°18′N, 26°42′E	CT	Herb	N	Y	N	Ovate	Pinnate	Serrate	Entire
Viburnum davidii Franch.10	Caprifoliaceae	40°27′N, 3°42′W4	M	Shrub	Y	Y	N	Elliptic/oval	Pinnate	Smooth	Entire
Vinca difformis L.10	Apocynaceae	40°27′N, 3°42′W	M	Herb	Y	Y	N	Ovate	Pinnate	Smooth	Entire
Vitis vinifera L.10	Vitaceae	36°43′N, 4°25′W	M	Woody vine	N	Y	N	Oval/orbicular	Palmate	Serrate	Palmitifid

¹ Species nomenclature follows the latest version of the W₃TROPICOS database (Missouri Botanical Garden, 2005) and Flora Europea (Tutin, 1964–1980).

² Sampled from greenhouse-grown plants.

³ Non-native species of South American origin.

⁴ Non-native species of Asian origin.

⁵ Non-native species of North-American origin.

⁶ Non-native species of South African origin.

⁷ Non-native species of European origin.

⁸ Non-native species of New Zealand origin.

⁹ Non-native species of Australian origin.

¹⁰ In this species, lamina and mid-rib were dissected into 1–5-cm strips to investigate the distribution of lamina mass.

¹¹ CT, cool temperate; M, Mediterranean or warm temperate; T, subtropical or tropical.

¹² Logical field (Yes/No).