Brain temperature and pH measured by ¹H chemical shift imaging of a thulium agent

Abstract

Temperature and pH are two of the most important physiological parameters and are believed to be tightly regulated because they are intricately related to energy metabolism in living organisms. Temperature and/or pH data in mammalian brain are scarce, however, mainly due to lack of precise and non-invasive methods. At 11.7T, we demonstrate that a thulium-based macrocyclic complex infused through the blood stream can be used to obtain temperature and pH maps of rat brain in vivo by ¹H chemical shift imaging (CSI) of the sensor itself in conjunction with a multi-parametric model that depends on several proton resonances of the sensor. Accuracies of temperature and pH determination with the thulium sensor – which has a predominantly extracellular presence – depend on stable signals during the course of the CSI experiment as well as redundancy for temperature and pH sensitivities contained within the observed signals. The thulium-based method compared well with other methods for temperature (¹H magnetic resonance spectroscopy (MRS) of N-acetyl aspartate and water; copper-constantan thermocouple wire) and pH (³¹P MRS of inorganic phosphate and phosphocreatine) assessment, as established by in vitro and in vivo studies. In vitro studies in phantoms with two compartments of differing pH values observed under different ambient temperature conditions generated precise temperature and pH distribution maps. In vivo studies in α-chloralose anesthetized and renal-ligated rats revealed temperature (33–34 °C) and pH (7.3–7.4) distributions in the cerebral cortex which are in agreement with observations by other methods. These results demonstrate that the thulium sensor can be used to measure temperature and pH distributions in rat brain in vivo simultaneously and accurately with ¹H CSI.

Introduction

Both pH and temperature are vital indicators of normal metabolism and physiology in the central nervous system. Usually departure from tightly regulated temperature and pH are considered to be warning signs of life abnormal conditions. Therefore temperature and pH measurements are extremely important for both assessment, and perhaps even treatment, of various pathophysiological states.

In vivo measurements of brain temperature and pH distributions are scarce mainly due to lack of non-invasive methods. Although thermocouple wires provide direct and absolute measure of brain temperature in vivo (1), the method is slightly invasive and temperature measurement across wide regions is quite impractical. On the other hand, infrared spectroscopy methods are far less invasive to provide better temperature distributions (2). However optical methods usually provide relative measurements near the dorsal cortical layers. In contrast, magnetic resonance imaging (MRI) and spectroscopy (MRS) allow measurements of both temperature (3) and pH (4) non-invasively using variations of relaxation times, diffusion constants, or chemical shifts of various molecules – both endogenous (e.g., water, N-acetyl aspartate (NAA), inorganic phosphate (Pi), phosphocreatine (PCr)) and exogenous (e.g., shift reagents).

One of the most common MRI methods used for temperature mapping is based on the calculation of water proton resonance frequency using the phase information obtained from gradient echo images (5). Two other water-based MRI methods use dependencies of longitudinal relaxation time (6) or molecular diffusion coefficient (7). With MRS, the water proton resonance frequency in relation to NAA has a temperature sensitivity of 0.01 ppm/°C and is more accurate than both the relaxation time and diffusion methods (8). However further applications of these methods could be pursued if the sensitivities were higher because many other factors (e.g., magnetic susceptibility) can affect the water signal.

The most reliable method for pH uses endogenous ³¹P intracellular signals of Pi and PCr (9). Recently other ³¹P methods involving exogenous agents such as 3-aminopropylphosphate have been used in mice (10). ¹H MRS provides various options for pH measurements in vivo with other exogenous agents. For example, a nontoxic reagent, 2-imidazole-1-yl-3-ethoxycarbonyl-propionic acid, has been used for imaging brain tumors in rodents (11). However these spectroscopic methods for pH determination have relatively low pH sensitivities.

Other ¹H MRS methods for pH are based on the chemical exchange saturation transfer or CEST technique (12). The method uses the exchange of hydrogen of either endogenous (amide protons of intracellular proteins and peptides (13)) or exogenous (5,6-dihydrouracil (12) or chelates containing paramagnetic ions called PARACEST agents (14)) molecules. Although the concentration requirement for PARACEST agents is smaller than that of CEST agents, both require determination of ratiometric curves at a given field strength. Recently PARACEST agents have also demonstrated temperature dependence of the hyperfine shift of lanthanide-bound water protons (15). Several ¹⁹F MRS methods for pH measurement have been reported. Fluorinated derivatives of vitamin B6 (6-fluoropyridoxol and 6-fluoropyridoxamine) allow the measurement of both intra- and extracellular pH in rodent tumors (16). Another ¹⁹F method is based on the extracellular pH dependence of the ZK-150471 probe (17). Although ¹⁹F has some advantages over ³¹P (i.e., high gyromagnetic ratio, large chemical shift dispersion, absence of endogenous ¹⁹F resonances), the fluorinated compounds are relatively unstable.

In the last decade, several complexes between lanthanide paramagnetic ions (e.g., thulium, ytterbium) and various macrocyclic chelates – such as 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetrakis(methylene phosphonate) (DOTP⁸⁻), 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetate (DOTA⁴⁻), or 1,4,7,10-tetramethyl 1,4,7,10-tetra azacyclodoecane-1,4,7,10-tetraacetic acetate (DOTMA⁴⁻) – have been proposed as temperature sensitive probes (18–25). Initially these types of complexes were used as shift reagents (26). As temperature probes they rely on the temperature dependence of their ¹H and/or ³¹P chemical shifts. In general the complexes with the highest temperature sensitivities are the ones containing thulium (Tm³⁺) as the paramagnetic ion (19). A comparison between the TmDOTP⁵⁻ and TmDOTA⁻ complexes indicate that all the TmDOTP⁵⁻ protons have higher temperature sensitivities than the corresponding protons in TmDOTA⁻ (24). The H6 proton of TmDOTP⁵⁻ has temperature sensitivity of 0.93±0.05 ppm/°C (27) which is higher than that of the corresponding methyl group of TmDOTMA⁻ (∼0.57 ppm/°C) (19). Therefore TmDOTP⁵⁻ represents an excellent temperature sensor. Moreover its proton chemical shifts are also pH dependent, which represents an advantage when trying to measure both temperature and pH. Previously we have shown that TmDOTP⁵⁻ is present in brain’s extracellular space and that temperature and pH can be calculated using two TmDOTP⁵⁻ proton resonances (27). Here we demonstrate that the majority of the TmDOTP⁵⁻ signal in a voxel is from extracellular space and that this signal can be successfully used to obtain temperature and pH maps of rat brain. The impact of signal-to-noise ratio (SNR) on chemical shift for accuracy of temperature and pH assessments is compared with other methods.

Materials and Methods

Database for TmDOTP⁵⁻ (¹H MRS)

A database for TmDOTP⁵⁻ was obtained from various samples containing 3 mM of 3-(Trimethylsilyl)propionic-2,2,3,3-d₄ acid (TSP) and 10% of D₂O with different Ca²⁺ concentrations (0–4 mM) at pH values between 6.9 and 7.7. For each sample, ¹H spectra were acquired on an 11.7T Bruker vertical bore spectrometer (Fig. 1) at temperatures between 26 and 40 °C. The spectra were line broadened (50 Hz) and then baseline (first order) and phase (zero order) corrected. The chemical shifts of each TmDOTP⁵⁻ proton (and water) were measured by fitting to a Lorentzian function. Longitudinal (T₁) and transverse (T₂) relaxation times of the TmDOTP⁵⁻ protons (Table 1) were measured at 35 °C and pH 7.4 using conventional inversion recovery and spin echo methods. The longest inversion recovery and spin echo times were 5 ms. Single exponential functions were fitted to the data to obtain T₁s and T₂s.

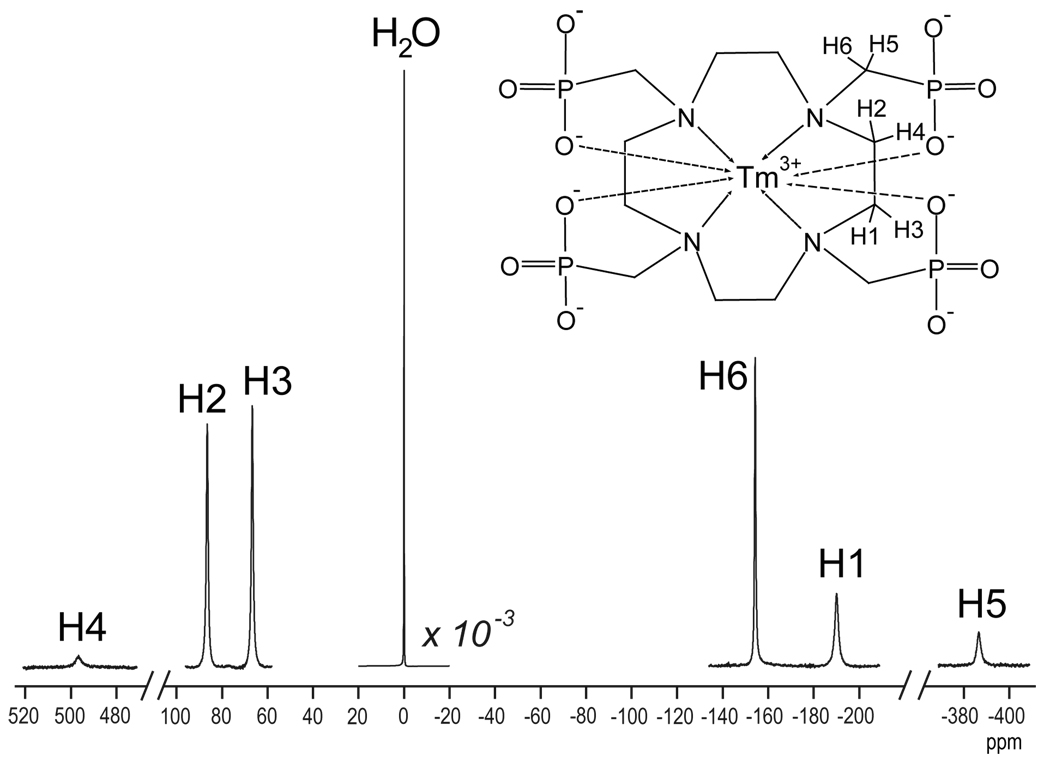
Figure 1.

¹H spectrum at 11.7T (500 MHz) of a sample containing 10 mM TmDOTP⁵⁻. The water signal (at 0 ppm) was decreased by three orders of magnitude, while for all the other resonances the vertical scale was the same. Assignment of the six non-exchangeable and non-equivalent proton resonances from the macrocyclic chelate are also shown.

Table 1.

Longitudinal (T₁) and transverse (T₂) relaxation times for H1, H2, H3 and H6 protons of TmDOTP⁵⁻ at 11.7T (temperature 35 °C, pH 7.4).

Proton	T1 (ms)	T2 (ms)
H1	0.40 ± 0.02	0.32 ± 0.03
H2	0.85 ± 0.03	0.47 ± 0.03
H3	0.88 ± 0.02	0.51 ± 0.04
H6	1.6 ± 0.1	0.73 ± 0.06

Phantom experiments with TmDOTP⁵⁻(¹H CSI)

The phantom used for in vitro experiments consisted of two concentric tubes containing 4 mM TmDOTP⁵⁻, 3 mM TSP, 10% D₂O, and 1 mM Ca²⁺ but the inner and outer tubes had different pH values (7.0 and 7.4, respectively). 2D CSI data were acquired on a modified 11.7T Bruker horizontal bore spectrometer using a ¹H surface coil radio frequency (RF) probe (1.4 cm diameter) using the following parameters: 32×32 or 16×16 encoding steps, dummy scans = 32, repetition time (TR) = 22 ms, number of averages = 16 or 64, field of view = 2.56×2.56 cm, acquisition time = 6 minutes. A 200 µs gaussian excitation pulse was used for selective excitation of a 4 mm slice and the phase encode gradient duration was 100 µs. Two free induction decays (FIDs) were acquired sequentially, one with the transmitter pulse at a frequency between the H2 and H3 protons and the other at the frequency of the H6 proton. These two transmitter frequencies (and the respective bandwidths of the excitations) were determined a priori from temperature and pH dependencies of the TmDOTP⁵⁻ protons within the physiological range (27). The temperature of the phantom was controlled by a water-heating blanket wrapped around the phantom. The ambient temperature inside the bore was measured by a thermocouple wire (∼100 µm diameter, copper-constantan; ±0.05 ºC; Oxford Optronix, Oxford, UK) positioned ∼5 cm away from the surface coil to avoid any interactions with the thermocouple. No magnetic susceptibility effects of the thermocouple wire were detected in the MRI data. Two different CSI datasets were obtained at two different bath temperatures, 45 and 35 °C, corresponding to respective temperatures of 37.3±0.1 and 30.1±0.1 °C inside the magnet bore as measured by the thermocouple. The spectra were processed as described above.

Temperature and pH by TmDOTP⁵⁻ (calibration)

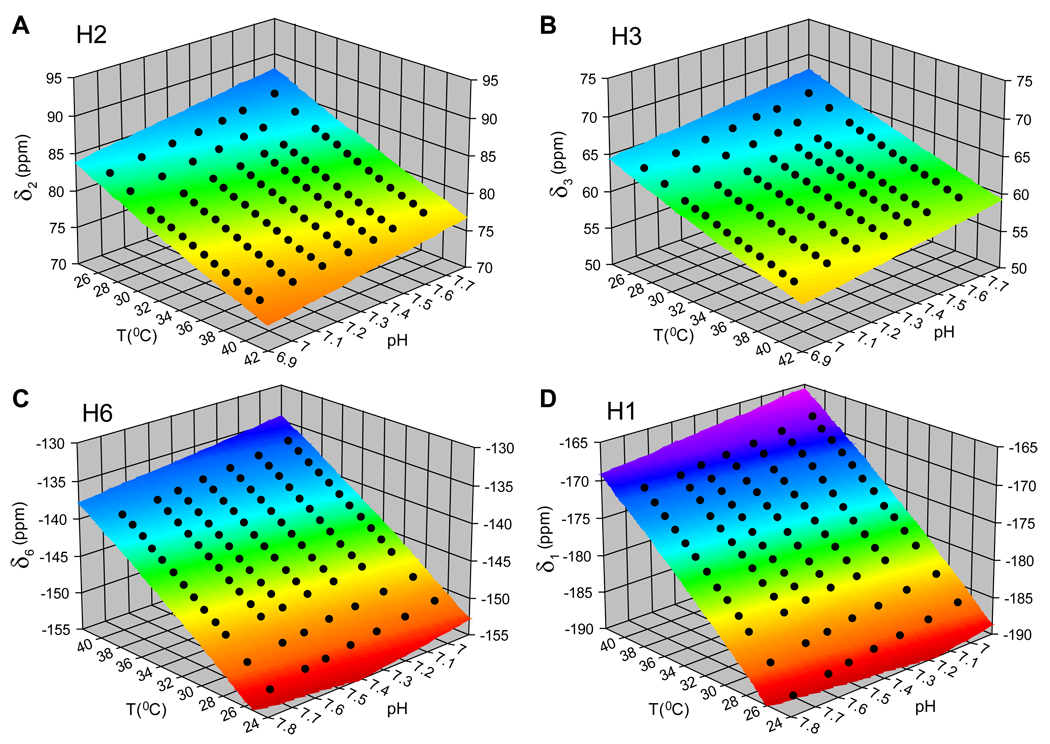
An example of the temperature and pH dependencies for the four observable proton resonances of TmDOTP⁵⁻ is shown in Fig. 2. Because the chemical shifts of these protons do not depend linearly on temperature and/or pH, at least a second order dependence of chemical shift on temperature and/or pH needs could be considered for each proton. The 3D surfaces in Fig. 2 represent the fitted results of chemical shift (δ) as a function of temperature (T) and pH,

$$\mathrm{\delta }=\mathrm{A}+\mathrm{B}\cdot \mathrm{T}+\mathrm{C}\cdot \text{pH}+\mathrm{D}\cdot {\mathrm{T}}^2+\mathrm{E}\cdot {\text{pH}}^2+\mathrm{F}\cdot \mathrm{T}\cdot \text{pH}$$ [1]

where A–F are coefficients which were determined analytically. As the temperature increases, all four protons move towards water. For H2 and H3 protons the temperature increase results in a decrease in their chemical shifts, whereas for H6 and H1 protons this results in an increase in their chemical shifts. The pH effect on the chemical shift movement is opposite to the temperature effect. Most importantly, the temperature and pH dependencies of these four protons are different from each other (i.e., each 3D sheet represented in Fig. 2 is unique from the others), providing the possibility to simultaneously determine temperature and pH by exploiting the internal redundancy of the thulium sensor for both physiological parameters (see Results).

Figure 2.

Temperature and pH dependencies of H2, H3 H6 and H1 proton chemical shifts (δ₂, δ₃, δ₆ and δ₁) of TmDOTP⁵⁻ are shown in (A), (B), (C) and (D), respectively, for an in vitro sample (4 mM TmDOTP⁵⁻, 1 mM Ca²⁺, 10% D₂O). The 3D surfaces represent the result of the fits of chemical shift δ as function of temperature T and pH (eq. [1]). The differential and independent “storage” of temperature and pH information by each of these protons is reflected by the non-overlapping 3D surfaces, a fact which can be appreciated by the variable extent of the different color tones.

Temperature by NAA and water (¹H MRS, calibration)

¹H spectra of NAA-water were acquired on an 11.7T Bruker horizontal bore spectrometer using a ¹H surface RF probe (1.4 cm diameter): voxel size = 6×3×6 mm³, TR = 2.5 s, number of averages = 384, dummy scans = 4. Samples containing 20 mM NAA, 20 mM phosphate buffer, and 1 mM TSP at pH values of 7.0, 7.2 and 7.4 were studied at temperatures within the range of 20 and 40 °C. Temperature (T) was calculated by

$$T=(309.7\pm 1.3)+(-102.7\pm 0.5)•({\delta }_{\text{water}}-{\delta }_{\text{NAA}})$$ [2]

where δ_water and δ_NAA represent the water and NAA chemical shifts. The slope and intercept were calculated by linear least-squares regression of water-NAA data for the different conditions described above.

pH by Pi and PCr (³¹P MRS, calibration)

³¹P spectra of Pi-PCr were obtained on a 9.4T Bruker horizontal bore spectrometer using a ³¹P surface coil RF probe (2 cm diameter): voxel size = 7×4×7 mm³, TR = 2 s, number of averages = 1024, dummy scans = 16. Samples containing 20 mM phosphate and 20 mM phosphocreatine at pH values between 6.6 and 7.7 were used. The pH was calculated by

$$\text{pH}={\text{pK}}_{\mathrm{a}}+\text{log}\left(\frac{\mathrm{\Delta }\mathrm{\delta }-{\mathrm{\delta }}_1}{{\mathrm{\delta }}_2-\mathrm{\Delta }\mathrm{\delta }}\right)$$ [3]

where Δδ represents the chemical shift difference between Pi and PCr resonances, δ₁ = 3.23 ppm and δ₂ = 5.70 ppm are the corresponding chemical shift differences at low and high pH, respectively (28), and pK_a = 6.915±0.002 was calculated by linear least-squares regression of Pi-PCr data for the different conditions described above.

Impact of spectral SNR on temperature and pH determination (simulations)

Since the accuracy of temperature/pH calculation by eqs. [1–3] depends on SNR, the effect of SNR on chemical shift determination was assessed by incremental addition of uniformly distributed random noise to the FID. A noise vector, representing a uniform distribution, was constructed with the same length as the complex FID vector. SNR was varied by increasing the noise amplitude. For each noise amplitude value, the modified FID was Fourier transformed and the peak of interest was fitted to a Lorentzian lineshape. No extra line broadening was used, whereas baseline (first order) and phase (zero order) corrections were applied. The SNR for the peak of interest was calculated from “signal” and “noise” measurements (29)

$$\text{SNR}=20\times {\text{log}}_{10}\left(\frac{\text{signal}}{\text{noise}}\right)$$ [4]

where the “signal” was defined as the height of the Lorentzian fitted peak and the “noise” was assessed from the intensity in a specified spectral region containing no resonances (based on a priori knowledge). At a designated noise amplitude, an averaged SNR value was obtained from 100 different runs of uniformly distributed random noise. For SNR calculations of TmDOTP⁵⁻ protons, the temperature and pH were calculated during each of the 100 runs using the model which is an extension of eq. [1] (see Results). Similar procedures were followed for NAA-water (by ¹H MRS; eq. [2]) and Pi-PCr (by ³¹P MRS; eq. [3]) data used for temperature and pH measurements, respectively.

In vivo studies

All animal experimental procedures were approved by the Institutional Animal Care and Use Committee (IACUC). Twelve Sprague-Dawley rats (200–300 g) were tracheotomized and artificially ventilated (70% N₂O, 30% O₂). Halothane (1–2 %) was used for induction and surgery. An intraperitoneal line was inserted for administration of α-chloralose (46±4 mg/kg/hr) and an intravenous line for administration of D-tubocurarine chloride (1 mg/kg/hr) and Na[TmDOTP⁵⁻] (1 mmol/kg). The rate of TmDOTP⁵⁻ infusion was adjusted to keep the animal within the autoregulatory range of cerebral perfusion. An arterial line was used for monitoring physiology (blood pH, pO₂, pCO₂) throughout the experiment. The anesthetized rats were prepared with renal ligation as previously described (27). A water-heating blanket was used to control and maintain the body temperature. Eight and four animals were used for MRS and thermocouple measurements, respectively, inside and outside the magnet. The procedures described above were common for both types of experiments. For the thermocouple measurements, a probe (Oxford Optronix Ltd., Oxford, UK) was inserted through a small burr hole to measure cortical temperature (1mm below the dura) continuously (μ1401, CED, Cambridge, UK). To minimize heat exchange with the environment, the head was covered with cotton balls.

The in vivo ¹H 2D CSI data from rat brain during TmDOTP⁵⁻ infusion were obtained on a modified 11.7 T Bruker horizontal bore spectrometer using data acquisition parameters for the phantom experiments (see above). The 2D CSI data sets were acquired using 16×16 phase encoding steps and processed similarly as indicated above. In vivo temperature and pH were assessed based on in vitro calibrations (see Results). The in vivo ¹H and ³¹P MRS data of metabolites (containing NAA-water and Pi-PCr, respectively) were acquired using single voxel spectroscopy (see above) to calculate temperature and pH, respectively (eq. [2] and eq. [3]).

The TmDOTP⁵⁻ concentration in vivo (in a CSI voxel) was estimated by comparison with a phantom of known TmDOTP⁵⁻ concentration, where both data sets were acquired under identical conditions (spatial resolution, acquisition time, data processing, etc.). We used the H2 and H3 protons for TmDOTP⁵⁻ concentration estimation. In both cases (i.e., in vivo and in vitro CSI voxels) the areas under the corresponding resonances were used for quantification. Shimming conditions did not adversely affect this procedure because the TmDOTP⁵⁻ proton peaks are intrinsically broad due to their extremely short T₂ values (Table 1). This procedure provided the total TmDOTP⁵⁻ concentration in the CSI voxel (C_t) which contains TmDOTP⁵⁻ in the blood (C_bl) and in the extracellular space (C_ex). In a specified cortical region, the blood volume is about 3% (30) and the extracellualar volume is about 20% (31) of the total volume. Since the thulium agent is localized within these two regions, the blood fraction (f_bl) contributes by ∼13% while the extracellular space fraction (f_ex) contributes by ∼87% to the total MRS signal. The TmDOTP⁵⁻ concentration in the extracellular space C_ex can be calculated using the total and blood concentrations according to the equation C_t = f_bl C_bl + f_ex C_ex. To determine the blood concentration, we removed blood (75–150 µl) from the sagittal sinus after 2 hours from the start of the infusion. The scalp was removed to expose the skull, a small hole was drilled on the sagittal suture, 1 mm above the lambda point and blood was extracted using a capillary glass tube. The blood samples were centrifuged, the supernatant portions were saved, and ex vivo samples were made by adding 50 µl of 10 mM TSP in D₂O and distilled water to bring the final volume to 500 µl. ¹H spectra were acquired on the 11.7T Bruker vertical bore spectrometer (see above).

Results

In vitro measurements

Two of the six non-exchangeable and non-equivalent protons of TmDOTP⁵⁻ (Fig. 1), H4 and H5, have resonances at approximately +500 ppm and −385 ppm, respectively, from the water resonance. Therefore simultaneous detection of all six protons requires an extremely large spectral bandwidth (∼1000 ppm). The smaller intensities of these two resonances are due to limited excitation over the far ends of the excited bandwidth. Thus the spectral bandwidth needs to be restricted to a smaller range (∼300 ppm) to acquire signals with reasonable SNR – namely the H1, H2, H3 and H6 resonances.

The presence of a paramagnetic ion (Tm³⁺) inside the DOTP⁸⁻ macrocyclic complex enhances T₁ and T₂ relaxation of the protons, most likely dominated by dipolar relaxation between the unpaired Tm³⁺ electron and the proton nuclear spin. Previous results at 7T suggest relaxation times on the order of several milliseconds (25). Such short relaxation times restrict the design of complex ¹H MRS pulse sequences (e.g., involving outer volume suppression or water suppression). Our 11.7T measurements at 35 °C (Table 1) indicate that, out of the four protons investigated, the H6 has the longest T₁ and T₂ relaxation times (1.6±0.1 ms and 0.73±0.06 ms, respectively). The extremely short T₂ values (less than 0.73 ms) drastically restrict the TR of the MRS pulse sequence (i.e., elapsed time between excitation and acquisition) to less than 1 ms. Under these conditions the most suitable method to obtain localized detection of TmDOTP⁵⁻ signals is 2D CSI. Water suppression was not required given the use of a frequency selective gaussian pulse and the fact that the TmDOTP⁵⁻ proton frequencies are at least 20 MHz away from the water frequency.

Temperature and pH calibration for TmDOTP⁵⁻

The different dependencies of TmDOTP⁵⁻ proton chemical shifts on temperature and pH (Fig. 2) can allow simultaneous prediction of these vital parameters. Our previous results showed that temperature and pH can be calculated simultaneously using chemical shifts of two different TmDOTP⁵⁻ protons (27). However this method did not fully account for presence of Ca²⁺ interactions with TmDOTP⁵⁻ in vivo. In rat brain, Ca²⁺ concentration in interstitial fluid is ∼1 mM (32–34). Since previous results indicate that Ca²⁺ forms a stable adduct with TmDOTP⁵⁻ (35), the in vitro calibration for temperature and pH should consider the involvement of Ca²⁺ and TmDOTP⁵⁻ interactions.

Given that the in vivo TmDOTP⁵⁻ concentrations measured in a CSI voxel and sagittal sinus were 4.0±0.1 mM and 5.7±0.3 mM respectively, the TmDOTP⁵⁻ concentration in the extracellular space was calculated to be 3.75±0.12 mM (Table 2). Therefore the in vitro calibrations were carried out with spectra from the database containing a range of Ca²⁺ and TmDOTP⁵⁻ concentrations (see above) to match the in vivo Ca²⁺:Tm³⁺ ratio of about 1:4. In addition, our results suggest that about 82% of the in vivo TmDOTP⁵⁻ signal in a CSI voxel is of non-blood origin and therefore the temperature and pH calculated using the TmDOTP⁵⁻ method would be sensitive to the extracellular compartment.

Table 2.

Measured TmDOTP⁵⁻ concentrations in vivo

Compartment	Fraction	[TmDOTP5−] (mM)
Blood	13 %	5.7 ± 0.3
Extracellular space	87 %	3.75 ± 0.12
Total	100 %	4.0 ± 0.1

The current multi-parametric model exploits the redundant temperature and pH information contained in the chemical shifts of TmDOTP⁵⁻ protons. Since the H1 proton has an extremely short T₂ (0.32±0.03 ms), the peak is very broad and under in vivo conditions this proton has a much lower SNR than the other three protons. Therefore the model is based on the chemical shifts of the H2, H3, and H6 protons. To find the combination of protons that produce the smallest error in temperature and pH determination, several scenarios were considered. For the model using two protons (x and y), the temperature (T_c^[x,y]) and pH (pH_c^[x,y]) were calculated from their respective chemical shifts (δ_x and δ_y) according to

$${\mathrm{T}}_{\mathrm{c}}^{[\mathrm{x},\mathrm{y}]}={\mathrm{a}}_1^{[\mathrm{x},\mathrm{y}]}+{\mathrm{a}}_2^{[\mathrm{x},\mathrm{y}]}{\mathrm{\delta }}_{\mathrm{x}}+{\mathrm{a}}_3^{[\mathrm{x},\mathrm{y}]}{\mathrm{\delta }}_{\mathrm{y}}+{\mathrm{a}}_4^{[\mathrm{x},\mathrm{y}]}{{\mathrm{\delta }}_{\mathrm{x}}}^2+{\mathrm{a}}_5^{[\mathrm{x},\mathrm{y}]}{{\mathrm{\delta }}_{\mathrm{y}}}^2+{\mathrm{a}}_6^{[\mathrm{x},\mathrm{y}]}{\mathrm{\delta }}_{\mathrm{x}}{\mathrm{\delta }}_{\mathrm{y}}$$ [5]

$${\text{pH}}_{\mathrm{c}}^{[\mathrm{x},\mathrm{y}]}={\mathrm{b}}_1^{[\mathrm{x},\mathrm{y}]}+{\mathrm{b}}_2^{[\mathrm{x},\mathrm{y}]}{\mathrm{\delta }}_{\mathrm{x}}+{\mathrm{b}}_3^{[\mathrm{x},\mathrm{y}]}{\mathrm{\delta }}_{\mathrm{y}}+{\mathrm{b}}_4^{[\mathrm{x},\mathrm{y}]}{{\mathrm{\delta }}_{\mathrm{x}}}^2+{\mathrm{b}}_5^{[\mathrm{x},\mathrm{y}]}{{\mathrm{\delta }}_{\mathrm{y}}}^2+{\mathrm{b}}_6^{[\mathrm{x},\mathrm{y}]}{\mathrm{\delta }}_{\mathrm{x}}{\mathrm{\delta }}_{\mathrm{y}}$$ [6]

Where the coefficients a_i^[x,y] and b_i^[x,y] (i=1 to 6) were calculated from the linear least-squares fits of temperature and pH, respectively, as function of chemical shifts (Table 3 and Table 4). For the model using all three protons, the temperature and pH were calculated in two ways. First, averaged temperature and pH values were obtained from three combinations of two protons: [H2,H6], [H3,H6] and [H2,H3]. Second, averaged temperature and pH values were obtained from two combinations of two protons: [H2,H6] and [H3,H6], [H2,H6] and [H2,H3], [H3,H6] and [H2,H3]. Assuming the same error in the chemical shift measurement for all protons (ε_δ) and with propagation of errors (36) it can be shown that the uncertainties in temperature (ε_T) and pH (ε_pH) are both proportional to the error in the chemical shift measurement. Our results indicated that the smallest error in both temperature and pH determination was obtained with the model based on two combinations of two protons, namely [H2,H6] and [H3,H6]. In this case, at 35 °C and pH of 7.4, we estimated that the errors in temperature and pH were ε_T = 2.63•ε_δ and ε_pH = 0.482•ε_δ, respectively. Based on this error analysis, the most reliable way to calculate temperature (T_c^•) and pH (pH_c^•) from H2, H3 and H6 resonances is by using

$${{\mathrm{T}}_{\mathrm{c}}}^{•}=({{\mathrm{T}}_{\mathrm{c}}}^{[\mathrm{H}2,\mathrm{H}6]}+{{\mathrm{T}}_{\mathrm{c}}}^{[\mathrm{H}3,\mathrm{H}6]})/2$$ [7]

$${{\text{pH}}_{\mathrm{c}}}^{•}=({{\text{pH}}_{\mathrm{c}}}^{[\mathrm{H}2,\mathrm{H}6]}+{{\text{pH}}_{\mathrm{c}}}^{[\mathrm{H}3,\mathrm{H}6]})/2$$ [8]

where T_c^[H2,H6], T_c^[H3,H6], pH_c^[H2,H6] and pH_c^[H3,H6] are given by eq. [5] and eq. [6]. The comparison between calculated (T_c^•) and measured (T_m) temperatures gave

$${{\mathrm{T}}_{\mathrm{c}}}^{•}=(0.016\pm 0.075)+(0.999\pm 0.002)•{\mathrm{T}}_{\mathrm{m}}$$ [9]

with a high correlation coefficient (R = 0.99978) as obtained by linear least-squares fit. A similarly good correlation (R = 0.99654) was found between calculated (pH_c^•) and measured (pH_m) pH.

$${{\text{pH}}_{\mathrm{c}}}^{•}=(0.058\pm 0.064)+(0.992\pm 0.009)•{\text{pH}}_{\mathrm{m}}$$ [10]

For both temperature and pH, the correlation between calculated and measured values was ∼1 with an intercept of ∼0 indicating excellent accuracy. Using the in vitro calibration at 1 mM Ca²⁺ and 4 mM TmDOTP⁵⁻, we calculated temperature sensitivities of TmDOTP⁵⁻ protons at 35 °C and pH of 7.4 to be 1.27, −0.59, −0.46 and 1.00 ppm/°C for H1, H2, H3 and H6 protons, respectively. The corresponding pH sensitivities were −4.23, 4.16, 3.61 and −3.91 ppm/pH units for H1, H2, H3 and H6 protons, respectively. This calibration holds for the wide range of temperature (26 to 40 °C) and pH (6.9 to 7.7) expected in vivo.

Table 3.

The coefficients a_i^[x,y] for temperature determination using chemical shifts of two TmDOTP⁵⁻ protons, x and y, for an in vitro sample (4 mM TmDOTP⁵⁻, 1 mM Ca^2+;, 10% D₂O). The coefficients were calculated from linear least-squares fits of temperature as function of chemical shifts according to eq. [5].

δx	δy	a1	a2	a3	a4	a5	a6
H2	H6	326.667	8.45179	7.68409	−0.0576860	0.0137429	−0.0193380
H3	H6	305.664	5.24485	4.94409	−0.1899355	−0.0193254	−0.1397433
H2	H3	176.503	52.60730	−70.54896	−16.2642940	−26.0607580	41.1884170

Table 4.

The coefficients b_i^[x,y] for pH determination using chemical shifts of two TmDOTP⁵⁻ protons, x and y, for an in vitro sample (4 mM TmDOTP⁵⁻, 1 mM Ca²⁺, 10% D₂O). The coefficients were calculated from linear least-squares fits of pH as function of chemical shifts according to eq. [6].

δx	δy	b1	b2	b3	b4	b5	b6
H2	H6	8.085	1.42126	0.77861	−0.0084096	0.0007837	−0.0030817
H3	H6	2.261	0.59475	0.16352	−0.0391725	−0.0072995	−0.0329490
H2	H3	−15.069	10.63741	−13.05446	−2.3389974	−3.6943872	5.8774425

Effect of spectral SNR on temperature and pH determination

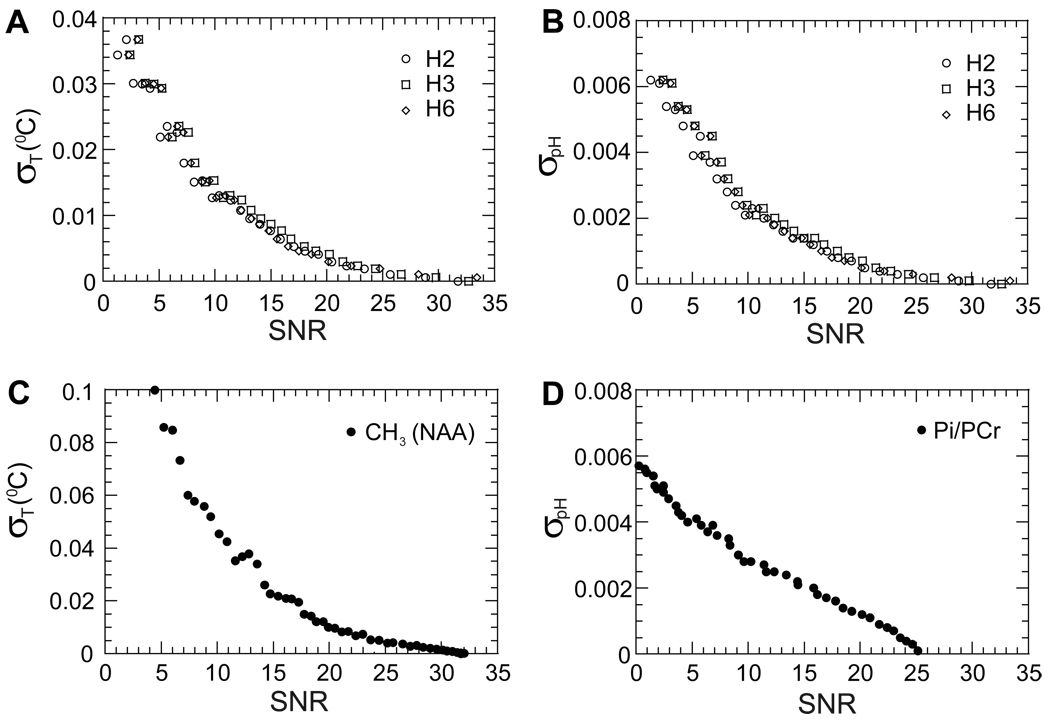
The error in temperature and pH determination depends on the error in chemical shift measurement, which in turn depends on the SNR for each proton resonance. Simulation results with TmDOTP⁵⁻ show that the standard deviation in the chemical shift for H1 proton is larger than for the H2, H3 and H6 protons at the same SNR value. The temperature and pH values were calculated with variable SNR values from the chemical shifts of H2, H3 and H6 (eq. [5] to eq. [8]) and the standard deviations for temperature and pH estimations were obtained (Figs. 3A and 3B, respectively). Typical in vivo SNR values for H2, H3 and H6 protons in a 2D CSI voxel (of a 1.6×1.6×4 mm³) is ∼15 with total acquisition time of 6 minutes. At this SNR the standard deviations of temperature and pH were 0.008 °C (Fig. 3A) and 0.0013 (Fig. 3B), respectively.

Figure 3.

Effect of spectral SNR on temperature and pH determination. Dependencies of temperature (A) and pH (B) standard deviations using the H2, H3 and H6 proton chemical shifts of TmDOTP⁵⁻. For a typical in vivo SNR value of ∼15, the standard deviations were 0.008 °C for temperature and 0.0013 for pH. The effect of SNR on temperature and pH accuracies was compared with the NAA-water method by ¹H MRS for temperature (C) and Pi-PCr method by ³¹P MRS for pH (D). Under similar in vivo conditions, the SNR values were ∼8 and ∼5, respectively, which corresponded to standard deviations of 0.06 °C for temperature and 0.004 for pH.

Similarly the standard deviations in temperature and pH using the NAA-water and Pi-PCr methods, respectively, were estimated for a range of SNR values (Figs. 3C and 3D). Under similar conditions (i.e., in terms of voxel size and total acquisition time of a 2D CSI experiment for TmDOTP⁵⁻), the SNR values for the methyl NAA group and Pi-PCr were ∼8 and ∼5, respectively. These SNR values for NAA-water and Pi-PCr methods corresponded to standard deviations of 0.06 °C for temperature and 0.004 for pH, respectively. The comparison of results from the different methods shows that the standard deviations in temperature and pH measured by the TmDOTP⁵⁻ method are at least as good as in the other methods, thereby suggesting that both temperature and pH can be measured rapidly and simultaneously using 2D CSI of TmDOTP⁵⁻. However both NAA-water and Pi-PCr methods reflect predominantly intracellular events, whereas the TmDOTP⁵⁻ method reflects mostly extracellular events.

Phantom measurements of temperature and pH

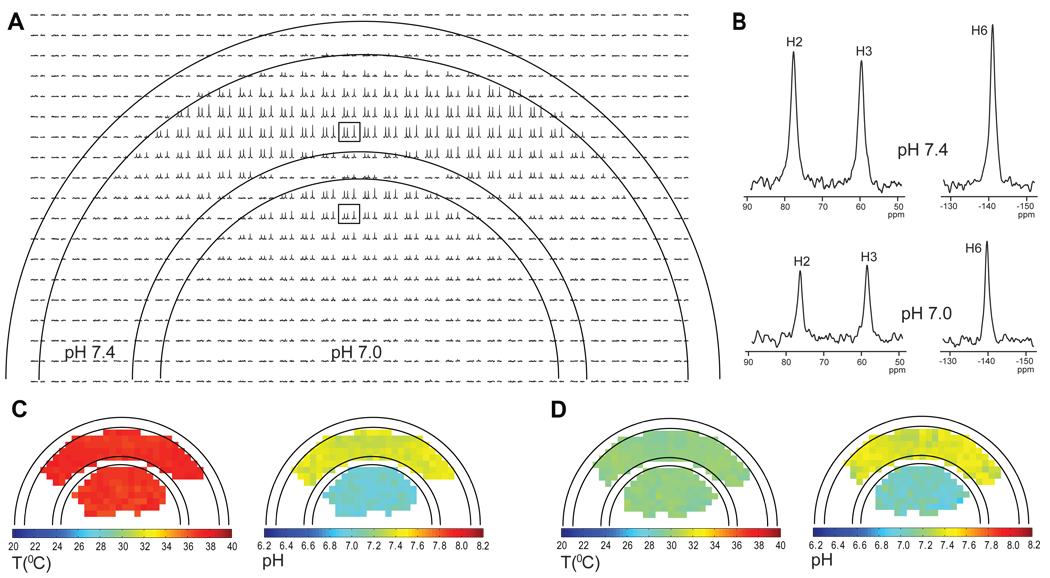
A phantom with two different pH values in each of its two compartments (inner at 7.0 and outer at 7.4) was used to demonstrate the feasibility of generating high resolution temperature and pH maps with TmDOTP⁵⁻, where the magnet bore temperature was varied by ∼7 °C (Fig. 4). Rapidly acquired high resolution 2D CSI data provided well resolved spectra of the entire phantom (Fig. 4A). Chosen voxels from the outer and inner compartments (Fig. 4B, upper and lower spectra, respectively) revealed that the chemical shifts move towards the water resonance as the pH decreases, as expected from the temperature and pH dependencies of TmDOTP⁵⁻ (Fig. 2). Using the H2, H3 and H6 protons, the temperature and pH values were calculated for each voxel according to the model described above. Temperature and pH maps were generated for two different ambient temperature conditions, one corresponding to a bore temperature of 37.3±0.1 °C (Fig. 4C) and another to 30.1±0.1 °C (Fig. 4D). For the first case (Fig. 4C), the results indicated that the average calculated temperatures in the outer and inner compartments were 37.2±0.3 °C and 37.0±0.3 °C, respectively, with average calculated pH values of 7.39±0.05 and 7.01±0.05. These results are in excellent agreement with the measured values of temperature (37.3±0.1 °C) and pH (7.4±0.1 and 7.0±0.1, respectively, in the two compartments). Similar agreements were found when the bore temperature was lowered (Fig. 4D). The average calculated temperatures in the outer and inner compartments were 30.0±0.3 °C and 29.9±0.3 °C, respectively, with average calculated pH values of 7.40±0.06 and 7.05±0.07. When voxels sizes of the CSI experiment in this phantom were increased (i.e., SNR was raised), the agreement between calculated and measured values improved slightly (data not shown), which agrees with the conclusions from the SNR-based simulations (Fig. 3).

Figure 4.

Examples of temperature and pH maps of a two compartment phantom containing 4 mM TmDOTP⁵⁻, 3 mM TSP and 1 mM Ca²⁺ in 10% D₂O at two different pH values (7.0 inner and 7.4 outer). (A) ¹H CSI of the phantom obtained in a 32×32 CSI experiment showing the resonances of H2, H3 and H6 protons. The bore temperature was initially maintained at 37.3±0.1 °C. The field of view used was 2.56×2.56 cm and the slice thickness was 4 mm, giving a voxel size of 0.8×0.8×4 mm³. (B) Examples of ¹H spectra from two different voxels (boxed in A) one from the outer compartment at pH of 7.4 (upper spectrum) and the other from the inner compartment at pH of 7.0 (lower spectrum). Temperature and pH maps of the phantom at bore temperatures of 37.3±0.1 °C (C) and 30.1±0.1 °C (D).

Brain temperature and pH maps

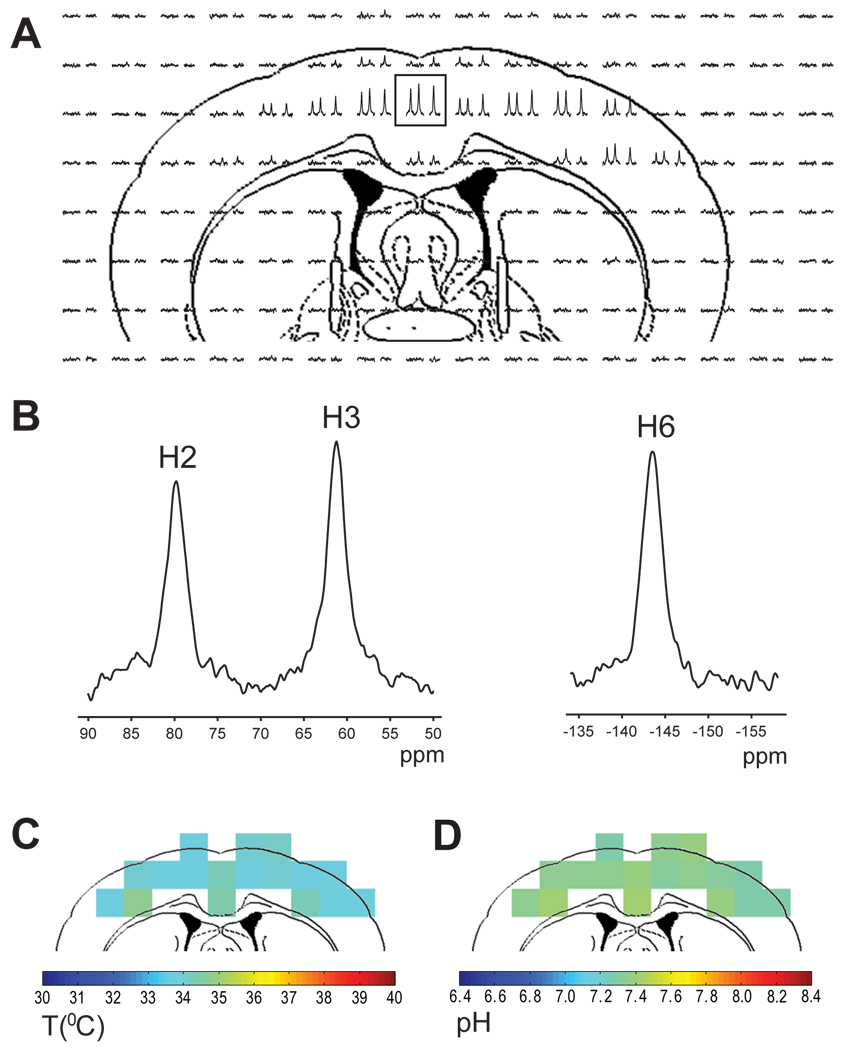
TmDOTP⁵⁻ concentration in the blood and in the extracellular spaces became quite stable within 2 hours of infusion (Table 2). Repeated measurements over several hours did not change significantly from these steady-state values, probably because renal ligation drastically diminished the amount of TmDOTP⁵⁻ lost over time. All CSI experiments were acquired during the stable period to ensure that the in vivo conditions were similar to those used for temperature and pH calibration (i.e., Ca²⁺:TmDOTP⁵⁻ ratio of 1:4). In vivo detection of TmDOTP⁵⁻ with high SNR (Fig. 5A) shows well resolved H2, H3 and H6 resonances in 10 µl voxels (Fig. 5B). The temperature (Fig. 5C) and pH (Fig. 5D) maps of rat brain show that the average cortical values were 34.3 °C and 7.40, respectively. The temperature in the upper cortical regions was between 33.7 and 34.2 °C and slightly higher ranges were found in deeper cortical regions (between 34.3 to 34.9 °C). Likewise the pH distribution was relatively uniform, with values ranging between 7.29 and 7.41 in upper cortical regions. The core body temperature was 35.8±0.1 °C, where the standard deviation of 0.1 °C represents the fluctuations of the body temperature during the acquisition period. Measurements with thermocouple wires in a separate group (n = 4) but under the same conditions indicated that the average temperatures in the cortex (1 mm below dura) and basal ganglia (4 mm below dura) were 35.4±0.8 and 37.2±0.7 °C, respectively, where the corresponding standard deviations indicate the variations about the mean for four animals investigated. Moreover the cortical temperature measured by the NAA-water method and pH using ³¹P MRS in slightly larger voxels (data not shown, under similar conditions) were 35.2±0.4 °C and 7.30±0.01, respectively. These independent temperature and pH values are in excellent agreement with the TmDOTP⁵⁻ results.

Figure 5.

Example of temperature and pH maps of rat brain. (A) ¹H CSI of rat brain after TmDOTP⁵⁻ infusion. The signal intensity is much higher in the cortical area mainly due to RF inhomogeneity of the surface coil. (B) Example of ¹H spectra from a 1.6×1.6×4 mm³ voxel (boxed in A) showing the H2, H3 and H6 proton resonances. (C) Temperature and (D) pH maps of rat brain.

Discussion

The method presented here demonstrates that two important parameters which are commonly used to discern various metabolic processes in vivo, temperature and pH, can be simultaneously measured using three proton chemical shifts of TmDOTP⁵⁻ (Fig. 1). Because the temperature and pH information is “stored” differentially and independently in each of the chemical shifts of these three protons (Fig. 2), their redundant dependencies can be used to increase the accuracies of temperature and pH predictions (Table 3 and Table 4). While the simultaneous dependence of chemical shifts on both temperature and pH can be seen as a drawback for accurate determination of these two parameters, we propose that simultaneous measurement of temperature and pH from TmDOTP⁵⁻ protons can instead be an experimental asset since the acid-base balance is inherently linked to temperature in most tissues (37). Thus with one exogenous agent both vital parameters can be measured by biosensor imaging of redundant deviation of shifts (BIRDS).

The error in temperature and pH calculation from any MRS measurement is dependent on spectral SNR through the error in chemical shift determination. Our simulations indicate that for typical in vivo SNR range with TmDOTP⁵⁻ (10 to 30) the range of errors for temperature and pH predictions are better than 0.02 °C and 0.003, respectively (Figs. 3A and 3B). Under similar in vivo conditions, the errors for temperature and pH measured by NAA-water and Pi-PCr methods, respectively, are quite similar (Figs. 3C and 3D). It should be noted, however, that the simulations for NAA-water and Pi-PCr methods did not take into account the additional confounds of spectral overlap between the assigned and other metabolites. For example, the in vivo NAA methyl group resonance at 2.01 ppm overlaps with a resonance from N-acetyl aspartatyl glutamate at 2.04 ppm and another resonance from glutamate at 2.05 ppm (28), thereby inducing deviations from Lorentzian lineshapes. In contrast, for the TmDOTP⁵⁻ method all proton resonances are well resolved and there are no concerns about spectral overlap with other resonances. However an important distinction between these MRS methods is that the NAA-water and Pi-PCr methods do not require infusion of an exogenous agent and no renal ligation is needed. However the extremely short T₁ and T₂ relaxation times of TmDOTP⁵⁻ protons, on the order of milliseconds, have two opposite effects on the corresponding SNR. A short T₂ produces a large linewidth to thereby decrease SNR, while a short T₁ allows for faster averaging which in turn increases the SNR. Fast averaging is extremely important for obtaining temperature and pH distributions in real time during various applications.

Our in vitro results showed that high resolution temperature and pH maps can be obtained using the BIRDS method using TmDOTP⁵⁻ (Fig. 4). Excellent agreement was observed between the bore temperatures and the average calculated temperatures in the two compartments. Also the calculated pH distributions showed excellent agreement with the measured pH values in the two compartments for two different bore temperatures. The similarity between the pH distributions in the two compartments (at both bore temperatures) demonstrates that the temperature determination is indeed independent of pH, and therefore this calibration may be applied in vivo. Although the in vivo toxicity of TmDOTP⁵⁻ has not been measured directly, it can be inferred from other observations. Results in our (27) and other (38) laboratories suggest that infusion dose of 1 mmol/kg results in stable systemic physiology without affecting normal brain function (HKT and FH unpublished results). Moreover the half lethal dose (LD₅₀) values for lanthanide complexes such as YbDOTMA⁻ (18) or GdDOTA⁻ (39) are 10.5 mmol/kg and 11.4 mmol/kg, respectively, suggesting that the LD₅₀ for TmDOTP⁵⁻ may be at least an order of magnitude higher than the doses used in our experiments.

It has been suggested (22,40) that TmDOTP⁵⁻ or other similar compounds (e.g., TmDOTMA⁻) do not cross the blood-brain barrier. Our previous (27) and current results suggest that TmDOTP⁵⁻ crosses the blood-brain barrier quite rapidly (1 hour). A plausible delivery route for TmDOTP⁵⁻ into the extracellular space may be through fenestrated blood vessels. Early in brain development, the endothelium of fenestrated vessels has small apertures which allow various solutes to cross into the extracellular space. However by fetal day 17, these fenestrated vessels disappear from the brain parenchyma (41) except for the circumventricular organs (42). We propose that fenestrated vessels of the circumventricular organs (43) may provide the path for delivery of agents like TmDOTP⁵⁻ or TmDOTMA⁻ (and perhaps even other similar agents). The observation of proton signals emanating from the TmDOTP⁵⁻ complex is drastically enhanced by renal ligation which minimizes its clearance from the body. The present measurements suggest that the in vivo TmDOTP⁵⁻ concentration in a CSI voxel in rat brain is 4.0±0.1 mM after about 2 hours of infusion, while the TmDOTP⁵⁻ concentration in the sagittal sinus is 5.7±0.3 mM. Based on these results we calculated that the concentration of TmDOTP⁵⁻ in the extracellular milieu is 3.75±0.12 mM, which represents about 82% of the total signal in a CSI voxel. Because of continuous fast exchange of water (and other molecules) between the inside and outside of the cell, it is possible that the extracellular temperature measured by the TmDOTP⁵⁻ method represents a good approximation of the intracellular situations measured by the NAA-water method (see Results).

In vivo results demonstrated that temperature and pH maps of rat brain can be obtained by conventional CSI requiring at most a few minutes to image the TmDOTP⁵⁻ complex (Fig. 5). The voxels situated at the brain surface had temperature values between 33 and 34 °C, while temperature values in deeper cortical regions were in the range of 34 to 35 °C (Fig. 5C). The results indicated that the anesthetized brain temperature (33–35 °C) can be slightly lower than the body temperature (∼36 °C) (44). These results are in good agreement with a recent study in rats (45) which shows that the brain temperature is lower than the body temperature and that deeper brain regions have higher temperature values than the superficial regions. The pH distribution in the cortex shows relative homogeneity between 7.3 and 7.4 (Fig. 5D). While the results in Fig. 5 are from one rat, similar data were obtained from all eight rats scanned.

The temperature and pH measurements from the BIRDS method using TmDOTP⁵⁻ are in good agreement with independent methods used for each of these physiological parameters (see Results). There is, however, a relatively small effect of Ca²⁺ ions on the chemical shift of the TmDOTP⁵⁻ protons. Although the calibration depends slightly on the Ca²⁺:TmDOTP⁵⁻ ratio, the CSI experiments were acquired after 2 hours of TmDOTP⁵⁻ infusion when the concentrations in the blood and in the extracellular space were stable (Table 2). Under these conditions, the TmDOTP⁵⁻ concentration in the extracellular space was 3.75±0.12 mM. Given that Ca²⁺ in the extracellular space is ∼1 mM (32–34) and the largest physiological variations in the extracellular space are in the nM range, the in vivo Ca²⁺:TmDOTP⁵⁻ ratio is within 5–7% of the in vitro calibration values. This systematic error corresponds to chemical shift changes of −0.035 ppm, −0.032 ppm, and 0.022 ppm for H2, H3, and H6 resonances, respectively. Therefore slight experimental variations of the Ca²⁺:TmDOTP⁵⁻ ratio in vivo could correspond to additional temperature and pH errors of 0.025 °C and 0.012, respectively. In total, the estimated error in temperature and pH prediction by the TmDOTP⁵⁻ method would be on the order of 0.04 °C and 0.015, respectively, which is within the margin of error of the other methods.

In a recent study in α-chloralose anesthetized rats, temperature dynamics in the brain during forepaw stimulation were measured with thermocouples (46). The model considered four simultaneous processes that contributed to temperature changes in a local region: metabolic heat production, removal/addition of heat through blood flow, conductive heat loss to adjacent regions in the brain, and dissipative heat loss to the environment from the brain. A similar approach can be used to model temperature dynamics in the rat brain using temperature distributions obtained using the TmDOTP⁵⁻ complex. The advantage of the CSI method based on TmDOTP⁵⁻ in such a study would be that it can be used to map temperature dynamics of the whole brain rather than just a local region.

In summary, in the present study we described a model which uses the redundant chemical shift information from three protons of TmDOTP⁵⁻ to generate independent and simultaneous temperature and pH distributions. Our results indicated that the BIRDS method using TmDOTP⁵⁻ compared well with other methods. Simultaneous temperature and pH maps of rat brain were obtained within several minutes using the BIRDS method. The present results open the way towards obtaining simultaneous temperature and pH distributions in a large variety of applications, such as functional activation (47), brain cooling (48) or cancer treatment (49).