Modeling repeated time-to-event health conditions with discontinuous risk intervals: an example of a longitudinal study of functional disability among older persons

Summary

Objectives

Researchers have often used rather simple approaches to analyze repeated time-to-event health conditions that either examine time to the first event or treat multiple events as independent. More sophisticated models have been developed, although previous applications have focused largely on such outcomes having continuous risk intervals. Limitations of applying these models include their difficulty in implementation without careful attention to forming the data structures.

Methods

We first review time-to-event models for repeated events that are extensions of the Cox model and frailty models. Next, we develop a way to efficiently set up the data structures with discontinuous risk intervals for such models, which are more appropriate for many applications than the continuous alternatives. Finally, we apply these models to a real dataset to investigate the effect of gender on functional disability in a cohort of older persons. For comparison, we demonstrate modeling time to the first event.

Results

The GEE Poisson, the Cox counting process, and the frailty models provided similar parameter estimates of gender effect on functional disability, that is, women had increased risk of bathing disability and other disability (disability in walking, dressing, or transferring) as compared to men. These results, especially for other disability, were quite different from those provided by an analysis of the first-event outcomes. However, the effect of gender was no longer significant in the counting process model fully adjusted for covariates.

Conclusion

Modeling time to the first event only may not be adequate. After properly setting up the data structures, repeated event models that account for the correlation between multiple events within subjects, can be easily implemented with common statistical software packages.

1. Introduction

Recurrent health conditions, which are common in epidemiological and medical research, can be classified as two types. The first type uses a continuous risk interval, which is appropriate for discrete health conditions, such as myocardial infarction, where the first occurrence does not preclude the possibility of a second occurrence immediately thereafter. Previously studies have mostly focused on recurrent health conditions with continuous risk intervals [1–9]. However, in medical research we more often encounter recurrent health conditions of a second type, that is, ones with discontinuous risk intervals. Examples of such health conditions include infections, disability episodes [10–12], hospitalizations, and nursing home admissions. When subjects have disability, they are not at risk of the second episode of disability until they have recovered from the first episode. To obtain valid estimates of incidence rates and model parameters, the duration of the heath condition should be excluded from the risk set when analyzing recurrent time-to-event outcomes with discontinuous risk intervals.

A systematic review of the literature [1] shows that researchers have often used rather naive approaches to analyze data of recurrent health conditions that either examine time to the first event only or treat multiple events as independent, thereby ignoring the correlation within subjects. However, methods have been developed that make use of all available data, while accounting for the lack of independence of multiple events within subjects. Popular approaches fall into two families: variance-corrected models and frailty/random effects models [2]. Variance-corrected models were developed to account for correlation by using robust standard errors. The correlation is of no substantive interest and is merely a nuisance parameter in variance-corrected methods.The theory behind frailty models is that some subjects are intrinsically more or less prone than others to experiencing the events of interest; frailty can be considered a random covariate in the model that corrects dependence among the multiple event times. Limitations of applying these variance-corrected models and frailty models include their complexity and difficulty in implementation without careful attention to forming the data structures, even with commercially available statistical software packages.

In this paper, we review six models for repeated time-to-event outcomes, and we demonstrate how to efficiently create the data structures with discontinuous risk intervals. We focus on the practical application of these techniques to generate the incidence rate, which is a core concept in epidemiology [13]. As an illustration, we apply these models to investigate the effect of gender on disability in essential activities of daily living (ADLs). We model bathing disability and other disability (disability in walking, dressing, or transferring) separately to determine whether bathing disability and other disability may differ by gender and the number of previous disability episodes. Finally, we provide some general guidance for analyzing recurrent health conditions with discontinuous risk intervals.

2. Data and Methods

2.1 Brief Description of the Models

We briefly describe four variance-corrected models and two frailty models in this section.

2.1.1 Poisson regression model

The Poisson regression model is frequently used to study disease incidence and mortality [13]. The conditional mean of Y (number of events) given T (person-time) is written as:

• (1)Ln(Y|T) = Ln(T) + X_iβ, where X_iβ = β₀ + β₁x₁ + … + β_px_p and β is a vector of parameters and X_i is a vector of fixed effects.

Liang and Zeger [14] developed a generalized estimating equation (GEE) method for the analysis of repeated data, which is a quasi-likelihood method used for modeling binary or discrete data. The GEE is a variance-corrected approach that requires the specification of a working correlation to derive the robust estimator of variance.

2.1.2. Extended Cox models

We examined three models that were extensions [2,15] of the Cox regression model [16]: counting process model (Anderson-Gill model or AG) [17], conditional model A (Prentice-Williams-Peterson counting process model or PWP-CP) [18] and conditional model B (Prentice-Williams-Peterson gap time model or PWP-GT) [18]. We calculated the robust sandwich variance estimators for standard errors of coefficients [19], which do not require specification of the correlation matrix. The three formulas below follow the general form of a Cox regression model where:

• λ_ik(t) represents the hazard function for the kth event of the ith subject at time t,

• λ₀ represents the common baseline hazard for all events,

• λ_0k represents the event-specific baseline hazard for the kth event, and

• X_ikβ represents the covariate vector (p fixed effects) for the ith subject with respect to the kth event where X_ik is the covariate matrix.

• (2)Counting process model (AG): λ_ik(t) = λ₀(t)e^X_ikβ
• (3)Conditional model A (PWP-CP): λ_ik(t) = λ_0k(t)e^X_ikβ
• (4)Conditional model B (PWP-GT): λ_ik(t) = λ_0k(t – t_k−1)e^X_ikβ

The counting process model (AG) is a simple extension of the Cox model where a subject contributes to the risk set for an event as long as s/he is under observation at the time the event occurs and shares the same baseline hazards function. In the conditional models (PWP), a subject is assumed not to be at risk for a subsequent event until a current event has terminated. There are two variations of PWP that depend on how the starting point of the risk interval is set. The conditional model A is similar to the counting process model but stratified by event. The conditional model B is similar to the conditional model A but assumes all events start at the time of study entry.

2.1.3. Frailty models

(5 and 6) λ_i(t) = λ₀(t)e^X_iβ+Z_iω, where X_i and Z_i are the covariate matrices and ω is a vector of unknown random effects that describe excess risk or frailty [2]. The distribution of p(ω) may be either log-Gamma or Gaussian, corresponding, respectively, to the Gamma or Gaussian frailty model. The frailty or the random effect varies across subjects but is constant over time within subject. Like the counting process model, the baseline hazard function for the frailty models does not vary by event; but the coefficient estimates of treatment effect from the frailty models may differ from those of the general Cox model or its extension if there is a meaningful contribution of the random term.

2.2 Data Example

We used data from the Precipitating Events Project (PEP), a longitudinal study of 754 community-living persons, who were aged 70 years or older and nondisabled in four essential ADLs (bathing, dressing, transferring, and walking) at baseline. There are two primary reasons why we selected this data set: (1) PEP is designed to observe the recurrent nature of disability; (2) we have previously implemented recurrent event models with this data set [10–12]. Complete details about the study design and the assessment of disability, including formal tests of reliability and accuracy, can be found elsewhere [20]. Briefly, after a comprehensive home-based assessment, subjects were interviewed monthly over the phone to ascertain disability using standard questions. For each of the four essential ADLs, we asked, “At the present time, do you need help from another person to (complete the task)?” Bathing disability was defined as the inability to wash and dry one’s whole body without personal assistance. Other disability was defined as the inability to dress, transfer from a chair, or walk inside the house. For this analysis, we require that the disability (both bathing and other) persist for at least two consecutive months, that is, a single month of disability was not considered as an outcome as justified in an early report [21]. We examined the occurrence of disability over a period of 72 months. During the follow-up period, 213 (28.2%) participants died after a median follow up of 40 months, and 32 (4.2%) dropped out of the study after a median follow-up of 21 months. Participants who died had more episodes of both bathing disability (p<0.001) and other disability (p<0.001) as compared with those did not die during the follow-up period.

2.3 Data Structures

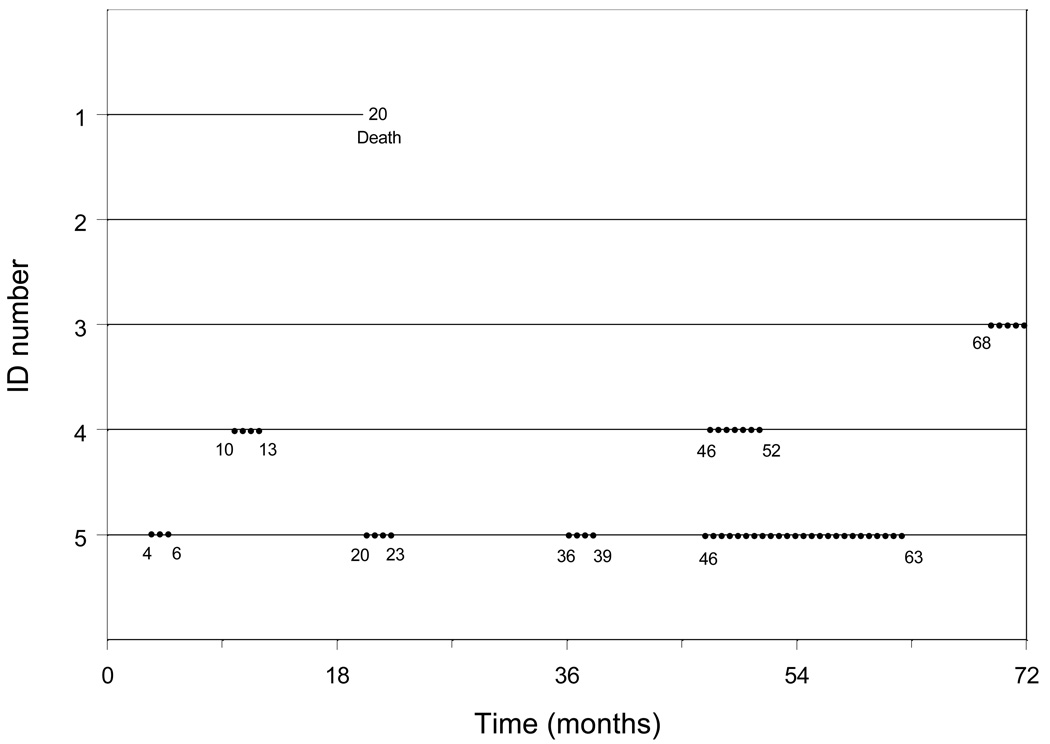
We define duration as the time between the start and end of a disability episode. An episode (event) of disability had to be preceded and followed by a time period with no disability except in the case of death and at the end of the 72-month follow-up period. Figure 1 provides information on five hypothetical study subjects (more complete details are provided in Appendix A). Subject 1 died after 20 months of follow-up without having a disability event, while subject 2 was censored at the end of follow-up (72 months) without having an event. Subject 3 had one event at 68 months. Subject 4 had two events at months 10 and 46 with durations of 4 months and 7 months, respectively. Subject 5 had four events at months 4, 20, 36, and 46. The corresponding durations were 3, 4, 4, and 18 months.

Fig. 1.

Disability data over the period of 72 months for five hypothetical subjects.

Dots denote episodes of disability; the values indicate the starting and ending months of each episode.

Appendix A.

Complete disability data over the period of 72 months for five hypothetical study subjects in the illustrative dataset

PTID	Follow-up period from month 1 to month 24
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	D	.	.	.
2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0	0	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0
5	0	0	0	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	0
PTID, subject identification number; 0, no disability; 1, disability; D, death.

continued
PTID	Follow-up period from month 25 to month 48
	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48
1	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.
2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1
5	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	0	0	0	0	0	0	1	1	1

continued
PTID	Follow-up period from month 49 to month 72
	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72
1	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.
2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1
4	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0

The data structures presented in Table 1 are based on the counting process data structure frame [4,22,23]. The idea is to divide the follow-up period into intervals based on disability episodes. The data are organized as one record per subject per event. The data structure for the counting process model consists of the first four columns in Table 1. A subject with multiple events is considered as multiple subjects for analytic purposes. For example, subject 5 in Table 1 is considered as five subjects: the first begins follow-up at time 0 and has an event at 4 months; the second has delayed entry at 7 months and is followed until an event occurs at 20 months; the third has delayed entry at 24 months and is followed until an event occurs at 36 months; the fourth has delayed entry at 40 months and is followed until an event occurs at 46 months; and the fifth subject has delayed entry at 64 months and is followed through 72 months without having an event. Because the counting process model does not consider the order of the events, it does not use the ‘interval’ column.

Table 1.

Data structures for modeling repeated time-to-event outcomes

PTID	Start	End	Event	Interval	Time	PrevEvent	Female
1	0	20	0	1	20	0	0
2	0	72	0	1	72	0	0
3	0	68	1	1	68	0	0
4	0	10	1	1	10	0	1
4	14	46	1	2	32	1	1
4	53	72	0	3	19	2	1
5	0	4	1	1	4	0	1
5	7	20	1	2	13	1	1
5	24	36	1	3	12	2	1
5	40	46	1	4	6	3	1
5	64	72	0	5	8	4	1

Column headings are defined as follows:

PTID, study subject identification number.

Start, the start time of the interval (in months).

End, the time (in months) at which the event occurs or the time of censoring (death, drop-out, or the end of study).

Event, the occurrence of disability event (yes=1, no=0).

Interval, the order of the events, which is used only for the conditional models.

Time, the number of months at risk that is calculated from the columns ‘Start’ and ‘End’

PrevEvent, the number of previous events.

Female, women=1, men=0.

In the conditional models, a subject is assumed not to be at risk for a subsequent event until the current event has terminated. In other words, one cannot be at risk for the second event without having experienced and completed the first event. The data structure for conditional model A is similar to that of the counting process model except that the fifth column in Table 1 is also used to identify the event interval. Conditional model B also uses time since the previous event (similar to model A) but the clock is reset to zero after each event interval. The data structure for conditional model B uses the first five columns of Table 1 but replaces ‘start’ with zero and ‘end’ with ‘time’ (see SAS and S_PLUS codes in Appendix B).

Appendix B.

SAS and S_PLUS codes [32,33] for modeling repeated and first time-to-event outcomes. Variables are in bold font and are defined in the footnote blow (see the data structures in Table 1).

	SAS code	S_PLUS code
GEE Poisson model	proc genmod data=dataname; class ptid; model event=female / dist=p offset=myoffset; repeated subject=ptid; run; (myoffset = log(time)).	glm(event ~ offset(log(time)) + female, data = dataname, corstr = “exch”, family=poisson) (For GEE Poisson model, please see ‘gee’ function in R at http://www.r-project.org/)
Extension of Cox model
Counting process	proc phreg data=dataname covs(aggregate) covm; model (start end)*event(0)=female / ties=exact; id ptid; run;	coxph(surv(start, end, event) ~ female + cluster(ptid), data=dataname)
Conditional model A	proc phreg data=dataname covs(aggregate) covm; model (start end)*event(0)=female/ ties=exact; strata interval; id ptid; run;	coxph(surv(start, end, event) ~ female + strata(interval), + cluster(ptid), data=dataname)
Conditional model B	proc phreg data=dataname covs(aggregate) covm; model (start end)*event(0)=female/ ties=exact; strata interval; id ptid; run; (start=0, end=time)	coxph(surv(start, end, event) ~ female + strata(interval), + cluster(ptid), data=dataname) (start=0, end=time)
Conditional model B (simple codes)	proc phreg data=dataname covs(aggregate) covm; model time*event(0)=female/ ties=exact; strata interval; id ptid; run;	coxph(surv(time, event) ~ female + strata(interval), + cluster(ptid), data=dataname)
Frailty model
Gamma	(please see SAS procedure NLMIXED of SAS/STAT at ‘http://support.sas.com/onlinedoc/913/docMainpage.jsp’)	coxph(surv(start, end, event) ~ female + frailty(ptid), data=dataname)
Gaussian	(please see SAS procedure NLMIXED of SAS/STAT at ‘http://support.sas.com/onlinedoc/913/docMainpage.jsp’)	coxph(Surv(start, end, event) ~ female + frailty(ptid, dist=“gauss”), data=dataname)
First event
Poisson model	proc genmod data=dataname; where interval=1; model event=female / dist=p offset=myoffset; run; (myoffset = log(time)).	glm(event ~ offset(log(time)) + female, data = dataname, corstr = “exch”, family=poisson)
Cox model	proc phreg data=dataname; where interval=1; model (start end)*event(0)= female/ ties=exact; run;	coxph(surv(start, end, event) ~ female + cluster(ptid), data=dataname)
Gamma frailty model	(please see SAS procedure NLMIXED of SAS/STAT at ‘http://support.sas.com/onlinedoc/913/docMainpage.jsp’)	coxph(surv(start, end, event) ~ female + frailty(ptid), data=dataname)
Gaussian frailty model	(please see SAS procedure NLMIXED of SAS/STAT at ‘http://support.sas.com/onlinedoc/913/docMainpage.jsp’)	coxph(Surv(start, end, event) ~ female + frailty(ptid, dist=“gauss”), data=dataname)

Dataname, name of the data set.

PTID, study subject identification number.

Start, the start time of the interval (in months).

End, the time (in months) at which the event occurs or the time of censoring (death, drop-out, or the end of study).

Event, the occurrence of disability event (yes=1, no=0).

Interval, the order of the events.

Time, the number of months at risk that is calculated from the columns ‘Start’ and ‘End’.

MMSE, the Mini-Mental State Examination²⁷, which was measured every 18 months in the PEP study, is a brief cognitive test with possible scores ranging from 0 (worse) to 30 (best).

Female, women=1, men=0.

2.4 Incidence Rate of Repeated Events

The incidence rate (density function), i.e., the number of events per 1000 person-months, can be easily calculated from Table 1 as follows $\frac{{\displaystyle \sum _{k=1}^n{\mathit{\text{event}}}_{ij}}}{{\displaystyle \sum _{k=1}^n{\mathit{\text{time}}}_{ij}}}\times 1000$ where: event_ij is the event status (1 or 0) for the ith subject in the jth interval; time_ij is the time at risk for the ith subject in the jth interval; and n is the number of subjects. The 95% confidence intervals (CIs) were calculated by bootstrapping samples with replacement, using the entire cohort. One thousand samples were created, and the 2.5th and 97.5th percentiles were used to form the CIs.

2.5 Relative Risk

We used the relative risks (RRs) to assess the effect of gender (women vs. men) on the development of disability. The RRs were calculated from the incidence rates (the incidence rate among women divided by the incidence rate among men) or were estimated by exponentiating the coefficients from the models as described above. The 95% CIs for the RRs based on the incidence rates were calculated by bootstrapping 1000 samples with replacement. The 95% CIs for the RRs based on the models were derived from robust variances.

2.6 Counting Process Model (AG) with Time-varying Covariates

As an illustration we ran a full counting process Cox model with time-varying covariates. We chose the counting process model because of its broader application in medicine and its greater suitability to disability data. The data structure with time-varying variable is listed in the Appendix. The covariates selected based on our previous publications [10–12, 21] were age in year at baseline, non-Hispanic white (vs. other races), education (years), living alone (vs. living with others), number of the nine chronic conditions (hypertension, myocardial infarction, congestive heart failure, stroke, diabetes mellitus, arthritis, hip fracture, chronic lung disease, and cancer), cognitive impairment (a score less than 24 on the Folstein Mini-Mental State Examination (MMSE)) [24], slow gait (< 10 seconds to walk back and forth over a 10-ft [3-meter] course as quickly as possible)[25] and depression symptoms (a scored 16 or higher on the CES-D)[26]. For comparison, we ran two separate models without and with the number of previous disability episodes.

3. Results

Table 2 provides information on the number, duration, and incidence of bathing disability and other disability for all subjects and by gender. About 60% of subjects did not develop an episode of bathing disability over the follow-up period, about 20% had only one episode, and 5% had 4 or more episodes. Similar results were found for other disability. As compared with men, women had more episodes of both bathing disability and other disability (both p<0.001, Chi-Square test).

Table 2.

Episodes of bathing and other disability by gender

	All (N=754)	Women (N=487)	Men (N=267)
Episodes of bathing disability per person, n (%)
0	443 (58.8)	270 (55.4)	173 (64.8)
1	159 (21.1)	100 (20.5)	59 (22.1)
2	72 (9.5)	52 (10.7)	20 (7.5)
3	42 (5.6)	32 (6.6)	10 (3.7)
≥4	38 (5.0)	33 (6.8)	5 (1.9)
Total no. of episodes	631	479	152
Duration of episode, mean (median)	8.8 (4.0)	9.1 (4.0)	7.7 (3.0)
Incidence rate (95% CI)	15.7 (13.6–17.9)	18.5 (15.7–21.5)	10.6 (8.3–13.0)
Episodes of other disability* per person, n (%)
0	466 (61.8)	295 (60.6)	171 (64.0)
1	143 (19.0)	86 (17.7)	57 (21.3)
2	66 (8.8)	46 (9.4)	20 (7.5)
3	41 (5.4)	28 (5.7)	13 (4.9)
≥4	38 (5.0)	32 (6.6)	6 (2.2)
Total no. of episodes	626	450	176
Duration of episode, mean (median)	6.5 (3.0)	6.8 (3.0)	5.7 (3.0)
Incidence rate (95% CI)	15.0 (13.1–17.2)	16.5 (14.0–19.6)	12.2 (9.2–15.6)

^*Includes disability in walking, dressing, or transferring.

Among all participants, the incidence rates for bathing disability and other disability were comparable (Table 2). As compared with men, women had higher incidence rates of both bathing disability and other disability, although the difference between women and men was not statistically significant for other disability based on the 95% CI. The RRs for gender (women vs. men) based on the incidence rates were 1.74 (1.33–2.27) for bathing disability and 1.36 (0.99–1.90) for other disability.

Table 3 provides the estimates for the effect of gender on the development of disability (unadjusted or adjusted for the number of previous events). The GEE Poisson and counting process models generated very similar results. After adjustment for the number of previous events (column ‘PrevEvent’ in Table 1) in the GEE Poisson and counting process models, the effect of gender on other disability did not change but was reduced for bathing disability.

Table 3.

Effect of gender (women vs. men) on disability estimated from various models

	Bathing disability (RR and 95% CI) *	Other disability (RR and 95% CI)*
GEE Poisson model	1.74 (1.32–2.29)	1.36 (1.00–1.85)
GEE Poisson model**	1.38 (1.06–1.79)	1.42 (1.12–1.81)
Extended Cox model
Counting process	1.74 (1.32–2.30)	1.36 (1.00–1.85)
Counting process**	1.37 (1.06–1.77)	1.39 (1.09–1.78)
Conditional model A	1.35 (1.09–1.67)	1.25 (1.01–1.54)
Conditional model B	1.27 (1.05–1.53)	1.18 (0.99–1.41)
Frailty model
Gamma	1.87 (1.56–2.24)	1.41 (1.19–1.68)
Gaussian	1.76 (1.47–2.12)	1.37 (1.15–1.64)
First event
Poisson model	1.31 (1.03–1.67)	1.06 (0.83–1.35)
Cox model	1.30 (1.02–1.66)	1.05 (0.82–1.34)
Gamma frailty model	1.30 (1.03–1.66)	1.05 (0.82–1.34)
Gaussian frailty model	1.31 (1.03–1.67)	1.05 (0.82–1.34)

^*Relative risk (95% confidence interval) calculated by exponentiating the coefficients of gender from the models.

^**Adjusted for the number of previous disability episodes; all others are univariate models.

The RRs from the two conditional models were smaller than those from the GEE Poisson and counting process (unadjusted for the number of previous events) models for both bathing disability and other disability (Table 3). The RRs from the two frailty models were similar to those from the GEE Poisson and counting process (unadjusted) models for both bathing disability and other disability (Table 3). This suggests that there may not be a strong random effect in this example that affects the coefficient estimate for gender.

We also estimated the effect of gender on the development of both bathing disability and other disability with the first-event approach, which only modeling time to the first event (Table 3). The RRs from the first-event approach, especially for other disability, were much smaller than those based on the GEE Poisson, the counting process (unadjusted), and the frailty models.

Table 4 listed the results of a full counting process model (AG) with time-varying covariates for both bathing disability and other disability. The effect of gender was no longer significant for bathing disability after fully adjusted for covariates including number of previous disability episodes.

Table 4.

Counting process models (AG) with time-varying covariates

	Bathing disability (RR and 95% CI)*	Other disability (RR and 95% CI)*
Model without number of previous disability episodes
Women (vs. men)	1.25 (1.01–1.55)	1.04 (0.84–1.28)
Age at baseline (years)	1.04 (1.02–1.06)	1.03 (1.02–1.05)
Non-Hispanic white (vs. other races)	1.26 (0.91–1.74)	1.31 (0.93–1.86)
Education (years)	1.01 (0.98–1.05)	1.01 (0.97–1.04)
Living alone**	0.80 (0.66–0.98)	0.77 (0.64–0.93)
Number of chronic conditions**	1.24 (1.16–1.33)	1.16 (1.08–1.25)
Cognitive impairment (MMSE<24)**	1.29 (0.98–1.68)	1.16 (0.91–1.48)
Slow gait**	2.72 (2.21–3.35)	2.75 (2.22–3.42)
Depression symptom**	1.49 (1.24–1.79)	1.47 (1.21–1.80)
Model with number of previous disability episodes
Women (vs. men)	1.15 (0.96–1.39)	1.01 (0.86–1.19)
Age at baseline (years)	1.04 (1.02–1.05)	1.03 (1.01–1.04)
Non-Hispanic white (vs. other races)	1.16 (0.87–1.54)	1.14 (0.87–1.51)
Education (years)	1.01 (0.98–1.04)	1.01 (0.99–1.04)
Living alone**	0.89 (0.75–1.06)	0.84 (0.72–0.97)
Number of chronic conditions**	1.18 (1.10–1.25)	1.13 (1.07–1.19)
Cognitive impairment (MMSE<24) **	1.22 (0.96–1.55)	1.07 (0.89–1.30)
Slow gait**	2.45 (2.01–2.99)	2.29 (1.89–2.77)
Depression symptom**	1.33 (1.14–1.57)	1.32 (1.13–1.54)
Number of previous disability episodes	1.13 (1.09–1.17)	1.18 (1.15–1.21)

^*Relative risk (95% confidence interval) calculated by exponentiating the coefficients.

^**Time-varying covariates whose detailed descriptions are in section 2.6.

4. Discussion

Although rather simple approaches, which examine time to the first event or treat multiple events within subjects as independent, have been commonly used to analyze recurrent event data¹, more sophistical methods have been developed that make use of all available data while accounting for the lack of independence among the recurrent events [2–9]. These models have also been applied in other disciplines and research areas [27–29]. We have demonstrated how to efficiently create the data structures with discontinuous risk intervals for these more sophisticated methods and to interpret the corresponding model results. For these analyses, the duration of the episode must be taken into account and excluded from the risk set. The basic counting process data structure that we have presented is easy to understand and master; and the incidence rates for repeated events can be easily calculated after forming the data structures. This counting process data structure and the corresponding models can easily incorporate multiple variables including those that are time-dependent (Appendix C).

Appendix C.

Data structure with time-dependent variable for GEE Poisson, Cox counting process and frailty models

PTID	Start	End	Event	Time	MMSE	Female
1	0	18	0	18	28	0
1	18	20	0	2	29	0
2	0	17	0	17	12	0
2	17	36	0	19	12	0
2	36	54	0	18	11	0
2	54	72	0	18	5	0
3	0	18	0	18	27	0
3	18	36	0	18	27	0
3	36	54	0	18	20	0
3	54	68	1	14	10	0
4	0	10	1	10	12	1
4	14	18	0	4	12	1
4	18	36	0	18	10	1
4	36	46	1	10	6	1
4	53	54	0	1	7	1
4	54	72	0	18	5	1
5	0	4	1	4	20	1
5	7	18	0	11	20	1
5	18	20	1	2	19	1
5	24	36	1	12	19	1
5	40	46	1	6	15	1
5	64	72	0	8	10	1

Column headings are defined as follows:

PTID, study subject identification number.

Start, the start time of the interval (in months).

End, the time (in months) at which the event occurs or the time of censoring (death, drop-out, or the end of study).

Event, the occurrence of disability event (yes=1, no=0).

Time, the number of months at risk that is calculated from the columns ‘Start’ and ‘End’.

MMSE, the Mini-Mental State Examination [24], which was measured every 18 months in the PEP study, is a brief cognitive test with possible scores ranging from 0 (worse) to 30 (best).

Female, women=1, men=0.

The counting process and GEE Poisson models showed, as expected given the mathematical relationship between the two models [30], consistently similar results for both bathing disability and other disability. The counting process (or AG) model is simple and easy to understand, requires few assumptions, and is comparably robust as the traditional Cox regression model. Based on the results of simulated data, Therneau and colleagues [2,4] have recommended the counting process model because of its efficiency and reliability. The choice between the counting process model and conditional models can depend on several factors, including: (1) the relationship between first event and subsequent events; (2) the set of covariates, especially those that are time-dependent; (3) the number of subjects without any event; and (4) whether an overall effect is of interest. Based on our experience [10–12], the counting process (or AG) model, with careful consideration of covariates, has broader application in epidemiological and medical research if one is interested in the overall effect, such as the treatment effect in a clinical trial, and if there is no clear biological mechanism underlying the relation between the first event and subsequent events. The conditional models assume that a subject is at risk for a subsequent event only if s/he has experienced a previous event. These models could significantly underestimate the overall effect if there is no strong biological relationship between events, especially in a sample that includes a large number of subjects with no event, as illustrated in our example for other disability. However, if there is a strong biological relationship between the first and subsequent events (e.g. an initial viral infection may reduce the risk of a subsequent viral infection because of the development of immunity), and if one is more interested in the separate risk for these events, then conditional models might be considered. We are focusing on the clinical relevance of the models. There are good reviews regarding the mathematical comparison and interpretations of the models [2, 3, 27–29].

Although frailty models generated similar results as GEE Poisson and counting process models in this study, procedures to specify a distribution of frailty, which certainly affects coefficient estimates, have not been published. We did not consider the marginal model (LWL) [31], which is similar to conditional model A because the underlying assumption that a subject is at risk for all events simultaneously was not applicable in our example, and is less likely to be widely applicable in medical research. Furthermore, the model often overestimates the overall effect [6]. Our primary aim was to practically model recurrent events of the same type, which has broader applicability in clinical medicine. When there are situations where multiple events of different types are of interest or multiple events of the same type can occur at the same time, then one should consider more complicated models that may incorporate the nature of both variance-corrected models and frailty/random effects models or consider both the heterogeneity between subjects and event correlation within subject. These topics, however, are beyond the scope of the current paper. Because of space constraints, we could not formally evaluate the effect of informative censoring. We found that participants who died had more episodes of both bathing disability and other disability as compared with those who did not die during the follow-up period. These findings suggest that drop out due to death, which was about 28%, might be informative and, hence, could have affected our results. However, concerns about informative censoring are diminished by the frequency of our assessments, which ensured that disability status was known within a month of death. One way to analyze how drop out due to death could affect the results is to do sensitivity analysis, by assuming that all persons were disabled or nondisabled, respectively, at the time of death. Another way is to model both disability and death simultaneously as we have done in an earlier study [12].

There is increasing evidence that modeling time to the first event is not adequate [2]. Our results indicate that the first event approach may generate biased results. All models with the first event approach showed that there is no association between gender and the development of other disability. However, all the models for multiple events suggested a clear relationship between gender and other disability, although the relation with other disability was weaker than that with bathing disability.

5. Conclusion

In summary, analyzing repeated event times requires accounting for the correlation between multiple events within subjects. Although there are a number of approaches available for analyzing recurrent events, the counting process model, which is a simple extension of the Cox model, is fairly robust and easy to interpret in accordance with the Poisson model and the incidence rate. One can include the previous events as covariates to further correct the dependence between the events within subject if one believes the occurrence of the previous events may influence the occurrence of current events. The counting process model should be the primary choice, especially if one is interested in the overall effect such as the treatment effect in a clinical trial. However, if one strongly believes that there is biological relationship between the first event and subsequent events and if one is more interested in modeling separate risk for specific event, the condition models should be considered. Forming data structures is critical to proper modeling and the duration of an event has to be excluded from the risk set in analyzing multiple failure events with discontinuous risk intervals.