Functional Assessment of the Kidney From Magnetic Resonance and Computed Tomography Renography: Impulse Retention Approach to a Multicompartment Model

Abstract

A three-compartment model is proposed for analyzing magnetic resonance renography (MRR) and computed tomography renography (CTR) data to derive clinically useful parameters such as glomerular filtration rate (GFR) and renal plasma flow (RPF). The model fits the convolution of the measured input and the predefined impulse retention functions to the measured tissue curves. A MRR study of 10 patients showed that relative root mean square errors by the model were significantly lower than errors for a previously reported three-compartmental model (11.6% ± 4.9 vs 15.5% ± 4.1; P < 0.001). GFR estimates correlated well with reference values by ^99mTc-DTPA scintigraphy (correlation coefficient r = 0.82), and for RPF, r = 0.80. Parameter-sensitivity analysis and Monte Carlo simulation indicated that model parameters could be reliably identified. When the model was applied to CTR in five pigs, expected increases in RPF and GFR due to acetylcholine were detected with greater consistency than with the previous model. These results support the reliability and validity of the new model in computing GFR, RPF, and renal mean transit times from MR and CT data.

MR renography (MRR) and computed tomography renography (CTR) are increasingly used for noninvasive measurement of single-kidney function (1–7). These dynamic imaging techniques record the transit of a tracer, such as Gd-DTPA or iodinated contrast agents, from the aorta through the renal system. Tracer activity versus time curves can then be derived for intrarenal regions such as renal cortex, medulla, and collecting system. Design of an appropriate physiologic model is an essential part of accurate quantification of renal function (1,2).

Several models have been proposed to estimate glomerular filtration rate (GFR) from MRR (3–6) and CTR (7). Baumann and Rudin (3) computed the GFR from the medullary uptake of the tracer using the cortical concentration as the input function. Another method (4) used a Patlak-Rutland plot to estimate GFR from the clearance of the tracer from the vascular compartment. This approach used whole-kidney concentration, obviating the need for regional segmentation of the kidneys. Both of these methods ignored the outflow of the tracer, and the results can be biased by improper selection of the “upslope” interval. Annet et al. (5) extended these techniques to account for tracer leaving the nephron space, thus enabling fitting of the model to measured data over a longer time period. All of these models assume instantaneous mixing of tracer within every compartment.

More recently, models have been proposed with the aim of extending physiologic measures beyond GFR. Krier et al. (7) represented the cortex and medulla curves as extended gamma-variate functions with parameters shown to yield renal plasma flow (RPF) and tubular transit times in addition to GFR. GFR and RPF measures were validated against the reference values in pig model using CT renography. Hermoye et al. (8) determined RPF and GFR in rabbits from the cortical impulse response function by numerical deconvolution of renal cortical enhancement curves. The impulse response function exhibited three sequential peaks presumed to reflect the contrast in glomeruli, proximal tubules, and distal tubules. Lee et al. (6) developed a multicompartment model that reflected the functional components of the nephron (such as proximal tubules and loops of Henle) and was the first to incorporate the process of water re-absorption. The model relied on simultaneous fitting of the cortical and medullary concentration versus time curves using a measured aortic input function. Besides RPF and GFR, vascular volume fraction and rates of tubular fluid re-absorption could be calculated. One limitation of the model of Lee et al. is that it assumes instantaneous compartmental mixing, thereby ignoring the time delay involved in the passage of the tracer through the glomerulus, proximal convoluted tubules, and loops of Henle. This assumption could possibly increase the bias and reduce precision in measures of renal function. Of particular concern is the ability to measure small changes in GFR required in pharmacologic challenge studies (e.g., angiotensin-converting-enzyme inhibitors or acetylcholine).

We have extended the multicompartment renal model of Lee et al. by incorporating a transit delay time for every compartment to reflect noninstantaneous mixing. Cortical and medullary retention versus time curves are represented as a convolution of the aortic input function with the model-based IRFs. We performed a parameter-sensitivity analysis and Monte Carlo simulation to verify the identifiability and stability of the model parameters. The model was then applied to patient data previously acquired by MRR and to a CTR study to detect the acetylcholine-induced response in pig kidneys. We hypothesized that, because of more realistic description of kidney physiology, the IRF approach can provide more precise measurements of parameters and better goodness of fit than the model of Lee et al.

THEORY

Plasma filtration and water re-absorption are carried out by the vascular–nephron system, which is composed of intrarenal arteries and veins, glomerulus, proximal tubules, loops of Henle, distal tubules, and collecting ducts. To analyze MRR data, Lee et al. (6) validated a three-compartment renal model (Fig. 1).

FIG. 1.

Schematic diagram of a three-compartment model, derived from Lee et al. (6). The plasma flows from the artery (Ao) into the renal vascular network (A) at a rate RPF (mL/min). From there, a fraction of plasma with tracer is filtered into proximal tubule (P) at the rate GFR (mL/min). The remainder leaves the kidney through the renal vein (downward solid arrow, rate = RPF-GFR). The filtered fluid traverses the loop of Henle (L) and exits the kidney through the ureter. Water free of tracer is reabsorbed from P and L compartments into the peritubular capillaries and vasa recta, respectively, at rates F_P and F_L, denoted by the dashed arrows.

The model can be extended by representing each of the three serial compartments A (renal vascular network), P (proximal tubules), and L (loops of Henle) as a composite of multiple parallel pathways that differ in length and diameter. Even within one path, the transit time of a tracer molecule can be variable due to laminar flow. As a result, it may take different time intervals for the fluid and tracer molecules to traverse a compartment. The distribution of the transit times required for traversal of a compartment is fully characterized using the concept of impulse retention function (IRF; Fig. 2). The IRF, R(t), represents the fraction of injected tracer residing in the compartment at time t after a unit impulse input applied at the entrance to the compartment at time 0 (9). To determine the amount of tracer that remains in the compartment after an actual input, we convolve IRF with the input function.

FIG. 2.

Impulse retention function R(t) represents the fraction of the injected tracer that remains in the compartment at time t after a unit impulse input at time 0. For a multipathway system with a minimum transit time t_i , R(t) = 100% for t ≤ t_i and decays at t > t_i.

In our model, the IRF for compartment i, R_i(t), is given by:

$$R_i(t)=\{\begin{array}{cc}1\hfill & t\le t_i\hfill \\ e^{-k_i(t-t_i)}\hfill & t>t_i\hfill \end{array}.$$ [1]

The parameter t_i is the minimum transit time. Before t_i, 100% of the input is assumed to reside in the compartment (Fig. 2). At later times, a mono-exponential washout with the rate constant k_i is assumed (10).

We also consider a derived parameter, the compartmental mean transit time, MTT_i (11), which represents the area under the IRF curve and, thus, is likely to be more robust than t_i and k_i:

$${\text{MTT}}_i={\displaystyle {\int }_0^{\infty }{R}_i(\tau )d\tau =t_i+1/k_i.}$$ [2]

A second form of IRF must be considered in a multicompartment system. This form, denoted as R^_i(t), describes tracer retention in the compartment i after the unit-impulse input applied at the entry of the entire system at time 0. Using the model in Figure 1 as an example, consider an impulse input at the entry of compartment A. The output of A, which is no longer an impulse function, serves as the input for P, resulting in R^_P(t), a global retention function for P. The retention of tracer in P at any given time can be expressed as the convolution of the input for the entire system and R^_P(t). For compartment A, R_A (t) = R^_A(t), but this is not the case for compartments P and L (see the Appendix for details).

To apply this IRF-based model to clinical MRR or CTR, we extract from the dynamic images three curves: (i) the input function Ao(t), commonly sampled in the abdominal aorta and expressed in units of tracer concentration; (ii) the cortical curve Cx(t) and the medullary curve Med(t), expressed in units of tracer mass integrated over the corresponding volumes, V_Cx and V_Med.

Let R^_Cx and R^_Med denote the IRFs for renal cortex and medulla. Renal cortical and medullary retention, Cx(t) and Med(t), are the convolution of input function and the regional IRFs:

$$\{\begin{array}{l}\text{Cx}=\frac{RPF}{1-Hct}\mathrm{A}o\otimes {\widehat{R}}_{Cx}\\ \text{Med}=\frac{RPF}{1-Hct}\mathrm{A}o\otimes {\widehat{R}}_{Med}\end{array},$$ [3]

where RPF is renal plasma flow, Hct is hematocrit and ⊗ denotes convolution.

Let w_A,Cx denote the fraction of the volume of compartment A that resides in renal cortex, with the remainder, 1-w_A,Cx, located in the medulla. If we assume that the entire compartment P is in the cortex and all of L in the medulla, from Eq. [3] the IRFs for renal cortex and medulla can be written as:

$$\{\begin{array}{cc}{\widehat{R}}_{Cx}=w_{A,Cx}{\widehat{R}}_A+{\widehat{R}}_P\hfill & \hfill \\ {\widehat{R}}_{Med}=(1-w_{A,Cx}){\widehat{R}}_A+{\widehat{R}}_L\hfill & \hfill \end{array}$$ [4]

As shown in the Appendix, our model contains nine parameters: RPF, w_INFA,Cx, GFR, and minimum transit times and washout rate constants for each compartment: t_A, k_A, t_P, k_P, t_L, and k_L. We note that RPF and w_INFA,Cx can be replaced by another pair of independent parameters: cortical plasma flow RPF_Cx = RPF × w_A,Cx (w_A,Cx can thus be termed as cortical flow fraction) and medullary plasma flow RPF_Med = RPF × (1-w_A,Cx). In fitting measured data, the model parameters are derived by minimizing the residual difference between the measured retention curves and the model-constructed ones (right side of Eq. [3]).

METHODS

MRR: Human Subjects

A total of 10 patients (5 female and 5 male patients; ages 38 to 90 years; mean age, 69.8 years ± 16.9; 20 kidneys) with suspected renovascular disease were included for this study. Serum creatinine levels ranged 0.6−3.0 mg/dL. The protocol was approved by the local institutional review board, and written informed consent was obtained from all subjects. All subjects underwent dynamic renal scintigraphy and MRR in the same morning. Immediately before each examination, subjects were asked to drink approximately 300 mL water and to void.

MRR: Reference Values Derived From Renal Scintigraphy

^99mTc-DTPA renal scintigraphy was performed to derive reference values for single-kidney GFR and RPF. Dynamic images (coronal projection, matrix 128 × 128, pixel 4.3 × 4.3 mm) were acquired with a large-field-of-view gamma camera after injection of 10 mCi (370 MBq) ^99mTc-DTPA. Images were collected at 3-s intervals for 1.5 min and then at 60-s intervals for 60 min. Total GFR was derived from plasma clearance of ^99mTc-DTPA computed from two venous blood samples, collected at 1 h and 3 h after contrast injection (12,13). Single-kidney GFR values were determined from the relative uptake of ^99mTc-DTPA by the left and the right kidney at 2–3 min, derived from scintigraphy. RPF was quantified from renal and aortic time-activity curves as the change of renal retention at the time of aortic-curve peak divided by the aortic peak (14–16).

MRR: Imaging Protocol

MR renography was performed on the same morning as scintigraphy (between the two venous blood samplings) after a bolus injection of 4 mL of Gd-DTPA (Magnevist, Berlex Laboratories, Wayne, NJ) followed by a 20-mL saline flush at 2 mL/s. Serial coronal three-dimensional (3D) spoiled GRE images were acquired on a 1.5 Tesla (T) system (Avanto, Siemens Medical Solutions, Erlangen, Germany) using the following parameters: repetition time/ echo time (TR/TE)/flip angle = 2.84 ms/1.05 ms/12°, partition matrix 161 × 256 × 20 interpolated to 256 × 256 × 40, field of view 400 × 400 × 100 mm, voxel size 1.6 × 1.6 × 2.5 mm, parallel imaging acceleration factor of 3, acquisition time 3 s. Before contrast administration, five 3D images were acquired during one 15-s breath-hold, to obtain a reliable precontrast signal for measurement of tissue concentration. Eight seconds after the start of Gd-DTPA injection, ten 3D acquisitions were repeated continuously for 30 s, during which the subject was asked to suspend respiration as long as possible. Twenty-six additional volumes were acquired during separate 3-s breath-holds for at least 10 min thereafter.

MRR: Patient Data Analysis

Semiautomated image registration and segmentation of the 3D MRR data sets were performed to produce aortic, renal cortical, and renal medullary signal intensity versus time curves (17). The signal intensity versus time curves were converted to concentration versus time curves (18). Model parameters were adjusted by the least-squares fitting using Levenberg-Marquardt algorithm (Matlab, MathWorks, Natick, MA) to minimize the residual difference between the model-constructed and the measured cortical and medullary tissue retention curves. In a preliminary study, it was observed that fixing two parameters, t_P at 0 s and t_L at 1/k_L, brought an increase of 1.1% ± 2.6 in root-meansquare (RMS) error, with similarly negligible effects on estimates for the important parameters (GFR decreased by 2.7% ± 3.6; RPF decreased by 0.4% ± 0.9). Hence, curve fitting of seven parameters, instead of nine, was performed: RPF_Cx, RPF_Med, GFR, t_A, k_A, k_P, k_L with the following initial parameter values: RPF_Cx = 100 mL/min, RPF_Med = 30 mL/min, GFR = 30 mL/min, t_A = 6 s, k_A = 0.1 1/s, k_P = 0.04 1/s and k_L = 0.07 1/s. To evaluate the goodness of fit, the relative RMS error (% RMS) was defined as the ratio of root mean square error between data and fitted curves and the average value of data across time samples. From the fitted parameters, MTTs were derived for the compartments (A, P, L) according to Eq. [2] and summed to give the total mean transit time for whole kidney: MTT_K = MTT_A + MTT_P + MTT_L. RPF was computed as the sum of cortical and medullary perfusion, RPF_Cx + RPF_Med, and cortical flow fraction w_A,Cx as RPF_Cx / RPF.

The estimates of GFR and RPF were compared with their reference values derived from scintigraphy and ^99mTc-DTPA plasma clearance using Pearson’s correlation coefficient, linear regression, and Bland-Altman plots. The %RMS of our model fitting and those of a previous model (6) applied to the same patient data were compared using paired Student’s t-test. Based on the model-derived GFR values, the kidney cases can be divided into two groups, those with GFR ≥ 30 mL/min and those with GFR < 30 mL/min. MTT_K estimates of these 2 groups were compared using two-sample Student’s t-test. Similar, t-test comparison was performed for MTT_K measured by the model of Lee et al. for these two groups. In this previous model, the compartmental MTTs were calculated as the ratio of the compartmental volume and flow (11). Statistical significance for the tests was judged at P < 0.05.

CTR: Acetylcholine-Induced Response in Pig Kidney

The proposed model was applied to previously described CTR experiment in which renal perfusion and filtration rates were measured in response to acetylcholine (ACH), a renal vasodilator (7). Five domestic female pigs (body weight 30–70 kg) were anesthetized, intubated, and mechanically ventilated. A tracker catheter was placed above the level of both renal arteries for ACH infusion. A second catheter was placed in the superior vena cava for subsequent injection of iopamidol tracer. Dynamic imaging was performed during respiratory suspension at end-expiration using an electron beam computed tomography (C-150, Imatron, South San Francisco, CA). Two contiguous 8-mm-thick sections were scanned through the hilar regions of both kidneys. The field of view was 260 × 260 mm with matrix 360 × 360, resulting in pixel size of 0.72 × 0.72 mm. Forty consecutive scans were obtained after a bolus injection (0.5 mg/kg over 1–2 s) of iopamidol. The first 20 scans were performed at high temporal resolution (0.6- to 2.5-s intervals) to sample rapid vascular changes, whereas the last 20 scans at 6- to 8-s intervals to follow tubular changes, with total scanning time of 3 min. Fifteen minutes after the baseline study, ACH (4.5 µg kg⁻¹ min⁻¹) was slowly infused for 20 min, after which the second CTR scan was done using the same protocol as the baseline scan. Following the above flow studies and 10 s after an injection of 0.5 mL/kg of iopamidol over 5–6 s, a separate high-resolution structural scan of both kidneys using contiguous 6-mm slices was acquired for measurement of cortical and medullary volumes.

Aortic, cortical, and medullary tracer concentration curves were generated from both sets of dynamic CTR data. Renal cortical and medullary retention versus time curves were then obtained by multiplying the tracer concentrations by the measured volumes. The proposed model was fitted to the baseline and ACH curves. For RPF and GFR, which were anticipated to increase after infusion of ACH, their baseline and after-ACH estimates were compared using paired Student’s t-test (one-tailed). For comparison, the same data were also analyzed using the model of Lee et al. (6).

Parameter-Sensitivity Analysis

Parameter-sensitivity analysis was performed to ensure that the clinically relevant changes in parameter values result in measurable changes in the model-constructed curves. We plotted the relative change (%) in the cortical and medullary retention versus time curves due to 1% change in each parameter. The reference parameter values were taken from fitting two representative kidneys: one healthy (patient no. 4R, GFR = 58.1 mL/min, RPF_Cx = 168.0 mL/min, RPF_Med = 43.1 mL/min, t_A = 8.7 s, k_A = 0.60 1/s, k_P = 0.015 1/s, and k_L = 0.034 1/s) and one dysfunctional kidney (patient no. 8L, GFR = 6.1 mL/min, RPF_Cx = 21.3 mL/min, RPF_Med = 2.9 mL/min, t_A = 7.6 s, k_A = 0.07 1/s, k_P = 0.005 1/s, and k_L = 0.021 1/s). The sensitivity curve reflects the relative influence of a parameter on the model fit at each time point. For good identifiability, the absolute value of its sensitivity function should be large enough, e.g. 0.5% , for multiple data points (19,20).

Monte Carlo Simulation

Monte Carlo simulation was performed to assess how reliable are the model parameters in the presence of data noise. An ideal arterial input function with a high (0.1 s) temporal resolution was generated by fitting a measured aortic curve to the sum of 3 gamma-variate functions (21). The functions represent the first pass and two recirculations of the contrast. The reference cortical and medullary IRFs were constructed from the healthy and dysfunctional kidneys used in the sensitivity analysis. Convolving the aortic curve with the constructed IRFs resulted in reference cortical and medullary retention curves. The ideal aorta, cortex, and medulla curves were then re-sampled at 3-s intervals. Random noise, with zero mean and SD equal to 5% of the mean magnitude of each curve, was repeatedly added to the curve. The model was then used to fit these noisy data. The mean and SD of each parameter estimate were obtained from simulation trials. The coefficient of variation CV = SD/mean, measures the precision (reliability) of the parameter estimation. The bias in the estimation of each parameter was computed by comparing its mean value across trials and the ideal value. For a robust estimation scheme, it is desirable that both the bias and CV be small. Since the calculated CV and bias converge with the number of trials (N_T), in a preliminary study, we have established that N_T = 4000 is sufficient for results to be within ± 3% of the asymptotic value at 95% confidence interval.

RESULTS

Patient Study

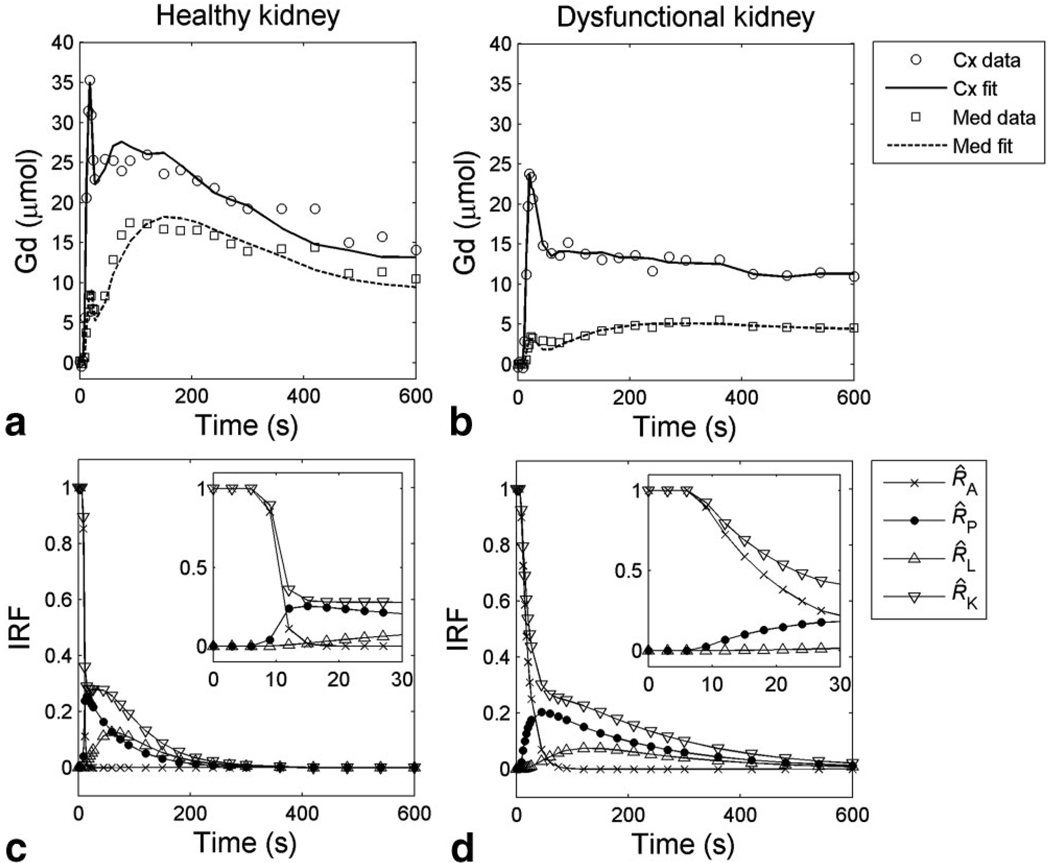
Figure 3 demonstrates the ability of the model to fit the measured cortical and medullary data for two representative kidneys. For the healthy kidney (Fig. 3a), both cortical and medullary retention curves display first a sharp vascular peak, then a second, broader peak that corresponds to tracer accumulation in P or L compartment. The cortical and medullary retention functions of the dysfunctional kidney (Fig. 3b) are lower and have less pronounced tubular peaks. The fitted curves capture the essential features of the data, with %RMS errors 9.7% for the healthy kidney and 8.6% for the dysfunctional kidney. The global retention functions, R^(t), are plotted in Figure 3c,d for the whole kidney and A, P, L compartments. R^(t) demonstrates wider intrinsic heterogeneity and slower tubular transit in the dysfunctional kidney than in the healthy one. Delayed transit times are manifest as differences in calculated mean transit times for all compartments. As shown in Table 1, the overall mean transit time, MTT_K, for the healthy kidney (4R) was 134 s compared with 311 s for the dysfunctional kidney (8L).

FIG. 3.

Representative MRR data and model fits. a,b: Cortical and medullary retention versus time curves and model fits for (a) a healthy kidney (patient no. 4R, GFR = 58.1 mL/min, RPF = 211.1 mL/min), and (b) a dysfunctional kidney (patient no. 8L, GFR = 6.1 mL/min, RPF = 24.2 mL/min). c,d: IRFs for compartments A, P, L, and whole kidney (K) for (c) healthy and (d) dysfunctional kidney. The initial 30 s is magnified in the insets.

Table 1.

Reference GFR and RPF Values (in Bold Font) and Parameter Estimates for 10 Patients. The last two columns (in italic font) list the relative RMS by the current model compared to the model of Lee et al. (6)

Patient no.	Reference GFR (mL/min)	Reference RPF (ml/min)	GFR (mL/min)	RPF (mL/min)	tA (s)	MTTA (s)	MTTP (s)	MTTL (s)	MTTK (s)		%RMS (%)
									Current model	Lee model	Current model	Lee model
1R	42.1	215.8	13.4	137.3	3.3	20.5	174.7	116.0	311	221	9.2	10.0
2R	63.3	202.2	50.4	197.9	6.0	8.7	76.6	64.8	150	124	9.4	12.7
3R	66.2	308.9	42.0	197.8	5.6	8.4	67.4	57.9	134	106	10.2	13.3
4R	80.1	282.9	58.1	211.1	8.7	10.4	65.7	58.3	134	107	9.7	13.0
5R	51.2	143.7	30.4	105.5	6.0	10.3	65.9	57.1	133	101	13.7	19.7
6R	53.4	148.9	34.8	160.5	6.0	9.9	68.8	67.9	147	124	11.5	14.2
7R	39.6	170.8	22.3	82.1	8.5	9.5	70.4	59.0	139	116	8.5	11.9
8R	17.2	49.6	5.7	21.0	6.0	20.4	198.7	69.0	288	451	10.8	18.3
9R	27.6	191.0	24.0	87.2	9.0	14.7	63.2	80.8	159	123	11.0	16.7
10R	43.8	200.2	18.7	95.0	9.0	12.6	122.4	78.6	214	158	9.9	13.4
1L	31.8	233.0	11.6	77.0	20.3	30.5	215.2	136.6	382	263	11.0	12.1
2L	59.5	284.1	59.4	197.5	6.0	9.2	76.2	61.5	147	120	9.5	13.2
3L	75.0	160.3	45.7	186.3	7.2	9.5	70.0	56.2	136	102	10.5	15.5
4L	75.0	222.3	55.2	181.4	6.8	9.4	51.6	55.9	117	94	9.6	12.4
5L	89.4	242.7	23.1	105.6	6.0	11.4	82.1	53.1	147	140	10.6	24.0
6L	18.2	36.3	11.8	51.4	12	21.2	82.1	85.1	188	139	15.7	19.5
7L	49.0	121.8	24.3	92.6	8.1	10.2	75.2	55.8	141	122	7.0	10.7
8L	11.3	61.0	6.1	24.2	7.6	21.5	194.2	95.0	311	419	8.6	16.3
9L	8.7	70.1	5.0	27.4	8.4	23.1	79.2	35.1	137	104	14.8	25.0
10L	3.5	0.0	2.2	6.0	15.0	25.0	71.4	151.5	248	104	30.9	17.7

Parameter values determined by the proposed model for the 20 kidneys are shown in Table 1 along with reference values of GFR and RPF from ^99mTc-DTPA renography and the %RMS errors by fitting. The improved fitting of model to the data is reflected in the lower relative root mean square errors with the new model compared with that reported by Lee (11.6% ± 4.9 vs 15.5% ± 4.1; P < 0.001).

GFR estimates by the proposed model range from 2.2 mL/min to 59.4 mL/min, as compared with reference values of 3.5–89 mL/min. Figure 4a shows a high correlation (r = 0.82; y = 0.61 × −0.3) between the model-derived GFR and reference values. Bland-Altman plot (Fig. 4b) shows that the model-derived GFR underestimates the reference GFR by an average of 18.1 mL/min. There is one outlier (no. 5L) with a drastic difference (89.4 mL/min by nuclear medicine vs 23.1 mL/min by our model). MR images for this case demonstrate the presence of several large cysts which were included in the regions of interest drawn on scintigraphy images but excluded during MRR image processing. After excluding this kidney, the correlation between model and reference GFR improves to r = 0.92, regression line y = 0.75 × −4.7, and an average difference of 15.5 mL/min. For GFR estimates by the model of Lee et al., the correlation with the reference values was r = 0.84, and the error averaged −11.9 mL/min with ± 1.96 SD at −38.9 mL/min and 15.2 mL/min.

FIG. 4.

Comparison of GFR values determined by the proposed model fitting (GFR_MR) and those by nuclear medicine (GFR_Nuc). a: Correlation plot: regression line y = 0.61 × −0.3, correlation coefficient r = 0.82; the solid line is the identity line, and the dotted line is the linear regression. b: Bland-Altman plot of the same data. The difference averages −18.1 mL/min (solid line) with ± 1.96SD between −46.9 mL/min and 10.8 mL/min (dotted lines).

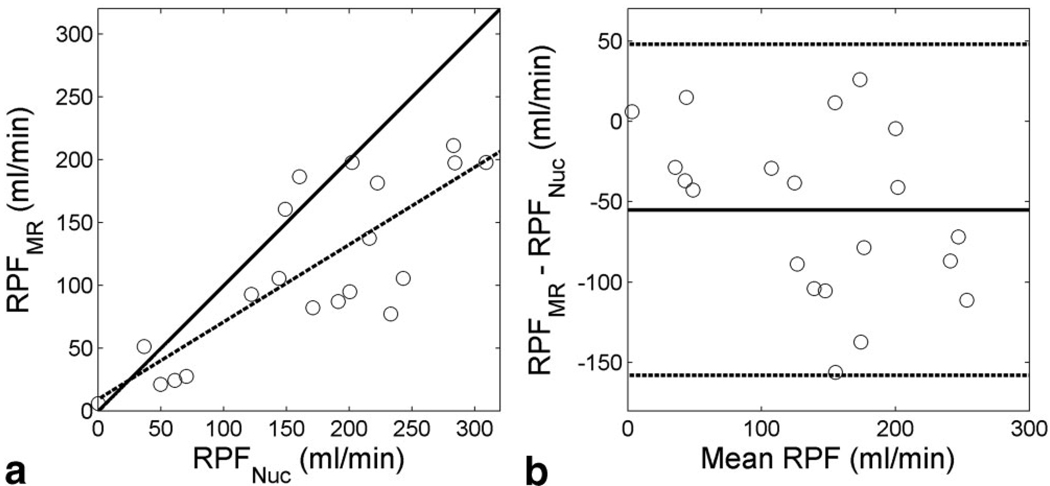
RPF estimates by the proposed model ranges from 6.0 to 211.1 mL/min. As shown in Figure 5, the model-derived RPF correlates well with the reference values, although there was an average difference of 55.0 mL/min between them.

FIG. 5.

Comparison of RPF values determined by the proposed model fitting (RPF_MR) and those by nuclear medicine (RPF_Nuc). a: Correlation plot: regression line y = 0.62 × + 9.3, correlation coefficient r =0.80. The solid line is the identity line, and the dotted line is the linear regression. b: Bland-Altman plot of the same data. The difference averages −55.0 mL/min (solid line) with ± 1.96 SD between −158.1 mL/min and 50.0 mL/min (dotted lines).

Derived from RPF_Cx (88.1 mL/min ± 52.2) and RPF_Med (24.1 mL/min ± 14.3), cortical flow fraction, w_A,Cx, averaged 0.77 ± 0.12. The two IRF parameters for the vascular compartment were t_A = 8.3 s ± 3.7 and k_A = 0.28 1/s ± 0.22. The outflow constants for P and L compartments were k_P = 0.012 1/s ± 0.004 and k_L = 0.030 1/s ± 0.010, both significantly lower than k_A (P < 0.001). The mean transit times MTT_A, MTT_P, and MTT_L were 14.8 s ± 6.6, 98.6 s ± 50.7, and 74.8 s ± 28.8, and their sum, MTT_K, was 188 s ± 77. For three cases with unilateral renal arterial stenosis by MR angiography (no. 9R, 6L, 10L), MTT_A values averaged 20.3 s ± 5.2. For the cases with model-derived GFR larger than 30 mL/min (n = 8), MTT_K were 137 s ± 11, significantly shorter than that (222 s ± 84) for the dysfunctional cases with GFR < 30 mL/min (n = 12) (P < 0.05). MTT_K estimates by the model of Lee et al. did not show significant difference between the 2 groups of kidney cases (P= 0.29).

Acetylcholine-Induced Renal Response

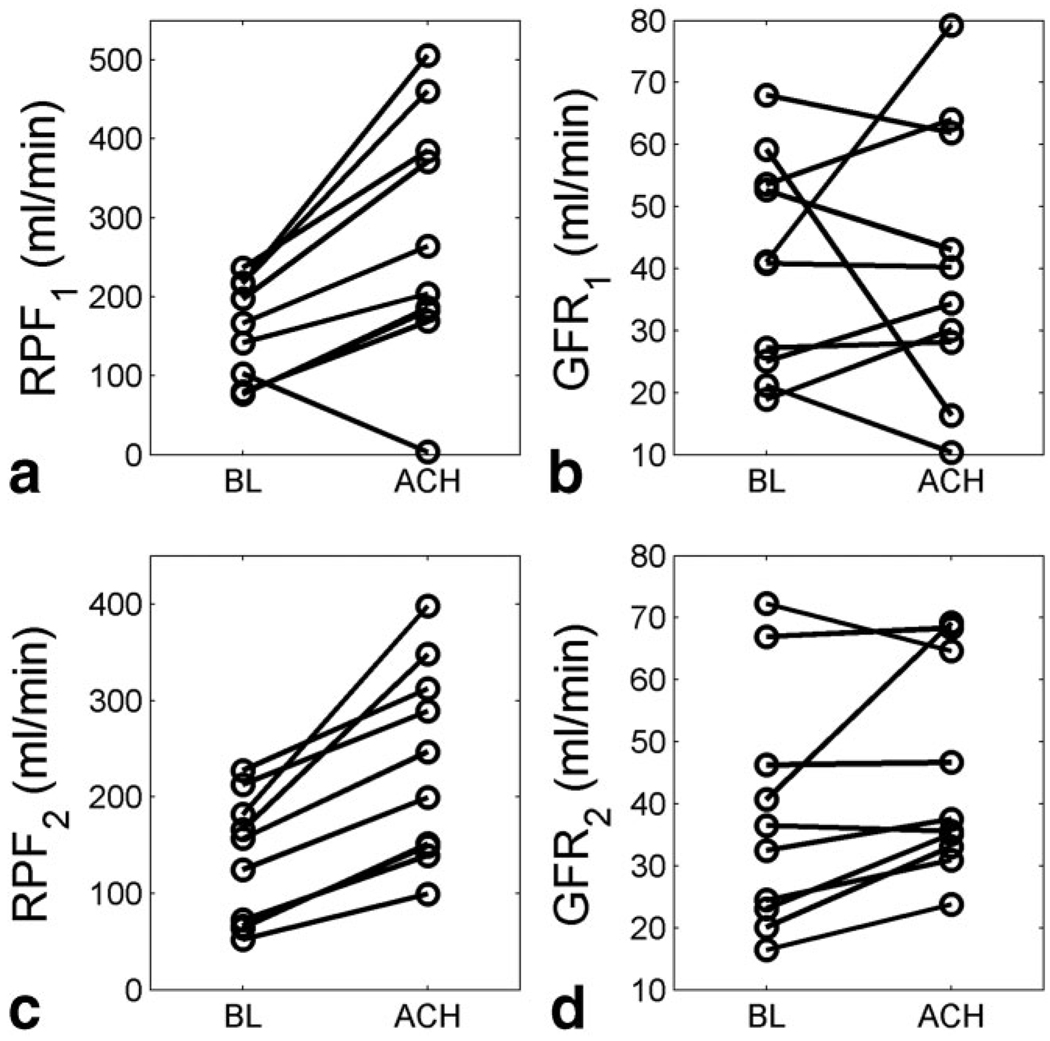
By the proposed model, the fitting of the CTR pig data gave %RMS of 10.3% ± 2.9. An example of CTR data fitting is shown in Figure 6. RPF from the baseline (BL) studies were estimated as 132.5 mL/min ± 62.4, and for the after-ACH studies, were 233.2 mL/min ± 95.6. Paired t-test indicated that the infusion of acetylcholine led to a significant increase in RPF (P < 0.001, T = 5.93), on average by 86.3% ± 36.9 (Fig. 7c). Similarly, GFR estimates of the ACH study, 44.5 mL/min ± 16.0, were significantly higher than the baseline values, 37.9 mL/min ± 18.2 (P < 0.05, T = 2.11), on average by 26.4% ± 29.7 (Fig. 7d). ACH-RPF as measured with the compartmental model of Lee et al. (6) was significantly higher than BL-RPF (273.0 ± 154.8 vs 151.3 ± 64.2 mL/min; P < 0.005, T = 3.64) (Fig. 7a), but this model failed to detect GFR response (40.8 ± 21.9 vs 40.8 ± 17.3 mL/min, P = 0.499, T = 0.0017; Fig. 7b).

FIG. 6.

Representative CTR pig data and model fits. HU, Hounsfield units.

FIG. 7.

Acetylcholine (ACH) -induced renal response in pigs measured using CTR. a,b: RPF₁ and GFR₁ as measured by the model of Lee et al ACH-RPF was significantly higher than baseline RPF (P < 0.005; T = 3.64); there was no significant increase in GFR (P = 0.499; T = 0.0017). c,d: RPF₂ and GFR₂ by the proposed model showed significant increase after ACH (RPF: P < 0.001, T = 5.93; GFR: P < 0.05; T = 2.11).

Parameter-Sensitivity Analysis

The sensitivity analysis (Fig. 8) demonstrates that, for both healthy and dysfunctional kidneys, the initial portions of both cortex and medulla curves are sensitive to their respective RPFs (RPF_Cx, RPF_Med). High (1%) sensitivity of RPFs is maintained from t = 3–5 s, which corresponds to the arrival of tracer in renal vascular space, for approximately 10–15 s and decreases below 0.5% at approximately t = 60 s. This finding indicates that under our experimental conditions, RPF_Cx and RPF_Med (and thus RPF) are mainly determined from the initial 30–60 s. At approximately t = 20 s, the sensitivity function for t_A displays a sharp peak with a height of approximately 2% for the healthy kidney, and a relatively broad peak with a height of 0.3% for the dysfunctional one. The sensitivity to k_A is lower, with a maximum below 0.2% for the healthy kidney and below 0.5% for the dysfunctional one.

FIG. 8.

The sensitivity functions of cortical and medullary retention versus time curves for 1% change in each of the fitted parameters (GFR, RPF_Cx, RPF_Med, t_A, k_A, k_P, k_L). The y-axis is the relative change in the retention curves. The sensitivity of the cortex is shown in a and b; the medulla in c and d; the healthy kidney is used in a and c; the dysfunctional kidney in b and d.

The sensitivity to GFR is relatively high and stable for cortex (~0.7% at t = 60 s) and even better (0.8%) for medulla. The sensitivity of cortex for k_P increases to approximately −0.8% from ~200 s for the healthy kidney and 400 s for the dysfunctional one. The sensitivity of medulla for k_P is 1%. From t = 60–80 s, the sensitivity of medullary curve to k_L increases and remains at approximtely −1% after t = 200–300 s.

Monte Carlo Simulation

Monte Carlo simulation (Table 2) shows that GFR, RPF_Cx, k_P, and k_L can be recovered reliably, with CV range of 1.0–3.7% and minimal bias of 0.0%–3.4%. The CV and bias of RPF are low, with 2.8% and 2.4% for the healthy case, and 2.9% and 0.8% for the dysfunctional case. We observed a relatively high bias (overestimation by the model) in RPF_Med, 10.9% for the healthy case and 6.9% for the dysfunctional one, which does not affect the precision of total RPF. CVs of t_A and k_A are relatively high (7.0%– 42.9%), indicating that these fitted parameters are less stable than other parameters. However, MTT_A, which is derived from t_A and k_A, can be estimated with a CV of 3.7% and a bias of 4.8% for the healthy case, and a CV of 4.1% and a bias of 1.9% for the dysfunctional case. Overall, Monte Carlo simulation shows that the proposed model can reliably identify GFR, RPF, MTT_A, k_P, and k_L from renal tissue retention curves.

Table 2.

Results of the Monte Carlo Simulation

		GFR (mL/min)	RPFCx (mL/min)	RPFMed (mL/min)	tA (s)	kA (1/s)	kP (1/s)	kL (1/s)	MTTA (s)	RPF (mL/min)
	True value	58.1	168.0	43.1	8.7	0.6	0.015	0.034	10.4	211.1
Healthy	Estimates	58.3 ± 0.6	167.7 ± 5.2	38.4 ± 1.0	8.9 ± 0.6	1.26 ± 0.54	0.015 ± 0.001	0.034 ± 0.001	9.9 ± 0.4	206.1 ± 5.7
	(CV, bias)	(1.0, 3.4)	(3.1, 0.2)	(2.6, 10.9)	(7.0, 2.3)	(42.9, 110.0)	(1.3, 0.0)	(1.2, 0.0)	(3.7, 4.8)	(2.8, 2.4)
	True value	6.1	21.3	2.9	7.6	0.07	0.005	0.021	21.5	24.2
Dysfunctional	Estimates	6.1 ± 0.1	21.3 ± 0.6	2.7 ± 0.1	7.6 ± 2.3	0.07 ± 0.01	0.005 ± 0.001	0.021 ± 0.001	21.9 ± 0.9	24.0 ± 0.7
	(CV, bias)	(2.0, 0.0)	(3.0, 0.0)	(4.0, 6.9)	(15.5, 0.0)	(7.7, 0.0)	(2.8, 0.0)	(3.7, 0.0)	(4.1, 1.9)	(2.9, 0.8)

For every parameter, mean, SD, CV (%) and bias (%) of the estimates are shown after subjecting data to Nt = 4000 trials containing random 5% noise.

DISCUSSION

A three-compartment model with seven free parameters can be applied to MRR and CTR data and allows renal curves to be modeled more realistically than a previous model (6) by introducing minimum transit times. Fitting MRR patient cases across a broad range of renal function (reference GFR 3.5–89.0 mL/min, RPF 0.0–308.9 mL/min) gave satisfactory goodness of fit. Several clinically useful parameters such as GFR, RPF, and vascular MTT, can be identified reliably. Furthermore, a proposed model fitting of CTR data successfully detected the anticipated increase in RPF and GFR in response to acetylcholine in the pig kidneys, suggesting that this model is independent of the modality, the indicator used, or the species.

Noninvasive measurement of single-kidney function is important for the diagnosis of a variety of renal diseases, and directs appropriate therapy. For analyzing the dynamic images acquired by MRR or CTR, several renal models have been proposed. Although some simple models, such as the Patlak plot, are able to measure GFR reliably, they can not provide information on renal tubular functions (4,5,22). Some other models do not eliminate the dependence of the identified renal parameters on aortic input function (7). The proposed model consists of three compartments: vascular, proximal tubules, and distal tubules, and requires a measured aortic curve as input. Although similar to the multicompartment model by Lee et al. (6), the proposed model offers several advantages. First, the proposed model fitted the MRR patient data well, with% RMS significantly lower than that of the previous model. Second, Monte Carlo simulation showed that, with 5% simulation noise, GFR and RPF could be recovered precisely with CV 1.0–2.9%, which were much lower than those of the previous model, 4.8–10.3% (6). In pig CTR experiments, the anticipated increase in GFR in response to ACH was successfully detected by the proposed model, whereas the previous model failed. Third, whole-kidney MTT measured by the proposed model was shown to be a more reliable parameter than that by the previous model in differentiating dysfunctional kidneys (GFR < 30 mL/min) from the others.

The advantages of the proposed model over the previous model can be attributed to the following new features. First, the proposed model does not assume instantaneous mixing and introduces a minimum transit time in every compartment. The non-negligible transit time of tracer through functional parts of the nephron such as from the glomerular capillary through proximal tubules and loops of Henle enables better fits for the retention functions of compartments such as P and L. Using the aorta as the input function, even the minimum vascular transit time, t_A, was not negligible, averaging 8.3 s ± 3.7. Second, the IRFs of renal cortex and medulla are expressed in explicit multiexponential form (see the appendix), which potentially improves the model reliability as compared with the previous model. Third, unlike the model of Lee et al., the proposed model does not require the knowledge of the relative volume fractions of P and L compartments. This ensures valid fits in kidneys with abnormal tubular volumes (23,24).

We also note that deconvolution, another variant of IRF approach, has been applied for analyzing MRR data (8). However, deconvolution is known to be noise-sensitive because it involves inversion of large matrices. Hermoye et al. (8) showed that numerical deconvolution, despite using a regularized approach, propagated 5% data noise into a CV of 15–30% for parameters such as GFR, renal perfusion and vascular MTT. In the proposed method, deconvolution was avoided by fitting the convolution of the measured input and a predefined IRF to the measured renal retention curves. A similar technique has been successful in simpler models in scintigraphy (16,25).

The sensitivity analysis shows that the proposed model can reliably identify GFR, as cortical and medullary retention curves are sensitive to GFR beyond the first 60 s. Monte Carlo simulations confirmed that GFR can be recovered with high precision and accuracy. For human kidney measured with MRR, the model-fitted GFR agrees with the reference values, and the agreement is comparable to GFR measured with the model of Lee et al. (r = 0.82 vs 0.84 for Lee et al. (6)).

The sensitivity analysis shows that RPF is mainly identified from the data of the initial 30–60 s after the tracer injection. In our study, MR imaging during the initial period was performed using relatively high temporal resolution with the aim of capturing more information about the fast vascular process. Including a minimum transit time for the vascular compartment (estimated as 8.3 s ± 3.7 for our patient study) enables accurate identification of RPF.

The underestimation of GFR and RPF by the proposed model and the model of Lee et al. (6) may be due to (a) neglecting intermediate transcytolemmal water-exchange kinetics when converting Gd-DTPA signal to concentration, (b) the flow effects in aorta (5), (c) overestimation of GFR by scintigraphy (26), and (d) simplification of complex renal system as three compartments. More work is needed to assess if a more comprehensive model can improve accuracy.

The proposed model was also applied to assess response of pig kidneys to the infusion of ACH using CT renography. Using CTR of high temporal resolution, some subtle features in renal retention curves potentially due to ACH can be reliably recorded, and with appropriate model fitting applied to the pre- and post-ACH retention curves, the ACH-induced responses are thus quantified as significant change in some model parameters. A large increase in RPF and a moderate increase in GFR due to the infusion of ACH were previously reported (27–29). In agreement with prior studies, our model detected a significant RPF increase averaging 86.3% ± 36.9 with lower but also significant GFR response (26.4% ± 29.7). This finding confirms improvement in reliability as compared with the compartmental model by Lee et al. (6) that failed to detect GFR changes.

Besides GFR and RPF, several other parameters can be identified with the proposed model. The cortical flow fraction, w_A,Cx averaged 0.77 ± 0.12, in agreement with the value of 0.67 measured in rats using 3D micro-CT (30). Mean vascular transit time derived from t_A can be identified reliably, as shown by the Monte Carlo simulation. The mean vascular transit time was estimated as 14.8 s ± 6.7. These estimates are longer than previous observations from normal cases (6.8 s ± 3.3 by Chaiwatanarat et al. (31), 8.5 s ± 1.6 by Koh et al. (16)). This finding may be due to the renovascular disease present in our subjects. For the tubular compartmental mean transit times, few reference values are available for human kidneys. Our estimates of MTT_K, 188 s ± 77, are in agreement with previous values for nonobstructive kidneys (16,32,33). The whole-kidney MTT has been shown to be useful in diagnosing obstructive uropathy (32) and in differentiating essential and renovascular hypertension with captopril renal scintigraphy (33).

MRR data used in the study were collected using low doses of Gd-DTPA (4 mL or approximately 0.02 mmol/kg). There are several benefits of using low doses of the gadolinium contrast agent. First, with low doses, signal loss that can be associated with concentrated gadolinium chelates (T2^* effect) is avoided. Second, with a standard intravenous injection rate, the low dose of contrast agent can be injected into the body within a shorter time, resulting in a sharper bolus. According to the intrarenal tracer kinetics, a sharp bolus partially decouples compartmental contributions to the tissue retention curves, which presumably helps the estimation of the related intrarenal parameters. Third, recent studies (34,35) showed that gadolinium-containing contrast agents, especially gadodiamide, may lead to nephrogenic systemic fibrosis (NSF) when injected at a high dose to patients with impaired renal function. Use of low doses may reduce the risk of NSF.

There are several limitations of our study. First, some renal compartments (e.g., distal tubules, collecting ducts) are ignored by our model. However, it is known (8) that tracer retention in distal tubule due to unit-impulse input from aorta, R^_D is much lower and more dispersed than R^_P so that its omission should not introduce large error, especially for vascular parameters and GFR. However, the tubular parameters such as k_P, k_L will likely be affected. Second, the measured aortic concentration versus time curve was used as the input function for the renal system. The signal intensity from aorta may be affected by flow-related signal enhancement. The inflow artifact was minimized in our data by using an oblique coronal imaging slab in the plane of aortic flow. Third, our validation studies were limited to 10 MRR subjects with suspected renovascular hypertension and five pigs that underwent CTR before and after ACH infusion. The validity of the proposed model needs to be tested in a broader patient population.

In conclusion, the proposed IRF model appears suitable to estimate important renal parameters such as GFR, RPF, MTT_A, and total renal MTT from MRR and CTR with satisfactory reliability. The additional tubular parameters provided by the model have potential clinical utility in evaluating the tubular function, but their validity need to be further verified.

APPENDIX

Derivation of Renal Cortical and Medullary IRFs

According to the three-compartment kidney model (Fig. 1), the renal cortex contains a part of compartment A and the whole compartment P. Given a unit-impulse input at the entrance of the entire system, the tracer retention versus time curve for renal cortex, R^_Cx can be written as:

$${\widehat{R}}_{Cx}=w_{A,Cx}{\widehat{R}}_A+{\widehat{R}}_P$$ [A1]

in which R^_A and R^_P are tracer retention functions for compartments A and P, and w_A,Cx is the volume fraction of A residing in renal cortex.

As the first compartment in renal system, compartment A receives the unit-impulse input into the system immediately. Hence, R^_A equals R_A as,

$${\widehat{R}}_A=R_A=\{\begin{array}{cc}1\hfill & t\le t_A\hfill \\ e^{-k_A(t-t_A)}\hfill & t>t_A\hfill \end{array}$$ [A2]

The input for compartment P is not a unit impulse, but the output from compartment A, which can be derived based on the mass-conservation principle. The change of tracer retention in a compartment equals the difference of its input and output. Hence, the output function for compartment i, O_i(t) can be written as,

$$O_i(t)=I_i(t)-\frac{d{\widehat{R}}_i}{dt}.$$ [A3]

O_i has unit of mass per unit time. For i = A, I_A(t) = δ(t), and R^_A = R_A. According to Eq. [A3],

$$O_A(t)=\{\begin{array}{cc}0\hfill & t\le t_A\hfill \\ k_A{e}^{-k_A(t-t_A)}\hfill & t>t_A\hfill \end{array}$$ [A4]

Only a fraction of plasma with tracer is filtered into proximal tubules from the glomeruli; the filtration fraction can be expressed as GFR/RPF. Therefore, I_P = (GFR/RPF)O_A. Hence, R^_P can be written as the convolution

$${\widehat{R}}_P=\frac{GFR}{RPF}{O}_A\otimes R_P$$ [A5]

where R_P is defined in Eq. [1]. Substituting R_P and O_A into Eq. [A5], we get

$$\begin{array}{cc}\hfill & \hfill \\ {\widehat{R}}_P\hfill & =\{\begin{array}{cc}0\hfill & t\le t_A\hfill \\ \frac{GFR}{RPF}[1-e^{-k_A(t-t_A)}]\hfill & t_A<t\le t_A+t_P\hfill \\ \frac{GFR}{RPF}[E_1-e^{-k_A(t-t_A)}]\hfill & t>t_A+t_P\hfill \end{array}\hfill \end{array},$$ [A6]

where $E_1=\frac{k_P{e}^{-k_A(t-t_A-t_P)}-k_A{e}^{-k_P(t-t_A-t_P)}}{k_P-k_A}.$

The renal medulla consists of part of compartment A and the whole compartment L. Similar to Eq. [A1], we have

$${\widehat{R}}_{Med}=(1-w_{A,Cx}){\widehat{R}}_A+{\widehat{R}}_L$$ [A7]

in which R^_A is in Eq. [A2], and R^_L is tracer retention in L compartment. The derivation of R^_L requires the output from compartment P (denoted as O_P) as the input for compartment L (I_L). Note that, because Gd-DTPA is not reabsorbed in the proximal tubules, O_P = I_L. With R_L defined in Eq. [1], R^_L can be derived as,

$$\begin{array}{cc}{\widehat{R}}_L=\hfill & O_P\otimes R_L\hfill \\ \hfill & =\{\begin{array}{cc}0\hfill & t\le t_A+t_P\hfill \\ \frac{GFR}{RPF}[1-E_1]\hfill & t_A+t_P<t\le t_A+t_P+t_L\hfill \\ \frac{GFR}{RPF}[E_2-E_1]\hfill & t>t_A+t_P+t_L\hfill \end{array}\hfill \end{array},$$ [A8]

where E₂

$$=\frac{k_P{k}_L{e}^{-k_A(t-t_A-t_P-t_L)}-k_A{k}_L{e}^{-k_P(t-t_A-t_P-t_L)}+k_A{k}_P{e}^{-k_L(t-t_A-t_P-t_L)}}{(k_P-k_A)(k_L-k_A)}.$$