Abstract
Purpose
To compare six methods for calculating the single-kidney glomerular filtration rate (GFR) from T1-weighted magnetic resonance (MR) renography (MRR) against reference radionuclide measurements.
Materials and Methods
In 10 patients, GFR was determined using six published methods: the Baumann-Rudin model (BR), the Patlak-Rutland method (PR), the two-compartment model without bolus dispersion (2C) and with dispersion (2CD), the three-compartment model (3CD), and the distributed parameter model (3C-IRF). Reference single-kidney GFRs were measured by radionuclide renography. The coefficient of variation of GFR (CV) was determined for each method by Monte Carlo analyses for one healthy and one dysfunctional kidney at a noise level (σn) of 2%, 5%, and 10%.
Results
GFR estimates in patients varied from 6% overestimation (BR) to 50% underestimation (PR and 2CD applied to cortical data). Correlations with reference GFRs ranged from R = 0.74 (2CD, cortical data) to R = 0.85 (BR). In simulations, the lowest CV was produced by 3C-IRF in healthy kidney (1.7σn) and by PR in diseased kidney ((2.2–2.4)σn). In both kidneys the highest CV was obtained with 2CD ((5.9–8.2)σn) and with 3CD in diseased kidney (8.9σn at σn = 10%).
Conclusion
GFR estimates depend on the renal model and type of data used. Two- and three-compartment models produce comparable GFR correlations.
Keywords: renal function, glomerular filtration rate, MR renography, tracer kinetics, gadolinium chelates, compartmental modeling
Quantitative dynamic contrast-enhanced T1-weighted magnetic resonance imaging (MRI) of the kidneys, or MR renography (MRR) (1–3), has emerged as a promising radiological measure of renal function. MRR provides high spatial and temporal resolution and can be performed in conjunction with anatomic imaging and angiography (4). Assessment of renal function with MRR is based on visualizing the passage of gadolinium contrast through the kidney and subsequent analysis of the contrast concentration in renal tissues. Determining renal functional parameters from MRR data requires several steps, which include image postprocessing, such as motion correction of dynamic images and segmentation of renal tissues, quantification of contrast concentration from MR signal intensity, and tracer kinetic modeling.
A variety of techniques for deriving the functional parameters from MRR data have been recently published (5–10), including several methods for estimating the glomerular filtration rate (GFR) (11–17) (Table 1). These models represent the kidney as a combination of a vascular and one or more tubular compartments, although the details of these compartments and the required input data vary among models. Simpler methods describe only the inflow of contrast from the renal vasculature into the tubules (11–13), while more advanced models account for both tubular inflow and outflow (14–17). Some models take into account the dispersion of the bolus during its passage from the abdominal aorta into the renal arteries and arterioles (14,16), whereas other models ignore this effect (13,15). While some models require both cortical and medullary enhancement curves (11, 16, 17), others can be applied to either cortical or whole kidney data (13–15). All but one (11) require the aortic enhancement curves as input function.
Table 1.
Tracer Kinetic Renal Models
| Model | Compartments | Input data | No of parameters | ||
|---|---|---|---|---|---|
| No | Vascular | Tubular | |||
| Baumann-Rudin (BR) (11,12) | 1 | ND | I | Cx and Med | 1 |
| Patlak-Rutland (PR) (13–15) | 2 | ND | I | Ao and K (or Cx) | 2 |
| 2C (15) | 2 | ND | IO | Ao and K (or Cx) | 3 |
| 2CD (14) | 2 | D | IO | Ao and K (or Cx) | 5 |
| 3CD (16) | 3 | D | IO | Ao, Cx, and Med | 6 |
| 3C-IRF (17) | 3 | D | I-IO | Ao, Cx, and Med | 7* |
2C and 3C, two- and three-compartment models; IRF, impulse residue function-based model; ND, no dispersion; D, dispersion; I, inflow; IO, inflow and outflow; I-IO, inflow only followed by inflow-outflow; Ao, aorta; Cx, cortex; Med, medulla; K, whole kidney parenchyma.
In 3C-IRF model (17), the number of adjustable parameters was reduced from 9 to 7, by fixing two parameters.
Applied to the analysis of computed tomography (CT) and MR renography data, these methods yield moderate to high correlation with reference GFR measurements and GFR estimates that vary from strong underestimation to strong overestimation (8,11–18). The direct comparison of model performance is difficult because of the discrepancies in acquisition and analysis techniques used by different groups. Annet et al (14), Buckley et al (15), and Sourbron et al (19) compared the Patlak–Rutland method against two-compartment models with tubular outflow; however, more extensive comparison of existing renal models has not been undertaken. The purpose of this study was to compare GFR estimates using six renal models (11–17) applied to the same MRR data against the reference GFR measured by the same-day 99mTc-DTPA renography. Monte Carlo simulations were used to evaluate the reliability of each method in the presence of data noise.
Renal Models
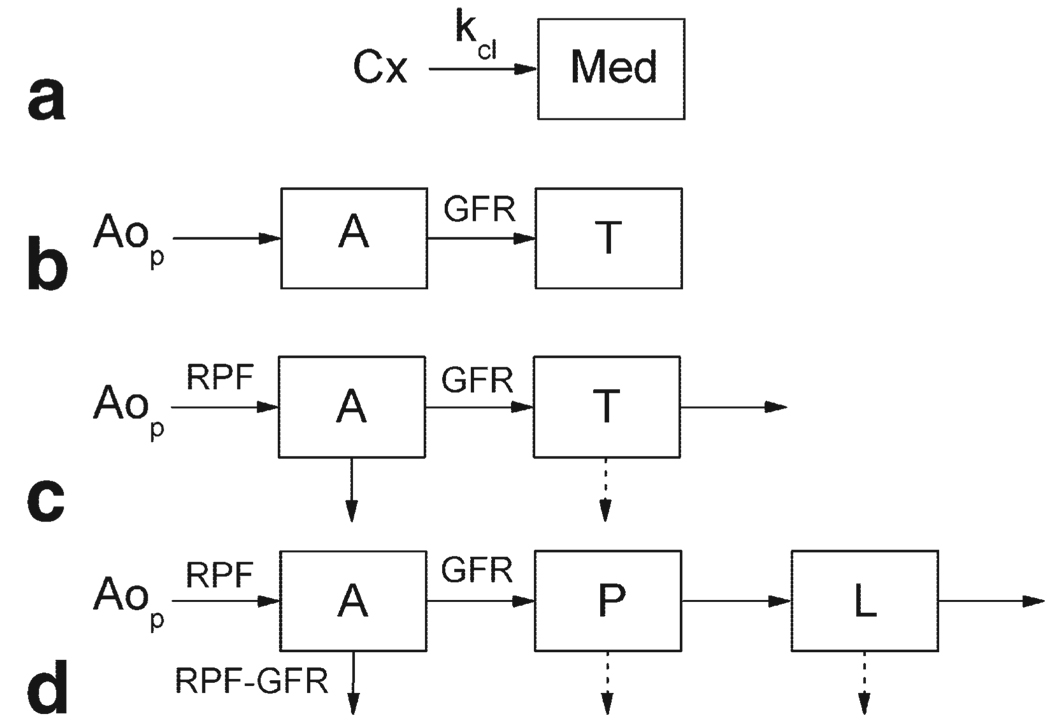
Six methods for calculating GFR from MRR data were studied: the Baumann–Rudin model (BR) (11,12), the Patlak–Rutland method (PR) (13–15,20), a two-compartment model with bolus dispersion (2CD) (14) and without dispersion (2C) (15), a three-compartment model with dispersion (3CD) (16), and a similar model based on impulse retention function (IRF) approach (3C-IRF) (17) (Fig. 1). These models have been developed for analysis of the gadolinium concentration versus time curves measured in renal tissues after an intravenous bolus injection of contrast agent. All models describe the kidney as a combination of a prefiltration (vascular) compartment and one or more postfiltration (tubular) compartment(s). GFR is identified with the flow from the prefiltration to postfiltration compartments. All but the 3C-IRF model assume instantaneous mixing of contrast within each compartment. The leakage of contrast into the interstitial space is neglected, and the venous compartment is also ignored. All concentrations are expressed per unit volume of plasma, unless stated otherwise. Each model is briefly described below and the mathematical details are given in the Appendix.
Figure 1.
Renal models: (a) Baumann-Rudin (BR), (b) Patlak-Rutland (PR), (c) 2C and 2CD, (d) 3CD and 3C-IRF. RPF is renal plasma flow; GFR is glomerular filtration rate. Aop is the contrast concentration in aortic plasma; Cx and Med are the cortical and medullary concentrations; A is the vascular concentration; and T, P, L are the concentrations in all tubules, proximal tubules, and loops of Henle, respectively. In BR (a), kcl is the clearance index related to GFR. In PR (b) and 2C (c), A = Aop. Solid arrows indicate the flow of contrast and dashed arrows show the reabsorption of water in the tubular compartments.
Baumann–Rudin Model
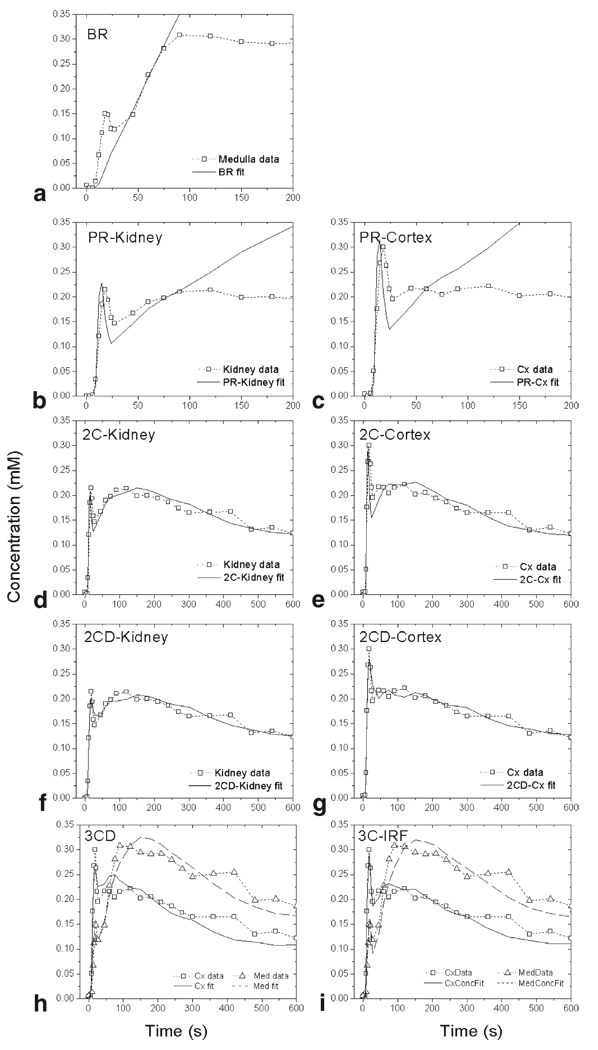
The model proposed by Baumann and Rudin (BR; Fig. 1a) describes the initial inflow of contrast from the cortex, which is identified with the vascular compartment, into the medulla (11,12). The outflow from the medulla is neglected. A single free parameter, the clearance index kcl, defined as the rate constant for unidirectional flow from cortex to medulla, was shown to correlate with GFR (12). An example of BR fit is given in Fig. 2a.
Figure 2.
Model fits for a kidney with radionuclide GFR = 80.1 mL/min: (a) BR, (b) PR-Kidney and (c) PR-Cortex, (d) 2C-Kidney and (e) 2C-Cortex, (f) 2CD-Kidney and (g) 2CD-Cortex, (h) 3CD, (i) 3C-IRF model.
Patlak–Rutland Method
The Patlak–Rutland method (PR) is based on a two-compartment model (Fig. 1b), in which the outflow of contrast from the tubular compartment is neglected (13–15). The dispersion of the bolus in renal vasculature is also ignored, and the vascular concentration is approximated by the plasma concentration in the aorta. The model yields two parameters, vascular volume fraction and GFR. The latter is found as the flow from the vascular to tubular compartment during the tubular uptake.
To ensure the “no-outflow” condition in the renal tubules, the PR method is often applied to the whole-kidney data (13,15,18). However, in animal MR and CT studies, significant correlations with the reference GFRs were obtained only from analyses of the cortical data (8,14). We evaluated both whole-kidney and cortical data fitting (PR-Kidney and PR-Cortex, respectively) (Fig. 2b,c).
Two-Compartment Models With Tubular Outflow
The two-compartment models that account for the outflow of contrast from the renal tubules are valid beyond the tubular uptake interval. Buckley et al (15) analyzed the whole-kidney human data with a two-compartment model (2C) which, similar to the PR model, neglects the bolus dispersion and yields three parameters: vascular volume, GFR, and tubular outflow rate (Fig. 1c). A similar, five-parameter model with bolus dispersion and delay (2CD) had been previously proposed by Annet et al (14) and applied to cortical data in rabbits (Fig. 1c). We considered both implementations of the two-compartment models and applied them to the whole-kidney and cortical data (2C-Kidney, 2C-Cortex, 2CD-Kidney, and 2CD-Cortex) (Fig. 2d–g).
Three-Compartment Model
The three-compartment model (3CD) proposed by Lee et al (16) describes the cortex and medulla as combinations of three serially connected compartments: vascular compartment, shared by cortex and medulla, proximal tubules, contained only in the cortex, and loops of Henle, contained only in the medulla (Fig. 1d). Simultaneous fitting of cortical and medullary concentrations yields five parameters including RPF, GFR, cortical and medullary vascular volumes, and water reabsorption fraction in proximal tubules and loops of Henle (Fig. 2h).
Three-Compartment IRF-Based Model
The model of Zhang et al (17) (3C-IRF) has the same structure as the 3CD model, but assumes that due to a distribution of pathways, the contrast takes a minimum transit time to traverse each compartment before emerging at the outlet (Fig. 1d). Until the minimum transit time, each compartment behaves like a no-outflow system and becomes an inflow-outflow system afterwards (Fig. 2i). While the 3C-IRF model includes nine parameters: RPF, GFR, cortical vascular volume fraction, minimum transit times, and outflow constants for each of the three compartments, only six parameters can be reliably identified: RPF, GFR, cortical vascular volume fraction, and mean transit times in three compartments.
MATERIALS AND METHODS
Patients
The study protocol was approved by the Institutional Review Board, and written informed consent was obtained from all subjects. Ten patients (five female, five male, mean age 69.8 years, range 38–90 years), all diagnosed with hypertension and one also with chronic renal failure, were referred for suspected renovascular disease. Serum creatinine levels ranged from 0.6 to 3 mg/dL. All patients underwent Gd-DTPA-enhanced, T1-weighted MRR. Reference GFRs were measured by the same-day radionuclide clearance and gamma camera renography.
Reference GFR Measurements
GFR values were measured using standard 99mTc-DTPA clearance and gamma camera renography methods (21,22). Radionuclide renography was performed 1–3 hours prior to MRR. Patients were manually injected with 10 mCi (370 MBq) of 99mTc-DTPA and 20 mL saline flush. Coronal images with pixel size of 4.3 mm × 4.3 mm were acquired every 3 seconds for the first 1.5 minutes and every 60 seconds afterwards for 1 hour maximum. The total GFR was determined from plasma clearance of 99mTc-DTPA from two blood samples collected 1 hour and 3 hours after the injection. GFR was calculated by multiplying the total GFR by the fractional uptake by each kidney determined from imaging.
MR Imaging
MR imaging was performed at 1.5 T (Avanto; Siemens Medical Solutions, Erlangen, Germany) and included T1-mapping (23) and Gd-DTPA-enhanced T1-weighted low-dose MRR using oblique coronal 3D spoiled gradient echo sequence: TR = 2.84 msec, TE = 1.05 msec, flip angle α = 12°, bandwidth 650 Hz/pixel, field of view 425 × 425 × 100 mm3, interpolated matrix 256 × 256 × 40, parallel imaging acceleration factor of 3, GRAPPA reconstruction with 24 central reference lines, and acquisition time 3 seconds. A bolus of 4 mL of Gd-DTPA (Magnevist; Berlex Laboratories, Wayne, NJ) and a 20-mL saline flush were both injected at a rate of 2 mL/sec with an automated injector (Spectris; Medrad, Indianola, PA). Five precontrast images were acquired to determine the baseline signal. Acquisition was started at 8 seconds after injection and repeated during separate breath-holds every 3 seconds up to 0.5 minutes, every 15 seconds between 0.5 and 1.5 minutes, 30 seconds at 1.5–5 minutes, and 60 seconds at 5–10 minutes.
Image and Data Analysis
Coregistration and segmentation of serial images was performed using a semiautomatic algorithm (24). After motion correction, kidney parenchyma (excluding the collecting system and renal pelvis) was segmented from the surrounding tissue, and afterwards cortex was segmented from medulla. Aortic signal was sampled in the abdominal aorta at the level of renal arteries. For each region, the average signal intensity (SI) was computed at each timepoint.
SI data were converted into gadolinium concentrations using previously validated phantom-based method (5,25). Precontrast parenchymal, cortical, and medullary T1 values required for conversion were determined from T1 maps (23); T1 of 1200 msec was assumed for aortic blood (26).
Nonlinear least squares fitting with Levenberg-Marquardt algorithm was performed in MatLab (Math-Works; Natick, MA). For curve fit models, the match between the fitted curves and data was assessed by the fit residual (root-mean-square (RMS) error) and expressed as percentage of the mean measured concentration. For three-compartment models the residual was calculated with equal weights for cortical and medullary RMS.
The fitted interval for BR model was selected between the trough after the vascular peak and the maximum of the tubular peak in the medullary concentration. To obtain GFR, the BR clearance index kcl was multiplied by the volume of medulla. The PR method was implemented as a nonlinear curve fit (15). A fixed interval between 0 and 120 seconds was selected for fitting the whole-kidney data and 0 to 90 seconds was chosen for fitting the cortical data. To account for bolus arrival into the kidney in models without dispersion, PR and 2C, the arterial input function was shifted forward by 3 seconds, which was the smallest sampling interval in our protocol. In 2CD, bolus delay was adjusted by minimizing the fit residual while shifting the time axis of the aortic curve.
The fit residuals were compared using two-sample paired Wilcoxon signed-rank test. The correlation between the model-derived and reference GFR was characterized by linear regression and Pearson’s correlation coefficient R.
Variability Due to Data Noise
The robustness of the models to data noise was evaluated by Monte Carlo analyses. Two representative experimental MRR datasets were assessed: one from a kidney with a normal reference GFR = 80.1 mL/min and the other from kidney with abnormally low GFR = 18.2 mL/min. Measured aortic curves were used as input functions. Aortic and renal data were perturbed by adding normally distributed noise with zero mean and standard deviation of σn = 2%, 5%, and 10% of the precontrast whole-kidney signal (for PR, 2C, 2CD models) or cortical signal (BR, 3CD, 3C-IRF). The signal curves were then converted into concentration (25) and fitted with each model. The coefficient of variation of GFR (CV(GFR)), or the ratio of the standard deviation to the mean value, was calculated from N = 1000 trials.
RESULTS
GFR Estimates With Six Renal Models
All 20 MRR datasets were analyzed with six renal models. Examples of model fits are shown in Fig. 2 and fit residuals are given in Table 2. The PR method produced the highest residuals that reached 30% over the fitted interval. The inclusion of outflow in 2C decreased the residuals by half (14.9% for 2C-Kidney and 17.5% for 2C-Cortex) and accounting for dispersion resulted in another 2-fold decrease in residual (8.3% for 2CD-Kidney and 9.1% and 2CD-Cortex). For 2C model, the residuals were significantly lower for whole-kidney data than for cortical data (P < 0.0001); however, in PR and 2CD models this difference did not reach significance (P > 0.05). The 3C-IRF model yielded significantly lower residuals than the 3CD model (11.6% vs. 15.5%, P = 0.0006). The residuals did not show any apparent trends in relation to GFR.
Table 2.
Average Fit Residuals Expressed as Percentages of Average Renal Concentration and Median Relative Differences ΔGFR=(GFRMR – GFRNuc)/GFRNuc Between Model-Derived GFRs (GFRMR) and Radionuclide GFRs (GFRNuc)
| Model | Residual (%) | ΔGFR (%) |
|---|---|---|
| BR | — | 6.0 |
| PR-Kidney | 30.3 | −36.4 |
| PR-Cortex | 30.7 | −52.7 |
| 2C-Kidney | 14.9 | −2.5 |
| 2C-Cortex | 17.5 | −26.8 |
| 2CD-Kidney | 8.3 | −17.1 |
| 2CD-Cortex | 9.1 | −51.2 |
| 3CD | 15.5 | −28.3 |
| 3C-IRF | 11.6 | −39.8 |
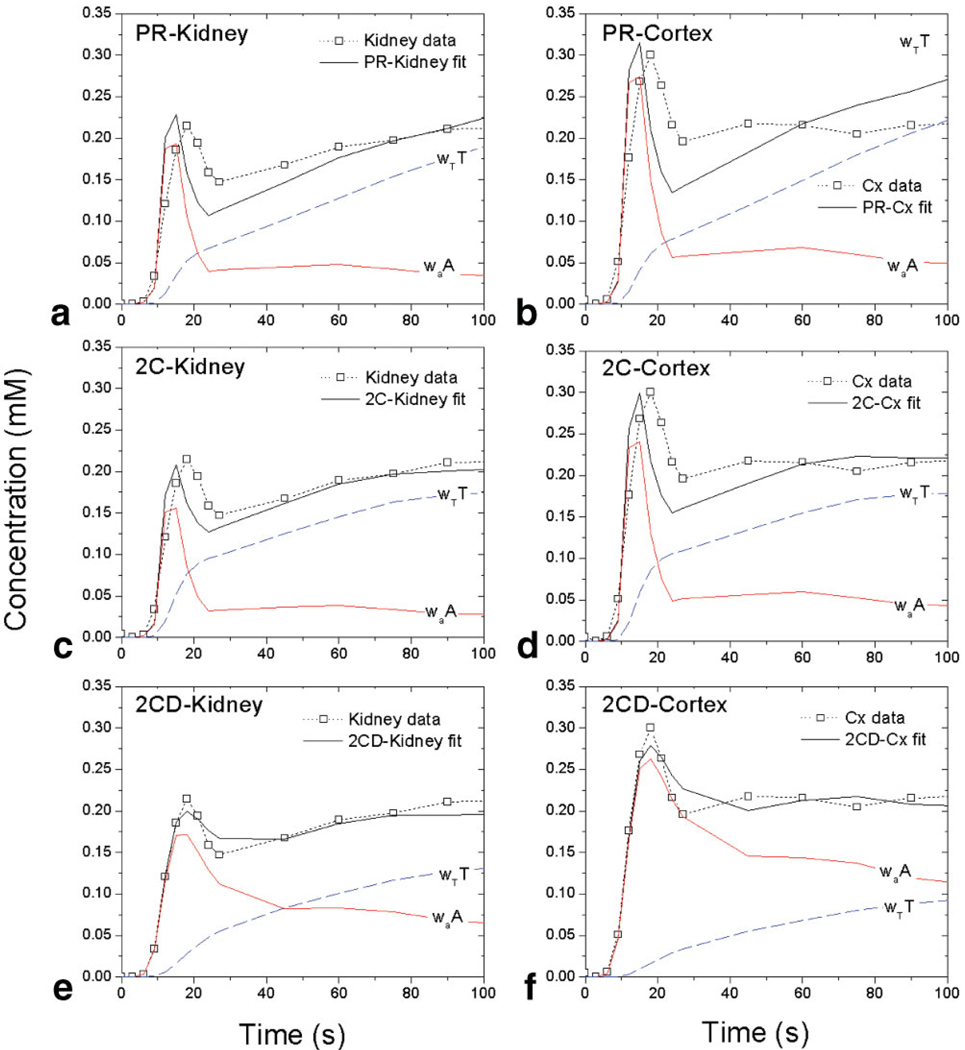
The model-estimated vascular and tubular compartmental contributions are illustrated in detail for two-and three-compartment models (Fig. 3 and Fig. 4, respectively). In models without dispersion (PR, 2C; Fig. 3a,d), the vascular contribution shows a narrow first-pass peak followed by a low washout tail. A considerable part of the renal vascular peak and most of the tubular peak are attributed to the tubular compartment. In 2CD, the vascular contribution is broader and has a higher tail, and the tubular contribution is lower than in 2C. In 2C-Kidney (Fig. 3c), the area under the curve (AUC) of the vascular contribution between 0 and 90 seconds accounts for 26% of the area under the renal concentration curve. In contrast, in 2CD-Kidney (Fig. 3e) the vascular AUC over the same time interval is 57% of the renal AUC. The fits to cortical data (Fig. 3d, f) show larger vascular and smaller tubular contributions than the corresponding whole-kidney fits (Fig. 3c,e).
Figure 3.
Two-compartment model fits (solid black lines) and vascular (solid red lines) and tubular (dashed blue lines) compartmental contributions for MRR data (symbols and dotted lines) of a kidney with radionuclide GFR = 80.1 mL/min: (a) PR-Kidney, (b) PR-Cortex, (c) 2C-Kidney, (d) 2C-Cortex, (e) 2CD-Kidney, (f) 2CD-Cortex. The vascular and tubular contributions are labeled waA and wTT, respectively, where A and T are concentrations and wa and wT are volume fractions (see Appendix). In no-dispersion models (PR and 2C, top and middle row), waA is narrower and lower and wTT is higher than in 2CD (bottom row).
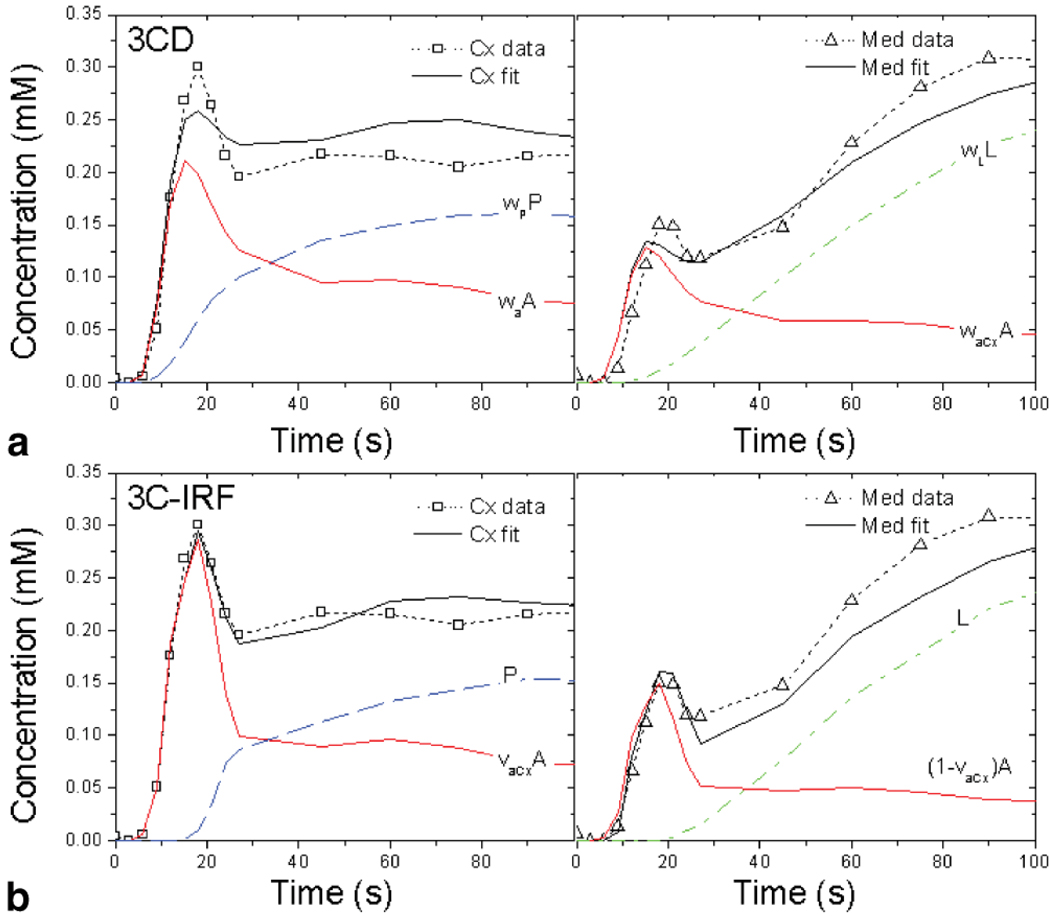
Figure 4.
Three-compartment model fits (solid black lines) with vascular (solid red line) and tubular (dashed blue and dash-dotted green lines) compartmental contributions for MRR data (symbols and dotted lines) of kidney with reference GFR = 80.1 mL/min. (a) 3CD and (b) 3C-IRF fits. Cortical fits are shown in the left panels and medullary fits in the right panels. In 3CD (a) the model-derived vascular contribution is labeled waA and the contributions of proximal tubules and loops of Henle are labeled wPP and wLL, where A, P, and L are concentrations in vasculature, proximal tubules, and loops, respectively, and wa, wP, and wL are the corresponding volume fractions. In 3C-IRF the concentrations are denoted the same way, but the volume fraction νaCx is defined as the fraction of vascular compartment residing in the cortex (see Appendix).
The 3CD model fits (Fig. 4a) are similar to the 2CD fits, with broadened vascular contributions. In 3C-IRF (Fig. 4b), the shapes of the vascular and tubular contributions appear to be intermediate between models with and without dispersion.
Radionuclide single-kidney GFRs ranged from 3.5–89.4 mL/min. The magnitude of model-derived GFRs varied among models from weak overestimation to strong underestimation (Table 2). The highest GFRs were obtained from the BR model, which produced the median 6% overestimation. All other models underestimated GFR by different amounts that varied from 2.5% for 2CD-Kidney to over 50% for the PR-Cortex and 2CD-Cortex models. GFRs derived using two-compartment models applied to cortical data were significantly lower than GFRs obtained using the same methods from whole-kidney data (P < 0.0001 in PR, 2C, and 2CD models). The correlations between the model-derived and radionuclide GFRs (Fig. 5) were significant in all cases (P < 0.0004) with the correlation coefficients ranging from R = 0.74 for 2CD-Cx to R = 0.85 for the BR model. There was one outlier kidney (radionuclide GFR = 89.4 mL/min).
Figure 5.
Model-derived GFR versus nuclear medicine GFR: (a) BR, (b) PR-Kidney, (c) PR-Cortex, (d) 2C-Kidney, (e) 2C-Cortex, (f) 2CD-Kidney, (g) 2CD-Cortex, (h) 3CD, (i) 3C-IRF models. Linear regressions are indicated by dotted lines and equations; identity lines are shown by solid lines.
Variability Due to Data Noise
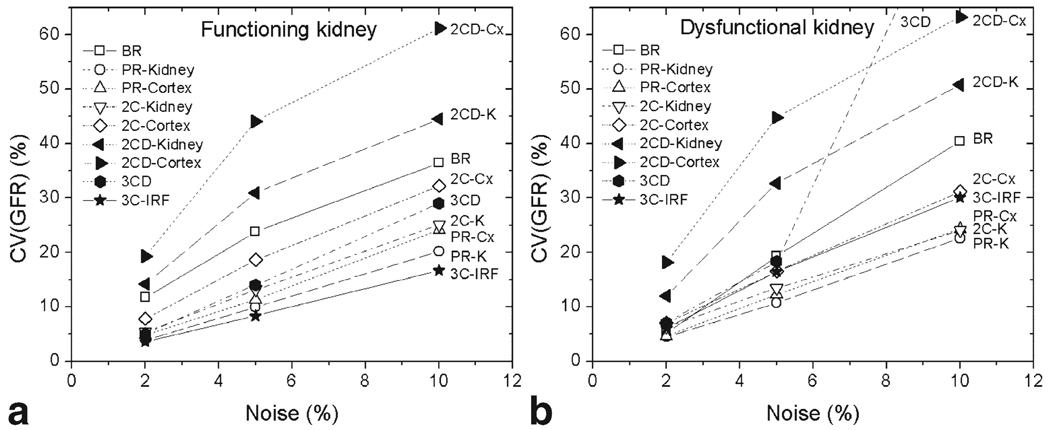
CV(GFR) estimated by Monte Carlo analyses in representative healthy and diseased kidneys shows that all models amplified data noise to different degrees (Fig. 6). Two-compartment models with two to three parameters (PR and 2C) amplified noise by factors of 2.0 to 3.6 in both functional and dysfunctional kidneys. The BR model produced higher errors (3.5–4.8σn). The 2CD model amplified noise more strongly, with CV(GFR) reaching on average 5.9σn (2CD-Kidney) and 8.2σn (2CD-Cortex) in both kidneys. The 3CD model yielded 2.7 times noise amplification in healthy kidney, but performed poorly in diseased kidney at 10% noise (CV = 8.9σn). In contrast, the 3C-IRF provided the lowest CV(GFR) among all models in healthy kidney (1.7σn) and consistent CV(GFR) values in diseased kidney at all noise levels (3.1σn).
Figure 6.
Coefficient of variation of GFR CV(GFR) at 2%, 5%, and 10% data noise for two kidneys: (a) functioning kidney (GFR = 80.1 mL/min), and (b) dysfunctional kidney (GFR = 18.2 mL/min). The two-compartment models with two or three parameters (PR and 2C) produce lower CV than the five-parameter model (2CD) or BR model. The 3CD model performs well in a normal kidney, yet fails at 10% noise in dysfunctional kidney. In contrast, the 3C-IRF produces the lowest CV(GFR) in healthy kidney and performs comparably with more rigid PR and 2C models in dysfunctional kidney.
DISCUSSION
We studied six models for calculating GFR from MRR data. As expected, the best fits (or the lowest fit residuals) were obtained using the most flexible model, the seven-parameter 3C-IRF model, and the worst fits (the highest residuals) were produced by the PR method and 2C model. Cortical data fitted with the 2C model tended to result in lower quality fits than whole-kidney data. We believe that this occurs because of the difficulty of describing the cortical curve, which contains features of the proximal and distal tubules, using a single tubular compartment in addition to vascular compartment. In the whole-kidney curve, all tubular features are lumped together and enveloped by the loop of Henle/collecting ducts peak in medulla, and thus a two-compartment description is more suitable.
The correlations between the model-derived and reference GFRs ranged from R = 0.74 (2CD-Cortex) to R = 0.85 (BR) and were not necessarily better for more so-phisticated models. The magnitude of GFR estimates varied greatly across models, even when the same data were used (eg, among PR-Kidney, 2C-Kidney, and 2CD-Kidney), and were lower for cortical data than for whole-kidney data.
Large variations of GFRs obtained from the same data are likely caused by the models. We believe that the primary source of these variations is the uncertainty in determination of the relative magnitude of the vascular and tubular contributions to the net renal concentration. This uncertainty is caused by the unfeasibility of direct measurements of arterial contrast concentration immediately at the filtration site, ie, at the glomerulus. Instead, the arterial concentration is usually measured in the abdominal aorta and the concentration in the renal vasculature is inferred from it using model-specific assumptions. We noticed that accounting for bolus dispersion results in lower GFRs. For example, the 2CD model produced significantly lower GFRs than the 2C model. When dispersion is ignored, as in 2C (Fig. 3c,d), the vascular contribution is equated to the aortic concentration scaled by the vascular volume fraction (see Appendix) and the amplitude of this contribution is set almost exclusively by the height of the renal vascular peak. As a result, the vascular volume fraction is forced to be quite low to scale the aortic first-pass peak down to a less prominent renal vascular peak. Consequently, the vascular contribution has a narrow peak followed by a low tail, and the rest of the renal curve is attributed to the tubular component. In contrast, in models with dispersion, such as in 2CD and 3CD (Fig. 3e,f and Fig. 4a,b) the vascular volume fraction adjusts both the height and width of the vascular contribution to match the renal vascular peak. This results in a vascular curve with a broadened first-pass peak and higher tail and a lower tubular component than in the no-dispersion case. Larger vascular and lower tubular contributions in models with dispersion suggest that GFR obtained using these models is expected to be lower than in no-dispersion models applied to the same data.
The description of the tubular compartment also affects GFR magnitude. Annet et al (14) first noticed that the PR method underestimated GFR relative to 2CD model and attributed this underestimation to neglecting the tubular outflow in the PR method. Similar observations were reported by Buckley et al for 2C (15) and by Sourbron et al for the 2CD model (19). Our results showed a similar trend: PR GFRs were lower than both 2C and 2CD GFRs applied to the same data. This observation is supported by the model solutions (see Appendix). In PR, GFR is multiplied by a monotonically increasing integral of the aortic concentration and is forced to be lower to compensate for this increase. In a similar 2C model, the aortic integral is reduced by the outflow term, and when applied to the same data this model yields higher GFR than PR method (Eq. [A4] vs. Eq. [A5]).
Another problem in the no-outflow models arises from the uncertainty of defining the uptake interval, the choice of which strongly affects GFR values. Hackstein et al (20) observed that PR GFR decreased considerably as the fitted interval was shifted toward later times. We observed the same trend in our PR analyses; however, we did not attempt to optimize the fitted PR interval. Hackstein et al (20) obtained the highest correlations of PR GFR with the reference from fitting 40–110 seconds interval after the aortic rise; the same interval was used by Sourbron et al (19). We implemented the PR method as a nonlinear curve fit, following Buckley et al (15), to take advantage of the initial portions of the kidney data that are discarded in the graphical implementation, and used the interval from 0 seconds to 120 seconds in whole-kidney data and 0 seconds to 90 seconds in cortical data. In healthy kidneys, as the ones studied in Refs. (19) and (20), the interval of 40–110 seconds corresponds mainly to the medullary uptake. In dysfunctional kidneys, as in some of our patients, this interval may be extended or shifted toward later times. We suspect that even with the fitted interval ending at 110–120 seconds the “no-outflow” condition is not fulfilled, especially in the cortical data, where the outflow from proximal tubules probably occurs before 60–75 seconds. The initial, “inflow-only” part of the tubular contribution is buried under the vascular peak, and the PR method relies on the exposed slope of the renal concentration instead. The methods proposed by Krier et al (27), Daghini et al (8), and Hermoye et al (5), which use gamma variate functions to estimate the upslope of the proximal tubular enhancement, may offer more accurate modeling.
For our experimental protocol, the PR method may be suboptimal. Lower temporal resolution of our breath-holding protocol results in few data points measured during the uptake interval. Furthermore, it has been shown that the PR results improve at higher injected doses of contrast (13), whereas in our study a low dose (4 mL, or ≍ 0.025 mmol/kg) of Gd-DTPA was used. Lower amounts of contrast minimize the signal loss associated with concentrated contrast (T2* effects) and may also be advantageous given the association of high doses of gadolinium chelates with the development of the nephrogenic systemic fibrosis (NSF) (28,29).
Using cortical data for GFR estimates seems to be preferable because glomerular filtration occurs pre-dominantly in the cortex. However, in addition to vascular and proximal tubular features, cortical enhancement also contains overlapping features of the distal tubules, which the contrast enters after passing through the medulla, and therefore the cortical concentration may not be a more direct indicator of filtration. In PR analysis of animal data, only cortical data yielded significant GFR correlations with the reference, but not the whole-kidney data (8,14). In human studies, whole-kidney enhancement is often used (13,15,18). In our study, both cortical and whole-kidney data provided similar correlations, but “cortical” GFRs were lower than GFRs obtained from whole-kidney data. We believe that this occurs because the inclusion of the medulla into whole-kidney enhancement alters the relative contributions of vascular and tubular components in favor of the tubules. In the whole-kidney curve the vascular peak is lower (because of lower vascular content in medulla) and the tubular peak is higher (mainly due to contrast in loops of Henle and collecting ducts) than in the cortical curve (Fig. 2d,e), which results in higher whole-kidney GFRs. Higher tubular enhancement in medulla also accounts for the higher GFR values obtained with the BR model.
Both three-compartment models provide good curve fits, especially the 3C-IRF model. GFR correlations provided by the three-compartment models were on par with the two-compartment models.
Among the studied models, the BR model is the only one that does not require measurements of the aortic input function (AIF). The use of the cortical data as an approximation of AIF is both a flaw and an advantage. Unlike other models, the BR model does not compute GFR directly, but only an index kcl that is proportional to GFR. The BR model ignores both the nonvascular contributions to cortical concentration and the vascular contribution in the medulla. This may be an appropriate assumption in animal studies (20), but not in human kidneys (Fig. 2). On the other hand, the BR model eliminates potentially large errors associated with AIF measurements, which can be unreliable due to flow artifacts and inadequate temporal sampling of the arterial peak. For our patient group, the BR model gave a good correlation with the reference GFR values, suggesting that AIF errors may be the dominant sources of GFR errors.
For methods that require arterial input function, variations of the aortic enhancement have a strong impact on the modeling results and are a major source of uncertainty in GFR. Aortic signal, particularly in a tortuous aorta, can be distorted by the inflow artifacts. In our study, this problem was reduced by imaging in coronal direction and sampling the abdominal aorta signal at the level of the renal arteries. Other methods of reducing errors in AIF, such as postprocessing corrections and population-averaged AIF curves, may also be helpful (30).
The stability of computed parameters in the presence of noise is always a concern, especially for more complex models. Our simulations show that curve-fit models with three or fewer parameters (PR and 2C) amplify noise by a factor of 2 to 3.6. In contrast, the five-parameter 2CD model amplifies noise 6–8-fold. The 3CD produces CV(GFR) = 89.0% in diseased kidney at 10% noise, which agrees with our routine experience with this model. On the other hand, due to its ability to capture correctly both the uptake and the washout portions of the data, the more complex 3C-IRF model amplifies noise by a factor of 1.7 in a healthy kidney and 3-fold in a dysfunctional kidney.
The models considered here share assumptions that may be sources of error. The distribution of parameters was considered homogeneous within a given tissue. In all but the 3C-IRF model, complete instantaneous mixing within each compartment was assumed, and concentration gradients in the renal tubules were ignored. Each kidney region (parenchyma, cortex, and medulla) was described by no more than two compartments (vascular and tubular), which is a gross oversimplification. The distribution of contrast agent over the interstitial space was also neglected. In normal kidneys, interstitial space occupies only about 10% of parenchymal volume; however, in patients with inflammatory renal disease, the interstitial space may be increased, and ignoring it was shown to cause overestimation of GFR (18). In the patients studied here, renal volumes were not obviously increased (154 ± 48 mL), and therefore neglecting the interstitial space was justified in the first approximation.
Our study suffered from the following limitations. First, the number of studied cases was small. Second, we explored only a single type of MRR protocol, and the influence of acquisition details on GFR results should be studied further. Third, we considered the PR method with an empirically selected fitted interval which was the same for all cases and not systematically optimized. Fourth, we used a fixed bolus delay in the no-dispersion models. Although this delay does not change the trends in GFR results, the best method for treating the bolus delay needs to be determined. Additionally, our Monte Carlo simulations were performed for only two sets of representative kidney parameters and did not explore a range of renal states. Finally, the reference radionuclide GFRs are imperfect and may contain about 10% errors (31).
Many other methods have been used to estimate renal functional parameters from MR and CT renography. Some investigators have used fast T1-measurements and phase contrast flow quantification to determine GFR from renal extraction fraction of gadolinium chelates (9,10); however, these methods require high spatial and temporal resolution. Other approaches, such as reported by Boss et al (6), are based on gadolinium clearance principles, similar to radionuclide clearance methods, and fit the exponential washout of gadobutrol contrast from the renal cortex. Unlike the models studied here, this method relies on estimates of extracellular fluid volume determined from patient height and weight to convert the washout constant into the total GFR.
In conclusion, compartmental models provide means for calculating GFR and other parameters from MRR data. The choice of renal model is determined by the parameters that need to be measured, availability and accuracy of tissue segmentation, quality of dynamic images, and patient’s kidney condition. It is important to know the biases and error propagation associated with each model, as these properties may strongly influence the resulting parameters. The three-parameter two-compartment model without dispersion enables calculation of GFR when either whole-kidney or cortical data are available. The four-parameter (with dispersion only) or five-parameter (with dispersion and delay) versions of this model also provide RPF, but should be used with caution, preferably in experiments with high signal-to-noise ratio (SNR), because of their lower stability. The three-compartment models require more involved image processing (24,32), but provide GFR, RPF, and other parameters and can characterize cortex and medulla separately. The distributed-parameter 3C-IRF model offers excellent curve fits and parameter stability and GFR estimates on par with other models. Reliable determination of aortic signal is crucial for models that require arterial input functions.
APPENDIX
Baumann–Rudin Model (11,12)
The clearance index kcl related to GFR is found from cortical and medullary concentrations, Cx(t) and Med(t):
| [A1] |
Patlak–Rutland Model (13–15)
The contrast concentration in renal tissue K(t) is found as a combination of vascular and tubular concentrations, A(t) and T(t), respectively:
| [A2] |
where wa = Va/V, wt = Vt/V, and Va and Vt are the compartmental volumes and V is the renal tissue volume. A(t) is equated to the plasma concentration in aorta, Aop(t), which can be found from whole-blood concentration Ao(t) and hematocrit Hct:
| [A3] |
During uptake of contrast by renal tubules, the PR model solution can be fitted to the renal data with two free parameters, vascular volume fraction wa and GFR:
| [A4] |
In traditional implementation of the PR method, Eq. [A4] is divided by Aop(t), and GFR and wa are found, respectively, from the slope and intercept of linear regression between y = K(t)/Aop(t) and normalized time .
2C and 2CD models (14,15)
In 2C and 2CD models, the kidney concentration K(t) has the form of Eq. [A2] and the model solution is given by:
| [A5] |
where kout is the tubular outflow rate constant. In the 2C model, A(t) = Aop(t). In the 2CD model, it is expressed as follows:
| [A6] |
where RPF is the renal plasma flow. 2C has three free parameters: wa, GFR, kout; and 2CD has an additional parameter, RPF. Fitted bolus delay τ was introduced in 2CD according to the original implementation of the model (14): Aop(t) → Aop(t − τ).
3C model (16)
Cortical and medullary concentrations, Cx(t) and Med(t), are expressed as combinations of concentrations in vasculature, A, proximal tubules, P, and loops of Henle L:
| [A7a] |
| [A7b] |
| [A8a] |
| [A8b] |
| [A8c] |
where waCx = VaCx/VCx, waMed = VaMed/VMed, and VaCx and VaMed are cortical and medullary vascular volumes, VCx and VMed are tissue volumes, and fp and fl are water reabsorption fractions in P and L. The volume fractions of P in the cortex, wp, and L in medulla, wl were found to be fully correlated with fp and fl and were fixed at constant values: wp = Vp/VCx = 0.3, wl = Vl/VMed = 0.5. The model yields six parameters: RPF, GFR, waCx, waMed, fp, and fl. Only a sum fp + fl can be reliably identified, thus reducing the number of parameters to five.
3C-IRF model (17)
The cortical and medullary contrast residues (in mass units), MCx and MMed are expressed through compartmental IRFs, R^A, R^P, and R^L, convolved with aortic concentration Aop(t):
| [A9a] |
| [A9b] |
Here υaCx is the fraction of vascular compartment in the cortex. “Inherited” IRFs (i = A, P, L) correspond to an ideal delta-function bolus applied to the entrance of the whole system and can be found as follows:
| [A10a] |
| [A10b] |
| [A10c] |
| [A10d] |
| [A10e] |
where Ri is a “native” IRF in response to an ideal bolus applied at the entrance of i-th compartment, ti is the minimum transit time (minTT), and Ii and Oi are the compartmental input and output fluxes of contrast (mass per unit time). The input to the first compartment, A, is equal to the ideal bolus applied to the whole system, ie, IA = δ(t). The model yields nine parameters: RPF, GFR, νaCx, minTTs tA, tP, tL, and outflow constants kA, kP, kL. To improve the stability of the model, two parameters were fixed: tP = 0 seconds and tL = 1/kL. Although kA could not be identified reliably, mean transit times MTTA = tA+ 1/kA was shown to be robust.
REFERENCES
- 1.Prasad PV. Functional MRI of the kidney: tools for translational studies of pathophysiology of renal disease. Am J Physiol Renal Physiol. 2006;290:F958–F974. doi: 10.1152/ajprenal.00114.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huang AJ, Lee VS, Rusinek H. Functional renal MR imaging. Magn Reson Imaging Clin N Am. 2004;12:469–486. doi: 10.1016/j.mric.2004.04.001. [DOI] [PubMed] [Google Scholar]
- 3.Michoux N, Vallée J-P, Pechère-Bertschi A, Montet X, Buehler L, Van Beers BE. Analysis of contrast-enhanced MR images to assess renal function. MAGMA. 2006;19:167–179. doi: 10.1007/s10334-006-0045-z. [DOI] [PubMed] [Google Scholar]
- 4.Lee VS, Rusinek H, Noz M, Lee P, Raghavan M, Kramer EL. Dynamic three-dimensional MR renography for the measurement of single kidney function: Initial experience. Radiology. 2003;227:289–294. doi: 10.1148/radiol.2271020383. [DOI] [PubMed] [Google Scholar]
- 5.Hermoye L, Annet L, Lemmerling P, et al. Calculation of the renal perfusion and glomerular filtration rate from the renal impulse response obtained with MRI. Magn Reson Med. 2004;51:1017–1025. doi: 10.1002/mrm.20026. [DOI] [PubMed] [Google Scholar]
- 6.Boss A, Martirosian P, Gehrmann M, et al. Quantitative assessment of glomerular filtration rate with MR gadolinium slope clearance measurements. Radiology. 2007;242:783–790. doi: 10.1148/radiol.2423060209. [DOI] [PubMed] [Google Scholar]
- 7.Michaely HJ, Schoenberg SO, Oesingmann N, et al. Renal artery stenosis: Functional assessment with dynamic MR perfusion measurements—feasibility study. Radiology. 2006;238:586–596. doi: 10.1148/radiol.2382041553. [DOI] [PubMed] [Google Scholar]
- 8.Daghini E, Julliard L, Haas JA, Krier JD, Romero JC, Lerman LO. Comparison of mathematic models of assessment of glomerular filtration rate in electron-beam CT in pigs. Radiology. 2007;242:417–424. doi: 10.1148/radiol.2422052144. [DOI] [PubMed] [Google Scholar]
- 9.Coulam CH, Lee JH, Wedding KL, et al. Noninvasive measurement of extraction fraction and single-kidney glomerular filtration rate with MR imaging in swine with surgically created renal arterial stenosis. Radiology. 2002;223:76–82. doi: 10.1148/radiol.2231010420. [DOI] [PubMed] [Google Scholar]
- 10.Niendorf ER, Grist TM, Lee FT, Jr, Brazy PC, Santyr GE. Rapid in vivo measurement of single-kidney extraction fraction and glomerular filtration rate with MR imaging. Radiology. 1998;206:791–798. doi: 10.1148/radiology.206.3.9494503. [DOI] [PubMed] [Google Scholar]
- 11.Baumann D, Rudin M. Quantitative assessment of rat kidney function by measuring the clearance of the contrast agent Gd(DOTA) using dynamic MRI. Magn Reson Imaging. 2000;18:587–595. doi: 10.1016/s0730-725x(00)00134-x. [DOI] [PubMed] [Google Scholar]
- 12.Laurent D, Poirier K, Wasvary J, Rudin M. Effect of essential hypertension on kidney function as measured in rat by dynamic MRI. Magn Reson Med. 2004;47:127–134. doi: 10.1002/mrm.10034. [DOI] [PubMed] [Google Scholar]
- 13.Hackstein N, Heckrodt J, Rau WS. Measurement of single-kidney glomerular filtration rate using a contrast-enhanced dynamic gradient-echo sequence and the Rutland-Patlak plot technique. J Magn Reson Imaging. 2003;18:714–725. doi: 10.1002/jmri.10410. [DOI] [PubMed] [Google Scholar]
- 14.Annet L, Hermoye L, Peeters F, Jamar F, Dehoux J-P, Van Beers BE. Glomerular filtration rate: assessment with dynamic contrast-enhanced MRI and a cortical-compartment model in the rabbit kidney. J Magn Reson Imaging. 2004;20:843–849. doi: 10.1002/jmri.20173. [DOI] [PubMed] [Google Scholar]
- 15.Buckley DL, Shurrab A, Cheung CM, Jones AP, Mamtora H, Kalra PA. Measurement of single kidney function using dynamic contrast-enhanced MRI: comparison of two models in human subjects. J Magn Reson Imaging. 2006;24:1117–1123. doi: 10.1002/jmri.20699. [DOI] [PubMed] [Google Scholar]
- 16.Lee VS, Rusinek H, Bokacheva L, et al. Renal function measurements from MR renography and a simplified multicompartmental model. Am J Physiol Renal Physiol. 2007;292:F1548–F1559. doi: 10.1152/ajprenal.00347.2006. [DOI] [PubMed] [Google Scholar]
- 17.Zhang JL, Rusinek H, Bokacheva L, et al. Functional assessment of the kidney from MR and CT renography: impulse retention approach to a multi-compartment model. Magn Reson Med. 2008;59:278–288. doi: 10.1002/mrm.21489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hackstein N, Bauer J, Hauck EW, Ludwig M, Kramer H-J, Rau WS. Measuring single-kidney glomerular filtration rate on single-detector helical CT using a two-point Patlak plot technique in patients with increased interstitial space. AJR Am J Roentgenol. 2003;181:147–156. doi: 10.2214/ajr.181.1.1810147. [DOI] [PubMed] [Google Scholar]
- 19.Sourbron SP, Michaely HJ, Reiser MF, Schoenberg SO. MRI-measurement of perfusion and glomerular filtration in the human kidney with a separable compartment model. Invest Radiol. 2008;43:40–48. doi: 10.1097/RLI.0b013e31815597c5. [DOI] [PubMed] [Google Scholar]
- 20.Hackstein N, Kooijman H, Tomaselli S, Rau WS. Glomerular filtration rate measured using the Patlak plot technique and contrast-enhanced dynamic MRI with different amounts of gadolinium-DTPA. J Magn Reson Imaging. 2005;22:406–414. doi: 10.1002/jmri.20401. [DOI] [PubMed] [Google Scholar]
- 21.Rowell KL, Kontzen FN, Stutzman ME, et al. Technical aspects of a new technique for estimating glomerular filtration rate using technetium-99m-DTPA. J Nucl Med Technol. 1986;14:196–198. [Google Scholar]
- 22.Russell CD, Rowell K, Scott JW. Quality control of technetium-99m DTPA: correlation of analytic tests with in vivo protein binding in man. J Nucl Med. 1986;27:560–562. [PubMed] [Google Scholar]
- 23.Bokacheva L, Huang AJ, Chen Q, et al. Single breath-hold T1 measurement using low flip angle TrueFISP. Magn Reson Med. 2006;55:1186–1190. doi: 10.1002/mrm.20845. [DOI] [PubMed] [Google Scholar]
- 24.Rusinek H, Boykov Y, Kaur M, et al. Performance of an automated segmentation algorithm for 3D MR renography. Magn Reson Med. 2007;57:1159–1167. doi: 10.1002/mrm.21240. [DOI] [PubMed] [Google Scholar]
- 25.Bokacheva L, Rusinek H, Chen Q, et al. Quantitative determination of Gd-DTPA concentration in T1-weighted MR renography studies. Magn Reson Med. 2007;57:1012–1018. doi: 10.1002/mrm.21169. [DOI] [PubMed] [Google Scholar]
- 26.Parker DL, Tsuruda JS, Goodrich KC, Alexander AL, Buswell HR. Contrast-enhanced magnetic resonance angiography of cerebral arteries. Invest Radiol. 1998;33:560–572. doi: 10.1097/00004424-199809000-00012. [DOI] [PubMed] [Google Scholar]
- 27.Krier JD, Ritman EL, Bajzer Z, Romero JC, Lerman A, Lerman LO. Noninvasive measurement of concurrent single-kidney perfusion, glomerular filtration, and tubular function. Am J Physiol Renal Physiol. 2001;281:F630–F638. doi: 10.1152/ajprenal.2001.281.4.F630. [DOI] [PubMed] [Google Scholar]
- 28.Kuo PH. Gadolinium-containing MRI contrast agents: important variations on a theme for NSF. J Am Coll Radiol. 2008;5:29–35. doi: 10.1016/j.jacr.2007.08.014. [DOI] [PubMed] [Google Scholar]
- 29.Sadowski EA, Bennett LK, Chan MR, et al. Nephrogenic systemic fibrosis: risk factors and incidence estimation. Radiology. 2007;243:148–157. doi: 10.1148/radiol.2431062144. [DOI] [PubMed] [Google Scholar]
- 30.Parker GJ, Roberts C, Macdonald A, et al. Experimentally-derived functional form for a population-averaged high-temporal-resolution arterial input function for dynamic contrast-enhanced MRI. Magn Reson Med. 2006;56:993–1000. doi: 10.1002/mrm.21066. [DOI] [PubMed] [Google Scholar]
- 31.Moonen M, Jacobsson L. Effect of administered activity on precision in the assessment of renal function using gamma camera renography. Nucl Med Commun. 1997;18:346–351. doi: 10.1097/00006231-199704000-00174. [DOI] [PubMed] [Google Scholar]
- 32.de Priester JA, den Boer JA, Giele ELW, et al. MR renography: an algorithm for calculation and correction of cortical volume averaging in medullary renographs. J Magn Reson Imaging. 2000;12:453–459. doi: 10.1002/1522-2586(200009)12:3<453::aid-jmri11>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]