Abstract
We present a multiscale agent-based non-small cell lung cancer model that consists of a 3D environment with which cancer cells interact while processing phenotypic changes. At the molecular level, transforming growth factor β (TGFβ) has been integrated into our previously developed in silico model as a second extrinsic input in addition to epidermal growth factor (EGF). The main aim of this study is to investigate how the effects of individual and combinatorial change in EGF and TGFβ concentrations at the molecular level alter tumor growth dynamics on the multi-cellular level, specifically tumor volume and expansion rate. Our simulation results show that separate EGF and TGFβ fluctuations trigger competing multi-cellular phenotypes, yet synchronous EGF and TGFβ signaling yields a spatially more aggressive tumor that overall exhibits an EGF-driven phenotype. By altering EGF and TGFβ concentration levels simultaneously and asynchronously, we discovered a particular region of EGF-TGFβ profiles that ensures phenotypic stability of the tumor system. Within this region, concentration changes in EGF and TGFβ do not impact the resulting multi-cellular response substantially, while outside these concentration ranges, a change at the molecular level will substantially alter either tumor volume or tumor expansion rate, or both. By evaluating tumor growth dynamics across different scales, we show that, under certain conditions, therapeutic targeting of only one signaling pathway may be insufficient. Potential implications of these in silico results for future clinico-pharmacological applications are discussed.
Contact: deisboec@helix.mgh.harvard.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Signaling pathways are responsible for coordinating incoming cues in an effort to regulate a diverse array of cellular processes including proliferation, migration, differentiation, and apoptosis. The deregulation of these signaling pathways induced by a variety of growth factors is one of the fundamental elements contributing to initiation and progression of many solid tumors (Hanahan and Weinberg, 2000), the most prevalent being cancer of the lung. It is estimated that in 2008 alone, ∼215 020 new cases of lung cancer will have been diagnosed in the United States and about 161 840 deaths will have occurred from the disease (Jemal et al., 2008). The epidermal growth factor receptor (EGFR) is often mutated and overexpressed in non-small cell lung cancer (NSCLC) (Hirsch et al., 2003). Epidermal growth factor (EGF) binds EGFR and promotes dimerization and subsequent autophosphorylation, resulting in the downstream activation of a number of key cell decision-making proteins such as phosopholipase Cγ (PLCγ), extracellular signal-regulated kinase (ERK), and many others (Friedl and Wolf, 2003). In addition, the secreted protein transforming growth factor β (TGFβ) is another ligand that plays a prominent role in regulating or mediating cellular and physiological processes in NSCLC (Anumanthan et al., 2005). Cancer cells often secrete excess TGFβ and induce autocrine signaling (Siegfried, 1987) resulting in enhanced invasion and metastasis, while in healthy cells or benign tumor cells, TGFβ halts proliferation and induces apoptosis (Blobe et al., 2000). Regardless of this, the functional consequences of TGFβ in NSCLC patients are still ambiguous, where TGFβ levels are generally elevated but show considerable variation (median of 21 ng/ml, range 5–103 ng/ml) compared to healthy individuals (range 4–12 ng/ml) (De Jaeger et al., 2004).
In an effort to first integrate and ultimately enhance understanding of the complex dynamics of growth factor mediated signaling networks, mathematical and computational modeling approaches combined with experiments have been utilized to probe cancer systems, and their continued improvement may advance the development of new cancer diagnostic and therapeutic techniques (Khalil and Hill, 2005). However, current in silico modeling efforts have been focusing primarily on the single-cell level (Albeck et al., 2006), which may not be sufficient for exploring cancer growth dynamics and predicting tumor response as these approaches fail to incorporate the tumor's interactions with its heterogeneous biochemical environment (Di Ventura et al., 2006). It is therefore desirable for computational cancer models to encompass multiple biological scales within a specific temporal, spatial and physiological context in order to generate more relevant predictions.
We have recently developed a multiscale agent-based computational model for the simulation of NSCLC (Wang et al., 2007). Using this model, tumor expansion dynamics have been studied across molecular and multi-cellular scales within a 2D biochemical environment. In a follow-up study (Wang et al., 2008) we identified key signaling events that are critical in determining the output behavior of the model (i.e. the tumor expansion rate) by employing sensitivity analysis techniques. Together, our previous modeling efforts provide a novel and functional computational platform for investigating and predicting cancer behaviors at the multi-cellular level in response to changes occurring at the molecular level.
In this article, we present a physiologically and clinically motivated extension to our previously developed 2D model. Here, we monitor the synchronized motion of individual lung cancer cells as they move through a 3D block of virtual lung tissue. At this multi-cellular (microscopic) level, we have designed a biochemical microenvironment with which cancer cells communicate and to which they may respond by growing into or moving to different locations, i.e. filling empty locations with daughter cells through replication or migrating to unoccupied sites. This model expansion is necessary en route to eventual clinical application of these types of computational platforms because (i) a 3D environment can provide a more accurate representation of an in vivo system and hence will generate more clinically relevant information, and (ii) findings from 2D and 3D models may differ (Zaman et al., 2006). In addition, we extend our previous NSCLC-specific EGFR signaling pathway at the molecular level by introducing TGFβ as a second stimulus (in addition to EGF). While some earlier models of TGFβ signaling have been proposed (Melke et al., 2006; Vilar et al., 2006), multi-cellular computational models that maintain even a partial focus on TGFβ are scarce. Studies that minimally incorporate TGFβ as a model parameter include investigation of malignant brain tumor immune cell interactions (Kronik et al., 2008), modeling of morphogenesis and pattern formation of mesenchymal condensation in the developing vertebrate limb (Christley et al., 2007; Kiskowski et al., 2004), and simulation of prostate stem cell movement (Lao and Kamei, 2008). However, none of these models adequately incorporates the effects of molecular-level variations of TGFβ on consequent cellular phenotypes and tumor patterns. We note that the autocrine secretion and interaction process of EGF (as a growth promoting factor) and TGFβ (as a growth inhibiting factor) were studied in a theoretical work on the growth of solid tumors (Chaplain et al., 2001), in which a novel numerical method to expedite the computation of reaction kinetics was also developed. However, still, the underlying signaling dynamics of EGF and TGFβ within a cell were not presented. In this study, we investigate both the individual and combinatorial effects of EGF and TGFβ fluctuation on multi-cellular behaviors. Within our model, EGF and TGFβ distinctly contribute to tumor volume and tumor expansion rate. We have also discovered an EGF- and TGFβ-dependent stable phenotypic region that partitions types of phenotypic response: changes within the region (comprised of a range of EGF and TGFβ concentrations) do not affect the stability of the robust tumor system; however, alterations outside this area cause substantial changes in multi-cellular behaviors, either in tumor volume or tumor expansion rate, or in both.
2 METHODS
2.1 Molecular scale: signaling network
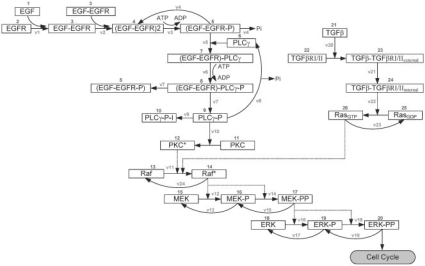
We have previously developed and implemented a NSCLC-specific protein signaling pathway that mediates EGF-induced proliferative and migratory responses of individual cancer cells (Wang et al., 2007). Cell stimulation with EGF induces an EGFR-mediated phenotypic response, through the downstream activation of the MAPK/ERK cascade. Recent experimental studies have shown that TGFβ also stimulates the rapid activation of ERK through activation of the oncogenic GTPase Ras (Derynck and Zhang, 2003), which necessitates the incorporation of such TGFβ signaling into our previous EGF-based pathway. For its part, TGFβ binds its type II receptors (TGFβRII) promoting their dimerization, followed by the recruitment of two type I receptors (TGFβRI) (Siegel and Massague, 2003). The resulting heterotetrameric complex is then subject to internalization (forming endosomes with kinase activity), recycling, and/or degradation. Cytosolic signaling proteins such as Ras are activated, leading to activation of Raf, the initiating kinase of the ERK signaling cascade. Figure 1 shows the kinetic scheme of the integrated EGF and TGFβ signaling pathway which is composed of 26 molecules and 23 chemical reactions. Signaling between the two sub-pathways converges at the reaction step for Raf activation (reaction step 11). While conventionally TGFβ signaling is processed through the SMAD pathway (Derynck and Zhang, 2003), we have initially chosen this simplified TGFβ-Ras-ERK signaling route because (i) Ras plays an important role in NSCLC tumorigenesis (Gupta et al., 2004), and (ii) it is reasonable to reduce the number of explicitly involved molecules as a starting point for computational modeling from which refinement can begin (Aldridge et al., 2006).
Fig. 1.
Kinetic scheme of the integrated signaling network. Both EGF and TGFβ can initiate the pathway, leading to the ultimate molecular response in doubly phosphorylated ERK (ERK-PP). Each component is identified by a specific number. The arrows represent the reactions specified in Supplementary Tables 1 and 2 and characterized by reaction rates v1-v23.
During EGF and TGFβ signaling, pathway dynamics within the model are regulated by material balance and kinetic equations, as well as reaction rates that are dependent on changes of species concentrations over time. The integrated pathway model is based on a total of 26 ordinary differential equations (ODEs) and is constructed as previously described (Kholodenko et al., 1999; Schoeberl et al., 2002). Supplementary Tables 1 and 2 summarize the kinetic parameters and ODEs used for the model. Most parameters, including initial concentrations and reaction rate constants, are obtained from the literature or estimated when unavailable. As in the previously developed 2D model (Wang et al., 2007), PLCγ and ERK are employed to determine two important phenotypic traits: PLCγ-dependent migration and ERK-dependent proliferation. Experimental studies have shown that transient acceleration of accumulating PLCγ levels leads to cell migration (Dittmar et al., 2002), while that of ERK leads to cell replication (Santos et al., 2007). Therefore, in our model, the rate of change of PLCγ determines whether a cell will migrate, and the rate of change of ERK dictates a cell's proliferation fate. Supplementary Figure 1 depicts a brief schematic of the cellular phenotype decision algorithm. We emphasize here that a cell must also meet other microenvironmental requirements such as sufficient local nutrient conditions and available adjacent space in order to process any phenotype transition [see Wang et al. (2007) for more details]. Finally, we note that, although TGFβ has an impact on both cancer cell proliferation and migration, only its impact on cell proliferation is explicitly implemented in the model. This is since, between ERK and PLCγ, only ERK is a direct downstream signaling molecule of TGFβ, whereas PLCγ is not. However, this does not mean that TGFβ variation cannot influence PLCγ signaling. Indeed, as we present in ‘Results’ section, our mathematical implementation demonstrates that alterations in TGFβ concentration also result in a change in the collective cell migration behavior, implying that TGFβ can indirectly modulate the activity of PLCγ.
2.2 Microscopic scale: tumor cell–microenvironment interaction
Illustrated in Supplementary Figure 2a is the structure of a 3D virtual microenvironment comprised of a discrete cubic space with 200 × 200 × 200 grid points, within which the nutrient source and seed cells are positioned. Each grid point may be occupied by a single cell or may remain empty. Each cell or agent has a self-maintained signaling network (Fig. 1). Over the course of a simulation, seed cells and their progeny respond to cellular and environmental biochemical cues that determine their phenotype at each time step. A simulation run is terminated when the first cell reaches the nutrient source. We use the number of elapsed time steps as a measure for ‘tumor expansion rate’ and the final number of live cells for ‘tumor volume’. We note here that, the expression of the expansion rate should have units of distance per time; however, for simplicity we use units of time in our model evaluation because under all simulations, cells must travel the same distance to the source (Supplementary Fig. 2b). Thus, a simulation that terminates after a greater number of time steps has a slower tumor expansion rate.
Four external diffusive chemical cues (EGF, TGFβ, glucose and oxygen tension) are normally distributed throughout the virtual lung tissue grid and are weighted by the distance of a grid point from the nutrient source. As a result, the nutrient source is assigned the highest weight for each of the four cues, making it the most attractive location for the chemotactically acting tumor cells. Moreover, throughout the simulation, the four chemical cues are continuously updated at a fixed rate, using the following equation [as described previously (Wang et al., 2007)]:
| (1) |
where C represents the concentration of one of the four external cues, DC corresponds to the diffusion coefficient of the corresponding species C, t represents the time step, and ijk is the 3D integer coordinate of a given grid location. Glucose is continuously taken up from the local environment by cells to support their metabolism, while EGF and TGFβ autocrine loops mediate the cellular phenotype and are also considered in the model; these cellular processes are described by Equations 2–4:
| (2) |
| (3) |
| (4) |
where rg, regf and rtgf represent the glucose uptake coefficient, the secretion rate of EGF, and the secretion rate of TGFβ, respectively. The values for the coefficients of Equations (1)–(4) are listed in Supplementary Table 3. Only at the nutrient source is glucose replenished at each time step. A main feature of our model is that, in each simulation, tumor expansion patterns due to cell proliferation and migration are neither pre-defined nor intuitive, but rather are the accumulated result of dynamic interactions between individual cells, and between cells and their biochemical microenvironment.
2.3 Cross-scale analysis
We have previously introduced an approach for identifying critical pathway components that have significant impact on the tumor's expansion rate within a 2D environment (Wang et al., 2008). Here, we further examine the effects of individual and combinatorial change in EGF and TGFβ concentrations on tumor volume and expansion rate within the 3D environment. We use a sensitivity coefficient as an index of the importance of how a change in a single sub-cellular model component affects the overall system response at the multi-cellular level (deemed the ‘multi-cellular readout’). This coefficient is calculated by the following equation:
| (5) |
where δM is the change in M (the response of the system) due to δp, the change in p [system parameter(s) varied during a simulation]. In this study, the system response M corresponds to either tumor volume (indicated by final live cell number) or tumor expansion rate (indicated by total simulation steps). Furthermore, we explore two types of variations in p: a single parameter change (altering either EGF or TGFβ levels) and a combinatorial change (altering EGF and TGFβ levels simultaneously).
3 RESULTS
Our agent-based model was implemented in C/C++ and all simulation runs were carried out on a 19-node dual-CPU cluster supercomputer (Intel® Xeon™ 3.06 GHz CPUs, each with 2.5 GB available RAM) provided by the Harvard University School of Engineering and Applied Sciences (SEAS). A total of 27 seed cells arranged in a 3 × 3 × 3 cube were initially positioned in the center of 3D environment (Supplementary Fig. 2a). Due to computation intensity, the maximum simulation step for all simulations was set to 250; simulations that require more than 250 time steps to finish are terminated at 250 time steps and are considered to represent a slow expansion system. In our simulations, each time step corresponds to 2.4 h, and one cell cycle requires 10–12 steps, in agreement with experimental data (Hegedus et al., 2000). For both single and combinatorial parameter changes, parameter variation ranges were set to [0.2, 0.3, 0.5, 0.7, 1.0, 2, 3, 5, 7, 10, 20, 30, 50]-fold of their corresponding reference (literature) values.
3.1 Multi-cellular patterns
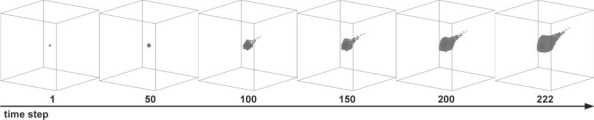
In this model emergent multi-cellular tumor growth patterns result from the collective behavior of individual cells and their repetitive interactions. The progression of a tumor expansion pattern under typical simulation conditions (i.e. when all kinetic parameters are set to their reference values; called the ‘standard simulation’) is shown in Figure 2. As expected, the cells tend to move toward the nutrient source, which, according to our model setup, is the most chemotactically attractive location. For this standard simulation, the final cell number is 16 417 and the number of elapsed time steps is 222. These values are then used for subsequent sensitivity analyses. According to our model setup (Supplementary Fig. 2a), the final tumor volume (including live and dead tumor cells and interstitial fractions within the tumor mass) is 3.75 × 10−2 mm3 with a diameter of 1.1 mm.
Fig. 2.
A typical tumor growth pattern over time in the full 3D environment; this is deemed the ‘standard simulation’.
3.2 Individual parameter change
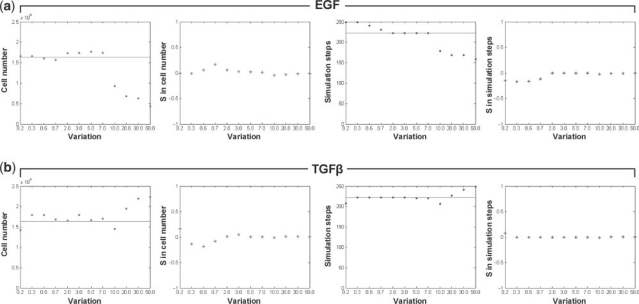
We varied concentration levels of EGF and TGFβ according to the aforementioned range in order to investigate the phenotypic changes of individual cells in response to either stimulus, and how they in turn collectively generate multi-cellular patterns over time. The final tumor volume and expansion rate were obtained for all simulations, and were compared to the results of the standard simulation (Fig. 2) for sensitivity coefficient calculations. Figure 3 shows the simulation results with varying concentrations of EGF or TGFβ (while keeping the other stimulus constant). Overall, increasing EGF concentrations leads to a decrease in both cell number and simulation steps (indicating a slowly proliferating but highly invasive phenotype); conversely, increasing TGFβ concentrations results in an increase in cell number while the simulation steps increase as well (describing a rapidly growing but less invasive phenotype). Specifically, EGF variation: in Figure 3a, the final cell number (i) remains relatively constant compared to the standard simulation if variation is <1.0-fold; (ii) slightly increases if the variation is >1.0 and <7.0; and (iii) decreases if variation is >10.0. However, the number of simulation steps slightly decreases prior to plateau for variations of up to 7.0-fold, beyond which it decreases significantly, indicating an acceleration of the cancer system (albeit with a smaller number of cells). In both sensitivity coefficient plots, a smaller variation in EGF concentration leads to a relatively large change in both the final cell number and simulation steps. TGFβ variation: in Figure 3b, as the TGFβ concentration increases, the simulation step plot stays relatively steady if the variation is <7.0-fold and increases continuously by a small margin if exposed to a variation of >10.0-fold (indicating a deceleration of the system). The final cell number plot shows fluctuations if the variation is <7.0-fold, and starts to show a consistent increase if >10.0. The sensitivity analysis demonstrates that a small variation in the TGFβ concentration also triggers a relatively substantial change in the final cell number, but not in the number of simulation steps.
Fig. 3.
The effects of individual changes in EGF and TGFβ concentration on tumor volume (cell number) and expansion rate [(inverse) simulation steps]. Illustrated are the two multi-cellular indices and corresponding sensitivity analysis results of (a) EGF and (b) TGFβ, where S is the sensitivity coefficient. Horizontal lines in the first and third columns of (a) and (b) represent the simulation results obtained from the standard simulation (final cell number: 16 417; simulation step: 222).
3.3 Synchronous combinatorial change
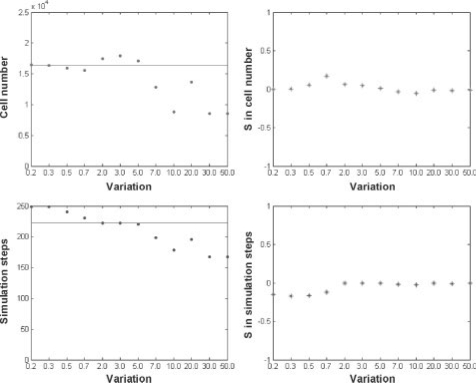
We next simultaneously varied the concentrations of EGF and TGFβ at equivalent rates in order to investigate the combinatorial effects on multi-cellular responses (Fig. 4). Our results indicated that the variation patterns for both cell number and simulation steps are similar to the corresponding simulation results for EGF variation alone (Fig. 3a). Indeed, a correlation analysis (Supplementary Table 4) showed that correlation coefficients between simulation results of this combinatorial (EGF and TGFβ concentration) change and the EGF concentration change are all positive and are all near 1.0, indicating a direct and strong relationship, whereas correlation coefficients between the combinatorial change and TGFβ concentration change are all negative and around −0.5, indicating an inverse and weak relationship. Together, these results indicate that the EGF signal prevails as the most influential stimulus on the cascade's resulting phenotypic output. Furthermore, the point at which the tumor system becomes more spatially aggressive than the standard simulation occurs already at a smaller EGF variation, i.e. from 10.0-fold (Fig. 3a) down to 7.0-fold (Fig. 4). This suggests that raising both EGF and TGFβ concentrations together increases the sensitivity of the tumor system to environmental stimuli that trigger invasiveness (as compared to increasing EGF alone).
Fig. 4.
The effects of synchronous combinatorial change in EGF and TGFβ concentrations on tumor volume (cell number) and expansion rate [(inverse) simulation steps]. Horizontal lines represent the simulation results obtained from the standard simulation (final cell number: 16 417; simulation step: 222).
3.4 Asynchronous combinatorial change
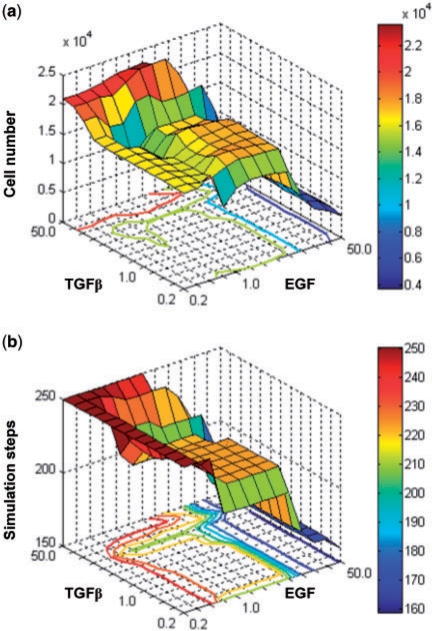
Based on the above findings on synchronous variation of EGF and TGFβ concentrations, we sought to gain insight into how asynchronous changes in the two stimuli affect tumor growth dynamics across different scales. The concentration variation range for both components included a total of 13 variations; this generated a total of 132 simulation runs, each of which has a unique pair of EGF and TGFβ concentration variations. It is noteworthy that the set of variation-pairs used in the previously described synchronous case is a subset of the variation-pairs used in this asynchronous case. Figure 5 shows the simulation results from changing EGF and TGFβ concentrations both simultaneously and asynchronously. As shown in Figure 5a, smaller EGF and greater TGFβ concentrations lead to larger final cell counts and thus increased tumor volume; however, when both EGF and TGFβ concentrations remain small, the cell number remains unaltered. In Figure 5b, increased EGF concentration leads to a smaller simulation step number and thus a faster tumor expansion rate, independent of TGFβ levels. Comparing both panels, there exists a common stable phenotypic region (generated by [2–7]-fold variation of EGF and [0.3–3]-fold variation of TGFβ) within which varying EGF and TGF concentrations only results in minimal changes in the final cell number (17 570 ± 250 cells; see Supplementary Table 5 for detail) and does not alter the tumor expansion rate. However, if a variation-pair does not reside within this stable phenotypic region, it leads to a relatively substantial change in either tumor volume or tumor expansion rate, or both.
Fig. 5.
The effects of asynchronous combinatorial change in EGF and TGFβ concentrations on (a) tumor volume (cell number) and (b) tumor expansion rate [(inverse) simulation steps]. In (a), the largest tumor volume (indicated by the red portion of the graph) is reached under conditions of high TGFβ and low or standard (with a variation of 1.0-fold) EGF concentrations. However, in (b), the most aggressive tumor expansion rate (fewest simulation steps, indicated by the blue portion of the graph) occurs under conditions of high EGF, regardless of TGFβ concentrations.
4 DISCUSSION
The significance of incorporating the underlying biological mechanisms at multiple scales is being increasingly recognized in developing computational cancer models that are more realistic and predictive of in vivo outcomes (Wang and Deisboeck, 2008). Focus at only the molecular level, which accounts for the vast majority of current cancer modeling efforts, is likely insufficient for achieving accurate predictions of cancer initiation and progression because even extrinsic environmental conditions alone, independent of genetic mutations, can induce the carcinogenic transformation of cells (Postovit et al., 2006). Here, we presented a multiscale agent-based computational model for NSCLC, the dynamical processes of which span both molecular and multi-cellular levels. Within the 3D biochemical environment, the effects of changing EGF and TGFβ expression levels, in an individual or concurrent manner, on tumor volume and expansion rate have been investigated. It is the first time, to our knowledge, that an in silico approach has been utilized to explore the differences in multi-cellular behaviors caused by various extrinsic stimuli within NSCLC.
Elevated expression of EGF leads to increase in tumor cell motility and invasiveness, thereby enhancing lung metastasis (Price et al., 1996; Xue et al., 2006). This clinical observation is consistent with our findings where increasing EGF concentrations engenders a more spatially aggressive tumor, with expansion rates greater than the standard simulation (Fig. 3a). However, experimental data indicate that excess TGFβ leads to an enhanced invasion and metastasis (Akhurst and Derynck, 2001) which, at first, appears to be in conflict with our simulation findings where increasing TGFβ concentrations ultimately results in a less spatially aggressive tumor. This disagreement may be in part due to our simplified TGFβ pathway design and, more so, to our modular approach of adding the TGFβ module to a preexisting phenotypic decision algorithm (Wang et al., 2007). While going ‘modular’ is a reasonable if not desirable first step from a computational perspective, in the resulting composite design PLCγ (Fig. 1) is responsible for the cell's migration decision and is a direct downstream effector of EGF but not TGFβ. As such, in the current network iteration, regulation of TGFβ does not have an immediate direct effect on changing the expression level of PLCγ nor in regulating subsequent cellular PLCγ-mediated phenotype decisions. This shortcoming can be addressed by rendering the TGFβ sub-pathway and its downstream components more directly responsible (via experimentally validated means) for determining the cell's migratory fate.
In examining the combinatorial synchronous change of EGF and TGFβ (Fig. 4), it was observed that EGF was the dominating stimulus of both tumor volume and expansion rate increases within our model design. Surprisingly, altering EGF and TGFβ synchronously yields a more chemotactically sensitive and thus spatially more aggressive tumor (as compared to altering EGF separately while keeping TGFβ constant). As such, the TGFβ signal when varied in context is not migration-limiting as in the case described above (compare Figs 3a and 4), but rather is in agreement with the experimental data. Also of note, we discovered a stable phenotypic region of EGF-TGFβ variation pairs when we altered concentrations of both stimuli, asynchronously and simultaneously (Fig. 5). If a variation-pair of EGF and TGFβ concentrations falls within this region, the tumor system appears to be robust with regards to its resulting multi-cellular performance patterns of volumetric increase and expansion rate. However, the tumor system becomes sensitive to external variations in EGF and/or TGFβ when they occur outside this region. Furthermore, within our multiscale simulation platform, we are not only able to monitor multi-cellular dynamics in response to molecular changes, but can also determine the fate of molecular components as the tumor system evolves. For instance, Supplementary Figure 3 tracks the activated form of PKC (PKC*) and GTPase Ras (RasGTP) (which are the final downstream effectors of the EGF- and TGFβ-induced sub-pathways, respectively; see Fig. 1) as well as Raf (the point of convergence of both sub-pathways). Monitoring these molecular components, it can be seen that while RasGTP levels change sharply as TGFβ concentration increases, levels of RasGTP's direct downstream target Raf are not affected and thus do not lead to major alterations in the ERK activation cascade. This behavior is a result of the cross-talk between the EGF and TGFβ branches of our implemented pathway: changes in downstream protein levels caused by TGFβ can be masked by EGF signaling. In fact, it has been demonstrated that such inherited cross-talk in the underlying signaling pathways may be the most challenging obstacle in the development of molecular-targeted cancer therapeutics (Adjei, 2006; McClean et al., 2007). Our combinatorial analysis results indeed suggest that adding TGFβ to an EGF signal up-regulates an EGF-dominated, invasive tumor growth pattern (Fig. 4), despite lacking direct interaction with the migration switching molecule PLCγ. Current NSCLC therapies still rely on monoclonal inhibitors that target EGF or TGFβ or their receptors, where only moderate clinical outcome has been achieved so far [see Janne et al. (2005) and Yingling et al. (2004) for reviews]. Our simulation results indicate that both EGF and TGFβ pathways need to be targeted to effectively regulate tumorigenesis.
To quantify cell motility, the expansion rate or the spreading speed of cell populations have been studied both experimentally and computationally (Dubin-Thaler et al., 2004; Edelstein-Keshet and Ermentrout, 2001; Mogilner and Edelstein-Keshet, 2002). The computationally determined expansion rate varies between these studies, which is not surprising as multiple cell types under unique biochemical or biophysical environments should behave differently. In our model, the expansion rate is 2.07 μm/h for the standard simulation; the fastest expansion rate is 2.88 μm/h (observed in simulations with pairs of 50.0-fold variation of EGF and [0.7–50.0]-fold variation of TGFβ). Our simulation results are in very good agreement with a recent study on growth regulation mechanisms in epithelial cell populations that shows a representative cellular expansion rate of 2.1 μm/h (Galle et al., 2005). Furthermore, our results are also comparable to in vitro experiments with cancer cell lines, where e.g., Bru et al. (2003) demonstrate expansion rates of 1.10–11.50 μm/h. Additionally, the diameter of the final tumor mass is ∼1 mm in all simulations. At this size, the simulated tumor could be reliably detected with existing technologies, e.g. helical computed tomography (CT) (McMahon et al., 2008).
The tumor microenvironment is known to influence both tumor progression and metastasis (Gatenby et al., 2006). A number of computational models, with a focus on tumor growth and invasion behaviors on and beyond the single-cell level, have been developed to investigate cell–matrix interactions and corresponding gradient-driven process (Gerlee and Anderson, 2009; Ramis-Conde et al., 2008, 2009). Moreover, cell–cell adhesion is another important component in cancer cell invasion (Hood and Cheresh, 2002), and corresponding biophysical properties have also been widely studied using a mathematical modeling approach [see Armstrong et al. (2006) and Gerisch and Chaplain (2008) and references presented therein]. Taken together, in an ongoing effort to create a more realistic cell phenotypic decision algorithm, especially in determining cell migration, the dynamic interactions among cells and between cells and their biological microenvironment will be integrated into our intracellular signal driven algorithm presented in here.
Alone, TGFβ has potent inhibitory effects on cell proliferation at the pre-tumor stage and stimulatory effects on cell invasion and metastasis in later tumor stages (Cui et al., 1996). This important multifunctional role of TGFβ has not yet been fully captured by our model where tumor volume (final cell number) fluctuates as TGFβ concentration increases (Fig. 3b). To address this limitation, the current TGFβ pathway can be supplemented with an SMAD-dependent one. The main targets of activation by TGFβ are the SMAD proteins, the complex of which can target specific genes, contributing to tumor formation in certain forms of cancer, including lung (Derynck and Zhang, 2003). Hence, the development of an SMAD-dependent pathway is ongoing in a continued effort to improve the model design at the molecular level. Finally, because in reality (cancer) cells rely on many more interacting signaling pathways to process phenotypic decisions, the combined effects of other pathway components (in addition to EGF and TGFβ) on tumor volume and expansion rate will be investigated. By doing so, we can further examine and validate the relationship between extrinsic stimuli variations, intracellular signaling dynamics and multi-cellular tumor readout. These model amendments will facilitate the identification of potential molecular-level biomarkers and/or critical pathway components that can be targeted to affect tumor progression at the multi-cellular level.
5 CONCLUSIONS
The effects of individual and combinatorial change of EGF and TGFβ at the molecular level on multi-cellular tumor behaviors, including tumor volume and expansion rate, have been investigated in a 3D in silico NSCLC model. We identify EGF as the dominant stimulus over TGFβ in regulating the two evaluation indices within our model and found that TGFβ's phenotypic signal output is context-dependent. We discovered a particular region of tumor system stability, generated by unique pairs of EGF and TGFβ concentration variations. When the variation-pair of EGF and TGFβ concentrations occurs on the edge of this region, we observed that changes caused by the two growth factors do not effectively transmit to the downstream activation cascade, potentially explaining the resulting robustness of the tumor system at the multi-cellular level. Together, our combinatorial analysis results demonstrate that changes in TGFβ can modulate the EGF downstream cascade, thereby affecting the motility of tumor cells through signaling cross-talk. With regard to pharmaceutical and clinical strategies, our findings, cautiously extrapolated, suggest that, future NSCLC therapies may need to target both of these pathways in order to achieve effective tumorigenic-signal disruption.
Funding: NIH grant CA 113004; Harvard-MIT (HST) Athinoula A. Martinos Center for Biomedical Imaging and the Department of Radiology at Massachusetts General Hospital.
Conflict of Interest: none declared.
REFERENCES
- Adjei AA. Novel combinations based on epidermal growth factor receptor inhibition. Clin. Cancer Res. 2006;12:4446s–4450s. doi: 10.1158/1078-0432.CCR-06-0623. [DOI] [PubMed] [Google Scholar]
- Akhurst RJ, Derynck R. TGF-beta signaling in cancer – a double-edged sword. Trends Cell Biol. 2001;11:S44–S51. doi: 10.1016/s0962-8924(01)02130-4. [DOI] [PubMed] [Google Scholar]
- Albeck JG, et al. Collecting and organizing systematic sets of protein data. Nat. Rev. 2006;7:803–812. doi: 10.1038/nrm2042. [DOI] [PubMed] [Google Scholar]
- Aldridge BB, et al. Physicochemical modelling of cell signalling pathways. Nat. Cell Biol. 2006;8:1195–1203. doi: 10.1038/ncb1497. [DOI] [PubMed] [Google Scholar]
- Anumanthan G, et al. Restoration of TGF-beta signalling reduces tumorigenicity in human lung cancer cells. Br. J. Cancer. 2005;93:1157–1167. doi: 10.1038/sj.bjc.6602831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong NJ, et al. A continuum approach to modelling cell-cell adhesion. J. Theor. Biol. 2006;243:98–113. doi: 10.1016/j.jtbi.2006.05.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blobe GC, et al. Role of transforming growth factor beta in human disease. N. Engl. J. Med. 2000;342:1350–1358. doi: 10.1056/NEJM200005043421807. [DOI] [PubMed] [Google Scholar]
- Bru A, et al. The universal dynamics of tumor growth. Biophys. J. 2003;85:2948–2961. doi: 10.1016/S0006-3495(03)74715-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaplain MA, et al. Spatio-temporal pattern formation on spherical surfaces: numerical simulation and application to solid tumour growth. J. Math. Biol. 2001;42:387–423. doi: 10.1007/s002850000067. [DOI] [PubMed] [Google Scholar]
- Christley S, et al. Patterns of mesenchymal condensation in a multiscale, discrete stochastic model. PLoS Comput. Biol. 2007;3:e76. doi: 10.1371/journal.pcbi.0030076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui W, et al. TGFbeta1 inhibits the formation of benign skin tumors, but enhances progression to invasive spindle carcinomas in transgenic mice. Cell. 1996;86:531–542. doi: 10.1016/s0092-8674(00)80127-0. [DOI] [PubMed] [Google Scholar]
- De Jaeger K, et al. Significance of plasma transforming growth factor-beta levels in radiotherapy for non-small-cell lung cancer. Int. J. Radiat. Oncol. Biol. Phys. 2004;58:1378–1387. doi: 10.1016/j.ijrobp.2003.09.078. [DOI] [PubMed] [Google Scholar]
- Derynck R, Zhang YE. Smad-dependent and Smad-independent pathways in TGF-beta family signalling. Nature. 2003;425:577–584. doi: 10.1038/nature02006. [DOI] [PubMed] [Google Scholar]
- Di Ventura B, et al. From in vivo to in silico biology and back. Nature. 2006;443:527–533. doi: 10.1038/nature05127. [DOI] [PubMed] [Google Scholar]
- Dittmar T, et al. Induction of cancer cell migration by epidermal growth factor is initiated by specific phosphorylation of tyrosine 1248 of c-erbB-2 receptor via EGFR. FASEB J. 2002;16:1823–1825. doi: 10.1096/fj.02-0096fje. [DOI] [PubMed] [Google Scholar]
- Dubin-Thaler BJ, et al. Nanometer analysis of cell spreading on matrix-coated surfaces reveals two distinct cell states and STEPs. Biophys. J. 2004;86:1794–1806. doi: 10.1016/S0006-3495(04)74246-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelstein-Keshet L, Ermentrout GB. A model for actin-filament length distribution in a lamellipod. J. Math. Biol. 2001;43:325–355. doi: 10.1007/s002850100102. [DOI] [PubMed] [Google Scholar]
- Friedl P, Wolf K. Tumour-cell invasion and migration: diversity and escape mechanisms. Nat. Rev. Cancer. 2003;3:362–374. doi: 10.1038/nrc1075. [DOI] [PubMed] [Google Scholar]
- Galle J, et al. Modeling the effect of deregulated proliferation and apoptosis on the growth dynamics of epithelial cell populations in vitro. Biophys. J. 2005;88:62–75. doi: 10.1529/biophysj.104.041459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatenby RA, et al. Acid-mediated tumor invasion: a multidisciplinary study. Cancer Res. 2006;66:5216–5223. doi: 10.1158/0008-5472.CAN-05-4193. [DOI] [PubMed] [Google Scholar]
- Gerisch A, Chaplain MA. Mathematical modelling of cancer cell invasion of tissue: local and non-local models and the effect of adhesion. J. Theor. Biol. 2008;250:684–704. doi: 10.1016/j.jtbi.2007.10.026. [DOI] [PubMed] [Google Scholar]
- Gerlee P, Anderson AR. Evolution of cell motility in an individual-based model of tumour growth. J. Theor. Biol. 2009;259:67–83. doi: 10.1016/j.jtbi.2009.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta AK, et al. Signaling pathways in NSCLC as a predictor of outcome and response to therapy. Lung. 2004;182:151–162. doi: 10.1007/s00408-004-0310-8. [DOI] [PubMed] [Google Scholar]
- Hanahan D, Weinberg RA. The hallmarks of cancer. Cell. 2000;100:57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
- Hegedus B, et al. Locomotion and proliferation of glioblastoma cells in vitro: statistical evaluation of videomicroscopic observations. J. Neurosurg. 2000;92:428–434. doi: 10.3171/jns.2000.92.3.0428. [DOI] [PubMed] [Google Scholar]
- Hirsch FR, et al. Epidermal growth factor receptor in non-small-cell lung carcinomas: correlation between gene copy number and protein expression and impact on prognosis. J. Clin. Oncol. 2003;21:3798–3807. doi: 10.1200/JCO.2003.11.069. [DOI] [PubMed] [Google Scholar]
- Hood JD, Cheresh DA. Role of integrins in cell invasion and migration. Nat. Rev. Cancer. 2002;2:91–100. doi: 10.1038/nrc727. [DOI] [PubMed] [Google Scholar]
- Janne PA, et al. Epidermal growth factor receptor mutations in non-small-cell lung cancer: implications for treatment and tumor biology. J. Clin. Oncol. 2005;23:3227–3234. doi: 10.1200/JCO.2005.09.985. [DOI] [PubMed] [Google Scholar]
- Jemal A, et al. Cancer statistics, 2008. CA Cancer J. Clin. 2008;58:71–96. doi: 10.3322/CA.2007.0010. [DOI] [PubMed] [Google Scholar]
- Khalil IG, Hill C. Systems biology for cancer. Curr. Opin. Oncol. 2005;17:44–48. doi: 10.1097/01.cco.0000150951.38222.16. [DOI] [PubMed] [Google Scholar]
- Kholodenko BN, et al. Quantification of short term signaling by the epidermal growth factor receptor. J. Biol. Chem. 1999;274:30169–30181. doi: 10.1074/jbc.274.42.30169. [DOI] [PubMed] [Google Scholar]
- Kiskowski MA, et al. Interplay between activator-inhibitor coupling and cell-matrix adhesion in a cellular automaton model for chondrogenic patterning. Dev. Biol. 2004;271:372–387. doi: 10.1016/j.ydbio.2004.03.038. [DOI] [PubMed] [Google Scholar]
- Kronik N, et al. Improving alloreactive CTL immunotherapy for malignant gliomas using a simulation model of their interactive dynamics. Cancer Immunol. Immunother. 2008;57:425–439. doi: 10.1007/s00262-007-0387-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lao BJ, Kamei DT. Investigation of cellular movement in the prostate epithelium using an agent-based model. J. Theor. Biol. 2008;250:642–654. doi: 10.1016/j.jtbi.2007.11.001. [DOI] [PubMed] [Google Scholar]
- McClean MN, et al. Cross-talk and decision making in MAP kinase pathways. Nat. Genet. 2007;39:409–414. doi: 10.1038/ng1957. [DOI] [PubMed] [Google Scholar]
- McMahon PM, et al. Adopting helical CT screening for lung cancer: potential health consequences during a 15-year period. Cancer. 2008;113:3440–3449. doi: 10.1002/cncr.23962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melke P, et al. A rate equation approach to elucidate the kinetics and robustness of the TGF-beta pathway. Biophys. J. 2006;91:4368–4380. doi: 10.1529/biophysj.105.080408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Edelstein-Keshet L. Regulation of actin dynamics in rapidly moving cells: a quantitative analysis. Biophys. J. 2002;83:1237–1258. doi: 10.1016/S0006-3495(02)73897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postovit LM, et al. Influence of the microenvironment on melanoma cell fate determination and phenotype. Cancer Res. 2006;66:7833–7836. doi: 10.1158/0008-5472.CAN-06-0731. [DOI] [PubMed] [Google Scholar]
- Price JT, et al. Epidermal growth factor (EGF) increases the in vitro invasion, motility and adhesion interactions of the primary renal carcinoma cell line, A704. Eur. J. Cancer. 1996;32A:1977–1982. doi: 10.1016/0959-8049(96)00207-9. [DOI] [PubMed] [Google Scholar]
- Ramis-Conde I, et al. Modeling the influence of the E-cadherin-beta-catenin pathway in cancer cell invasion: a multiscale approach. Biophys. J. 2008;95:155–165. doi: 10.1529/biophysj.107.114678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramis-Conde I, et al. Multi-scale modelling of cancer cell intravasation: the role of cadherins in metastasis. Phys. Biol. 2009;6:16008. doi: 10.1088/1478-3975/6/1/016008. [DOI] [PubMed] [Google Scholar]
- Santos SD, et al. Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat. Cell Biol. 2007;9:324–330. doi: 10.1038/ncb1543. [DOI] [PubMed] [Google Scholar]
- Schoeberl B, et al. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat. Biotechnol. 2002;20:370–375. doi: 10.1038/nbt0402-370. [DOI] [PubMed] [Google Scholar]
- Siegel PM, Massague J. Cytostatic and apoptotic actions of TGF-beta in homeostasis and cancer. Nat. Rev. Cancer. 2003;3:807–821. doi: 10.1038/nrc1208. [DOI] [PubMed] [Google Scholar]
- Siegfried JM. Detection of human lung epithelial cell growth factors produced by a lung carcinoma cell line: use in culture of primary solid lung tumors. Cancer Res. 1987;47:2903–2910. [PubMed] [Google Scholar]
- Vilar JM, et al. Signal processing in the TGF-beta superfamily ligand-receptor network. PLoS Comput. Biol. 2006;2:e3. doi: 10.1371/journal.pcbi.0020003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, et al. Cross-scale sensitivity analysis of a non-small cell lung cancer model: linking molecular signaling properties to cellular behavior. Bio Syst. 2008;92:249–258. doi: 10.1016/j.biosystems.2008.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Deisboeck TS. Computational modeling of brain tumors: Discrete, continuum or hybrid? Sci. Model. Simulat. 2008;15:381–393. [Google Scholar]
- Wang Z, et al. Simulating non-small cell lung cancer with a multiscale agent-based model. Theor. Biol. Med. Model. 2007;4:50. doi: 10.1186/1742-4682-4-50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue C, et al. Epidermal growth factor receptor overexpression results in increased tumor cell motility in vivo coordinately with enhanced intravasation and metastasis. Cancer Res. 2006;66:192–197. doi: 10.1158/0008-5472.CAN-05-1242. [DOI] [PubMed] [Google Scholar]
- Yingling JM, et al. Development of TGF-beta signalling inhibitors for cancer therapy. Nat. Rev. Drug Discov. 2004;3:1011–1022. doi: 10.1038/nrd1580. [DOI] [PubMed] [Google Scholar]
- Zaman MH, et al. Migration of tumor cells in 3D matrices is governed by matrix stiffness along with cell-matrix adhesion and proteolysis. Proc. Natl Acad. Sci. USA. 2006;103:10889–10894. doi: 10.1073/pnas.0604460103. [DOI] [PMC free article] [PubMed] [Google Scholar]