Hemodynamic Patterns of Anterior Communicating Artery Aneurysms: A Possible Association with Rupture

Abstract

BACKGROUND AND PURPOSE: The anterior communicating artery (AcomA) is a predilect location of aneurysms which typically carry higher rupture risks than other locations in the anterior circulation. The purpose of this study was to characterize the different flow types present in AcomA aneurysms and to investigate possible associations with rupture.

MATERIALS AND METHODS: Patient-specific computational models of 26 AcomA aneurysms were constructed from 3D rotational angiography images. Bilateral images were acquired in 15 patients who had both A1 segments of the anterior cerebral arteries, and models of the whole anterior circulation were created by fusing the reconstructed left and right arterial trees. Computational fluid dynamics simulations were performed under pulsatile flow conditions measured on a healthy subject. Visualizations of flow velocity, instantaneous streamlines, and wall shear stress (WSS) were performed. These were analyzed for flow patterns, size of the impaction zone, and peak WSS and then correlations were made with prior history of rupture.

RESULTS: Aneurysms with small impaction zones were more likely to have ruptured than those with large impaction zones (83% versus 63%). Maximum intra-aneurysmal WSS (MWSS) for the unruptured aneurysms ranged from 10 to 230 dyne/cm² (mean, 114 dyne/cm²) compared with ruptured aneurysms, which ranged from 35 to 1500 dyne/cm² (mean, 271 dyne/cm²). This difference in MWSS was statistically significant at 90% confidence levels (P = .10).

CONCLUSIONS: Aneurysms with small impaction zones, higher flow rates entering the aneurysm, and elevated MWSS are associated with a clinical history of previous rupture.

The anterior communicating artery (AcomA) is a recognized site of aneurysm predilection accounting for nearly one fourth of all cerebral aneurysms in several large studies.^1-3 Because of the complexity and diversity of the geometry and flow conditions in the AcomA, it is not surprising that aneurysms of the AcomA are considered the most complex of the anterior circulation.⁴ It is widely believed that the initiation, growth, and, ultimately, rupture of cerebral aneurysms are related to the interaction between hemodynamic forces with the arterial wall biology, resulting in a focalized weakening of the wall. Observations in patients with AcomA aneurysms have lent support to this hypothesis. Aneurysms of the AcomA complex are more likely to have asymmetric A1 segments⁵ and, furthermore, to have exclusive filling angiographically from 1 A1 segment in up to 78% cases.⁶ Experimentally, AcomA aneurysms can be produced in hypertensive rats by unilateral ligation of the common carotid artery,⁷ further supporting a causative relationship between increased flow and aneurysm formation.

Previous studies based on 3D rotational angiography (3DRA) images excluded aneurysms of the AcomA because these images included only 1 of the 2 feeding arteries.^8,9 This work has pointed to connections between intra-aneurysmal flow structures and the clinical history of prior aneurysmal rupture. Since then, new methodologies for modeling arterial networks from multiple-injection 3DRA images¹⁰ have been developed, which now allow us to study the hemodynamics of AcomA aneurysms on a patient-specific basis. The purpose of this work was to use these new methods to explore possible relationships between hemodynamic characteristics and aneurysm rupture in the subset of AcomA aneurysms.

Materials and Methods

Patients and Imaging

Twenty-six consecutive patients with AcomA aneurysms and rotational angiography were selected from our data base. Rotational angiography images were obtained during a 180° rotation and imaging at 15 frames per second for a total of 8 seconds, by using an Integris system (Philips Medical Systems, Best, the Netherlands). The corresponding 120 projection images were reconstructed into a 3D dataset of 128 × 128 × 128 voxels covering an FOV of 54.02 mm on a dedicated Philips workstation. Independent 3DRA images were acquired for each internal carotid artery (ICA) in patients having both A1s angiographically visible on conventional angiography. The voxel data were exported into a PC for mathematic vascular modeling by using a previously developed methodology.¹⁰

The patient's medical and radiologic records were reviewed and evaluated for evidence of aneurysmal intracranial hemorrhage. In patients with multiple aneurysms, clinical and radiologic information was considered, and the most likely source of the hemorrhage was determined. The other coincident aneurysms were classified as unruptured. All clinical evaluations were performed by an experienced interventional neuroradiologist. The study of these patients was approved by the local institutional review board.

Vascular Modeling

Realistic vascular models were constructed for each patient from the corresponding 3DRA images by using region-growing segmentation followed by geometric deformable models.^8,11 This segmentation procedure tends to place the vessel surface at the vessel boundaries detected on the 3D images, thus making the reconstructions independent from the selected threshold level. The anatomic models included segments of the ICAs, the middle cerebral arteries, and the A1 and A2 segments of the anterior cerebral arteries. The upstream portion of the parent arteries was extended as much as possible (ie, the entire portion of the ICAs visible in the 3DRA image was modeled, typically extending down through the carotid siphon). In AcomA aneurysms receiving inflow from bilateral A1s, left and right models were independently reconstructed and fused by using a surface-merging algorithm^10,12 after rigid registration of the 2 images. These geometric models were used to generate volumetric finite element grids with an advancing front technique.^13-15 A minimum mesh resolution of 0.16 mm was prescribed, which resulted in grids containing between 2 and 3 million elements for unilateral A1 models and between 3 and 4.5 million elements for bilateral A1 models.

Blood-Flow Simulations and Analysis

Blood was modeled as an incompressible and Newtonian fluid with density ρ = 1.0 g/cm³ and viscosity μ = 0.04 poise. The governing equations were the unsteady Navier-Stokes equations in 3D.¹⁶ Vessel walls were assumed to be rigid, and no-slip boundary conditions were applied at the walls. Pulsatile flow conditions derived from phase contrast (PC) MR imaging measurement in a healthy subject were imposed at the inlet of the ICAs. The inflow waveform amplitude was scaled with the radius of each ICA to obtain a mean wall shear stress (WSS) of <τ> = 15 dyne/cm² by using the Poiseuille formula.¹⁷ Fully developed pulsatile velocity profiles were prescribed by using the Womersley solution.^18,19 The outlet boundary conditions assumed a flow division according to the areas of the vessels at the outlet boundaries. This assumption implies that the flow resistances of the distal vascular beds are roughly proportional to the area of the feeding vessels. The Navier-Stokes equations were numerically integrated by using a fully implicit finite element formulation.⁸ Two cardiac cycles were computed by using 100 time steps per cycle. All the results reported correspond to the second cardiac cycle.

The aneurysmal flow patterns were visualized by using cine animations from velocity magnitude maps at selected cut planes and instantaneous streamlines at peak systole. These visualizations were examined for similarities in flow structure and grouped into flow types. Flow types were assigned by using a previously reported classification of intra-aneurysmal flow⁹: type I, stable inflow jet direction with a single vortex; type II, stable direction of the inflow jet with 2 or more unchanging vortices; type III, changing direction of the inflow jet with creation or destruction of a single vortex during the cardiac cycle; and type IV, changing direction of the inflow jet with multiple varying vortices.

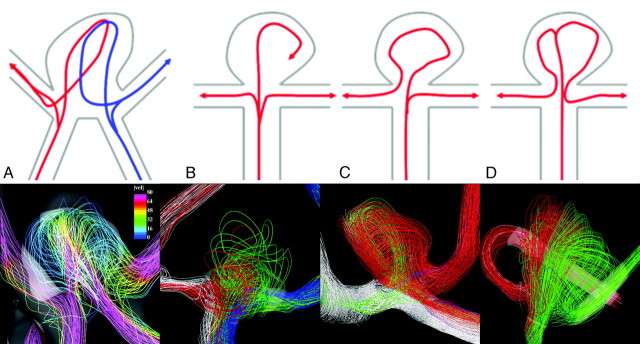
Instantaneous streamline visualizations were examined and grouped into 4 categories by the flow patterns of entry into the aneurysm and associated arteries as follows: First, aneurysms were divided into 2 groups. The first consisted of aneurysms that accept blood flow from the 2 A1 segments (flow type A). The remaining aneurysms, filled exclusively from a single A1 segment, were divided into 3 flow types. In the first of these groups (flow type B), the main jet splits into 3 secondary jets directed toward the aneurysm and the 2 A2 segments. In the second group (flow type C), the inflow jet in the dominating A1 segment splits into 2 secondary jets, 1 of which impacts on the aneurysm before being directed to 1 of the A2 segments, while the other reaches the contralateral A2 segment without entering the aneurysm. In the third group (flow type D), the jet first enters the aneurysm, where it splits into 2 secondary jets directed toward each of the A2 segments. Sketches of the different flow types are presented in Fig 1 (top row), along with examples of aneurysms in each category (bottom row).

Fig 1.

A–D, Different flow patterns found in AcomA aneurysms are shown in the top row. Pictures of the streamlines colored by the magnitude of the velocity and their path from the A1 segment to the A2 segments in 4 selected aneurysms for each flow type are shown in the bottom row.

Each aneurysm was also classified on the basis of the size of the inflow jet and the size of the impaction zone. Additionally, visualizations of instantaneous peak WSS were done for each aneurysm. These were analyzed to identify the zones of elevated WSS within the aneurysm. From these areas, the maximum intra-aneurysmal WSS magnitude at the systolic peak (MWSS) was computed for each aneurysm, and the average was calculated for each group. Comparisons were then made with the clinical history of aneurysmal rupture to look for associations between peak WSS, size of the impaction zone, and flow type with the frequency of prior rupture. A nonparametric Wilcoxon rank sum test was used to test the statistical significance of the association between hemodynamic variables (peak WSS and flow type) and aneurysm rupture.

Results

A total of 26 patient-specific AcomA aneurysm models were constructed from 3DRA images, of which 11 had only 1 A1 and 15 had both A1 segments present. The average aneurysm size was 7.0 ± 2.3 mm with a range from 3.4 to 11.5 mm. Seventy percent (18/26) of the aneurysms had a clinical history of previous rupture and were almost evenly distributed between aneurysms associated with a single A1 versus bilateral aneurysms (73% versus 67%). Only 4 aneurysms were associated with symmetric A1 inflows, of which 25% were ruptured, versus 77% for aneurysms with asymmetric A1 inflows.

Results of the intra-aneurysmal flow type analysis are summarized in Table 1. All flow types were found in the sample, with most (54%) of the aneurysms exhibiting unstable flow types (types III and IV). Only 15% had the simple stable pattern of flow type I. Ruptured aneurysms were more common in all flow types with no statistical trends.

Table 1:

Number and percentage of ruptured and unruptured aneurysms in each flow type based on velocity magnitude maps at selected cut planes

Flow Type	Ruptured (%)	Unruptured (%)	Total
I	3 (75)	1 (25)	4
II	6 (75)	2 (25)	8
III	1 (100)	0 (0)	1
IV	8 (62)	5 (38)	13
Total	18 (70)	8 (30)	26

Aneurysms with small impaction zones outnumbered those with large impaction zones by greater than a 2:1 majority (69% versus 31%). Aneurysms with small impaction zones were more likely to have ruptured than those with large impaction zones (83% versus 63%), though this trend did not reach statistical significance for this sample size.

Streamline analysis of the flow entry to the aneurysms and peak WSS values are summarized in Table 2. Bilateral aneurysms accounted for 58% of the aneurysms, whereas 42% were unilateral (only 1 A1 segment). Only 27% of the bilateral aneurysms accepted blood from both A1 segments (flow type A). The remaining 73% of bilateral aneurysms together with the unilateral aneurysms (85% of the sample) accepted blood from a single A1 segment. The relative number of ruptured aneurysms varied with the flow type. Most aneurysms in group A were unruptured (75%). In contrast, ruptured aneurysms accounted for 50%, 87%, and 67% of aneurysms in groups B, C, and D, respectively. These differences did not reach statistical significance.

Table 2:

Number, percentage, and average peak WSS of ruptured and unruptured aneurysms in each flow type group

Flow Type	Ruptured		Unruptured		Total
	No. (%)	WSS (dyne/cm2)	No. (%)	WSS (dyne/cm2)
A	1 (25)	700	3 (75)	63	4
B	2 (50)	78	2 (50)	60	4
C	13 (87)	283	2 (13)	225	15
D	2 (67)	160	1 (33)	150	3
Total	18 (70)	271	8 (30)	114	26

Note:—WSS indicates wall shear stress.

MWSS was diverse across the sample with values ranging from 10 to 1500 dyne/cm² and a mean of 222 dyne/cm². No value separated ruptured from unruptured aneurysms. MWSS for the unruptured aneurysms ranged from 10 to 230 dyne/cm² (mean, 114 dyne/cm²) compared with ruptured aneurysms from 35 to 1500 dyne/cm² (mean, 271 dyne/cm²). However, this difference in MWSS was statistically significant at 90% of confidence levels (P = .10). All the unruptured aneurysms in group A had a low WSS (63 dyne/cm²), whereas the only ruptured aneurysm in that flow type had an MWSS 1 order of magnitude higher. Aneurysms in group B showed a relatively small MWSS, which was slightly higher in ruptured aneurysms (78 dyne/cm²) than in unruptured ones (60 dyne/cm²). In contrast, aneurysms in groups C and D, which had higher rupture rates, had larger MWSSs. Specifically, the average MWSSs for unruptured and ruptured aneurysms in group C were 225 and 306 dyne/cm², whereas those for group D were 150 and 163 dyne/cm², respectively (Table 2).

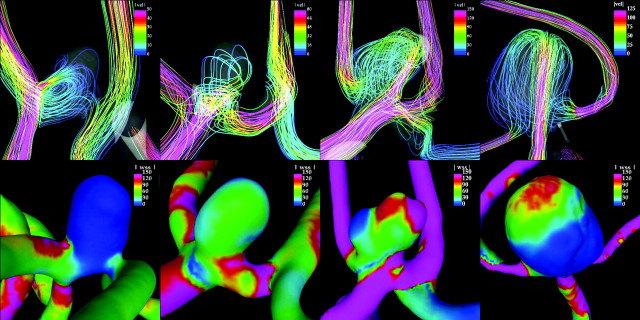
Figure 2 shows visualizations of the flow pattern (top row) and corresponding WSS distributions (bottom row) for 4 selected aneurysms, 1 of each flow type group. This figure shows that for flow types A and B, the inflow jets disperse before entering the aneurysm, producing low WSSs in the aneurysm. In contrast, in flow types C and D, the inflow jets impact on the aneurysm body and dome, respectively, producing higher values of WSS. In particular, in flow type C, the inflow jet slides along the aneurysm wall, producing the highest values of WSS. The main difference between types C and D is that in type C, the flow splits at the neck of the aneurysm, with 1 secondary jet entering the aneurysm close to the wall and the other flowing to 1 of the daughter branches. In contrast, in type D, the flow enters the aneurysm and travels to the dome where it impacts and splits, creating 2 secondary streams that flow to each of the daughter branches.

Fig 2.

Streamlines colored with the velocity magnitude (top row) and instantaneous WSS distributions (bottom row) at the peak systole for 4 selected aneurysms with different flow types (from left to right: flow types A, B, C, and D) whose MWSS is of 10, 60, 200, and 150 dyne/cm², respectively. The same color scale of 150 dyne/cm² is used for all the WSS images. Only flow type C aneurysm is ruptured.

Discussion

Aneurysms in this study group were more commonly associated with asymmetric inflow whether related to hypoplastic A1s or receiving inflow from 1 A1. Intra-aneurysmal flow patterns were most often complicated with unstable jets (flow types III and IV) or multiple intra-aneurysmal vortices (flow types II and IV). Complex intra-aneurysmal flow was similarly found by Kerber et al²⁰ in a study of a ruptured lethal AcomA, by using an acrylic flow model manufactured from a postmortem specimen. In contrast to a study of aneurysms excluding AcomA aneurysms,⁹ where a simple stable flow type I was most common, we found type IV (50%) to be the most common flow type. We were unable to find a statistical association between these intra-aneurysmal flow types and the clinical history of previous rupture. Using a similar analysis of impaction zone size, we also found an increased incidence of rupture in aneurysms with small impaction zones when compared with those with large impaction zones (83% versus 63%), but we could not confirm a statistical association as in Cebral et al.⁹

The asymmetric nature of the AcomAs in this study population led to many of the AcomAs being configured analogous to terminal or bifurcation aneurysms. As such, there was the potential for the aneurysm to receive differing proportions of the parent artery inflows. Our classification of inflow patterns from the parent artery was an attempt to group them in a logical manner. Only a small minority of the aneurysms shared a portion of inflow from both A1s in type A, of which most (75%) were not ruptured. As aneurysms receive a greater proportion of the parent artery flows, the frequency of being ruptured appears to increase (types C and D were 87% and 67%, respectively). Receiving a larger proportion of parent artery inflow appears to account for the higher MWSS found in these aneurysms.

At first glance, our finding that type C exceeds type D in MWSS and incidence of rupture is confusing. However, review of the streamline visualizations has shown that the type C aneurysms tend to have inflow jets that are asymmetric to the aneurysm dome, so the jets often impact against the side of the dome at a short distance from the neck. This would cause a shorter and, therefore, less dispersed inflow jet, which impacts at a more tangential angle. Together this would tend to generate higher localized WSS. When considered alone, MWSS appears to be the most important factor in determining whether an aneurysm had ruptured in our study group. Ruptured aneurysms had a mean MWSS of 271 dyne/cm² compared with 114 dyne/cm² for the unruptured aneurysms, which was statistically significant at a 90% confidence level. Considering that the small size of this sample would yield an expected statistical power of only 37%, we believe that achieving any statistical result argues that this association may be significant.

It is possible that the size of the impaction zone, flow patterns, and WSS is a surrogate marker for a different, more relevant hemodynamic variable. There are numerous other possible variables that can be studied, such as the gradient of WSS, oscillating shear index, and measures of stagnation. Also, there could be multiple concomitant effects, such as a smaller impaction zone, which might imply a larger region of low WSS. Until a better understanding of the biomechanical relationships in aneurysm pathophysiology is obtained, it will be difficult to systematically exclude the large number of hemodynamic measures that we can construct. Our goal was to obtain an indication of where to look so that we could examine more closely the most likely variables.

The findings of this study may have important implications in our understanding of the mechanisms responsible for aneurysmal rupture. We have found more ruptured aneurysms with small impaction zones, higher inflows, and, consequently, higher MWSS. If this finding is confirmed in further work, it may imply that flow concentrations within aneurysms play a role in inducing mechanisms within the aneurysmal wall that lead to the mechanical failure responsible for the rupture. It may also imply that aspect ratio may be predictive of aneurysmal rupture not as a predictor of the low-flow recirculation (ie, low WSS) but because narrow necks in large aneurysms geometrically induce narrow inflow jets and small concentrated impaction zones. Furthermore, MWSS potentially could be used as a predictor of aneurysms at increased rate of future rupture. Computational fluid dynamics (CFD) analysis could be used clinically to help select those aneurysms at higher risk for progression and rupture, which, therefore, should be treated.

Although interesting trends and associations have been found in this study, care must be taken in extending these findings to aneurysms in general. The study is of a unique hemodynamic situation found in the anterior communicating complex. Although the study is large by standards of previous CFD works, the absolute size is quite small, accounting for the lack of strong statistical results, on which we commonly rely. The sample demographics do compare well with previous works. The patient population considered for this study was composed of 16 patients (58%) with bilateral A1 segments and 11 patients (42%) with 1 A1 segment missing. Similar findings were reported in a previous study in which 45% of the patients with AcomA aneurysms showed a hypoplastic A1 segment.⁵ Exclusive filling of the AcomA aneurysm from 1 of the A1 segments was observed in 75% of our computational models of the bilateral group. This is in good agreement with 78% of the cases reported in a previous study.⁶ Similarly, the large majority of our AcomA aneurysms were ruptured. Ideally, an equally large cohort of unruptured aneurysms would be available for our analysis.

Our study relies on the 3DRA performed on the aneurysms, many of which had already ruptured. The event of rupture could affect the geometry of the aneurysms study, potentially influencing the intra-aneurysmal hemodynamics. Rupture most frequently occurs at the aneurysm dome; therefore, the hemodynamic variables related to the flow jet in the parent vessel and its split into the aneurysm and daughter vessels will not change dramatically. The size of the impaction zone can be influenced by the incident angle of the contact between the jet and the aneurysmal wall at the dome, but this effect is likely small in the absence of formation of a clear daughter sac (bleed). However, no data exist to corroborate (or disprove) this assumption. This limitation is found in any retrospective study performed to date on aneurysm rupture. Only a prospective study of aneurysms before and after rupture could answer this question.

Computational methods are based on assumptions that could affect the results of CFD simulations. From previously reported sensitivity analyses,^8,21 the most important factor for accurate modeling of the intra-aneurysmal hemodynamics is the geometry of the aneurysm and the parent vessel. We used vascular models from the highest resolution and contrast imaging techniques currently available (3DRA) and took great care to compare the constructed 3D models with the conventional cerebral angiography images to avoid errors. Because hemodynamic information was not available for each of the patients in this study, we used representative flow conditions obtained from healthy volunteers. These parameters could be obtained from noninvasive imaging (PC-MR or transcranial Doppler) or invasive means through angiographic techniques but were not practical for the patients in our study group.

The representative flow conditions were scaled to match the vessel diameter to reach a mean wall shear measured experimentally.¹⁷ Previous sensitivity analysis showed that varying these parameters in the expected physiologic range does not significantly alter the major flow structures in the parent artery or intra-aneurysmally.⁸ However, this approximation may have a significant influence on the measured peak WSS. Because the intra-arterial flow conditions are likely to vary within a given individual from moment to moment due to differences in the level of blood pressure, activity, etc, we believe that there may be not be a single set of “correct” conditions. Using an approximate representative set of conditions seems to be a reasonable method until we are able to isolate a single set of variables that have the most influence on aneurysmal rupture.

Unlike most aneurysms previously studied, AcomA aneurysms have the potential of inflow from 2 sources. Asymmetry in the inflow waveforms of bilateral AcomA aneurysms can have an important effect on the intra-aneurysmal hemodynamics.²² These effects are important in aneurysms with symmetric geometries of the contributing A1 segments. These represented only a small minority of our patient population. The extent of this influence on our simulations is not certain because it is not known how much asymmetry of flow conditions exists in vivo. Wall compliance, non-Newtonian properties of blood, outflow conditions, and the numeric technique used to solve the governing equations can also affect the hemodynamics.^8,23,24 However, if the vascular geometry is correctly modeled, all these other factors are likely to affect the small scale details of the flow patterns. Because our flow classification is based on macroscopic characteristics of the flow pattern, it is likely that it will not be significantly affected by these limiting assumptions. Finally, the modeling that we used neglects the influence of the perianeurysmal environment, which has recently been found to exert some influence on aneurysmal progression and rupture.²⁵

Conclusions

In this study, the flow dynamics in 26 AcomA aneurysms was analyzed by using image-based computational fluid dynamics methods. Aneurysms with small impaction zones, higher flow rates into the aneurysm, and elevated maximum WSS were more likely to be ruptured.