Structural transitions in ion coordination driven by changes in competition for ligand binding

Abstract

Transferring Na⁺ and K⁺ ions from their preferred coordination states in water to states having different coordination numbers incurs a free energy cost. In several examples in nature, however, these ions readily partition from aqueous-phase coordination states into spatial regions having much higher coordination numbers. Here we utilize statistical theory of solutions, quantum chemical simulations, classical mechanics simulations and structural informatics to understand this aspect of ion partitioning. Our studies lead to the identification of a specific role of the solvation environment in driving transitions in ion coordination structures. Although ion solvation in liquid media is an exergonic reaction overall, we find it is also associated with considerable free energy penalties for extracting ligands from their solvation environments to form coordinated ion complexes. Reducing these penalties increases the stabilities of higher-order coordinations and brings down the energetic cost to partition ions from water into over-coordinated binding sites in biomolecules. These penalties can be lowered via a reduction in direct favorable interactions of the coordinating ligands with all atoms other than the ions themselves. A significant reduction in these penalties can, in fact, also drive up ion coordination preferences. Similarly, an increase in these penalties can lower ion coordination preferences, akin to a Hofmeister effect. Since such structural transitions are effected by the properties of the solvation phase, we anticipate that they will also occur for other ions. The influence of other factors, including ligand density, ligand chemistry and temperature, on the stabilities of ion coordination structures are also explored.

Introduction

Na⁺ and K⁺ ions play vital roles in numerous biochemical reactions as their binding affects activities of several globular proteins^{1, 2} and RNA³ enzymes. In addition, their direct interactions with functional groups in ion channels enables regulation of their concentration gradients across cellular membranes, which allows a wide variety of high-level physiological tasks to be accomplished: from nutrient uptake and volume control in individual cells, to the generation and propagation of nerve signals and regulation of muscle activity such as in a heartbeat.⁴ Direct interactions or chelation of these ions with biological molecules occur only when they partially or completely shed the water molecules present within their inner coordination shells in the aqueous phase. Here we carry out a combination of quantum chemical simulations, classical molecular dynamics (MD) simulations and structural informatics studies to understand the details of one specific aspect of this ion-partitioning phenomenon.

Recent studies based on neutron diffraction experiments^5-7 and ab initio molecular dynamics (AIMD) simulations^8-11 strongly suggest that in aqueous phase Na⁺ and K⁺ ions coordinate with five and six water molecules, respectively. These values correspond to the average numbers of water oxygens within the spherical sub-volume Γ = 4/3 πr³ bounded by the principal minima of their radial distribution functions g(r), that is, for r ≤ 3.0 Å for Na⁺ and r ≤ 3.5 Å for K⁺. Data from these AIMD simulations,^8-11 and also from longer time-scale trajectories generated as part of this work, show how coordination numbers, n, are distributed within Γ (figure 1). Several noteworthy observations regarding these distributions can be made. First, the preferred coordination numbers P_Γ(n) for sub-volumes Γ(r = 3.0) for Na⁺ and Γ(r = 3.5) for K⁺ need not match the respective average coordination numbers of these ions. This results from asymmetric distribution of P_Γ(n) around the most preferred values. Furthermore, the values of both preferred and average coordinations depend upon the size of Γ chosen for analysis and, most importantly, the probability P_Γ(n) of finding a coordination number n within Γ decreases sharply as one departs further away from the most preferred numbers. If the sub-volume around the ion were chosen to be smaller, for example, where r = 3.0 Å for K⁺, the preferred coordination number drops to four,^10-12 and the probability of finding greater than six water molecules within this sub-volume becomes negligible (figure 1). A similar trend is also seen for Na⁺ ions, where decreasing the size of the sub-volume by setting r = 2.5 Å reduces the preferred coordination number to three. In other words, there is a free energy cost ΔG_Γ associated with transferring ions from their respective preferred coordination states to a different coordination state inside a given Γ,

$$\Delta G_{\Gamma }=-RT\ln (P_{\Gamma }\left(n\right)∕P_{\Gamma }\left(n_{\text{preferred}}\right)).$$ [1]

This energetic cost gets progressively larger as n takes up values much larger or smaller than n _preferred.

Figure 1.

Probability P_Γ(n) to find n water oxygens within a spherical sub-volume Γ = 4/3 πr³ around the ion, where r is the distance from the ion in ångström units. These probabilities were estimated from separate AIMD trajectories of (a) Na⁺ and, (b) K⁺ ions. Probabilities are plotted in energy scale (kcal/mol).

There are, however, several exceptional cases in nature^{1, 2, 13-19} where these ions readily partition from such aqueous-phase coordination states into spatial regions having much higher coordination numbers. For example, low temperature x-ray data show that the binding sites in lysozymes, neurotransmitter transporters, dialkylglycine decarboxylases, and thrombins coordinate Na⁺ ions using five or six ligands, and that all these ligands lie within 2.5 Å from the Na⁺ ion (table 1). At the same time, other biomolecules like potassium channels, nonactin, pyruvate kinases, and chaperons coordinate K⁺ ions using more than six ligands, and all these ligands lie within 3.0 Å from the K⁺ ion. In particular, crystallographic data for the celebrated potassium channels^20-23 show that their binding sites coordinate K⁺ using eight carbonyl ligands, all of which are within 3.0 Å from the K⁺ ion. This makes for twice as many ligands as seen preferentially around K⁺ in aqueous phase, which according to equation 1 and the data in figure 1, indicates that the transfer of a K⁺ from liquid water to the binding sites in K-channels requires an enormous uphill transition on the free energy surface.

Table 1.

Examples of proteins that bind Na⁺ and K⁺ ions in states of over-coordination (higher than the coordination in water).

Ion	Biomolecule	PDB ID	# Ligands	rave (Å)
Na+	Neurotransmitter Transporter	2A65a	5	2.3
	Dialkylglycine decarboxylase	2DKBb	6	2.4
	Lysozyme	1V7Tc	6	2.4
	Neurotransmitter Transporter	2A65a	6	2.4
	Thrombokinase	1BOKd	6	2.5
K+	Chaperon Hsc70	1HPMe	7	3.0
	Pyruvate Kinase	1A49f	7	2.8
	Chaperon Hsc70	1HPMe	8	2.9
	Potassium Channel	1K4Cg	8	2.8
	Nonactin	n.a.h	8	2.8

^aReference ¹³

^bReference ¹⁴

^cReference ¹⁵

^dReference ¹⁶

^eReference ¹⁸

^fReference ¹⁷

^gReference ²⁰

^hReference ¹⁹

Clearly, there cannot be large free energy costs associated with such processes as ions are readily able to transfer back-and-forth between aqueous phase and biological molecules under standard physiological conditions. What physical principles explain such structural transitions? Do the binding site environments in these biological molecules somehow trigger a transition in ion coordination preferences? Or, are there any special chemical and/or structural features present in the binding environments of biological molecules that simply reduce the energetic cost associated with over-coordination (relative to the low coordinations in water), without actually altering ion coordination preferences? Or, do the specific chemistries of the ligands present in these binding sites effect such structural transitions?

An approach toward understanding the underlying basis of this ion coordination phenomenon begins with identifying the roles of various factors that affect the energetics of ion-ligand association reactions in solutions, such as ligand number, solvation environment and ligand chemistry. This task becomes easier if the energetics of the ion-ligand association reactions in solutions could be estimated as functions of such determinants, thus providing insights into their explicit and combined roles and leading to clues for explaining the above anomaly. One way to accomplish this is to utilize the quasi-chemical organization of solution theory.^24-30 In this theory, the chemical potential of the solute is formulated in such a way that the 3-dimensional space around the solute is divided into separate inner- and outer-shell domains, enabling an estimation of energetic contributions to ion-ligand association arising from local and distant solvation environments.

Using the quasi-chemical approach, we first estimate solvation free energies of Na⁺ and K⁺ ions in three different liquid media, each representing a different ligand chemistry offered by the binding sites in biological molecules. Such a strategy provides estimates of the explicit roles of ligand chemistry and solvation phase in driving ion-ligand association reactions. In addition, the inner-shell clusters in the cluster implementation are built up by incrementally solvating the ion with increasing numbers of surrounding solvent molecules, which provides an estimate of the role of ligand numbers in driving ion solvation. We then carry out a series of other case studies using classical molecular dynamics (MD) simulations, probing the inferences derived from the earlier quasi-chemical analysis. Finally, we scrutinize our findings from the quasi-chemical and MD analyses against the structural and chemical properties of the ion binding sites listed in table 1, where ion binding occurs in states of over-coordination relative to water.

We find that the local solvation environment of ligands, which also includes ligand concentrations and structural flexibility, plays a significant role in driving transitions in ion coordination structures. Although important to other aspects of ion-host interactions, ligand chemistry appears to be less important in driving ion coordination transitions.

Methods

A) Quasi-chemical theory of solutions

The quasi-chemical organization of solution theory^24-30 enables calculation of solvation free energy in terms of individual contributions arising from local and distant solvation effects. The volume surrounding the solute is divided into an inner- and an outer-shell domain, where the inner-shell domain captures the solute and a subset of the solvent molecules. Solvent occupation statistics are then collected for the inner domain, where clustering equilibria occur, thus providing an estimate of the effect of coordination number on solvation energy. Since details of the theory are described elsewhere,^24-30 here we outline only those results of the formulation that show how the free energy is partitioned into individual components, which provide insight into the driving forces of ion solvation by any medium.

The Gibbs free energy or the chemical potential of a solute particle (A) can be written as,^{30, 31}

$${\mu }_A=RT\ln \left(\frac{{\rho }_A{\Lambda }_A^3}{q_A^{\mathrm{int}}}\right)+{\mu }_A^{ex},$$ [2]

where ρ_A is the number density of the solute, Λ_A is the thermal de Broglie wavelength and $q_A^{\mathrm{int}}$ is the partition function of a single solute particle without translational degrees of freedom. The first term in equation 2 is the ideal gas contribution to the chemical potential, while the second term, which is the quantity of primary interest for the present work, is the excess chemical potential. The potential distribution theorem^{25, 30} defines this excess chemical potential as

$${\mu }_A^{ex}=-RT\ln {\langle \langle e^{-\beta \Delta U_A}\rangle \rangle }_0$$ [3]

where, β = 1/RT and ΔU_A is the potential energy of interaction between the solute and solvent molecules. The double brackets indicate averaging over the thermal motions of the solute and the solvent molecules. The subscript zero, in line with Widom’s particle insertion method,²⁵ emphasizes that this average is obtained in the absence of solute-solvent interactions. This excess chemical potential can be separated into two terms:^{24-27, 29, 30}

$$\beta {\mu }_A^{ex}=\ln \left[x_{\Gamma ,n=0}\right]-\ln {\langle \langle e^{-\beta \Delta U_A}\prod _j[1-b_{\Gamma }\left(j\right)]\rangle \rangle }_0.$$ [4]

The first term provides the inner-shell contribution to the excess chemical potential of solute A, while the second term provides the outer-shell contribution. The quantity x_Γ,_n=0 in the first term is the probability that an arbitrarily defined inner-shell domain Γ contains the solute particle without any solvent molecules (n = 0). b_Γ(j) is an indicator function that takes up a value of one when the j^th solvent molecule is inside Γ and zero otherwise. This formulation can be utilized directly in conjunction with standard molecular simulation techniques, such as MD or Monte Carlo simulations, to determine solvation energies as functions of, for example, the shapes and volumes³² of the inner-shell domain Γ. It is straightforward to see that while the net excess chemical potential of a solute ${\mu }_A^{ex}$ will be independent of the shape or the volume of the inner-shell domain Γ, as can also be seen in figure 3 of reference ³², the relative contributions arising from inner- and outer-shell domains will change with the definition of Γ.

Figure 3.

Schematic illustrating the general idea that when an ion is transferred from one environment (say liquid water l_W) to another (say biological ion binding site ξ), then the free energy cost ΔΔG_lW→ξ(n_lW → n_ξ) associated with changes in the coordination number of the ion (n_lW → n_ξ) can be overcome through modifications in free energy penalties ΔΔΦ^R-O(l_W →ξ) associated with extracting ligands from the their environments.

For the present study, we are particularly interested in probing solvation free energies as functions of the numbers (n > 0) of solvent molecules inside the inner-shell domain of the solute. This can be accomplished by expressing the probability x_Γ,n=0 as a function of the equilibrium constants K_n of the solute-solvent association reactions that occur inside the inner-shell domain of the solute particle. In a specific scenario where solute A interacts with n solvent particles of type B inside volume Γ to form cluster AB_n,

$$A+nB\stackrel{K_n}{\to }A{B}_n,$$ [5]

the probability to find zero solvent molecules within Γ is,

$$x_{\Gamma ,n=0}\equiv \frac{C_{A{B}_0}}{\sum _n{C}_{A{B}_n}}=\frac{1}{\sum _n{K}_n{\left[C_B\right]}^n}.$$ [6]

Here C_ABn and C_B are, respectively, the concentrations of the cluster and solvent particles. Inserting this into equation 4 yields

$$\beta {\mu }_A^{ex}=-\ln \left[\sum _{n\ge 0}{K}_n{C}_B^n\right]-\ln {⟪e^{-\beta \Delta U_A}\prod _j[1-b_{\Gamma }\left(j\right)]⟫}_0.$$ [7]

For the specific association reactions defined by equation 5, the equilibrium constants K_n can be expressed as³⁰

$$K_n=K_{n,\Gamma }^{\left(0\right)}\frac{{⟪e^{-\beta \Delta U_{A{B}_n}}⟫}_{0,\Gamma }}{{⟪e^{-\beta \Delta U_{A{B}_0}}⟫}_{0,\Gamma }{\left\{{⟪e^{-\beta \Delta U_B}⟫}_0\right\}}^n}$$ [8]

Here, $K_{n,\Gamma }^{\left(0\right)}$ are the “ideal” equilibrium constants of the association reactions given by equation 5. They differ from K_n as they do not include any effects of the complementary region Γ^C outside the inner-shell domain. The specific effects of Γ^C on K_n are incorporated through the ensemble averages in equation 8. Note that the ideal equilibrium constant $K_{n,\Gamma }^{\left(0\right)}$ should not be confused with the gas-phase equilibrium constant $K_n^{\left(g\right)}$. $K_{n,\Gamma }^{\left(0\right)}$ are obtained under the condition that the association equilibrium occurs within a predefined inner-shell domain Γ, whereas the estimations of $K_n^{\left(g\right)}$ are free from any such impositions. The quantity 〈〈e^-βΔU_ABn〉〉_0,Γ is the ensemble average of the distribution that is the product of the distributions for the solvent molecules in Γ^C and for the complex enclosed within the region Γ. The ensemble average 〈〈e^-βΔU_B〉〉₀, just like in equation 3, is related to the excess chemical potential of the solvent molecule B as:

$${\mu }_B^{ex}=-RT\ln {⟪e^{-\beta \Delta U_B}⟫}_0.$$ [9]

The ensemble average 〈〈e^-βΔU_AB0〉〉_0,Γ in equation 8 is, in fact, precisely equal to the ensemble average in the second term of equation 7, that is,

$${⟪e^{-\beta \Delta U_{A{B}_0}}⟫}_{0,\Gamma }={⟪e^{-\beta \Delta U_A}\prod _j[1-b_{\Gamma }\left(j\right)]⟫}_0.$$ [10]

Introducing the relationships in equations 8 and 10 into equation 7 and rearranging yields

$$\beta {\mu }_A^{ex}=-\ln \left[\sum _{n\ge 0}{K}_{n,\Gamma }^{\left(0\right)}\left[\frac{{⟪e^{-\beta \Delta U_{A{B}_n}}⟫}_{0,\Gamma }}{{\left\{{⟪e^{-\beta \Delta U_B}⟫}_0\right\}}^n}\right]C_B^n\right].$$ [11]

This quasi-chemical formulation shows how the excess chemical potential of a solute A can be estimated in terms of individual contributions arising from inner- and outer-shell domains: $K_{n,\Gamma }^{\left(0\right)}$ provides the contribution from the inner-shell domain while the ratio of the ensemble averages within the inner square brackets provides the contribution from the outer-shell domain.

We now describe how we implement this quasi-chemical framework to determine the solvation free energies of Na⁺ and K⁺ ions in three different liquid media: methanol, water and formamide. Under standard conditions, these solvents have different dielectric constants of 33, 78.5 and 109.5, respectively. In addition, they provide different chemistries for ion-ligand association that are representative of the chemistries offered to ions in the binding sites of biological molecules.

Implementation

Following the formulation in equation 11, the solvation free energy, $\Delta G_n^A\left(l_B\right)$, of an ion of type A in the liquid phase (l) of solvent molecules of type B can be computed as the sum of four separate terms:^{24-27, 29, 30}

$$\Delta G_n^A\left(l_B\right)=\Delta G_{n,\Gamma }^A\left(g_B\right)+n.\Delta G_{\mathit{conc}}^B+\Delta G_{n,\Gamma }^{A{B}_n}\left(l_B\right)-n.\Delta G^B\left(l_B\right).$$ [12]

These four terms are:

1. The “intrinsic” free energies $\Delta G_{n,\Gamma }^A\left(g_B\right)$ of ion-ligand association reactions estimated in the gas phase, but under the condition that the ion-ligand association equilibria occur within a predefined volume Γ around the ion. $\Delta G_{n,\Gamma }^A\left(g_B\right)$ can occasionally be equal to the ion-ligand association energies in gas phase, but in general $\Delta G_{n,\Gamma }^A\left(g_B\right)\ge \Delta G_n^A\left(g_B\right)$;

2. The contribution from the actual concentration of the solvent molecules, $\Delta G_{\mathit{conc}}^B$, which may be different from their concentrations in gas phase used in the estimation of the previous term $\Delta G_{n,\Gamma }^A\left(g_B\right)$;

3. The solvation free energies, $\Delta G_{n,\Gamma }^{A{B}_n}\left(l_B\right)$, or the excess chemical potentials of individual clusters (AB_n) in the solvent l_B;

4. The solvation free energy, ΔG^B(l_B), or the excess chemical potential of the solvent molecule B in its bath l_B;

Note that while we evaluate solvation free energies, $\Delta G_n^A\left(l_B\right)$, for various ion-ligand coordination complexes, an ion’s excess chemical potential will result from formation of the most probable complex, that is, the one for which $\Delta G_{n=n_{\text{preferred}}}^A\left(l_B\right)$ has the lowest most favorable value.

One way to determine these contributions to ion solvation is to utilize the ab initio level of theory to describe explicitly the complex interactions between the ion and the ligands inside the inner-shell domain Γ, while the remaining longer-range interactions can be described using an implicit solvent model. The radius chosen to define the spherical boundary for the inner-shell domain essentially determines the number of solvent molecules that will be treated explicitly at the ab initio level of theory. Choosing a large radius can result in expensive calculations on a large number of association reactions, whereas choosing a small radius may not provide sufficient information to understand the dependency of solvation energy on relevant ligand numbers. Note that while the net solvation free energy of an ion, $\Delta G_n^A\left(l_B\right)$, will not depend upon the choice of the radius of the inner-shell domain Γ, the relative contributions arising from the inner- and outer-shell domains will change with the choice of the radius.

To select a radius for defining the spherical boundary of the inner-shell domain, we first examine the low temperature x-ray data in table 1. We see that, despite the apparent over-coordination in the biological ion binding sites, the average distance of ligands from Na⁺ is less than 2.6 Å, while the average distance of ligands from K⁺ is less than 3.1 Å. From the AIMD simulations in liquid water,^8-11 we also know that the average distances of Na⁺ and K⁺ ions from the water oxygens within their respective canonical inner-shells are also less than 2.6 Å and 3.1 Å. We therefore define the inner-shell boundary around Na⁺ using a radius of 2.6 Å, and around K⁺ using a radius of 3.1 Å. As we will demonstrate using molecular dynamics simulations, these boundaries also naturally accommodate the average inner-shell ion-carbonyl distances for fully flexible ligands under conditions of room temperature. Note that for these chosen volumes of the inner-shell domains, the packing penalties are small³² and expected to be equivalent in magnitude but opposite in sign to the van der Waals interaction between the inner- and outer-shell molecules. Neither of these contributions is determined explicitly in this work as they are expected to cancel out.

The intrinsic Gibbs free energies $\Delta G_{n,\Gamma }^A\left(g_B\right)$ of the ion-ligand association reactions were determined by describing all interactions at the ab initio level of theory. The 3-dimensional structures of the ligands and their respective inner-shell coordination complexes with the ions were first optimized using the hybrid B3LYP^{33, 34} density functional theory (DFT). All ion-ligand coordination distances were found to be less than the respective radii chosen to describe the boundary of the inner-shell domain. See supplementary text for illustration of the Na⁺-water and K⁺-water optimized configurations and note that the configurations of the ion-methanol and ion-formamide optimized complexes resemble those of the ion-water optimized configurations.

Each optimized structure was then analyzed to determine its individual free energies G^A(g), G^B(g) and $G_{n,\Gamma }^{A{B}_n}\left(g\right)$. Entropies for all reactant and product species were determined separately from partition functions³⁵ evaluated at their respective potential energy minima and at a temperature (T) of 298 K and pressure (P) of 1 atmosphere. In particular, harmonic expansions (Hessian analysis) about these potential energy minima produce estimates of the vibrational frequencies, thereby capturing the effects of thermal fluctuations within each potential energy well. If optimization algorithms fail and the final geometry does not correspond to a stable minimum on the potential energy surface, the computed vibrational frequencies end up imaginary. All frequencies were found to be real, confirming the existence of energetically optimized structures. Next, these free energies were combined to obtain gas-phase reaction free energies for the various inner-shell association reactions,

$$\Delta G_{n,\Gamma }^A\left(g_B\right)=\Delta G_{n,\Gamma }^{A{B}_n}\left(g\right)-G^A\left(g\right)-n.G^B\left(g\right).$$ [13]

Note that in these computations we do not account for: (a) anharmonicities in the vibrational motions of the ion complexes, and (b) fluctuations due to configurational changes within the inner-shell domain, as each of the different n-fold inner-shell coordination states of the ions are represented using single optimized structures. Separate calculations in fact demonstrate a significant effect on energetics due to the presence of anharmonicity and configurational fluctuations only in higher order (n > 5) ion-ligand clusters. While corrections for these anharmonicities and configurational fluctuations result in more exothermic association reactions, they do not alter any of the conclusions drawn from this study. The details of these calculations are not included here as they are subject of a separate publication. (See reference ³² for a description of methods used for explicitly calculating free energy contributions due to anharmonicities.)

All optimization and subsequent frequency calculations were carried out with the Gausssian 03 suite of programs³⁶ using the following basis sets: a 6-31G(d) basis set for Na⁺ ions, a 6-31++G(d,p) basis set for H, C, N and O atoms, and a 6-311+G(2d) basis set for K⁺ ions. Our reasons for selecting these basis sets are summarized in the legend of table 2. Guided by previous investigations dealing with the effects of basis sets on estimating gas-phase H₂O-H₂O and H₂O-HF interactions,³⁷ we systematically explored several possibilities until we arrived at this combination of basis sets, which yields ion-water dissociation energies in excellent agreement with experiment.^38-40

Table 2.

Effect of Na⁺ and K⁺ basis sets on computed gas phase Gibbs free energies (kcal/mol).^†

Basis Set	ΔGNa+(H2O)3→Na+(H2O)2+(H2O)(g)		ΔGK+(H2O)3→K+(H2O)2+(H2O)(g)
	Estimated	% Error	Estimated	% Error
Expt.a	9.5		6.3
6-31G(d)	9.6	1.1	5.8	7.9
6-31+G(d)	9.6	1.1	5.6	11.1
6-31+G(2d)	-	-	5.4	14.3
6-311+G(2d)	-	-	6.4	1.6

^†Our goal here is to find the smallest basis set that estimates the experimental free energy difference between two randomly selected ion-water complexes within a 2% error. To accomplish this, we start with the 6-31G(d) basis set for each ion and gradually increase its size. We keep the basis set for the water molecule fixed at 6-31++G(d,p) in accord with the observation³⁷ that it yields the energetic and structural properties of dipole-dipole interactions, H₂O-H₂O and H₂O-HF, in excellent agreement with experiment.

^aReference ³⁹

The favorable gain in reaction free energy $\Delta G_{\mathit{conc}}^B$ associated with a higher concentration (or, alternatively, higher pressure) of solvent molecules in the liquid phase (C_l > C_g) was determined as follows. Since the translational term of the molecular partition function can be singled out,^{30, 35, 41} allowing the chemical potential of a solvent molecule B to be written as a summation,

$${\mu }_B\left(l\right)={\mu }_B\left(g\right)-RT\ln {\langle e^{-\Delta U_B∕kT}\rangle }_N-RT\ln (C_l∕C_g),$$ [14]

this translational contribution was determined as a function of the ratio of solvent molecule concentrations (or pressures) in liquid (C_l) and gas (C_g) phases, that is, as

$$\Delta G_{\mathit{conc}}^B=-{\beta }^{-1}\ln (C_l∕C_g).$$ [15]

The gas phase concentration was taken as 0.041 M, while the liquid phase concentrations of methanol, water and formamide were taken as 24.7 M, 55.6 M and 25.2 M, respectively.

The excess chemical potentials of the solvent molecules, ΔG^B(l_B), and individual clusters, $\Delta G_{n,\Gamma }^{A{B}_n}\left(l_B\right)$, were determined by treating the outer-shell domain as an implicit solvent. The finite difference (FD) scheme of the APBS package⁴² with a finest grid spacing of 0.1 Å was used for solving the Poisson’s equation. Partial charges of atoms in the ligands and complexes were obtained from separate DFT/B3LYP calculations using the optimized structures and the ChelpG method,⁴³ and were distributed over the FD grids using cubic B-spline discretization. Atomic radii required for defining solvent exclusion regions were taken from Stefanovich & Truong;⁴⁴ and the diameters of the solvent molecules required to create the molecular surfaces on the FD grids were taken as the distances corresponding to the principal maxima of their oxygen-oxygen pair distribution functions in liquid state, that is, 1.4 Å for water, 1.4 Å for methanol⁴⁵ and 2.15 Å for formamide.⁴⁶ The radii needed to partition the inner- and outer-shell domains were taken as 2.6 Å for Na⁺ ions and 3.1 Å for K⁺ ions.

We note that the method used above for estimating atomic partial charges does not account for the perturbation of the solvent reaction field onto the solute Hamiltonian. To test the effect of the solvent reaction field on the estimation of partial charges and ultimately on the estimation of the excess chemical potentials of clusters, $\Delta G_{n,\Gamma }^{A{B}_n}\left(l_B\right)$, we utilized the Integral Equation Formalism Polarizable Continuum Model⁴⁷ (IEFPCM) implemented in the Gausssian 03 suite of programs³⁶ and computed the excess chemical potentials for two test cases, $\Delta G_{4,\Gamma }^{N{a}^{+}{W}_4}\left(l_W\right)$ and $\Delta G_{4,\Gamma }^{K^{+}{W}_4}\left(l_W\right)$. Consistent with other studies of closed-shell systems,⁴⁸ we found that the incorporation of the perturbation of the solvent reaction field onto the solute Hamiltonian had a minimal effect on the results.

We also note that treating the outer-shell domain Γ^C as an implicit solvent can lead to errors in the estimation of free energy components $\Delta G_{n,\Gamma }^{A{B}_n}\left(l_B\right)$ and ΔG^B(l_B).^49-51 The broad phenomena we observe in this work, however, appear sufficiently robust and are not likely to be compromised by this inaccuracy. In addition, the treatment of the outer-shell domain as an implicit solvent is expected to result in the overestimation of both terms, resulting in a partial-to-complete cancellation when the final solvation free energies $\Delta G_n^A\left(l_B\right)$ are computed. For example, the calculation of ΔG^B(l_B) in the case of ion solvation in water yields a value of -8.4 kcal/mol, which in comparison to other values,⁵² is overestimated by ∼2 kcal/mol. The radii chosen to define the dielectric boundaries, that is, 2.6 Å for Na⁺ ions and 3.1 Å for K⁺ ions, places the low dielectric boundary of the cluster in such a way that it protrudes into the high dielectric region, causing the solvent in the outer-shell domain to be physically closer to the cluster than seen in AIMD simulations.^8-11 This should lead to an overestimation of the values of $\Delta G_{n,\Gamma }^{A{B}_n}\left(l_B\right)$, and as the cluster size increases, this overestimation should also increase, ultimately resulting in a minimization of errors when the summation $\Delta G_{n,\Gamma }^{A{B}_n}\left(l\right)-n.\Delta G^B\left(l\right)$ is computed in equation 11.

B) Ab initio molecular dynamics

Two separate AIMD trajectories were generated within the Born-Oppenheimer scheme⁵³ using the PW91 functional⁵⁴ implemented in VASP⁵⁵ version 4.2: one involving a Na⁺ ion embedded in a box of 64 waters, while the other involving a K⁺ ion embedded in a box of 64 waters. Both trajectories are extensions of previously reported trajectories¹¹ to longer time scales of 20 ps for Na⁺ and 40 ps for K⁺. Note that the K⁺-O pair distribution functions from the 40 ps trajectory of K⁺ have been reported elsewhere.⁵⁶ The following parameters were used for running the simulations in NVE ensembles and with periodic boundaries: cubic box of length 12.4171 Å to emulate water density under standard conditions; Ewald summation with background neutralizing charge; projector augmented-wave method^{57, 58} for description of core-valence electron interactions; explicit treatment of the 2P electrons of Na⁺ and the 3P electrons of K⁺; deuterium mass assigned to protons; kinetic energy cutoff of 500 eV for the expansion of plane waves; gamma-point Brillouin zone sampling; cutoff of 10^-6 eV for energy convergence; and an integration time step of 0.5 fs. The average temperature in the simulation with Na⁺ was 294 ± 11 K, while it was 313 ± 21 K for the simulation with K⁺. Data from these trajectories were used for estimating the probabilities illustrated in figure 1.

C) Classical molecular dynamics

All classical molecular dynamics simulations were carried out using GROMACS⁵⁹ version 3.1.4. Unless otherwise stated, the following parameters were used to carry out simulations in an NVT ensemble: cubic box of length 30 Å; periodic boundaries in all directions; PME with real space cut-off of 10 Å, background neutralizing charge, dipole correction, Fourier spacing of 1.5 Å, a sixth order interpolation and a tolerance of 10^-5 units; a cut-off of 10 Å for van der Waals interactions; recently revised van der Waals parameters⁶⁰ for K⁺; SPC/E⁶¹ charges and van der Waals parameters for description of water models; all atom OPLS⁶² charges and van der Waals parameters for description of all other types of atoms and molecules; an integration time-step of 2 fs; the SETTLE algorithm⁶³ for constraining bond lengths in water molecules; the LINCS algorithm⁶⁴ to constrain all other bond lengths; and a Berendsen method⁶⁵ with a coupling constant of 0.1 ps to maintain temperature at 298.15 K. In simulations involving only an ion and water molecules, the box was filled with 893 water molecules to emulate the density of water under standard conditions. When other molecules were introduced in this simulation box, appropriate numbers of water molecules were deleted to maintain the water densities.

Results and Discussion

(A) Quasi-chemical analysis - Determinants of ion solvation

To determine how ions are able to partition from liquid water (l_W) to higher coordinations in the binding sites of some proteins (ξ) without uphill transitions on the free energy surface, we first need to understand the explicit roles of the various factors that drive the energetics of ion-ligand association reactions in solution. To this end, we first utilize the quasi-chemical framework of solution theory^24-30 to estimate the solvation free energies of Na⁺ and K⁺ ions in liquid water. As described in the methods section, the solvation free energies are estimated as functions of coordination numbers and in terms of individual contributions arising from local and distant solvation effects, which provide an opportunity to inspect their individual and combined roles during ion solvation.

Ion solvation in liquid water

The results of the calculation of the solvation free energies of Na⁺ and K⁺ ion in liquid water using the quasi-chemical framework of solution theory^24-30 are given in table 3.

Table 3.

Quasi-chemical components (in kcal/mol) in the calculation of hydration free energy of Na⁺ and K⁺ ions.

A	n	$\Delta G_{n,\Gamma }^A\left(g_W\right)$a$[\mathrm{Exp}.]$b	$n.\Delta G_{\mathit{conc}}^W$c	$\Delta G_{n,\Gamma }^A\left(g_W\right)+n.\Delta G_{\mathit{conc}}^W$	$\Delta G_{n,\Gamma }^{A{W}_n}\left(l_W\right)$d	n.ΔGW(lW)e	$\Delta G_n^A{\left(l_W\right)}^f$f
Na+	1	-18.6 [-18.8]	-4.3	-22.8	-61.2	-8.4	-75.6
	2	-34.2 [-31.9]	-8.5	-42.7	-60.2	-16.7	-86.2
	3	-43.3 [-40.9]	-12.8	-56.1	-59.8	-25.1	-90.9
	4	-49.4 [-46.9]	-17.1	-66.5	-60.2	-33.5	-93.3
	5	-49.0 [ - ]	-21.4	-70.4	-59.6	-41.9	-88.1
	6	-45.6 [ - ]	-25.6	-71.3	-59.1	-50.2	-80.1
K+	1	-12.0 [-11.8]	-4.3	-16.3	-52.9	-8.4	-60.8
	2	-21.7 [-20.7]	-8.5	-30.3	-53.7	-16.7	-67.2
	3	-27.7 [-27.0]	-12.8	-40.6	-55.0	-25.1	-70.4
	4	-32.0 [ - ]	-17.1	-49.0	-56.3	-33.5	-71.8
	5	-29.8 [ - ]	-21.4	-51.1	-56.1	-41.9	-65.4
	6	-26.9 [ - ]	-25.6	-52.5	-54.3	-50.2	-56.6
	7	-28.8 [ - ]	-29.9	-58.7	-54.9	-58.6	-55.0
	8	-30.6 [ - ]	-34.2	-64.8	-56.2	-67.0	-53.9

^a$\Delta G_{n,\Gamma }^A\left(g_W\right)$ is the intrinsic Gibbs free energy of ion-ligand association reaction at T = 298 K and P = 1 atm, and is estimated using equation 13. Computed values are compared to the experimental estimates of Tissandier et al.,⁴⁰ but the comparison is limited to lower order clusters, n ≤ 4 for Na⁺ and n ≤ 3 for K⁺. This is because separate calculations⁶⁷ at the MP2 level of theory show that the experimental estimates for higher order gas-phase clusters correspond to configurations where waters do not directly coordinate the ion, a scenario entirely different from the one considered for this quasi-chemical analysis.

^bReference ⁴⁰

^c$\Delta G_{\mathit{conc}}^W$ refers to the favorable gain in reaction free energy associated with a higher concentration of water molecules in the liquid phase as compared to the gas phase.

^d$\Delta G_{n,\Gamma }^{A{W}_n}\left(l_W\right)$ refers to the solvation free energy of an n-fold ion-water cluster in liquid water.

^eΔG^W (l^W) is the solvation free energy of a single water molecule W in liquid water.

^f$\Delta G_{n,}^A\left(l_W\right)$ is the solvation free energy of the ion coordinating with n water molecules in liquid water and is equal to the summation given by equation 12. The lowest most favorable value of $\Delta G_{n,}^A\left(l_W\right)$ corresponds to the ion’s absolute hydration free energy, as it is the dominant term.

For the specific radii used to define the inner-shell domains, that is, 2.6 Å for Na⁺ and 3.1 Å for K⁺, we find that both ions prefer to coordinate with four water molecules, consistent with the results from AIMD simulations illustrated in figure 1.^† The resulting absolute hydration free energies of both ions, that is, values corresponding to $\Delta G_n^A\left(l_W\right)$ when n = n _preferred = 4, are within 3% of their respective experimental estimates.⁶⁶

For Na⁺, the computed absolute hydration free energy $\Delta G_4^{N{a}^{+}}\left(l_W\right)=-93.3$ kcal/mol is only slightly overestimated with respect to the experimental value⁶⁶ of -90.8 kcal/mol. This is perhaps due in part to the slightly larger^{38, 40} value of the predicted gas phase Na⁺-water association free energy $\Delta G_{4,\Gamma }^{N{a}^{+}}\left(g_W\right)=\Delta G_4^{N{a}^{+}}\left(g_W\right)$ (see column 3 of table 3) and in part to the use of implicit solvent in the treatment of long-range interactions.^{32, 52} These errors could be reduced⁶⁷ by switching to a Møller-Plesset⁶⁸ second order perturbation theory (MP2) and/or by using explicit solvent molecules in the outer-shell domain Γ^C .³²

The computed absolute hydration free energy of K⁺, $\Delta G_4^{N{a}^{+}}\left(l_W\right)=-93.3$ kcal/mol, is slightly underestimated with respect to the experimental value⁶⁶ of -74.1 kcal/mol. Unlike the case of Na⁺, there is no experimental estimate for $\Delta G_{4,\Gamma }^{K^{+}}\left(g_W\right)$, but given that the values of $\Delta G_1^{K^{+}}\left(g_W\right)$, $\Delta G_2^{K^{+}}\left(g_W\right)$ and $\Delta G_3^{K^{+}}\left(g_W\right)$ are in excellent agreement with experiment,^{38, 40} it seems unlikely that this underestimation could result from a choice of functional or basis set. Treating solvent molecules in the outer domain explicitly may improve this value. Another option would be to extend the boundary to larger distances that include more solvent explicitly in the inner-shell domain, but then calculations become more time-consuming and the larger clusters that result may require explicit treatment of anharmonicity and configurational fluctuations. Nevertheless, correcting these small errors will not alter the trend in the dependence of solvation free energies $\Delta G_n^A\left(l_W\right)$ on coordination number observed for these specific inner-shell volumes, and is not the primary objective of this study.

We now assess the effect of the various terms that contribute to the solvation properties of these two ions. From the data in column 4 of table 3, we see that ligand concentration plays a vital role in stabilizing ion-ligand complexes. When ligand concentration is increased from its value in gas phase (C_g = 0.041 M) to its value in liquid phase (C_l = 55.6 M), the stability of each gas phase ion-water cluster is enhanced, that is, the sum $\Delta G_{n,\Gamma }^A\left(g_W\right)+n.\Delta G_{\mathit{conc}}^W$ in column 5 of table 3 is less than the corresponding value of $\Delta G_{n,\Gamma }^A\left(g_W\right)$ in column 3. How is this relevant to ion binding in biological molecules?

Although biological molecules cannot or do not have the isotropic high densities of ligands found in liquids or solids, they can certainly ensure the presence of high local densities in their ion binding regions through specific 3-dimensional folds or topologies and increase their propensities to bind ions. Note that these densities do not correspond to the densities of ligands in the ion-complexed state, but to the densities of ligands in the empty binding sites. The need for high local densities to stabilize ion binding can therefore, at times, result in close similarities between the ion-complexed and apo-state structures of ion binding sites. This aspect of ion binding has been observed for numerous proteins, with more recent examples coming from K-channels,⁶⁹ thrombins⁷⁰ and cytosolic phospholipases,^{71, 72} where the structures of the apo and ion-complexed states are similar in the sense that they do not have different orders of ligand densities in their binding sites. Note also that the dependence of free energies on ligand concentrations is logarithmic, which allows binding sites the freedom to explore configurational space before changes in ligand densities begin to alter the energetics of ion binding appreciably. This freedom to explore configurational changes can be vital to biological molecules, especially to acclimatize to the presence or absence of high charges in their binding sites.⁷²

From column 6 of table 3, we see that the excess chemical potential $\Delta G_{n,\Gamma }^{A{W}_n}\left(l_W\right)$ of each ion-water cluster is favorable. In addition to the gas phase and the ligand concentration free energy terms in equation 12, that is, $\Delta G_{n,\Gamma }^A\left(g_W\right)$ and $n.\Delta G_{\mathit{conc}}^W$, this term also serves to stabilize the formation of ion-water complexes in liquid water. Unlike the concentration term $\Delta G_{n,\Gamma }^{A{W}_n}\left(l_W\right)$, however, solvation of the clusters does not depend strongly on the coordination number of ions.

In the final step in the estimation of ion solvation free energies in liquid water, the excess chemical potential of the water molecule, ΔG^W(l_W), is multiplied by the total number of solvent molecules in the inner-shell domain (column 7 of table 3) and subtracted out. This makes each successively larger coordination complex in liquid phase less favorable. More importantly, this solvent contribution disrupts the stabilities of larger clusters more than the smaller clusters, shifting the coordination preferences in favor of lower values. This process of subtracting out the excess chemical potential of a water molecule ΔG^W(l_W) from the total solvation free energy of an ion is physically analogous to accounting for the penalty ΔΦ^W(l_W) associated with desolvating (extracting) a water molecule ligand from its aqueous environment to place it into a coordination complex, where ΔΦ^W(l_W)=-ΔG^W(l_W). There is a higher overall penalty associated with extracting larger numbers of water molecules from their natural bulk environment to place them in the coordination complex, which leads to a shift in the ion coordination preferences in favor of smaller numbers.

Note from the data in table 3 that the structural and thermodynamic properties of ion solvation in liquid water arise from a coupling or a balance between contributions arising from both the inner- and outer-shell domains. If this coupling or balance is disturbed, such as due to changes in temperature and pressure and/or due to changes in properties of the local or distant environments, ion solvation properties may change. For example, it is well known that increasing the temperature and pressure of salt solutions to very high values reduces the probability of the formation of higher order coordinations to such an extent that the coordination preferences of ions shift in favor of lower values as compared to those found under ambient conditions of temperature and pressure.^73-77 The physical principles that drive these structural transitions, however, still remain unclear. In another well known example, increasing the concentration of ions in water also results in reducing their average coordination numbers.^{5, 7, 78} This result can, in fact, be understood in the context of the free energy terms given in equation 12. We shall take up this discussion in the next section, where we also argue that this observation is actually part of a broader phenomenon known as the Hofmeister effect.^79-82 Nevertheless, neither these nor any of the previous studies explain how Na⁺ and K⁺ ions partition from liquid water to higher-order coordinations in the binding sites of proteins without any apparent uphill transitions on the free energy surface.

In order to find clues regarding the underlying physics that allows this structural transition in ion coordination, we now examine more carefully two of the above determinants of ion solvation that will most likely undergo modifications as the ion partitions from liquid water into protein binding sites: (a) the outer-shell environment Γ^C, and (b) the chemistry of the ligands, B.

Role of the outer-shell environment

When ions partition from liquid water (l_W) to binding sites in proteins (ξ), the structural and chemical properties of their outer-shell environments change. This should alter ion solvation energies via modifications in two free energy terms, $\Delta G_{n,\Gamma }^{A{B}_n}\left(\xi \right)$ and ΔG^B(ξ) (or ΔΦ^B(ξ)), in equation 12.

When ions bind to proteins, which have much lower dielectric constants than water,^83-87 the ions retain only a partial exposure to the high dielectric water. As a result, the strength of the interaction energies between the clusters AB_n and their outer-shell domains Γ^C decrease, consequently making the term $\Delta G_{n,\Gamma }^{A{B}_n}\left(\xi \right)$ less favorable in comparison to $\Delta G_{n,\Gamma }^{A{B}_n}\left(l_W\right)$. Although this will destabilize clusters of all sizes, it is not expected to alter the relative stabilities between different n-fold clusters. In contrast, modifications in the desolvation penalty of the ligand molecule ΔΦ^B(ξ) will significantly affect the relative stabilities between different ion coordination structures. A decrease in its magnitude will stabilize all complexes, but more importantly, it will stabilize the higher-order coordinations more than the lower-order coordinations. An increase in its magnitude will have the opposite effect.

Consider a scenario in which this desolvation penalty ΔΦ^B(ξ) could somehow be eliminated. For the purpose of reference, let us call the environment that results in negligible values of ΔΦ^B(ξ) a quasi-liquid (qL) environment, that is, ΔΦ^B(qL) ∼ 0. If such a hypothetical scenario is encountered in liquid water, the data in table 3 shows that this will lead to more favorable solvation free energies of all ion-water complexes, that is,

$$\Delta G_n^A\left(q{L}_W\right)=\Delta G_{n,\Gamma }^A\left(g_W\right)+n.\Delta G_W^{\mathit{conc}}+\Delta G_{n,\Gamma }^{A{W}_n}\left(qL\right)<\Delta G_n^A\left(l_W\right).$$ [16]

Note that in this model scenario, we continue to consider the local concentration of ligands to be of the same order as that found in liquid water. Setting the desolvation penalty to zero will also lead to an increase in the coordination preferences of both Na⁺ and K⁺ ions. In this analysis, the 6-fold cluster ends up the most stable cluster for Na⁺, while the 8-fold cluster becomes the most stable cluster for K⁺.

One obvious model environment in which the desolvation penalty takes up a value of zero is where the static dielectric constant ε of the outer-shell environment Γ^C is equal to unity. In this model situation, both terms $\Delta G_{n,\Gamma }^{A{B}_n}(\epsilon =1)$ and ΔΦ^B(ε = 1) will be zero, which will result in each progressively larger cluster to be more stable, and therefore will result in an increase in the coordination preferences of an ion. But this value of dielectric constant does not represent the environments of biological molecules, which have higher dielectric constants.^83-87 So how large can the dielectric constant be before, for example, the desolvation penalty of a water molecule ΔΦ^W(ε) takes up values large enough to make the coordination number preferences drop back to their original low values in liquid water? Separate calculations of ΔΦ^W(ε) and re-estimations of n_preferred for progressively increasing values of ε show that coordination preferences remain high until ε takes up a value greater than three (data not shown). Such low values of the static dielectric constants that yield increased coordination preferences still do not quite represent the environments of biological ion binding sites.^83-87

Even though such low values of the macroscopic dielectric constant are unlikely descriptors of Γ^C in biological molecules, an alternative mechanism for reducing electrostatic interactions between binding-site ligands and their environment presents itself upon recognition of the local nature of polar ligand (dipole) solvation in dielectric phases. Dipole-dipole interactions decay as 1/r³ , and as a result, in contrast to charged species, dipoles should receive the majority of their electrostatic stabilization from direct favorable interactions.⁸⁸ This can be demonstrated by computing the free energy penalty ΔΦ^W(ξ) associated with extracting a water molecule from a “pseudo-liquid-water” environment in which the high dielectric boundary of liquid water has been radially pushed away to a distance beyond, say, 6 Å from the water molecule (see figure 2). The free energy penalty ΔΦ^B(ξ) associated with extracting any dipolar ligand B can therefore be substantially reduced without actually setting the macroscopic dielectric constant of the entire solvation environment to a very low value. ΔΦ^B(ξ) can be substantially reduced by simply eliminating direct favorable interactions of the coordinating ligands with everything else but the binding ion.

Figure 2.

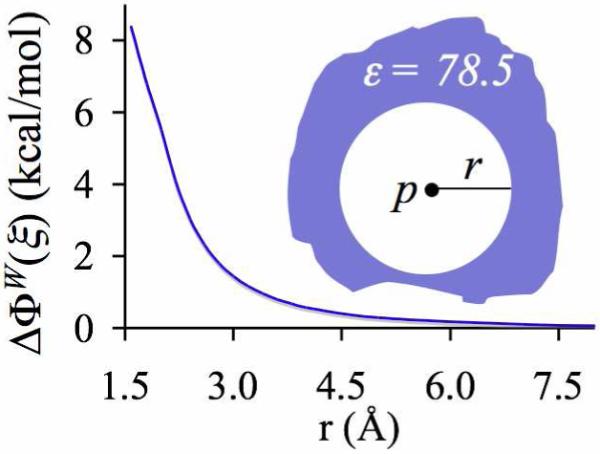
Free energy penalty ΔΦ^W(ξ) associated with extracting a water molecule (dipole, p) into gas phase from the center of a spherical low dielectric (ε = 1) cavity (radius, r) embedded in liquid water (ε = 78.5).

In the case of biological ion binding sites, the specific conditions that would yield reduced electrostatic penalties for extracting the coordinating ligands for ion complexation consist of:

1. A proximal environment devoid of only those chemical groups that can directly and favorably interact with the coordinating ligands. For example, in cases where the coordinating ligands are hydroxyl or carbonyl oxygens, the chemical groups that can engage in direct favorable interactions with them are hydrogen bond donors. In proteins, these hydrogen bond donors or competing groups can be supplied either by the protein backbone or by the side chains of some amino acids, including Arg, Lys, His, Cys, Tyr, Thr, Trp, Ser, Gln and Asn. Their proximity to coordinating ligands in binding sites, and also their conformational freedom, together determine their potency toward favorably interacting with the coordinating ligands and influencing the values of the average desolvation penalties 〈ΔΦ^B(ξ)〉. In addition, the values of 〈ΔΦ^B(ξ)〉 can also be influenced by the exposure of binding sites to solvent molecules, which can either be water molecules for soluble proteins or a combination of specific lipid headgroups and water molecules for membrane proteins. If the binding sites are exposed to such solvents, the probability to form higher-order coordination structures will be lower, and perhaps that is why all the binding sites listed in table 1 are mostly buried in the protein matrix. In line with the above argument, the presence of proximal hydrogen bond acceptors can also reduce desolvation penalties by making the ligands more readily accessible to the binding cations.

2. Specific architectural constraints on the coordinating ligands to prevent them from favorably interacting with any other atoms but the ion. Given the ingrained flexibility in the architectures of many biomolecules, however, it is not straightforward to envision how this strategy can by itself significantly reduce ligand extraction penalties. Nevertheless, we explore its contribution to reducing ligand extraction penalties a little later.

Now consider the opposite scenario in which the desolvation penalty of a ligand molecule, ΔΦ^B(ξ), is somehow increased, rather than lowered. This will destabilize each and every n-fold ion complex, and in theory could also lead to a reduction in ion coordination preferences. Based on the arguments above, one way to achieve this in experiments is to add certain solutes into water, along with the ions, that will compete with the ions for favorable interactions with the waters. For example, this could occur if the concentration of salt in water is itself increased to values where ions begin to compete with each other for coordination with water molecules. In such a case, an ion will have to “pull” waters away from its neighboring ions to fill its own inner coordination shell, a process that will result in an increase in the desolvation penalty of a water molecule, that is, $\Delta {\Phi }^W\left({\tilde{l}}_W\right)>\Delta {\Phi }^W\left(l_W\right)$, where the tilde over l_W indicates the water solution having the requisite high concentration of ions. This could ultimately lead to a reduction in ion coordination numbers with water, but at the same time it could also lead to a coagulation of ions or an increase in their probability to form cation-anion pairs because, as a pair, they would require wetting by fewer water molecules. In reality, this indeed happens,^{5, 7} and from this perspective it can be clubbed together into a more general phenomenon popularly referred to as the Hofmeister effect.^79-82 Analogous to the process in which adding salt coagulates proteins in solution, the process for which this phenomenon is most famous, here salt is “salting-out” itself under conditions of high concentrations. Recent molecular dynamics simulations⁷⁸ of Rb⁺ and Cs⁺ ions in water also show that as their concentrations are increased from millimolar levels to a few molars, their average ion-water coordination numbers drop from 7.5 and 9 to ∼6.

Together, the analysis above provides the first clue to explaining how Na⁺ and K⁺ ions are able to partition readily from aqueous-phase into the spatial regions in proteins having much higher coordination numbers, such as those listed in table 1. We find that increased accessibility of ions to ligands not only enhances the individual stability of each n-fold complex, especially the higher-order complexes, but can also lead to an increase in ion coordination preferences. A schematic of this idea is illustrated in figure 3. The binding sites in such proteins are, however, not always made up of hydroxyl ligands,^{1, 2, 13-19} such as those provided by water molecules. This raises the question of what role ligand chemistry plays in modulating ion complexation energies.

Role of ligand chemistry

From equation 12 and from the data in table 3, we can see that ligand chemistry will primarily affect ion solvation energies $\Delta G_{n,}^A\left(\xi \right)$ by modulating the values of the two terms, ΔG^B(ξ) and $\Delta G_{n,\Gamma }^A\left(g_B\right)$. A ligand B that has an electric dipole moment and/or polarizability stronger than water will bind to the ion more tightly, which will make the enthalpic components $\Delta H_{n,\Gamma }^A\left(g_B\right)$ of cluster free energies more favorable. Concurrently, the same ligand will be repelled electrostatically more by the other ligands in the cluster. This will in turn reduce the stabilities of the clusters (n ≠ 1). In addition, a ligand with a stronger dipole moment will also have a higher free energy penalty, ΔΦ^B(ξ)=-ΔG^B(ξ), associated with extracting it from a given environment. This will also decrease the stability of the ion-ligand complex. The overall contribution of ligand chemistry to ion binding will therefore emerge from a balance between at least these three competing physical effects.

The analyses in the previous sections were carried out using water molecules, which are an acceptable representative for the hydroxyl ligands found in biological cation binding sites. Nevertheless, we supplement the study of the effect of hydroxyl ligands on ion binding by carrying out a similar quasi-chemical analysis of ion solvation in liquid methanol, which has a static dielectric constant of 33. Methanol molecules have an electric dipole moment of 1.7 Debye,⁸⁹ which is similar to that of water (1.85 Debye), but more importantly they have a neighboring methyl group that makes them a better representative of the hydroxyl groups found in ion-binding sites in proteins. In numerous cases,^{1, 2, 13-19} including those listed in table 1, Na⁺ and K⁺ binding sites also contain carbonyl ligands. In order to understand how carbonyl ligands differ from hydroxyl ligands (water and methanol) with respect to their contributions to ion binding, we carry out a quasi-chemical analysis of the solvation of Na⁺ and K⁺ ions in liquid formamide. We choose formamide (NH₂CHO) because it has a gas phase electric dipole moment of 3.73 Debye,⁸⁹ which is almost twice as strong as that of a water molecule. Furthermore, formamide under standard conditions exists as a liquid with a static dielectric constant of 109.5, which is similar to that of liquid water.

Table 4 lists the gas phase enthalpies $\Delta H_{n,\Gamma }^A\left(g_B\right)$ for complexation of Na⁺ and K⁺ ions with methanol and formamide molecules. We find that for each cluster size, the ion-methanol and ion-formamide complexes are more stable than their corresponding ion-water complexes. This does not appear surprising for formamide, as it has a stronger dipole moment than water. In the case of methanol, however, this occurs despite the weaker gas phase dipole moment of methanol, suggesting strongly that methanol is more polarizable than water. Nevertheless, more pertinent to this study is the observation that a ligand that has an electric dipole moment and/or polarizability stronger than water binds to Na⁺ and K⁺ ions more tightly than water, regardless of the relevant coordination numbers (n ∈ {1,2,...,8}). This is contrary to our earlier expectations that increasing the electric dipole moment could destabilize the overall complexation energy via increased ligand-ligand repulsion. The effect of increased ligand-ligand repulsion is certainly visible in larger ion-formamide clusters, but it is not sufficient to override the stability achieved via increased ion-ligand attraction.

Table 4.

Intrinsic enthalpies (in kcal/mol) of complexation of Na⁺ and K⁺ ions with methanol (CH₃OH) and formamide (NH₂CHO) molecules, presented relative to their corresponding values with water molecules.

n	$\Delta \Delta H_{n,\Gamma }^A(g_W\to g_B)=\Delta H_{n,\Gamma }^A\left(g_B\right)-\Delta H_{n,\Gamma }^A\left(g_W\right)$
	B ≡ CH3OH		B ≡ NH2CHO
	A ≡ Na+	A ≡ K+	A ≡ Na+	A ≡ K+
1	-2.1	-1.3	-11.5	-9.3
2	-3.4	-2.1	-19.0	-15.4
3	-3.9	-2.6	-21.0	-18.3
4	-3.9	-2.7	-20.0	-18.7
5	-3.9	-3.3	-19.4	-25.3
6	-5.0	-4.4	-14.8	-25.6
7		-5.4		-25.6
8		-5.1		-24.3

The finding above identifies an important role of ligand chemistry in stabilizing ions through short-range interactions within ion-ligand complexes, which has seldom been considered in the context of ion binding to proteins. As can be seen from the data in table 3, apart from the fact that both Na⁺ and K⁺ ions receive a significant degree of their stability in liquid water from direct interactions with water molecules in their inner-shell domain, they also receive a significant degree of their stability from interactions with the distant high dielectric environment. This is primarily a consequence of the long-range nature of electrostatic interactions. When ions bind to proteins, which have a much lower dielectric constant than water,^83-87 the ions retain only a partial exposure to the high dielectric water, and therefore, receive reduced stability from the distant environment. Since both carbonyl ligands from formamide and the hydroxyl ligands from methanol bind ions more tightly than water, their presence in biological ion binding sites can help compensate for the loss associated with the reduced exposure of ions to the high dielectric environment. In line with this observation, higher coordination numbers in the binding sites as compared to those found in water can also serve the same purpose; however, such binding sites need to be accompanied with a local quasi-liquid environment for reduced penalties for ligand extraction.

Ligand chemistry also dictates the thermodynamic cost of extracting ligands from a given environment for ion coordination. Recall that implicit solvent calculations yielded ΔΦ^W(l_W)= 8.4 kcal/mol as the electrostatic penalty to extract a water molecule ligand from bulk water (see data in table 3). The same calculations show that the electrostatic penalty to extract a methanol molecule from bulk water is 6.2 kcal/mol, while the electrostatic penalty to extract formamide molecule from bulk water is 10.7 kcal/mol. As expected, the stronger the dipole moment, the higher the desolvation penalty of the ligand. A realization of this aspect of ion solvation can be useful in explaining certain observations, such as in the selectivity filters of NaK channels, where ligands with a weaker dipole moment (hydroxyl) preferentially replace ligands with a stronger dipole moment (carbonyl).⁹⁰

Figure 4 illustrates the solvation free energies of Na⁺ and K⁺ ions in liquid methanol and in liquid formamide. The radii chosen to define the boundaries of the inner-shell domains were identical to those used for the calculations in liquid water, that is, 2.6 Å for Na⁺ and 3.1 Å for K⁺. We see that ligand chemistry, which had altered the gas phase enthalpies, does not change ion coordination preferences in these liquids, as both ions still prefer to coordinate with four ligands. In addition, setting the desolvation penalties to zero results in increased coordination preferences, identical to those found in the case of water (data not shown).

Figure 4.

Solvation free energies of $\Delta G_n^A\left(l_B\right)$ of ions A ∈ {Na⁺,K⁺} in liquid formamide (l_B ≡ l_formamide, triangles connected using solid lines) and liquid methanol (l_B ≡ l_methanol, circles connected using broken lines) estimated using the quasi-chemical framework.

Together, this analysis highlights the importance of ligand chemistry in ion binding; however, it does not provide any clues with respect to the ability of ions to partition from their low coordinations in water to over-coordinated binding sites in proteins without energetic barriers.

(B) Classical MD analysis

The analysis using the quasi-chemical framework suggested one explanation for how Na⁺ and K⁺ ions readily partition from aqueous phase into the spatial regions in proteins having much higher coordination numbers. If the accessibility of the ion to ligands is increased via a substantial decrease in the desolvation penalty of ligands (〈ΔΦ^B(ξ)〉 → 0), then the individual stabilities of the higher-order complexes can be increased, even to values that increase ion coordination preferences. For the sake of reference, we collectively termed the conditions that yielded negligible penalties for ligand extraction a “quasi-liquid” environment. Given the physical nature of interaction of dipoles with their environments (as illustrated in figure 2), we noted that this penalty could be substantially reduced if direct favorable interactions of the coordinating ligands with all atoms, except the ion, were eliminated. We identified two different mechanisms to eliminate such direct favorable interactions: (a) presence of a proximal environment around the coordinating ligands devoid of only those chemical groups that can directly and favorably interact with the coordinating ligands, and (b) specific architectural constraints on the coordinating ligands that prevented them from favorably interacting with any other atoms but the ion. In order to reaffirm and further explore these ideas, we now switch to classical MD simulations and study the various factors that control the coordination numbers of K⁺ ions.

If the condition where the proximal environment is devoid of chemical groups that can directly and favorably interact with the coordinating ligands is by itself sufficient to allow ion partitioning from low coordinations in aqueous phase to over-coordinated states in protein binding sites, then the following test case should hold. If a K⁺ ion is introduced in a box of water in a state of over-coordination by, for example, 8 water oxygens, and the partial charges on all the water molecules that are not directly coordinating the ion are turned off (no hydrogen bond donors), then the ion should remain in its original state of over-coordination indefinitely. Note that this does not happen when all the waters in the simulation box carry their natural partial charges.

To test this, we introduce a K⁺ ion in a cubical box (length, 30 Å) containing 893 water molecules. We turn off the partial charges on all but a subset of randomly selected water molecules n_w, and generate 4 ns long MD trajectories with periodic boundaries under NVT conditions. Data from the final 1 ns of each trajectory is analyzed and the results of 5 such simulations, where n_w ∈ {4,5,...,8}, are illustrated in figure 5. As expected, the number distributions n_oxy(r) around K⁺ of the oxygen atoms that carry their natural partial charges change with the value of n_w. Interestingly, however, not more than four such oxygens on average are found to coordinate K⁺ directly despite availability of additional water oxygens that carry their natural partial charges. The remaining n_w water molecules prefer to occupy the outer-shell domain Γ^C of K⁺, where they line up behind the water molecules that occupy the inner-shell domain. Their dipoles are on average aligned with the electric field of the ion while their oxygens are favorably interacting with the hydrogen atoms of the water molecules occupying the inner-shell domain. This is discernible from the discrete jumps in the n_oxy(r) profiles and can also be seen in a representative snapshot of a simulation in figure 5.

Figure 5.

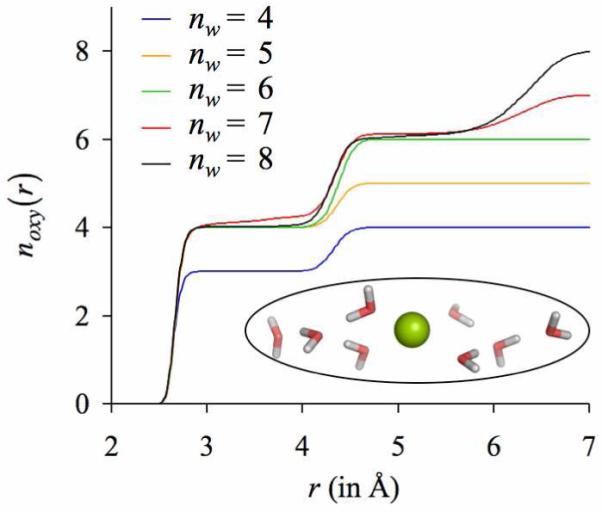
Number distributions n_oxy(r) of water oxygens around K⁺. Each curve represents an individual simulation in which the natural partial charges of only a subset of randomly selected water molecules n_w in the simulation box are turned on, while the natural partial charges on the remaining water molecules in the simulation box are turned off. The inset illustrates a representative configuration when the partial charges on exactly n_w = 8 water molecules are turned on.

The reason that over-coordination is not achieved in the test scenario above is because lower coordinations are energetically preferred over higher coordinations when the water molecules have the option to drop out of the inner-shell, which is essentially what happens in gas phase, as noted in a previous quantum chemical (MP2) study.⁶⁷ This suggests that to achieve over-coordination, a specific variety of rigidity on the coordinating ligands is also required; an architectural constraint that prevents the ligands from dropping out of the inner shell. In the over-coordinated binding sites in proteins, this role invariably needs to be taken up by the protein matrix.

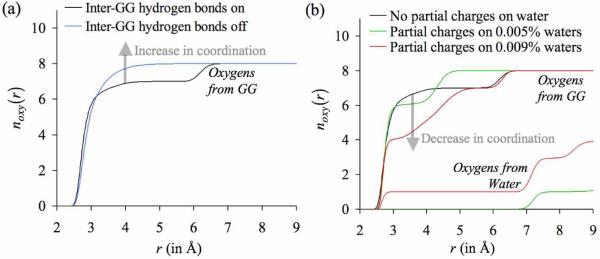
One strategy to specifically test the role of architectural rigidity on ligands is to tether the ligands together, which may prevent them from dropping out of the inner-shell and lining up one behind the other. For this, we choose bidentate ligands in the form of glycine dipeptide (GG) molecules. Each of these bidentate ligands provides two oxygens for ligation, instead of the one oxygen supplied by a monodentate water molecule. We retain the simulation protocol used in the previous study, except that in these simulations appropriate numbers of water molecules are substituted with n_GG ∈ {1,...,4} GG molecules, and the partial charges on all the remaining water molecules are turned off. The results of these simulations are illustrated in figure 6. We now see that K⁺ coordinates directly with more than four GG oxygens. Nevertheless, the discrete jumps observed in the previous n_oxy(r) profiles, which indicate that some ligands have dropped out of the inner-coordination shell, are still present in simulations where n_GG = 3 or n_GG = 4. An inspection of the trajectories reveals that the ligands that drop out of the inner-shell are those which hydrogen bond with the amino groups of the adjacent GG molecules. In other words, instead of coordinating the K⁺ ion, some oxygen atoms of GG molecules engage in hydrogen bond interactions with the amino groups of the neighboring GG molecules. Essentially, even though there are no water molecules in the simulation box that carry their natural partial charges and can reduce the ion coordination numbers by introducing penalties for ligand extraction, the GG molecules can themselves introduce penalties for ligand extraction by supplying hydrogen bond donors in the form of amino groups. Turning off such inter-GG hydrogen bond interactions and regenerating the MD trajectories eliminates the discrete jumps in the number distribution profiles, and increases the coordination numbers of K⁺ ions (figure 7a).

Figure 6.

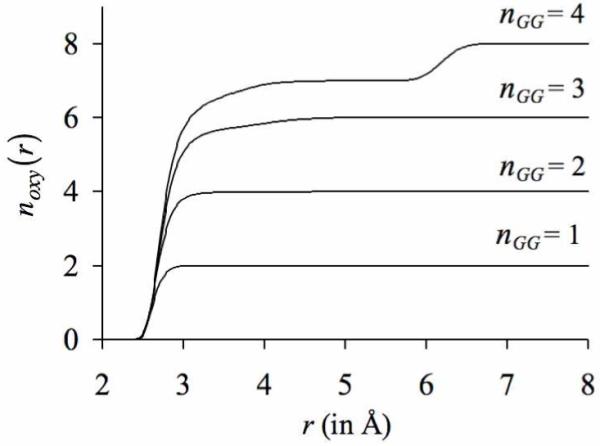
Number distributions n_oxy(r) of the oxygens belonging to the glycine dipeptide (GG) molecules around K⁺. Each curve represents an individual simulation in which n_GG glycine dipeptide molecules are present in the simulation box. Note that glycine dipeptide molecules are bidentate ligands, and in contrast to water molecules, provide two oxygen ligands for ion coordination.

Figure 7.

Effect of altering the densities of hydrogen bond donors in Γ^C on the number distributions of oxygens n_oxy(r) around K⁺. The final configuration of the simulation with four glycine dipeptide (GG) molecules in the simulation box (n _GG = 4 case in figure 6) was used as the starting configuration for two separate sets of simulations: one in which the densities of hydrogen bond donors were decreased, and another in which the densities of hydrogen bond donors were increased. (a) Since the oxygen atoms of GG molecules showed a tendency to hydrogen bond with the amino groups in adjacent GG molecules, the densities of hydrogen bond donors were effectively reduced by turning-off all inter-GG hydrogen bond interactions. This increased the number of oxygens directly coordinating the K⁺ ion, as indicated by a transparent arrow. (b) The densities of hydrogen bond donors were increased by turning on the natural partial charges of a certain percentage of water molecules in the simulation box. This decreased the total number of oxygen atoms directly coordinating the K⁺ ion, as also indicated by a transparent arrow. Note that in the case where the partial charges on 0.009% of the waters are turned on, this reduction in coordination number occurs despite one oxygen atom from water substituting for the oxygen atoms from the GG molecule.

Now what happens if, instead of turning off the inter-GG hydrogen bond interactions, the density of hydrogen bond donors in Γ^C is further increased? In line with our findings from the quasi-chemical analysis, this should further decrease the number of oxygen atoms directly coordinating the K⁺ ion. We test this by re-introducing the natural partial charges on some randomly selected water molecules in the simulation box. As illustrated in figure 7b, increased population of hydrogen-bond donors does indeed decrease the average numbers of oxygens directly coordinating the K⁺ ion. Another point to observe from figure 7b is that in one of the simulations in which the natural partial charges on 0.009% of water molecules were turned on, one water molecule directly coordinates the K⁺ ion, preferentially replacing a carbonyl oxygen atom from the GG molecules. This is an example of a situation described in the previous section where a ligand with a weaker dipole moment (hydroxyl) preferentially replaces a ligand with a stronger dipole moment (carbonyl), primarily because the desolvation penalty associated with extracting a ligand with a weaker dipole moment is smaller.

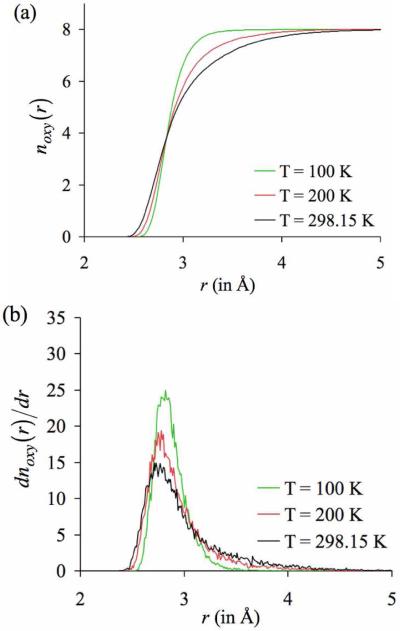
In the analysis above, ion coordination properties were studied under conditions of ambient temperature (298.15 K). In contrast, the x-ray data of bio-molecules in table 1, where ions were found to be over-coordinated with respect to ion coordinations in liquid water, was collected after flash freezing the crystals to very low temperatures below 200 K. Is it legitimate to compare our findings at physiological temperatures to those obtained under conditions of very low temperatures? In other words, does flash freezing of crystals introduce any artifacts in the ion coordination structures? It is common knowledge that temperature manifests itself as fluctuations in interacting particles, so from that standpoint it seems that the process of flash freezing should basically dampen thermal fluctuations and “trap” the ion coordination structures in their minimum energy configurations. Despite the fact that temperature does not alter potential energy surfaces (PES), it can alter transition probabilities across energy barriers on the PES, ultimately modifying the overall topologies of the ion coordination structures. No hard-and-fast rules, however, can predict the temperature-response of electrostatically interacting particles, as each such system will have its unique PES.⁹¹ Nevertheless, we test this for our candidate 8-fold K⁺-GG complex.

We start with the final snapshot of the trajectory of a K⁺ ion generated with four GG molecules in the absence of hydrogen bond donors (including inter-GG hydrogen bond interactions), and generate new 4 ns long trajectories at lower temperatures of 200 and 100 K. The results of these simulations are illustrated in figure 8, where they are also compared to the results of the simulation at ambient temperature (298.15 K). Despite the observation that the volume of coordination shell contracts, none of the ligands drop out into the second shell of the ion. In addition, the average ion coordination structures at lower temperatures remain similar to the average ion coordination structure at ambient temperature. In other words, we find that lowering the temperature did not alter the overall topology of this 8-fold complex, and congruous with our expectations, lowering the temperature reduced thermal fluctuations and in effect “tightened” this coordination complex. Furthermore, when the temperature was lowered, the average K⁺-O distances decreased only marginally. At a temperature of 298.15 K, the average K⁺-O distance was 2.90 ± 0.06 Å. When the temperature was lowered to 200 K, the average K⁺-O distance decreased to 2.86 ± 0.05 Å, and when the temperature was further lowered to 100 K, the average K⁺-O distance decreased to 2.82 ± 0.03 Å. This strongly suggests that the average ion-ligand distances collected at low temperatures are likely to be only slightly smaller than their values at physiological temperature, and it is indeed legitimate to compare our findings at physiological temperatures to those obtained under conditions of very low temperature.

Figure 8.

Effect of temperature on (a) the number distributions of oxygen atoms n_oxy(r) and (b) their derivatives dn_oxy(r)/dr around K⁺. The final snapshot of the simulation of K⁺ at a temperature T = 298.15 K with four GG molecules embedded in a simulation box without any hydrogen bond donors (including inter-GG hydrogen bonds interactions) was used as the starting configuration for simulations at lower temperatures. Lowering the temperature “tightened” this coordination complex, without altering its overall topology. Note that while the volume of coordination shell contracts, none of the ligands drop out into the second shell of the ion.

Together, the classical MD analysis reaffirms the finding from quasi-chemical analysis that ion coordination preferences can be altered via changes in the penalty associated with extracting ligands from their solvation environments. This penalty can be altered not only via specific modifications in the local environments of the coordinating ligands, but also via modifications in the conformational flexibility (or rigidity) of the coordinating ligands.

(C) Environmental analysis of over-coordinated binding sites in biomolecules

It is straightforward to see that the local structural and chemical factors that lead to a substantial reduction in the desolvation penalties of ligands (or lead to the formation of local quasi-liquid pockets around the ligands) and enable formation of over-coordinated structures without energetic barriers will be unique to each biological ion-binding setting. In this section, we undertake a structural and chemical analysis of the environments of all the over-coordinated binding sites listed in table 1.

We first identify indications of the presence of a local quasi-liquid environment around the binding sites of potassium channel selectivity filters, where K⁺ ions are seen to coordinate directly with 8 ligands in the x-ray structure.^20-23 First, the concentration of ligands in the empty binding site is ∼23 M, which is comparable to the concentration of water ligands in aqueous phase. This was estimated by dividing the total number of carbonyl ligands available in the selectivity filter of the apo state of potassium channels⁶⁹ by the volume of the selectivity filter. Second, there are no side chain hydrogen bond donors within the local environments of the ligands in any of the four known structures^20-23 of potassium channels (KcsA, MthK, KvAP & KirBac1.1), as can be seen in an illustration of KirBac1.1 in figure 9. Third, all the proximal backbone hydrogen bond donors are hydrogen bonded to other functional groups in the protein and involved in maintaining the integrity of the protein’s 3-dimensional fold. Fourth, there are some hydrogen bond acceptor groups present in the vicinity of the filter in the form of Asp and Glu residues. The negative charges on these residues will serve to prevent the carbonyl ligands from turning away from the ion binding sites. And finally, the packing of residues and the hydrogen bond network behind the selectivity filter also provide a certain degree of structural rigidity to the ligands themselves, as supported by the finding that deformation of the filter structure requires an appreciable energetic cost.⁹² These observations indicate how potassium channels can sustain K⁺ ions bound in states of high coordination.

Figure 9.

Distribution of hydrogen bond donor and acceptor side chains in a representative structure of potassium channels, KirBac1.1 (PDB ID: 1P7B). The orientation of the channel is as viewed from its extra-cellular end. The selectivity filter, which provides the backbone carbonyl oxygens to form 8-fold K⁺ binding sites, is colored green. The side chains of amino acids H, R, K, N, Q, T, Y, W, S and C that contain hydrogen bond donors and do not belong to the selectivity filter are illustrated as sticks and colored blue. The side chains of amino acids D and E that contain hydrogen bond acceptors are colored red. In the crystallographic configuration, all relevant side chain hydrogen bond donor groups are at a distance of at least 6.8 Å from the coordinating carbonyl oxygens of the selectivity filter.

Table 5 presents a survey of the environments of the coordinating ligands in the remaining ion binding sites of table 1. Columns 2 and 3 list the number densities η_H-donor of side chain hydrogen bond donors in the distant (r_d ∈ (6,12]) and local (r_d ∈ [0,6]) environments of the coordinating ligands, where r_d is the distance in ångström units from the ligand and not from the ion. Barring the case of pyruvate kinase, the local environments carry far fewer hydrogen bond donors than found in the distant environment. Irrespective, the densities of hydrogen bond donors in the local environments are almost two orders of magnitude smaller than the density of hydrogen bond donors offered by liquid water. Based on the analysis above, this will reduce the penalties associated with extracting these ligands for ion coordination, and increase the stability of ions in these proteins. Now, if only those hydrogen bond donors are considered that are not engaged in other favorable interactions, such as salt-bridges and hydrogen bonds with other groups in the proteins, then we find that the number densities η_free-H-donor drop to negligible values. In other words, hardly any freely available side chain hydrogen bond donors are present in the local neighborhoods of the coordinating ligands that can engage in favorable interactions with them and disrupt the formation of higher order ion-ligand complexes.

Table 5.

Normalized number densities of hydrogen bond donors around the ligands in the ion binding sites of proteins listed in table 1.^†

Biomolecule	ηH-donor/ηw × 100 (rd ∈ (6,12])	ηH-donor/ηw × 100 (rd ∈ (0,6])	ηfree-H-donor/ηw × 100 (rd ∈ (0,6])
Pyruvate Kinase (1A49)	6.90	6.17	0.00
Chaperone (1HPM)	6.58	1.30	0.47
Lysozyme (1V7T)	8.07	1.63	0.00
Neurotransmitter Transporter (2A65)	4.84	2.22	0.26
Dialkylglycine Decarboxylase (2DKB)	2.65	0.52	0.26
Thrombokinase (2BOK)	2.95	0.98	0.33

^†The normalization factor η_w is the number density of bulk water. For a given binding site, individual number densities were first estimated for all of its ligands, and then averaged. These average number densities were computed for two different spherical sub-volumes around the ligand, one limited to a region within 6 Å from the ligand, while the other extending from 6 to 12 Å from the ligand. In the estimation of η_H-donor, hydrogenbond donors from all side chain residues were considered, including Arg, Lys, His, Cys, Tyr, Thr, Trp, Ser, Gln and Asn; while in the estimation of η_free-H-donor, only thosehydrogen bond donors were considered that were not engaged in other favorable interactions, including salt-bridges and hydrogen bonds.

In the local neighborhood of the ligands, the non-zero values of η_H-donor are, in fact, expected to play a special role during ion binding. In the absence of bound ions, the coordinating ligands in the binding site will experience large electrostatic repulsions from each other. On the one hand, in a scenario where proximal hydrogen bond donors are absent, the binding site will build up significant strain energy and may have to undergo large structural changes. On the other hand, if proximal hydrogen bond donors are present, then this strain can be relieved through favorable interactions, as has been seen recently in the case of cytosolic phospholipases.⁷² This brings us to believe that, although the presence of proximal hydrogen bond donors can disrupt formation of higher-order complexes, they can at the same time relieve the strain energy that builds up in the absence of bound cations without need for large structural changes. Perhaps there exists an optimum density of proximal hydrogen bond donors that benefits both aspects of the ion-binding process, with its implication being tightly intertwined with the individual functions of ion binding sites. We note that this analysis is based on static x-ray structures, and an analysis using Monte Carlo sampling or MD simulations is expected to provide a better perspective on the distributions and the dual roles of proximal hydrogen bond donors in ion binding, especially those belonging to the protein backbone that were not considered during analysis other than in the case of potassium channels.

Conclusions and Summary

In this work, we focused our efforts to understand one specific aspect of the ion-binding phenomenon in biomolecules. When ions, such as Na⁺ and K⁺, dissolve in liquid water, they exhibit strong preferences toward the numbers of ligands inside their inner-coordination shells. Alternatively phrased, there is a free energetic cost associated with transferring ions from their preferred coordination states in water to states having different coordination numbers. Such free energetic costs become exceedingly large if transitions are considered to coordination numbers that are very different from preferred values. Nevertheless, there are several biomolecules^{1, 2, 13-19} that, based primarily on x-ray data, appear to bind these ions using coordinations that are much higher than those preferred in liquid water. Why don’t energetic costs surface during such structural transitions from water to over-coordinated binding sites (relative to water) in biomolecules? What deflates these energetic costs and allows ions to readily partition back-and-forth between liquid water and the binding sites in biomolecules? What physical principles explain such structural transitions in ion coordinations?

We utilized a three-way strategy to first expand our understanding of the essential nature of ion solvation in liquid media and then determine the underlying physics that explains this ion coordination anomaly. First, quantum chemical simulations within the statistical framework of the quasi-chemical theory of solutions^{24-27, 29, 30} was invoked to understand the individual and combined roles of the various factors that drive ion solvation in liquid media. Note that the goal here was not to determine the exact contributions arising from the various factors that drive ion solvation, but only to assess their participation in a qualitative manner. Then classical MD simulations were carried out to probe the inferences derived from the quasi-chemical analysis. Finally, the findings from the quasi-chemical and MD analyses were examined in the context of the architectures and chemical compositions of the over-coordinated binding sites in biomolecules.

This analysis revealed an important ingredient to the recipe for lowering the energetic costs associated with partitioning ions from liquid water into any given over-coordinated binding site. If the penalty associated with extracting ligands from their solvation environments to form ion coordination complexes is substantially reduced, that is ΔΦ^B(ξ) ∼ 0, then the stabilities of higher-order complexes are dramatically increased, even to extents that can drive up the coordination preferences of ions. For the sake of reference, we collectively term the conditions that yield negligible penalties for ligand extraction a “quasi-liquid” environment. Given the physical nature of interaction of ligands (dipoles) with their environments (as illustrated by figure 2), this penalty can be substantially reduced by simply eliminating direct favorable interactions of the coordinating ligands with all atoms except the ion. Biomolecules can utilize two different strategies to accomplish this:

1. Tune the local environments of their coordinating ligands: The local environments of the coordinating ligands can be tuned such that the local number densities of competing groups that can favorably interact with the coordinating ligands are either significantly reduced, or made exceedingly less accessible for interaction through specific steric and electrostatic interactions in the protein matrix.

2. Impose specific architectural constraints on the ligands themselves: Specific architectural constraints can be imposed on the coordinating ligands to prevent them from favorably interacting with any other atoms but the ion. Given the ingrained flexibility in the architectures of biomolecules, however, it is not straightforward to envision how this strategy can by itself significantly reduce ligand extraction penalties.

If a substantial reduction in the local densities of competing groups, which can favorably interact with the coordinating ligands, can increase ion coordination preferences, then a substantial increase in the number densities of such competing groups should lead to a drop in coordination preferences. This is indeed true, as was demonstrated using classical MD simulations. In fact, this is reminiscent of the effect of salt concentrations on an ion’s coordination number. When the concentration of salt in water is increased to values where ions begin to compete with each other for coordination with water molecules, the ion-water coordination numbers decrease. This has been observed both experimentally^{5, 7} and theoretically.⁷⁸ It is also tempting to compare this phenomenon to the famous Hofmeister effect.^79-81 Analogous to the process in which adding salt precipitates proteins, the process for which the Hofmeister effect is most famous, here salt is “salting-out” itself under conditions of high concentrations.

The complete absence of competing groups in the local neighborhoods of binding sites will maximize the stabilities of the higher-order complexes. In such a scenario, however, when there are no ions present in the binding sites, the coordinating ligands in the binding site will experience large electrostatic repulsions from each other. As a result, the binding site will build up significant strain energy and may have to undergo large structural changes. In contrast, if proximal competing groups are present, then this strain can be relieved through favorable interactions, as has been seen recently in the case of cytosolic phospholipases.⁷² This brings us to believe that although the presence of proximal competing groups can disrupt formation of higher-order complexes, they can at the same time relieve the strain energy that builds up in the absence of bound ions without need for large structural changes. The advantage of preventing the binding site from undergoing large structural changes in the absence of ions is that it helps maintain high ligand concentrations, which enhances ion binding energies. In theory, there should exist an optimum density of proximal competing groups that benefits both aspects of the overall ion-binding process. What are these optimum densities? Has evolution indeed carved out such optimum densities in biomolecules to boost their function? Can we harness them to engineer desirable environmental responses? Answers to such questions require a more extensive study of this phenomenon, which we anticipate will be the focus of future studies.

Our studies also show that modifying ligand chemistries need not alter ion coordination preferences and/or ion solvation energies. On the one hand, ligands that have larger dipole moments or polarizabilities (field strengths) are energetically more expensive to extract from their solvation environment for ion coordination. This will serve to decrease the stabilities of coordination complexes. On the other hand, ligands that have stronger field strengths will bind more strongly to the ion, which will increase the stabilities of coordination complexes. It is easy to see that these competing effects can on certain occasions cancel each other out and yield unchanged ion coordination preferences and/or ion solvation energies. This we argue is the primary reason why ion solvation structures or energies need not differ between solvents that have vastly different dielectric properties. For example, the solvation energies of Na⁺ and K⁺ ions in liquid water are similar to their corresponding values in liquid formamide, despite the fact that formamide has a dipole moment twice as large as water.

Investigations concerning the effect of temperature on ion coordination led to the finding that lowering the temperature “tightens” coordination complexes, at least for the particular case considered in this study. When MD simulations were carried out at lower temperatures of 100 and 200 K, temperatures to which crystals are flash frozen for use in structure determination by x-ray studies, the thermal fluctuations decreased without altering the overall topology of the coordination complex. In addition, the average ion-ligand coordination distances were minimally affected. This strongly suggests that (a) the average ion-ligand distances collected at low temperatures are likely to be a good representative of their values at physiological temperature, and (b) it is indeed legitimate to compare our findings at physiological temperatures to those obtained under conditions of very low temperature.

Our overall findings testify to the intricate designs of the over-coordinated binding sites in biomolecules. So why had evolution taken the trouble to design such binding sites? Are they mere remnants of the act of serendipity or do they serve any purpose? We identify two important roles of over-coordination in biomolecules:

1. Over-coordinating ions can increase ion stability in special cases where ions are required to bind within the interiors of biomolecules. When ions bind to buried-sites in biomolecules, over-coordination can serve to compensate for the loss in exposure of the ion to the high dielectric water. For example, the binding energy of K⁺ ion with six or more carbonyl ligands (supplied by three of more glycine dipeptide ligands) is similar to the hydration energy of the K⁺ ion.⁵⁶ This will allow K⁺ ions to readily partition from water into such over-coordinated binding sites without need for stability from the high dielectric water. It is interesting to note that such an outcome simultaneously requires that the ion-binding site has reduced exposure to water for reduced penalties for ligand extraction.

2. Over-coordination is a potent mechanism for K⁺/Na⁺ selectivity^{56, 90, 92-96} in the fluctuating (but not liquid)^{56, 90, 93, 94, 97} ion binding sites of potassium channels. Reducing the extent of over-coordination decreases ion selectivity,^{56, 90, 93, 94, 98} which appears to have been utilized by nature to create different varieties of potassium channels that exhibit weak, intermediate and strong K⁺/Na⁺ selectivity.^{56, 90, 99} Certainly, binding ions into states of over-coordination may provide other advantages to biomolecules, and it will be interesting to see what future investigations reveal.