Flow patterns and heat convection in a rectangular water bolus for use in superficial hyperthermia

Abstract

This paper investigates both numerically and experimentally the spatio-temporal effects of water flow in a custom made water bolus used for superficial hyperthermia generated by a 915-MHz, 4 × 3 microwave applicator array. Similar hyperthermia models referenced in the literature use a constant water temperature and uniform heat flux to describe conduction and convection energy exchange within the heating apparatus available to cool the tissue surface. The results presented in this paper show that the spatially varying flow pattern and rate are vital factors for the overall heat control applicability of the 5 mm thick bolus under study. Regions with low flow rates and low heat convection clearly put restrictions on the maximum microwave energy possible within the limits of skin temperature rise under the bolus. Our analysis is illustrated by experimental flow front studies using a contrast liquid setup monitored by high definition video and complemented by numerical analysis of liquid flow and heat exchange within the rectangular water bolus loaded by malignant tissue. Important factors for improvement of future bolus designs are also discussed in terms of diameter and configuration of the water input and output tubing network.

1. Introduction

During hyperthermia treatment, the basic idea is to create a sufficiently high temperature of 41–45°C in regions inside the human body where cancer cells live. Although this elevated temperature itself may damage and kill malignant tissue, hyperthermia is normally combined with radiation therapy or/and chemotherapy to gain synergistic effects of the treatment modalities while minimizing injury to nearby normal tissues (Overgaard et al. 1995,Issels 1999, Jones et al. 2003, Sugahara et al. 0301, Van der Zee et al. 2008). Thermal therapy applied to recurrent breast cancer resulted in a complete response rate increase from 31% to 65% in tumors of size smaller than 3 cm (Van der Zee et al. 1999). Other multi-institutional randomized trials on the same disease all showed similar improvement from adding hyperthermia to radiotherapy (Vernon et al. 1996, Jones et al. 2005). Hyperthermic treatment of large (>40 mm) and deeper (>20 mm) tumors still remains a challenge (Overgaard et al. 1996, Vernon et al. 1996, Perez et al. 1991, Sherar et al. 1997). A key factor affecting treatment efficiency of larger tumors is tissue temperature heterogeneity, since this imposes an upper limit to the maximum sustainable temperature that can be induced to avoid erythema and blistering in the patient (44–45° C subcutaneously (Sneed et al. 1995) and 43° C skin temperatures (Lindholm et al. 1995)).

Microwave array applicators are commonly used for heating in hyperthermia, in which the imperative water bolus between applicator and skin plays a central role in the MW-heat budget. Two basic parameters, namely electromagnetic power distribution and bolus temperature, are central quantities for optimization of temperature distribution within the volume under treatment (Van der Gaag et al. 2006). Together with applicator design, water bolus shape and size have been subject to combined experimental and theoretical studies (Van Rhoon et al. 1998,Kumeradas and Sherar 2002,Kumeradas and Sherar 2003). Nevertheless, quantitative thermal loading effects of the water bolus within clinical hyperthermia systems are less known. In addition to function as a dielectric coupling medium for the antenna applicator, the bolus is also essential for heat regulation both at the skin-applicator interface as well as deeper tissue levels (Lagendijk 2000). Furthermore, the near field antenna deposition pattern is typically very energetic and non-uniform. The bolus thus provides an effective buffer zone (Underwood et al. 1992) between the applicator and the patient. To avoid thermal blisters, the skin temperature must be controlled by active use of the water temperature and flowrate during microwave heating. Thermal convection and conduction in the bolus compartment also spread the heating energy spatially. Finally, the bolus effective thickness directly influences the resulting SAR distribution (effective field size) of each microwave antenna (de Bruijne et al. 2006, Neuman et al. 2002)

Low cost and expandable printed circuit board (PCB) array construction facilitates development of antennas without the shortcomings of early superficial heating devices. Now lightweight and low profile multi-element array designs have been introduced such as the current sheet applicator (CSA) (Gopal et al. 1992), the contact flexible microstrip applicator (CFMA-12) (Lee et al. 2004), the microstrip spiral applicator (Lee 1995), the annular aperture and horseshoe applicators (Carlier et al. 2002), and the Dual Concentric Conductor applicator (DCC) (Rossetto and Stauffer 2001). One such applicator developed by this group, for concurrent heating an brachytherapy treatment of large area surface disease such as chest wall recurrence of breast cancer, was reported by (Stauffer et al. 2005). The use of a multilayered conformal applicator (Juang et al. 2006a) further emphasizes the need for a thin water bolus. The requirement of reduced thickness (<10 mm) is also essential to prevent standing waves within boli (Neuman et al. 2002); however, with the trade-off that larger thickness (and volume) will increase the thermal cooling capacity of the bolus.

The electromagnetic and thermal effects in applicator-bolus-tissue hyperthermia treatment setups have been investigated in terms of spatio-temporal effects of radiation patterns from microwaves applicators (Lagendijk 2000,Jacobsen and Stauffer 2007). However in these references, and elsewhere in the literature, the heating/cooling effects of the water bolus are assumed to result from a spatially uniform flow rate of water at a fixed temperature. In practice there are several design considerations for the water bolus that influence the water flow pattern, and as water passes through the bolus it clearly picks up heat either directly from the electromagnetic field or through heat transfer or cooling from the skin. Hence, it is obvious that the mutual thermal and electromagnetic coupling between the applicator, bolus and patient is the source of a complicated thermal control system faced by the hyperthermia operator

The focus of this study is to quantify the flow pattern in an existing water bolus design, and describe its spatial electro-thermal characteristics during hyperthermia treatment. Based on Navier-Stokes equations for flow in incompressible media and Brinkman’s equation for flow in porous media, the flow pattern in the water bolus was investigated both experimentally and numerically. These results are thereafter incorporated into a numerical model of superficial hyperthermia induced by a conformal array of microwave antennas coupled to skin with a 5 mm thick water layer (Jacobsen and Stauffer 2007) to investigate the lateral thermal variations across the antenna array.

The paper is organized as follows. The experimental and numerical models are described in Section 2, while results are presented in Section 3. In Section 4 we discuss our results in terms of the established theoretical and practical background, and finally conclude our findings in Section 5.

The results from the numerical simulations described in this paper have been produced using the high performance computing facilities at the University of Tromsø.

2. Methodology

2.1. Experimental setup

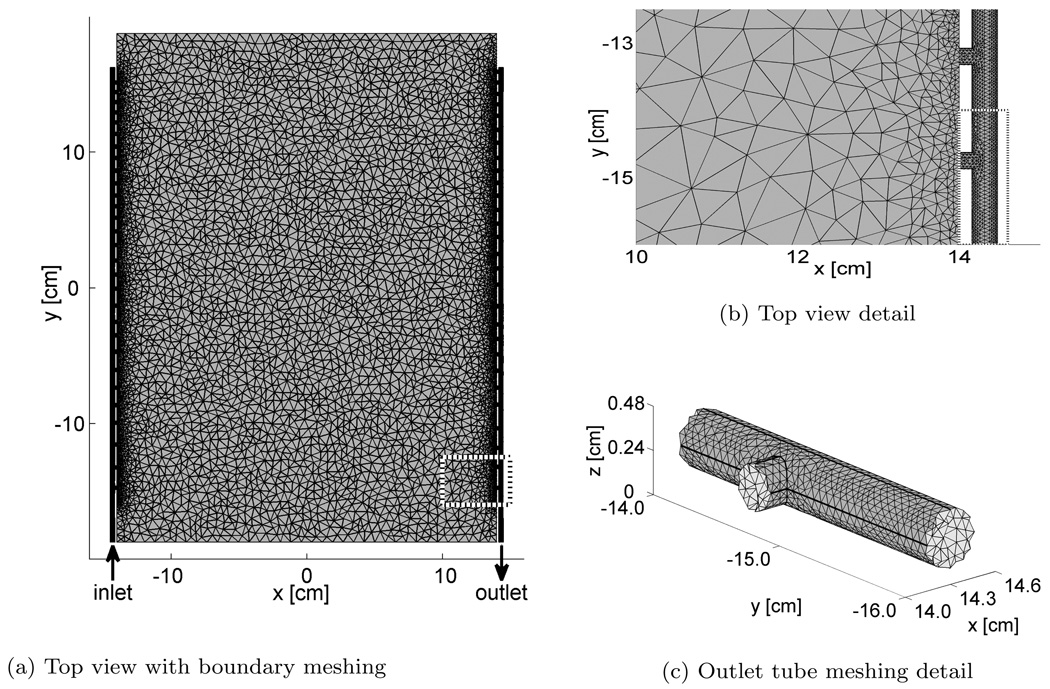
The bolus under investigation is a rectangularly shaped compartment of dimensions 375×280×4.8 mm³ formed between two layers of 0.2 mm (8 mil) thick Polyurethane fabric with perforated Tygon tubes for distribution of water from the bolus inlet tubing, across the thin layer compartment, and to the outlet tubing. An open pore Polyurethane filter foam, with 20 pores per inch (PPI), is used inside the bolus to stabilize its thickness and ensure free water flow. This particular bolus is based on an early water bolus design used in superficial microwave hyperthermia as described in (Stauffer 2000,Jacobsen et al. 2000). The experimental setup for testing flow dynamics is shown in figure 1, whereas physical properties of the study are summarized in Table 1. Note that there are in total 29 and 28 holes in the inlet and outlet tubes, respectively, and that the holes have a slightly closer spacing at the end of the tubes. The experimental setup used to study flow through the bolus consisted of a video camera aimed at the top surface of the bolus while circulating skimmed milk as a contrast fluid into the bolus inlet and monitoring the advancing front of milk across the bolus surface. Although the viscosity of water and skimmed milk is somewhat different, 0.0010 sPa as compared to 0.0015 sPa at 20°C (Phillips et al. 1995), the flow patterns of water and skimmed milk in bolus are expected to be close to that of a water circulated bolus. Numerical runs (data not shown) showed marginal differences of fluid velocity distribution vs space-time for the two cases of milk and water.

Figure 1.

Experimental setup. 1: Rectangular bolus, 2: Inlet tube, 3: Outlet tube, 4: Peristaltic pump, 5: Air trap, 6: Flow meter, 7: HD video camera.

Table 1.

Dimensional and material constants in experimental setup.

Medium	Parameter	Notation	Value
Bolus	Width	W	280 mm
	Length	L	375 mm
	Thickness	T	4.8 mm
Tube	Inner diameter	di	3.175 mm
	Outer diameter	do	6.3 mm
	Hole diameter	dh	2.5 mm
Water	Viscosity	ηw	0.001 sPa
	Density	ρw	1000 kg/m3
	Specific heat	cw	4200 J/kg °C
	Thermal conductivity	kw	0.60 W/m °C
	Heat flux (water)	hw	4 W/m2 °C
Polyurethane	Density	ρp	1300 kg/m3
	Specific heat	cp	1500 J/kg °C
	Thermal conductivity	kp	0.16 W/m °C
	Heat flux (polyurethane)	hp	0.4 W/m2 °C
Tissue	Density	ρt	1000 kg/m3
	Specific heat	ct	3500 J/Kg °C
	Thermal conductivity	kt	0.56 W/m °C
	Heat flux (body)	ht	40 W/m2 °C
	Blood heat capacity	ωbcb	1912.5 J/Kg °C

The inlet and outlet tubes in the water bolus are connected to a Stöckert Shiley heart-lung machine roller pump driving water through the closed system including a 500 mL air trap bulb. The pump has a variable speed adjustment which provides readout of both flowrate in liters per minute (l/min) and pump speed in rotations per minute (RPM). To compensate for high pressure and possible backflow in the pump at the highest pump speeds, a Digimesa FHK Arnite Ø3.3 mm flow meter was used to calibrate the flow measurements. The water and contrast fluid temperatures were held at room temperature T=22°C during the different experiments with pump speeds providing flow rates in the range from 0.25–1.0 l/min.

Initially in the experiment, the bolus compartment was filled with water and the air trap with contrast fluid. The bolus is lying flat (horizontal) and the closed loop fluid system ensures that the bolus maintains a constant thickness close to specified 4.8 mm during the experiment. A Canon HV20 camcorder was used to capture the flow pattern as the contrast fluid was suddenly pumped into the bolus inlet using 0.25, 0.5, 0.75 and 1 l/min flow rates. Because of the closed loop system the mixed fluid were pumped out of the bolus outlet at the same rates. The taped film is rendered in HDV quality (1440×1024 pixels) with 25 frames per second. The movie was post-processed in Matlab for cropping (showing only bolus), gray tone (simplicity for black/white contrast) and finally a front line position estimate was generated, based on gray tone thresholds of a smoothed difference between the current frame compared to the initial frame without contrast fluid.

2.2. Multi-physical numerical model

To quantitatively study the water flow velocity u in the system, a numerical model of the bolus was constructed in Comsol Multiphysics^†; a commercial software for solution of partial differential equations using the finite element method. The numerical model has a rectangular central part, with external cylinders representing the water-bearing part of the perforated tubes. The full model is shown in figure 2a, and the water inlet and outlet are located in the lower left and right part of the model, respectively.

Figure 2.

Numerical model. Detailed areas perimeter shown as dotted white and black line.

The conservation of flow momentum in the bolus is described through Navier-Stokes equations for incompressible media combined with Brinkman’s term for the porous media (Slattery 1972, Verleye et al. 2005)

$${\rho }_w\left(\frac{d\mathit{u}}{dt}+\mathit{u}·\nabla \mathit{u}\right)-\frac{\eta }{\kappa }\mathit{u}+\nabla p-\eta {\nabla }^2\mathit{u}=\mathit{F}.$$ (1)

Here ρ_w is the water density, κ is the permeability, p is the pressure, η is the viscosity and F is the external force vector. ∇ denotes the gradient operator, ∇² denotes the Laplace operator, and $\frac{d}{dt}$ is the time derivative. We will in this study assume a steady state flow pattern, so that the derivative term in Eq. (1) is set to zero.

From Eq. (1) we can identify the two main contributors to the flow pattern, the pressure p and any other external forces F. In our case, the external forces are represented by the rigid walls of the tubes and bolus, which are represented by the boundary conditions of zero flow velocity in the direction normal to the wall. In addition a “no-slip” boundary, meaning that also the tangential velocity component equals zero immediately adjacent to the wall, is commonly applied to solve Navier-Stokes equations for flow in rigid bodies (Lauga et al. 2007). This leaves us with pressure as the only active driving force for the flow, and under the influence of ∇p water flows mainly in the direction of lower pressure.

While the pressure contributes to the water velocity, we can also identify two other restrictions to the flow pattern in Eq. (1). First, the fluid viscosity, in the η∇²u term, acts as a diffusion of water momentum trying to equalize the velocity of nearby particles/positions. Second, the permeability of the porous material in the rectangular middle part of the bolus acts as a unidirectional energy dissipation parameter which also de-emphasizes sharp derivatives in the velocities as e.g., jets and eddies (Pilotti et al. 2002). Lastly, the second order velocity term ∇²u describes the flow inertia which maintains the current direction of the flow.

As the filter foam only fills the rectangular part, the permeability term in Eq. (1) is dropped in the inlet and outlet flow cylinders. In addition to Eq. (1), conservation of mass ∇ · u, artificial diffusion and no-slip walls were used when solving for flow velocity u in the bolus.

While Eq. (1) is easily solved numerically for laminar flow, the use of artificial diffusion and fine meshing is important to get credible results for higher flow rates. Reynolds number (Landau and Lifšic 1959)

$$Re=\frac{{\rho }_{w}q{d}_i}{\eta A},$$ (2)

where A is the tube cross-section area and q is the tube flow rate, is a dimensionless parameter commonly used to classify the flow pattern inside a tube. For Re < 2000 the flow is laminar, while the Re > 4000 case indicates turbulent flow. These limits are not exact, and the transition region between laminar and turbulence flow is particularly difficult to model in numerical solvers (Zabaleta 2007).

The final meshing of the model is done using the extra fine option in the software, producing a mesh consisting of a total of 455510 tetrahedral voxels. The meshing is irregular, with smaller elements where a greater detail in the solution is expected. A closer look at the intersection between the rectangular inner part and the tube reveals a denser mesh near the tube holes, as shown in figure 2b. The fine meshing around the last hole in the outlet tube is shown in figure 2c. The numerical model was solved for flow rates q=0.25, 0.50, 0.75, and 1 l/min on Stallo ^‡, using approximate 200 hours CPU time and 22 GByte of memory.

Using the steady state numerical solution of flow direction and velocity in Comsol, a front propagation estimate was created in Matlab^§. This numerical front propagation is initialized by introducing a set of particles located in a straight line inside the rectangular inner part close to the inlet tube. For closely spaced time samples, T_S=0.5 s, the new position of each particle is estimated using the old position according to

$${\mathit{x}}_{i+1}={\mathit{x}}_i+\mathit{u}({\mathit{x}}_i)·T_S,$$ (3)

where x_i is the particle position at instant i and u(x_i) is the velocity vector at that position. As the velocity changes accordingly to the depth z, an averaged velocity is used and the particle position is calculated along the z = 0.24 mm plane. This front propagation method creates an effect similar to the time-dependent step temperature gradient procedure used in (Juang et al. 2006b), but in our case the flow dynamics are more precise as all heat conduction effects are ignored in the numerical method.

2.3. Microwave hyperthermia

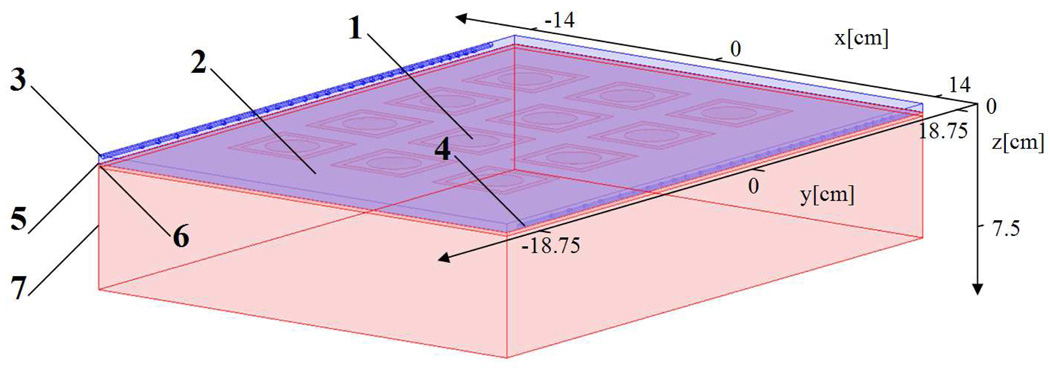
The microwave applicator used in this study is a 4×3 array of Dual-Concentric Conductor (DCC) antennas operating at 915-MHz. The DCC antenna has a square slot aperture with outer diameter of 50 mm surrounding, a 5 mm wide rim of copper with central opening of 30 mm, thus producing a 5 mm radiating slot. The spacing from center to center between the antenna elements were selected to 70 mm; which produces a maximum effective field size at about 10 mm depth in tissue. A simplified anatomical model was used to illustrate the temperature load effects of the water bolus and microwave heating on tissue. Using the rectangular shaped water bolus as the basic outline, this model had the microwave DCC array applicator on top, and a 0.2 mm thick polyurethane fabric followed by 2 mm skin and 68 mm homogenous malignant tissue beneath the bolus. The model is depicted in figure 3.

Figure 3.

Hyperthermia model. 1: Microwave antenna array, 2: Water bolus, 3: Inlet, 4: Outlet, 5: Polyurethane, 6: Skin, 7: Malignant tissue.

The steady state heat transfer inside the bolus can be written as a combination of convection and conduction

$${\rho }_w{c}_w\mathbf{u}\nabla T-\nabla ·(k_w\nabla T)=Q,$$ (4)

where c_w and k_w are water specific heat and thermal conductivity, respectively, T is the temperature, u is the velocity vector and the source term Q is the power density produced by the DCC microwave antenna array. The in- and outflow bolus boundaries are assumed to be dominated by forced convective heat flux from the water, while other boundaries have conductive heat transfer to the surroundings.

The polyurethane layer represents a thermal barrier between the bolus and the tissue so that a thin layer is essential for its functionality (Jacobsen and Stauffer 2007). The heat transfer can in our study be written as

$$-\nabla ·(k_p\nabla T)=Q,$$ (5)

where k_p is the polyurethane thermal conductivity. The tissue thermal response, both for skin and underlying tissue, can be written by the steady state Pennes’ bio-heat transfer equation as (Pennes 1948)

$$w_b{c}_b(T-T_b)-\nabla ·(k_t\nabla T)=Q,$$ (6)

where w_b and c_b is the blood perfusion rate and specific heat, respectively, T_b is the arterial blood temperature and k_b is the thermal conductivity of the tissue. The polyurethane and tissue boundaries both have conductive heat transfer to their surroundings, with room (22 °C) and body temperatures (37 °C), respectively. Heat flux parameters are listed in Table 1.

Meshing of the microwave model is undertaken using Comsol’s extremely fine rectangular option at the top boundary of the bolus, and swept mesh from this layer through the bolus, polyurethane, skin and malignant tissue with 10, 2, 5, and 20 layers, respectively. In the deepest tissue subdomain, an exponential distribution of layers where applied, and the total model consisted of 123,950 hexahedral elements with 1,022,625 degrees of freedom. Flow results from the high resolution water bolus simulations are used in Eq. (4), while power density results from each antenna are imported from CST Microwave Studio^¶. Properties and further results from the electromagnetic simulations can be found in (Jacobsen and Stauffer 2007). Each antenna in the microwave array is set to the same power level, and the total power is matched to give skin temperatures below 43°C. For each flow rate, this leads to a hyperthermia simulation solvable in 2–3 hours CPU time using approximately 26 GByte of RAM on Stallo.

3. Results

3.1. Front propagation

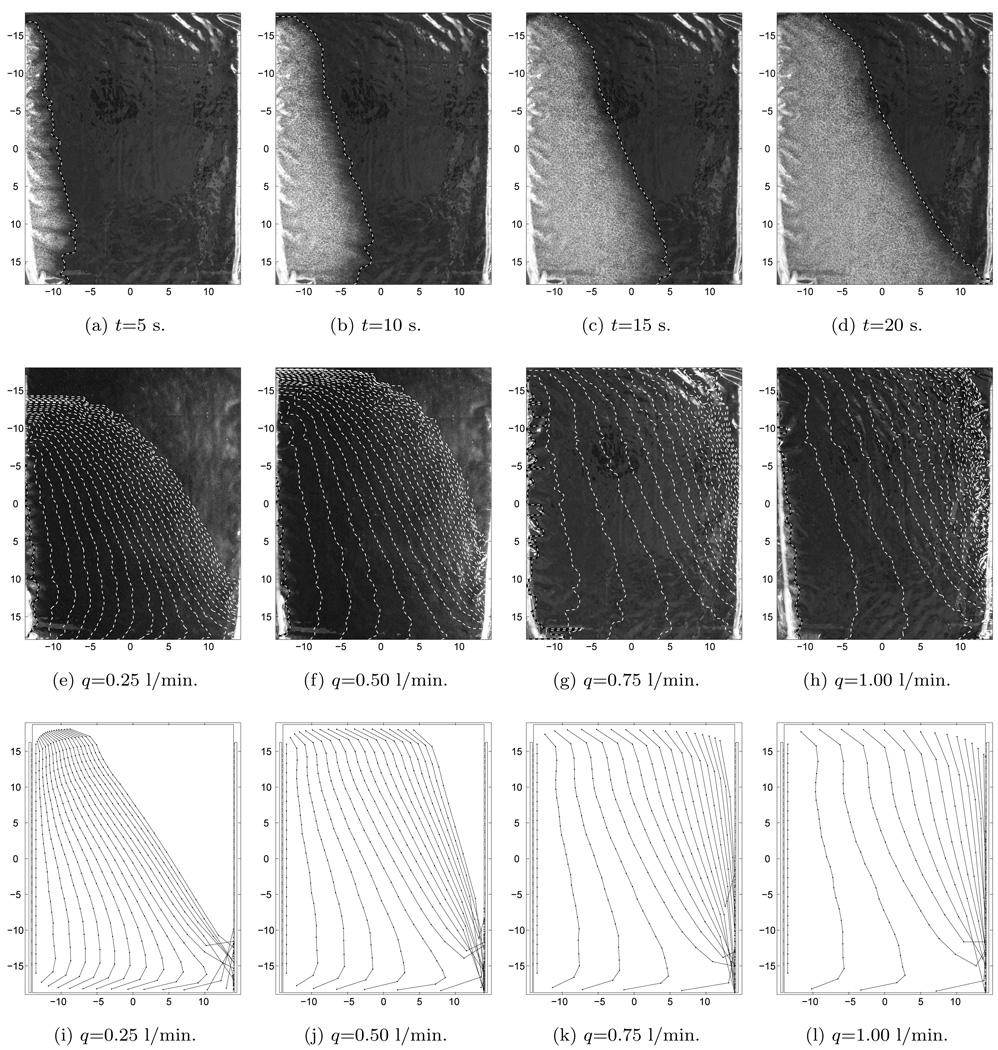
In the upper row of figure 4, we have shown four different images of the bolus taken from the contrast fluid experiment with a flow rate of 0.75 l/min. The contrast fluid front 5 s into the experiment, shown in figure 4a, indicates an almost uniform and synchronized inflow pattern of fluid into the bolus although the front near the first hole in the tube has moved slightly further than at the end of the inlet tube (top). The white dashed line in this plot shows the front line as determined by the detection algorithm. After 10 s, the contrast fluid front line has moved approximately 50 mm to the right (see figure 4b). For t=15 s into the experiment, shown in figure 4c, the front line of the lower part of the bolus clearly has moved further towards the outlet tube compared to the front in the upper part of the bolus. The contrast fluid distribution in the bolus at t=20 s is shown in figure 4d, at which time the contrast fluid has reached only half way across the bolus at the top and all the way to the outlet in the lower right corner. The front line is tilted, clearly indicating that flow velocity near the first hole in the outlet tube is significantly higher than in the upper right corner of the bolus.

Figure 4.

Flow pattern of moving front. Upper row: Time line of contrast fluid distribution experiment with q = 0.75l/min. Middle row: Superimposed moving front lines from experiments, 5 s between lines. Lower row: Numerical simulation of moving front, 5 s between lines.

The second row of figure 4, shows from left to right successive moving front lines in the experiment for different flowrates. In all these plots, the time distance between each line is kept constant at T = 5s. For the lowest flow rates, q=0.25 and 0.50 l/min, we find that it takes some time before the contrast fluid reaches the upper part of the bolus. The last front line shown is taken 100 s after the contrast fluid entered the bolus, and still the upper right part of the bolus is without any white contrast liquid. For higher flow rates, q=0.75 and 1.00 l/min, we find that the contrast fluid is pushed to the end of the inlet tube. Thus, the flow velocity is almost uniform in x-direction in the left part of the bolus. As the fluid moves close to the outlet tube, the front lines becomes more tilted; again indicating high flow velocity near the first hole in the outlet tube.

3.2. Numerical flow patterns

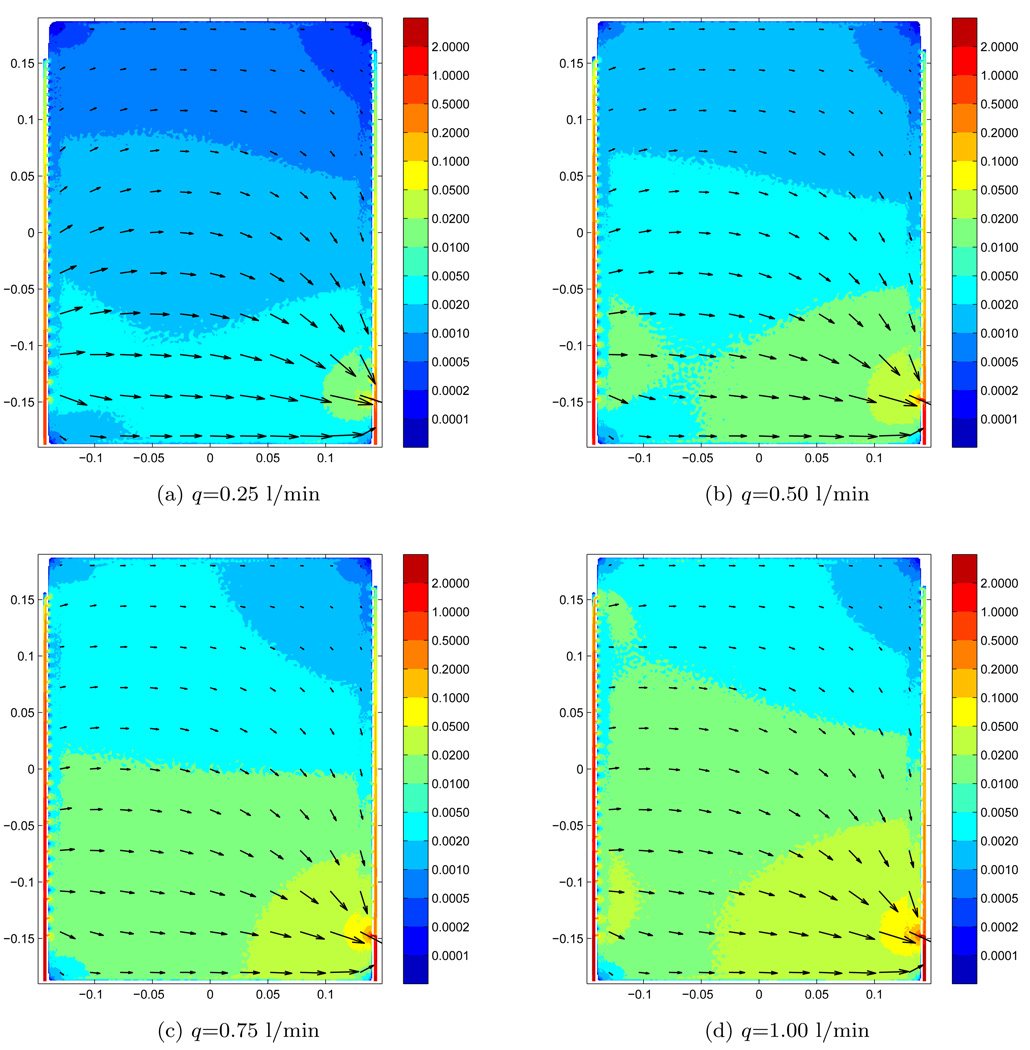
The resulting flow velocity magnitude and direction, in the center of the water bolus at z=2.4 mm, are shown for different flow-rates as color levels and arrows in figure 5. The water inlet and outlet are located at the lower left and right sides, respectively. For the lowest flow rate, q=0.25 l/min as shown in figure 5a, we find that most of the water enters the bolus through the first couple of holes in the inlet tube. Similarly, most of the water leaves the bolus through the first couple of holes in the outlet tube. The flow pattern is in this case nearly symmetric with respect to the y=0-plane. As for the flow rates q=0.5 and 0.75 l/min, shown in figure 5b and figure 5c, respectively, the majority of water is moved further into the inlet tube before entering the bolus. In contrast, the flow pattern along the outlet tube stays almost constant in terms of direction and relative velocities. In the highest flow rate case q=1.0 l/min, shown in figure 5d, water enters the bolus in a nearly uniform pattern along the tube length with velocities ranging from 0.015 to 0.01 m/s near the inlet and tube end, respectively. This uniform flow pattern along the y-direction breaks down about one-third of distance across the bolus at x > −5cm, and most of the water exits the bolus through the first couple of holes in the outlet tube (as seen before).

Figure 5.

Fluid velocity distribution for different flow rates. Numerical results.

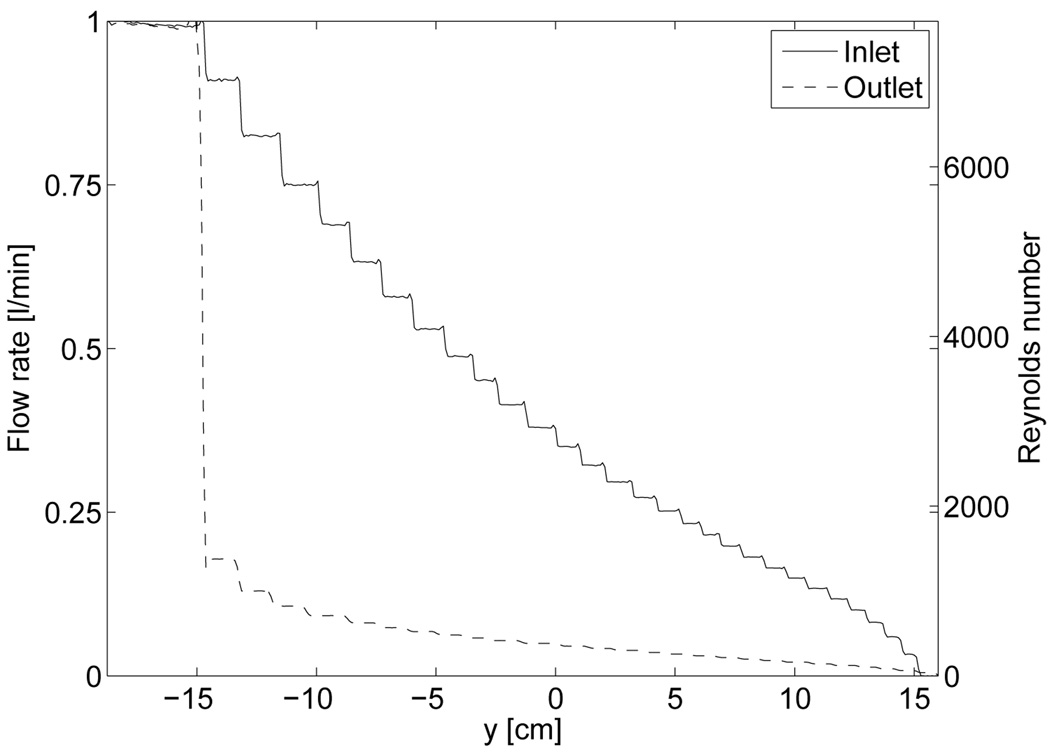
For the q = 1 l/min case, figure 6 shows the vertical flow rate as a function of the longitudinal coordinate y in the inlet and outlet. In the inlet tube, we find that the flow rate drops almost linearly passing each hole in the tube, while it is clear that most of the water flow enters the outlet tube through the last few holes. Note that the placement of holes in the inlet- and outlet tube are not entirely symmetric, as this numerical model resembles the actual hole placements in the water bolus prototype which has somewhat irregular spacing of holes but generally closer spaced near the end of the tubes. Based on Eq. (2), an estimate of the average Reynolds number along the tubes are shown in the right hand ordinate-axis. A closer look near the first hole of the outlet tube reveals that this volume is especially prone to turbulent flow as a result of high Reynold numbers and rapid change of flow direction as the water comes through the hole and turns into the outlet tube at an abrupt angle.

Figure 6.

Flow rate and Reynolds number along inlet- and outlet tubes with q =1 l/min.

Based on the flow velocity and directions of the numerical model in figure 5, we have shown the calculated front lines using Eq. (3) for particles in the bolus in the lowest row of figure 4. These plots from left to right, showing results from flow rates q=0.25, 0.50, 0.75 and 1.00 l/min, respectively, are almost identical to the experimental results in the middle row. There is some discrepancy in the low velocity flow regions as e.g., in the upper left part for q=0.25 l/min and the upper right part of q=1.00 l/min. However, overall the flow lines from the numerical and experimental results are very similar both spatially and temporally.

3.3. Bolus convection effects on superficial tissue heating

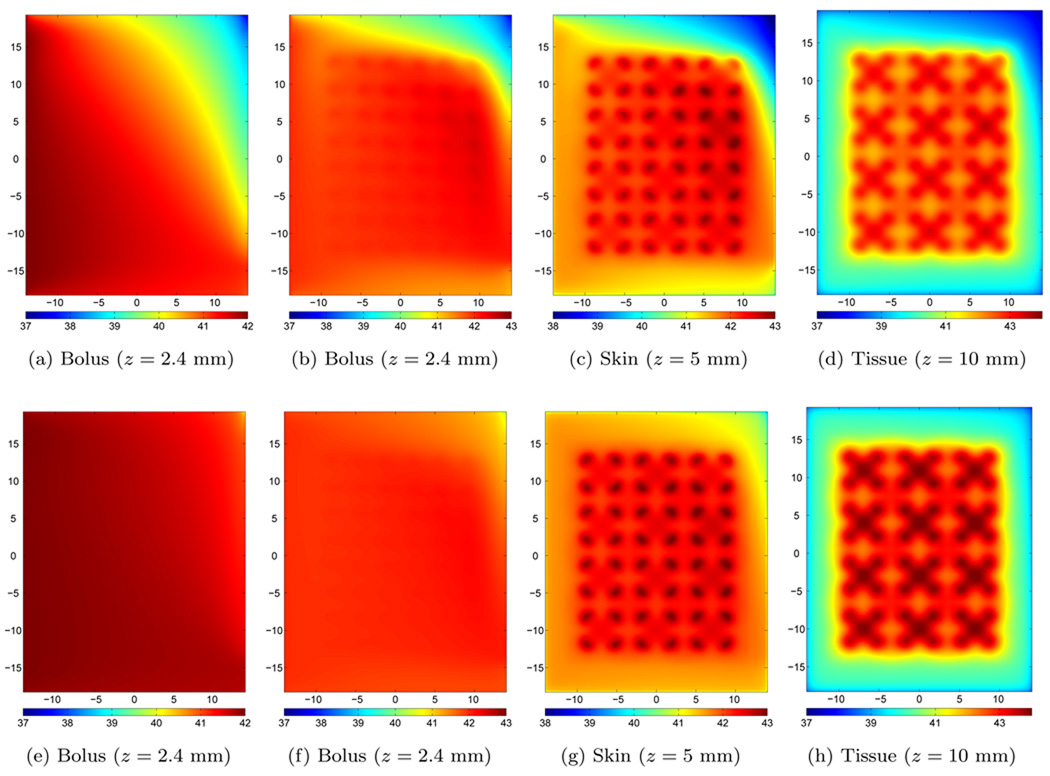
In the upper row of plots in figure 7, we have shown different temperature distributions using a flow rate of q=0.25 l/min. The bolus temperature without microwave heating is shown in figure 7a. Near the inlet tube, the skin temperature increased to the inlet water temperature 42 °C. As the water passes through the bolus, the temperature drops as a result of the constant load from the underlying body at cooler temperature (37 °C). Since the flow rate is low and non-uniform, the temperature drops quickly with a gradient similar to the front lines in figure 4i. With the microwave applicators turned on, the temperature distributions in the bolus compartment, at the skin-bolus interface and in the tissue are shown as figure 7b, figure 7c and figure 7d, respectively. In the bolus, we find that the temperature increases above 42 °C as the water passes under the microwave antennas. A maximum temperature of 42.5 °C is observed under the rightmost second upper microwave antenna. For the skin temperature, we find almost the same distribution as in the bolus case. The maximum temperature under each antenna at the skin interface varies from 42.7 to 43 °C, where the latter is the design temperature for the experiment corresponding to a power P=2.9 Watt from each antenna. For the target tissue, the difference of the maximum temperature under each antennas is also approximately 0.3 °C with a global maximum at 43.5 °C.

Figure 7.

Steady state temperature distributions without (left panels) and with (columns 2–4) microwave heating. Upper row: q=0.25 l/min and P=2.9 Watt per antenna, lower row: q=1.00 l/min and P=3.6 Watt per antenna.

At the highest flow rate, q=1.0 l/min, we have shown the corresponding temperature distributions in the lower row of figure 7. Without the microwave applicator array turned on, the higher water flow rate keeps the temperature close to 42 °C across most of the bolus (shown in figure 7e). Only in the upper right part of the bolus, where the flow rate is significantly lower than in the lower right part, we find a temperature decrease of about two degrees centigrade, about half the drop seen in the q=0.25 l/min case. With the microwave power on, the water temperature again starts increasing while passing under the microwave antennas (shown in figure 7f), but now the maximum water temperature is limited to 42.2 °C. The skin temperature is shown in figure 7g. The maximum skin temperatures under each antenna have a difference of approximately 0.1 °C, and the variations are mainly found along the horizonal x-axis, as the variations vertically under the different antennas is small. In this case, the design criteria of 43 °C allowed for a power P=3.6 Watt from each antenna. Finally, the tissue temperature 5 mm into the tissue (z = 10 mm) is shown in figure 7h. Here we find that the maximum tissue temperature under each antenna varies marginally from 44.0 to 44.1 °C.

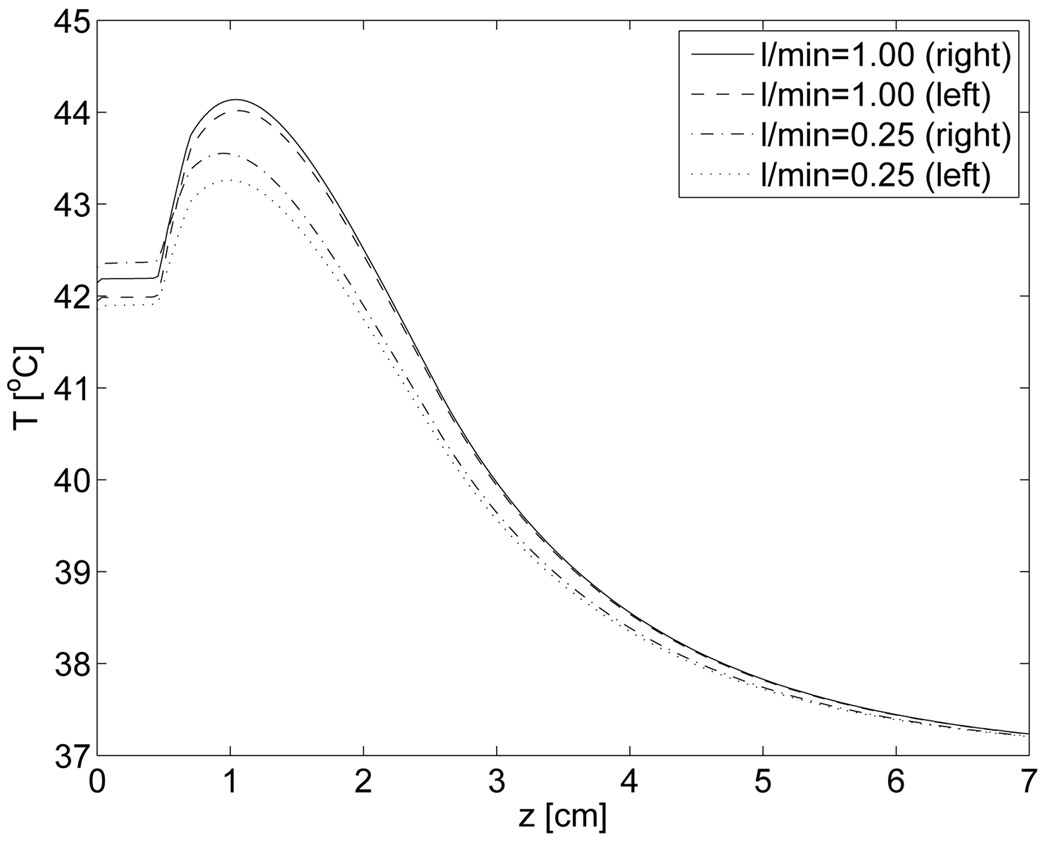
The temperature profile along the z-direction into tissue are shown in figure 8 under the hottest antenna at the outlet side (right) and the corresponding antenna near the inlet side (left). These results shows that the temperature for z=10 mm are close to the maximum temperature, and that the temperature falls approximately exponentially down to the body temperature of 37 °C. As the lateral temperature distribution is under investigation in this study, we have chosen to restrict our presented results to z=10 mm which corresponds well to superficial hyperthermia.

Figure 8.

Vertical temperature profiles under center of two antennas at positions: x=−7cm (left), x=7cm (right) and y=3.5cm (both).

4. Discussion

4.1. Finite element numerical method vs real world

Some differences between the numerical and the experimental fluid dynamic findings are expected, especially within the filter foam where fat particles in the contrast fluid can be trapped for low flow velocities. This may explain the discrepancies between the numerical and experimental moving front lines in figure 4. The physical parameters describing the bolus are also difficult to quantify precisely. For instance, the permeability of the filter foam depends on material compression. The numerical model has a constant thickness, and it is not trivial to keep the bolus strictly rectangular and uniform in thickness between exactly parallel inlet- and outlet tubes. The real bolus thus performs slightly worse than the numerical model predicts, a result not surprising in the world of computation vs reality. Even so the agreement seen in figure 4 is acceptable.

While the numerical results from the finite element method in COMSOL provide values of both flow speed and direction for an almost unlimited set of points inside the bolus, there is to our knowledge no method to measure these parameters accurately (without perturbing the flow lines) in practice. The adopted procedure of using contrast fluid and moving front lines in the experiment can not provide accurate flow velocity results (speed and direction) for all points at all times in the bolus. Nevertheless, our frontline evaluation clearly indicates that the applied numerical model is reliable as verified by the overall concordance between simulations and experiments.

From the Reynolds number defined in Eq. (2), and numerically obtained values in figure 6, it is clear that parts of the bolus (inlet and outlet tubes) are prone to turbulence as the flow rate exceeds q = 0.5 l/min. In our numerical model the effect of turbulence is included in the inlet- and outlet tubes through fine tuned artificial diffusion. This creates a more uniform flow velocity cross-section inside the tube, as also observed for turbulent flow. The use of artificial diffusion is essential to provide convergence in the q = 0.75 and 1 l/min cases, and we find that our numerical solution also closely resembles the turbulent effect present in the real water bolus case. From the flow velocities obtained in the numerical model, we identify the most important features of the bolus construction that can be adjusted to improve the flow pattern in future water bolus designs.

First, as the flow rate increases the second order velocity term in Eq. (1) dominates. In the investigated bolus, this gives rise to two distinct effects: As the inlet tube water is pushed past the first couple of holes (as a consequence of large moment of inertia) to the outlet, the high-velocity water meets a 90-degrees bend which increases the possibility of eddies. This shows the possibility of creating a well distributed flow pattern of water entering the rectangular bolus from a perforated inlet tube. Note that smaller spacing between holes at the end of the input tube also contribute to this almost uniform flow pattern. But, even with a uniform input of water to the left, the flow distribution is quite non-uniform by the time it reaches the perforated tube along the right side outlet, which produces much higher flow in the last few holes close to the tube exit.

Second, the high flow rate combined with small diameter tubes and holes give rise to turbulence and high pressure drops. In the experiment, the high quality roller pump could not provide the highest available flow rate. While the pump speed indicated a flow rate of 1.6 l/min the measured flow rate using the flow meter was only 0.97 l/min (denoted q=1.0 l/min in our presented results). This indicates large resistance against high flow velocities in the bolus, with possible turbulence and back resistance in the high-quality heart-lung machine pump. The difference between measured and direct flow rate readings of the pump was observed to be significantly smaller for lower pump speeds. From this we conclude that somewhat larger diameter input and output tubing will reduce inefficient pumping from the peristaltic pump. However, from a practical point of view, that is the prerequisite of bolus conformability to contoured anatomy, the tube diameter should be kept to a minimum. As higher total flow rate in general gives superior cooling capacity by the bolus, this limitation reduces the effectiveness of this bolus in microwave hyperthermia.

Third, and last, we find that while uniform flow pattern is possible to obtain from a tube with one inlet, we can not get a uniform velocity distribution along the outlet using only one outlet tube. Large spacing between the first couple of holes in the outlet tube does not reduce this outlet effect significantly. Future water boli likely need at least two outlets, but also two inlets could improve the total flow rate in the bolus as indicated by preliminary studies in (Arunachalam et al. 2009).

4.2. Adequacy of water bolus for superficial microwave hyperthermia treatment

The results from our numerical hyperthermia model clearly show that the water bolus is essential in homogenizing the temperature distribution, not only at the skin, but also further down into the tissue. The inlet water temperature is used both to heat the skin above its natural temperature, but also acts to remove excess energy (homogenize temperature distribution) which is flushed out with convection. With this in mind, it is no surprise that the bolus performs better as the flow rate is increased.

Although the lower flow rate of q=0.25 l/min (upper row of figure 7) does not provide a uniform and high temperature heat pattern as the higher flow rate cases (lower row of figure 7), these results illustrate another important problem that can arise from a non-uniform flow pattern in the coupling bolus. Regions with slow flow rate are more sensitive to the applied microwave power as the heat convection term becomes smaller. This limited flushing of excess heat produces hot spots under the antennas. As a result, the microwave power must be reduced, which leads to less effective penetration depth and lower maximum temperature inside the tissue as shown in figure 8. Thus, adjusting the power levels across the different microwave antennas can produce a more uniform skin temperature, e.g. reducing the power under the hottest antenna, but this will not necessarily maintain optimum (uniform) heating deeper in tissue.

Using the highest possible flow rate in the numerical model, in our case q=1.0 l/min, further improves the bolus performance in terms of closely matched temperature distribution under each antenna. Compared to the q=0.25 l/min case, the tissue temperature is significantly higher and more uniform for q=1.0 l/min flow rate case, as a direct result of a uniform skin temperature. A small temperature increase downstream (from left to right) can not be avoided. In both cases, the lowest flow region is located near the end of the outlet tube and the low heat convection in this area limits this bolus use in hyperthermia treatment. Higher total flow rates in the system will reduce the problem, but the flow pattern does not change along the outlet tube and most water exits the tube through the holes nearest the water outlet connector.

However, somewhat more alarming is the fact that our experimental study indicated a more extreme flow pattern than our numerical model. In particular, figure 4h shows that the front lines where dense and almost stopped up in the upper right part of the bolus in the experiment, while front lines entered the output bolus in the numerical model case shown in figure 4l. This could be an artifact of the applied contrast fluid (trapping of fat particles in low flow regions), but we can not rule out that this region at the end of the single outlet tube could potentially be problematic even for the highest flow rates available in practice.

5. Conclusion

The main focus of this study was to characterize the uniformity of fluid flow through a rectangular water bolus with a secondary purpose of characterizing the ability to produce uniform cooling of the skin surface under a large microwave array that is coupled to the tissue surface through this bolus. Both thermal simulations and experimental measurements revealed two main problems with the prototype rectangular water bolus available for this investigation. Non-uniform flow patterns give rise to problematic regions with lower flow rate, and current design with small holes in the inlet and outlet tubes exhibited a strong limitation in terms of maximum flow rate in the system. As higher flow rate in general gives superior cooling capacity by the bolus, these limitations reduces the effectiveness of this bolus in microwave hyperthermia.

Despite its limitations, the single side feed water bolus under investigation still provides acceptable temperature control of the skin surface, but small changes to its design clearly would improve its applicability. Several tube and polyurethane parameters listed in Table 1 clearly affects the flow pattern, and the small difference between the tube inner diameter and the feeding holes plays a significant role in the flow pattern near the outlet. Reducing the hole size will reduce the flow in the hole closest to the outlet, but this at the cost of higher velocities, turbulence and pressure in the system. Preliminary results indicate that both larger diameter and two-sided inlet and outlet tubes will improve the flow pattern in the bolus. This again will reduce internal tubing turbulence effects that produce dissipative heat and decrease overall flow capacity. Although the prototype bolus of this study provides an adequate homogenization of temperature under the large 4×3 microwave applicator, future efforts will investigate design changes in the water inlet and outlet configuration in order to improve uniformity of temperature, both on the skin surface and at superficial tissue depths beneath the microwave antennas.