Abstract
Mechanical signals are important factors that control plant growth and development. External mechanical loadings lead to a decrease in elongation and a stimulation of diameter growth, a syndrome known as thigmomorphogenesis. A previous study has demonstrated that plants perceive the strains they are subjected to and not forces or stresses. On this basis, an integrative biomechanical model of mechanosensing was established (“sum-of-strains model”) and tested on tomato (Solanum lycopersicum) elongation but not for local responses such as diameter growth or gene expression. The first aim of this interdisciplinary work was to provide a quantitative study of the effect of a single transitory bending on poplar (Populus tremula × alba) diameter growth and on the expression level of a primary mechanosensitive transcription factor gene, PtaZFP2. The second aim of this work was to assess the sum-of-strains model of mechanosensing on these local responses. An original bending device was built to study stem responses according to a controlled range of strains. A single bending modified plant diameter growth and increased the relative abundance of PtaZFP2 transcripts. Integrals of longitudinal strains induced by bending on the responding tissues were highly correlated to local plant responses. The sum-of-strains model of mechanosensing established for stem elongation was thus applicable for local responses at two scales: diameter growth and gene expression. These novel results open avenues for the ordering of gene expression profiles as a function of the intensity of mechanical stimulation and provide a generic biomechanical core for an integrative model of thigmomorphogenesis linking gene expression with growth responses.
Attention is currently being refocused on mechanical signals as major cues that control plant growth and development and, thereby, the acclimation of plants to their mechanical environment (Moulia et al., 2006; Hamant et al., 2008). The modification of growth by external mechanical loading is known as thigmomorphogenesis. The thigmomorphogenetical syndrome was reported by Boyer (1967) and Jaffe (1973) and has been subsequently described at the whole plant level in herbaceous plants (Biddington and Dearman, 1985; Latimer et al., 1986; for review, see Biddington, 1986) as well as woody plants (Telewski and Pruyn, 1998; Coutand et al., 2008). In plant stems, this syndrome generally combines a reduction of elongation and a stimulation of diameter growth, in comparison with unstimulated plants (Telewski and Pruyn, 1998; Coutand et al., 2008), and involves local as well as long-distance signaling (Coutand et al., 2000). This syndrome is believed to be involved in the acclimation of the architecture of the plant to its chronic wind environment (Rodriguez et al., 2008). As a corollary, the reduction of mechanical loading (tether staking, individual shelter) induces a reduction of diameter growth to the benefit of growth in height (Jacobs, 1954; Larson, 1965; Meng et al., 2006; Coutand et al., 2008).
However, quantitative data about mechanosensing are lacking (Telewski, 2006). Most thigmomorphogenesis studies use different types of mechanical solicitations, and the mechanical loadings applied to the plants are generally uncontrolled. Comparisons between these experiments are thus difficult, and no quantitative relationship can be assessed between the thigmomorphogenetical stimulus and the plant response (except as in Jaffe et al., 1980; Coutand and Moulia, 2000). Moreover, in most cases, the mechanical loading is applied every day for a few weeks, whereas the effect of these repetitive stimuli in terms of growth in height and/or diameter is often only assessed at the end of the experiment. Coutand et al. (2008) found no correlation between repetitive bending strains and Prunus avium responses, probably because trees acclimated when they were regularly loaded, so that their sensitivity to a given loading was dependant on the preceding loading (mechanical history). The study of the effect of a single mechanical loading thus appears to be a prerequisite for studying the effect of different loading frequencies. Nevertheless, such studies of the effect of a single mechanical stimulus on plant growth remain rare. Measuring the effect of a single loading on growth requires tools capable of measuring small amounts of growth (especially for diameter growth). The linear voltage differential transducer (LVDT) makes this possible (Daudet et al., 2005; Giovannelli et al., 2007). Using this device, Coutand et al. (2000) were able to characterize the kinetics of transient elongation cessation after a single stem bending. But, to our knowledge, the effect of a single bending on diameter growth has never been documented.
Using a detailed biomechanical analysis of the effect of a single bending on stem elongation growth response on plants with varying tissue rigidities and sizes, Coutand and Moulia (2000) demonstrated that tissue strains (ε, relative length changes of each element) and not forces or stresses (σ, internal forces per unit area) are sensed (as was also found in animal cells; for a comparative review, see Moulia et al., 2006). On the basis of this fact, they proposed an integrative model of mechanosensing. This model was based on two assumptions: (1) that each small volume of mechanosensitive tissue dV produces a secondary signal dS proportional to the strain of the small tissue element
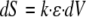 |
(1) |
(provided that the strains are small so that the primary responses of the mechanosensing pathway can be linearized), and (2) that these secondary elementary signals dS add up to a cumulated signal S over all of the competent tissues involved in the mechanoperception
 |
(2) |
The thigmomorphogenetical signal S then comes to be proportional to the sum of applied strains (Sstrains), so that Sstrains provides a quantitative model of the integrated mechanical stimulus on the plant tissues. Note that strain is a dimensionless variable (relative change in length of an infinitesimal element dV), but the sum of longitudinal strains is a volumic integral on the stem volume and thus has a unit of mm3 (for more details, see Coutand and Moulia, 2000). In that study, as the mechanical stimulus was a bending in the range of small displacements and small strains, the longitudinal bending strains were the major strain components (the calculation of the sum of longitudinal strains is detailed in “Materials and Methods”).
The strain-sensing hypothesis (Eq. 1) and the “sum-of-strains” integrative model for mechanoperception (Eq. 2) have been shown to explain univocally the variation in primary growth for different applied loads and tissue rigidities. Indeed, Coutand and Moulia (2000) found a close log dose-response curve between the duration of the primary growth inhibition response D and the sum of longitudinal strains Sstrains
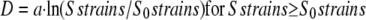 |
(3) |
whereas no relation could be found with force, stresses, or mechanical energy (Coutand et al., 2000, Coutand and Moulia, 2000). Equation 3 means the inhibition of primary growth through systemic long-distance signaling depends log linearly on the sum of strains over a threshold S0strains with a sensitivity equal to a.
The sum-of-strains mechanoperceptive model (Eqs. 1 and 2) has been considered as a step forward for quantifying the local mechanical signal to cells (tissue strains) and integrating it into whole plant responses (Braam, 2005; Moulia et al., 2006; Telewski, 2006). Indeed, Equations 1 and 2 constitute more than a dose-response model, as Equation 1 also integrates the quantitative effect of the size and anatomy of the plant defining the “perceptive structure” of the plant (i.e. more mechanocompetent cells at the same strain level produce more thigmomorphogenetical signal S, but more rigid tissues and organs are less strained for the same force and, hence, sense less; Coutand and Moulia, 2000). This model generalizes the first quantitative response curve obtained by Jaffe et al. (1980) in bean (Phaseolus vulgaris), where the mechanical stimulus was quantified in terms of force or “degree of bending” but not in terms of strains, and a log linear relationship between the applied force and the stem elongation was found. Indeed, the study of Jaffe et al. (1980) was using very standardized plants with, consequently, very similar rigidity, so that in this case the bending force is almost proportional to the sum of strains.
However, the assessment of the sum-of-strains model has been conducted on a global response, elongation growth. The underlying local assumptions of the sum-of-strains mechanoperceptive model have not been directly assessed. This would require the analysis of two types of local responses: responses specific to a position along the stem, such as the diameter growth (Daudet et al., 2005), and cellular responses involved in the mechanosensing pathway, such as the expression of a primary mechanosensing marker gene. Indeed, Equation 1 predicts that the closer the response to the primary reaction of the local mechanosensing pathway, the more linear the relationship between the response and the sum of strains in the strained sensing tissue (in the range of small strains).
At the cellular level, 760 genes were regulated 30 min after touching the rosette leaves in Arabidopsis (Arabidopsis thaliana). They represent 2.5% of the Arabidopsis genome (Lee et al., 2005) and include TOUCH genes first identified by Braam and Davis (1990). In woody plants, a primary mechanosensitive gene called JrZFP2 has recently been found in walnut (Juglans regia; Leblanc-Fournier et al., 2008). The homolog of this gene has also been found in poplar (Populus tremula × alba ‘717-1B4’) and called PtaZFP2 (Martin et al., 2009). The deduced amino acid sequence of PtaZFP2 contains all typical conserved regions of Cys-2/His-2 transcription factors with two zinc fingers (Ciftci-Yilmaz and Mittler, 2008; Martin et al., 2009). In both walnut and poplar, transcript levels of ZFP2 are much higher after mechanical loading than after other abiotic factors such as saline and cold stresses (Leblanc-Fournier et al., 2008; Martin et al., 2009). Moreover, after stem bending, ZFP2 is only expressed in the mechanically strained tissues (Leblanc-Fournier et al., 2008; Martin et al., 2009). Finally, in poplar, this gene has been shown to be expressed as soon as 5 min after bending, with a maximum level of expression 30 min later and then decreasing 1 h after bending. Since PtaZFP2 is mechanosensitive and expresses (1) rapidly after mechanical loading is applied (i.e. during the perception-transduction phase) and (2) only in the tissues undergoing mechanical strains, it is an ideal candidate to test the biophysical model of mechanosensing at the cellular level.
In summary, this work hypothesized that the mechanosensing model initially established for tomato (Solanum lycopersicum) stem elongation also applied for local responses. This hypothesis was assessed by quantifying short-term local responses of plants to a single controlled mechanical loading and determining whether or not this mechanosensing model also applies quantitatively to two local responses occurring at two spatial scales: (1) modification of diameter growth at the macroscopic scale, along the stem, and (2) expression level of the mechanosensitive gene, PtaZFP2, at the cellular scale. Young poplar stems were subjected to a single transitory bending using an original experimental device (Fig. 1), allowing us to control the level of applied bending strains. The plant responses were studied according to a range of applied strains. The effective thigmomorphogenetical stimulus S was assumed to be proportional to the sum of longitudinal strains computed on the local responding zone. The plant responses (modification of diameter growth and expression level of PtaZFP2) were then plotted against the sums of longitudinal strains. The results demonstrated that the maximal diameter growth rate reached after bending, as well as the relative abundance of PtaZFP2 mRNAs, were linearly correlated to the integrals of longitudinal strains. The biomechanical model of perception developed for tomato stem elongation thus appeared to apply to diameter growth and even at the cellular level for a mechanosensitive gene. This provides a way to enhance the quantitative modeling of the macroscopic aspects of the thigmomorphogenetic syndrome and to establish a novel quantitative action law for the expression of a mechanosensitive primary gene over mechanically strained tissues.
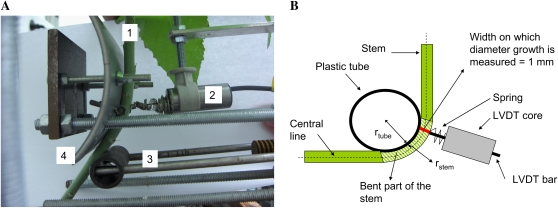
Figure 1.
Bending device. A, The stem (1) was equipped with a linear voltage displacement transducer (2) in order to monitor the diameter growth of the stem before, during, and after bending was applied. A moving arm (3) pushed the stem against a plastic tube; the stem was thus bent around the tube (4). Therefore, the stem was subjected to a controlled curvature in terms of strains. The moving arm was then driven back and the stem was reset to its initial position. B, Scheme of the stem in the bent state. Locally, the applied strain is the product of the curvature of the central line and the stem radius (rstem). In the case of small curvature, the curvature of the central line is given by the inverse of the sum of the stem radius and of the radius of the plastic tube (rtube).
RESULTS
Tests of the Experimental Design
An original experimental device delivering a controlled and quantified level of longitudinal strains to the plants was designed (Fig. 1; for more details, see “Materials and Methods”). The basal part of the stem was curved homogeneously on a plastic tube whose diameter is known. The longitudinal strain in the stem tissues is then dependent on the tube radius as well as on the stem radius. Taking the variability of stem diameters into account, plastic tubes of different diameters were used to create a range of applied strains. In order to study the response in terms of diameter growth, the experimental device also included a LVDT placed within the bent part of the stem and dedicated to monitor continuously the stem diameter growth before and after bending (Fig. 1A). Such a device records all diameter variations, which mainly include diameter growth and elastic diameter variations due to changes of plant water status. Nevertheless, in our hydroponic experiments with low evaporative demand, the diameter variations attributed to changes in plant water status appeared very limited. Indeed, there was no typical wavy signal characterizing stem diameter variations due to stem water status changes (Daudet et al., 2005), except a small reversible component in diameter observed at the transition between night and day periods and also the time of temperature variations, and a transient viscoelastic effect of the mechanical compression during bending to be presented below. Apart from these transitions, the LVDT recording thus represents essentially stem diameter growth, so its output has been called diameter growth in this article. If variations of growth rate are observed, they are attributed to internal biological rhythm.
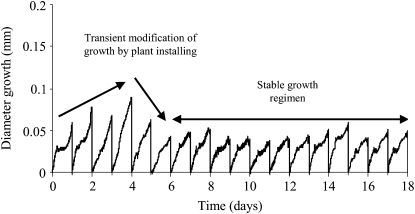
Since plant installation necessarily involves uncontrolled mechanical perturbations, we first assessed the time for the plant to recover an undisturbed state by following the growth after installing the plants on the bending device (without any subsequent mechanical treatment). Plant diameter growth rate increased for 2 or 3 d and then decreased and stabilized (Fig. 2). When stabilized, plants exhibited a rhythmic growth with higher growth rates in the dark period and at the end of the light period. For the tested stems, the average daily increment of diameter was 0.056 ± 0.031 mm. Controlled bending was applied after the plant diameter growth rate had stabilized (i.e. at least 5 d after plant installation) for all bending experiments so as to avoid uncontrolled effects of mechanical strain due to plant installation.
Figure 2.
Representative example of diameter growth of a control plant. The daily recorded diameter growth is plotted against time. Just after plant installation, the diameter growth rate exhibited an increase for 3 or 4 d, followed by a decrease, and finally reached a stable growth rate after 5 to 6 d. The daily growth appeared to be rhythmic, with higher growth rates during the dark period and at the end of the light period.
As shown in Figure 1A, pushing the plant stem against the plastic tube led to a homogeneous bending of the stem around the tube, which made it possible to assimilate the stem to a flexed beam and therefore to apply beam theory for flexural strains computation (Moulia and Fournier, 1997).
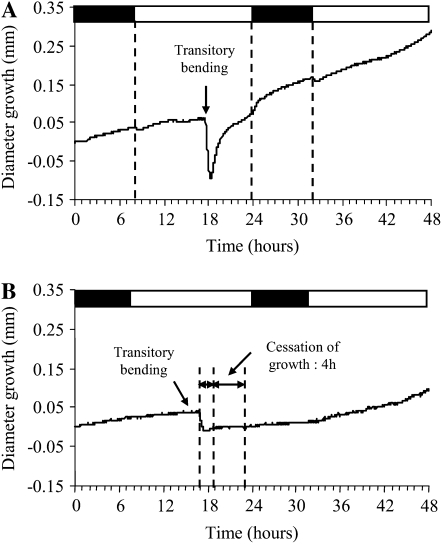
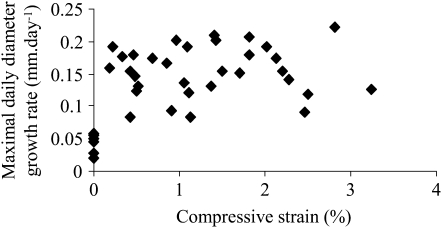
Since bending can affect growth within minutes (Coutand et al., 2000), we checked the growth recorded just after bending. When a single bending was applied, the LVDT signal decreased for 1 to 2 h, suggesting a decrease of the stem diameter (Fig. 3A), and then progressively increased for several hours before it returned to the position it had before bending. This decrease of stem diameter just after bending was mainly attributed to the direct mechanical effect of the pressure exerted on the stem when the plant is pushed against the plastic tube during bending, leading to a transient viscoelastic compression strain in the radial direction. Indeed, when plants were subjected to bending without the plastic tube (and thus to bending strain without radial compression), the phenomenon was largely reduced (Fig. 3B). Nevertheless, even without the plastic tube, bending induced a slight decrease of stem diameter, which may reflect a variation of turgor pressure due to bending. After this slight decrease of stem diameter, the diameter growth stopped for 4 h. A proxy of this compression strain against the tube was computed by dividing the initial variation of stem diameter by the stem diameter. The average value of the compression strain was 1.4% ± 0.8%.
Figure 3.
Representative examples of short-term diameter growth plant responses after a single transitory bending. A, Representative example of a short-term monitoring of the LVDT signal after bending applied by curving the stem against a plastic tube. The diameter decreased just after bending and returned to its former prebending value within a few hours. The decrease of stem diameter was due to the compression of the stem against the tube during bending. B, Representative example of the short-term monitoring of the LVDT signal after manually bending the plant without a plastic tube. Bending induced a slight decrease of the stem diameter, followed by a cessation of diameter growth for 4 h. Diameter growth then slowly began again for 6 h and subsequently reached values that were higher than those before bending was applied.
Effect of a Single Bending on Plant Diameter Growth
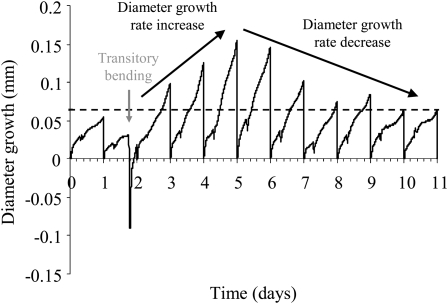
A representative example of the effect of a single controlled bending on stem diameter growth is shown in Figure 4. Bending induced a long-lasting increase in the diameter growth rate. Diameter growth rate reached its maximal value on day 2 (65% of the plants) or day 3 (35% of the plants) after bending. The maximal diameter growth rate reached after bending was variable between stems, ranging from 0.09 to 0.22 mm d−1, with an average value of 0.16 ± 0.03 mm d−1. After this peak, the diameter growth rate regularly decreased and finally reverted to the values found before bending. The duration of the response was considered as the time between the application of bending and the time when diameter growth reverted back to the values observed before bending. Once the peak of diameter growth rate was reached, the time for the plant to recover a growth rate similar to the one before bending was highly variable and estimated between 2 and 11 d, with an average value of 4.8 ± 2.7 d.
Figure 4.
Representative example of the effect of a single transitory bending on stem diameter growth. Before the application of a transitory bending, the diameter growth rate was stable. The application of a transitory bending (gray arrow) led to an increase in diameter growth. The daily diameter growth rate increased for 3 d and then decreased for several days before returning to its prebending value.
Relationship between Diameter Growth and Thigmomorphogenetical Stimulus
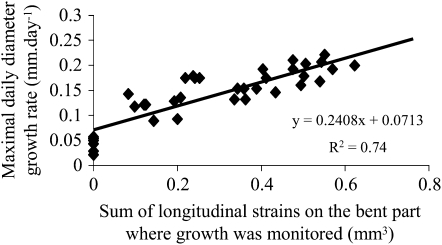
We assessed the relationship between the sum of longitudinal strains induced by bending and the plant responses using the model of mechanosensing (Eqs. 1 and 2). A highly significant correlation (r2 = 0.74) was found between the sum of applied strains on the portion of the stem where the LVDT recorded diameter growth and the growth response quantified as the maximal daily cambial rate reached after bending (Fig. 5). In contrast, no significant correlation was found between the compression strain and the diameter growth response (Fig. 6).
Figure 5.
Relationship between the sum of applied longitudinal strains and the diameter growth response. A linear relationship was observed between the imposed sum of longitudinal strains computed on the width of the stem where the diameter growth was monitored and the maximal daily diameter growth rate reached after bending.
Figure 6.
Relationship between the compressive strain and the diameter growth response. No correlation was found between the compression strain induced by bending on the plastic tube and the maximal daily diameter growth rate reached after bending.
Relationship between PtaZFP2 Transcript Levels and Applied Strains
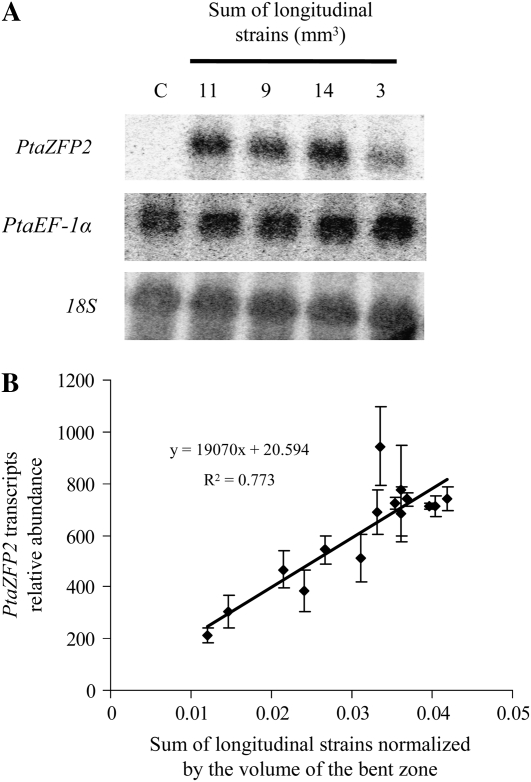
The accumulation of PtaZFP2 mRNAs after controlled bending was investigated by northern-blot analysis and by real-time quantitative reverse transcription (RT)-PCR analysis (Fig. 7). Different levels of PtaZFP2 transcripts were observed according to the applied sum of strains (Fig. 7A). With this method, no transcripts were detected in control plants (i.e. not bent). In contrast with PtaZFP2 transcripts, levels of PtaEF-1α mRNAs and 18S rRNAs did not vary with the applied sum of strains.
Figure 7.
Expression analysis of the poplar PtaZFP2 gene by northern blot and the relationship between the level of expression of PtaZFP2 (quantified by real-time quantitative RT-PCR) and the applied strain. A, Northern-blot analysis revealed the induction of PtaZFP2 transcript accumulation 30 min after stem bending on five representative stem samples. Total RNAs (15 μg) were separated on a formaldehyde gel, blotted, and probed with 32P-labeled PtaZFP2 gene-specific probe. RNAs were extracted from the 3-cm-long bent part of the stems that were subjected to different levels of strains as indicated or from the same stem portion on the control (not bent) plant (C). Expressions of PtaEF-1α and 18S rRNA were used as loading and transfer controls. B, Real-time quantitative RT-PCR analysis of the expression of PtaZFP2 in 15 stems bent within a range of standardized sums of applied strains from 0.012 to 0.042. Each point corresponds to one plant. All values were standardized to PtaEF-1α transcript levels. Errors bars correspond to se. The expression level of PtaZFP2 was correlated with the standardized sum of longitudinal strains. The relative abundance of PtaZFP2 transcripts increased linearly with the increase of the standardized sum of applied strains.
For a better quantification of the plant response at the cellular level, real-time quantitative RT-PCR was used to quantify the relative abundance of PtaZFP2 transcripts on 15 independent bent samples. All values were standardized to PtaEF-1α transcript accumulation, which was previously found to be unaffected by bending in northern-blot analysis, and used as an internal control of segment volume and RNA extraction efficiency. For consistency, the values of the sum of strains were standardized by the volume of the bent segment that had been used for RNA extraction. The standardized sum of strains thus has no unit. PtaZFP2 transcript accumulation was highly correlated to the level of the standardized applied sum of longitudinal strains (Fig. 7B). The whole set of data was well fitted by a linear function (r2 = 0.77), consistent with Equations 1 and 2.
DISCUSSION
Effect of a Single Bending on Stem Diameter Growth
Unexpectedly, the first response of diameter growth to a transitory bending is a cessation of growth, similar to what has been observed for elongation growth. For tomato elongation, cessation of growth was observed a few minutes after bending was applied (Coutand et al., 2000). The reaction time to induce the cessation of diameter growth after bending in poplar was approximately 2 h. The duration of growth cessation was approximately 1 h for tomato primary elongation, whereas it was about 4 h for diameter growth in poplar. In tomato, after the cessation of growth, elongation restarted and the elongation rate progressively reverted to the values observed before bending (Coutand et al., 2000). In the case of diameter growth, the growth stopped, restarted, but progressively reached higher values than those observed before bending for most of the plants for a period of 3 d. Detailed anatomical and growth kinematical analyses would be necessary to attribute this increase to an increment of the size of the cambial zone, to an increase of growth rate of growing cells, or both. After the peak of diameter growth rate was reached, the rate decreased for several days before it reverted back to values observed before bending. Globally, the response appeared to be longer than for tomato elongation: the maximal duration of the observed response was 10 h in tomato elongation and 11 d in poplar diameter growth.
Two hypotheses can be raised to explain these differences in reaction time: (1) the triggering of the growth response is slower in poplar than in tomato, and (2) the triggering of the growth response in poplar is as fast as in tomato but the onset of growth cessation might be obscured by the recovery of stem diameter after the compression induced by bending. The differences in the duration of the growth response could be also due to the level of applied strains: indeed, the sum of strains computed on the whole bent zone (for the purpose of comparison with the tomato experiment) ranged from 0 to 20 mm3 in this experiment with poplar stems, whereas it was much smaller in the tomato stem experiments, ranging from 0 to 3 mm3. However, experiments monitoring elongation and diameter growth on the same plants would be necessary to differentiate genetic differences in mechanosensitivity from differences in the responses in terms of elongation and diameter growth.
Quantitative Relationship between Thigmomorphogenetical Stimulus and Growth Response
When quantifying the growth response by the maximal daily diameter growth rate reached after bending, the plant growth response was correlated with the sum of longitudinal strains. This demonstrated that the biomechanical model of mechanosensing established on tomato (modification of elongation by bending of a zone distant from the primary growth zone) was also applicable in the case of diameter growth, a local response measured at the loaded zone. These results also suggested that in the case of diameter growth, the mechanosensitive control of the response is local.
In contrast to what was found on tomato (Coutand and Moulia, 2000), the linear fit gave better results than a log shape function, in accordance with the assumption of a linear local mechanosensing in the model.
Despite their different contexts, our results can also be compared with the recent results of Soga et al. (2006) on the effect of hypergravity on the gravimorphism of azuki bean (Vigna angularis) epicotyls. Their work revealed that elongation is reduced by hypergravity and that diameter growth is increased. These physiological responses are characteristic of the thigmomorphogenetical syndrome, despite the fact that they are presented as “gravity resistance” responses by Soga et al. (2006). As suggested by Telewski (2006), gravimorphism and thigmomorphogenesis involve a common core of mechanosensing. Interestingly Soga et al. (2006) also found a correlation between the modification of growth and the intensity of hypergravity. Hypergravity is a mechanical loading that induces compression strains in tissues, proportional to the weight of the plant divided by Young's modulus of the tissue and the area of stem cross-section. Since their plant material was probably very homogeneous, tissue strain levels were probably proportional to the intensity of hypergravity, and the results of Soga et al. (2006) are consistent with our results. However, it should be observed that expressing responses in terms of gravity or stress levels rather than tissue strain can be misleading, since only tissue strains are sensed and they may vary for the same gravity or stress level as long as the size and mechanical properties of the plants vary (Coutand and Moulia, 2000).
Quantitative Relationship between Mechanical Loading and Gene Expression
The expression level of PtaZFP2 was highly correlated with the level of applied sum of strains in the range of 3 to 24 mm3, corresponding to a standardized sum of strain (i.e. volume-averaged strain) in the range of 1% to 4%. The global fitting was linear (r2 = 0.77). Even if not significant with our data set, the relative abundance of PtaZFP2 may start to reach a plateau phase for levels of standardized sums of strains higher than 4%. This could be explained by a slight ovalization of the stem that would reduce the level of applied longitudinal strains so that the computation of sum of strains by the classical equation of beam theory may overestimate the computed sum of strains. In addition, a plateau phase could also be due to a saturation of the mechanosensing apparatus. Care should thus be taken before extending the sum-of-strains model to very large strain levels.
Nevertheless, in the range of small sums of longitudinal strains (3–12 mm3, corresponding to volume-averaged strains in the range of 1%–4%), the induction factor of PtaZFP2 was linearly dependent on the sum of longitudinal strains. The relative abundance of PtaZFP2 transcripts over the control was thus proportional to the level of applied sums of longitudinal strains, as assumed in the model (Eq. 1). The model of mechanosensing, therefore, was also valid at the cellular level for the earliest primary responding gene known in the mechanotransduction pathway. To our knowledge, the only studies that present a quantitative relationship between mechanical loading and the level of gene expression are those focused on the effects of hypergravity conditions (Soga et al., 2007); VaXTHS4 is down-regulated by hypergravity, and the level of VaXTHS4 expression is correlated with the applied level of hypergravity with a logarithmic function. The α-tubulin gene is up-regulated by hypergravity, and the level of expression is dependent on the level of hypergravity (Saito et al., 2003). As argued previously, plant responses in these studies are characteristic of thigmomorphogenetic responses and may reflect the quantitative cellular response to strain sensing, although they were initially described as gravity resistance responses. But, as argued earlier, the relation of gene expression with hypergravity level is likely to be casual to the fact that plant material with homogeneous sizes and mechanical properties were used and to reflect a more integrative and mechanically sound relation with the sum of the strains.
It thus appears that mechanosensing can quantitatively control the level of expression of some genes in plants. Mechanosensitive activation of genes following quantified mechanical tissue strain has also been reported in animals (TWIST expression in Drosophila; Supatto et al., 2005), but no quantitative action law for gene expression has yet been established.
How mechanosensing alters the transcription of genes remains an open question. The mechanoperception/transduction of external mechanical signals is thought to be ensured, at least partly, by stretch mechanosensitive channels of the plasma membrane releasing cytoplasmic calcium, which in turn modulates gene expression through a cascade of molecular events (Haswell et al., 2008; Chehab et al., 2009). Recently, the study of Xiong et al. (2004) indicated that the nucleus has the capacity to perceive mechanical signals resulting in autonomous calcium movements into the nucleoplasm. These calcium movements are conditioned by the environment of the nucleus, notably by the cytoplasmic pH. The ability of the nucleus to directly perceive mechanical signals implies that mechanical external signals have to be transferred to the nucleus. This possibility is in accordance with the ideas of Ingber (2006, 2008) on cellular tensegrity. Ingber (2008) proposed the animal cell to be composed of different and hierarchized tensegrity structures (implying integrins, local adhesions, and the cytoskeleton linking the extracellular matrix to the nucleus) that span from the macroscale to the nanoscale and that focus stresses on specific mechanotransducer molecules and structures, such as the nucleus. Such a system has not been so precisely described in plants, but integrin-like proteins have been identified (Sakurai et al., 2004), a continuum of cytoskeleton-plasma membrane-cell wall has been described (Baluska et al., 2003), and local adhesions of plasma membrane-cell wall have been demonstrated (Hayashi et al., 2006). The mechanical models of cellular tensegrity proposed in animals could thus also be a good candidate model for mechanosensing in plants. But systems biology models quantitatively integrating strain sensing with gene expression and growth responses are still lacking in both plants and animals.
CONCLUSION
This article presents the effect of a single controlled bending on the diameter growth of young poplars and on the expression of a mechanosensitive gene, PtaZFP2. The results showed that a single transitory bending was sufficient to modify plant diameter growth for several days. Bending first stopped diameter growth, the diameter growth rate then increased for several days, and finally it returned to basal values. Beam theory was used to compute the longitudinal strains induced by the controlled loading for each bent stem. Using the model of mechanosensing initially developed in a study of thigmomorphogenesis on tomato primary growth, we were able to establish that relationships between the applied mechanical stimulus and the plant responses exist. This analysis revealed that the biomechanical sum-of-strains model of mechanosensing established for tomato stem elongation was also applicable in the case of radial growth. It is interesting that the sum-of-strains model was also applicable at the cellular level; the results showed that the relative abundance of PtaZFP2 transcripts was highly and linearly correlated to the applied sum of strains. To our knowledge, this is the first time that a quantitative relationship between the mechanical loading (the applied level of longitudinal strains in the stem tissues) and the level of expression of a mechanosensitive gene has been established. This approach can be extended to other genes from the mechanosensitive transcription network and should prove insightful in the ordering of gene expression during increasing mechanical stimulation and in defining possible differences in the sensitivity of their expression. Moreover, a common generic integrative model for the various responses to stem mechanical stimulation can been defined combining the sum-of-strains model for mechanosensing and the dose-response curves for elongation, diameter growth, and even the expression of a primary mechanosensing gene. These results open up new perspectives in the area of systems biology of plant growth under mechanical loading.
Quantification of the strains that plants are subjected to under natural conditions is still lacking (Rodriguez et al., 2008). However, the range of applied strains in this study was wide enough to cover the ecological range of strains. Moreover, now that the effect of a single controlled bending has been characterized, it is possible to use these results as a basis to analyze plant responses after several mechanical loadings. This will allow us to understand the regulation of mechanosensitivity and its consequences on the acclimation to wind through thigmomorphogenesis (Moulia et al., 2006). In particular, it is now possible to determine whether or not plant growth or molecular responses are dependent on plant mechanical history (i.e. if the plant response is the same, higher, or lower after several bendings) in order to characterize and quantify the acclimation process that is taking place while the plant is mechanically stimulated.
MATERIALS AND METHODS
Plant Material and Culture Conditions
Young poplars (Populus tremula × alba ‘717-1B4’) were obtained by in vitro micropropagation and grown on nutrient solution (Morizet and Mingeau, 1976) after acclimation (for more details, see Martin et al., 2009). Trees were grown in a growth chamber (16 h/8 h light/dark at 40 μmol m−2 s−1 at 24°C/20°C with relative humidity of 60% ± 10%). Two months after micropropagation, the poplars were ready to be used in experiments; stems were about 35 cm high at this stage. The diameters of tested stems ranged from 4.3 to 6.3 mm, with an average diameter of 5.18 ± 0.51 mm.
Bending Experiments
For bending experiments, plants were transferred to another growth chamber with the same environmental conditions as for breeding. Plants were aligned in a vertical position along a metal bar to which they were attached with individual clamping rings. Foam was rolled around each stem in order to avoid stem wounds when the clamping ring was tightened. During the entire experiment, roots were bathed in a nutrient solution that was oxygenated by four aquarium pumps generating microbubbles from foam tubes placed at the bottom of the vat. Two vats (containing 100 L of nutrient solution) were available in the same growth chamber, with the possibility of experimenting on a set of eight plants (four plants on each vat) at the same time. During plant installation, plant leaves were removed in the basal part of the stem that was to be bent, in order to avoid uncontrolled mechanical stimuli on leaves during controlled bending (see below).
Bending Device
An original experimental device was developed in order to impose a controlled level of strains to the stem; the basal part of the stem was pushed against a plastic tube in order to curve the stem and then returned to its initial position.
This bending device was used for growth experiments as well as for experiments to study the level of expression of PtaZFP2. Because the installation induced mechanical perturbation of plant growth, plants in both types of experiments were installed and left for 5 d before the application of a controlled bending in order to avoid interactions of the installation with the effects of the controlled bending.
In growth experiments, the diameter growth of each plant was monitored by a LVDT (DF/5.0 LIN 3M; Solartron Metrology) before, during, and after the transitory stem bending. The LVDT was placed at approximately 10 cm from the stem collar in the middle of an internode. Each LVDT was linked to an Omega bus (Omega D5131, ±5 V) linked to a computer on which an in-house data-acquisition program (LVDT.exe; B. Adam, INRA UMR PIAF) recorded average growth per minute. Each plant of the two vats was equipped with a LVDT so that each of the two Omega buses gathered data from four plants.
For each plant, the imposed state of deformation induced by bending was computed using the beam theory principle.
Quantification of the Applied Strains
The stem was pushed against a plastic tube whose diameter was known so that the stem was thus subjected to a single bending controlled in terms of curvature. The longitudinal strain state that the plant was subjected to could be computed. Within the framework of beam theory, under the assumption of small curvature and small strain, the cross-section remains a plane in the bent state and the maximal longitudinal strain is given by the product of the stem radius (rstem) and the curvature of the neutral line (κ):
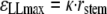 |
(4) |
The curvature of the central line can be computed as the inverse of the sum of the radius of the tube and the stem (Fig. 1B):
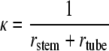 |
(5) |
That results in:
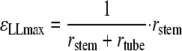 |
(6) |
Following the conceptual framework developed by Coutand and Moulia (2000), if we consider that the perception dS is at the local level and that these perceptions add up to generate a signal S that triggers plant reaction, the signal perceived by the plant is the integral of local perceptions dS and is proportional to the sum of longitudinal applied strains (Eq. 1).
Taking the model of mechanosensing established from the work on tomato (Solanum lycopersicum; i.e. assuming a sensory function with no threshold and a scattering of the sensory function in the stem), the effective signal is proportional to the sum of strains on the bent part and was computed by Coutand and Moulia (2000) as:
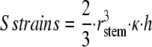 |
(7) |
where rstem is the radius of the stem in the middle of the bent part, κ is the imposed curvature, and h is the length of the considered zone.
The diameter of the tube to be used to impose a given sum of strains is thus written as:
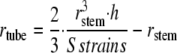 |
(8) |
Given the length of the bent zone (taken equal to 30 mm) and the radius of the stems, we used Equation 6 to create a range of applied sums of strains.
The imposed level of the sums of strains ranged from 0 to 20 mm3. Tubes of different diameters (40, 50, 75, 90, 140, 160, and 200 mm) were used to control the level of applied strains.
Assuming that the perception is local and that the sensory function is scattered along the stem, we assumed that the effective thigmomorphogenetical signal was proportional to the sum of strains computed over the length of the response site: 1 mm for diameter growth and 30 mm for PtaZFP2 expression (Fig. 1B).
Quantification of the Growth Response
Before checking the capacity of these strain integrals to explain the observed growth response, it was necessary to find a way to quantify the growth response. The diameter growth response was quantified by the maximal average daily diameter growth rate reached by the plant after bending.
Quantification of Gene Expression
Plants were bent as explained above for growth experiments and harvested 30 min after bending was applied. Thirty millimeters of the bent part of each plant was cut and immediately placed in liquid nitrogen.
Since the aim of this study was to determine if some quantitative relationship could be found between the applied level of strains and the expression level of PtaZFP2, the mRNA abundance of PtaZFP2 was measured plant by plant. Five plants were used as controls.
RNA Isolation and cDNA Synthesis
Total RNAs were extracted from about 150 mg of bent stems using hexadecyl-trimethyl-ammonium bromide extraction buffer as described by Chang et al. (1993) and then treated with RNase-free RQ1 DNase (Promega). RNA was quantified spectrophotometrically and checked by agarose gel electrophoresis. First-strand cDNA was synthesized from 1 μg of total RNA using oligo(dT) and SuperScript III (Invitrogen), according to the manufacturer's instructions.
Northern-Blot Hybridization
For northern-blot analysis, a PtaZFP2 gene-specific probe of 287 bp was generated by PCR with a specific pair of primers, Pe1S (5′-CGTGCGAGTCACAAGAAACC-3′) and Pe1AS (5′-CACAGAACTCTCTTGCTGCT-3′), labeled with [α-32P]dCTP using a Ready-To-Go, DNA Labeling Beads kit (Amersham), and then purified with a Cleanmix kit (Euromedex), according to the manufacturer's recommendations. Total RNAs (15 μg) were separated by 1% agarose gel electrophoresis after denaturation with formaldehyde and blotted onto a nylon Hybond-N+ membrane (Amersham). The northern hybridization was carried out with a northernMax kit (Ambion). Membranes were then exposed to a phosphoimager screen (Kodak) for 4 h. Signal quantification was made using Quantify One software (Bio-Rad).
Real-Time Quantitative RT-PCR Experiments
Real-time RT-PCR amplifications were done using an iCycler IQ (Bio-Rad) and SYBR Green as a fluorescent dye. Each PCR reaction (30 μL) contained the following: cDNA (4 μL of 1:40 dilution of the first cDNA strands), PCR buffer (1×), MgCl2 (1.66 mm), deoxyribonucleotide triphosphate mix (200 μm each), primers (0.3 μm each), Platinium Taq DNA polymerase (0.5 unit; Invitrogen), and SYBR Green I (1:1,000; Sigma).
After a heat step at 94°C for 5 min, PCR cycling conditions were as follows: 40 cycles of denaturation (94°C, 15 s), annealing (61°C, 15 s), and elongation (72°C, 20 s), ending with a final elongation step at 72°C for 5 min.
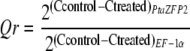
PtaZFP2 transcripts were detected by amplifying 287 bp with primers Pe1S and Pe1AS. The reference gene EF-1α (for elongation factor-1α) transcripts were amplified using the primers EF1S (5′-GACAACTAGGTACTACTGCACTGTC-3′) and EF1AS (5′-TTGGTGGACCTCTCGATCATG-3′). Relative quantitative abundance of PtaZFP2 transcripts was calculated by comparison with the expression of EF-1α using the delta-delta method mathematical model (McMaugh and Lyon, 2003):
 |
(9) |
where C is the cycle number of PCR to reach the quantitative detection threshold. Specificity of amplification was confirmed by determining the melt curves for the PCR products at the end of each run and by gel electrophoresis.
Sequence data from this article can be found in the GenBank/EMBL data libraries under accession number FM172949.
Acknowledgments
We are grateful to Ginette Faure and Christelle Boisselet for their help with plant production and preparation of nutrient solutions. We thank Prof. Georges Jeronimidis for general discussion about this work and Gail Wagman for reading and correcting the English.
This work was supported by the Department of Environment and Agronomy of INRA (innovating project grant no. PSI–EA–3729B).
The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (www.plantphysiol.org) is: Catherine Coutand (coutand@clermont.inra.fr).
References
- Baluska F, Samaj J, Wojtaszek P, Volkmann D, Menzel D (2003) Cytoskeleton-plasma membrane-cell wall continuum in plants: emerging links revisited. Plant Physiol 133 482–491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biddington NL (1986) The effects of mechanically-induced stress in plants: a review. Plant Growth Regul 4 103–123 [Google Scholar]
- Biddington NL, Dearman AS (1985) The effect of mechanically induced stress on the growth of cauliflower, lettuce and celery seedlings. Ann Bot (Lond) 55 109–119 [Google Scholar]
- Boyer N (1967) Modification de la croissance de la tige de bryone (Bryonia dioica) à la suite d'irritations tactiles. C R Acad Sci Paris 267 2114–2117 [Google Scholar]
- Braam J (2005) In touch: plant responses to mechanical stimuli. New Phytol 165 373–389 [DOI] [PubMed] [Google Scholar]
- Braam J, Davis RW (1990) Rain-induced, wind-induced, and touch-induced expression of calmodulin and calmodulin-related genes in Arabidopsis. Cell 60 357–364 [DOI] [PubMed] [Google Scholar]
- Chang SJ, Puryear J, Cairney J (1993) A simple and efficient method for isolating RNA from pine trees. Plant Mol Biol Rep 11 113–116 [Google Scholar]
- Chehab EW, Eich E, Braam J (2009) Thigmomorphogenesis: a complex plant response to mechano-stimulation. J Exp Bot 60 43–56 [DOI] [PubMed] [Google Scholar]
- Ciftci-Yilmaz S, Mittler R (2008) The zinc finger network of plants. Cell Mol Life Sci 65 1150–1160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutand C, Dupraz C, Jaouen G, Ploquin S, Adam B (2008) Mechanical stimuli regulate the allocation of biomass in trees: demonstration with young Prunus avium trees. Ann Bot (Lond) 101 1421–1432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coutand C, Julien JL, Moulia B, Mauget JC, Guitard D (2000) Biomechanical study of the effect of a controlled bending on tomato stem elongation: global mechanical analysis. J Exp Bot 51 1813–1824 [DOI] [PubMed] [Google Scholar]
- Coutand C, Moulia B (2000) Biomechanical study of the effect of a controlled bending on tomato stem elongation: local strain sensing and spatial integration of the signal. J Exp Bot 51 1825–1842 [DOI] [PubMed] [Google Scholar]
- Daudet FA, Ameglio T, Cochard H, Archilla O, Lacointe A (2005) Experimental analysis of the role of water and carbon in tree stem diameter variations. J Exp Bot 56 135–144 [DOI] [PubMed] [Google Scholar]
- Giovannelli A, Deslauriers A, Fragnelli G, Scaletti L, Castro G, Rossi S, Crivellaro A (2007) Evaluation of drought response of two poplar clones (Populus x canadensis Monch ‘I-214’ and P. deltoides Marsh. ‘Dvina’) through high resolution analysis of stem growth. J Exp Bot 58 2673–2683 [DOI] [PubMed] [Google Scholar]
- Hamant O, Heisler MG, Jonsson H, Krupinski P, Uyttewaal M, Bokov P, Corson F, Sahlin P, Boudaoud A, Meyerowitz EM, et al (2008) Developmental patterning by mechanical signals in Arabidopsis. Science 322 1650–1655 [DOI] [PubMed] [Google Scholar]
- Haswell ES, Peyronnet R, Barbier-Brygoo H, Meyerowitz EM, Frachisse JM (2008) Two MscS homologs provide mechanosensitive channel activities in the Arabidopsis root. Curr Biol 18 730–734 [DOI] [PubMed] [Google Scholar]
- Hayashi T, Harada A, Sakai T, Takagi S (2006) Ca2+ transient induced by extracellular changes in osmotic pressure in Arabidopsis leaves: differential involvement of cell wall-plasma membrane adhesion. Plant Cell Environ 29 661–672 [DOI] [PubMed] [Google Scholar]
- Ingber DE (2006) Cellular mechanotransduction: putting all the pieces together again. FASEB J 20 811–827 [DOI] [PubMed] [Google Scholar]
- Ingber DE (2008) Tensegrity-based mechanosensing from macro to micro. Prog Biophys Mol Biol 97 163–179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs MR (1954) The effect of wind sway on the form and development of Pinus radiata D. Don. Aust J Bot 2 35–51 [Google Scholar]
- Jaffe MJ (1973) Thigmomorphogenesis: the response of plant growth and development to mechanical stimulation. Planta 114 143–157 [DOI] [PubMed] [Google Scholar]
- Jaffe MJ, Biro R, Bridle K (1980) Thigmomorphogenesis: calibration of the parameters of the sensory function in beans. Physiol Plant 49 410–416 [Google Scholar]
- Larson PR (1965) Stem forms of young Larix as influenced by wind and pruning. For Sci 11 412–424 [Google Scholar]
- Latimer JG, Pappas T, Mitchell CA (1986) Growth-responses of eggplant and soybean seedlings to mechanical-stress in greenhouse and outdoor environments. J Am Soc Hortic Sci 111 694–698 [PubMed] [Google Scholar]
- Leblanc-Fournier N, Coutand C, Crouzet J, Brunel N, Lenne C, Moulia B, Julien JL (2008) Jr-ZFP2, encoding a Cys2/His2-type transcription factor, is involved in the early stages of the mechano-perception pathway and specifically expressed in mechanically stimulated tissues in woody plants. Plant Cell Environ 31 715–726 [DOI] [PubMed] [Google Scholar]
- Lee D, Polisensky DH, Braam J (2005) Genome-wide identification of touch- and darkness-regulated Arabidopsis genes: a focus on calmodulin-like and XTH genes. New Phytol 165 429–444 [DOI] [PubMed] [Google Scholar]
- Martin L, Leblanc-Fournier N, Azri W, Lenne C, Henry C, Coutand C, Julien JL (2009) Characterization and expression analysis under bending and other abiotic factors of PtaZFP2, a poplar gene encoding a Cys2/His2 zinc finger protein. Tree Physiol 29 125–136 [DOI] [PubMed] [Google Scholar]
- McMaugh SJ, Lyon BR (2003) Real-time quantitative RT-PCR assay of gene expression in plant roots during fungal pathogenesis. Biotechniques 34 982–986 [DOI] [PubMed] [Google Scholar]
- Meng SX, Lieffers VJ, Reid DEB, Rudnicki M, Silins U, Jin M (2006) Reducing stem bending increases the height growth of tall pines. J Exp Bot 57 3175–3182 [DOI] [PubMed] [Google Scholar]
- Morizet J, Mingeau M (1976) Effect of environment on water-uptake, as studied on beheaded exudating tomato. 1. Role of nutrients. Ann Agron 27 183–205 [Google Scholar]
- Moulia B, Coutand C, Lenne C (2006) Posture control and skeletal mechanical acclimation in terrestrial plants: implications for mechanical modeling of plant architecture. Am J Bot 93 1477–1489 [DOI] [PubMed] [Google Scholar]
- Moulia B, Fournier M (1997) Mechanics of the maize leaf: a composite beam model of the midrib. J Mater Sci 32 2771–2780 [Google Scholar]
- Rodriguez M, De Langre E, Moulia B (2008) A scaling law for the effects of architecture and allometry on tree vibration modes suggests a biological tuning to modal compartmentalization. Am J Bot 95 1523–1537 [DOI] [PubMed] [Google Scholar]
- Saito Y, Soga K, Wakabayashi K, Hoson T (2003) Increase in expression level of alpha-tubulin gene in Arabidopsis seedlings under hypergravity conditions. Biol Sci Space 17 177–178 [PubMed] [Google Scholar]
- Sakurai M, Pak JY, Muramatsu Y, Fukuhara T (2004) Integrin-like protein at the invaginated plasma membrane of epidermal cells in mature leaves of the marine angiosperm Zostera marina L. Planta 220 271–277 [DOI] [PubMed] [Google Scholar]
- Soga K, Wakabayashi K, Kamisaka S, Hoson T (2006) Hypergravity induces reorientation of cortical microtubules and modifies growth anisotropy in azuki bean epicotyls. Planta 224 1485–1494 [DOI] [PubMed] [Google Scholar]
- Soga K, Wakabayashi K, Kamisaka S, Hoson T (2007) Effects of hypergravity on expression of XTH genes in azuki bean epicotyls. Physiol Plant 131 332–340 [DOI] [PubMed] [Google Scholar]
- Supatto W, Debarre D, Moulia B, Brouzes E, Martin JL, Farge E, Beaurepaire E (2005) In vivo modulation of morphogenetic movements in Drosophila embryos with femtosecond laser pulses. Proc Natl Acad Sci USA 102 1047–1052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telewski FW (2006) A unified hypothesis of mechanoperception in plants. Am J Bot 93 1466–1476 [DOI] [PubMed] [Google Scholar]
- Telewski FW, Pruyn ML (1998) Thigmomorphogenesis: a dose response to flexing in Ulmus americana seedlings. Tree Physiol 18 65–68 [DOI] [PubMed] [Google Scholar]
- Xiong TC, Jauneau A, Ranjeva R, Mazars C (2004) Isolated plant nuclei as mechanical and thermal sensors involved in calcium signalling. Plant J 40 12–21 [DOI] [PubMed] [Google Scholar]