INFERRING GENOME-WIDE MOSAIC STRUCTURE

Abstract

Genetic recombination plays two essential biological roles. It ensures the fidelity of the transmission of genetic information from one generation to the next and it generates new combinations of genetic variants. Therefore, recombination is a critical process in shaping arrangement of polymorphisms within populations. “Recombination breakpoints” in a given set of genomes from individuals in a population divide the genome into haplotype blocks, resulting in a mosaic structure on the genome. In this paper, we study the Minimum Mosaic Problem: given a set of genome sequences from individuals within a population, compute a mosaic structure containing the minimum number of breakpoints. This mosaic structure provides a good estimation of the minimum number of recombination events (and their location) required to generate the existing haplotypes in the population. We solve this problem by finding the shortest path in a directed graph. Our algorithm’s efficiency permits genome-wide analysis.

1. Introduction

Ancestral genetic recombination events play a critical role in shaping extant genomes. Characterizing the patterns of recombination (e.g. the recombination locations and rates), is a crucial step for reconstructing evolutionary histories, performing disease association mapping, and solving other population genetics problems.

During meiosis diploid organisms recombine two homologous genome copies on a chromosome by chromosome basis to form a haploid gamete, which contributes half of the genetic content to its offspring. This mixing of genomes leads to mosaic chromosome (haplotype) structure composed of segments from each grandparent. We refer to the boundaries between the segments of each haplotype as the recombination breakpoints in this paper. Recombination breakpoints represent locations where the crossovers have occurred, either during the generation of the haplotype itself, or in previous generations.

In this paper, we are interested in inferring the possible mosaic structure of a given set of related haplotypes. This is accomplished by finding a set of recombination breakpoints that divide the haplotypes into compatible blocks according to the Four-Gamete Test (FGT)^?. The FGT states that, under the infinite-sites assumption^?, all pairs of polymorphisms should co-occur in only three out of their four possible configurations. Thus, when four configurations are observed in a pair of markers, it implies that either a recombination or a homoplastic event has occurred between them. We propose an efficient algorithm to solve the “Minimum Mosaic Problem”, which finds the mosaic with the minimum number of breakpoints. The algorithm is suitable for genome-wide study.

2. Related Work

Many algorithms have been developed for estimating a lower bound on the minimum number of recombination events necessary to generate a given set of haplotypes. Hudson and Kaplan^? proposed a lower bound (HK bound) computed using the FGT^?. Their algorithm computes a minimum set of non-overlapping intervals where all pairs of SNPs in an interval are compatible according to the FGT. This number of intervals, less one, is the HK bound. Myers and Griffiths^? proposed a tighter bound, RecMin. However, it is only computationally tractable to find the optimal RecMin in relatively small data sets. Myer and Song et al.^? proposed a RecMin approximation algorithm known as HapBound using Integer Linear Programming (ILP). They also proposed an algorithm, SHRUB, which finds a plausible evolutional history for the given haplotypes, called an Ancestral Recombination Graph (ARG). The ARG establishes an upper-bound on the minimum number of recombinations. Different from RecMin or SHRUB, our algorithm focuses on the mosaic structure of a set of sample sequences without explicitly computing the evolutionary history, assuming that the genomic structures of the sample sequences are of more interest. However, the breakpoints on the sample sequences may reflect possible recombination events happened in the history.

In addition to estimating lower-bounds on the number of recombinations, algorithms have also been proposed for finding a set of founders which generate a given set of recombinant sequences. Ukkonen first proposed the founder set reconstruction problem ^?. A dynamic programming algorithm was developed to compute a minimum number of founders with a given set of sample haplotype sequences, where a segmentation of all the sequences in the sample set can be derived which contains the minimum number of segments. Wu and Gusfield ^? studied a slightly different problem to compute a set of K founders where a segmentation of the given sequences can be derived with a minimum number of segments. They proposed a polynomial time algorithm for genotype sample sequences with only two founders. Different from these works, we do not construct the founder sequences, or rely on the existence of a founder set for segmentation and inferring the mosaic structures on the genome.

3. Problem Formulation

Suppose that we have a set of n haplotypes over m SNPs, represented by a binary data matrix D = [d_ij]_{i=1‥n,j=1‥m}. Row i in D corresponds to a haplotype h_i, and column j in D corresponds to a SNP s_j. Matrix entry d_ij is either 0 or 1, representing the majority allele or minority allele at SNP s_j respectively. In this paper, we only consider crossover recombination events, ignoring gene conversion and homoplasy (assuming they do not have a significant role).

Over any pair of SNPs s_j and s_j′, a haplotype takes one of four possible gametes 00, 01, 10, 11 (the combination of alleles at s_j and s_j′). We denote the set of haplotypes taking 00, 01, 10, or 11 at SNP pair (s_j, s_j′) as ${\mathit{\text{HapSet}}}_{00}^{j,j\prime }$, ${\mathit{\text{HapSet}}}_{01}^{j,j\prime }$, ${\mathit{\text{HapSet}}}_{10}^{j,j\prime }$, ${\mathit{\text{HapSet}}}_{11}^{j,j\prime }$ respectively. If all four sets are nonempty, according to the FGT^?, a historical recombination event must have occurred between s_j and s_j′. In this case, we say that the SNP pair (s_j, s_j′) is incompatible. We represent a recombination breakpoint as a tuple (h_i, s_b), where the breakpoint locates on haplotype h_i between SNPs s_b and s_b+1. It is possible that multiple haplotypes may have breakpoints at the same location since they may “inherit” the breakpoint from a common ancestor sequence.

We define a compatible block of SNPs as a continuous set of SNPs such that any two SNPs inside the block are compatible. Two SNP blocks are incompatible with each other if there exist two incompatible SNPs, one from each block.

A complete set of breakpoints creates a haplotype mosaic structure over the set of genome sequences. A Mosaic M over a SNP data matrix D is defined as a set of recombination breakpoints M = {(h_i, s_b)}, i ∈ [1, n], b ∈ [1, m]. The set of distinct^a locations of breakpoints s_b in M divides the entire range of SNPs [s₁, s_m] into blocks that satisfy: 1) each block is a compatible block, 2) any two neighboring blocks are incompatible, and 3) any two neighboring blocks (assume the boundary is between s_b and s_b+1) would become compatible if the set of haplotypes that have breakpoints between s_b and s_b+1 are excluded. In this paper, we develop an efficient algorithm for computing Minimum Mosaic (denoted as M_min) – the mosaic structure that contains the least number of breakpoints. We refer to this problem as the Minimum Mosaic Problem.

4. Inferring the Local Mosaic

4.1. Maximal Intervals

We begin by defining the concept of maximal interval. An interval I = [s_b, s_e] is a set of consecutive SNPs which are compatible with each other starting from s_b and ending at s_e. We define an interval I as a maximal interval if and only if there is no other interval I′, I′ ≠ I, $I\prime =[s_b^{\prime },s_e^{\prime }]$, which contains I: $s_b^{\prime }\le s_b$, and $s_e^{\prime }\ge s_e$. The complete set of maximal intervals can be computed in O(mn) time^?, assuming that the compatibility test of any two SNPs using FGT takes O(1) time^?.

4.2. Finding Local Breakpoints

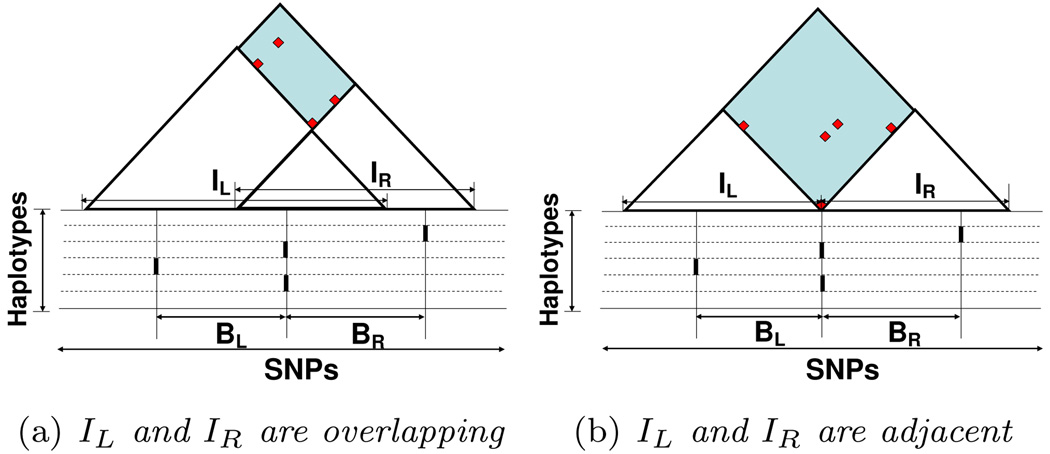
Maximal intervals are useful for inferring the local mosaic. The set of distinct breakpoint locations s_b in a mosaic M = {(h_i, s_b)} divide the entire SNP range [s₁, s_m] into compatible blocks, where neighboring blocks are incompatible. The set of breakpoints in M is the union of the set of breakpoints on the boundary of each pair of neighboring blocks. We first consider the breakpoints on the boundary of a pair of neighboring blocks. We observe that, every pair of neighboring blocks in M fall inside a pair of overlapping or adjacent maximal intervals, as stated in the following Lemma:

Lemma 4.1

For any pair of neighboring blocks (B_L, B_R) deduced by a mosaic, there exists a pair of overlapping or adjacent maximal intervals (I_L, I_R), where B_L completely falls inside I_L (B_L ⊆ I_L) but not I_R (B_L \ I_R ≠ ϕ), and B_R completely falls inside I_R (B_R ⊆ I_R) but not I_L (B_R \ I_L ≠ ϕ). We refer to (I_L, I_R) as (B_L, B_R)’s containing interval pair; and (B_L, B_R) as (I_L, I_R)’s contained block pair (Fig. 1).

Figure 1.

Neighboring blocks B_L, B_R fall inside overlapping/adjacent maximal intervals I_L, I_R respectively. The dots in the shaded region represent incompatible SNP pairs of I_L and I_R.

Proof

Details of the proof are presented in ^?.

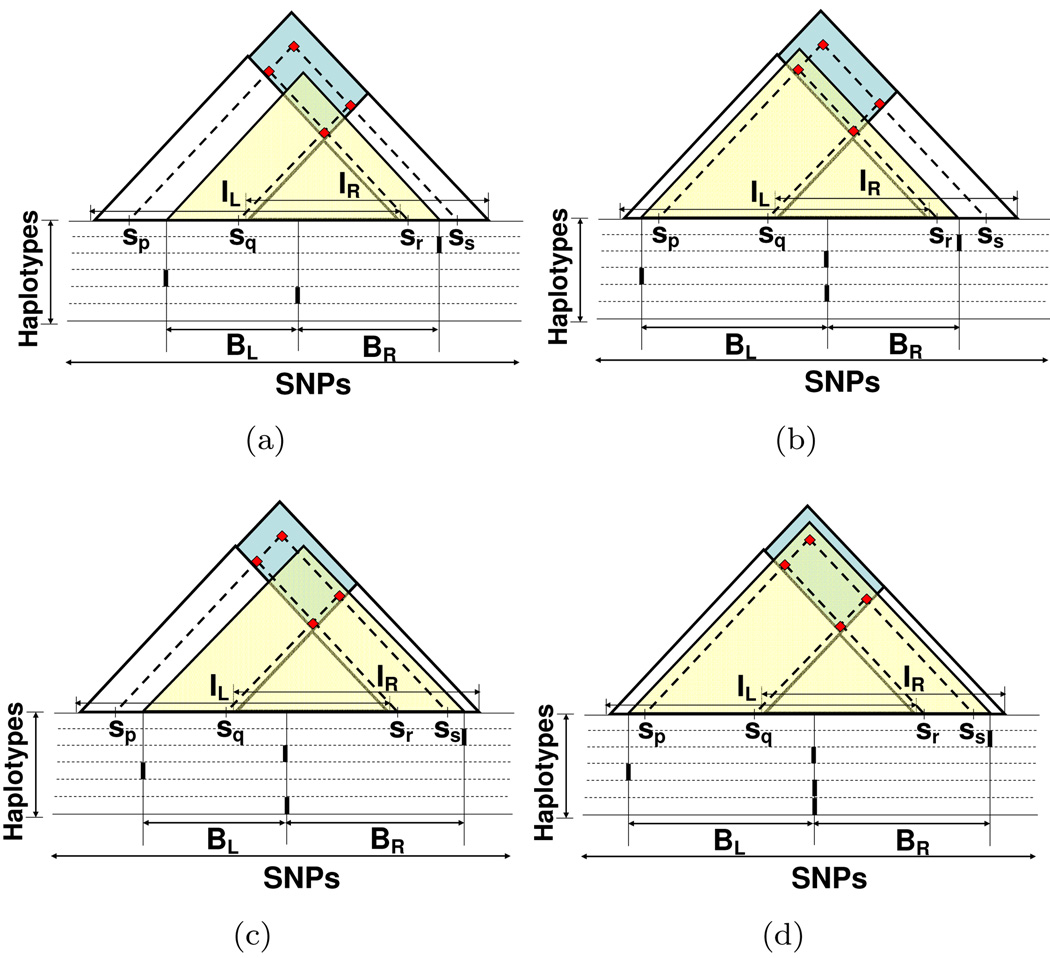
For each pair of overlapping or adjacent intervals (I_L, I_R), there exists a set of incompatible SNP pairs SNPPair(I_L, I_R) = {(s_l, s_r)}, where l < r, s_l and s_r are incompatible, and s_l ∈ I_L\I_R, s_r ∈ I_R\I_L. For example, in Fig. 1(a) and 1(b), each dot represents an incompatible SNP pair. Let (B_L, B_R) be a contained block pair of the interval pair (I_L, I_R). We denote the incompatible SNP pairs contained in (B_L, B_R) as SNPPair(B_L, B_R) = {(s_l, s_r)}, where l < r, s_l and s_r are incompatible, and s_l, s_r ∈ B_L ∪ B_R. Apparently, SNPPair(B_L, B_R) is a subset of SNPPair(I_L, I_R). The incompatible SNP pairs in SNPPair(B_L, B_R) determine the minimum number of the breakpoints on the boundary of B_L and B_R, as well as the corresponding set of haplotypes having these breakpoints. Given an interval pair, several candidate block pairs may be derived, each of which corresponds to a different SNPPair(B_L, B_R). Fig. 2(a)–2(d) show four different candidate block pairs derived from the same interval pair. The exact set of incompatible SNP pairs in SNPPair(B_L, B_R) depends on the positions of B_L and B_R, i.e., the leftmost SNP of B_L, and the rightmost SNP of B_R. Formally, we define the start range R_s, the end range R_e of a block pair (B_L, B_R) as the ranges where SNPPair(B_L, B_R) remains unchanged if the leftmost SNP of B_L changes within R_s and the rightmost SNP of B_R changes within R_e. Moreover, the breakpoint range R_b of (B_L, B_R) is defined as the range where the boundary of B_L and B_R falls into. The breakpoint range is the overlapping region of I_L and I_R (if I_L and I_R overlap), or the boundary of I_L and I_R (if I_L and I_R are adjacent to each other). For example, in Fig. 2(a), SNPPair(B_L, B_R) contains only one incompatible SNP pair (s_q, s_r). The start range R_s(B_L, B_R) is (s_p, s_q], the end range R_e(B_L, B_R) is [s_r, s_s), and the breakpoint range R_b(B_L, B_R) is I_L ∩ I_R. In Fig. 2(b), SNPPair(B_L, B_R) contains two incompatible SNP pairs (s_q, s_r) and (s_p, s_r). The start range R_s(B_L, B_R) is [s*, s_p] (s* denotes the leftmost SNP of interval I_L), and the end range R_e(B_L, B_R) is [s_r, s_s), and the breakpoint range R_b(B_L, B_R) is I_L ∩ I_R.

Figure 2.

Neighboring blocks B_L, B_R contain different subsets of the incompatible SNP pairs. The dots represent the incompatible SNP pairs contained in the overlapping maximal intervals I_L, and I_R. The dots inside the shaded triangle are contained in the neighboring block pair B_L and B_R.

Any contained block pair (B_L, B_R) of any overlapping/adjacent maximal interval pair (I_L, I_R) can be a possible neighboring block pair inside a mosaic M. A subset of these block pairs constitute a mosaic. Specifically, for any neighboring block pair (B_L, B_R) which is inside a Minimum Mosaic M_min, we have the following Lemma:

Lemma 4.2

Let (B_L, B_R) be a neighboring block pair in a Minimum Mosaic M_min, and Breakpoints(B_L, B_R) be the set of breakpoints on the boundary of B_L and B_R in M_min, and HapSet(Breakpoints(B_L, B_R)) be the set of haplotypes having breakpoints in Breakpoints(B_L, B_R). Then Breakpoints(B_L, B_R) is the smallest number of breakpoints which satisfies:

$$\begin{array}{c}\forall (s_l,s_r)\in \mathit{\text{SNPPair}}(B_L,B_R)\hfill \\ ({\exists }_{\mathit{\text{gl}},r}\in \{00,01,10,11\},\mathit{\text{HapSet}}(\mathit{\text{Breakpoints}}(B_L,B_R))\supseteq {\mathit{\text{HapSet}}}_{gl,r}^{l,r})\hfill \end{array}$$ (1)

Proof

Details of the proof are presented in ^?.

It is easy to compute Breakpoints(B_L, B_R) if SNPPair(B_L, B_R) only contains one pair of incompatible SNPs (as shown in Fig. 2(a)). We can choose the smallest set of ${\mathit{\text{HapSet}}}_{00}^{l,r}$, ${\mathit{\text{HapSet}}}_{01}^{l,r}$, ${\mathit{\text{HapSet}}}_{10}^{l,r}$ and ${\mathit{\text{HapSet}}}_{11}^{l,r}$ to be Breakpoints(B_L, B_R). If SNPPair(B_L, B_R) contains more than one pair of incompatible SNPs (as shown in Fig. 2(b), 2(c), and 2(d)), we need to find the smallest set of haplotypes which is a superset of at least one of ${\mathit{\text{HapSet}}}_{00}^{l,r}$, ${\mathit{\text{HapSet}}}_{01}^{l,r}$, ${\mathit{\text{HapSet}}}_{10}^{l,r}$ and ${\mathit{\text{HapSet}}}_{11}^{l,r}$, for each pair of incompatible SNPs (s_l, s_r). The computation complexity is O(4^k), where k = |Breakpoints(B_L, B_R)|. In practice, k is small. Moreover, many incompatible SNP pairs are caused by a small number of SNP patterns, which enables further reduction in computation.

5. Finding Minimum Mosaic - A Graph Problem

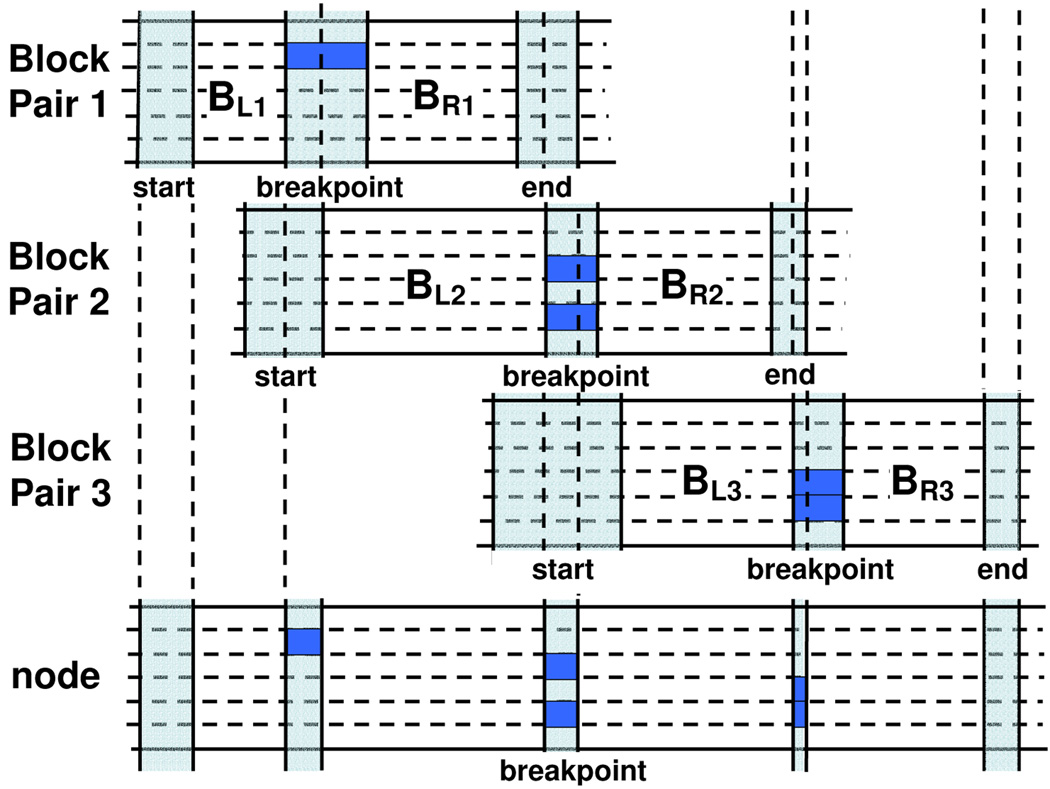
The set of all possible block pairs {(B_L, B_R)} of all overlapping/adjacent maximal interval pairs are the building blocks of a mosaic. We can use them and construct a graph as follows. A node nd in this graph represents the combination of three block pairs BP₁ = (B_L1, B_R1), BP₂ = (B_L2, B_R2), BP₃ = (B_L3, B_R3) that satisfy the following constraints: 1) the breakpoint range of BP₁ overlaps with the start range of BP₂: R_b(BP₁)∩R_s(BP₂) ≠ ϕ; 2) the end range of BP₁, the breakpoint range of BP₂, and the start range of BP₃ overlap: R_e(BP₁) ∩ R_b(BP₂) ∩ R_S(BP₃) ≠ ϕ; 3) the end range of BP₂ overlaps with the breakpoint range of BP₃: R_e(BP₂) ∩ R_b(BP₃) ≠ ϕ. As shown in Fig. 3, BP₁, BP₂, and BP₃, are the left block pair, middle block pair, and right block pair of nd, respectively. The breakpoint range of nd is the intersection of the end range of BP₁, the breakpoint range of BP₂, and the start range of BP₃: R_b(nd) = R_e(BP₁)∩R_b(BP₂)∩R_s(BP₃). The set of breakpoints associated with nd is the same as Breakpoints(BP₂), denoted as Breakpoints(nd). The weight of the node is the number of breakpoints in Breakpoints(nd), weight(nd) = |Breakpoints(nd)|.

Figure 3.

Three block pairs form a node. Block pair 1, 2, and 3 are the left, middle, and right block pair of the node respectively. The breakpoint range of the node is the intersection of the end range of block pair 1, the breakpoint range of block pair 2, and the start range of block pair 3. The vertical stripes correspond to the start range, breakpoint range, and end range of a block. The marked haplotypes in the stripes are the haplotypes which have breakpoints in the corresponding region.

We also create two special kinds of nodes – starting nodes and ending nodes to model the two ends of a chromosome. We first identify all block pairs with start range beginning from the first SNP s₁, referred to as starting block pairs. We create a starting node nd_s for every combination of a starting block pair BP_s and another block pair BP satisfying 1) the breakpoint range of BP_s overlaps with the start range of BP: R_b(BP_s) ∩ R_s(BP) ≠ ϕ, and 2) the end range of BP_s overlaps with the breakpoint range of BP: R_e(BP_s) ∩ R_b(BP) ≠ ϕ. BP_s is the middle block pair of the starting node nd_s, BP is the right block pair of nd_s. There is no left block pair for nd_s. The set of breakpoints associated with nd_s is the same as Breakpoints(BP_s): Breakpoints(nd_s) = Breakpoints(BP_s). The weight of nd_s is weight(nd_s) = |Breakpoints(nd_s)|. Similarly we create a set of ending nodes {nd_e} associated with the set of ending block pairs {BP_e}.

After generating all nodes, we connect nodes with directed edges according to the following rule. For nodes nd₁ and nd₂, if nd₁’s middle block pair is the same as nd₂’s left block pair and nd₁’s right block pair is the same as nd₂’s middle block pair, we add an edge from nd₁ to nd₂. The nodes and edges form a directed graph. A Minimum Mosaic corresponds to a shortest path from any starting node to any ending node in this graph. The weight of the path is the sum of all node weights on the path. The set of breakpoints {Breakpoints(nd)} associated with all nodes on the shortest path is the Minimum Mosaic solution. We can use any shortest path algorithm to compute the solution. The details of the complete algorithm and the correctness proof are presented in ^?.

6. Experimental Studies

Our algorithm is implemented in C++ and all experiments were performed on a machine with an Intel Core2 Duo processor of 1.60GHz and 3GB RAM.

6.1. Kreitman’s ADH Data

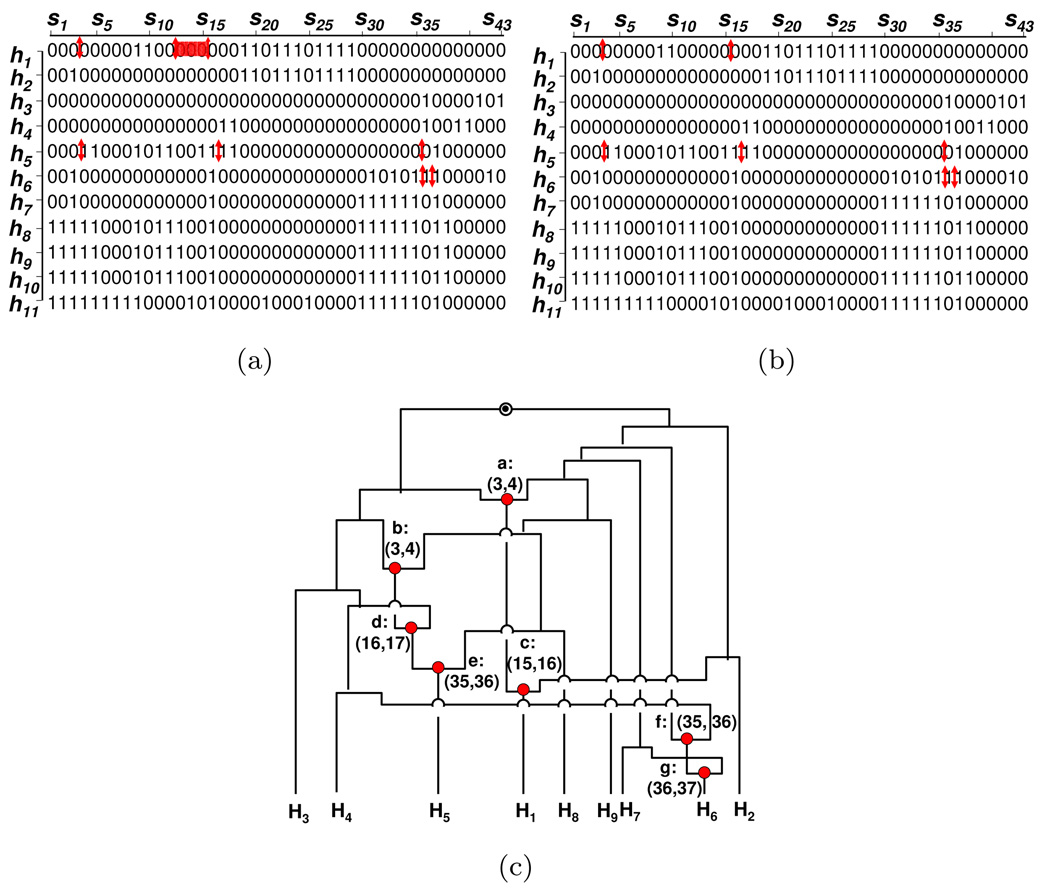
The alcohol dehydrogenase (ADH) data of Kreitman^? consists of 11 haplotypes over 43 polymorphic sites of the ADH locus of fruit fly, Drosophila melanogaster. The haplotypes were sampled from 5 geographically distinct populations: Washington, Florida, Africa, France, and Japan^?. Our algorithm detected 7 breakpoints shown in Fig. 4(a). We can estimate the exact locations of 6 out of 7 breakpoints: H₁ : (S₃, S₄), H₅ : (S₃, S₄), H₅ : (S₁₆, S₁₇), H₅ : (S₃₅, S₃₆), H₆ : (S₃₅, S₃₆), H₆ : (S₃₆, S₃₇). For the remaining breakpoint on H₁, its location can be either (S₁₂, S₁₃), or (S₁₃, S₁₄), or (S₁₄, S₁₅), or (S₁₅, S₁₆) with equal probability.

Figure 4.

Comparison of Minimum Mosaic and Hapbound/SHRUB results on ADH data, (a): the Minimum Mosaic result; (b): the result inferred from the ARG in (c); (c): the ARG computed using SHRUB^?. The bars in (a) and (b) represent the breakpoints. The dots in (c) represents the recombination events.

Note that 7 is the lower and upper bounds of the minimum number of recombinations, estimated by HapBound and SHRUB, respectively^?. Therefore, 7 is the exact number of minimum number of recombination events for the ADH data. The corresponding ARG generated by SHRUB is shown in Fig. 4(c). The breakpoints in the ARG are illustrated in a SNP matrix in Fig. 4(b). By comparing Fig. 4(a) and 4(b), we observe that almost the same set of breakpoints are inferred by our algorithm and SHRUB.

6.2. Running Time and Scalability Analysis

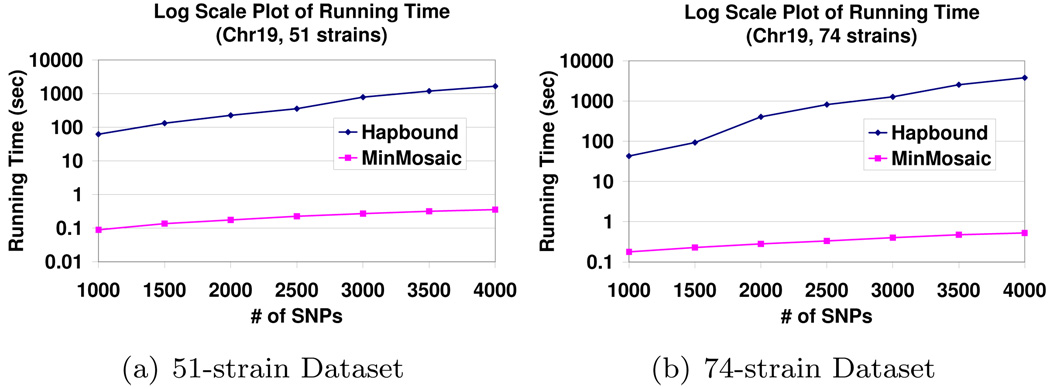
We tested the performance of our algorithm on two genome-wide SNP data sets from mouse. Both sets represent a combination of experimental and imputed genotypes^? in two overlapping sets of laboratory inbred strains available from the Center of Genome Dynamics at the Jackson’s Laboratory^?. The 51-strain data set contains 51 inbred mouse strains with 7,870,134 SNPs^b. The 74-strain data set contains 74 inbred mouse strains with 7,989,200 SNPs^c.

Fig. 5 shows the running time comparison of Hapbound and our algorithm using the first w SNPs from Chromosome 19 of both data sets where w varies from 1000 to 4000. Our algorithm is 250× – 7000× faster than Hapbound on 74-strain dataset, and 350× – 4000× faster on 51-strain dataset.

Figure 5.

Comparison of the running times of MinMosaic and Hapbound over varying number of SNPs (in log scale). The datasets used are from Chrl9 of 51-strain dataset and 74-strain dataset. The number of SNPs included varies from 1000 to 4000.

Our algorithm is efficient enough to finish on all chromosomes (Chr 1–19 and Chr X). Results from the 51-strain data set are shown in Table 1. Genome-wide, the number of breakpoints in the Minimum Mosaic varies between 15253 (Chr X) and 266006 (Chr 1), and the number of derived blocks in the Minimum Mosaic varies between 9888 (Chr X) and 68261 (Chr 1). The average number of breakpoints per neighboring block pair is 2.2.

Table 1.

The result on genome-wide 51-strain mouse data set.

Chr	# of SNP	# of breakpoints	# of blocks	Runtime (min)
1	694809	266006	68261	6.87
2	524667	210797	47793	11.27
3	509892	113715	52487	8.90
4	476425	100702	43776	7.84
5	496888	110157	49938	33.98
6	509547	97740	49562	6.42
7	405733	94973	46884	38.83
8	444910	87659	45796	37.10
9	361571	86755	40189	3.89
10	399126	64806	35764	3.21
11	259028	65092	27575	23.52
12	396114	89243	42159	1.30
13	399930	75323	39914	3.03
14	345783	67304	34089	2.54
15	337461	78181	35776	4.08
16	305078	57257	28449	1.14
17	266421	73542	31517	0.75
18	291266	69546	31271	8.61
19	222031	49276	22839	1.46
X	223456	15253	9888	0.96

7. Conclusions

Genetic recombination during meiosis generates a mosaic structure of the genome, where each resulting haplotype consists of segments from different ancestral sequences. In this paper, we study the Minimum Mosaic model that contains a minimum number of breakpoints to generate the haplotypes present within extant populations. The resulting blocks are compatible where no recombinations can be inferred within a block according to the FGT. We proposed a novel algorithm to compute the minimum mosaic structure of genomes. the efficiency of our algorithm allows for genome-wide analysis.