Patterns of structural complexity in Alzheimer's disease and frontotemporal dementia

INTRODUCTION

Changes in brain structure during aging are complex and it is often hard to distinguish the effects of normal aging from early changes resulting from neurodegenerative pathologies, such as Alzheimer's disease (AD) and frontotemporal dementia (FTD) [Dickstein et al., 2007; Tononi, 2005; Zhang et al., 2007]. Subtle changes in structure can nonetheless lead to severe consequences that can be highly specific for a given pathology. In particular, AD and FTD are sometimes difficult to clinically differentiate because of overlapping symptoms [McKhann et al., 1984; Neary et al., 1998; Siri et al., 2001]. Definite diagnosis currently requires histopathological examination of brain tissue. Although structural MRI data depicts characteristic patterns of brain atrophy in AD and FTD, aiding a differentiating diagnosis between the dementias [Frisoni et al., 1999; Gee et al., 2003; Grossman et al., 2004; Kitagaki et al., 1998; Laakso et al., 2000; Lipton et al., 2004; Rosen et al., 2002], a complete separation based on MRI has not been accomplished. Histopathological studies have indicated that AD and FTD pathology are associated with damage to specific cortical layers, e.g., Layer II of the entorhinal cortex and Layer III of the neocortex in AD and Layers III and V of frontal and temporal lobes in FTD [Gomez‐Isla et al., 1996; Kersaitis et al., 2004; Lewis et al., 1987; Pearson et al., 1985]. Even though current MRI methods lack power to resolve individual cortical layers, these histological observations led to a MRI‐based study of cortical thickness [Du et al., 2007], in the hopes that such estimates would improve differential diagnosis between AD and FTD. However, since the cortex is a highly folded structure and its surface is rarely aligned with any of the cardinal axes in MRI, estimates of cortical thickness are difficult, especially in the presence of pathological alterations. Although elegant techniques have recently been developed for estimating cortical thickness from MRI [Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 1999; Lerch et al., 2005], they were not shown to be substantially more effective than brain volume estimates for distinguishing AD and FTD subjects [Du et al., 2007]. This raises the possibility that specialized volumetric and thickness estimates may not be the most effective way to extract available information by the given current MRI resolution and geometry. In particular, a number of combined effects such as variations in sulcal depth, cortical area, and cortical thickness are likely involved in different pathologies and such effects would appear in combination at current MRI resolution. This suggests the use of image markers that capture some degree of combined global and local variability in brain structures while also supplying some degree of interpretability. To this end, we have explored the use of information theoretic quantities that provide quantitative measures of structural complexity as image markers [Crutchfield and Young, 1989; Feldman and Crutchfield, 2003; Hopcroft and Ullman, 2000; Young and Schuff, 2008; Young et al., 2005]. This approach seems particularly compelling in light of recent evidence that distributed changes in structural complexity of the brain have been shown to occur in specific forms in both normal and pathological age‐related loss of cognitive function [Dickstein et al., 2007].

Since its introduction as a means of studying communication over noisy channels [Cover and Thomas, 2006; Shannon, 1948], information theory has been successfully applied in a variety of scientific settings, including neuroimaging [Pluim et al., 2004] and modeling of brain function [Tononi, 2005]. Information theoretic methods provide a convenient framework for summarizing information in the form of quantitative measures. The particular information theoretic measures chosen for the analysis, presented in this article, were initially introduced via a graph theoretical, optimal prediction‐based formalism that provided estimates of dynamical complexity in time series data [Crutchfield and Young, 1989]. These methods were later generalized to allow for the study of structure in multidimensional, multivariate data sets, in particular multimodal medical images, such as structural and spectroscopic MRI [Young and Schuff, 2008; Young et al., 2005]. The fundamental hypothesis is that the complexity of spatial patterns in neuroimages, such as the convoluted spatial distribution of human cortex evident in MRI, can effectively be captured by structure‐based information theoretic measures that correspond well with visual impressions of image complexity. Hence, the specific information theoretic quantities discussed in this article will be referred to as complexity measures.

The specific objectives of this study were to (1) determine the extent to which structural complexity measures capture the characteristic spatial patterns of tissue loss and cortical thinning in AD and FTD relative to cognitive normal (CN) subjects, (2) compare the sensitivity and specificity of complexity measures for differentiating between AD and FTD with that provided by current state of the art MRI estimates of cortical volume loss and thinning.

SUBJECTS AND METHODS

Subjects

Twenty‐three CN subjects, 24 patients diagnosed with AD, and 19 patients diagnosed with FTD were included in the study (Table I). Patients with FTD and AD were recruited from the Memory and Aging Center of the University of California, San Francisco, for a previously described study [Du et al., 2006]. All patients were diagnosed based upon information obtained from an extensive clinical history and physical examination. MRI data were used to rule out other major neuropathologies such as tumor, stroke, severe white matter disease, or inflammation but not for diagnosis of dementia. Inclusion criteria were age between 35 and 80 years and no history of brain trauma, brain tumor, stroke, epilepsy, alcoholism, psychiatric illness, or systemic disease that affects brain function. FTD was diagnosed according to the established consensus criteria. Patients with FTD, who had motor neuron disease‐related symptoms, were excluded. Patients with AD were diagnosed according to the criteria of the National Institute of Neurological and Communication Disorders and Stroke/Alzheimer's Disease and Related Disorders Association [McKhann et al., 1984]. All subjects received a standard battery of neuropsychological tests. This included assessment of global cognitive impairment by Mini‐Mental State Examination (MMSE) [Folstein et al., 1975] and global functional impairment by Clinical Dementia Rating (CDR) Scale [Morris, 1993]. In addition, the California Verbal Learning Test (CVLT)‐Short Form was administered to assess episodic memory, and a modified version of the Trail‐Making Test (TMT) was administered to evaluate executive function. Two patients with FTD and two CN subjects, who had MRI of inferior quality, were eliminated as the MRI was not suitable for tissue segmentation and spatial normalization processing with FreeSurfer (http://surfer.nmr.mgh.harvard.edu).

Table I.

Study demographics

	Number (F/M)	Age	MMSE	CDR box score
Control	23 (14/9)	61.9 ± 6.3	29.9 ± 0.3	0 ± 0
AD	24 (8/16)	63.5 ± 7.4	19.1 ± 6.1	5.0 ± 2.7
FTD	19 (3/16)	61.7 ± 7.5	25.1 ± 5.7	6.3 ± 3.7

Data Acquisition and Processing

Data acquisition has also been described in detail [Du et al., 2007]. MRI data were obtained on a 1.5 T Siemens Vision™ System (Siemens, Iselin NJ), including coronal T1‐weighted images using a volumetric magnetization‐prepared rapid gradient echo sequence (MPRAGE, TR/TE/TI = 10/7/300 ms timing, 15° flip angle, 1.00 × 1.00 mm² in‐plane resolution, and 1.40‐mm thick coronal partitions. The 3D MPRAGE images were segmented into gray matter, white matter, CSF, and non‐brain tissue and then mapped to the Montreal neuroimaging (MNI) brain atlas [Tzourio‐Mazoyer et al., 2002] for spatial normalization using the FreeSurfer software.

Assessments of Image Complexity

Three information theoretic measures, the statistical complexity (SC), the entropy (H), and the excess entropy (EE), introduced in [Crutchfield and Young, 1989; Feldman and Crutchfield, 2003], described in more detail in the appendix, and applied to medical image analysis [Young and Schuff, 2008; Young et al., 2005], were estimated from the spatially normalized, segmented images. As outlined [Young and Schuff, 2008], SC measures the degree of spatially correlated structure in the image. It accomplishes this by quantifying the amount of information required for predicting the image values in a region given the image values in a neighboring region, averaged over the entire image or region under consideration. H measures the degree of apparent randomness in the image and thus corresponds to the usual notion of entropy in physics. It is a complimentary measure of complexity to SC in that it measures the number of patterns observed in an image or region without regard to their correlation structure. While H is a maximum for completely uncorrelated sets of patterns, SC is a minimum for such sets. Lastly, EE provides a quantitative complexity measure of the spatial scaling properties of the image. In particular, EE quantifies how long it takes the average of H over a volume to converge to a constant value as a function of increasing volume. As simple examples: (1) the ordered pattern of a black and white checkerboard (without noise) would have low H, low SC, and low EE; (2) in contrast, a completely random black and white pattern would have high H, low SC, and low EE. More complicated patterns, like an image of the cortex, would have intermediate values of H, and higher values of SC and EE relative to these two simpler patterns.

STATISTICS

To determine the ability of H, SC, and EE to detect structural changes in the brain in AD and FTD, the measures were obtained for 13 brain regions that MRI studies reported, e.g. [Varma et al., 2002], to be affected by AD, FTD, or both. These regions included the anterior cingulum, posterior cingulum, inferior frontal lobe, superior frontal lobe, Heschl gyrus, hippocampus, insula, inferior parietal lobe, superior parietal lobe, precentral gyrus, precuneus, putamen, and inferior temporal lobe.

H, SC, and EE estimates were obtained for the 13 brain regions using the methods described in the appendix at a scale of 2 mm for H and SC and a range of scales from the voxel size to the size of the region for EE. Classification accuracy between paired groups, i.e., AD or FTD versus CN and AD versus FTD was tested using Platt's sequential minimal optimization algorithm for training a support vector classifier. The algorithm used a linear kernel, cache size 250007, and complexity parameter 1.0. Sensitivity, specificity, and overall classification accuracy was assessed using 10‐times 10‐fold stratified cross validation [Hastie et al., 2001].

In addition, to test how well‐structural complexity estimation performed when trying to separate all three classes at once, linear discriminant analysis (LDA) was performed for various sets of regions for a combined three group analysis using the structural complexity estimates and compared with a similar LDA analysis using cortical thickness estimates.

RESULTS

The variability of the three complexity measures in different brain regions is illustrated in Figure 1, separately for single, representative CN, AD, and FTD subjects. An additive red‐green‐blue (RGB) color space is used to represent simultaneous values of H, EE, and SC. In this color space, the value of H is represented on the red axis, EE on the green axis, and SC on the blue axis. In this representation, a higher saturation of red represents a higher value of H, implying lack of correlation of structural patterns in an image region. Similarly, a higher saturation of green represents a higher value of EE, implying increased long‐range correlations of structural patterns and a higher saturation of blue represents a higher value of SC, implying an increase of locally correlated patterns. Accordingly, a simultaneous increase/decrease of all three complexity measures results in brighter/darker levels of gray. The most prominent effects in the AD subject when compared with the CN and FTD subjects, as seen in this representation, are decreased correlation in the hippocampus (faint red regions, yellow arrows in Columns 1 and 2) and diminished long‐range correlations of structural patterns in superior parietal lobe regions (faint green regions, arrows in Column 6). In contrast, the most prominent effect in the FTD subject when compared with the CN and AD subjects is greater long‐range correlation in medial frontal lobe and anterior cingulum (intense green regions, arrows in Columns 5 and 6). Somewhat surprisingly, AD and FTD show little change of the complexity measures in the posterior cingulum (gray regions, arrows in Column 4) relative to CN. In addition to differences between the groups, the color scheme also illustrates anatomical differences in that inferior brain regions seem dominated by decreased correlation in spatial patterns (red, H), whereas superior brain regions are dominated by greater long‐range correlations of patterns (green, EE) and subcortical structures, such as the basal ganglia, by more locally correlated patterns (blue, SC). This representation was provided to convey a direct visual impression of how the complexity measures vary across individual subjects in different groups but to increase its utility, for example, as it might be used for clinical assessment, a way to additionally provide a visual characterization of group variability for the various groups (and in particular normal subjects) would be necessary.

Figure 1.

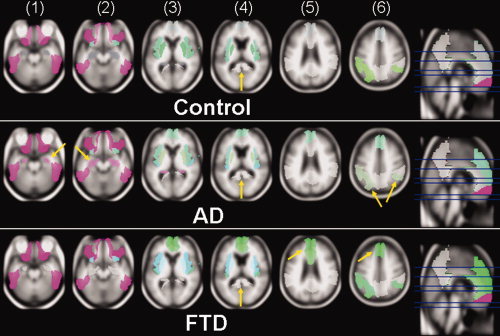
Simultaneous variability of entropy (H), excess entropy (EE), and statistical complexity (SC) of different brain regions in a single control subject, a single subject diagnosed with AD, and a single subject diagnosed with FTD, represented in an additive red‐green‐blue (RGB) color space.

Table II compares results using the structural complexity estimation against results on the use of cortical thickness estimation using the FreeSurfer software on the same set of subjects. In the table, comparisons are between classification accuracy based on structural complexity estimation and classification accuracy based on tissue volume and cortical thickness estimation (the parietal lobes provided the best separation between AD and CN subjects and the only significant separation between AD and FTD subjects for the volume and thickness estimates). For each, complexity or FreeSurfer, the regions providing the best separation between the groups are listed, i.e. for complexity, the hippocampus, parietal lobe, precuneus, and Heschl gyrus taken together, and for FreeSurfer, the thickness of parietal lobe gray matter. This shows that structural complexity measures slightly outperformed volume and cortical thickness measures for the differential classification between AD and FTD as well as between FTD and CN. For the classification between AD and CN, volume and cortical thickness estimation achieved slightly higher classifications than structural complexity estimation. In addition to classification accuracy, used in the direct comparison with the cortical thickness and volume study, Table III lists the sensitivity and specificity obtained for structural complexity estimation for the two group comparisons.

Table II.

Comparison of classification accuracy (in percent of total subjects) between AD/CN groups, FTD/CN groups, and AD/FTD groups for complexity estimation methods and cortical thinning

Measure	AD vs. CN (%)	FTD vs. CN (%)	AD vs. FTD (%)
Parietal gray matter volume (FreeSurfer)	95 ± 4	81 ± 7	85 ± 6
Parietal gray matter thickness (FreeSurfer)	96 ± 3	82 ± 6	86 ± 6
Complexity estimates (hippocampus, parietal lobe, precuneus, heschel gyrus)	92 ± 0.8	87 ± 0.7	91 ± 0.8

Table III.

Classification accuracy, sensitivity, and specificity (in percent of total subjects) between AD/CN groups, FTD/CN groups, and AD/FTD groups for structural complexity estimation

	Sensitivity	Specificity	Classification Accuracy
AD vs. CN (%)	91 ± 0.8	92 ± 0.8	92 ± 0.8
FTD vs. CN (%)	86 ± 0.7	88 ± 0.7	87 ± 0.7
AD vs. FTD (%)	90 ± 0.8	92 ± 0.8	91 ± 0.8

Table IV lists the prediction accuracy of structural complexity and FreeSurfer measures when trying to separate all three groups at once, using LDA based on either complexity or FreeSurfer volume and thickness estimates. The prediction accuracy is also illustrated graphically in Figure 2a–c, which depicts the projections onto the first two linear discriminants (labeled LD1 and LD2 in the figures) from the LDA corresponding to the region selections for complexity estimation. This shows first that group separation prominently increased from global measures, such as whole brain, to more focal measures, such as each of the 13 regions, as expected. Second, structural complexity measures outperformed cortical thickness and volume estimates when utilizing specific focal information. In detail, using the structural complexity estimates from all 13 brain regions produced an LDA prediction accuracy of 96%, whereas a similar LDA for volume and cortical thickness (illustrated in Fig. 3) estimates in the same regions [Du et al., 2007] achieved a prediction accuracy of 90%.

Table IV.

Linear discriminant analysis (LDA) results for application of structural complexity estimation to separation of AD/FTD/CN groups

	Thickness and volume	LDA prediction accuracy
Whole brain	N/A	0.64
Hippocampus, subiculum, and precuneus	N/A	0.80
13 regions treated separately	0.90	0.96

Figure 2.

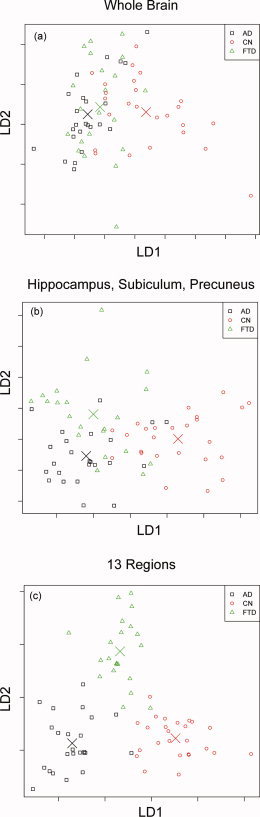
Results of linear discriminant analysis (LDA) using structural complexity estimates with x and y axes representing projections of complexity estimates onto the 1st and 2nd linear discriminants. Complexity analysis results for (a) only the whole brain, (b) the hippocampus, subiculum, and precuneus, and (c) all 13 regions.

Figure 3.

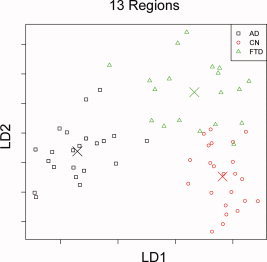
Results of linear discriminant analysis (LDA) using cortical thickness and volume estimates with x and y axes representing projections of thickness and volume estimates onto the 1st and 2nd linear discriminants using a set of regions similar to that used for Figure 2.

To provide some indication of the baseline complexity measures for normal subjects compared with those for AD and FTD subjects, Table V shows comparisons of average H and EE values in the frontal lobe and hippocampus, respectively, for the various subject groups analyzed in the article. Significance values for between‐group t‐tests are provided in Table V as well.

Table V.

Means and standard deviations for Hippocampal EE and Frontal H, and P‐values for between group t‐tests

	Hippocampal EE	Frontal H
CN	2.00 ± 0.12	1.32 ± 0.05
AD	2.26 ± 0.15	1.30 ± 0.04
FTD	2.26 ± 0.16	1.22 ± 0.09
P‐value CN/AD	<0.001	NS
P‐value CN/FTD	<0.001	<0.001
P‐value AD/FTD	NS	0.005

DISCUSSION

This article provides two main results: (1) it was shown that use of structural complexity estimates is effective at capturing systematic differences on brain MRIs, exhibiting a variety of effects such as cortical volume loss and thinning, and (2) it was demonstrated that use of structural complexity estimates can achieve similar classification results between dementia and controls as well as between AD and FTD as highly specialized measures of cortical thinning. It should be noted that complexity estimation achieved similar group classifications to cortical thickness estimates using FreeSurfer for the same brain regions (e.g., parietal lobe). In selected brain regions (i.e., the hippocampus), complexity estimates achieved even better classification than FreeSurfer thickness and volume estimates. The classification accuracy provided by both methods is in fact at the limit of the ability to reliably diagnose subjects and so further comparisons between classification methods will require improved clinical testing methods, much larger samples, or some other, more accurate means of classification to account for test variability. Nonetheless, the results suggest that the complexity‐based formalism for image analysis shows promise for classification of neurodegenerative diseases.

Similar to conventional image processing, the analysis involved tissue segmentation and spatial normalization to a brain atlas. It should be noted, however, that structural complexity estimation does not in principal require prior segmentation or spatial normalization of the images. The appendix provides a description of how continuous intensity images are processed by the complexity estimation method. The reason for performing the initial FreeSurfer gray/white/CSF tissue segmentation was to bring the computational dimensionality to a manageable size by using a few tissue classes rather than the continuum of image intensities. In addition, it was felt that decoupling the segmentation step from the structural complexity estimation by using a method that is widely used for segmentation (FreeSurfer) in thickness and volume studies provided a better basis for comparison of methods. Although various segmentation methods could well affect complexity estimation results, the fact that complexity estimation methods performed well at separating the classes when using segmented images generated with FreeSurfer suggests that, at least initially, the utility of the complexity estimation methods can be evaluated independently. But further exploration of the effects of segmentation algorithms on the complexity estimation methods is an important step, both to gain a better understanding of the interaction, as well as to attempt to improve the sensitivity of the complexity estimation methods in the face of neural abnormalities such as white matter lesions.

Similarly, spatial normalization was used for region‐based comparisons with conventional volume and thickness estimates but global (or arbitrary region) versions of the structural complexity estimates can be obtained without the step of spatial normalization. This offers the possibility of eliminating the difficult problem of choosing appropriate group specific atlases for the analysis [Lorenzen et al., 2005; Mega et al., 2005].

Despite their simplicity and fully automated application, the structural complexity estimates provided classification accuracy similar to that from volume and thickness estimates. As expected, the parietal lobe volume and thickness estimates already yielded excellent separation between CN and AD groups. It was difficult to match by structural complexity estimates, as specific local tissue volume changes are expected to provide a good image marker for AD related changes [Laakso et al., 2000] and such prior information should certainly be taken into account if available. In contrast, structural complexity estimation yielded a better separation between the CN and FTD groups as well as the AD and FTD groups, especially in regions considered to be affected by both AD and FTD. Both frontal and temporal lobe volume and thickness estimates provided comparable separation of the CN and FTD groups to structural complexity estimation but did not do as well at separating the CN and AD groups and showed no significant separation between the AD and FTD groups. This suggests that structural complexity estimation potentially provides a more robust overall method of separating and classifying populations in a realistic setting where subjects generally exhibit a variety of conditions. The general nature of the method allows it to be applied with a minimum of assumptions about the locality of disease specific effects as well as at which anatomical locations the effects are expect to appear in the images. Thus, the method should be particularly effective for simultaneous examinations of spatially scalable effects that may occur across the wide spectrum of neurodegenerative diseases.

In both AD and FTD effects are expected in a number of regions and the structural complexity estimation analysis was effective at distinguishing those situations. However, discrimination between the three groups based on global structural complexity estimates was not particularly effective, as depicted in Figure 2a. The reason for this is that on the level of the whole brain, CN subjects are reasonably well separated from those suffering from neurodegeneration but as might be expected for a measure that does not provide for any regional distinctions, AD and FTD yield similar values for the structural complexity estimates. That is, a whole brain analysis ignores the clear regional differences in neurodegeneration exhibited in AD and FTD patients; this would also be true of a whole brain cortical thickness and/or volume analysis. On the other hand if three regions, known to be strongly affected in one or both AD and FTD, are considered, i.e., the hippocampus, subiculum, and precuneus, the prediction accuracy is considerably improved, as seen in Table III and Figure 2b. Finally, including more predetermined regions that are considered strongly affected by FTD and/or AD achieves an excellent separation of the three groups, as shown Figures 2c and 3.

Although it is a long‐term goal of the authors to establish baseline estimates of H, SC, and EE for normal subjects, given the that this work is in its early stages, the primary goal of this article is to determine useful image classification methods based on between‐group differences. This must be viewed as a limitation to clinical application of the complexity estimation methods, but this situation is similar to other image‐based classification methods such as those based on thickness and volume estimates. Establishing baseline complexity estimates will involve identifying sources of variability such as changes in normal aging. Some indication of the differences between H and EE between baseline values for normal subjects and values for AD and FTD subjects in regions affected in AD and FTD is provided by the data in Table V. The measures and regions used for Table V were chosen for illustration based on the relatively well‐understood clinical effects in those regions. Hippocampal atrophy (represented as a slower decay of spatial entropy represented by higher EE) has been found in MRI studies of both AD and FTD subjects. Frontal lobe atrophy (represented as lower spatial entropy, H) has been found in MRI studies of FTD subjects and to a lesser degree in advanced stage AD subjects.

Although the complexity estimation results were promising in terms of providing image‐based classification of subjects with AD and FTD, a number of issues remain before the methods can provide a concrete, interpretable tool suitable for clinical use. Future work will extend structural complexity estimation to multimodal imaging, as demonstrated [Young et al., 2005], to studies of neurodegenerative disease. This approach is expected to be particularly effective as it does not depend on spatially confined effects in the different modalities for its classification power as is the case for multivariate image analysis [Worsley et al., 2004]. In addition, it provides a more general and interpretable approach to understanding structural image properties than methods such as fractal [Zhang et al., 2007] and texture analysis [Freeborough and Fox, 1988]. In contrast to methods such as that described by Bocti et al. [ 2006] which provide accurate classification via exploratory analysis, the methods described in this article are fully automatic and independent of operator bias.

In conclusion, information theory‐based structural complexity estimation shows promise for use in the study and classification of neurodegenerative disease.

In this appendix, a brief mathematical description of the quantities, H, SC, and EE, and how they are obtained is provided. This discussion closely follows that contained in [Young and Schuff, 2008].

Definitions

The components required for defining SC and H are an index set I representing a set of spatial or space/time coordinates and a feature space F defined over I, representing some set of variables defined at each index. The feature space used in this article consists of the values at each voxel of a set of coregistered images in a standardized space, in particular, the one‐dimensional space of intensity values from T1 images.

Definition of the complexity measures requires the conditional probability

(A1)

defined in terms of the joint empirical distribution over observed patterns

(A2)

where the template pair, T ${}_{\mathit{\text{j}}}^{\text{1}}$ and T ${}_{\mathit{\text{i}}}^{\text{2}}$, are ordered sets of indices forming distinct but possibly overlapping regions of voxels, in the underlying index set I, at positions j and i, respectively. N is the total number of template pairs observed over the whole image or region. 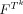is a product feature space, which is the product space of values in the image(s) at voxels in the template T^k. The mapping 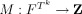, maps the set of all patterns observed in the image or region over the product feature space 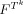, to the integers. That is M indexes the observed patterns, assuming that the set of patterns form a discrete set. The sums are taken over all particular instances, T ${}_{\mathit{\text{i}}}^{\mathit{\text{k}}}$, that is, instances of template k “located” at index i. The functional δ(·) is the indicator “function,” yielding 1 if a particular pair of patterns is observed, 0 otherwise. Thus 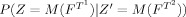effectively constitutes a 2D histogram of counts of feature space patterns observed when parsing over the index space with the templates T ${}_{\mathit{\text{j}}}^{\text{1}}$ and T ${}_{\mathit{\text{i}}}^{\text{2}}$. Further restrictions can be imposed such as requiring that T ¹ and T ² be nonoverlapping and/or contiguous. In the analysis presented in this article, T ¹ and T ² are linear sets of contiguous voxels of a given length L. Hence, the analysis effectively studies local correlation structure at scale L. In the following, we will simplify the notation using the conversion 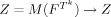. The marginal distribution is then defined as follows:

(A3)

To estimate SC, the set of optimally predictive states must be determined from the images.

Determination of States

For this article, the states are determined after tissue segmentation of the univariate T1. Better segmentation algorithms provide some benefit in obtaining better complexity estimates but complexity estimation as a whole, given the global nature of the analysis, can be viewed as less sensitive to the accuracy of segmentation algorithms than techniques that rely on accurate “local” information such as cortical thickness estimation.

The next step in the algorithm is to choose templates and parse the image using those templates. The templates are moved over the image and the image values over the templates are recorded as counts in a joint histogram. The number of joint histogram bins s ${}^{\mathit{\text{v}}{}_{\text{1}}}$ × s ${}^{\mathit{\text{v}}{}_{\text{2}}}$ is determined by the number of segmentation values, s, in the image and the number of voxels, v ₁ and v ₂, in the templates. s ${}^{\mathit{\text{v}}{}_{\text{1}}}$ is the number of possible patterns that can be observed over template 1 and s ${}^{\mathit{\text{v}}{}_{\text{2}}}$ is the number of possible patterns that can be observed over template 2. For this article, the two template structures are identical, simple linear sequences of voxels, and s ${}^{\mathit{\text{v}}{}_{\text{1}}}$ and s ${}^{\mathit{\text{v}}{}_{\text{2}}}$ are identical.

From the joint histogram, the conditional histograms defined in Eq. (A1) are obtained. The conditional histograms are then grouped, based on a measure of similarity for probability distributions; there are a number of choices for similarity measure between distributions. In this article, a hard clustering algorithm, PAM [Dimitriadou et al., 2004], is used with the Euclidean distance between bin counts as the similarity measure. Note that the grouping of conditional histograms into states is the step that specifically characterizes structure in the image and distinguishes the complexity‐based method from simply estimating entropies from the joint histogram as a co‐occurrence matrix [Young and Schuff, 2008]. This step is also what distinguishes SC from the joint entropy though in the special case where there is a one‐to‐one correspondence between joint histograms and states, SC reduces to the joint entropy. This can occur when there are a small number of joint histograms that are too distinct to be clustered into states.

The ability to specify arbitrary template structures also distinguishes the complexity estimation methods from standard co‐occurrence analysis. In addition, while the joint histogram, analogous to a co‐occurrence matrix, is a convenient representation of the results of the image parsing step, the underlying construction is based on a rigorously defined and general set of graph theoretic methods described in [Crutchfield and Young, 1989].

Statistical Complexity

Given the set of states s, accumulated as just described, SC can then be defined as follows:

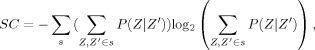(A4)

This quantifies the information contained in the distribution of observed patterns, conditioned and summed over all states, s. Note that as mentioned earlier, via conditioning over the states s, SC is distinct from the conditional entropy of the histogram and measures something quite different. For example, when the set of N conditional histograms making up the joint histogram are identical, the joint entropy would equal N times the entropy of one of the conditional histograms; but SC would equal zero as there is only a single state.

Although not explicitly represented in Eq. (A4), SC is dependent on the particular templates T ¹ and T ² over which the patterns are observed and implicitly on the scale of the template patterns. However, as is demonstrated by the results reported earlier, as long as the choice of template patterns is consistently applied, the results can be used to detect systematic group differences exposed in the images.

Entropy (H)

The standard measure of the number and distribution of observed patterns produced by a system is the entropy

(A5)

where the joint probabilities are defined in Eq. (A2). The entropy in the current case is over the joint distribution defined in Eq. (A2), accumulated over the underlying template pairs and summed over the indices of the observed patterns.

Excess Entropy

EE measures the convergence rate of H as a function of increase in volume. Despite some subtleties in interpreting EE, discussed in [Feldman and Crutchfield, 2003], it provides a useful and complimentary measure to H and SC. EE was defined and initially discussed in [Feldman and Crutchfield, 2003]. We first define the metric entropy as the limit of entropy per unit volume as the volume is taken to infinity, initially without specifying explicitly how the volume is to be taken to infinity:

(A6)

EE is then defined as

(A7)

where V is the volume of the templates in index space. Despite the subtleties involved with estimating EE in dimensions higher than 1, any particular choice, consistently applied, results in a useful method for comparing structure in images. In particular, note that if the entropy per unit volume converges quickly to h_μ as a function of scale then EE is small indicating a lack of large scale structures in the image.

EE provides an estimate of the scaling properties in image data that compliments information obtained using SC and H. Specifically, H provides a measure of the number and distribution of structures observed at a given template scale, SC provides a measure of the complexity of the spatial correlation of those structures at a given template scale, and EE provides a measure of the variation in the number of observed structures as a function of template scale.

Implementation

For the particular case of classifying neurodegenerative disease via T1 MRI, the steps for obtaining sets of states and calculating SC, H, and EE are as follows:

• 1Feature space reduction: For the analysis in this article, feature space reduction had already been performed given that the complexity estimation steps were applied to the segmented T1 image data. That is, the feature space consists of a single value, the intensity of a T1‐weighted MR brain image, and the feature space reduction corresponds to standard tissue segmentation of the brain image into 3 classes, gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) via FreeSurfer.
• 2Parsing: The index space is parsed according to the specified templates. The observed patterns over all instances of the templates in the index space are then catalogued via the joint histogram. In this study, parsing is done for the three‐dimensional index space in the cardinal directions (x, y, z), and templates consist of linear sequences of voxels in those directions.

  To obtain the list of distinct states, as described earlier, a robust hard clustering algorithm (PAM [Dimitriadou et al., 2004] in the current implementation) is used to group the conditional distributions. There are various similarity measures that could be used to group the conditional histograms into states, but the use of PAM for clustering based on Euclidean distance between histogram bin counts proved to be relatively robust in being transparent to numerical problems resulting from histogram bins with zero counts.

• 3Complexity estimation: The total probabilities of the states, that is the normalized sums of the histogram counts in the conditional histograms in that cluster, are obtained and used to estimate SC using Eq. (A4). H is estimated over all histogram bins treated independently using Eq. (A5).

The software implementation of the above methods is an open source package written in Python [van Rossum and Drake, 2001] and SciPy [Jones et al., 2001], and uses the Rpy [Moreira, 2004] package to provide access to the statistical and graphical capabilities of the R statistical language [R Development Core Team, 2004] and supplemental libraries. The cluster and e1071 [Dimitriadou et al., 2004] R packages were used for clustering and the AnalyzeFMRI [Marchini, 2004] package for MR image processing. Image analysis was performed using this package on a 46‐processor Beowulf cluster using the PyPAR [Nielsen et al., 2003] Python wrapper for the message passing interface MPI. Complete (fully automated) processing of a single subject takes on the order of 40 min on a single 3‐GHz processor.