Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Dec 1.
Published in final edited form as: J Mech Behav Biomed Mater. 2008 Dec 13;2(6):613–619. doi: 10.1016/j.jmbbm.2008.11.008

DIFFERENCES IN THE MECHANICAL BEHAVIOR OF CORTICAL BONE BETWEEN COMPRESSION AND TENSION WHEN SUBJECTED TO PROGRESSIVE LOADING

Jeffry S Nyman 1,2, Huijie Ling 3, Xuanliang Dong 4, Xiaodu Wang 4
PMCID: PMC2736133  NIHMSID: NIHMS83967  PMID: 19716106

Abstract

The hierarchical arrangement of collagen and mineral into bone tissue presumabley maximizes fracture resistance with respect to the predominant strain mode in bone. Thus, the ability of cortical bone to dissipate energy may differ between compression and tension for the same anatomical site. To test this notion, we subjected bone specimens from the anterior quadrant of human cadaveric tibiae to a progressive loading scheme in either uniaxial tension or uniaxial compression. One tension (dog-bone shape) and one compression specimen (cylindrical shape) were collected each from tibiae of nine middle aged male donors. At each cycle of loading-dwell-unloading-dwell-reloading, we calculated maximum stress, permanent strain, modulus, stress relaxation, time constant, and 3 pathways of energy dissipation for both loading modes. In doing so, we found that bone dissipated greater energy through the mechanisms of permanent and viscoelastic deformation in compression than in tension. On the other hand, however, bone dissipated greater energy through the release of surface energy in tension than in compression. Moreover, differences in the plastic and viscoelastic properties after yielding were not reflected in the evolution of modulus loss (an indicator of damage accumulation), which was similar for both loading modes. A possible explanation is that differences in damage morphology between the two loading modes may favor the plastic and viscolelastic energy dissipation in compression, but facilitate the surface energy release in tension. Such detailed information about failure mechanisms of bone at the tissue-level would help explain the underlying causes of bone fractures.

Keywords: Bone, Post-yield, Toughness, Damage, Compression, Tension

INTRODUCTION

Being a biological tissue, bone has a hierarchical arrangement of its primary constituents, such as carbonated apatite and type I collagen (for reviews, see (Rho et al., 1998; Weiner and Traub, 1992)). This arrangement – from mineralized fibrils through alternating thick and thin lamellae to the alignment of trabeculae or cortices – gives rise to numerous toughening mechanisms and tissue strength as discussed in several reviews (Akkus et al., 2004; Hernandez and Keaveny, 2006; Nyman et al., 2005). Given the complexity of bone structure, the mechanistic cause for its failure is most likely multifactorial involving bone consituents and each hierarchical level of organization of the tissue. Such information is extremely important for accurately modeling the failure behavior of bone, thus facilitating predictions of bone fractures for elderly and osteoporotic patients and/or in skeletal implant systems.

Altough bone tissue may fail under any given mode of loading, few studies have directly compared failure mechanisms of bone under different loading modes (Burstein et al., 1976; Smith and Smith, 1976). Certainly, the mechanical behavior of human cortical bone has been investigated in single loading mode, such as unixial tension (Dickenson et al., 1981; Evans, 1976; McCalden et al., 1993), uniaxial compression (Walsh and Guzelsu, 1994), torsion (Jepsen et al., 1999), pure shear (Turner et al., 2001), and bending (Wang et al., 2002; Zioupos and Currey, 1998). From these studies, a number of determinants of bone strength and toughness have been identified (e.g., mineral density and collagen integrity). Nonetheless, failure mechanisms are still not fully understood, only with suggestions ranging from microcracks immanating at the lamellar interface (Jepsen et al., 1999) to heterogeneity of local tissue modulus affecting the coallescence of microcracks into macrocracks (Zioupos et al., 2007).

To better understand the failure mechanisms of bone, we recently developed a progressive loading scheme that could provide detailed information regarding the evolution of mechanical properties over increasing deformation (Wang and Nyman, 2007). This mechanical test not only detects changes in elastic modulus and stress relaxation with increasing strain but also measures several forms of energy dissipiation related to permanent deformation, hysteresis, and microdamage accumulation (i.e., modulus loss). In the present study, we applied the progressive scheme to cortical bone from human cadaveric tibiae in order to determine differences in the post-yield behavior and energy dissipation of the tissue in both uniaxial compression and uniaxial tension. We hypothesize in this study that the mechanism for the post-yield energy dissipation in cortical bone differ between compression and tension.

MATERIALS AND METHODS

Specimen preparation

Nine human cadaveric tibiae (5 male, 51.6±2.2 years of age and 4 female, 54.3±1.3 years of age) were obtained from the Willed Body Program (The University of Texas Southwestern Medical Center at Dallas, TX) with no known bone disease reported. Both tensile and compression specimens were collected from the anterior quadrant of the mid-diaphysis of each tibia. For tensile specimens, longitudinal sections were initially extracted using a diamond saw (Isomet 2000, Buehler, Lake Bluff, IL) and then machined into the final dog-bone shape (10mm×2mm×2mm in gage region) using a CNC machine (ProLIGHT 1000, Light Machines, Manchester, NH). For compression specimens, a benchtop precision lathe was used to turn the longitudinal sections into cylindrical specimens (ϕ3mm×5mm). All cutting occurred under constant irrigation; and all specimens were wrapped in gauze, soaked in phosphate buffered saline (PBS), and stored then at -20 °C until testing.

Mechanical testing

We conducted both tension and compression tests using the progressive loading scheme described elsewhere (Nyman et al., 2008; Nyman et al., 2007; Wang and Nyman, 2007). This method involves a series of cycles of load-dwell-unload-dwell-reload with incremental strains based on the observation that bone biomechanics is dependent on the level of strains (Winwood, et al., 2006). Such a scheme allows for measuring elastic, plastic, and viscous responses of bone and estimating the post-yield energy dissipation in different pathways as a function of incremental strains (Nyman et al., 2007).

Tensile tests were performed on a bench-top mechanical testing system (EnduraTEC ELF 3300, Bose Corporation, Minnetonka, MN) with an extensometer of 8mm gage length (MTS, Eden Prairie, MN). In each cycle of progressing loading, the specimen was loaded under displacement control to a designated displacement level at a rate of 0.5mm/min; then held for 30s for stress relaxation. Thereafter, the specimen was unloaded to zero force at a rate of 300N/min, held for 30s for anelastic relaxation, and then reloaded again at 0.5mm/min to the next strain level under displacement control. This procedure repeated until failure of the bone specimen.

Compressive tests were done using the same progressive loading scheme on a MTS mechanical testing system (Insight 5000, MTS, Eden Prairie, MN) with an extensometer of 3mm gage length (MTS, Eden Prairie, MN). Upon establishing a pre-load of 20N, the bone specimen was loaded at a rate of 0.3mm/min to the initial crosshead displacement of 0.03mm. The specimen was next held at the stain level under displacement control for 30s (stress relaxation dwell), unloaded to 20N force under load control, held at 20N under load control for 30s, and reloaded to the next level of crosshead displacement. In the succeeding cycles, the same loading procedure repeated with a series of sequential increment of crosshead displacement, thereby recording changes in the post-yield behavior of the specimen over increasing strain. Finally, the test stopped when the specimen either entirely or partially failed within the travel limit of the extensometer.

Quantification of mechanical properties

For both tensile and compressive tests, the initial modulus (E0) was the initial slope of the stress-strain curve in the linear elastic region (Fig.1). The instantaneous modulus (Ei) was determined as the slope between two points in each cycle: one at the end of stress relaxation dwelling that occurred before unloading and the other at the end of anelastic deformation dwelling that occurred after unloading. The plastic strain (εp) was the residual strain at the end of each load-dwell-unload-dwell cycle. The yield strain (εy) was estimated to be the strain at which plastic deformation began to occur (εp>0). Maximum stress (σmax) occurred at the end of loading and prior to stress relaxation (i.e., before the dwell period). We estimated the viscoelastic time constant (τ) and the magnitude of total stress relaxation (Δσ) by fitting the stress-time curve during the stress relaxation dwelling with an exponential equation,

Figure 1.

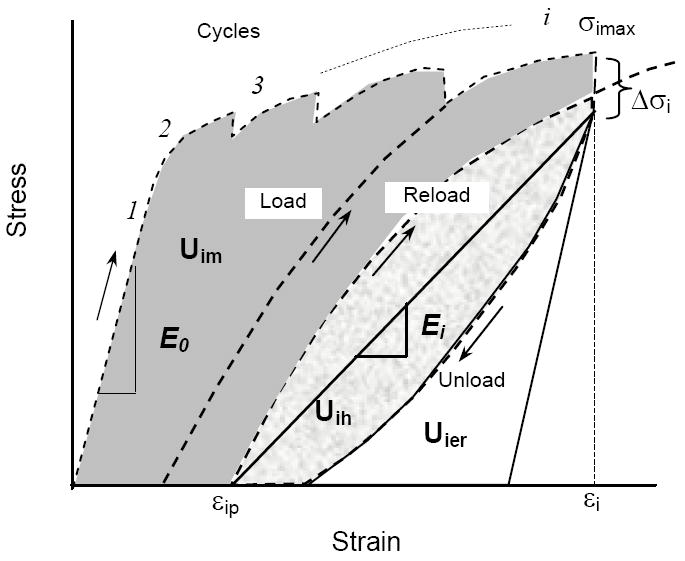
Figure 1

Open in a new tab

Whether in the compression or tension mode, the cortical bone specimen was subjected to multiple cycles of loading-dwell-unloading-dwell-reloading. The last cycle before failure is only shown here to provide greater clearity in how we calculated the mechanical properties.

σ=Δσ·e−t·τ (1)

The post-yield energy dissipation terms (i.e., released elastic strain energy: Uer, hysteresis energy: Uh, and plastic strain energy: Up) were determined according to the following procedures (Figure 1): The elastic release strain energy (Uer) was the area under the unloading curve (the total elastic strain energy) minus the triangular area (the elastic strain energy without stiffness loss). The hysteresis energy (Uh) was the area between the loading and unloading curves. The plastic strain energy (Up) was the cumulative area minus the hysteresis energy and the elastic release strain energy. The aforementioned properties were calculated at the maximum strain of each incremental cycle using a custom MATLAB script (Mathworks, Natick, MA).

Statistical analysis

To detect differences between tension and compression in the various mechanical properties at different strain levels, we grouped data within predefined strain ranges based on the different deformation stages (Table 1). Then, a two-side Student’s paired t-test was performed to examine statistically significant differences between tension and compression for each mechanical property of bone at each strain range. The significance was considered only if p<0.05 (Table 2).

Table 1.

In comparing tension to compression, the mechanical properties of bone were grouped in the following strain ranges such that the difference in strain between the two modes was not statistically significant (p>0.2) and that each tibia provided both a tension and a compression specimen (paired).

Strain Range Deformation Stage Tension Compression p-value
0.00340-0.00427 Pre-yield n=5 n=5 0.2276
0.00631-0.00864 Yielding n=6 n=6 0.2901
0.0100-0.0128 Transition n=7 n=7 0.8326
0.0147-0.0174 Early post-yield n=7 n=7 0.3923
0.0209-0.0247 Post-yield n=5 n=5 0.2772
Open in a new tab

Table 2.

p-values are given for the comparisons of mechanical properties between tension and compression modes as determined by an uniaxial, progressive loading scheme. Bold or italics indicates that the property is higher or lower for compression than tension, respectively.

Mechanical Property Pre-yield Yielding Transition Early post-yield Post-yield
Permanent strain (εp) 0.6103 0.0151 0.0005 0.0082 0.0102
Modulus (Ei) 0.4485 0.6609 0.3378 0.4734 0.7519
Maximum stress (σmax) 0.0913 0.0258 0.0001 0.0010 0.0395
Stress relaxation (Δσ) 0.8027 0.7706 0.0038 0.000003 0.0001
Time constant (τ) 0.1361 0.3442 0.00001 0.00004 0.0086
Elastic Release Energy (Uer) 0.6232 0.3162 0.2174 0.0050 0.0027
Plastic Strain Energy (Up) 0.0028 0.0405 0.0077 0.0002 0.0007
Hysteresis Energy (Uh) 0.0118 0.0130 0.0021 0.0002 0.0818
Open in a new tab

RESULTS

Changes in the maximum stress with increasing strain prior to yielding were similar for both compression and tension, showing a linear relationship (Figure 2 and Table 2). However, a significant difference occurred during the transition from yielding of the tissue to post-yield deformation in that the maximum stress of bone was greater in compression than in tension (Table 2). Such a difference diminished gradually with increasing strain at the late stages of post-yield deformation (ε>0.025).

Figure 2.

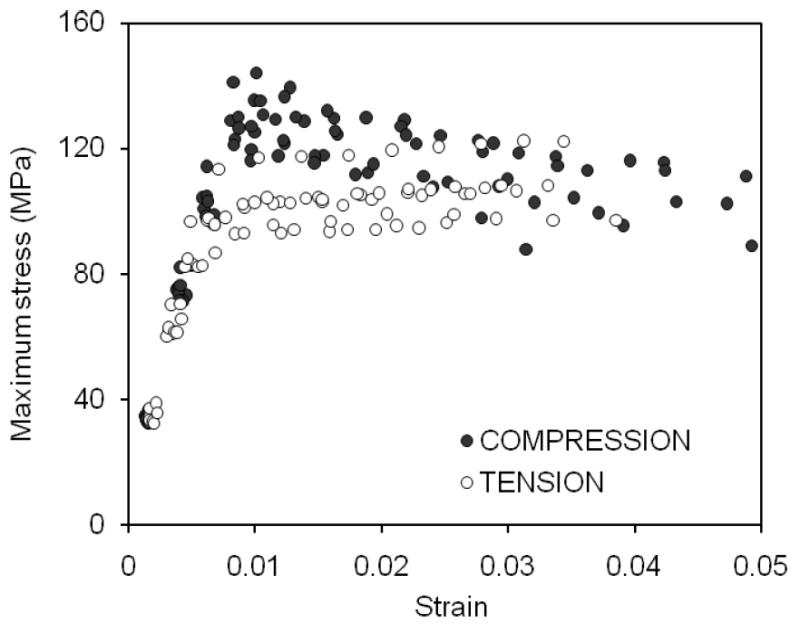
Figure 2

Open in a new tab

The maximum stress of each cycle is plotted against the maximum strain of each cycle. The relationships were similar to that obtained by a monotomic test with bone being stronger in compression than in tension.

When determined as the strain at which permanent strain departs from zero (Figure 3) yield strain was greater in compression (εy=8,070±340με) than in tension (εy=4,310±230με). After the bone yields, permanent deformation or plastic strain accumulated in the tissue, and this increase had a nearly linear relationship with increasing strain for both tension and compression (Figure 3). The degree of permanent deformation was greater for compression than for tension after yielding (Table 2). Similarly, the permanent strain energy dissipation in bone also exhibited a linear increase with an increase in post-yield strain in both tension and compression (Figure 4), and bone dissipated considerably more energy (about 13×) through this mechanism when loaded in compression than in tension (Table 2).

Figure 3.

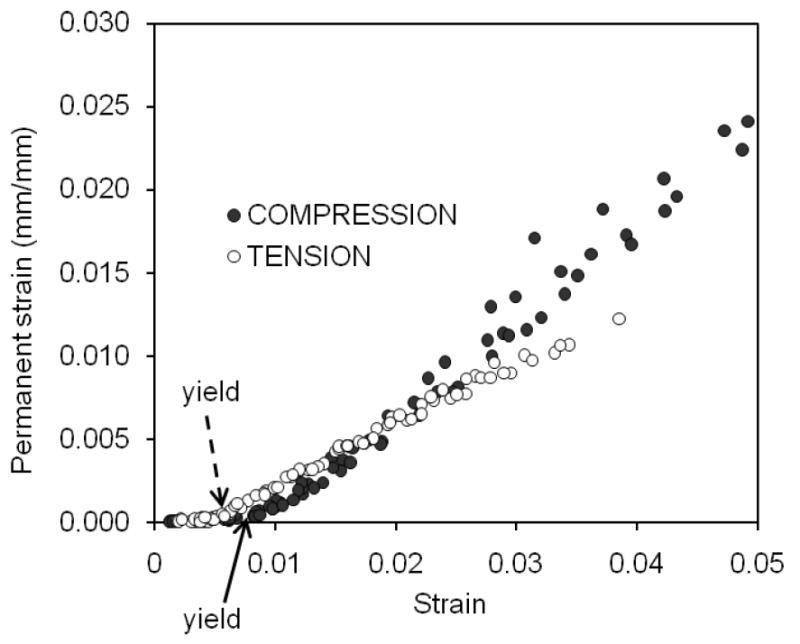
Figure 3

Open in a new tab

Permanent or plastic strain is the amount of unrecoverable deformation after unloading and a period of rest. When plotted against the maximum strain of the cycle, this strain departed from zero at the defined yeild point. Although this departure occurred at a higher yield strain in compression than in tension, the permanent strain generated in compression exceeded that in tension at post-yield strains.

Figure 4.

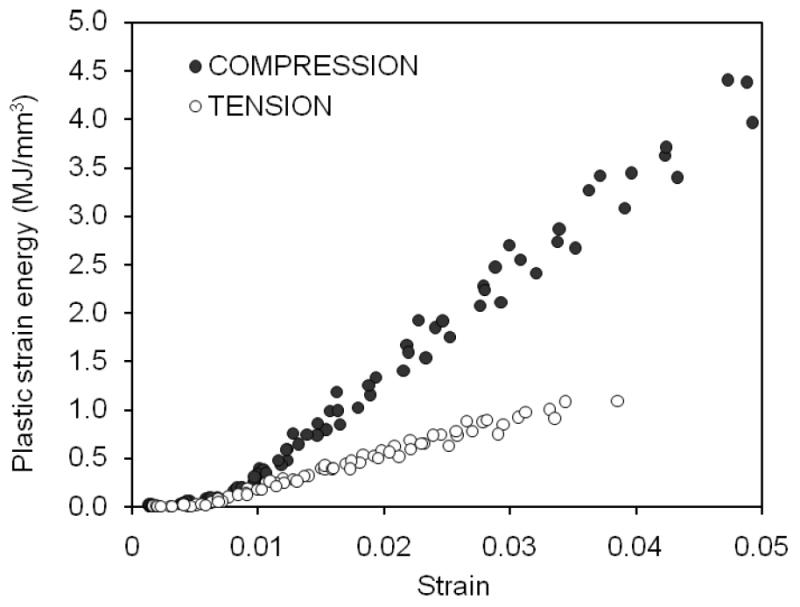
Figure 4

Open in a new tab

The energy dissipated by plastic deformation linearly increased after yielding as the strain increased with each successive cylce of loading. This pathway of toughness was greater for compression than for tension.

As the strain increased with successive cycles of loading, the modulus of the bone specimen decreased in both tension and compression (Figure 5). Moreover, the rate in modulus loss with increasing strain was strikingly similar between tension and compression. Not surprisingly then, there were no significant differences in modulus at all between the two modes (Table 2).

Figure 5.

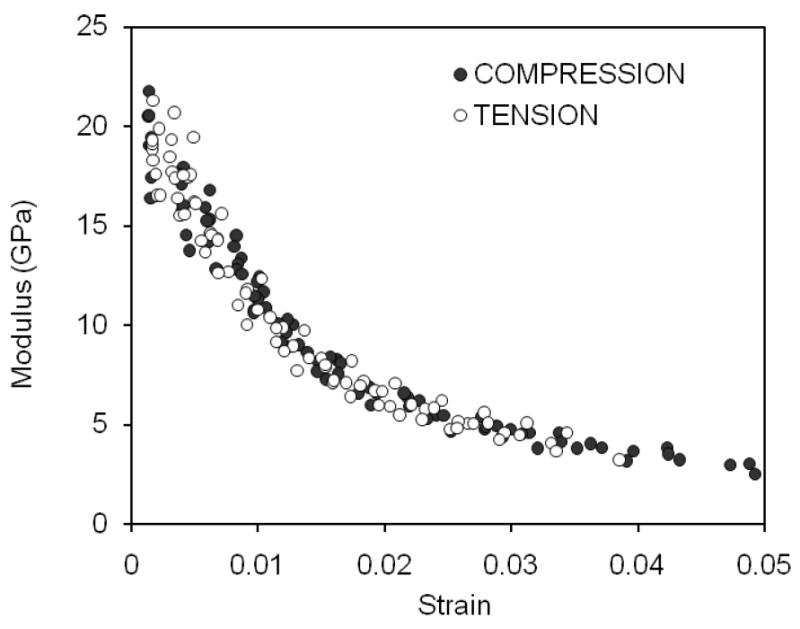
Figure 5

Open in a new tab

With each cycle of prgoressive loading, the modulus of cortical bone decreased for both modes of loading in a similar fashion. The rate of change with respective to the strain of the cycle was greater through yielding but slowed through the post-yield strains.

As for the viscoelastic response of bone, there was much greater stress relaxation when the cortical bone was loaded in compression than in tension (Table 2). In addition, the maximum in stress relaxation peaked in tension at 1% strain, whereas it remained constant after 1.3% strain in compression (Figure 6). Until the transition stage of deformation, the rate change to reach equilibrium (i.e., time constant of stress relaxation) decreased for both two loading modes with no differences in the property (Table 2). Thereafter (ε>0.01), the time constant became nearly constant (Figure 7) and was greater in compression than in tension (Table 2).

Figure 6.

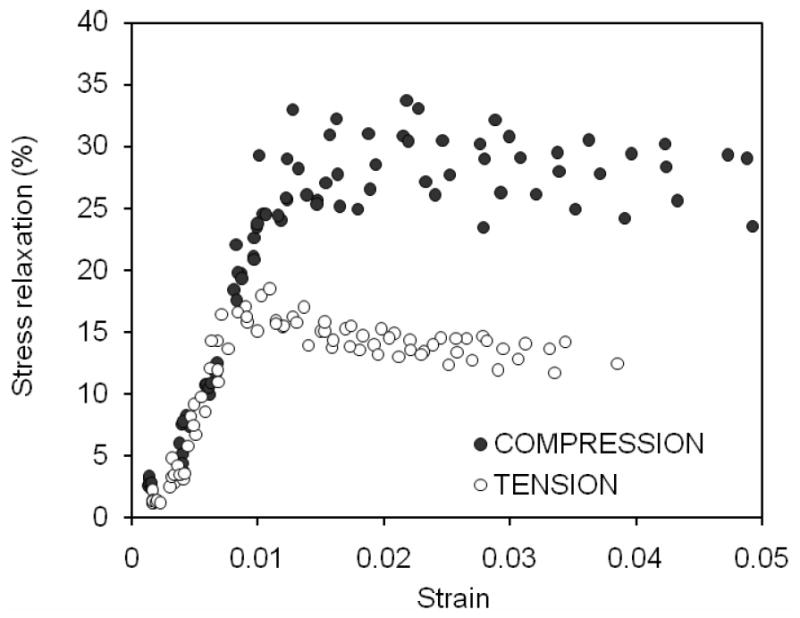
Figure 6

Open in a new tab

The degree to which bone relaxed is plotted against the strain during the dwell period (i.e., maximum strain of each cycle). As damage was introduced into the bone at increasing strains, stress relaxation increased in both modes but reached maximum after yielding. Bone sustained greater stress relaxation in compression than in tension.

Figure 7.

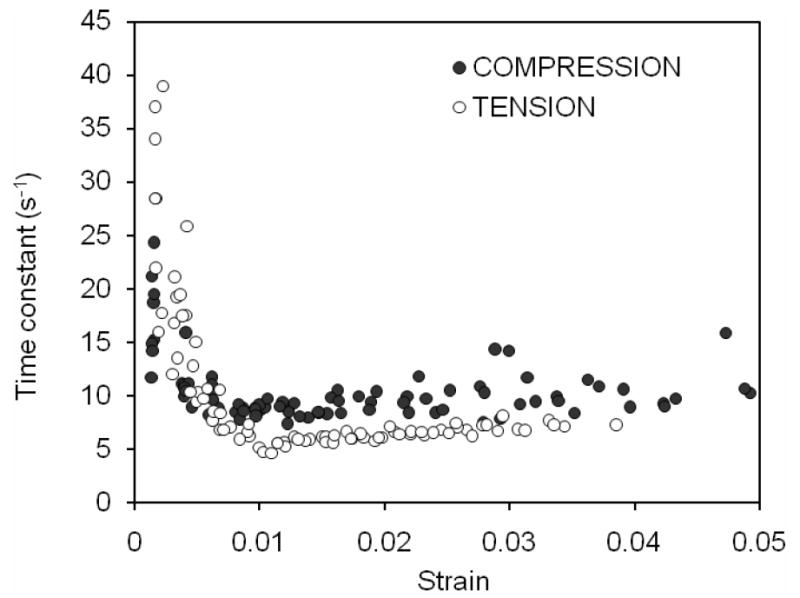
Figure 7

Open in a new tab

The time constant for the period of stress relaxation is plotted against the constant strain of that period for each cycle. For both modes of loading, the rate change in stress to reach equalibrium dropped as the strain increased with each cycle. It remained at a nearly constant value in the post-yield region.

As strain applied to bone progressed beyond yielding, dissipation of hysteresis energy (Uh) increased with increasing strain in both compression and tension (Figure 8). The rate of increase was different in compression (approximately a power law relationship) compared with tension (almost a linear relationship), with Uh being slightly greater for compression than for tension. However, such a difference diminished as the applied strain exceeded 2% (Table 2). Cortical bone dissipated considerably less energy in compression than in tension through the mechanism of elastic release strain energy that is presumably due to creation of new crack surfaces (Table 2). In addition, the capacity of bone to dissipate such energy diminished in compression with increasing strain (Figure 9).

Figure 8.

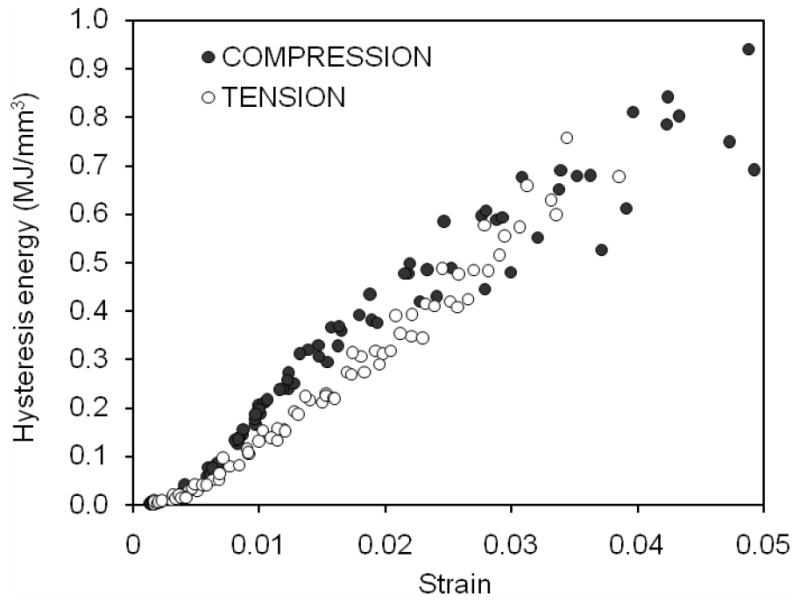
Figure 8

Open in a new tab

With increasing strain as the cycles progressed, the bone dissipated increasing hysteresis energy in both modes of loading.

Figure 9.

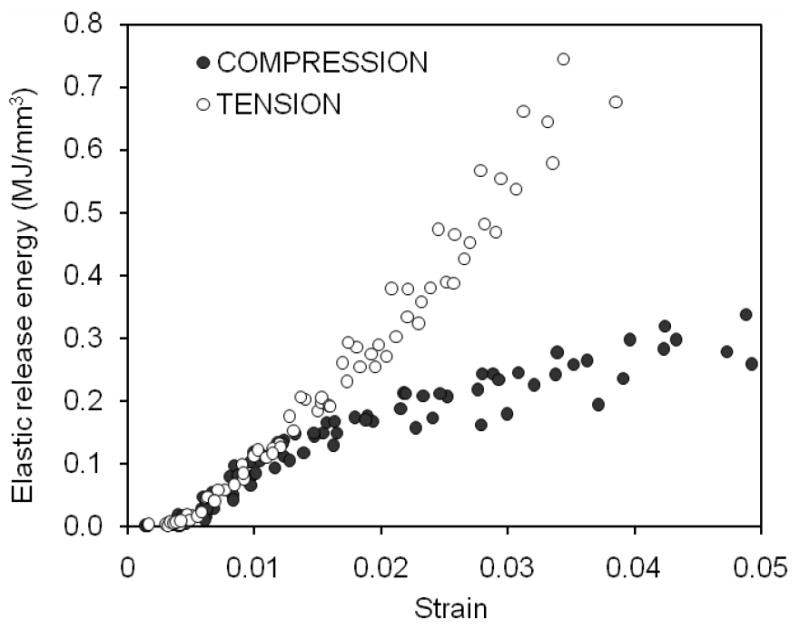
Figure 9

Open in a new tab

Bone dissipated more elastic release energy in tension than in compression as the strain on the bone increased with each cycle.

DISCUSSION

Using a novel loading scheme, we examined differences in the mechanical behavior between tension and compression tests of cortical bone from human tibiae. Over similar strain ranges, bone sustained greater permanent and viscous energy dissiaption (Figures 4 and 8, respectively) in compression than in tension. However, the released elastic strain energy dissipation that is associated with modulus loss (or damage accumulation) was less in compression than in tension (Figure 9) although the evolution of modulus loss was strikingly similar in both loading modes (Figure 5).

Since the yield strain and the rate of permanent strain accumulation were both greater in compression than in tension (Figure 3), the initiation and progression of plastic deformation in bone likely encounters higher resistance in the compression mode. As further evidence of this resistance, the plastic strain energy dissipation (Up) was more than two times greater in compression than in tension at similar post-yield strain levels. The contributing factors to the much higher plastic energy dissipation in compression than in tension are most likely 1) higher stress levels (Figure2) and 2) a greater plastic deformation at the same strain applied (Figure 3). A possible explanation for the greater plastic deformation is that the damages formed within bone tissue by compression (crosshatch type damages) allow for more plastic deformation than the damages induced in tension (most likely diffuse damages (Ebacher et al., 2007).

Since hysteresis energy dissipation is viscoelastic in nature, it is most likely dependent on the viscous phases in bone (i.e., collagen and water). Previous studies have shown that the viscous nature of bone depends on hydration condition of the tissue (Yamashita et al., 2002), and such viscoelastic properties as storage modulus and loss modulus of bone increase with increasing damage density (Yeni et al., 2004; Yeni et al., 2007). In this study, a much higher total stress relaxation (Δσ) and a slightly greater time constant (τ) were observed in compression than in tension (Figures 6 and 7). Physically speaking, Δσ reflects the contribution of viscous phases to load bearing, while τ is a measure of the damping capability of the viscous phases. Thus, the viscous phases of bone exhibit a greater contribution to loading bearing, but a lower damping capability in compression than in tension. For hysteresis energy dissipation, a positive effect due to an increase in Δσ could be actually cancelled out by a negative effect induced by a decrease in damping (τ). This could possibly explain the fact that only a slight difference in hysteresis energy dissipation between compression and tension was observed in this study.

The present testing methodology provides information on the evolution of modulus loss as the bone sustains increasing strain. Such degradation in modulus has often been used as an indicator of damage accumulation sustained by the tissue in fatigue studies (Cotton et al., 2005; Pattin et al., 1996; Pidaparti and Vogt, 2002; Schaffler et al., 1989; Zioupos et al., 1996) as well as in overloading studies (Fondrk et al., 1999; Jepsen and Davy, 1997; Morgan et al., 2005). Interestingly, we did not observe much of a difference in modulus loss of bone between compression and tension. This implies that the effect of damage accumulation on modulus loss of bone tissue was similar in both modes of loading. However, it is not necessarily the case that the type of damages induced in the two loading modes was the same. From previous work investigating the effect of fatigue on microdamage morphology in cortical bone, there is evidence that diffuse patches of sub-micron cracks tend to accumulate in regions subjected to tension and linear microcracks tend to accumulate in regions under compression (Boyce et al., 1998).

In fact, differences in microdamage accumulation between the two loading modes also could be reflected in the differences in the prominent mechanisms of energy dissipation. As shown in this study, the plastic strain energy dissipation (Up) was much greater (> 2×) in compression than in tension, whereas the elastic release strain energy (Uer) was less in compression than in tension. It is unlikely that this significant discrepancy in plastic energy dissipation is solely due to the difference in maximum stress levels because only about 20% of such a difference was observed between the two loading modes and for just strains between 1% and 2% (Figure 2). In addition, Up was much greater (13×) than Uer in compression, whereas Up and Uer were similar in tension. All these results suggest that the damage accumulation in compression (possibly crosshatch linear microcracks) expends minimal energy dissipation through creation of new crack surfaces (i.e., elastic release strain energy), but instead promotes a large amount of permanent energy dissipation through cross-hatched damage formation than is necessary for damage accumulation in tension (presumably less hazardous diffuse damage).

Finally, we point out that the results obtained in this study may not be necessarily true for bone specimens acquired from anatomical sites where the tissue has distinct orientations of mineral crystals and collagen fibrils. Since in vivo strain mode in bone tends to dictate collagen orientation through tissue adaptation process (Takano et al., 1999), such preferential orientation would in turn influence both tensile and compressive behavior of bone tissue (Ascenzi et al., 1985). From the viewpoint of bone adaptation, the tissue within anterior quadrant of the tibia mid-shaft appears more suited to resist compression than tension load, with collagen fibrils presumabely being oriented primarily transverse to the loading axis (Carando et al., 1989; Portigliatti Barbos et al., 1984).

In conclusion, the ability of bone to sustain post-yield deformation is unlikely equal across various loading modes, and domanint mechanisms of energy dissipation may vary among the modes. Such variation appears to be most likely due to the difference in the mechanisms of damage accumulation and responses of bone constituents including collagen orientations. Therefore, a complete mechanistic understanding of failure mechanism of bone in relation to the loading modes is necessary to study age- and disease-related bone fractures.

Acknowledgments

This is study was partially supported by a NIH/NIA grant (R01AG022044-A1) and a gift from the San Antonio Area Foundation.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Akkus O, Yeni YN, Wasserman N. Fracture mechanics of cortical bone tissue: a hierarchical perspective. Crit Rev Biomed Eng. 2004;32:379–426. doi: 10.1615/critrevbiomedeng.v32.i56.10. [DOI] [PubMed] [Google Scholar]
  2. Ascenzi A, Benvenuti A, Mango F, Simili R. Mechanical hysteresis loops from single osteons: technical devices and preliminary results. J Biomech. 1985;18:391–398. doi: 10.1016/0021-9290(85)90294-5. [DOI] [PubMed] [Google Scholar]
  3. Boyce TM, Fyhrie DP, Glotkowski MC, Radin EL, Schaffler MB. Damage type and strain mode associations in human compact bone bending fatigue. J Orthop Res. 1998;16:322–329. doi: 10.1002/jor.1100160308. [DOI] [PubMed] [Google Scholar]
  4. Burstein AH, Reilly DT, Martens M. Aging of bone tissue: mechanical properties. J Bone Joint Surg Am. 1976;58-A:82–86. [PubMed] [Google Scholar]
  5. Carando S, Portigliatti Barbos M, Ascenzi A, Boyde A. Orientation of collagen in human tibial and fibular shaft and possible correlation with mechanical properties. Bone. 1989;10:139–142. doi: 10.1016/8756-3282(89)90012-4. [DOI] [PubMed] [Google Scholar]
  6. Cotton JR, Winwood K, Zioupos P, Taylor M. Damage rate is a predictor of fatigue life and creep strain rate in tensile fatigue of human cortical bone samples. J Biomech Eng. 2005;127:213–219. doi: 10.1115/1.1865188. [DOI] [PubMed] [Google Scholar]
  7. Currey JD. Mechanical properties of bone tissues with greatly differing functions. J Biomech. 1979;12:313–319. doi: 10.1016/0021-9290(79)90073-3. [DOI] [PubMed] [Google Scholar]
  8. De Laet CE, Van Hout BA, Burger H, Weel AE, Hofman A, Pols HA. Hip fracture prediction in elderly men and women: validation in the Rotterdam study. J Bone Miner Res. 1998;13:1587–1593. doi: 10.1359/jbmr.1998.13.10.1587. [DOI] [PubMed] [Google Scholar]
  9. Dickenson RP, Hutton WC, Stott JR. The mechanical properties of bone in osteoporosis. J Bone Joint Surg Br. 1981;63-B:233–238. doi: 10.1302/0301-620X.63B2.7217148. [DOI] [PubMed] [Google Scholar]
  10. Duda GN, Schneider E, Chao EY. Internal forces and moments in the femur during walking. J Biomech. 1997;30:933–941. doi: 10.1016/s0021-9290(97)00057-2. [DOI] [PubMed] [Google Scholar]
  11. Ebacher V, Tang C, McKay H, Oxland TR, Guy P, Wang R. Strain redistribution and cracking behavior of human bone during bending. Bone. 2007;40:1265–1275. doi: 10.1016/j.bone.2006.12.065. [DOI] [PubMed] [Google Scholar]
  12. Evans FG. Mechanical properties and histology of cortical bone from younger and older men. Anat Rec. 1976;185:1–11. doi: 10.1002/ar.1091850102. [DOI] [PubMed] [Google Scholar]
  13. Evans FG, Vincentelli R. Relation of collagen fiber orientation to some mechanical properties of human cortical bone. J Biomech. 1969;2:63–71. doi: 10.1016/0021-9290(69)90042-6. [DOI] [PubMed] [Google Scholar]
  14. Fondrk MT, Bahniuk EH, Davy DT. A damage model for nonlinear tensile behavior of cortical bone. J Biomech Eng. 1999;121:533–541. doi: 10.1115/1.2835084. [DOI] [PubMed] [Google Scholar]
  15. Hernandez CJ, Keaveny TM. A biomechanical perspective on bone quality. Bone. 2006;39:1173–1181. doi: 10.1016/j.bone.2006.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Jepsen KJ, Davy DT. Comparison of damage accumulation measures in human cortical bone. J Biomech. 1997;30:891–894. doi: 10.1016/s0021-9290(97)00036-5. [DOI] [PubMed] [Google Scholar]
  17. Jepsen KJ, Davy DT, Krzypow DJ. The role of the lamellar interface during torsional yielding of human cortical bone. J Biomech. 1999;32:303–310. doi: 10.1016/s0021-9290(98)00179-1. [DOI] [PubMed] [Google Scholar]
  18. Kalmey JK, Lovejoy CO. Collagen fiber orientation in the femoral necks of apes and humans: do their histological structures reflect differences in locomotor loading? Bone. 2002;31:327–332. doi: 10.1016/s8756-3282(02)00828-1. [DOI] [PubMed] [Google Scholar]
  19. Kanis JA, Johnell O, Oden A, Dawson A, De Laet C, Jonsson B. Ten year probabilities of osteoporotic fractures according to BMD and diagnostic thresholds. Osteoporos Int. 2001;12:989–995. doi: 10.1007/s001980170006. [DOI] [PubMed] [Google Scholar]
  20. Martin RB, Boardman DL. The effects of collagen fiber orientation, porosity, density, and mineralization on bovine cortical bone bending properties. J Biomech. 1993;26:1047–1054. doi: 10.1016/s0021-9290(05)80004-1. [DOI] [PubMed] [Google Scholar]
  21. Martin RB, Burr DB, Sharkey NA. Skeletal Tissue Mechanics. Springer-Verlag; New York: 1998. [Google Scholar]
  22. McCalden RW, McGeough JA, Barker MB, Court-Brown CM. Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure. J Bone Joint Surg Am. 1993;75-A:1193–1205. doi: 10.2106/00004623-199308000-00009. [DOI] [PubMed] [Google Scholar]
  23. Morgan EF, Lee JJ, Keaveny TM. Sensitivity of multiple damage parameters to compressive overload in cortical bone. J Biomech Eng. 2005;127:557–562. doi: 10.1115/1.1933916. [DOI] [PubMed] [Google Scholar]
  24. Nyman JS, Reyes M, Wang X. Effect of ultrastructural changes on the toughness of bone. Micron. 2005;36:566–582. doi: 10.1016/j.micron.2005.07.004. [DOI] [PubMed] [Google Scholar]
  25. Nyman JS, Roy A, Reyes MJ, Wang X. Mechanical behavior of human cortical bone in cycles of advancing tensile strain for two age groups. J Biomed Mater Res A. 2008 doi: 10.1002/jbm.a.31974. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Nyman JS, Roy A, Tyler JH, Acuna RL, Gayle HJ, Wang X. Age-related factors affecting the postyield energy dissipation of human cortical bone. J Orthop Res. 2007;25:646–655. doi: 10.1002/jor.20337. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pattin CA, Caler WE, Carter DR. Cyclic mechanical property degradation during fatigue loading of cortical bone. J Biomech. 1996;29:69–79. doi: 10.1016/0021-9290(94)00156-1. [DOI] [PubMed] [Google Scholar]
  28. Pidaparti RM, Vogt A. Experimental investigation of Poisson’s ratio as a damage parameter for bone fatigue. J Biomed Mater Res. 2002;59:282–287. doi: 10.1002/jbm.1243. [DOI] [PubMed] [Google Scholar]
  29. Portigliatti Barbos M, Bianco P, Ascenzi A, Boyde A. Collagen orientation in compact bone: II. Distribution of lamellae in the whole of the human femoral shaft with reference to its mechanical properties. Metab Bone Dis Relat Res. 1984;5:309–315. doi: 10.1016/0221-8747(84)90018-3. [DOI] [PubMed] [Google Scholar]
  30. Rho JY, Kuhn-Spearing L, Zioupos P. Mechanical properties and the hierarchical structure of bone. Med Eng Phys. 1998;20:92–102. doi: 10.1016/s1350-4533(98)00007-1. [DOI] [PubMed] [Google Scholar]
  31. Schaffler MB, Radin EL, Burr DB. Mechanical and morphological effects of strain rate on fatigue of compact bone. Bone. 1989;10:207–214. doi: 10.1016/8756-3282(89)90055-0. [DOI] [PubMed] [Google Scholar]
  32. Skedros JG, Mason MW, Nelson MC, Bloebaum RD. Evidence of structural and material adaptation to specific strain features in cortical bone. Anat Rec. 1996;246:47–63. doi: 10.1002/(SICI)1097-0185(199609)246:1<47::AID-AR6>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
  33. Smith CB, Smith DA. Relations between age, mineral density and mechanical properties of human femoral compacta. Acta Orthop Scand. 1976;47:496–502. doi: 10.3109/17453677608988727. [DOI] [PubMed] [Google Scholar]
  34. Takano Y, Turner CH, Owan I, Martin RB, Lau ST, Forwood MR, Burr DB. Elastic anisotropy and collagen orientation of osteonal bone are dependent on the mechanical strain distribution. J Orthop Res. 1999;17:59–66. doi: 10.1002/jor.1100170110. [DOI] [PubMed] [Google Scholar]
  35. Taylor ME, Tanner KE, Freeman MA, Yettram AL. Stress and strain distribution within the intact femur: compression or bending? Med Eng Phys. 1996;18:122–131. doi: 10.1016/1350-4533(95)00031-3. [DOI] [PubMed] [Google Scholar]
  36. Turner CH, Wang T, Burr DB. Shear strength and fatigue properties of human cortical bone determined from pure shear tests. Calcif Tissue Int. 2001;69:373–378. doi: 10.1007/s00223-001-1006-1. [DOI] [PubMed] [Google Scholar]
  37. Walsh WR, Guzelsu N. Compressive properties of cortical bone: mineral-organic interfacial bonding. Biomaterials. 1994;15:137–145. doi: 10.1016/0142-9612(94)90263-1. [DOI] [PubMed] [Google Scholar]
  38. Wang X, Nyman JS. A novel approach to assess post-yield energy dissipation of bone in tension. J Biomech. 2007;40:674–677. doi: 10.1016/j.jbiomech.2006.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Wang X, Shen X, Li X, Agrawal CM. Age-related changes in the collagen network and toughness of bone. Bone. 2002;31:1–7. doi: 10.1016/s8756-3282(01)00697-4. [DOI] [PubMed] [Google Scholar]
  40. Weiner S, Traub W. Bone structure: from angstroms to microns. Faseb J. 1992;6:879–885. [PubMed] [Google Scholar]
  41. Winwood K, Zioupos P, Currey JD, Cotton JR, Taylor M. Strain patterns during tensile, compressive, and shear fatigue of human cortical bone and implications for bone biomechanics. J Biomed Mater Res A. 2006;79:289–297. doi: 10.1002/jbm.a.30796. [DOI] [PubMed] [Google Scholar]
  42. Yamashita J, Li X, Furman BR, Rawls HR, Wang X, Agrawal CM. Collagen and bone viscoelasticity: a dynamic mechanical analysis. J Biomed Mater Res. 2002;63:31–36. doi: 10.1002/jbm.10086. [DOI] [PubMed] [Google Scholar]
  43. Yeni YN, Christopherson GT, Turner AS, Les CM, Fyhrie DP. Apparent viscoelastic anisotropy as measured from nondestructive oscillatory tests can reflect the presence of a flaw in cortical bone. J Biomed Mater Res A. 2004;69:124–130. doi: 10.1002/jbm.a.20128. [DOI] [PubMed] [Google Scholar]
  44. Yeni YN, Shaffer RR, Baker KC, Dong XN, Grimm MJ, Les CM, Fyhrie DP. The effect of yield damage on the viscoelastic properties of cortical bone tissue as measured by dynamic mechanical analysis. J Biomed Mater Res A. 2007;82:530–537. doi: 10.1002/jbm.a.31169. [DOI] [PubMed] [Google Scholar]
  45. Zioupos P, Currey JD. Changes in the stiffness, strength, and toughness of human cortical bone with age. Bone. 1998;22:57–66. doi: 10.1016/s8756-3282(97)00228-7. [DOI] [PubMed] [Google Scholar]
  46. Zioupos P, Gresle M, Winwood K. Fatigue strength of human cortical bone: Age, physical, and material heterogeneity effects. J Biomed Mater Res A. 2007 doi: 10.1002/jbm.a.31576. [DOI] [PubMed] [Google Scholar]
  47. Zioupos P, Wang XT, Currey JD. Experimental and theoretical quantification of the development of damage in fatigue tests of bone and antler. J Biomech. 1996;29:989–1002. doi: 10.1016/0021-9290(96)00001-2. [DOI] [PubMed] [Google Scholar]

RESOURCES